Roc кривая – Roc-кривая — Википедия

ROC кривые — Язык и среда R — ЖЖ

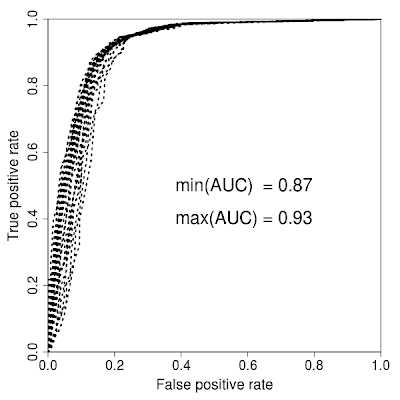
Перевод записи в моем английском блоге.

ROC — Receiver operating characteristic, это график, позволяющий оценить качество разделения двух классов. Кроме визуальной составляющей, есть численная характеристика ROC AUC — Area under ROC curve (AUROC, ROC AUC), площадь под ROC кривой, чем выше значение — тем лучше, 0.5 — плохая классификация, не отличающаяся от равновероятностной, больше 0.75 — считается хорошая классификация, и по моему мнения больше 0.8 — уже прекрасно и публикабельно, если значение 0.2 — то вам необходимо обратить лейблы. ROC curve является все навсего графиком двух значений: соотношения количества правильно и неправильно классифицированных признаков при каком-то выбранном значений (см.алгоритм построения ROC кривых здесь pdf — язык простой, но заморский).

История этого метода прозаичная — необходимо было определить качество распознавания сигналов радаров японцев среди всех остальных. В дальнейшем алгоритм был использован для всех исследований, где присутствует классификационные методы, т.к. является простым и емким методом визуализации. Были разработаны различные модификации, к примеру: CROC — A CROC Stronger than ROC: Measuring, Visualizing, and Optimizing Early Retrieval. Метод изначально создан для бинарных значений — т.е. два класса, но есть различные модификации для нескольких классов.

В R я обычно использую ROCR, хотя алгоритм реализован во многих других пакетах. Код, с комментированием каждой строки, приведен ниже, подствека сделана с помощью Online syntax highlighter. ROCR позволяет создавать самые различные графики для результатов классификации и является очень мощным инструментом визуализации.

# ROC curve(s) with ROCR
# [email protected]
# loading ROCR library
library("ROCR")
# loading active compounds, or compounds with label1
active <- read.table("sample.active", sep=",", header=FALSE)
# loading inactive compounds, or compounds with label2
inactive <- read.table("sample.inactive", sep=",", header=FALSE)
# binding them and converting to matrix because ROCR works with matrix data
target_pred <- as.matrix(rbind(active,inactive))
# because number of the colums should be the same - making additional param
ncol <- ncol(inactive)
# generating classes (1 for active, 0 for inactive, but it can be 1 and -1 - there is no difference)
class.active <- matrix(sample(1, (ncol(active)*nrow(active)), replace=T), ncol=ncol)
class.inactive <- matrix(sample(0, (ncol(inactive)*nrow(inactive)), replace=T), ncol=ncol)
# binding the classes
target_class <- rbind(class.active,class.inactive)
#target_class1 <- target_class[,1]
# calculating the values for ROC curve
pred <- prediction(target_pred, target_class)
perf <- performance(pred,"tpr","fpr")
# changing params for the ROC plot - width, etc
par(mar=c(5,5,2,2),xaxs = "i",yaxs = "i",cex.axis=1.3,cex.lab=1.4)
# plotting the ROC curve
plot(perf,col="black",lty=3, lwd=3)
# calculating AUC
auc <- performance(pred,"auc")
# now converting S4 class to vector
auc <- unlist(slot(auc, "y.values"))
# adding min and max ROC AUC to the center of the plot
minauc<-min(round(auc, digits = 2))
maxauc<-max(round(auc, digits = 2))
minauct <- paste(c("min(AUC)  = "),minauc,sep="")
maxauct <- paste(c("max(AUC) = "),maxauc,sep="")
legend(0.3,0.6,c(minauct,maxauct,"\n"),border="white",cex=1.7,box.col = "white")
#

r-statistics.livejournal.com

ROC-кривая — WikiModern

ROC-кривые трёх методов предсказания эпитопов

ROC-кривая (англ. receiver operating characteristic, рабочая характеристика приёмника) — график, позволяющий оценить качество бинарной классификации, отображает соотношение между долей объектов от общего количества носителей признака, верно классифицированных как несущих признак, (англ. true positive rate, TPR, называемой чувствительностью алгоритма классификации) и долей объектов от общего количества объектов, не несущих признака, ошибочно классифицированных как несущих признак (англ. false positive rate, FPR, величина 1-FPR называется специфичностью алгоритма классификации) при варьировании порога решающего правила.

Также известна как кривая ошибок. Анализ классификаций с применением ROC-кривых называется ROC-анализом.

Количественную интерпретацию ROC даёт показатель AUC (англ. area under ROC curve, площадь под ROC-кривой) — площадь, ограниченная ROC-кривой и осью доли ложных положительных классификаций. Чем выше показатель AUC, тем качественнее классификатор, при этом значение 0,5 демонстрирует непригодность выбранного метода классификации (соответствует случайному гаданию). Значение менее 0,5 говорит, что классификатор действует с точностью до наоборот: если положительные назвать отрицательными и наоборот, классификатор будет работать лучше.

Основная концепция

Задача классификации состоит в том, чтобы относить ранее неизвестные сущности к тому или иному классу. Примером такой задачи может быть постановка диагноза по медицинским анализам. В этом случае есть два класса результатов: положительный (positive) и отрицательный (negative). Тогда на выходе классификатора может наблюдаться четыре различных ситуации:

• Если результат классификации положительный, и истинное значение тоже положительное, то речь идет об истинно-положительном значении (true-positive, TP)
• Если результат классификации положительный, но истинное значение отрицательное, то речь идет о ложно-положительном значении (false-positive, FP)
• Если результат классификации отрицательный, и истинное значение тоже отрицательное, то речь идет об истинно-отрицательном значении (true-negative, TN)
• Если результат классификации отрицательный, но истинное значение положительно, то речь идет о ложно-отрицательном значении (false-negative, FN)

Возвращаясь к примеру с тестом на какое-либо заболевание, предположим, что врач на основе каких-либо медицинских анализов собирается поставить диагноз рака или его отсутствие. Тогда:

• true-positive, TP — пациент болен раком, диагноз положительный
• false-positive, FP — пациент здоров, диагноз положительный
• true-negative, TN — пациент здоров, диагноз отрицательный
• false-negative, FN — пациент болен раком, диагноз отрицательный

Четыре возможных выхода могут быть сформулированы и оформлены в виде таблицы сопряжённости размера 2×2.

Тогда значение Sen=TP/(TP+FN), способность алгоритма «видеть» больных, называется чувствительность, Spe=TN/(TN+FP) — специфичность, способность алгоритма не принимать здоровых за больных.

Бывает, что классификатор выдаёт не бит «здоров-болен», а число: «явно здоров» — «скорее всего, здоров» — «неопределённо» — «скорее всего, больной» — «явно больной». Это лучше, но всё равно набор принимаемых решений конечный, а зачастую и бинарный: отправлять ли пациента на дообследование? Должен ли сработать толкатель, сбрасывающий деталь в контейнер с браком? В таком случае, меняя порог, можно варьировать чувствительность и специфичность: чем выше одно, тем ниже другое.

Пробежимся порогом от −∞ до ∞ и нанесём на график соответствующие X=1−Spe и Y=Sen — это и будет ROC-кривая. Когда порог −∞, классификатор считает всех больными, Sen=1, 1−Spe=1. Когда +∞ — все «здоровые», Sen=0, 1−Spe=0. Так что ROC-кривая всегда идёт от (0,0) до (1,1).

Случай непрерывных случайных величин

Классификация часто основывается на непрерывных случайных величинах. В этом случае удобно записать вероятность принадлежности к тому или иному классу в виде функциираспределения вероятностей, зависящей от некоего порогового (граничного) значения параметра T{\displaystyle T} в виде P1(T){\displaystyle P_{1}(T)}, а вероятность непринадлежности как P0(T){\displaystyle P_{0}(T)}. Тогда количество ложно-положительных (false-positive rate,FPR) решений можно выразить в виде FPR(T)=∫T∞P0(T)dT{\displaystyle FPR(T)=\int _{T}^{\infty }P_{0}(T)dT}. В то же время количество истинно-положительных решений (true-positive rate, TPR) можно выразить в виде TPR(T)=∫T∞P1(T)dT{\displaystyle TPR(T)=\int _{T}^{\infty }P_{1}(T)dT}. При построении ROC-кривой по оси Y{\displaystyle Y} откладывают TPR(T){\displaystyle TPR(T)} и по оси X{\displaystyle X} — FPR(T){\displaystyle FPR(T)}, полученных при разных значениях параметра T{\displaystyle T}.

Например, представим, что уровни какого-нибудь белка в кровираспределены нормально с центрами, равными 1 г/дЛ и 2 г/дЛ у здоровых и больных людей соответственно. Медицинский тест может давать показатель уровня какого-либо белка в плазме крови. Уровень белка выше определенной границы может рассматриваться как признак заболевания. Исследователь может сдвигать границу (черная вертикальная линия на рисунке), что приведет к изменению числа ложно-положительных результатов. Результирующий вид ROC-кривой зависит от степени пересечения двух распределений.

Частные случаи

Если генеральная совокупность конечная (что обычно и бывает на реальных наборах данных), по ходу движения порога t от −∞ до ∞ возможны такие события.

• Пока t не задевает ни одной точки, ROC-кривая стоит на месте.
• При некотором t один или несколько членов переходят из ложно-положительных в истинно-отрицательные. Sen не меняется, Spe увеличивается — кривая делает горизонтальный отрезок.
• При некотором t один или несколько членов переходят из истинно-положительных в ложно-отрицательные. Здесь уменьшается Sen, и кривая делает вертикальный отрезок.
• Если происходит одновременно и то, и другое, ROC-кривая делает косой отрезок.

Поскольку вероятность четвёртого события мизерна, ROC-кривая конечной генеральной совокупности имеет ступенчатый вид, с небольшим количеством косых отрезков там, где погрешности сбора и обработки данных дали одинаковый результат на членах разных классов.

ROC-кривая бинарного классификатора, выдающего 0 или 1 (например, решающего дерева), выглядит как два отрезка (0,0)—(1−Spe,Sen)—(1,1).

В идеальном случае, когда классификатор полностью разделяет положительные и отрицательные члены генеральной совокупности, сначала все ложно-положительные становятся истинно-отрицательными (отрезок (1,1)—(0,1)), затем — все истинно-положительные становятся ложно-отрицательными (отрезок (0,1)—(0,0)). То есть, ROC-кривая идеального классификатора, независимо от того, какие цифры выдаёт критерий и конечна ли генеральная совокупность, выглядит как два отрезка (0,0)—(0,1)—(1,1).

При тех пороговых t, где ROC-кривая ниже диагонали 1−Spe = Sen, можно инвертировать критерий (всё, что меньше t, объявить положительным), и классификатор будет действовать лучше.

Применение

ROC-кривые впервые использованы в теории обработки сигналов в США во время Второй мировой войны для повышения качества распознавания объектов противника по радиолокационному сигналу. После атаки на Перл Харбор в 1941 году, американские военные начали новые исследования, направленные на попытки увеличения точности опознавания японскихсамолетов по радиолокационным сигналам.

Впоследствии широкое применение ROC-кривые получили в медицинской диагностике. ROC-кривые используется в эпидемиологии и медицинских исследованиях, часто упоминаются в одном контексте с доказательной медициной. В радиологии ROC-кривые используются для проверки и тестирования новых методик. В социальных науках ROC-кривые используются для того, чтобы делать суждения о качестве вероятностных моделей. Также кривые используются в вопросах управления качеством продукции и кредитном скоринге.

Как уже было отмечено, ROC-кривые широко используются в машинном обучении. Впервые в этом контексте они были использованы в работе Спакмена, который продемонстрировал применение ROC-кривых при сравнении нескольких алгоритмовклассификации.

Дополнительные варианты использования

Площадь под кривой

В нормированном пространстве площадь под кривой (AUC — Area Under Curve, AUROC — Area Under Receiver Operating Characteristic) эквивалентнавероятности, что классификатор присвоит больший вес случайно выбранной положительной сущности, чем случайно выбранной отрицательной. Это может быть показано следующим образом: площадь под кривой задаётся интегралом (ось X{\displaystyle X} развёрнута со знаком минус — большему значению координаты соответствует меньшее значение параметра T{\displaystyle T}):A=∫∞−∞y(T)x′(T)dT=∫∞−∞TPR(T)FPR′(T)dT=∫−∞∞TPR(T)P0(T)dT=⟨TPR⟩{\displaystyle A=\int _{\infty }^{-\infty }y(T)x'(T)dT=\int _{\infty }^{-\infty }TPR(T)FPR'(T)dT=\int _{-\infty }^{\infty }TPR(T)P_{0}(T)dT=\langle TPR\rangle }. Угловые скобки обозначают операцию взятия среднего.

Было показано, что AUC тесно связана с U-критерием Манна — Уитни, который является показателем того, присваивается ли позитивным элементам больший вес, чем негативным. Величина AUC также связана с

infosphere.top

ROC-кривая

TR | UK | KK | BE | EN |
roc кривая линия, roc кривая лаффера
ROC-кривая англ receiver operating characteristic, рабочая характеристика приёмника — график, позволяющий оценить качество бинарной классификации, отображает соотношение между долей объектов от общего количества носителей признака, верно классифицированных как несущих признак, англ true positive rate, TPR, называемой чувствительностью алгоритма классификации и долей объектов от общего количества объектов, не несущих признака, ошибочно классифицированных как несущих признак англ false positive rate, FPR, величина 1-FPR называется специфичностью алгоритма классификации при варьировании порога решающего правила

Также известна как кривая ошибок Анализ классификаций с применением ROC-кривых называется ROC-анализом

Количественную интерпретацию ROC даёт показатель AUC англ area under ROC curve, площадь под ROC-кривой — площадь, ограниченная ROC-кривой и осью доли ложных положительных классификаций Чем выше показатель AUC, тем качественнее классификатор, при этом значение 0,5 демонстрирует непригодность выбранного метода классификации соответствует случайному гаданию Значение менее 0,5 говорит, что классификатор действует с точностью до наоборот: если положительные назвать отрицательными и наоборот, классификатор будет работать лучше

Содержание

• 1 Основная концепция
• 2 Случай непрерывных случайных величин
• 3 Частные случаи
• 4 Применение
• 5 Дополнительные варианты использования
  • 51 Площадь под кривой
• 6 ROC-кривые в небинарных задачах классификации
• 7 См также
• 8 Примечания

Основная концепцияправить

См также: Ошибки первого и второго рода

Задача классификации состоит в том, чтобы относить ранее неизвестные сущности к тому или иному классу Примером такой задачи может быть постановка диагноза по медицинским анализам В этом случае есть два класса результатов: положительный positive и отрицательный negative Тогда на выходе классификатора может наблюдаться четыре различных ситуации:

• Если результат классификации положительный, и истинное значение тоже положительное, то речь идет об истинно-положительном значении true-positive, TP
• Если результат классификации положительный, но истинное значение отрицательное, то речь идет о ложно-положительном значении false-positive, FP
• Если результат классификации отрицательный, и истинное значение тоже отрицательное, то речь идет об истинно-отрицательном значении true-negative, TN
• Если результат классификации отрицательный, но истинное значение положительно, то речь идет о ложно-отрицательном значении false-negative, FN

Возвращаясь к примеру с тестом на какое-либо заболевание, предположим, что врач на основе каких-либо медицинских анализов собирается поставить диагноз рака или его отсутствие Тогда:

• true-positive, TP — пациент болен раком, диагноз положительный
• false-positive, FP — пациент здоров, диагноз положительный
• true-negative, TN — пациент здоров, диагноз отрицательный
• false-negative, FN — пациент болен раком, диагноз отрицательный

Четыре возможных выхода могут быть сформулированы и оформлены в виде таблицы сопряженности размера 2×2

Тогда значение Sen=TP/TP+FN, способность алгоритм

www.turkaramamotoru.com

ROC-кривая Википедия

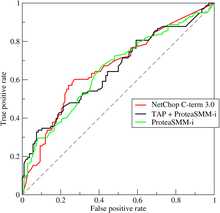ROC-кривые трёх методов предсказания эпитопов

ROC-кривая (англ. receiver operating characteristic, рабочая характеристика приёмника) — график, позволяющий оценить качество бинарной классификации, отображает соотношение между долей объектов от общего количества носителей признака, верно классифицированных как несущие признак (англ. true positive rate, TPR, называемой чувствительностью алгоритма классификации), и долей объектов от общего количества объектов, не несущих признака, ошибочно классифицированных как несущие признак (англ. false positive rate, FPR, величина 1-FPR называется специфичностью алгоритма классификации) при варьировании порога решающего правила.

Также известна как кривая ошибок. Анализ классификаций с применением ROC-кривых называется

ROC-анализом.

Количественную интерпретацию ROC даёт показатель AUC (англ. area under ROC curve, площадь под ROC-кривой) — площадь, ограниченная ROC-кривой и осью доли ложных положительных классификаций. Чем выше показатель AUC, тем качественнее классификатор, при этом значение 0,5 демонстрирует непригодность выбранного метода классификации (соответствует случайному гаданию). Значение менее 0,5 говорит, что классификатор действует с точностью до наоборот: если положительные назвать отрицательными и наоборот, классификатор будет работать лучше.

Задача классификации состоит в том, чтобы относить ранее неизвестные сущности к тому или иному классу. Примером такой задачи может быть постановка диагноза по медицинским анализам. В этом случае есть два класса результатов: положительный (positive) и отрицательный (negative). Тогда на выходе классификатора может наблюдаться четыре различных ситуации:

• Если результат классификации положительный, и истинное значение тоже положительное, то речь идет об истинно-положительном значении (true-positive, TP)
• Если результат классификации положительный, но истинное значение отрицательное, то речь идет о ложно-положительном значении (false-positive, FP)
• Если результат классификации отрицательный, и истинное значение тоже отрицательное, то речь идет об истинно-отрицательном значении (true-negative, TN)
• Если результат классификации отрицательный, но истинное значение положительно, то речь идет о ложно-отрицательном значении (false-negative, FN)

Возвращаясь к примеру с тестом на какое-либо заболевание, предположим, что врач на основе каких-либо медицинских анализов собирается поставить диагноз рака или его отсутствие. Тогда:

• true-positive, TP — пациент болен раком, диагноз положительный
• false-positive, FP
   — пациент здоров, диагноз положительный
• true-negative, TN — пациент здоров, диагноз отрицательный
• false-negative, FN — пациент болен раком, диагноз отрицательный

Четыре возможных выхода могут быть сформулированы и оформлены в виде таблицы сопряжённости размера 2×2.

Тогда значение Sen=TP/(TP+FN), способность алгоритма «видеть» больных, называется чувствительность, Spe=TN/(TN+FP) — специфичность, способность алгоритма не принимать здоровых за больных. Экономический эффект от этих ошибок разный: ложно-отрицательный больной придёт с запущенной болезнью, на дообследование ложно-положительного будут потрачены ресурсы.

Бывает, что классификатор выдаёт не бит «здоров-болен», а число: «явно здоров» — «скорее всего, здоров» — «неопределённо» — «скорее всего, больной» — «явно больной». Это лучше, но всё равно набор принимаемых решений конечный, а зачастую и бинарный: отправлять ли пациента на дообследование? Должен ли сработать толкатель, сбрасывающий деталь в контейнер с браком? В таком случае, меняя порог, можно варьировать чувствительность и специфичность: чем выше одно, тем ниже другое.

Пробежимся порогом от −∞ до ∞ и нанесём на график соответствующие X=1−Spe и Y=Sen — это и будет ROC-кривая. Когда порог −∞, классификатор считает всех больными, Sen=1, 1−Spe=1. Когда +∞ — все «здоровые», Sen=0, 1−Spe=0. Так что ROC-кривая всегда идёт от (0,0) до (1,1).

ruwikiorg.ru