Многоугольники. Выпуклый многоугольник. Четырехугольник 8 класс онлайн-подготовка на Ростелеком Лицей
Многоугольники. Выпуклый многоугольник. Четырехугольник.
Треугольник – это частный случай многоугольника.
В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т.е. больше, чем три. Например, изобразим пятиугольник – фигуру с пятью углами.
Многоугольник – фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки – сторонами. При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.
Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю. Внутреннюю область также относят к многоугольнику.
Иными словами, например, когда говорят о пятиугольнике А1А2А3А4А5, имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника.
Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).
Периметр многоугольника – сумма длин сторон многоугольника.
Отрезок, соединяющий любые две противоположные вершины, называется диагональю многоугольника.
Многоугольники делятся на выпуклые и невыпуклые. Например, многоугольник, изображенный на рисунке выше, является выпуклым, а на рисунке ниже – невыпуклым.
Многоугольник называется выпуклым, если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой.
Невыпуклыми являются все остальные многоугольники.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны.
Существенное отличие четырехугольника от треугольника в том, что он может быть выпуклым или невыпуклым.
Очень важное различие, о котором знает каждый плотник, состоит в том, что треугольник – «жесткая» фигура, а четырехугольник (как и все остальные многоугольники) – «нежесткая».
У треугольника невозможно изменить его форму, не изменив длин сторон. При этом у любого четырехугольника можно изменить его форму, не меняя длины сторон. На практике это будет означать, что треугольник, сколоченный из трех дощечек, будет жестким, не будет сминаться даже при сильных воздействиях, а четырехугольник при достаточной нагрузке со стороны изменит свою форму.
Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольникаитеорема о сумме внешних углов выпуклого многоугольника.
Теорема. О сумме внутренних углов выпуклого многоугольника (n-угольника).
Сумма углов n-угольника равна 180°·(n-2).
Математическая запись: ∠A1+∠A2+…+∠An=180°(n-2), где n – количество его углов (сторон).
Вспомним, что любой четырехугольник состоит из двух треугольников (достаточно провести диагональ). Но сумма углов каждого из них одинакова и равна 1800, значит, сумма углов четырехугольника 3600.
Теорема. О сумме внешних углов выпуклого многоугольника (n-угольника).
∠1’+∠2’+…+∠n’=360°, где n – количество его углов (сторон), а ∠1′,…,∠n’ – внешние углы, по одному от каждой вершины.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Многоугольники |
| Определение многоугольника |
| Диагонали n – угольника |
| Внешний угол многоугольника |
| Свойства углов треугольника |
| Свойства углов многоугольника |
| Свойства углов правильного n – угольника |
| Доказательства теорем о свойствах углов многоугольника |
Определение многоугольника
Рассмотрим n отрезков
| [A1 A2], [A2 A3], … , [An An +1] | (1) |
причём таких, что два любых отрезка, имеющих общий конец, не лежат на одной прямой (рис.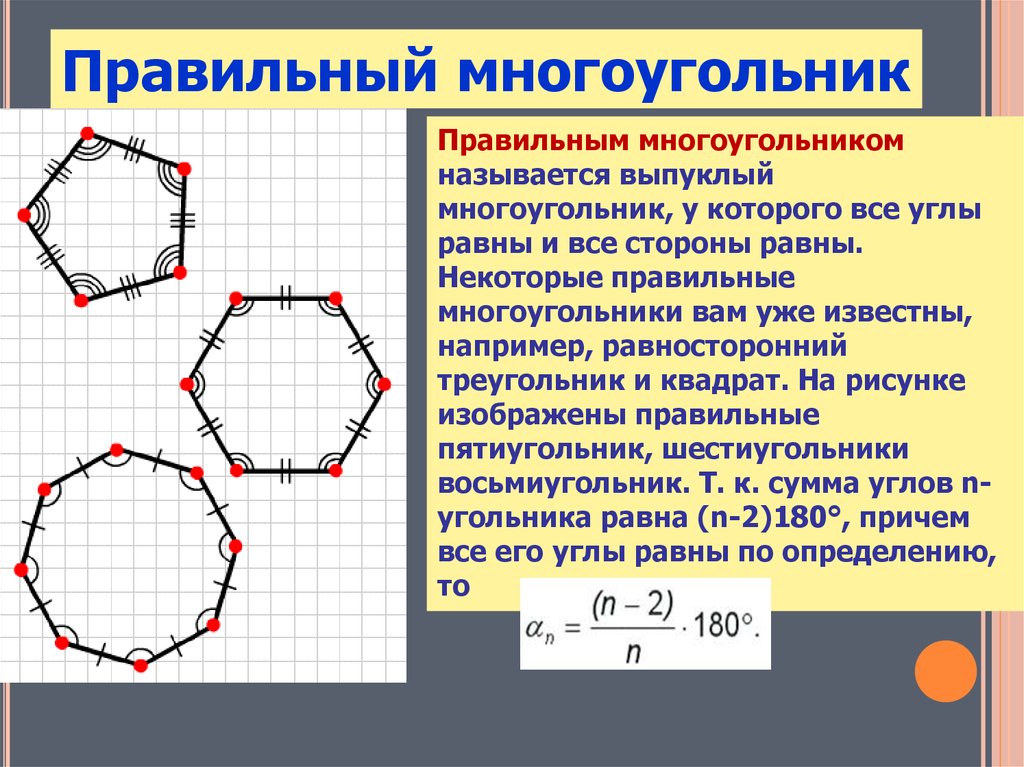
1).
Рис. 1
Определение 1. Ломаной линией с n звеньями называют фигуру L, составленную из отрезков (1), то есть фигуру, заданную равенством
L = [A1 A2] U [A2 A3] U …
… U [An An +1]
В случае, когда точки
Рис. 2
Определение 2. Многоугольником называют часть плоскости, ограниченную замкнутой ломаной линией без самопересечений (рис. 3). Отрезки, составляющие ломаную линию (звенья), называют сторонами многоугольника. Концы отрезков называют вершинами многоугольника.
Рис. 3
Определение 3. Многоугольник называют n – угольником, если он имеет n сторон.
Таким образом, многоугольник, имеющий 3 стороны, называют треугольником, многоугольник, имеющий 4 стороны, называют четырёхугольником и т.д.
Определение 4 . Периметром многоугольника называют сумму длин всех сторон многоугольника.
Величину, равную половине периметра, называют полупериметром.
Диагонали n — угольника
| Фигура | Рисунок | Описание |
| Диагональ многоугольника | Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника | |
| Диагонали n – угольника, выходящие из одной вершины | Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника | |
| Все диагонали n – угольника | Число диагоналей n – угольника равно |
| Диагональ многоугольника |
Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Диагонали n – угольника, выходящие из одной вершины |
Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника |
| Все диагонали n – угольника |
Число диагоналей n – угольника равно |
Внешний угол многоугольника
Определение 5 .
Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).
Рис.1
Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).
Рис.2
Замечание. Мы рассматриваем только выпуклые многоугольникивыпуклые многоугольники.
Свойства углов треугольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы треугольника | Сумма углов треугольника равна 180° α + β + γ = 180° Посмотреть доказательство | |
| Внешний угол треугольника | Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним δ = α + β Посмотреть доказательство |
| Углы треугольника |
Сумма углов треугольника равна 180° α + β + γ = 180° Посмотреть доказательство |
| Внешний угол треугольника |
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним δ = α + β Посмотреть доказательство |
Свойства углов многоугольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы n – угольника | Сумма углов многоугольника равна Посмотреть доказательство | |
| Внешние углы n – угольника | Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360° Посмотреть доказательство |
| Углы n – угольника |
Сумма углов многоугольника равна Посмотреть доказательство |
| Внешние углы n – угольника |
Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360° Посмотреть доказательство |
Свойства углов правильного n – угольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы правильного n – угольника | Все углы правильного n – угольника равны | |
| Внешние углы правильного n – угольника | Все внешние углы правильного |
| Углы правильного n – угольника |
Все углы правильного n – угольника равны |
| Внешние углы правильного n – угольника |
Все внешние углы правильного |
Доказательства свойств углов многоугольника
Теорема 1.
В любом треугольнике сумма углов равна 180°.
Доказательство. Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).
Рис.3
Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE. Поскольку углы ABD, ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180°. Теорема доказана.
Теорема 2. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.Доказательство. Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).
Рис.4
Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные.
Поэтому внешний угол BCD равен сумме углов BAC и ABC. Теорема доказана.
Замечание. Теорема 1 является следствием теоремы 2.
Теорема 3. Сумма углов n – угольника равна
Доказательство. Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).
Рис.5
OA1A2, OA2A3, … OAnA1
Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O. Поэтому сумма всех углов n – угольника равна
что и требовалось доказать.
Теорема 4. Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°.
Доказательство. Рассмотрим рисунок 6.
Рис.6
В соответствии рисунком 6 справедливы равенства
Теорема доказана.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Геометрический многоугольник Бесшовный векторный рисунок
- Совершенно новый
- Тенденции
- вневременной
- Дети
- Цветочный
- Животные
- Культуры
- Сезонный
- Формы
- Вкусный
Поделиться
| Ключевые слова | ||||
|---|---|---|---|---|
| ID | #30557 | |||
| Конструктор | Игорь Серазетдинов | Идентификационный номер 30557 | ||
| Описание | Современный геометрический векторный рисунок с многоугольными формами. | |||
| Сведения о лицензии | Цены | |||
| Цены Сведения о лицензии | Вектор без ограничений | SVG, EPS, PDF, JPEG без лицензионных отчислений | 35,20 $ | |
| Печать в формате JPEG | Ограниченная лицензия 1181×1181 пикс. | 8,10 $ | ||
| Экран JPEG | Ограниченная лицензия 150 x 150 пикс. | 2,70 $ | ||
| Дизайн добавлен в корзину Добавить в корзину Перейти в корзину | ||||
Другие похожие конструкции
Polygon: оптогенетика и фотостимуляция с клеточным разрешением
Свяжитесь с нами
Polygon
DMD Pattern Illuminator
for Targeted
Photostimulation
DMD Pattern Illuminator
for Targeted Photostimulation
Polygon
- Overview/Features
- Applications
- Models
- Resources
- Contact Us
Overview/ Характеристики
Более 600 лабораторий по всему миру, более 100 публикаций, использующих Polygon
Ведущий на рынке осветитель Polygon DMD компании Mightex обеспечивает точное пространственно-временное управление светом с субклеточным разрешением, что делает его идеальным инструментом освещения для исследований в области биологических наук.
Cellular-Resolution Optogenetics and Photostimulation
Simultaneous Multi-Region Illumination
Subcellular Resolution
Compatible with Any Microscope
Polygon Brochure & Specifications
State-of-the- Art Illumination Technology
Polygon использует технологию цифрового зеркального устройства (DMD) для одновременного освещения нескольких областей. DMD состоит из сотен тысяч микрозеркал, которые можно включать по отдельности, чтобы отражать свет на образец. Таким образом, вы можете управлять каждым зеркалом, чтобы управлять областью (областями) освещения и создавать любое количество узоров разного размера. Осветитель полигона Polygon DMD можно установить на бесконечном пути любого микроскопа.
Основные характеристики многоугольника
Выберите освещение отдельных клеток, экспрессирующих ChR2, в срезе с помощью многоугольника (любезно предоставлено Мэтью Траном и доктором Блейком Ричардсом, Университет Макгилла).
Одновременная оптогенетическая стимуляция отдельных клеток или субклеточных компонентов
Многоугольник позволяет ученым точно контролировать, где свет будет падать на их образец. С субклеточным разрешением Polygon может одновременно освещать любые клеточные элементы любой формы и размера на своем образце.
Стимуляция любого зонда для оптогенетики или фотостимуляции
Полигон обеспечивает большую гибкость при выборе длины волны. Polygon может проецировать свет разных цветов, от УФ до видимого/ближнего ИК-диапазона, подходящего для ваших светочувствительных конструкций.
Выберите градиентное освещение клетки, экспрессирующей новую оптогенетическую конструкцию, с помощью полигона (любезно предоставлено Эллиотом Дайном и доктором Джаредом Тетчером, Принстонский университет).
Пространственно-временной контроль и управление интенсивностью света
Контроль начала, продолжительности и интенсивности световой стимуляции с помощью полигона. Создавайте различные формы волны, чтобы контролировать интенсивность и продолжительность света, выводимого из полигона.
УФ-фотошаблон (предоставлено Гайлой Берг, Колорадский университет).
УФ-микропаттерн с субмикронным разрешением
Polygon совместим с источниками УФ-излучения (350 нм+) и обеспечивает субмикронное освещение для экспериментов по фотопаттерну и микрообработке.
Интегрируется в любой электрофизиологический, двухфотонный или конфокальный микроскоп
Polygon предназначен для подключения к бесконечному пространству любой модели микроскопа (Leica, Nikon, Olympus, Zeiss) с адаптерами Mightex для конкретных микроскопов.
Polygon оснащен триггерным входом и выходом TTL с разъемом BNC для легкой синхронизации с различным лабораторным оборудованием.
Модели освещения с использованием многоугольника, синхронизированного с электрофизиологическими записями срезов (любезно предоставлено Мэтью Траном и доктором Блейком Ричардсом, Университет Макгилла).
Выберите освещение отдельных клеток, экспрессирующих ChR2, в срезах, используя Polygon (любезно предоставлено Мэтью Траном и доктором Блейком Ричардсом, Университет Макгилла).
Неврология Оптогенетика
Оптогенетика продвинула область нейробиологии, предоставив точный метод управления активностью нейронов. Возможность выполнять оптогенетику с клеточным разрешением позволяет исследователям стимулировать отдельные экспрессирующие оптогенез нейроны (например, ChR2, NpHr, Chrimson и т. д.) в срезе или культуре во время электрофизиологических записей или визуализации кальция для картирования нейронных цепей.
Соответствующие публикации с использованием полигона:
Kauver IV et al. (2020). Наблюдение за корой головного мозга с помощью синхронной мультифокальной оптической выборки выявляет широко распространенное популяционное кодирование действий. Нейрон.
Chong E et al. (2020). Манипуляции с синтетическими запахами раскрывают логику кодирования обонятельного восприятия. Наука.
Kissinger ST et al. (2020). Колебания, зависящие от визуального опыта, и основные изменения подключения схемы ухудшаются в Fmr1 KO Мыши.
Отчеты сотовых.
Грувер К.М. и Ватт А.Дж. (2019). Оптимизация оптогенетической активации аксонов клеток Пуркинье для исследования клетки Пуркинье — синапса DCN. Границы синаптической нейронауки .
Табор К.М. и др. (2018). Пресинаптическое торможение избирательно направляет слуховую передачу на цепь вздрагивания ствола мозга. Актуальная биология.
Андраси и др. (2017). Дифференциальное управление возбуждением двух параллельных корзинчатых клеточных сетей в микросхемах миндалевидного тела. ПЛОС Биология .
Клеточная биология Оптогенетика
Оптогенетические инструменты расширились, чтобы предложить клеточным биологам беспрецедентный пространственно-временной молекулярный и клеточный контроль. От миграции клеток до регуляции генов или процессов развития, клеточные биологи теперь имеют возможность с невероятной точностью вызывать специфические биологические реакции в конкретных клетках организмов или субклеточных областях отдельных клеток с помощью оптогенетики.
Выберите градиентное освещение клетки, экспрессирующей новую оптогенетическую конструкцию, с помощью полигона (любезно предоставлено Эллиотом Дайном и доктором Джаредом Тетчером, Принстонский университет).
Соответствующие публикации с использованием Polygon:
Johnson HE et al. (2020). Оптогенетическое спасение паттернирующего мутанта. Актуальная биология.
Дайн Э. и др. (2018). Разделение белковых фаз обеспечивает долговременную память о переходных пространственных стимулах. Клеточные системы.
ван Харен Дж. и др. (2018). Локальный контроль динамики внутриклеточных микротрубочек с помощью фотодиссоциации EB1. Природа Клеточная биология.
Johnson HE et al. (2017). Пространственно-временные ограничения передачи сигналов Erk в процессе развития.
Развивающая ячейка.
Адриан М. и др. (2017). Фотопереключатель на основе фитохрома для внутриклеточного транспорта. Синтетическая биология ACS.
Фотоактивация/фотоконверсия
Достижения в технологии флуоресцентных белков сделали методы фотоактивации широко доступными в лабораториях клеточной биологии. Используя эти методы, исследователи могут флуоресцентно выделять/маркировать определенные популяции белков в клетке, чтобы можно было отслеживать их движение и поведение с течением времени. Кроме того, методы фотоактивации могут применяться в различных масштабах, что позволяет исследователям отслеживать белки внутри клеток или, альтернативно, отслеживать клетки в тканях.
Соответствующие публикации с использованием полигона:
Tabor KM et al.
(2018). Пресинаптическое торможение избирательно направляет слуховую передачу на цепь вздрагивания ствола мозга. Актуальная биология.
Осгасавара и др. (2018). Транскрипция, управляемая обратимым фотоконтролем гиперстабильных G-квадраплексов. Синтетическая биология ACS.
Создание фотошаблонов
Для управления различными свойствами клеточного микроокружения было разработано множество методов. Недавно появление светоиндуцированных биохимических соединений позволило ученым определить биохимические и структурные особенности клеточного матрикса с помощью фотомикроструктурирования и фотолитографии. Ученые могут точно определить пространственное распределение УФ-излучения для создания уникальной клеточной микросреды без использования масок или физического контакта с субстратом.
УФ-фотошаблон (предоставлено Гайлой Берг, Колорадский университет).
Соответствующие публикации с использованием полигона:
Geisterfer ZM et al.
(2020). Скорость роста микротрубочек чувствительна к глобальным и локальным изменениям плотности плюс-конца микротрубочек. Актуальная биология.
Fattahi N et al. (2020). Фоторазлагаемые гидрогели для быстрого скрининга, выделения и генетической характеристики бактерий с редкими фенотипами. Биомакромолекулы .
Норен Б.Е. и др. (2019). Клеточная печать в сложных гидрогелевых каркасах. транзакции IEEE по нанобиологии.
ван дер Влис А.Дж. и др. (2019). Высвобождение по требованию и извлечение бактерий из микролуночных матриц с использованием фоторазлагаемых гидрогелевых мембран. Прикладные биоматериалы ACS.
Оптоэлектронный пинцет для перемещения определенных клеток (любезно предоставлено доктором Шуайлун Чжаном, Университет Торонто).
Микрофлюидика
Микрофлюидные устройства изготавливаются путем нанесения тонкопленочных материалов-предшественников на подложку с фотоструктурированием для создания микроскопических каналов, камер и даже механизмов управления потоком.
Небольшие количества жидкостей, содержащих реакционноспособные химикаты или другие вещества, могут затем проходить через микроканалы и смешиваться в микрокамерах устройства и вступать в реакцию с другими веществами, которые могут осаждаться в микроканалах.
Модели
Различные модели, оптимизированные для медико-биологических приложений
Различные модели, оптимизированные для медико-биологических приложений
Mightex предлагает несколько моделей Polygon, которые были разработаны с различными функциями для удовлетворения потребностей широкого спектра приложений, использующих шаблоны. освещение. Пожалуйста, смотрите ниже все доступные модели Polygon.
Polygon1000-G
Polygon1000-G — это гибкое решение для направленного освещения, поскольку этот узорчатый осветитель можно использовать с любым источником света (350–700 нм), который принимает световод с сердечником диаметром 3 мм. Таким образом, Polygon1000-G обеспечивает будущую гибкость для различных длин волн и источников света, в зависимости от вашего приложения.
- Длина волны: 350–700 нм
- Источник света: со световодом
- Дополнительная передняя трубка для большого поля зрения
Polygon1000-DL
применения в высокомощном узорчатом освещении, так как этот узорчатый осветитель можно использовать с любым оптоволоконным источником света (400–700 нм), например, с мощными лазерами. Эта модель Polygon1000 была разработана для высокопроизводительных приложений, таких как оптогенетика in vivo.
- Длина волн: 400-700 нм
- Lightsource: волокно-связанное
- Длина волны: 400-700 нм
- Источник света: со световодом
*Снято с производства.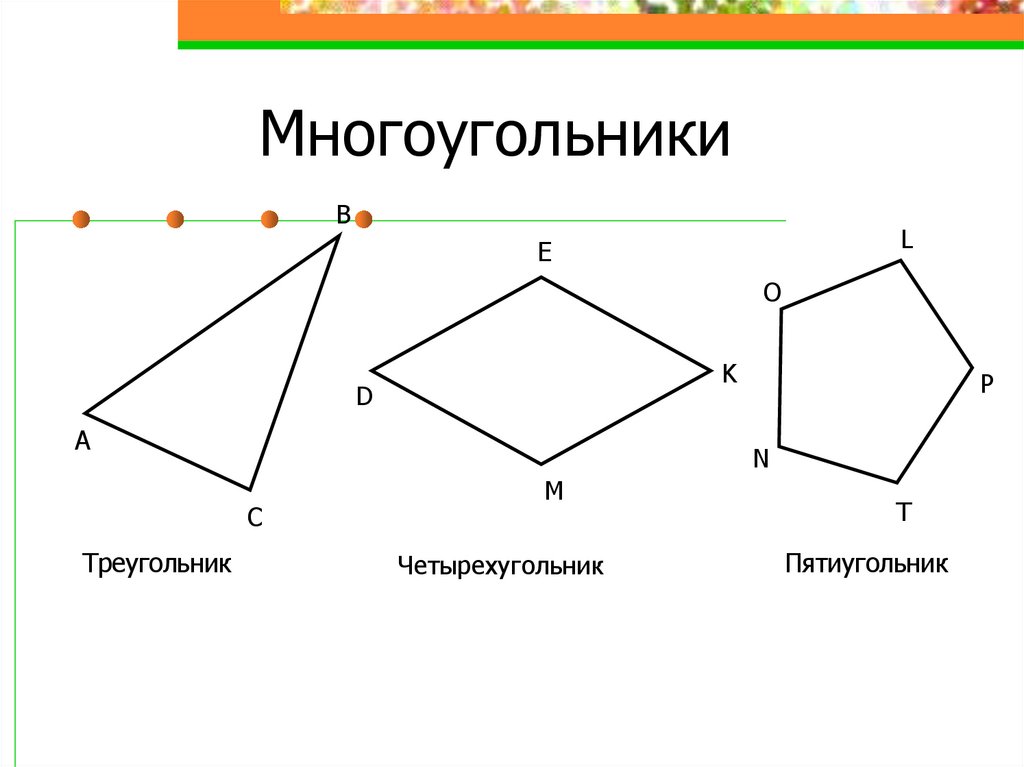
Заменена серией Polygon1000.
Resources
Webinars
White Paper/Applications Notes
Contact Us
600+ Labs Worldwide, 100+ Publications Using Polygon
Mightex’s market-leading Polygon DMD pattern illuminator provides precise spatiotemporal control of light with subcellular resolution , что делает его идеальным инструментом освещения для исследований в области наук о жизни.
Cellular-Resolution Optogenetics and Photostimulation
Simultaneous Multi-Region Illumination
Subcellular Resolution
Compatible with Any Microscope
Polygon Brochure & Specifications
State-of-the- Art Illumination Technology
Polygon использует технологию цифрового зеркального устройства (DMD) для одновременного освещения нескольких областей. DMD состоит из сотен тысяч микрозеркал, которые можно включать по отдельности, чтобы отражать свет на образец.
Таким образом, вы можете управлять каждым зеркалом, чтобы управлять областью (областями) освещения и создавать любое количество узоров разного размера. Осветитель полигона Polygon DMD можно установить на бесконечном пути любого микроскопа.
Основные характеристики многоугольника
Одновременная оптогенетическая стимуляция отдельных клеток или субклеточных компонентов
Выберите освещение отдельных клеток, экспрессирующих ChR2, в срезе с помощью многоугольника (любезно предоставлено Мэтью Траном и доктором Блейком Ричардсом, Университет Макгилла).
Многоугольник позволяет ученым точно контролировать, где свет будет падать на их образец. С субклеточным разрешением Polygon может одновременно освещать любые клеточные элементы любой формы и размера на своем образце.
Стимуляция любого зонда для оптогенетики или фотостимуляции
Полигон обеспечивает большую гибкость при выборе длины волны. Polygon может проецировать свет разных цветов, от УФ до видимого/ближнего ИК-диапазона, подходящего для ваших светочувствительных конструкций.
Пространственно-временной контроль и управление интенсивностью света
Выберите градиентное освещение клетки, экспрессирующей новую оптогенетическую конструкцию, с помощью полигона (любезно предоставлено Эллиотом Дайном и доктором Джаредом Тотчером, Принстонский университет).
Контролируйте начало, продолжительность и интенсивность световой стимуляции с помощью полигона. Создавайте различные формы волны, чтобы контролировать интенсивность и продолжительность света, выводимого из полигона.
УФ-микроструктурирование с субмикронным разрешением
УФ-фотоструктурирование (любезно предоставлено Гайлой Берг, Университет Колорадо).
Polygon совместим с источниками УФ-излучения (350 нм+) и обеспечивает субмикронное освещение для экспериментов по фотопаттерну и микрообработке.
Встраивается в любой электрофизиологический, двухфотонный или конфокальный микроскоп
Модели освещения с использованием полигона, синхронизированного с электрофизиологическими записями срезов (любезно предоставлено Мэтью Траном и доктором Блейком Ричардсом, Университет Макгилла).
Polygon предназначен для подключения к бесконечному пространству любой модели микроскопа (Leica, Nikon, Olympus, Zeiss) с помощью адаптеров Mightex для конкретных микроскопов. Polygon оснащен триггерным входом и выходом TTL с разъемом BNC для легкой синхронизации с различным лабораторным оборудованием.