Дифференциальная геометрия: первое знакомство
Дифференциальная геометрия: первое знакомство
ОглавлениеПредисловиеГЛАВА 1.  § 1. ПОНЯТИЕ КРИВОЙ 2°. Плоские кривые, задаваемые параметрически 3°. Пространственные кривые 4°. Кривая как линия пересечения поверхностей 5°. Кривая как годограф векторной функции § 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ КРИВЫЕ 2°. Гладкие кривые 3°. Дифференцирование и интегрирование векторных функций 4°. Достаточные условия гладкости кривой 5°. Регулярные кривые § 3. ДЛИНА ДУГИ КРИВОЙ 2°. Достаточные условия спрямляемости § 4. СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ 1°. Определение соприкасающейся плоскости 2°. Достаточные условия существования соприкасающейся плоскости 3°. Главная нормаль и бинормаль кривой. Основной триэдр § 5. КРИВИЗНА И КРУЧЕНИЕ. ФОРМУЛЫ ФРЕНЕ 2°. Кручение кривой 3°. Формулы Френе 4°. Вид кривой вблизи данной точки 5°. Натуральные уравнения кривой § 6. СОПРИКОСНОВЕНИЕ КРИВЫХ 2°. Достаточные условия соприкосновения 3°. Соприкасающаяся окружность 4°. Эволюта и эвольвента плоской кривой СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ ГЛАВА 2.  ТЕОРИЯ ПОВЕРХНОСТЕЙ§ 1. ПОНЯТИЕ ПОВЕРХНОСТИ 1°. Плоские области 2°. Простая поверхность 3°. Локально простая поверхность 4°. Общая поверхность § 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ ПОВЕРХНОСТИ 1°. Касательная плоскость к поверхности 2°. Гладкие поверхности 3°. Дифференцирование и интегрирование векторных функций двух аргументов 4°. Дифференцируемость векторной функции и касательная плоскость 5°. Достаточные условия гладкости поверхности 6°. Регулярные поверхности § 3. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ. ИЗМЕРЕНИЯ НА ПОВЕРХНОСТИ 1°. Первая квадратичная форма поверхности 2°. Длина кривой на поверхности 3°. Угол между кривыми на поверхности 4°. Площадь поверхности 5°. Внутренняя геометрия поверхности. Изометричные поверхности § 4. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА 2°. Классификация точек регулярной поверхности 3°. Кривизна кривой на поверхности 4°. Индикатриса Дюпена 5°. 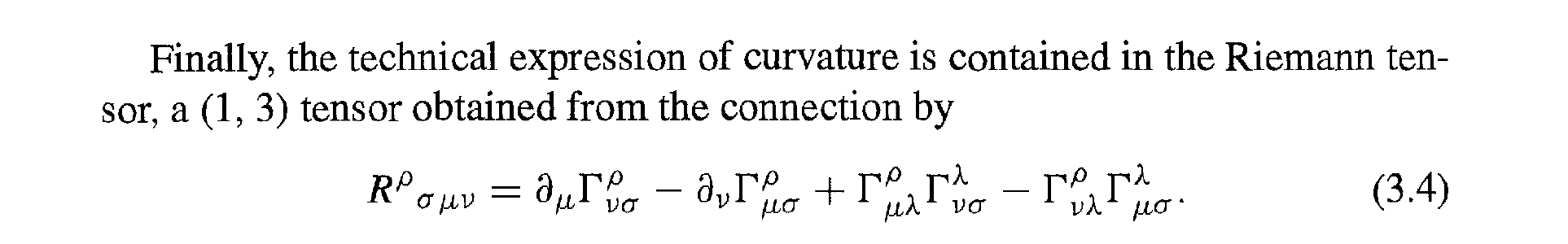 Главные кривизны6°. Линии кривизны 7°. Формула Родрига 8°. Асимптотические направления 9°. Асимптотические линии 10°. Формула Эйлера 11°. Средняя и гауссова кривизны 12°. Поверхности вращения § 5. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ 2°. Основные уравнения теории поверхностей 3°. Теорема Бонне § 6. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ 1°. Геодезическая кривизна кривой на поверхности 2°. Геодезические линии 3°. Полугеодезические координатные системы 4°. Полугеодезические полярные координаты 5°. Экстремальные свойства геодезических 6°. Поверхности постоянной кривизны СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ ГЛАВА 3. ОСНОВЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ 1°. Определение тензора 2°. Корректность определения тензора 3°. Равенство тензоров § 2. АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ НАД ТЕНЗОРАМИ 1°. Определение алгебраических операций над тензорами 2°. Правило суммирования 3°. Теорема об алгебраических операциях над тензорами 4°.  Операции над кососимметричными тензорами5°. Внешние формы § 3. МЕТРИЧЕСКИЙ ТЕНЗОР 2°. Опускание и поднятие индексов Б. АФФИННОЕ (ТОЧЕЧНОЕ) ПРОСТРАНСТВО § 4. ТЕНЗОРЫ В ТОЧЕЧНЫХ ПРОСТРАНСТВАХ 2°. Аффинные координаты 3°. Тензоры в точечном пространстве § 5. ТЕНЗОРНОЕ ПОЛЕ § 6. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 2°. Тензоры в криволинейных координатах 3°. О способе задания тензорного поля § 7. МЕТРИЧЕСКИЙ ТЕНЗОР В ТОЧЕЧНОМ ПРОСТРАНСТВЕ 2°. Длина дуги гладкой кривой 3°. Вычисление объема § 8. СИМВОЛЫ КРИСТОФФЕЛЯ 2°. Специальные системы координат 3°. Символы Кристоффеля 1-го и 2-го рода § 9. КОВАРИАНТНОЕ ДИФФЕРЕНЦИРОВАНИЕ 2°. Свойства операции ковариантного дифференцирования 3°. Тензор Римана-Крнстоффеля типа (1 3) 4°. Ковариантное дифференцирование и метрический тензор 5°. Тензор Римана-Кристоффеля типа (0 4) В. АРИФМЕТИЧЕСКОЕ (КООРДИНАТНОЕ) ПРОСТРАНСТВО § 10.  ТЕНЗОРЫ В КООРДИНАТНОМ ПРОСТРАНСТВЕ2°. Преобразования координат 3°. Понятие тензора 4°. Основные алгебраические операции над тензорами 5°. Метрический тензор в координатном пространстве 6°. Символы Кристоффеля и операция ковариантного дифференцирования 7°. Тензор Римана-Кристоффеля ГЛАВА 4. РИМАНОВА ГЕОМЕТРИЯ 2°. Примеры римановых пространств § 2. ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О РИМАНОВОЙ ГЕОМЕТРИИ 2°. Преобразование координат в римановом и касательном пространствах 3°. Локально нормальные координаты 4°. Каноническое разложение метрического тензора § 3. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВЕКТОРОВ И ТЕНЗОРОВ 2°. Векторы в римановом пространстве 3°. Параллельный перенос векторов в римановом пространстве 4°. Параллельный перенос тензоров 5°. Абсолютный дифференциал и абсолютная производная 6°. Техника абсолютного дифференцирования 7°. Еще раз о параллельном переносе тензоров 8°. Параллельный перенос некоторых важных тензоров § 4.  ГЕОДЕЗИЧЕСКИЕ ЛИНИИ В РИМАНОВОМ ПРОСТРАНСТВЕ2°. Геодезические как экстремали § 5. СПЕЦИАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ В РИМАНОВОМ ПРОСТРАНСТВЕ 2°. Полугеодезические координаты СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ ГЛАВА 5. ГЛАДКИЕ МНОГООБРАЗИЯ § 1. НЕКОТОРЫЕ ПОНЯТИЯ ТОПОЛОГИИ 1°. Топология координатного пространства 2°. Топологическое пространство 3°, Топологическое подпространство 4°. Непрерывное отображение. Гомеоморфизм 6°. Связность 7°. Отделимость 8°. Компактность 9°. Топологическое многообразие § 2. ГЛАДКИЕ МНОГООБРАЗИЯ 2°. Гладкие функции 3°. Разбиение единицы 4°. Произведение гладких многообразий § 3. КАСАТЕЛЬНОЕ ПРОСТРАНСТВО 1°. Касательный вектор 2°. Касательное пространство § 4. ГЛАДКИЕ ОТОБРАЖЕНИЯ 1°. Гладкое отображение. Диффеоморфизм 2°. Дифференциал гладкого отображения 3°. Ранг гладкого отображения § 5. ПОДМНОГООБРАЗИЯ § 6. ВЕКТОРНЫЕ И ТЕНЗОРНЫЕ ПОЛЯ 2°.  Риманова метрика3°. Внешние дифференциальные формы на многообразии § 7. ИНТЕГРИРОВАНИЕ ПО МНОГООБРАЗИЮ 2°. Многообразие с краем 3°. Интеграл от дифференциальной формы по гладкому многообразию 4°. Формула Стокса СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ ГЛАВА 6. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ 2°. Движение точки в поле сил 3°. Движение точки в параллельном поле сил 4°. Движение точки в центральном поле сил 5°. Движение в поле сил тяготения 6°. Движение заряженной частицы в электромагнитном поле 7°. Движение заряженной частицы в постоянном электромагнитном поле § 2. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ ОТРИЦАТЕЛЬНОЙ КРИВИЗНЫ 2°. Изометрические погружения плоскости Лобачевского в евклидово пространство Е3 3°. Доказательство теоремы Гильберта о невозможности в евклидовом пространстве Е3 полной плоскости Лобачевского 4°. Доказательство существования регулярного решения уравнения синус-Гордона на всей плоскости 5°.  Геометрическая интерпретация произвольных решений уравнения синус-Гордона6°. Понятие солитонных решений дифференциальных уравнений 7°. Физическая интерпретация поверхностей постоянной отрицательной кривизны § 3. ОСНОВНЫЕ ОПЕРАЦИИ ВЕКТОРНОЙ АЛГЕБРЫ И ВЕКТОРНОГО АНАЛИЗА В ТЕНЗОРНЫХ ОБОЗНАЧЕНИЯХ 3°. Ортонормированные базисы в пространстве En 4°. Дискриминантный тензор 5°. Ориентированный объем 6°. Векторное произведение 7°. Двойное векторное произведение 8°. Расходимость вектора 9°. Оператор Бельтрами — Лапласа 10°. Оператор Бельтрами — Лапласа в криволинейных координатах § 4. ПСЕВДОЕВКЛМДОВО И ПСЕВДОРИМАНОВО ПРОСТРАНСТВА 2°. Галилеевы координаты. Преобразования Лоренца 3°. Пространство Минковского. Преобразования Лоренца в пространстве Минковского 4°. Псевдориманово пространство. Метрический тензор псевдориманова пространства § 5. ПРОЕКТИРОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ 2°. Уравнение криволинейного четырехугольника 3°. 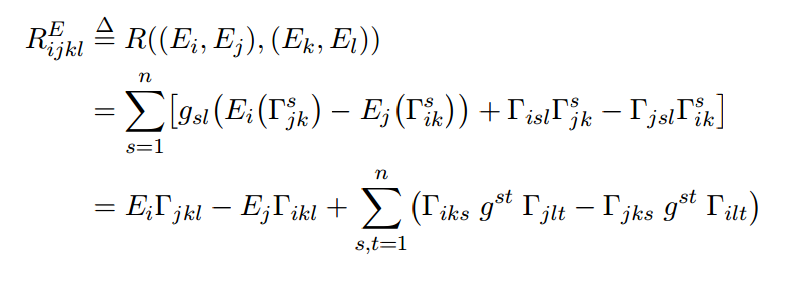 Составные кривые4°. Составные поверхности |
Метрический тензор Римана: новая теорема Пифагора. Гиперпространство
Метрический тензор Римана: новая теорема ПифагораРиману понадобилось несколько месяцев, чтобы оправиться от последствий нервного срыва. Его доклад, наконец прочитанный в 1854 г., приняли с воодушевлением. В ретроспективе это был, бесспорно, один из наиболее выдающихся публичных докладов в истории математики. По Европе быстро распространилось известие, что Риман решительно сбросил оковы евклидовой геометрии, которой математики подчинялись на протяжении двух тысячелетий. О докладе вскоре узнали во всех центрах образования Европы, вклад Римана в математику приветствовали повсюду в научных кругах. Доклад Римана перевели на несколько языков, он произвел фурор в математике. К евклидовой геометрии раз и навсегда перестали относиться так, как прежде.
Суть выдающегося труда Римана, как и суть многих величайших работ в области физики и математики, уловить довольно просто.
Риман начал со знаменитой теоремы Пифагора, одного из важнейших достижений древнегреческих математиков. Эта теорема устанавливает соотношения между длинами сторон прямоугольного треугольника. Согласно ей, сумма квадратов коротких сторон, катетов, равна квадрату длинной стороны, гипотенузы; если
Эту теорему легко сформулировать для трехмерного пространства. Она гласит, что сумма квадратов трех смежных сторон куба равна квадрату его диагонали; или если а, Ь и с — стороны куба, ad — его диагональ, тогда а2 + b2 + с2 = d2 (рис. 2.1).
Рис. 2.1. Длину диагонали куба дает трехмерный вариант теоремы Пифагора: a2 + Ь2 + c2 = d2.
Простого добавления новых переменных в теорему Пифагора достаточно, чтобы записать формулу для диагонали гиперкуба в N-мерном пространстве. Таким образом, несмотря на сложность визуализации высших измерений, представить N-мерность математически довольно просто.
Теперь так же просто можно сформулировать ту же теорему для N-мерного пространства. Представим себе N-мерный куб. Если а, Ь, с… — длины сторон «гиперкуба», а z — длина его диагонали, тогда а2 + Ь2 + с2 + d2 +… = z2. Примечательный момент: хотя наш мозг не в состоянии представить N-мерный куб, формулу для его сторон и диагонали записать несложно. (Это типичная особенность работы с гиперпространством. С математической, точки зрения манипулировать N-мерным пространством не труднее, чем трехмерным пространством. Поразительно, как на простом листе бумаги можно математически описать свойства многомерных объектов, которые не в силах вообразить наш мозг.
)
Затем Риман записал эти уравнения для пространств с произвольным количеством измерений. Эти пространства могут быть либо плоскими, либо искривленными. К плоским применяются обычные аксиомы Евклида: кратчайшее расстояние между двумя точками — прямая, параллельные линии никогда не пересекаются, сумма внутренних углов треугольника составляет 180°. Вместе с тем Риман обнаружил, что поверхности могут иметь «положительную кривизну», как поверхность сферы, где параллельные всегда пересекаются и сумма углов треугольника может быть больше 180°. Бывают и поверхности с «отрицательной кривизной»: например, седлообразные или воронкообразные. На этих поверхностях сумма углов треугольника меньше 180°. Если взять линию и точку вне этой линии, то через такую точку можно провести бесконечное множество линий, параллельных данной (рис. 2.2).
Рис. 2.2. Плоскость имеет нулевую кривизну. Согласно евклидовой геометрии сумма углов треугольника равна 180°, параллельные не пересекаются. В неевклидовой геометрии сфера имеет положительную кривизну.
Сумма углов треугольника превышает 180°, параллельные линии всегда пересекаются. (К параллельным линиям относятся дуги, центры которых совпадают с центром сферы. Широтные линии в эту категорию не входят.) У седлообразной поверхности отрицательная кривизна. Сумма углов треугольника меньше 180°. Через конкретную точку можно провести бесконечное множество линий, параллельных данной.
Целью Римана было ввести в математику новый элемент, позволяющий описывать все поверхности независимо от их сложности. Как и следовало ожидать, эта цель побудила его обратиться к фарадеевой концепции поля.
Как мы помним, поле Фарадея представляло собой подобие крестьянского, занимающего двумерный участок пространства. Фарадеево поле занимает часть трехмерного пространства; любой точке этого пространства мы присваиваем ряд параметров, описывающих магнитное или электрическое взаимодействие в этой точке. Идея Римана заключалась в том, чтобы присвоить каждой точке пространства ряд параметров, которые описывали бы степень его деформации или кривизны.
К примеру, для обычной двумерной поверхности Риман вводил набор из трех параметров для каждой точки, полностью описывающих искривление этой поверхности. Риман обнаружил, что в четырех пространственных измерениях для описания свойств каждой точки требуется набор из десяти параметров. Каким бы «скомканным» или искривленным ни было пространство, этих десяти параметров для каждой точки оказывалось достаточно, чтобы зашифровать всю информацию о данном пространстве. Обозначим эти десять параметров как g11, g12, g13, и т. д. (при анализе четырехмерного пространства нижний индекс меняется от единицы до четырех). В этом случае риманов набор из десяти параметров можно симметрично расположить, как показано на рис. 2.3[15]. (Несмотря на то что компонентов всего 16, g12 = g21, g13 = g31 и т. д., т. e. в действительности независимых компонентов только десять.) В настоящее время этот набор параметров называется римановым метрическим тензором.
Грубо говоря, чем больше значение метрического тензора, тем сильнее скомкан лист. Как бы ни был смят лист бумаги, метрический тензор дает нам простое средство измерения его кривизны в любой точке. Если же мы полностью расправим скомканный лист, сделаем его плоским, то снова вернемся к теореме Пифагора.
Рис. 2.3. Метрический тензор Римана содержит всю информацию, необходимую для математического описания изогнутого N-мерного пространства. Для каждой точки четырехмерного пространства требуется метрический тензор с 16 параметрами. Эти числа можно расположить в виде квадратной матрицы (из этих параметров шесть на самом деле избыточны, следовательно, в метрический тензор входит десять независимых параметров).
Метрический тензор позволил Риману построить эффективный аппарат для описания пространств с любым количеством измерений и произвольной кривизной. К своему изумлению, Риман обнаружил, что все эти пространства четко определены и логически последовательны. Ранее считалось, что при исследовании запретного мира высших измерений непреодолимые противоречия неизбежны.
Но, как ни странно, Риман не заметил ни одного. Напротив, переход к N-мерным пространствам оказался почти пустяковым делом. Метрический тензор приобрел сходство с шахматной доской размером NxN клеток. Это обстоятельство приобретет глубокий физический смысл в следующих главах, когда мы перейдем к объединению всех сил.
(Как мы убедимся, секрет объединения кроется в расширении метрического тензора Римана до N-мерного пространства с последующим его нарезанием на прямоугольные части. Каждый прямоугольник соответствует одному взаимодействию. В этом случае можно описывать различные силы природы, размещая их в метрическом тензоре, как элементы в головоломке. Таково математическое выражение принципа, согласно которому многомерное пространство объединяет законы природы так, что для их объединения «хватает места» в N-мерном пространстве. Точнее, для объединения сил природы «достаточно места» в метрическом тензоре Римана.)
Риман предсказал еще одно направление развития физики: он первым заговорил о многосвязных пространствах, или «червоточинах».
Для наглядного представления этой концепции возьмите два листа бумаги, положите один на другой. Сделайте ножницами короткий разрез на каждом листе. Потом склейте листы друг с другом вдоль разрезов (рис. 2.4). (Топологически получается то же самое, что и на рис. 1.1, только горловина «червоточины» имеет нулевую длину.)
Рис. 2.4. Разрез Римана и два листа, соединенных друг с другом по одной линии. Если обойти разрез, мы останемся в пределах одного и того же пространства. Если пройти в разрез, мы перейдем с одного листа на другой. Таковы многосвязные пространства.
Жучок, живущий на верхнем листе, может когда-нибудь случайно заползти в разрез и очутиться на нижнем листе. И озадачиться, так как все вокруг изменится. После многочисленных экспериментов жучок наверняка поймет, что можно вернуться в привычный мир, если проползти через разрез в обратном направлении. Стоит только сделать это — и мир станет обычным, но любые попытки пройти через разрез в надежде сократить путь чреваты проблемами.
Разрез Римана — пример «червоточины» (с нулевой длиной), соединяющей два пространства. Римановы разрезы с успехом применил математик Льюис Кэрролл в книге «Алиса в Зазеркалье». Зеркало — это и есть риманов разрез, соединяющий Англию и Страну чудес. Сегодня римановы разрезы сохранились в двух видах. Во-первых, о них упоминают в учебных курсах математики всего мира применительно к конформному отображению или теории электростатики.
Во-вторых, римановы разрезы фигурируют в сериале «Сумеречная зона» (следует отметить, что сам Риман никогда не рассматривал эти разрезы как средство перемещения между вселенными).
Данный текст является ознакомительным фрагментом.
Новая сказка о любопытном слоненке
Новая сказка о любопытном слоненке
Нет, это сказка не о том скверном Слоненке, котором писал Киплинг, Слоненке, который жил Африке и которого колошматили его дорогие родственники, пока он не научился колошматить их сам.
)то сказка о другом, о хорошем Слоненке, которого
Глава 14. По ком звонит теорема Белла
Глава 14. По ком звонит теорема Белла “Вы верите в Бога, который играет в кости, а я — в абсолютный закон и порядок в объективно существующем мире, который я чисто умозрительно стараюсь понять, — написал Эйнштейн Борну в 1944 году. — В это я твердо верю и надеюсь, что
Наследие Римана
Наследие Римана Риман упорно продолжал исследования в области физики. В 1858 г. он даже объявил, что наконец сформулировал единое описание для света и электричества. Он писал: «Я полностью убежден, что моя теория верна и что через несколько лет ее признают таковой»[16].
Новая вероятность
Новая вероятность
Новая вероятность принципиально отличалась от той, которую Максвелл положил в основу статистической физики, а Эйнштейн применил в задаче броуновского движения.
Там речь шла об учете огромного числа факторов — например, толчков множества молекул. В
Нужна новая физика
Нужна новая физика Как видим, опытное подтверждение существует лишь для стандартной модели. Однако своей проверки ждут многие теории. Вот некоторые из
На службе новая техника…
На службе новая техника… Помните, начиная разговор о «ненормальных» галактиках, мы привели целый список новых внегалактических объектов. Большинство из них так далеки от Земли и от Галактики, что сведения, которыми располагают о них специалисты, буквально ничтожны.
Новая сказка о любопытном слоненке
Новая сказка о любопытном слоненке
Нет, это сказка не о том скверном Слоненке, о котором писал Киплинг, Слоненке, который жил в Африке и которого колошматили его дорогие родственники, пока он не научился колошматить их сам.
Это сказка о другом, о хорошем Слоненке, которого
Новая классификация камней
Новая классификация камней М.Дж. Оппенгейм Ниже приводится классификация камней, применимая ко всем разновидностям и рекомендуемая для всеобщего использования. Эта классификация, с одной стороны, совершенно четкая и жесткая, с другой стороны – весьма гибкая и удобная.
Третья глава Новая разновидность молотка
Третья глава Новая разновидность молотка Геометрия, несмотря на весьма насыщенную историю и впечатляющие достижения, которыми она может похвастаться на сегодняшний день, не является завершенным произведением, она по-прежнему развивается, постоянно открывая заново
Как вывести тензор кривизны Римана
Итак, я решил стиснуть зубы и изучить общую теорию относительности .
Я довольно долго откладывал это, но мысль о том, что моя жизнь закончится, так и не изучив одну из самых глубоких и фундаментальных физических теорий, была столь же тревожной, сколь и мотивирующей. Я буду публиковать случайные материалы по мере поступления и, возможно, вернусь позже, чтобы отредактировать их, поскольку мое понимание теории (надеюсь) углубляется.
Решил посмотреть видео-лекции профессора Зюскинда, которые есть в открытом доступе на YouTube. Они мне нравились, потому что Сасскинд уделяет особое внимание физическому аспекту вещей, а не формализму математики. Конечно, необходимы и то, и другое, но для начала я думаю, что лучше сначала развить интуицию.
Наша сегодняшняя цель — придумать инструмент для измерения кривизны пространства. Вообще говоря, изменение направления вектора , параллельно перемещаемого по замкнутому контуру , является способом измерения именно этого. Рассмотрим следующий вектор, который параллельно переносится через \(A \rightarrow N \rightarrow B \rightarrow A\).
\sigma \), потому что индексы \(\lambda\) и \(\sigma\) используются только как фиктивные индексы для суммирования. 92}};
InverseMetric[g_] := Simplify@Inverse@g
ChristoffelSymbol[g_, xx_] :=
Блок[{n, ig, res},
п = 2;
ig = обратная метрика [g];
разрешение = Таблица[
(1/2) Сумма [ig[[\[лямбда], \[сигма]]]*
(-D[g[[\[Mu], \[Nu]]], xx[[\[Sigma]]]] +
D[g[[\[Sigma], \[Nu]]], xx[[\[Mu]]]] +
D[g[[\[Sigma], \[Mu]]], xx[[\[Nu]]]]),
{\[Сигма], 1, п}],
{\[Lambda], 1, n}, {\[Mu], 1, n}, {\[Nu], 1, n}];
Упростить[res]](*\[Lambda],\[Mu],\[Nu]*)
ChristoffelSymbol[gmn, {\[Theta], \[CurlyPhi]}][[1]]
(* {{0, 0}, {0, -Cos[\[Theta]] Sin[\[Theta]]}} *)
ChristoffelSymbol[gmn, {\[Theta], \[CurlyPhi]}][[2]]
(* {{0, Кот[\[Тета]]}, {Кот[\[Тета]], 0}} *) 9\лямбда\) означает:
Изображение взято отсюда.
Теперь мы приступаем к вычислению тензора кривизны Римана:
RiemannTensor[g_, xx_] :=
Блок[{n, Chr, res},
п = 2;
Chr = ChristoffelSymbol[g, xx];
разрешение = Таблица[
D[Chr[[\[Rho], \[Nu], \[Sigma]]], xx[[\[Mu]]]] -
D[Chr[[\[Rho], \[Mu], \[Sigma]]], xx[[\[Nu]]]] +
Сумма[Chr[[\[Rho], \[Mu], \[Lambda]]]*
Chr[[\[Lambda], \[Nu], \[Sigma]]], {\[Lambda], 1, n}] -
Сумма[Chr[[\[Rho], \[Nu], \[Lambda]]]*
Chr[[\[Lambda], \[Mu], \[Sigma]]], {\[Lambda], 1, n}],
{\[Rho], 1, n}, {\[Sigma], 1, n}, {\[Mu], 1, n}, {\[Nu], 1, n}];
Упростить[res]](*\[Rho],\[Sigma],\[Mu],\[Nu]*) 9{2} - 1)/12 $
необходимы.
Между последними не возникает никаких дополнительных зависимостей из перечисленных выше свойств. Когда $ n = 2 $
тензор Римана имеет одну существенную координату, $ R _ {1212} $;
он является частью определения внутренней, или римановой, кривизны поверхности: $ K = R _ {1212} / \mathop{\rm det} g _ {ij} $(
см. кривизну Гаусса).
Тензор Римана был определен Б. Риманом в 1861 г. (опубликовано в 1876 г.).
Каталожные номера
Между последними не возникает никаких дополнительных зависимостей из перечисленных выше свойств.| [1] | ПК. [П.К. Рашевский] Рашевский, "Риманская геометрия и тензорный анализ", Дойч. Verlag Wissenschaft. (1959) (Перевод с русского) |
| [2] | Л. П. Эйзенхарт, "Риманова геометрия", Princeton Univ. Press (1949) |
| [3] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen", Springer (1968) |
Комментарии
Литература
| [a1] | С. Кобаяши, К. Номидзу, "Основы дифференциальной геометрии", 1–2 , Interscience (1969) | Нью-Джерси Хикс, «Заметки по дифференциальной геометрии», v. Nostrand (1965) |
| [a3] | J.A. Схоутен, Д.Дж. Struik, "Einführung in die neueren Methoden der Differentialgeometrie", 2 , Noordhoff (1924) |
| [a4] | М. Спивак, «Всестороннее введение в дифференциальную геометрию», 1979 , Publish or Perish, стр. 1–5 |
| [a5] | В. Клингенберг, «Риманова геометрия», де Грюйтер (1982) (перевод с немецкого) |
| [a6] | Л. П. Эйзенхарт, «Введение в дифференциальную геометрию с использованием тензорного исчисления», Princeton Univ. Пресс (1947) |
| [а7] | Дж.А. Schouten, "Исчисление Риччи. |