Решение нелинейных уравнений маткад: Решение нелинейных уравнений в Matlab

MathCAd => Решение систем нелинейных уравнений (I часть)

MathCAd => Решение систем нелинейных уравнений (I часть)

Решение систем нелинейных уравнений
I часть

Цель работы:

– изучить форматы некоторых встроенных функций
– освоить приемы решения систем нелинейных уравнений
– приобрести навыки решения простейших инженерных задач

Задание №1: Ответить на следующие контрольные вопросы:

–     как отыскать корни нелинейных уравнений в системе MathCAD;
–     как решить систему нелинейных уравнений в MathCAD’e;
–     что должен делать пользователь, если MathCAD не может найти корни;
–     как графически проверить наличие действительных корней системы двух уравнений;
–     как задать точность поиска корней;
–     как найти корни при аналитических преобразованиях;
–     перечислите способы решения системы линейных уравнений в системе MathCAD;
–     как решить обыкновенное дифференциальное уравнение в системе MathCAD;
–     как решить систему двух дифференциальных уравнений.

Краткие ответы оформить в виде отчета.

Задание №2: Решить два нелинейных уравнения с точностью до 0.0001:

a∙x³+ b∙x² + c∙x +d = 0 и f₁(x) + f₂(x) = f₃(x)

Вместо компонентов a, b, c, d, f₁(x), f₂(x) и f₃(x) записать значения из табл., приведенной ниже. Корни отделить графически.

№ Варианта	Коэффициенты полинома				Тригонометрическое уравнение:
	a	b	c	d	f1(x)	f2(x)	f3(x)

Задание №3: Решить систему двух нелинейных уравнений с точностью до 0. 0001:

Вместо компонентов f

1(x), f₂(x), f₃(x), f₄(x), f₅(x) и f₆(x) записать значения из табл., приведенной ниже. Корни отделить графически.

№ Варианта	Компоненты 1-го уравнения			Компоненты 2-го уравнения
	f1(x)	f2(x)	f3(x)	f4(x)	f5(x)	f6(x)

Задание №4: Решить дифференциальные уравнения первого и второго порядка с точностью до 0. 0001:

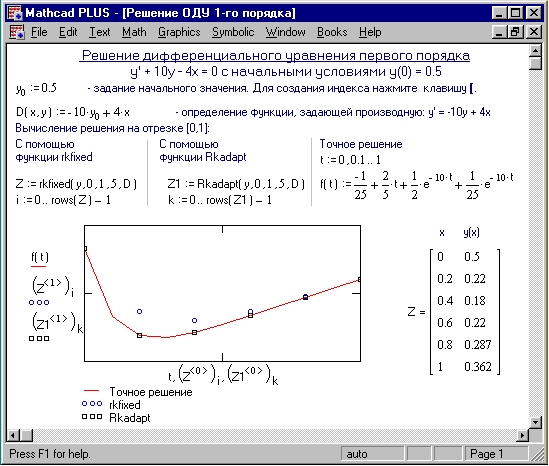
с помощью функций Odesolve() и rkfixed(). Вместо компонентов f(t,y(t)), a,b,c, f(x) записать значения из табл., приведенной ниже. Результаты, полученные разными функциями сравнить. Отсутствующие начальные условия выбрать самостоятельно.

таблица!

Задание №5: Решить систему двух дифференциальных уравнений первого порядка с точностью до 0.0001:

Вместо компонентов μ₀, ν₀, λ₀, μ₁, ν₁, λ₁, x₀

, x₁ записать значения из табл., приведенной ниже.

таблица!

Пример Выполнения Работы (Чать I и II)

Скачать работу (Чать I и II)…(16,2 КБ)

MathCAD — это просто! Часть 5. Системы нелинейных уравнений

Добрый день, уважаемые читатели и читательницы, мы с вами продолжаем грызть гранит науки. Делаем мы это с целью — напомню, если кто вдруг успел позабыть — овладеть замечательным математическим пакетом под названием MathCAD. И в прошлый раз мы с вами закончили на решении систем линейных алгебраических уравнений, для простоты также обозначаемых как СЛАУ. Что ж, линейные уравнения — это, конечно же, спору нет, замечательно. Однако на них, к величайшему сожалению многих поколений школьников и студентов, математические задачи далеко не заканчиваются, а даже, я бы сказал, напротив. То есть СЛАУ — это только частный случай систем уравнений, которые могут в обыкновенной вычислительной практике оказаться совсем даже и не линейными, а, напротив, нелинейными (да, именно так их и называют математики). Системы нелинейных уравнений без использования MathCAD или какого-либо другого математического пакета решать обычно не просто трудно, а очень трудно, но в MathCAD подход к ним не слишком отличается от подхода к СЛАУ — в этом вы сейчас получите возможность убедиться лично.

Аналитическое решение

В общем-то, основные аспекты аналитического решения систем уравнений мы с вами уже, по большому счету, обсудили.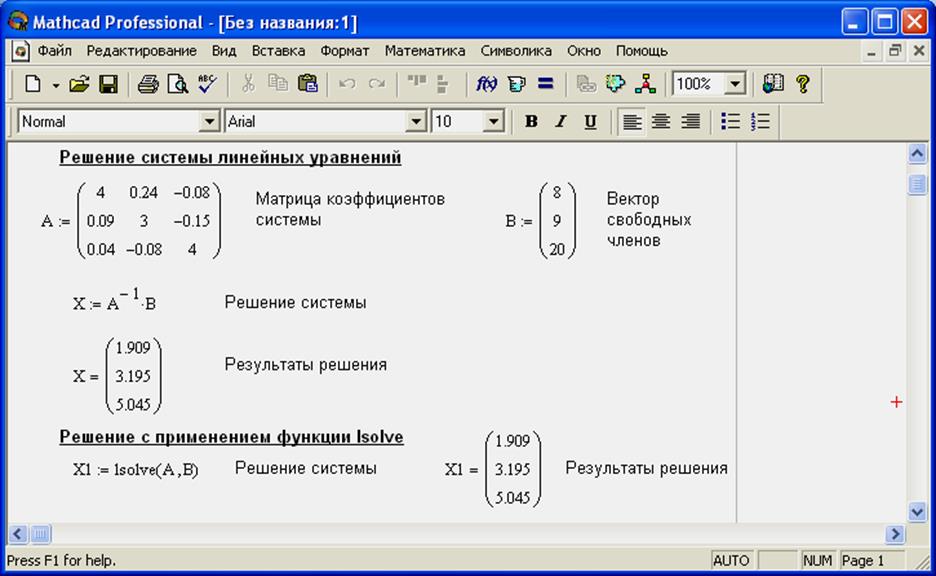 Когда это мы так лихо успели? А вот именно тогда, когда обсуждали аналитическое решение систем линейных уравнений с помощью оператора solve. Оказывается, все те же методы вполне применимы для решения систем нелинейных уравнений. Тем не менее, чтобы вы лучше их усвоили, повторю еще раз кратко алгоритм их решения с помощью MathCAD’а и приведу небольшой пример решения подобной системы. Давайте попробуем решить следующую систему уравнений: ex + y + z(xyz)1/2 = 0

(x + y+ z)1/2 = c
x +y + cz = 0

Система выглядит несложной, но для того, чтобы решить ее без использования MathCAD’а, даже очень хорошему математику потребуется не такое уж малое количество времени. Естественно, MathCAD с этой системой справится в два счета. Для ее решения создайте матрицу размером 3 на 1 (3 строки, 1 столбец), в которую и поместите уравнения нашей системы. Напомню, что для того, чтобы MathCAD распознавал уравнения как уравнения, знак «равно» нужно нажимать, удерживая клавишу Ctrl. После того, как система будет введена в виде матрицы, найдите на панели Symbolic оператор solve — мы им уже неоднократно пользовались для решения и простых уравнений, и СЛАУ, так что вы, по идее, уже должны были запомнить, где именно он находится. После оператора через запятые укажите переменные, которые входят в нашу систему уравнений — это пусть будут для начала x, y и z. Поскольку при вводе solve с панели Symbolic MathCAD сам добавляет нужную стрелочку для аналитического решения нашей с вами системы уравнений, то больше ничего, в общем-то, делать не нужно — дальше MathCAD будет решать систему. Сколько это времени у него займет, зависит, конечно же, от мощности вашего компьютера, ну и от самой системы. Нашу систему он решит быстро, а вот если поизвращаться и написать какую-нибудь систему тригонометрических и логарифмических уравнений, да еще и с комплексными переменными (о них мы потом еще поговорим отдельно), то решать такое MathCAD может на слабых компьютерах и не один час.Для чистоты эксперимента поменяем переменные: пусть теперь произвольной константой в нашей системе будет не c, а z. В этом случае нас ожидает совершенно другое, куда как более громоздкое, решение этой самой системы.

Как видите, аналитическое решение систем нелинейных уравнений с помощью MathCAD’а — вещь несложная, только, к сожалению, возможная далеко не всегда. Как обычно, на помощь символьному процессору MathCAD, который опускает в бессилии руки перед сложными системами, спешат численные методы. Вот здесь уже начинаются различия с системами линейных уравнений.

Численное решение нелинейных систем

В целом алгоритм решения систем нелинейных уравнений в MathCAD для пользователя мало чем отличается от него же для СЛАУ. Мы точно так же задаем начальные приближения, пишем «Given», записываем под этим словом наши уравнения и запрягаем функцию Find, которая должна вывести эти самые уравнения на чистую воду. Все точно так же, как тогда, когда мы решали СЛАУ.

Почему же я так пугал вас буквально двумя абзацами выше, говоря о том, что решать системы нелинейных уравнений намного сложнее, чем СЛАУ? Дело в том, что в случае нелинейных уравнений намного сложнее подобрать такие начальные значения, чтобы численное решение сходилось к реальным значениям корней уравнений. Честно говоря, со СЛАУ тоже не всегда все так просто, как я в прошлый раз сказал, однако в крайнем случае можно заставить MathCAD решить СЛАУ аналитически, а затем просто подставить конкретное численное значение какого-нибудь коэффициента. С нелинейными системами такой прием, что называется, «не покатит». Именно поэтому для получения максимального точного решения многих из таких систем придется озадачиться такими вещами, как задание начальных значений для наших переменных.

Первый способ, который я вам предложу, сразу предупреждаю, для людей неленивых. Заключается он в банальном подборе значений переменных собственными руками. То есть для начала берем начальные значения «с потолка» и решаем систему с помощью Find’а. Подставляем значения, выданные этой функцией, в исходные уравнения и смотрим, насколько они похожи на истинные решения.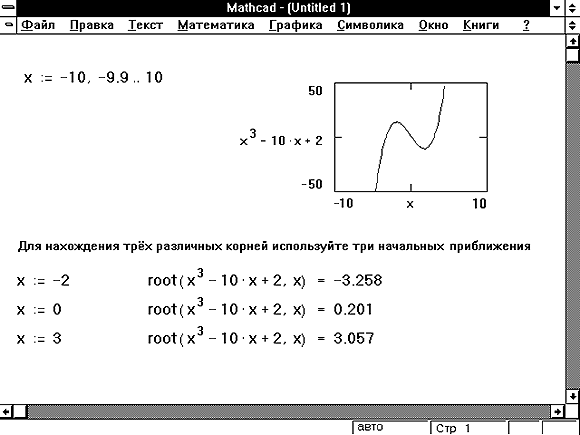 Если уравнения обращаются при подстановке в верные равенства, то все хорошо: либо система была простой, либо в вас дремлет талант подбирателя корней уравнений. Но если равенством после подстановки и близко не пахнет, то придется попотеть. Нужно начать изменять значения начальных приближений для каждой переменной и смотреть, как это отразится на близости выражений, получившихся после подстановки решений в уравнения, к равенствам. Таким нехитрым методом можно за не столь долгое время, как может сначала показаться, добиться хорошего приближения начальных значений к реальным решениям. И, несмотря на явный садомазохистский характер данного метода, он имеет то неоспоримое преимущество, что действует железно на любые системы и любые переменные — было бы терпение.

Второй метод, который я хочу предложить, этим достоинством не обладает, но зато и не требует от пользователя столь деятельного участия в решении. Думаю, вы сами сможете сформулировать главный его недостаток, если я скажу, что с этим методом мы уже сталкивались, и заключается он в построении графиков для уравнений, входящих в систему. Да, главный недостаток — это сложность в применении к системам уравнений, содержащим более трех переменных. Сложно, сами понимаете, изобразить на мониторе компьютера 25-мерное пространство для отображения решений системы с 25-ю переменными. Но для тех систем, которые содержат две или три переменные, построить график мы вполне сможем. Однако для этого сначала нужно научиться строить графики уравнений.

Построение графиков параметрических кривых

Наиболее простым способом построения графика уравнения в MathCAD’е является параметризация входящих в него переменных друг через друга или через какую-то третью переменную. Что это означает? Поясню на примере. Например, у нас есть уравнение окружности x2 + y2 = 5. Если вы попытаетесь записать функцию f(x, y) = x2 + y2 — 5, а потом построить ее график от x или от y, то вас ожидает разочарование. То, что в итоге выдаст на экран MathCAD, будет так же мало похоже на окружность, как сам MathCAD — на пасьянс «Косынка». Придется придумывать что-то другое. Например, можно подобрать такие функции переменной t, которые, будучи возведенными в квадрат, в сумме тоже дадут пять. Естественно, такими функциями будут тригонометрические — синус и косинус от переменной t, помноженные на корень из пяти. Если мы выразим таким образом x и y через t, то мы параметризуем наше уравнение и уже сможем успешно построить график x(t) от y(t) или же y(t) от x(t) — впрочем, в данном случае в силу симметричности это будет уже не столь важно.

<скриншот: MathCAD_5_4.png>

Для того, чтобы решить систему уравнений, нужно просто подобным образом параметризовать и второе уравнение. Вполне возможно, что, как и в нашем примере, оно вполне подойдет для того, чтобы банально выразить x через y или наоборот, после чего построение графика окажется особенно простым (см. соответствующий скриншот). Для нахождения начальных приближений достаточно воспользоваться уже знакомой нам с вами трассировкой — само собой, решением будет точка пересечения двух кривых на уравнении. Для того, чтобы получить более точное значение решения, чем предлагает нам трассировка, нужно, конечно же, подставить полученные с ее помощью координаты точки пересечения графиков в численное решение системы перед Given’ом. Последний скриншот иллюстрирует, что графики мы с вами построили правильно, и с его помощью действительно намного легче искать решение системы двух исходных уравнений. А легче хотя бы уже просто потому, что видно, какого количества корней мы вправе ожидать от нашей системы.

Но работа с трехмерными графиками в MathCAD’е не так проста, как с двумерными, поскольку и сама по себе поверхность — более сложный объект, чем кривая. С поверхностями можно ожидать немалого количества не самого приятного рода сюрпризов, так что лучше о них поговорить более подробно. Этим мы с вами и займемся в следующей статье из цикла о MathCAD’е.

SF, [email protected]

Компьютерная газета. Статья была опубликована в номере 17 за 2008 год в рубрике soft

Решение системы уравнений в Mathcad

Первоначально рассмотрим СЛАУ в Mathcad. Для их решения может использоваться блок given …find() или специальная функция lsolve(). Применение блока given …find() предопределяет необходимость задания начальных значений искомых переменных. Далее после ключевого слова given описывается СЛАУ и с помощью find() находится решение. Следует указать, что в том случае, когда СЛАУ в Mathcad имеет бесконечное множество решений блок given …find() дает конкретный результат, что несомненно следует отнести к недостаткам. В случае отсутствия решения будет выдано сообщение “Matrix is singular. Cannot compute its inversу – Матрица сингулярная. Нельзя вычислить эту инверсию”.

Применение функции lsolve( ) позволяет избежать этого недостатка. Функция lsolve(M,b) имеет два аргумента. M – матрица коэффициентов при неизвестных, b – вектор свободных членов. На листинге приведен пример решения СЛАУ.

Пример решения СЛАУ:

Для решения системы нелинейных уравнений используются два блока: given…find() и given…minerr (). Так как система нелинейных уравнений может иметь несколько решений, то полученные результаты зависят от начальных значений искомых переменных. В обоих случаях получаются приближенные решения, для которых рекомендуется делать проверку. Обычно в Mathcad требуется, чтобы количество уравнений было равно количеству искомых переменных, но в некоторых случаях, когда с точки зрения классической математики может быть получено точное решение и при меньшем количестве уравнений, данное условие может быть нарушено. На листинге представлены примеры использования блоков given…find() и given…minerr () для решения систем нелинейных уравнений.

Метод хорд в маткаде

БлогNot. Методы решения нелинейных уравнений в MathCAD

Методы решения нелинейных уравнений в MathCAD

Реализуем для некоторого уравнения 4 наиболее популярных численных метода для решения нелинейных уравнений.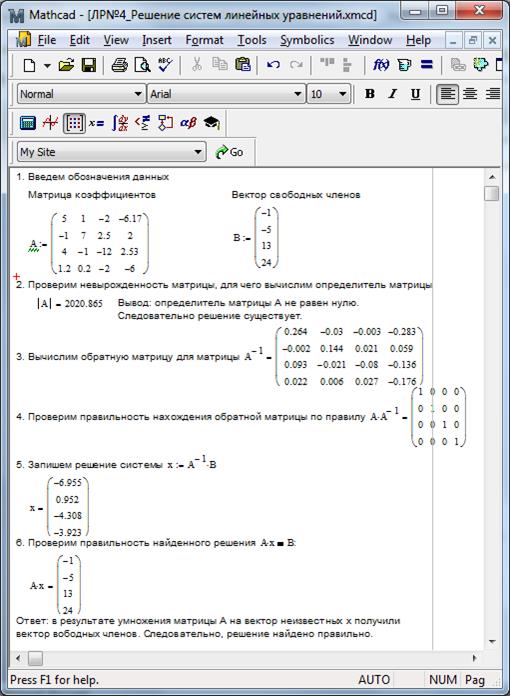 При этом мы стремимся именно запрограммировать методы, а не воспользоваться встроенным инструментом Given. Find или функциями root , polyroot . Об этих способах решения почитайте, например, здесь.

Определим функцию уравнения f(x)=0 как функцию пользователя, интервал поиска решения зададим переменными a и b . Найти этот интервал можно, например, табличным или графическим методом:

Начальный интервал [a,b] должен быть таким, чтобы значения f(a) и f(b) имели противоположные знаки. Если искомый корень уравнения окажется единственным на интервале, то совсем хорошо 🙂

Логика метода дихотомии (возможно, более правильные названия – метод бисекции, метод половинного деления) довольно проста: если на концах выбранного интервала [a,b] знаки функции совпадают (произведение f(a)*f(b)>0 ), то вернуть результат «недопустимый интервал» (вернём в этом случае ответ «бесконечность»), в противном случае до тех пор, пока длина интервала не станет меньше заданной погрешности ε , будем находить середину текущего интервала c=(a+b)/2 , считать в ней значение функции и проверять, какую из половин отрезка [a,c] или [c,b] нужно отбросить для выполнения следующего шага – а именно, ту, в которой знак f(c) совпадает со знаком функции на левой или правой границе интервала (в листинге – проверка f(a)*f(c)>0 ). Для большей точности вернём середину «последнего» интервала [a,b] , меньшего ε :

В методе простой итерации исходное уравнение f(x)=0 представляется в эквивалентном виде φ(x)=x (что, вообще говоря, можно сделать бесконечным числом способов), а затем шаг метода выполняется по формуле x_k+1 = φ(x_k) , пока не будет достигнута заданная точность |x_k+1-x_k| . Если выбрать φ(x)=x-c*f(x) , то константу c целесообразнее всего искать методом релаксации, для которого c=2/(M+m) , где M – максимальное из значений первой производной на концах отрезка или в находящихся на нём точках перегиба функции (точках, где f”(x)=0 ), а m – минимальное из таких значений. Вот соответствующий расчёт в MathCAD:

Если заданной сходимости нет в течение 10000 шагов, в подпрограмме предусмотрен аварийный выход.

Численный метод Ньютона решения нелинейного уравнения основан на формуле вида x_k+1 = x_k-f(x_k)/f'(x_k) , обеспечивающей наилучшую сходимость, но требующей дополнительного вычисления производной на каждом шаге. Так как производные для MathCAD – не проблема, можно всё сделать «в лоб»:

Видно, что сходимость метода – на 2 порядка выше (погрешность найденного решения

Наконец, существует метод хорд, в котором кривая f(x) заменяется прямой линией (хордой), стягивающей точки (a, f(a)) и (b, f(b)) . Формула этого метода зависит от знака выражения f(a)*f”(a) , то есть, имеет два варианта:
Если f(a)*f”(a)>0 , то x_{=b , xk+1=a-(f(a)(xk-a))/(f(xk)-f(a))
Если f(a)*f”(a) , то x=a , xk+1=xk-(f(xk)*(b-xk))/(f(b)-f(xk))}

Вот примерная реализация на MathCAD, как и в предыдущих двух случаях, контролируется максимальное число итераций, равное 10000:

Видно, что сходимость метода оказалась в нашем случае не столь высока.

Подсчитать, сколько шагов какому методу потребовалось, можете сами, немного поменяв выдачу подпрограмм.

Скачать этот пример в формате .xmcd (107 Кб)

05.09.2013, 15:07; рейтинг: 72153

В этом методе нелинейная функция f(x) на отделенном промежутке

[a,b] заменяется хордой, проходящей через точки (a,f(a))и (b,f(b))

Рис.2.4. Метод хорд. Неподвижен правый конец промежутка b

Уравнение хорды: . Найдем точку пересечения хорды с горизонтальной осью. Полагая и , получим

.

Точку x₁ принимаем за новую границу отрезка, где содержится корень. Через эту точку с координатами (x₁,f(x₁)) и соответствующую границу предыдущего интервала (b,f(b)) опять проводим хорду, находим и т.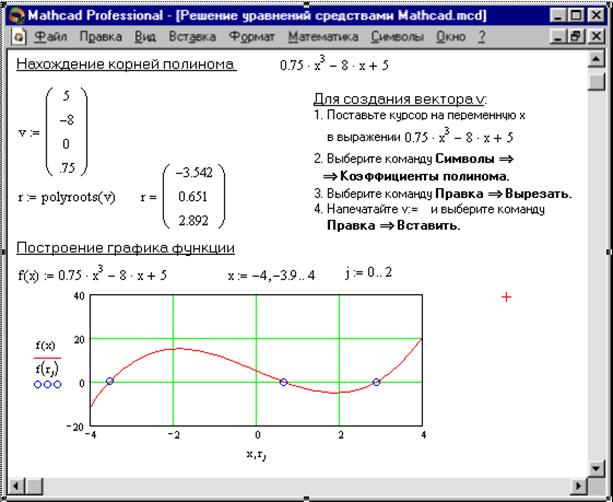 д., получая последовательность x₁,x₂,x₃,…x_n,…, сходящуюся к корню уравнения.

Вторая производная сохраняет постоянный знак на . Следовательно, возможны два случая. Если f(b)·f «(b)>0, то хорда имеет правый фиксированный конец, причем последовательность x_,x1,…xn приближается к корню слева. За начальное приближение x_{, естественно, берут a}

; ; ;

.

Рис.2.5. Метод хорд. Неподвижен левый конец промежутка a

Если f(a)·f «(a)>0, то хорда имеет левый фиксированный конец, причем последовательность x_,x1,…xn … приближается к корню справа. За начальное приближение x, берут b

; ; ;

.

Для оценки точности можно воспользоваться формулой

,

где -точный корень, – приближенный корень, , на промежутке [a,b]. Считаем до тех пор пока, не выполнится условие . Если имеет место неравенство , то счет можно прекратить, когда.

Пример 2.4. Найти методом хорд корень уравнения x 4 -x-1=0

Решение находим, используя пакет Mathcad.

Функция монотонна на промежутках (-∞, 0.63), (0.63, ∞) и меняет на концах промежутков знак. Уравнение имеет два корня. Сузим промежутки отделения корней методом проб, т.е. подстановкой.

Первый корень принадлежит промежутку (-1,-0.5)

Второй корень принадлежит промежутку (1,1.5)

Будем находить корень на промежутке (-1,-0.5)

Вторая производная всюду положительна, функция положительна в точке a = -1, значит, этот конец неподвижен.

-максимальное, a -минимальное значение модуля производной на промежутке

так как , множитель

нужно учитывать при оценке точности решения,

Нашли корень исходного уравнения с точностью .

Рис. 2.6. Вычисления в Mathcad, реализующие метод хорд для примера 2.4

2.2.3. Метод Ньютона – метод касательных

Пусть – корень уравнения отделен на отрезке , причем и непрерывны и сохраняют определенные знаки на этом же отрезке . Найдя какое-нибудь n-е значение корня ( ), уточним его по методу Ньютона. Для этого положим , где – считаем малой величиной. Разложим функцию f(x) в ряд Тейлора в окрестности точки x _n по степеням h _n . Тогда можно записать:

Ограничимся двумя членами ряда и так как , то:

.

Учитывая найденную поправку h_n:,получим (n=0,1,2,…).

Рис.2.7 Метод касательных. Начальное приближение x_=b

По-другому этот метод называется методом касательных. Если в точке провести касательную к функции f(x) , то ее пересечение с осью ОХ и будет новым приближением x₁ корня уравнения

Хорошим начальным приближением является то значение, для которого выполнено неравенство . Погрешность вычислений Счет можно прекратить, когда

Теорема 2.2: Если , причем и отличны от нуля и сохраняют определенные знаки при , то, исходя из начального приближения , удовлетворяющего условию , можно вычислить методом Ньютона единственный корень уравнения с любой степенью точности.

Пример 2.5. Найти методом Ньютона корень уравнения x 4 -x-1=0,

1-я производная

2-я производная положительна

один корень лежит на промежутке (-1.-0.5), второй на промежутке (1.1.5) Уточним левый корень методом Ньютона

Нашли корень исходного уравнения -0.7245 с точность 0.00007.

Рис. 2.8. Вычисления в Mathcad, реализующие метод касательных для примера 2.5

Численные методы решения нелинейных уравнений. Метод хорд.

Метод хорд ( метод также известен как Метод секущих ) один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения . Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность .

В отличие от метода половинного деления, метод хорд предлагает, что деление рассматриваемого интервала будет выполняться не в его середине, а в точке пересечения хорды с осью абсцисс (ось – Х). Следует отметить, что под хордой понимается отрезок, который проведен через точки рассматриваемой функции по концам рассматриваемого интервала. Рассматриваемый метод обеспечивает более быстрое нахождение корня, чем метод половинного деления, при условии задания одинакового рассматриваемого интервала.

Геометрически метод хорд эквивалентен замене кривой хордой, проходящей через точки и (см. рис.1.).

Рис.1. Построение отрезка (хорды) к функции .

Уравнение прямой (хорды), которая проходит через точки А и В имеет следующий вид:

Данное уравнение является типовым уравнением для описания прямой вы декартовой системе координат. Наклон кривой задается по ординате и абсциссе с помощью значений в знаменателе и , соответственно.

Для точки пресечения прямой с осью абсцисс записанное выше уравнение перепишется в следующем виде:

В качестве нового интервала для прохождения итерационного процесса выбираем один из двух или , на концах которого функция принимает значения разных знаков. Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:

или .

Итерационный процесс уточнения корня заканчивается, когда условие близости двух последовательных приближений станет меньше заданной точности, т.е.

.

Рис. 2. Пояснение к определению погрешности расчета.

Следует отметить, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.

Алгоритм нахождения корня нелинейного уравнения по методу хорд

1. Найти начальный интервал неопределенности одним из методов отделения корней. З адать погрешность расчета (малое положительное число ) и начальный шаг итерации ( ) .

2. Найти точку пересечения хорды с осью абсцисс:

3. Необходимо найти значение функции в точках , и . Далее необходимо проверить два условия:

– если выполняется условие , то искомый корень находится внутри левого отрезка положить , ;

– если выполняется условие , то искомый корень находится внутри правого отрезка принять , .

В результате находится новый интервал неопределенности, на котором находится искомых корень уравнения:

4. Проверяем приближенное значение корня уравнения на предмет заданной точности, в случае:

– если разность двух последовательных приближений станет меньше заданной точности , то итерационный процесс заканчивается. Приближенное значение корня определяется по формуле:

– если разность двух последовательных приближений не достигает необходимой точности , то необходимо продолжить итерационный процесс и перейти к п.2 рассматриваемого алгоритма.

В качестве примера, рассмотрим решение нелинейного уравнения методом хорд. Корень необходимо найти в рассматриваемом диапазоне с точностью .

Вариант решения нелинейного уравнения в программном комплексе MathCAD .

Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага итерации представлены в графической форме (см. рис.1).

Рис.1. Результаты расчета по методу хорд

Для обеспечения заданной точности при поиске уравнения в диапазоне необходимо выполнить 6 итераций. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением: .

Примечание:

Модификацией данного метода является метод ложного положения ( False Position Method ), который отличается от метода секущих только тем, что всякий раз берутся не последние 2 точки, а те точки, которые находятся вокруг корня.

Следует отметить, что в случае если от нелинейной функции можно взять вторую производную алгоритм поиска может быть упрощен. Предположим, что вторая производная сохраняет постоянный знак, и рассмотрим два случая:

Случай №1: 0,

Из первого условия получается, что неподвижной стороной отрезка является – сторона a .

Случай №2: 0″ w />

Из второго условия получается, что неподвижной стороной отрезка является – сторона b .

В общем виде, для выявления неподвижного конца можно записать следующее условие: 0″ w /> , где или .

Рис. 3. Примеры убывающей или возрастающей функции

Таким образом, в зависимости от вида функции получаются два выражения для упрощения поиска корня функции:

– если функция соответствует первому случаю (см. рис. 3), тогда формула будет иметь следующий вид:

, где k =0,1,2,…

– если функция соответствует второму случаю (см. рис. 3), тогда формула будет иметь следующий вид:

, где k =0,1,2,…

Случай сводится к рассматриваемому , если уравнение записать в форме: .

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

Моделирование в электроэнергетике — Численные методы решения нелинейных уравнений. Метод Ньютона для решения уравнений с одной переменной

Численные методы решения нелинейных уравнений. Метод Ньютона для решения уравнений с одной переменной

Метод Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643-1727), под именем которого и обрёл свою известность.

Метод был описан Исааком Ньютоном в рукописи De analysi per aequationes numero terminorum infinitas(лат.Об анализе уравнениями бесконечных рядов), адресованной в 1669 году Барроу, и в работе De metodisfluxionum et serierum infinitarum (лат.Метод флюксий и бесконечные ряды) или Geometria analytica(лат.Аналитическая геометрия) в собраниях трудов Ньютона, которая была написана в 1671 году. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения x_n, а последовательность полиномов и в результате получал приближённое решение x.

Впервые метод был опубликован в трактате Алгебра Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работеAnalysis aequationum universalis (лат. Общий анализ уравнений). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений x_n вместо более трудной для понимания последовательности полиномов, использованной Ньютоном.

Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.

В соответствии с данным методом задача поиска корня функции сводится к задаче поиска точки пересечения с осью абсцисс касательной, построенной к графику функции .

Рис. 1. График изменение функции

Проведенная в любой точке касательная линия к графику функции определяется производной данной функции в рассматриваемой точке, которая в свою очередь определяется тангенсом угла α (). Точка пересечения касательной с осью абсцисс определяется исходя из следующего соотношения в прямоугольном треугольнике: тангенс угла  в прямоугольном треугольнике определяется отношением противолежащего катета к прилежащему катету треугольнику. Таким образом, на каждом шаге строится касательная к графику функции в точке очередного приближения .Точка пересечения касательной с осью Ox будет являться следующей точкой приближения  .  В соответствии с рассматриваемым методом расчет приближенного значения корня на i-итерации производится по формуле: 

Наклон прямой подстраивается на каждом шаге наилучшим образом, однако следует обратить внимание на то, что алгоритм не учитывает кривизну графика и следовательно в процессе расчета остается неизвестно в какую сторону может отклониться график.

Условием окончания итерационного процесса является выполнение следующего условия:

,

где  ˗ допустимая погрешность определения корня.

Метод обладает квадратичной сходимостью. Квадратичная скорость сходимость означает, что число верных знаков в приближённом значении удваивается с каждой итерацией.

Математическое обоснование

Пусть дана вещественная функция , которая  определена и непрерывна на рассматриваемом участке. Необходимо найти вещественный корень  рассматриваемой функции.

Вывод уравнения основано на методе простых итераций, в соответствии с которым уравнение  приводят к эквивалентному уравнению  при любой функции . Введем понятие сжимающего отображения, которое определяется соотношением .

Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие . Данное требование означает, что корень функции  должен соответствовать экстремуму функции .

Производная сжимающего отображения определяется в следующем виде:

Выразим из данного выражение переменную при условии принятого ранее утверждения о том, что при  необходимо обеспечить условие . В результате получим выражение для определения переменной :

С учетом этого сжимающая функция прием следующий вид:

Таким образом, алгоритм нахождения численного решения уравнения  сводится к итерационной процедуре вычисления:

Алгоритм нахождения корня нелинейного уравнения по методу Ньютона для уравнения с одной переменной

1. Задать начальную точку приближенного значения корня функции , а также погрешность расчета (малое положительное число  ) и начальный шаг итерации ().

2. Выполнить расчет приближенного значения корня функции в соответствии с формулой:

3. Проверяем приближенное значение корня на предмет заданной точности, в случае: 

— если разность двух последовательных приближений станет меньше заданной точности , то итерационный процесс заканчивается.

— если разность двух последовательных приближений не достигает необходимой точности , то необходимо продолжить итерационный процесс  и перейти к п.2 рассматриваемого алгоритма.

Пример решения уравнений

по методу Ньютона для уравнения с одной переменной

В качестве примера, рассмотрим решение нелинейного уравнения   методом Ньютона для уравнения с одной переменной. Корень необходимо найти с точностью   в качестве первого приближения .

Вариант решения нелинейного уравнения в программном комплексе MathCADпредставлен на рисунке 3.

Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага итерации представлены в графической форме (см. рис.2).

Рис.2.  Результаты расчета по методу Ньютона для уравнения с одной переменной

Для обеспечения заданной точности  при поиске приближенного значения корня уравнения в диапазоне  необходимо выполнить 4 итерации. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением: .

Рис.3. Листинг программы в MathCad

Модификации метода Ньютона для уравнения с одной переменной

Существует несколько модификаций метода Ньютона, которые направлены на упрощение вычислительного процесса.

Упрощенный метод Ньютона

В соответствии с методом Ньютона требуется вычислять производную функции f(x) на каждом шаге итерации, что ведет к увеличению вычислительных затрат. Для уменьшения затрат, связанных с вычислением производной на каждом шаге расчета, можно произвести замену производной f’(x_n) в точке x_n в формуле на производную f’(x₀) в точке x₀. В соответствии с данным методом расчета приближенное значение корня определяется по следующей формуле:

Таким образом, на каждом шаге расчета строятся прямые, которые параллельны касательной к кривой y=f(x) в точке B₀ (см. рис.4). Преимуществом данного метода является то, что производная функции вычисляется один раз.

 
Рис.4. Модифицированный метод Ньютона

Разностный метод Ньютона

В соответствии с методом Ньютона требуется вычислять производную функции f(x) на каждом шаге итерации, что не всегда удобно, а иногда практически невозможно. Данный способ позволяет производную функции  заменить разностным отношением (приближенным значением):

В результате приближенное значение корня функции f(x) будет определяться выражением разностного метода Ньютона:

 

Двух шаговый метод Ньютона

В соответствии с методом Ньютона требуется вычислять производную функции f(x) на каждом шаге итерации, что не всегда удобно, а иногда практически невозможно. Данный способ позволяет производную функции  заменить разностным отношением (приближенным значением):

В результате приближенное значение корня функции f(x) будет определяться следующим выражением:

где

 

Рис.5. Двух шаговый метод Ньютона

Метод секущих является двух шаговым, то есть новое приближение определяется двумя предыдущими итерациями  и . В методе необходимо задавать два начальных приближения  и . Скорость сходимости метода будет линейной.

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

Курсы и материалы по системе Mathcad

 

Курсы и материалы по системе Mathcad

Представляем вам курсы и книги для самостоятельного обучения системе Mathcad

Mathcad – широко распространенное приложение, на основе которого изучают технические науки студенты во многих университетах мира.
Все курсы переведены на русский язык компанией PTS и соответствуют актуальным версиям.
Руководитель направления Mathcad в PTS – к.ф.-м.н. Дмитрий Кирьянов, имеющий 15-летний опыт работы с Mathcad, автор нескольких десятков курсов и книг, опубликованных в России и США.
Некоторые из ресурсов доступны онлайн и помогут вам, если вы планируете самостоятельное обучение работе в Mathcad.

Видеокурс Д.Кирьянова по работе в Mathcad на YouTube

Мультимедийный учебник по Mathcad  Кириянова Д.В. доступен также в хорошем качестве на  http://polybook.ru/mathcad/

Уроки по применению Mathcad для решения математических задач в свободном доступе есть на Интуит.ру (требуется регистрация)

Урок 1. Основные сведения о Mathcad: 
Введение. Знакомство с интерфейсом. Специфика приложения Mathcad. Документ Mathcad – простейшие расчеты. Числовой ввод, вывод, выделение формул. Панели инструментов. Редактирование формул. Вычисления. Численные и символьные расчеты. Об аналитических вычислениях. Функции. Производные. Автоматические и ручные вычисления. Интегралы. Графики.

Урок 2. Дифференцирование и интегрирование:
Дифференцирование. Оператор первой производной. Аналитическое дифференцирование. Об определении производной. О погрешности численного дифференцирования. Частные производные. Численное дифференцирование в Mathcad. Производные высших порядков. Интегрирование. Определенный интеграл. Неопределенный интеграл. Кратные интегралы .

Урок 3. Системы нелинейных уравнений:
О постановке задач. Одно нелинейное уравнение. Аналитическое решение. Графическая интерпретация. Численное решение (градиентный алгоритм). Зависимость решения от начального приближения. Алгоритм секущих. Сканирование. Система уравнений. Аналитическое решение. Численное решение. Алгоритмы продолжения по параметру. О постановке задач. Реализация алгоритма в Mathcad. Поиск разных ветвей решения .

Урок 4. Оптимизация:
Локальная минимизация. Зависимость решения от начального приближения. Аналитические вычисления. Многомерная минимизация. Приближенное решение нелинейных уравнений .

Урок 5. Системы линейных алгебраических уравнений:
«Хорошие» СЛАУ. О постановке задач СЛАУ в матричном виде. Встроенные методы Mathcad «Плохие» СЛАУ. Пример СЛАУ с неточной правой частью. Переопределенные СЛАУ. Псевдорешение. Минимизация невязки СЛАУ. Недоопределенные СЛАУ. Нормальное псевдорешение. Плохо обусловленные СЛАУ .

Урок 6. Обыкновенные дифференциальные уравнения:
Одно уравнение. О постановке задач. Решение в Mathcad. Зависимость от начальных условий. Решение при больших аргументах. Системы ОДУ. Пример. Графики решения. График в фазовом пространстве ОДУ высших порядков. Пример: колебания маятника. Фазовый портрет. Автоколебания .

Урок 7. Краевые задачи:
Краевые задачи для ОДУ. О постановке задач. Решение средствами Mathcad. Объяснение алгоритма стрельбы. Обсуждение О разностных схемах. Задачи на собственные значения. Постановка задачи: волновое уравнение. Решение методом стрельбы .

Урок 8. Дифференциальные уравнения в частных производных:
О постановке задач – уравнение теплопроводности. Решение средствами Mathcad. Пример: волновое уравнение. Метод сеток. Неявные схемы. О методе прогонки. Устойчивость. О многомерных задачах: уравнение Пуассона .

Урок 9. Анализ данных:
Ввод данных из файлов. Интерполяция и регрессия. Интерполяция. Линейная регрессия (МНК). Устранение тренда. Полиномиальная регрессия. «Простая» статистика. Среднее и дисперсия. Гистограммы. Корреляция. Методы Монте-Карло. Спектральный анализ БПФ. Обратное. Примеры. Маскировка частот. Спектр смеси сигнал+шум. Влияние конечности выборки.

Книги по Mathcad

 Книга по Computational science c «живыми» примерами на Mathcad (по-русски, бесплатно, PDF)

Поиск решения системы уравнений в Mathcad

Во-первых, давайте рассмотрим набор линейных алгебраических уравнений в Mathcad. Чтобы найти решение уравнений, можно использовать модуль с… find () или специальную функцию lsolve () . Применение модуля given… find () предопределяет необходимость присвоения начальных значений искомым переменным. Позже, после ввода ключевого слова, создается набор линейных алгебраических уравнений, и find () помогает найти решение.Следует отметить, что в случае, если система линейных алгебраических уравнений в Mathcad имеет бесконечный набор решений, случай задан… find () дает конкретный результат, что, безусловно, является недостатком. В случае отсутствия решения выдается сообщение «Матрица — сингулярная. Невозможно вычислить обратное значение ”.

Функция lsolve () может помочь избежать упомянутого выше недостатка. Функция lsolve (M, b) имеет два аргумента. M — матрица коэффициентов, определяющих неизвестные переменные, b — вектор абсолютных членов.В листинге программы показан пример решения такой системы линейных алгебраических уравнений.

Пример:

Чтобы найти решение системы нелинейных уравнений, используются два модуля: задано… find () и задано… minerr () . Поскольку система нелинейных уравнений может иметь несколько решений, полученные результаты зависят от начальных значений искомых переменных. В обоих случаях мы получаем приблизительные решения, которые требуют проверки решения. Обычно в Mathcad требуется, чтобы количество уравнений было равно количеству искомых переменных, но в некоторых случаях, когда с точки зрения классической математики правильное решение может быть найдено с меньшим количеством уравнений, это условие можно пренебречь.В листинге программы показаны примеры блоков , заданных… find () и , заданных… minerr () , используемых для поиска решения наборов нелинейных уравнений.

Уравнения с использованием блока решения Mathcad для оценки неизвестных переменных …

Контекст 1

… при заданном значении реактивного сопротивления возбуждения X c. Чтобы инициировать и поддерживать нарастание напряжения в обмотках генератора, внешний источник должен согласовывать магнитную и индуктивную реактивную мощность генератора с требованиями нагрузки.Это означает, что чистый вольт-ампер в эквивалентной схеме генератора, показанной на вставке к рис. 3, и подключенной нагрузке должны быть равны нулю в любой момент, иначе напряжение упадет. Общая проводимость узла на намагничивающем элементе составляет …

Контекст 2

… принимать в качестве решения для переменных. Принцип узловой проводимости используется для разделения проводимости машины на действительную и мнимую составляющие, где уравнение (1) представляет реальные составляющие, а уравнение (2) представляет мнимые составляющие.Два уравнения решаются одновременно для требуемой переменной, как показано на рис. …

Контекст 3

… Эквивалентная схема системы, показанная на рис. 3, связывает две переменные. Первая переменная — это «а», отношение, связывающее рабочую частоту и базовую частоту. Это зависит от скорости вращения и оказывает доминирующее влияние на рабочее скольжение и, следовательно, количество мощности, передаваемой нагрузке. Решение уравнения (1) приведет к оценке на единицу…

Контекст 4

… Определите узловые допуски Y LC1, Y m и Y 2; iv Укажите начальные предполагаемые значения для переменных a = 1.01, b = 1.1 и X m = 3; v Решите с «заданными» узловые уравнения, которые приравниваются к нулю, и «найдите» переменные a, b и X m, которые удовлетворяют условиям. Рис. 3 иллюстрирует вышеупомянутые процедуры ввода данных в лист MathCAD с использованием блоков решения «Дано» и «Найти». Теперь индукционный генератор открыт для исследования переменных.Например, требуемая емкость возбуждения для поддержания постоянного напряжения может быть оценена для каждого значения нагрузки. Также влияние …

Context 5

… прогнозировать набор данных при изменении нагрузки, необходимо несколько циклов программирования, чтобы повторить алгоритм, представленный на рис. 3, чтобы охватить требуемый рабочий диапазон . Используя вырезание и вставку уравнений, перечисленных для решений переменных, и применение новых наборов ограничений и значений нагрузки, генерируются новые наборы значений.Процедуры могут быть повторены, в которых нагрузка увеличивается с новыми ограничениями из предыдущего шага. Диапазон данных …

Эффективное использование решателя »MathCadHelp.com» Номер 1 в MathCad Assignments

В этом разделе представлены некоторые идеи о том, как эффективно использовать способность Mathcad решать системы одновременных уравнений.

Многократное решение уравнения

Приведенные до сих пор методы, хотя они и эффективны для решения конкретной системы уравнений, ограничены двумя вещами:

• Каждый раз, когда вы используете находку, вы должны иметь оставшуюся часть блока решения, чтобы идти вместе с ним.

• Если вы хотите изменить некоторые параметры или константы в вашей системе уравнений, чтобы увидеть, как они влияют на решение, вы должны полностью вернуться к блоку решения, чтобы изменить их.

Оба эти недостатка преодолеваются благодаря способности Mathcad определять функцию в терминах блока решения.

Если вы определяете функцию с помощью Find где-нибудь справа, эта функция будет решать систему уравнений каждый раз, когда вы ее используете. Это преодолевает первую проблему.

Если эта функция имеет в качестве аргументов те же параметры, которые вы хотите изменить в блоке решения, вы можете просто изменить параметры, изменив числа, которые вы помещаете в список аргументов функции. Это решает вторую проблему.

На рис. 15-14 показан конкретный пример. Коэффициент трения трубы f зависит от диаметра трубы D, ее шероховатости E и числа Рейнольдса R. Вполне возможно, что вы захотите поэкспериментировать с трубами разного размера (D), сделанными из разных типов бетона (E). .

Уравнение на рисунке 15-14 показывает взаимосвязь между этими параметрами. Уравнение слишком сложно, чтобы определить функцию от R, D и E, просто решая для f в терминах R, D и E. Однако вы можете определить функцию в терминах блока решения.

Каждый раз, когда вы просите Mathcad оценить функцию FricFac (E, D, R), Mathcad берет предоставленные вами E, D и R, заменяет соответствующие переменные в блоке решения, решает для f и возвращает значение.

Решение одной и той же задачи для разных переменных

Иногда вы сталкиваетесь с проблемой, в которой хотите изменить роли известных и неизвестных в уравнении.Например, рассмотрим уравнение, которое связывает процентную ставку, сумму ссуды, срок ссуды и платежи. Если вам известны три из этих четырех величин, вы можете найти недостающее.

Таблица на рис. 15-17 показывает, что для 12% -ной ссуды по 30-летней ипотеке и платежа в размере 1000 долларов в месяц наибольшая возможная ссуда составляет 97 218,33 долларов.

Погашение кредита в ипотеку.

С несколькими простыми изменениями тот же рабочий лист можно использовать для расчета процентной ставки.Предположим теперь, что известно, что сумма ссуды составляет 120 000 долларов. Насколько снизятся процентные ставки, прежде чем выплаты упадут до 1000 долларов в месяц? Рисунок 15-18 показывает ответ.

Если вы сравните рисунки 15-17 и 15-18, вы увидите, что они очень похожи. Основное отличие заключается в аргументе функции Find. Чтобы изменить фиксированное и переменное значение в уравнении, просто измените аргументы функции «Найти».

Расчет процентной ставки по ипотеке.

Примерные решения

Mathcad предоставляет функцию, очень похожую на Find, которая называется Minerr. Эта функция использует тот же алгоритм, что и Find. Разница в том, что если решающая программа не может внести никаких дальнейших улучшений в решение, Minerr все равно возвращает значение. Функция Find, с другой стороны, вернет сообщение об ошибке, указывающее, что она не может найти решение. Вы используете Minerr точно так же, как и Find.

Minerr обычно возвращает ответ, который сводит к минимуму ошибки в ограничениях.Однако Minerr не может проверить, что его ответы представляют собой абсолютный минимум ошибок в ограничениях. Если вы используете Minerrin как блок решения, вы всегда должны включать дополнительные проверки обоснованности результатов. Встроенная переменная ERR дает размер вектора ошибок для приближенного решения. Нет встроенной переменной для определения размера ошибки для отдельных решений неизвестных.

Minerr особенно полезен для решения некоторых нелинейных задач наименьших квадратов.На рисунке 15-19 показан пример, в котором Minerr используется для получения неизвестных параметров в распределении Вейбулла. Функция genfit также полезна для решения нелинейных задач наименьших квадратов. См. «Статистические функции» для получения дополнительной информации о genfit.

Использование функции minerr для нелинейной аппроксимации методом наименьших квадратов.

Использование символьного решателя

Обычно вы можете быстро и точно найти числовые корни с помощью корневой функции Mathcad. Но есть некоторые обстоятельства, в которых вы можете захотеть использовать символьный решатель Mathcad для поиска точных или приблизительных корней:

• Если уравнение, которое вы решаете, имеет параметр, символическое решение может позволить вам выразить ответ непосредственно через параметр.Затем вместо того, чтобы заново решать уравнение для каждого нового значения параметра, вы можете просто подставить его значение в свое символическое решение.

• Если вам нужны все комплексные корни многочлена степени 4 или меньше, символьный решатель выдаст их вам в виде одного вектора, точно или численно. Символьный решатель также найдет полные решения для некоторых многочленов более высокой степени.

См. Раздел «Символьное решение уравнений» в Главе 17 для получения дополнительной информации о символьном решении уравнений

Численные методы для нелинейных уравнений в Mathcad для общего машиностроения, специальность

Предпосылки для изучения Ньютона-Рафсона Метод [PDF] [DOC]

Цели метода Ньютона-Рафсона [PDF] [DOC]

Как работает метод Ньютона-Рафсона? [PDF] [DOC]

Вывод метода Ньютона-Рафсона. [YOUTUBE 8:24]

Пример метода Ньютона-Рафсона [YOUTUBE 10:06]

Преимущества и недостатки метода Ньютона-Рафсона Метод: Часть 1 из 2 [YOUTUBE 7:09]

Преимущества и недостатки метода Ньютона-Рафсона Метод: часть 2 из 2 [YOUTUBE 4:43]

Вывод из серии Тейлора Ньютона-Рафсона Метод [YOUTUBE 7:56]

Суперкомпьютеры не имеют разделительного блока — A Подход с использованием метода Ньютона-Рафсона [YOUTUBE 10:14]

Суперкомпьютеры не имеют разделительной единицы — Пример [YOUTUBE 5:23]

Нахождение квадратного корня числа — A Подход с использованием метода Ньютона-Рафсона [YOUTUBE 6:34]

Нахождение квадратного корня числа — пример [YOUTUBE 7:03]

Презентация в Power Point по методу Ньютона-Рафсона [PDF] [PPT]

Рабочий лист метода Ньютона-Рафсона [PDF] [MCD]

Таблица сходимости метода Ньютона-Рафсона [PDF] [MCD]

Ловушка: деление на ноль в рабочем листе метода Ньютона-Рафсона [PDF] [MCD]

Ловушка: медленная конвергенция при перегибе Точки в рабочем листе метода Ньютона-Рафсона [PDF] [MCD]

Ловушка: корень перепрыгивает через несколько корней в рабочем листе метода Ньютона-Рафсона [PDF] [MCD]

Ловушка: корни колеблются вокруг локальных максимумов и минимумов в Ньютон-Рафсоне Рабочий лист метода [PDF] [MCD]

Контрольная работа Ваше знание метода Ньютона-Рафсона [HTML] [ВСПЫШКА] [PDF] [DOC]

% PDF-1.5 % 1 0 obj> эндобдж 2 0 obj> эндобдж 3 0 obj> эндобдж 4 0 obj> поток конечный поток эндобдж xref 0 5 0000000000 65535 ф 0000000016 00000 н. 0000000075 00000 н. 0000000120 00000 н. 0000000210 00000 н. трейлер ] >> startxref 3379 %% EOF 1 0 obj> / OCG [37 0 R] >>>> эндобдж 2 0 obj> эндобдж 3 0 obj> эндобдж 5 0 obj null эндобдж 6 0 obj> / XObject> / ProcSet [/ PDF / Text] / ExtGState >>> / StructParents 3 >> эндобдж 7 0 obj> эндобдж 8 0 obj> эндобдж 9 0 obj> / ProcSet [/ PDF / Text] >> / Subtype / Form / FormType 1 / Matrix [1.0 0,0 0,0 1,0 0,0 0,0] / PieceInfo >>> / LastModified (D: 20071029172212-07’00 ‘) >> поток HA 0D1 = BL час» п, (xz {sx 9SN ޭ

Основы Mathcad Prime 5.0 | Корневые решения

Описание

Этот курс знакомит с основами Mathcad Prime, включая его уникальный интерфейс доски и математические панели инструментов. Он усиливает обширную функциональность Mathcad с помощью понятных, простых инструкций и примеров под руководством инструктора.Этот курс познакомит пользователя со многими критически важными функциями Mathcad, чтобы обеспечить немедленное применение продукта. Курс также можно разделить на два дня: первый для базовых техник, а второй — для продвинутых.

Доступны все версии Mathcad Prime

Узнайте, как записывать инженерные расчеты в стандартизированном формате.

Темы

Откройте и сохраните файлы Mathcad.

Навигация в рабочем пространстве Mathcad

Определение и форматирование математических и текстовых областей.

Разрабатывайте и редактируйте математические выражения.

Определите, оцените и используйте переменные.

Задним числом присвоить выражение

Определение и оценка пользовательских и встроенных функций.

Определите, оцените и используйте переменные диапазона.

Используйте единицы в расчетах.

Постройте двухмерные и трехмерные графики.

Найдите корни функции с одной независимой переменной.

Решите численно и символически систему линейных и нелинейных уравнений.

Решать задачи оптимизации без ограничений и с ограничениями.

Решайте обыкновенные уравнения и уравнения в частных производных.

Создайте программу на рабочем листе Mathcad, используя функции программирования Mathcad.

Импорт и экспорт данных.

Сглаживание, интерполяция и регрессия данных.

Даты курсов

Основы физики и технологий ускорителей

PTC Mathcad (PTC 2018) — мощный программный вычислительный инструмент. Он позволяет пользователю создавать, решать и анализировать различные математические задачи. Здесь мы представляем некоторые из основных возможностей Mathcad , а затем применяем их для расчета некоторых реальных параметров ускорителя.2} {13} = 11,841 \]

2. Давайте создадим две переменные и решим одно и то же уравнение. Скопируйте только что созданное уравнение в другое место на листе. Вы можете сделать это, щелкнув в любом месте поля уравнения, нажимая клавишу пробела, пока все уравнение не окажется внутри синих линий редактирования, а затем использовать функции копирования и вставки. Замените «7» на переменную, скажем «a», а «13» на другую, например «\ (\ beta \)» в уравнении, набрав их. Один из способов вставить бета-версию греческого символа — выбрать «Панели инструментов» в меню «Вид», удерживать кнопку мыши и отпустить ее, когда курсор находится на греческом языке, а затем выбрать нужный символ.2} {\ beta} = 11.841 \] Попробуйте ввести разные значения для a и \ (\ beta \).

   3. Mathcad выполняет итерационные вычисления с использованием переменных диапазона . Каждый раз, когда Mathcad встречает Range Varíable , он вычисляет уравнение для каждого значения этой специальной переменной.

      Скопируйте существующее уравнение и переменную «\ (\ beta \)» и вставьте их в другую область. Теперь превратите «a» в переменную диапазона, набрав a: 7,14; 70 .