Re число: расчет, формула, физический смысл, калькулятор

Число Рейнольдса • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Характер потока жидкости или газа — ламинарный или турбулентный — определяется безразмерным числом, зависящим от скорости потока, вязкости и плотности жидкости и характерной длины элемента потока.

Осборн Рейнольдс был, в некотором смысле, последним приверженцем старых добрых традиций классической механики Ньютона. В конце жизни он даже разработал тщательно продуманную механическую модель светоносного эфира (см. Опыт Майкельсона—Морли), согласно которой эфир представлял собой систему мельчайших шарообразных частиц, свободно перекатывающихся друг относительно друга подобно дробинкам в мешке. До конца своих дней он считал, что «прогрессу механики нет конца… и то, что современники полагают ее пределом и тупиком… со временем окажется лишь новым поворотом на пути ее развития».

Чтобы понять всю важность главного открытия его жизни, нужно сначала немного рассказать о так называемых безразмерных величинах. Предположим, нам нужно измерить геометрические размеры комнаты. Допустим, мы взяли рулетку и определили, что длина комнаты равна 5 метрам. Однако, если мы возьмем рулетку, проградуированную в футах, окажется, что длина комнаты равна 15 с небольшим футов. То есть полученные нами при измерении цифры будут зависеть от используемых единиц, в то время как реальная длина комнаты остается постоянной.

Есть, однако, и такие характеристики геометрии комнаты, которые никак не зависят от единиц измерения. В частности, такой величиной является отношение длины комнаты к ее ширине — так называемое характеристическое соотношение. Если комната имеет длину 20 футов и ширину 10 футов, ее характеристическое соотношение равно 2. Измерив длину и ширину комнаты в метрах, мы получим, что размеры комнаты равны 6,096 м × 3,048 м, однако характеристическое соотношение останется прежним: 6,096 м : 3,048 м = 2. В данном случае 2 — безразмерная характеристика комнаты.

Теперь давайте обратимся к потоку жидкости.

Различные жидкости при течении в трубах, растекании по поверхности или обтекании препятствий обладают различными свойствами. Густая, клейкая жидкость (например, мед) обладает, как говорят физики, большей вязкостью, нежели легкая и подвижная жидкость (например, бензин). Степень вязкости жидкости определяется так называемым коэффициентом вязкости, который принято обозначать греческой буквой η («эта»). У густых, клейких жидкостей коэффициент вязкости η в десятки и сотни раз выше, чем у легких и текучих.

Рейнольдсу удалось обнаружить безразмерное число, описывающее характер потока вязкой жидкости. Сам ученый получил его экспериментально, проведя изнурительную серию опытов с различными жидкостями, однако вскоре было показано, что его можно вывести и теоретически из законов механики Ньютона и уравнений классической гидродинамики. Это число, которое теперь называют числом Рейнольдса и обозначают 

Re, характеризует поток и равно:

    Re = vLρ/η

где ρ — плотность жидкости, v — скорость потока, а L — характерная длина элемента потока (в этой формуле важно помнить, что Re — это одно число, а не произведение R × e).

Теперь давайте посмотрим на размерность составляющих числа Рейнольдса:

• размерность коэффициента вязкости η — ньютоны умножить на секунды разделить на кв. метры, или н·с/м². Если вспомнить, что, по определению, н = кг·м/c², мы получим кг/м·с
• размерность плотности ρ — килограммы разделить на кубические метры, или кг/м³
• размерность скорости v
   — метры разделить на секунды, или м/с
• размерность длины элемента потока L — метры, или м

Отсюда получаем, что размерность числа Рейнольдса равна:

    (м/с) × (м) × (кг/м³) : (кг/м·с)

или, после упрощения,

    (кг/м·с) : (кг/м·с)

Итак, все единицы измерения в размерности числа Рейнольдса сокращаются, и оно действительно оказывается безразмерной величиной.

Рейнольдсу удалось выяснить, что при значении этого числа 2000–3000 поток становится полностью турбулентным, а при значении Re меньше нескольких сотен — поток полностью ламинарный (то есть не содержит завихрений). Между двумя этими значениями поток носит промежуточный характер.

Можно, конечно, считать число Рейнольдса чисто экспериментальным результатом, однако его можно интерпретировать и с позиции законов Ньютона. Жидкость в потоке обладает импульсом, или, как иногда говорят теоретики, «инерционной силой». По сути, это означает, что движущаяся жидкость стремится продолжить свое движение с прежней скоростью. В вязкой жидкости этому препятствуют силы внутреннего трения между слоями жидкости, стремящиеся затормозить поток. Число Рейнольдса как раз и отражает соотношение между двумя этими силами — инерции и вязкости. Высокие значения числа Рейнольдса описывают ситуацию, когда силы вязкости относительно малы и не способны сгладить турбулентные завихрения потока.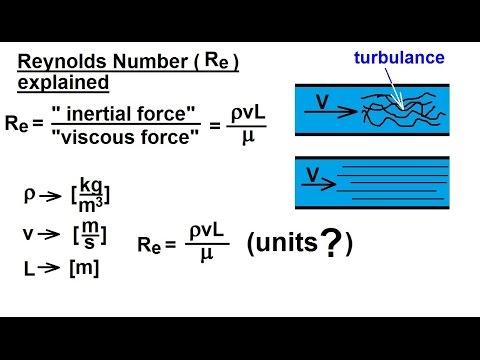 Малые значения числа Рейнольдса соответствуют ситуации, когда силы вязкости гасят турбулентность, делая поток ламинарным.

Число Рейнольдса очень полезно с точки зрения моделирования потоков в различных жидкостях и газах, поскольку их поведение зависит не от реальной вязкости, плотности, скорости и линейных размеров элемента потока, а лишь от их соотношения, выражаемого числом Рейнольдса. Благодаря этому можно, например, поместить в аэродинамическую трубу уменьшенную модель самолета и подобрать скорость потока таким образом, чтобы число Рейнольдса соответствовало реальной ситуации полномасштабного самолета в полете. (Сегодня, с развитием мощной компьютерной техники, нужда в аэродинамических трубах отпала, поскольку воздушные потоки можно смоделировать на компьютере. В частности, первым гражданским авиалайнером, полностью спроектированным исключительно с использованием компьютерного моделирования, стал «Боинг-747». В этой связи любопытно отметить, что при проектировании гоночных яхт и высотных зданий до сих пор практикуется их «обкатка» в аэродинамических трубах.

)

Mathway | Популярные задачи

1	Найти число нейтронов	H
2	Найти массу одного моля	H_2O
3	Баланс	H_2(SO_4)+K(OH)→K_2(SO_4)+H(OH)
4	Найти массу одного моля	H
5	Найти число нейтронов	Fe
6	Найти число нейтронов	Tc
7	Найти конфигурацию электронов	H
8	Найти число нейтронов	Ca
9	Баланс	CH_4+O_2→H_2O+CO_2
10	Найти число нейтронов	C
11	Найти число протонов	H
12	Найти число нейтронов	O
13	Найти массу одного моля	CO_2
14	Баланс	C_8H_18+O_2→CO_2+H_2O
15	Найти атомную массу	H
16	Определить, растворима ли смесь в воде	H_2O
17	Найти конфигурацию электронов	Na
18	Найти массу одного атома	H
19	Найти число нейтронов	Nb
20	Найти число нейтронов	Au
21	Найти число нейтронов	Mn
22	Найти число нейтронов	Ru
23	Найти конфигурацию электронов	O
24	Найти массовую долю	H_2O
25	Определить, растворима ли смесь в воде	NaCl
26	Найти эмпирическую/простейшую формулу	H_2O
27	Найти степень окисления	H_2O
28	Найти конфигурацию электронов	K
29	Найти конфигурацию электронов	Mg
30	Найти конфигурацию электронов	Ca
31	Найти число нейтронов	Rh
32	Найти число нейтронов	Na
33	Найти число нейтронов	Pt
34	Найти число нейтронов	Be	Be
35	Найти число нейтронов	Cr
36	Найти массу одного моля	H_2SO_4
37	Найти массу одного моля	HCl
38	Найти массу одного моля	Fe
39	Найти массу одного моля	C
40	Найти число нейтронов	Cu
41	Найти число нейтронов	S
42	Найти степень окисления	H
43	Баланс	CH_4+O_2→CO_2+H_2O
44	Найти атомную массу	O
45	Найти атомное число	H
46	Найти число нейтронов	Mo
47	Найти число нейтронов	Os
48	Найти массу одного моля	NaOH
49	Найти массу одного моля	O
50	Найти конфигурацию электронов	Fe
51	Найти конфигурацию электронов	C
52	Найти массовую долю	NaCl
53	Найти массу одного моля	K
54	Найти массу одного атома	Na
55	Найти число нейтронов	N
56	Найти число нейтронов	Li
57	Найти число нейтронов	V
58	Найти число протонов	N
59	Упростить	H^2O
60	Упростить	h*2o
61	Определить, растворима ли смесь в воде	H
62	Найти плотность при стандартной температуре и давлении	H_2O
63	Найти степень окисления	NaCl
64	Найти атомную массу	He	He
65	Найти атомную массу	Mg
66	Найти число электронов	H
67	Найти число электронов	O
68	Найти число электронов	S
69	Найти число нейтронов	Pd
70	Найти число нейтронов	Hg
71	Найти число нейтронов	B
72	Найти массу одного атома	Li
73	Найти эмпирическую формулу	H=12% , C=54% , N=20	, ,
74	Найти число протонов	Be	Be
75	Найти массу одного моля	Na
76	Найти конфигурацию электронов	Co
77	Найти конфигурацию электронов	S
78	Баланс	C_2H_6+O_2→CO_2+H_2O
79	Баланс	H_2+O_2→H_2O
80	Найти конфигурацию электронов	P
81	Найти конфигурацию электронов	Pb
82	Найти конфигурацию электронов	Al
83	Найти конфигурацию электронов	Ar
84	Найти массу одного моля	O_2
85	Найти массу одного моля	H_2
86	Найти число нейтронов	K
87	Найти число нейтронов	P
88	Найти число нейтронов	Mg
89	Найти число нейтронов	W
90	Найти массу одного атома	C
91	Упростить	na+cl
92	Определить, растворима ли смесь в воде	H_2SO_4
93	Найти плотность при стандартной температуре и давлении	NaCl
94	Найти степень окисления	C_6H_12O_6
95	Найти степень окисления	Na
96	Определить, растворима ли смесь в воде	C_6H_12O_6
97	Найти атомную массу	Cl
98	Найти атомную массу	Fe
99	Найти эмпирическую/простейшую формулу	CO_2
100	Найти число нейтронов	Mt

Число Рейнольдса

Число Рейнольдса — безразмерная скорость — может быть определена как отношение

• сила инерции (ρ u L) к сила вязкости или трения (μ)

и интерпретируется как отношение

• Динамическое давление (ρ u ² ) до Сдвигающегося напряжения (μ U / L)

Рейнольдс, следовательно, можно выразить как

Re = ρ U L / μ RE = ρ U L / μ re = ρ U L / μ re = ρ U L / μ RE = ρ U L / μ

0030

= ρ U ² / (μ U / L)

= U L / ν (1)

, где

RE = Номер REYNOLDS (неразмерный ρ = плотность (кг/м ³ , фунт _м /фут ³ )

u = скорость, основанная на фактической площади поперечного сечения воздуховода или трубы (м/с, фут/ у)

μ = dynamic viscosity (Ns/m ² , lb _m /s ft)

L = characteristic length (m, ft)

ν = μ / ρ = кинематическая вязкость (м ² /с, фут ² /с)

Число Рейнольдса для потока в трубе или воздуховоде

Для трубы или воздуховода характеристической длиной является гидравлический диаметр.

L = d _h

где

d _h = гидравлический диаметр (м, фут)

Число Рейнольдса для потока в воздуховоде или трубе может быть выражено как μ

= U D _H / ν (2)

, где

D _H = гидравлический диаметр (M, FT)

reynold nments nmole ntrys ntryls nments nments nments nments nments ntryls ntryls ntryls ntriots ntrylds ntrylds ntrinols ntrylds ntrinols ntrylds ntrylds ntrylds ntrylds ntrylds №

Число Рейнольдса для трубы или протока, выраженного в имперских единицах

RE = 7745,8 U D _H / ν (2A)

, где

RE = Reynolds № 3

RE = Reynolds (немерное мнение) 3

RE = Reynolds (немерное мнение) 9

re = reynolds (нерезовый u = скорость (фут/с)

d _h = гидравлический диаметр (дюймы)

ν = кинематическая вязкость (сСт) (1 сСт = 10 ^-6 м ²

Число Рейнольдса можно использовать для определения того, является ли поток ламинарным, переходным или турбулентным.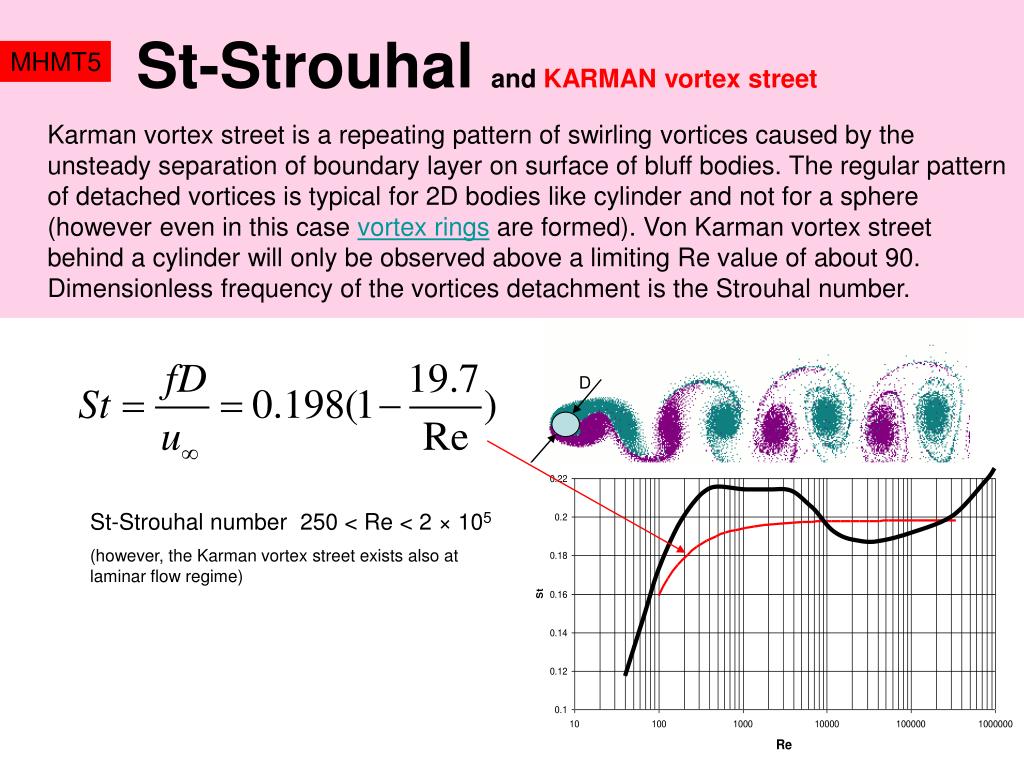 Поток составляет

• Ламинар — Когда RE <2300
• Transient — Когда 2300
• Turbulent — Когда

11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111 актуален только для вязких жидкостей, таких как сырая нефть, мазут и другие масла.

Пример — расчет числа Рейнольдса

Ньютоновская жидкость с динамической или абсолютной вязкостью 0,38 Нс/м ² и удельным весом 0,91 течет по трубе диаметром 25 мм со скоростью 2,6 м/с .

Плотность может быть рассчитана по удельному весу жидкости и удельному весу эталонной воды

    = 910 кг/м ³

Затем число Рейнольдса можно рассчитать с помощью уравнения (1) аналогично

Re = (910 кг/м 3 ^{) 25 мм) (10 -3 м/мм) / (0,38 Нс/м 2 )}

    = 156 ((кг м/с ² )/Н) 5 6

900 мин расход

1 (N) = 1 (кг м/с ² )

Связанные мобильные приложения из Engineering ToolBox

• Число Рейнольдса — Приложение-калькулятор

— бесплатные приложения для автономного использования на мобильных устройствах.

Онлайн-калькулятор Рейнольдса

Плотность и абсолютная (динамическая) вязкость известны

Этот калькулятор можно использовать, если известны плотность и абсолютная (динамическая) вязкость жидкости. Калькулятор действителен для несжимаемого потока — потока с жидкостями или газами без сжатия — что характерно для потоков воздуха в системах ОВКВ и т.п. Калькулятор является универсальным и может использоваться для метрических и имперских единиц, если использование единиц согласовано.

Плотность — ρ — (кг/м ³ , фунт _м /фут ³ )

Скорость — u — (м/с, фут/с) 90 0 -82 _ч — (или с характеристическая длина — L) (м, фут)

Абсолютная (динамическая) вязкость — мк — (Нс/м ² , фунт _м /с фут)

0 Значения по умолчанию для воздуха при 60 ^o F , 2 атм давление и плотность 0,146 фунта _м /фут ³ , текучий 20 фут/с между двумя металлическими листами характеристической длины 0,5 фута . Динамическая (абсолютная) вязкость равна 1,22 10 ^-5 фунтов _м /с фут .

• Сделать ярлык для этого калькулятора на главном экране?

Кинематическая вязкость известна

Приведенный ниже калькулятор можно использовать, когда известна кинематическая вязкость жидкости. Калькулятор является универсальным и может использоваться для метрических и имперских единиц, если использование единиц согласовано.

Скорость — u — (м/с, фут/с)

Гидравлический диаметр — d _h — (или c характеристическая длина — L) (м, фут) 30 вязкость — ν — (м ² /с, фут ² /с)) (1 сСт = 10 ^-6 м ² /с)

C с кинематической вязкостью 1,004 10 ^-6 м ² /с в стальной трубе сортамента 40. Характерная длина (или гидравлический диаметр) трубы 0,102 м .

• скачать Диаграмма числа Рейнольдса для расхода воды в стальной трубе Shedule 40 в формате pdf

Что такое число Рейнольдса? | SimWiki

Безразмерное число Рейнольдса играет заметную роль в предсказании моделей поведения жидкости. Число Рейнольдса, называемое Re, используется для определения того, является ли течение жидкости ламинарным или турбулентным. Это один из основных управляющих параметров во всех вязких течениях, где численная модель выбирается в соответствии с предварительно рассчитанным числом Рейнольдса.

Хотя число Рейнольдса включает в себя как статические, так и кинетические свойства жидкостей, оно определяется как свойство потока, поскольку исследуются динамические условия. С технической точки зрения число Рейнольдса — это отношение сил инерции к силам вязкости. Это соотношение помогает отделить ламинарные течения от турбулентных.

Силы инерции сопротивляются изменению скорости объекта и являются причиной движения жидкости. Эти силы являются доминирующими в турбулентных течениях. В противном случае, если силы вязкости, определяемые как сопротивление течению, преобладают – течение ламинарное. Число Рейнольдса может быть указано следующим образом:

$$ Re=\frac{сила~инерции}{сила~вязкости}=\frac{свойства~жидкости~и~течения}{свойства~жидкости} \tag{1}$$

Например, стакан вода, стоящая на статической поверхности, независимо от каких-либо сил, кроме силы тяжести, находится в состоянии покоя, и ее свойства текучести игнорируются. 2\). Он провел экспериментальные исследования, чтобы изучить взаимосвязь между скоростью и поведением потока жидкости. С этой целью Рейнольдс установил экспериментальную установку (рис. 2а) с использованием окрашенной воды, которая выпускалась в середине площади поперечного сечения в основную чистую воду, чтобы визуализировать движение потока жидкости через стеклянную трубку (рис. 2b). .

Рис. 2: а) Экспериментальная установка, созданная Осборном Рейнольдсом; б) Экспериментальная визуализация ламинарного и турбулентного течения

Исследование Осборна Рейнольдса под названием «Экспериментальное исследование обстоятельств, определяющих, должно ли движение воды в параллельных каналах быть прямым или извилистым» относительно безразмерного числа было опубликовано в «Philosophical Transactions of Королевское общество». Согласно статье, безразмерное число, открытое Рейнольдсом, подходило для предсказания течения жидкости в широком диапазоне от течения воды в трубе до течения воздуха над аэродинамическим профилем\(^2\). 4\)

Число Рейнольдса также предсказывает поведение вязкости потока в случае ньютоновских жидкостей. Поэтому очень важно воспринимать физический случай, чтобы избежать неточных прогнозов. Переходные режимы и внутренние и внешние потоки являются основными областями для всестороннего исследования числа Рейнольдса. Ньютоновские жидкости – это жидкости с постоянной вязкостью. Если температура остается неизменной, не имеет значения, какое напряжение приложено к ньютоновской жидкости; она всегда будет иметь одинаковую вязкость. Примеры включают воду, спирт и минеральное масло.

Переход от ламинарного к турбулентному

Поток жидкости можно задать в двух различных режимах: ламинарном и турбулентном. Переход между режимами является важной проблемой, которая определяется как свойствами жидкости, так и свойствами потока. Как упоминалось ранее, критическое число Рейнольдса можно разделить на внутреннее и внешнее. Тем не менее, в то время как число Рейнольдса, относящееся к ламинарно-турбулентному переходу, может быть разумно определено для внутреннего течения, трудно дать определение для внешнего течения.

Внутренний поток

Течение жидкости в трубе как внутренний поток был проиллюстрирован Рейнольдсом на рис. 2b. Критическое число Рейнольдса для внутреннего потока: \ (4 \)

Тип потока	Рейнольдс.
Турбулентный режим	Re>4000

Таблица 1: Числа Рейнольдса для различных типов режимов внутреннего течения

Течение в открытом канале, течение жидкости в объекте и течение с трением в трубе — это внутренние течения, в которых число Рейнольдса прогнозируется на основе гидравлического диаметра \(D\) вместо характерной длины \(L\). В случае цилиндрической трубы за фактический диаметр цилиндра принимается гидравлический диаметр \(D\), т.е. число Рейнольдса следующее:

$$ Re=\frac{F_{inertia}}{F_{ вязкая}}=\frac{ρVD_H}{μ} \tag{5}$$

Форма трубы или воздуховода может варьироваться (например, квадратная, прямоугольная и т. д.). В этих случаях гидравлический диаметр определяется следующим образом:

$$ D_H=\frac{4A}{P} \tag{6}$$

, где \(A\) — площадь поперечного сечения и \( P\) — смоченный периметр.

Трение на поверхности трубы из-за шероховатости является эффективным параметром для рассмотрения, поскольку оно вызывает переход от ламинарного к турбулентному и потери энергии. «Диаграмма Муди» (рис. 4) была создана Льюисом Ферри Муди (19 лет).2\). На приведенной ниже диаграмме вы можете увидеть логарифмическую шкалу внизу, шкалу коэффициента трения слева и относительную шероховатость трубы справа.

Рисунок 4: Диаграмма Муди для трения в трубах с гладкими и шероховатыми стенками чрезвычайно полезна для прогнозирования числа Рейнольдса и, следовательно, типа потока для труб с внутренним трением.

Внешний поток

Внешний поток, при котором русло не имеет районных границ, подобен внутреннему потоку, также имеющему переходный режим. Потоки над телами, такими как плоская пластина, цилиндр и сфера, являются стандартными случаями, используемыми для исследования влияния скорости во всем потоке. В 195\). Обтекание плоской поверхности показано на рис. 5 с режимами, где \(x_c\) — критическая длина перехода, \(L\) — полная длина пластины и \(u\) — скорость свободного поток. 6\)

Низкое и высокое число Рейнольдса

Число Рейнольдса также эффективно в уравнениях Навье-Стокса для усечения математических моделей. В то время как \ (Re → ∞ \), вязкие эффекты считаются незначительными, когда вязкие члены в уравнениях Навье-Стокса опущены. Упрощенная форма уравнений Навье-Стокса, называемая уравнениями Эйлера, может быть определена следующим образом:

$$ \frac{Dρ}{Dt}=-ρ∇\times{u} \tag{8}$$

$$ \frac{Du}{Dt}=-\frac{∇p}{ρ}+g \tag{9}$$

$$ \frac{De}{Dt}=-\frac{p} {ρ}∇\times{u} \tag{10}$$

где \(ρ\) — плотность, \(u\) — скорость, \(p\) — давление, \(g\) — ускорение свободного падения, а \(e\) — удельная внутренняя энергия.\( 6\) Хотя вязкие эффекты относительно важны для жидкостей, модель невязкого потока частично обеспечивает надежную математическую модель для прогнозирования реального процесса для конкретных случаев. Например, высокоскоростное внешнее обтекание тел является широко используемым приближением, в котором разумно подходит невязкий подход.

В то время как \(Re≪1\), инерционные эффекты считаются незначительными, и связанные с ними члены в уравнениях Навье-Стокса могут быть опущены. Упрощенная форма уравнений Навье-Стокса называется потоком ползучести или потоком Стокса: 96)\ Имея ощутимые эффекты вязкости, ползучее течение является подходящим подходом, который можно использовать для исследования, например, поток лавы, плавание микроорганизмов, поток полимеров, смазка и т. д.

Применение числа Рейнольдса

Численное решение потока жидкости основано на математических моделях, которые были созданы как экспериментальными исследованиями, так и соответствующими физическими законами. Одним из важных этапов численного исследования является определение подходящей математической модели, моделирующей физическую область. Чтобы получить достаточно хорошее предсказание поведения флюидов при различных обстоятельствах, число Рейнольдса было принято в качестве важной предпосылки для анализа потока флюидов. Например, движение глицерина в круглом канале можно предсказать по числу Рейнольдса следующим образом: \(^7\) 9\ Circ C \) 1259 Динамическая вязкость \ ((PA. S) \) 0,950 Диаметр Duct \ (M) \) 0,0450505050505050505050505050505050505050505050505ern. расход на входе \((м/с)\) 0,5 }{μ} = \frac{1259\times{0,5}\times{0,05}}{0,950} ≈ 33,1 \tag{13}$$

, где поток глицерина является ламинарным в соответствии с критическим числом Рейнольдса для внутреннего потока.

Число Рейнольдса SimScale

Число Рейнольдса никогда не отображается в проектах моделирования SimScale, поскольку оно вычисляется автоматически, но влияет на многие из них. Вот несколько интересных сообщений в блогах, которые можно прочитать о числе Рейнольдса в связи с его использованием в SimScale:

• Что все должны знать о CFD
• Как ямочки на мяче для гольфа влияют на его полет и аэродинамику
• 10 Моделирование проектирования трубопроводов: анализ потока жидкости и напряжений

Ссылки

• Стоукс, Джордж. «О влиянии внутреннего трения жидкостей на движение маятников». Труды Кембриджского философского общества. 9, 1851, стр. 8–106.
• Рейнольдс, Осборн. «Экспериментальное исследование обстоятельств, определяющих, будет ли движение воды прямым или извилистым, и закона сопротивления в параллельных каналах». Философские труды Королевского общества. 174 (0), 1883, стр. 935–982.
• Зоммерфельд, Арнольд. «Ein Beitrag zur hydrodynamischen Erkläerung der turbulenten Flussigkeitsbewegüngen (Вклад в гидродинамическое объяснение турбулентных движений жидкости)». Международный конгресс математиков, 1908 г., стр. 116–124.
• Уайт, Фрэнк. Механика жидкости. 4-е издание. Высшее образование McGraw-Hill, 2002 г., ISBN: 0-07-228192-8.
• https://en.wikipedia.org/wiki/Ludwig_Prandtl
• Берд, Р.Б., Стюарт, В.Е. и Лайтфут, Э.Н. «Транспортные явления». 2-е издание. Сыновья Джона Уили, 2001, ISBN 0-471-41077-2.