Размерность матрицы: Размер матрицы. Что это такое?

Виды матриц

Матрица, состоящая из одной строки, называется матрицей (вектором) — строкой, а из одного столбца — матрицей (вектором)- столбцом:

A=(a₁₁,a₁₂,…,a_1n) — матрица — строка

B=

Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n.

Например, 

Элементы матрицы a_ij, у которых номер столбца равен номеру строки образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы a₁₁, a₂₂,…,a_nn.

Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.

Операции над матрицами

Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциями над числами, а некоторые — специфические.

1. Умножение матрицы на число. Произведение матрицы А на число  называется матрица B=A, элементы которой b_ij=a_ij для i=1,2,…m; j=1,2,…n

Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы.

В частности, произведение матрицы А на число 0 есть нулевая матрица.

2. Сложение матриц. Суммой двух матриц А и В одинакового размера m называется матрица С=А+В, элементы которой c_ij=a_ij+b_{ijдля i=1,2,…m; j=1,2,…n (т. е. матрицы складываются поэлементно).}

3. Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: A-B=A+(-1)∙B.

4. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц A_m∙B _kназывается такая матрица C_m, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:

i=1,2,…,m; j=1,2,…,n

Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из этих операций):

A+B=B+A

(A+B)+C=A+(B+C)

λ (A+B)= λA+ λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ (AB)=( λA)B=A(λB)

A(BC)=(AB)C

Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:

a)      Если АВ существует, то после перестановки сомножителей местами произведение матриц ВА может и не существовать.

b)      Если АВ и ВА существуют, то они могут быть матрицами разных размеров.

5. Транспонирование матрицы — переход от матрицы А к матрице А’, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица А’ называется транспонированной относительно матрицы А:

Из определения следует, что если матрица А имеет размер m, то транспонированная матрица А’ имеет размер n

В литературе встречаются и другие обозначения транспонированной матрицы, например, А^Т

Связанные определения:
Вырожденная матрица
Обобщенная обратная матрица
Обратная матрица
Плохо обусловленная матрица
Псевдообратная матрица
Эрмитова матрица
Эрмитово-сопряженная матрица

В начало

Содержание портала

Изменение размерности матриц, выбор значений из NumPy массивов по условию

До этого момента индексы и срезы использовать для извлечения подмножеств. В этих методах используются числовые значения.

Предположим, что нужно выбрать все значения меньше 0,5 в матрице размером 4х4, которая содержит случайные значения между 0 и 1.

>>> A = np.random.random((4, 4))
>>> A
array([[ 0.03536295, 0.0035115 , 0.54742404, 0.68960999],
       [ 0.21264709, 0.17121982, 0.81090212, 0.43408927],
       [ 0.77116263, 0.04523647, 0.84632378, 0.54450749],
       [ 0.86964585, 0.6470581 , 0.42582897, 0.22286282]])

Когда матрица из случайных значений определена, можно применить оператор условия. Результатом будет матрица из булевых значений: True, если элемент соответствовал условию и False — если нет. В этом примере можно видеть все элементы со значениями меньше 0,5.

>>> A < 0.5
array([[ True, True, False, False],
       [ True, True, False, True],
       [False, True, False, False],
       [False, False, True, True]], dtype=bool)

На самом деле, булевы массивы используются для неявного извлечения частей массивов.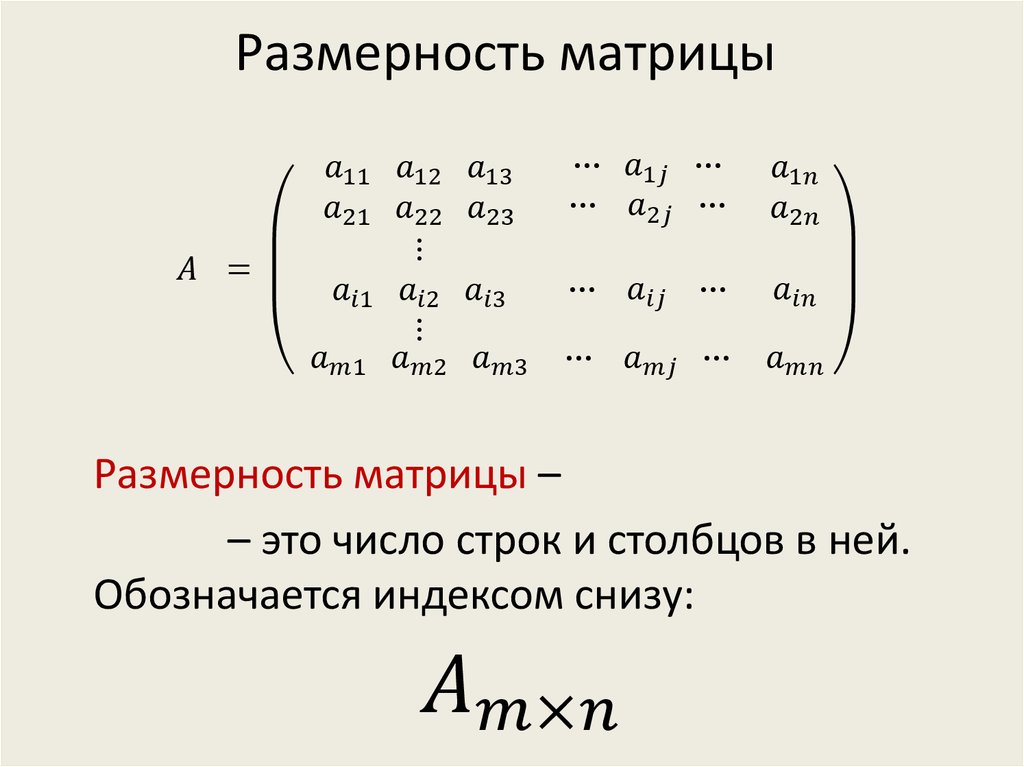 Добавив прошлое условие в квадратные скобки, можно получить новый массив, который будет включать все элементы меньше 0,5 из предыдущего.

>>> A[A < 0.5]
array([ 0.03536295, 0.0035115 , 0.21264709, 0.17121982, 0.43408927,
        0.04523647, 0.42582897, 0.22286282])

Вы уже видели, как можно превращать одномерный массив в матрицу с помощью функции reshape().

>>> a = np.random.random(12)
>>> a
array([ 0.77841574, 0.39654203, 0.38188665, 0.26704305, 0.27519705,
        0.78115866, 0.96019214, 0.59328414, 0.52008642, 0.10862692,
        0.41894881, 0.73581471])
>>> A = a.reshape(3, 4)
>>> A
array([[ 0.77841574, 0.39654203, 0.38188665, 0.26704305],
       [ 0.27519705, 0.78115866, 0.96019214, 0.59328414],
       [ 0.52008642, 0.10862692, 0.41894881, 0.73581471]])

Функция reshape() возвращает новый массив и таким образом может создавать новые объекты. Но если необходимо изменить объект, поменяв его форму, нужно присвоить кортеж с новыми размерностями атрибуту shape массива.

>>> a.shape = (3, 4)
>>> a
array([[ 0.77841574, 0.39654203, 0.38188665, 0.26704305],
       [ 0.27519705, 0.78115866, 0.96019214, 0.59328414],
       [ 0.52008642, 0.10862692, 0.41894881, 0.73581471]])

Как видно на примере, в этот раз оригинальный массив изменил форму, и ничего не возвращается. Обратная операция также возможна. Можно конвертировать двухмерный массив в одномерный с помощью функции

>>> a = a.ravel()
array([ 0.77841574, 0.39654203, 0.38188665, 0.26704305, 0.27519705,
        0.78115866, 0.96019214, 0.59328414, 0.52008642, 0.10862692,
        0.41894881, 0.73581471])

Или прямо повлиять на атрибут shape самого массива.

>>> a.shape = (12)
>>> a
array([ 0.77841574, 0.39654203, 0.38188665, 0.26704305, 0.27519705,
        0.78115866, 0.96019214, 0.59328414, 0.52008642, 0.10862692,
        0.41894881, 0.73581471])

Еще одна важная операция — транспонирование матрицы. Это инверсия колонок и рядов. NumPy предоставляет такую функциональность в функции transpose().

>>> A.transpose()
array([[ 0.77841574, 0.27519705, 0.52008642],
       [ 0.39654203, 0.78115866, 0.10862692],
       [ 0.38188665, 0.96019214, 0.41894881],
       [ 0.26704305, 0.59328414, 0.73581471]])

Максим

Я создал этот блог в 2018 году, чтобы распространять полезные учебные материалы, документации и уроки на русском. На сайте опубликовано множество статей по основам python и библиотекам, уроков для начинающих и примеров написания программ.

Python Q https://yandex.ru/q/loves/python Online

линейная алгебра — Какова размерность матрицы?

Задавать вопрос

спросил

Изменено 5 лет, 10 месяцев назад

Просмотрено 165 тысяч раз

$\begingroup$ 9н$. 3$ имеет размерность $2$, поскольку каждая точка плоскости может быть описана двумя параметрами, даже если реальная точка будет иметь вид $(x,y, г) $.

Если взять строки матрицы за основу векторного пространства, размерность этого векторного пространства даст вам количество независимых строк. Для векторного пространства, базисные элементы которого сами являются матрицами, размерность будет меньше или равна количеству элементов в матрице, это $\dim[M_2(\mathbb{R})]=4$

$\endgroup$

$\begingroup$

Здесь может быть полезна следующая литература из «Линейной алгебры» Фридберга:

Определения. Векторное пространство называется конечномерным , если оно имеет базис, состоящий из конечного числа векторов. Уникальное число векторов в каждом базисе $V$ называется размерностью $V$ и обозначается $\dim(V)$.

Базис, если вы еще не знали, это набор линейно независимых векторов, которые охватывают некоторое векторное пространство, скажем, $W$, являющееся подмножеством $V$.

$\endgroup$

$\begingroup$

Размерность — это количество оснований в ПРОСТРАНСТВЕ СТОЛБЦА матрицы, представляющей линейную функцию между двумя пространствами. т. е. если у вас есть отображение линейной функции R3 ->

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

линейная алгебра — Очень запуталась размерность матрицы

Задавать вопрос

спросил

Изменено 5 лет, 8 месяцев назад

Просмотрено 4к раз

$\begingroup$

Меня очень раздражает и смущает размер матрицы. До сих пор я думал, что размерность матрицы равна ее рангу. Но, похоже, это не так. Или так бывает иногда, в особых случаях?.. Вы видите мое замешательство прямо здесь.

Возьмем в качестве примера эту матрицу $A= \begin{pmatrix} 1 и 3 и 2\\ 2 и 4 и 4\\ 3 и 5 и 6 \end{pmatrix}$

Ранг этой матрицы равен $2$. Я использовал Gauss, и это был последний результат, который я получил (я хочу быть кратким):

$$A= \begin{pmatrix} 6 и 18 и 12\\ 0 и -8 и 0\\ 0 и 0 и 0 \end{pmatrix}$$

Но почему размерность $3$? Неужели просто потому, что в этой матрице $3$ столбцов?

Почему говорят, что размерность равна рангу? Или они имеют в виду размер изображения, когда говорят это?

Пожалуйста, пожалуйста, я сейчас в отчаянии, потому что до сих пор ничего не знаю об этом, и прошу разъяснений.

• линейная алгебра
• матрицы
• векторные пространства
• векторы

$\endgroup$

5

$\begingroup$

Путаница, вероятно, возникает из-за того, что слово «измерение(я)» используется для разных вещей. Однако в контексте векторных пространств это имеет очень специфическое значение.

Матрица, состоящая из $m$ строк и $n$ столбцов, называется $m \times n$-матрицей. Это дает вам размером матрицы, но иногда «$m$ на $n$» называют «размерами» матрицы. Когда $m=n$, это число иногда называют просто размерностью квадратной матрицы.

Существует ряд эквивалентных способов описания ранга матрицы, например количество линейно независимых столбцов (или строк). В контексте векторных пространств это размерность пространства столбцов (или строк) матрицы. Слово «размерность» имеет в этом контексте очень конкретное значение, а именно количество элементов в основе подпространства.

$\endgroup$

$\begingroup$

Использование термина размерность лучше отнести только к векторным пространствам и их элементам.

Таким образом, для матрицы из $m$ строк и $n$ столбцов мы можем сказать, что это матрица размера $m \times n$ , которая представляет собой линейное преобразование из векторного пространства размерности $n$ ( его область определения) в векторное пространство размерности $m$ (его область значений) и что его ранг может быть числом $p \le \mbox{min}(m,n)$.

Можно также сказать, что такая матрица является элементом векторного пространства размерности $q=n \cdot m$, поскольку набор матриц имеет структуру векторного пространства: векторное пространство матриц , т.е. отличается от домена и доменного пространства.