Непрерывные, цепные дроби онлайн
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Числитель
Анализ таких цепей при разных начальных условиях, дает широкую возможность оценить свои силы и возможности понимания этой части такой науки как арифметика.
Угол между ними.
Матрица смежности онлайнНепрерывные (цепные) дроби онлайн
С помощю этого онлайн калькулятора можно преобразовать обыкновенную дробь, смешанное число или десятичное число в непрерывную (цепную) дробь.
Дается подробное решение с пояснениями. Для построения непрерывной дроби введите числа в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Цепной (или непрерывной) дробью называется выражение вида
где a0− целое число, а a1,a2,…− целые положительные числа. Числа a0, a1, a2,…−называются элементами цепной дроби.
Цепная дробь может быть конечным или бесконечным. Число может быть представлено конечной цепной дробью тогда и только тогда, когда оно рационально. Ирациональные числа представляются в виде бесконечной цепной дроби.
Алгоритм разложения вещественного числа на цепную дробь имеет следующий вид:
Если на i-ом шаге xi=0, то процесс останавливается. Цепная дробь принимает вид:
Пример 1. Построить цепную дробь для числа 25/11.
Преобразуем дробь в смешанное число:
Отделим целую и дробную части и обозначим через a0 и x0, соответственно:
Перевернем дробную часть:
Преобразуем дробь в смешанное число:
Отделим целую и дробную части и обозначим через a1 и x1, соответственно:
Перевернем дробную часть:
Преобразуем дробь в смешанное число:
Отделим целую и дробную части и обозначим через a2 и x2, соответственно:
Перевернем дробную часть:
Отделим целую и дробную части и обозначим через a3 и x3, соответственно:
Дробная часть равна нулю.
Процедуру останавливаем.
Непрерывная (цепная) дробь имеет вид:
Таким образом исходный дробь можно представить в виде следующей цепной дроби:
Пример 2. Построить цепную дробь для числа -7.56.
Преобразуем дробь в смешанное число:
Представим число в виде суммы целой и дробной частей и обозначим через a0 и x0, соответственно:
Перевернем дробную часть:
Преобразуем дробь в смешанное число:
Отделим целую и дробную части и обозначим через a1 и x1, соответственно:
Перевернем дробную часть:
Преобразуем дробь в смешанное число:
Отделим целую и дробную части и обозначим через a2 и x2, соответственно:
Перевернем дробную часть:
Преобразуем дробь в смешанное число:
Отделим целую и дробную части и обозначим через a3 и x3, соответственно:
Перевернем дробную часть:
Отделим целую и дробную части и обозначим через a4 и x4, соответственно:
Дробная часть равна нулю.
Процедуру останавливаем.
Непрерывная (цепная) дробь имеет вид:
Таким образом исходный дробь можно представить в виде следующей цепной дроби:
Калькулятор непрерывных дробей
Калькулятор непрерывных дробей Предыдущий ☜ Навигация по страницам Золотого сечения ☞ СледующийАвтоматический расчет непрерывных дробей для (простых) выражений или десятичных чисел.
Краткое пояснение
Непрерывная дробь — это дробь, которая не сокращается. Обычно вас учат приводить дроби к их простейшим формам. Но можно пойти и другим путем, и разверните их, и то, что получится, может показать вам кое-что о числе. Непрерывные дроби (сокращенно CF) полезны при поиске рациональных приближений к иррациональным числам.
Именно этот аспект КФ проливает свет на золотое сечение φ.
Попробуйте сами
Чтобы найти CF для значения или выражения, просто введите его в текстовое поле с синей рамкой и нажмите клавишу Tab или клавишу возврата.
Десятичное число, такое как «1,5», будет работать, как и дробь, такая как «3/7». Или используйте одну из кнопок ниже, чтобы увидеть некоторые интересные CF.
Для опытных пользователей: обратите внимание, что если у вас нет только одного выражения, такого как «exp(3)», вы должны использовать нотацию JavaScript. Например, «Math.exp(3) + Math.cos(5)». Если есть только одно выражение, «Математика». добавляется автоматически.Выражение для xДесятичное расширение x
=
Непрерывная дробь для x в короткой форме
Непрерывная дробь в длинной форме
Интересные значения, чтобы попробовать
- x = Повторяется как десятичная дробь, но непрерывная дробь останавливается.
- x = любимая всеми константа. Или должно быть 2π?
- x = Основание натурального логарифма. Как десятичная она не повторяется, но цепная дробь имеет четкую закономерность!
- x = Еще одно иррациональное число с шаблоном.
- x = Чем это отличается от предыдущего примера?
- x = Это наш ключевой пример: Фи, золотое сечение.
- x = постоянная Фейгенбаума.
- x = малоизвестный, i i . Убедите себя, что это то же самое, что и е -π/2 .
Примечания
Это может показаться загадочным, но найти CF довольно просто. Возьмем знакомый пример π. Перепишите его как
π = 3 + 0,14159…
Теперь найдите обратную дробную часть, то есть 1/0,14159.… = 7,0625… (Обратите внимание, что обратная величина гарантированно больше 1, поэтому всегда будет целая часть, которую нужно сорвать, как красную вишню.)
Теперь у нас есть
π = 3 + 1/7,0625…
Теперь повторите процедуру с частью 7.0625…:
π = 3 + 1/(7 + 0,0625…)
и найти обратную дробную часть, то есть 1/0,0625… = 15,996…, значит:
π = 3 + 1/(7 + 1/15,996…)
Повторение этого процесса дает CF.
Если число рационально, то КФ конечна. Но, как показывает приведенный выше пример с 3/7, хотя CF конечен, десятичная дробь — нет. Таким образом, в некотором смысле CF более удобен, чем повторяющаяся неконечная десятичная дробь.
Если число иррациональное, то и его десятичная дробь, и его CF бесконечно длинные. Но хотя в десятичном числе не будет (обычно ✻) шаблона, есть может быть шаблоном в CF. Примеры e и φ ясно показывают это. Если и есть хорошее объяснение шаблона для e, то я его никогда не видел.
Интересно, что если мы ослабим ограничение канонической формы, согласно которому все числители должны быть равны 1, то для e будет обнаружена еще одна очень структурированная цепная дробь:
Наверняка существует интуитивный вывод e, использующий эту CF для улучшения обоснования «сложных процентов». Который никогда не казался мне таким интуитивным.
На следующей странице мы обсудим, что мы можем узнать о φ из ее особенно простой CF.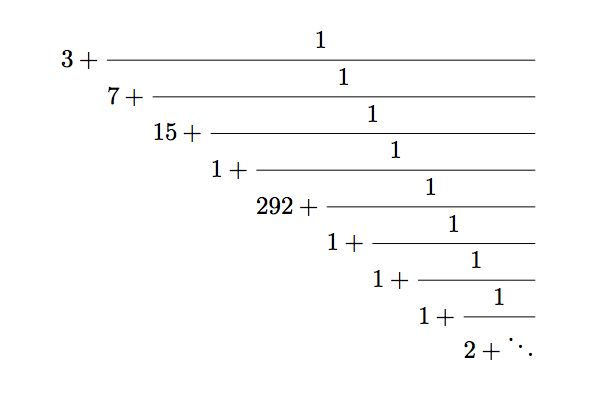
✻ Термин «шаблон», конечно, очень общий. Например, число 1.01001000100001… иррационально, но имеет четкую закономерность. (Поэтому мы имеем право использовать многоточие… чтобы показать, что вы уловили закономерность.) Но нет ни одного повторяющегося блока цифр.
Предыдущий ☜ Навигация по страницам Золотого сечения ☞ Следующий
Непрерывные дроби
Непрерывные дроби(примечания Р. Бигони)
1. Разложение рационального числа в цепную дробь
Рациональное число по определению может быть представлено в виде дроби, то есть как частное двух целых чисел. На самом деле, термин рациональное происходит от латинского слова отношение , что означает частное .
Из каждой положительной дроби , сведенная к низшим терминам, конечная последовательность натуральных чисел можно получить следующим образом
, где a 0 — максимальное натуральное число.
≤ , то есть целой части частного n разделить на d , r 0 это целый остаток от этого деления и d 0 совпадает со знаменателем d .
Например: . В этом случае a 0 =2 и r 0 =3.
Если r 0 равно 0, то есть если числитель кратен знаменателю, процедура завершается. В противном случае из (1) имеем
Очевидно, что d 0 больше, чем r 0 , и дробь можно обрабатывать как дробь, то есть
, где a 1 — целое частное от 9.0106 d 0 разделить на r 0 и r 1 остаток этого раздела. Из (2) и (3) получаем
В приведенном выше примере у нас есть
Опять же, если r 1 равно 0, процедура завершается. В противном случае из (4) получаем
Аналогично предыдущим случаям можно записать как
.
, где a 2 — целое частное r 0 , деленное на r 1 и r 2 остаток этого раздела.
Из (5) и (6) получаем
В приведенном выше примере у нас есть
В этом примере мы видим, что r 2 , последний полученный остаток, равен 1. Когда остаток равен 1, следующий остаток, очевидно, будет равен 0, поэтому мы можем остановить процедуру, предполагая предыдущий остаток. как последний срок a n последовательности . В примере у нас есть a 3 = 2. Пока остаток отличен от 1, процедуру необходимо повторить.
В примере мы видели, что из дроби получаем последовательность [2;1,1,2]. Эта последовательность называется расширением непрерывной дроби дроби .
Элементы разложения в непрерывную дробь можно быстро получить из алгоритм Евклида для вычисления наибольшего общего делителя двух натуральных чисел, запись на каждом шаге последовательных частных, пока остаток больше 0,
| 13 | 5 | 3 | 2 | 1 |
| частное | 2 | 1 | 1 | 2 |
| остаток | 3 | 2 | 1 | 0 |
Чуть более сложный пример:
| 157 | 2791 | 157 | 122 | 35 | 17 | 1 |
| частное | 0 | 17 | 1 | 3 | 2 | 17 |
| остаток | 157 | 122 | 35 | 17 | 1 | 0 |
Поэтому разложение непрерывной дроби равно
[0; 17, 1, 3, 2, 17].
Этот второй пример демонстрирует интересное свойство: в разложении дроби меньше 1 первый член равен 0, а второй следующие члены совпадают с его обратными.
При расширении непрерывной дроби производящая дробь может быть получена путем обращения ранее представленной процедуры: мы должны вычислить обратную величину последнего члена разложения и добавить его к предыдущему члену; затем мы вычисляем обратную часть этой суммы и прибавляем ее к предыдущему члену и так далее, пока не будет достигнут первый член. Взяв первый пример выше, мы имеем:
Во втором примере имеем:
2. Калькулятор.
Следующее приложение JavaScript может быть полезно для вычисления расширения непрерывной дроби и выполнения обратной операции.
Кнопка в продолжение расширяет число, записанное либо в виде дроби, либо в виде десятичного числа.
Кнопка из продолжения выполняет обратную операцию.
Поле длиной позволяет установить максимальное количество элементов расширения.
Примеры.
- с
по продолжение
из продолжения
3. Разложение иррационального числа в цепную дробь.
Иррациональное число по определению не может быть представлено отношением между двумя целыми числами, тогда мы не можем применить
алгоритм Евклида к иррациональному числу, чтобы получить его разложение в виде конечной цепной дроби по той же причине, по которой
мы не можем получить конечное представление числа, какое бы основание ни было принято.
Известно, что десятичное представление иррационального числа представляет собой неповторяющееся десятичное число, но,
если бы мы хотели представить его по основанию два, мы получили бы неповторяющееся двоичное число, или, если бы мы хотели представить его по основанию шестнадцать,
мы получили бы неповторяющееся шестнадцатеричное число.
Однако, по крайней мере, в некоторых случаях достаточно просто, используя процедуру, аналогичную
к тому, что используется для рациональных чисел, выведите его разложение как бесконечную цепную дробь.
Возьмем, к примеру, квадратный корень из двух — первое иррациональное число, открытое в истории человечества. Западная математика в пифагорейской школе. У нас есть
Так
Если мы рекурсивно применим это тождество к корням двойки в знаменателях, мы получим
Очевидно, что эту рекурсивную процедуру всегда можно повторить, поэтому процедура не заканчивается, но не опасно сказать, что разложение квадратного корня из двух в непрерывную дробь равно
Квадратный корень из 2, который, будучи представленным в десятичной системе счисления, представляет собой неповторяющуюся десятичную дробь, если его представить в виде непрерывной дроби. имеет бесконечное повторяющееся расширение.
Еще один очень интересный пример дает золотое число Φ.
У нас есть
Затем
Если мы рекурсивно применим это тождество к числам Φ внутри знаменателей, мы получим
Следовательно, разложение Φ в непрерывную дробь равно
В общем, для любого действительного числа x :
, где [ x ] — максимальное целое число ≤ x , то есть его целая часть, а { х } = х — [ х ] — его дробная часть. Если дробная часть больше 0, обратное является действительным числом больше 0, что, в свою очередь, может быть выражено в виде суммы его целой и дробной частей.
Если мы представим x i+1 обратную дробную часть x i , мы можем бесконечно повторять это процедуру и получать на каждом шаге новый член бесконечной последовательности целых частей чисел x i ; поэтому разложение x в виде непрерывной дроби равно
. Если вы хотите использовать калькулятор в разделе 2 для получения непрерывной дроби квадратного корня из 2,
нет смысла писать на входе десятичное приближение к нему, например 1,41421356,
потому что вы получите расширение рационального числа, которое будет завершено.
Вы можете в этом и подобных случаях использовать селектор функции , что вводит одно из имен наиболее часто используемых функций реальных переменных.
Вы также можете использовать селектор констант , который вводит на вход одну из самых известных реальных констант, таких как e , π и Φ .
Примеры.
Те же результаты можно получить с Mathematica , если у вас установлено это программное обеспечение, или бесплатно с WolframAlpha (документация), которая позволяет использовать некоторые возможности Математика .
- 20 членов разложения квадратного корня из 2 в виде цепной дроби;
- 20 членов разложения Φ в виде цепной дроби;
- порождающая дробь разложения Φ в виде непрерывной дроби с 16 членами.
3. Периодические цепные дроби.
В общем, разложение иррационального числа в виде непрерывной дроби — хороший способ получить рациональное приближение.
к самому номеру. Например, число Φ, которое может быть аппроксимировано частным числом
Последовательность Фибоначчи и предыдущая, с лучшими приближениями
по мере того, как мы идем по последовательности Фибоначчи, также можно по желанию аппроксимировать из ее разложения в непрерывную дробь, состоящего
бесконечной последовательности 1. Мы также можем использовать этот факт для определения Φ: это число, представленное
, где линия над второй 1
указывает на его периодичность.
То же самое относится к .
В общем, квадратные корни натуральных чисел имеют периодические расширения.
Это довольно легко доказать, если подкоренное число — это число, непосредственно следующее за квадратом. На самом деле
, затем
Рекурсивно применяя тождество (10), получаем
В заключение
Из (11)
- вместо n =1 получаем разложение квадратного корня из 2;
- вместо n =2 получаем разложение квадратного корня из 5:
- вместо n =3 получаем разложение квадратного корня из 10:
- вместо n =4 получаем разложение квадратного корня из 17:
- . ..
..
Если подкоренное число превышает квадрат натурального числа на 2 единицы, получаем
, затем
Рекурсивно применяя это тождество, мы получаем
Последний полученный знаменатель совпадает со знаменателем первой строки, поэтому цикл регулярно повторяется. В заключение
От (13)
- вместо n =1 получаем разложение квадратного корня из 3:
- вместо n =2 получаем разложение квадратного корня из 6:
- вместо n =3 получаем разложение квадратного корня из 11:
- вместо n =4 получаем разложение квадратного корня из 18:
- …
И наоборот, повторяющаяся цепная дробь может быть выражена решением квадратного уравнения с натуральными коэффициентами .
Пример: дробь с двумя повторяющимися цифрами.
Число x задается положительным решением уравнения
Из (14) получаем особо простые случаи для c = 2 a и кратного b .
Примеры:
4. Правильные цепные дроби.
Из (9), если мы примем х = котанг (1) и воспользуемся калькулятором, мы получим
Если воспользоваться калькулятором в пункте 2, получится получить
Очевидно, разложение cotanh (1) в непрерывную дробь не является периодическим, но оно показывает замечательную регулярность: мы можем предположить, что она задается последовательностью нечетных чисел.
На самом деле гипотеза верна и была продемонстрирована Эйлером.
База E натуральной экспоненты, т. е. числа Эйлера.
Также и в этом случае можно отметить четкую закономерность: начиная с третьего слагаемого мы видим четные числа, за которыми следует пара единиц. Мы можем предположить, что разложение e на непрерывную дробь равно
.