Работа с векторами: Solving Problems with Vectors

Решение задач с векторами

Горячая математика

Мы можем использовать векторы для решения многих задач, связанных с физическими величинами, такими как скорость, скорость, вес, работа и так далее.

Скорость:

Скорость движущегося объекта моделируется вектором, направление которого является направлением движения, а величина — скоростью.

Пример :

Мяч брошен с начальной скоростью 70 футов в секунду, под углом 35 ° с горизонталью. Найдите вертикальную и горизонтальную составляющие скорости.

Позволять в представить скорость и использовать данную информацию, чтобы написать в в форме единичного вектора:

в «=» 70 ( потому что ( 35 ° ) ) я + 70 ( грех ( 35 ° ) ) Дж

Упрощая скаляры, мы получаем:

в ≈ 57,34 я + 40. 15 Дж

Поскольку скаляры являются горизонтальной и вертикальной компонентами в ,

Следовательно, горизонтальная составляющая 57,34 футов в секунду, а вертикальная составляющая 40.15 футов в секунду.

Сила:

Сила также представлена ​​вектором. Если на объект действуют несколько сил, результирующая сила, испытываемая объектом, представляет собой векторную сумму этих сил.

Пример :

Две силы Ф 1 и Ф 2 с величинами 20 и 30 фунт соответственно действуют на объект в точке п как показано. Найдите результирующие силы, действующие на п .

Сначала мы пишем Ф 1 и Ф 2 в виде компонентов:

в ≈ 57,34 я + 40. 15 Дж

Упрощая скаляры, мы получаем:

Ф 1 «=» ( 20 потому что ( 45 ° ) ) я + ( 20 грех ( 45 ° ) ) Дж «=» 20 ( 2 2 ) я + 20 ( 2 2 ) Дж «=» 10 2 я + 10 2 Дж Ф 2 «=» ( 30 потому что ( 150 ° ) ) я + ( 30 грех ( 150 ° ) ) Дж «=» 30 ( − 3 2 ) я + 30 ( 1 2 ) Дж «=» − 15 3 я + 15 Дж

Итак, результирующая сила Ф является

Ф «=» Ф 1 + Ф 2 «=» ( 10 2 я + 10 2 Дж ) + ( − 15 3 я + 15 Дж ) «=» ( 10 2 − 15 3 ) я + ( 10 2 + 15 ) Дж ≈ − 12 я + 29Дж

Работа:

Работа Вт сделано силой Ф при движении по вектору Д является Вт «=» Ф ⋅ Д .

Пример :

Сила задается вектором Ф «=» 〈 2 , 3 〉 и перемещает объект из точки ( 1 , 3 ) к точке ( 5 , 9) . Найдите проделанную работу.

Сначала мы находим Displacement.

Вектор смещения

Д «=» 〈 5 − 1 , 9 − 3 〉 «=» 〈 4 , 6 〉 .

По формуле совершенная работа равна

Вт «=» Ф ⋅ Д «=» 〈 2 , 3 〉 ⋅ 〈 4 , 6 〉 «=» 26

Если единицей силы являются фунты, а расстояние измеряется в футах, то совершенная работа равна 26 фут-фунт

Введение в векторы — Math Insight

Определение вектора

Вектор — это объект, который имеет как величину, так и направление.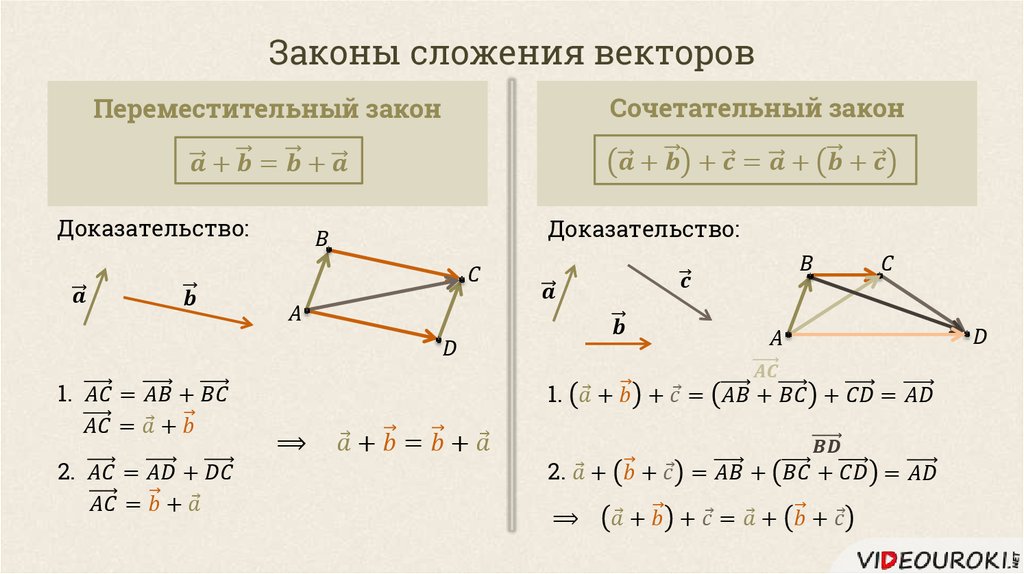 Геометрически мы можем изобразить вектор как направленный отрезок линии, длина которого равна величине вектора и со стрелкой, указывающей направление. Направление вектора от хвоста к голове.

Два вектора одинаковы, если они имеют одинаковую величину и направление. Это означает, что если мы возьмем вектор и переместим его в новое положение (не поворачивая его), то вектор, который мы получим в конце этого процесса, будет тем же вектором, который у нас был в начале.

Два примера векторов представляют силу и скорость. И сила, и скорость имеют определенное направление. Величина вектор будет указывать силу силы или скорость, связанную со скоростью.

Мы обозначаем векторы жирным шрифтом, как в $\vc{a}$ или $\vc{b}$. Особенно при письме от руки, где нельзя легко писать полужирным шрифтом, люди иногда обозначают векторы стрелками, как в $\vec{a}$ или $\vec{b}$ или используют другие обозначения. Здесь нам не нужно будет использовать стрелки. Обозначим величину вектора $\vc{a}$ через $\|\vc{a}\|$.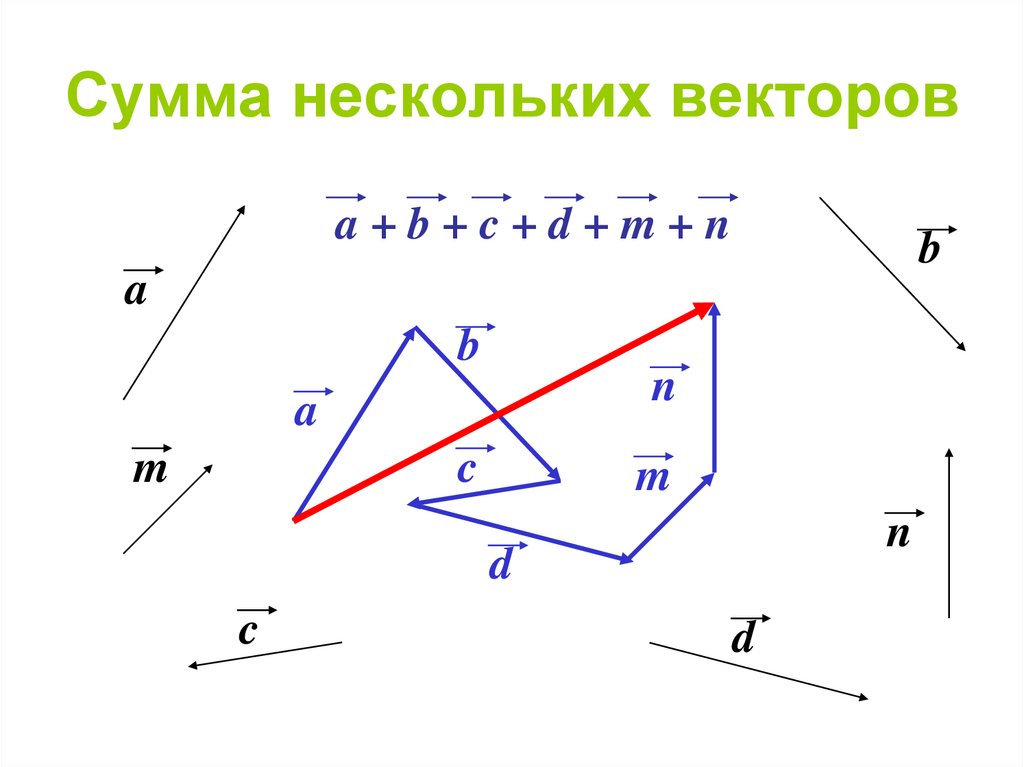 Когда мы хотим сослаться на число и подчеркнуть, что это не вектор, мы можем назвать это число скаляром. Мы будем обозначать скаляры с курсивом, как в $a$ или $b$.

Вы можете изучить понятие величины и направления вектора, используя приведенный ниже апплет. Обратите внимание, что перемещение вектора не меняет вектор, так как положение вектора не влияет на величину или направление. Но если вы растянете или повернете вектор, перемещая только его голову или хвост, величина или направление изменятся. (Этот апплет также показывает координаты вектора, о которых вы можете прочитать на другой странице.)

Величина и направление вектора. Синяя стрелка обозначает вектор $\vc{a}$. Два определяющих свойства вектора, величина и направление, показаны красной полосой и зеленой стрелкой соответственно. Длина красной полосы — это величина $\|\vc{a}\|$ вектора $\vc{a}$. Зеленая стрелка всегда имеет длину единицу, но ее направление совпадает с направлением вектора $\vc{a}$. Единственным исключением является случай, когда $\vc{a}$ является нулевым вектором (единственным вектором с нулевой величиной), для которого направление не определено.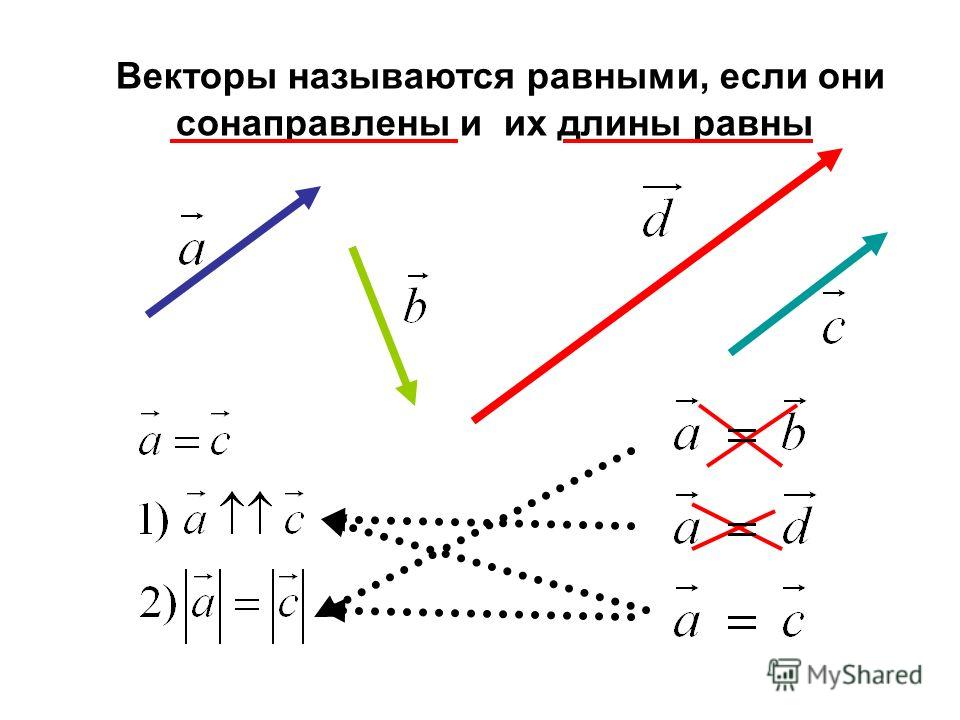 Вы можете изменить любой конец $\vc{a}$, перетащив его мышью. Вы также можете переместить $\vc{a}$, перетащив середину вектора; однако изменение положения $\vc{a}$ таким образом не меняет вектор, так как его величина и направление остаются неизменными.

Дополнительная информация об апплете.

Существует одно важное исключение для векторов, имеющих направление. ноль вектор, обозначенный полужирным шрифтом $\vc{0}$, является вектором нулевой длины. Поскольку у него нет длины, он не указывает ни в каком конкретном направлении. Существует только один вектор нулевой длины, поэтому мы можем говорить о нулевом векторе .

Операции над векторами

Мы можем определить ряд операций над векторами геометрически без ссылка на любую систему координат. Здесь мы определяем сложение, вычитание и умножение скаляром. На отдельных страницах мы обсуждаем два разных способа умножения двух векторов: скалярное произведение и перекрестное произведение.

Сложение векторов

По двум векторам $\vc{a}$ и $\vc{b}$ образуем их сумму $\vc{a}+\vc{b}$ следующим образом.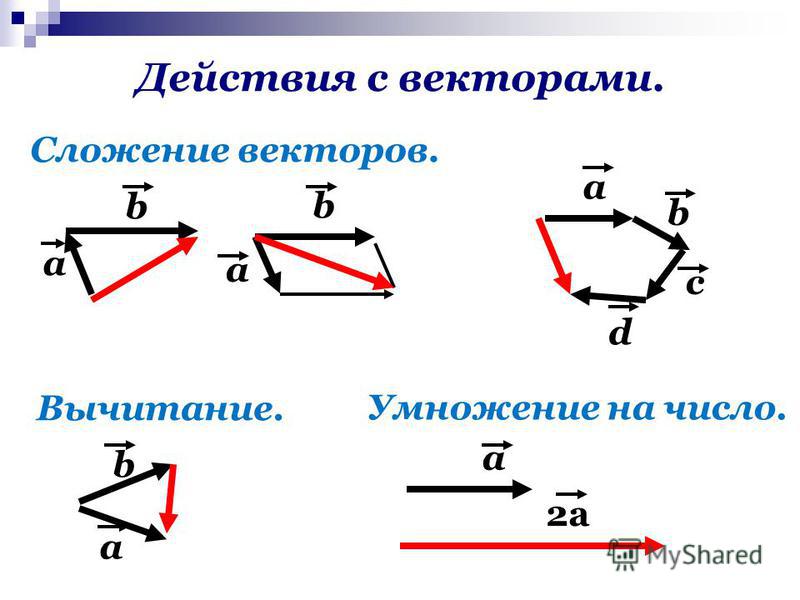 2}=20\sqrt{2}$ миль в час относительно земли.

Добавление векторов удовлетворяет двум важным свойствам.

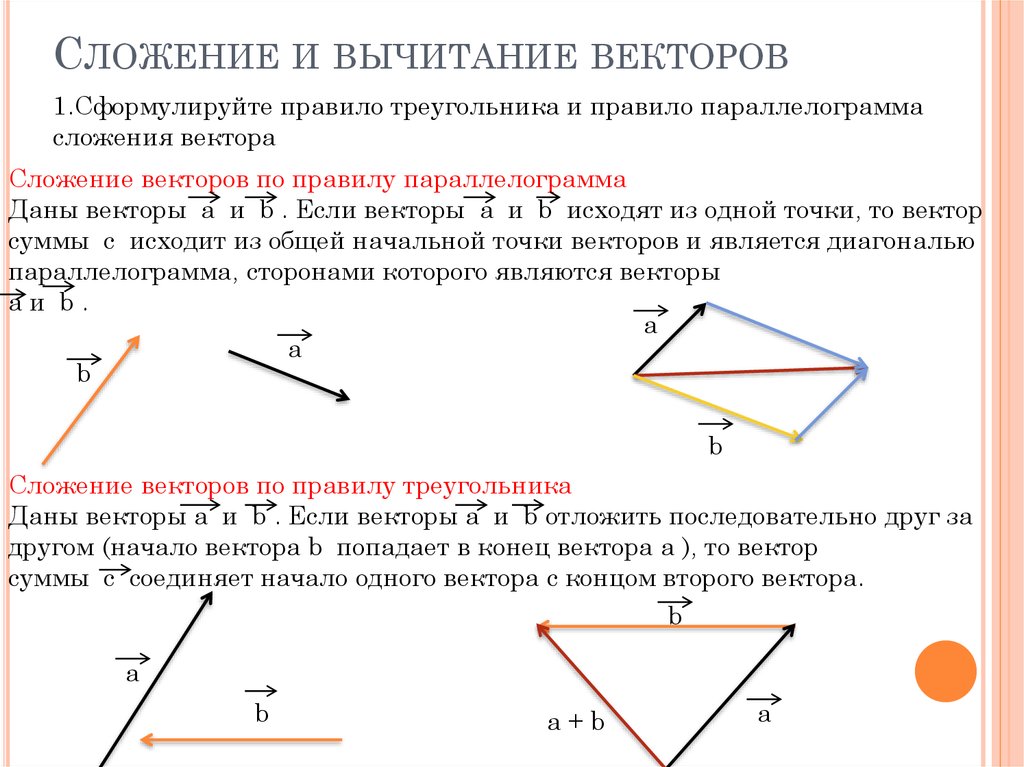
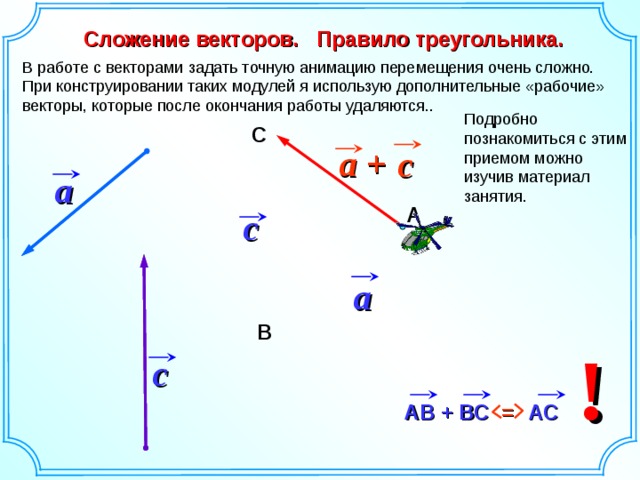
1. Коммутативный закон, который гласит, что порядок сложения не имеет значения: $$\vc{a}+\vc{b}=\vc{b}+\vc{a}.$$ Этот закон также называется законом параллелограмма, как показано на рисунке ниже. изображение. Два ребра параллелограмма определяют $\vc{a}+\vc{b}$, а другая пара ребер определяет $\vc{b}+\vc{a}$. Но обе суммы равны равна той же диагонали параллелограмма.

2. Ассоциативный закон, утверждающий, что сумма трех векторов не зависит от того, какая пара векторов добавляется первой: $$(\vc{a}+\vc{b})+\vc{c} = \vc{a} + (\vc{b}+\vc{c}).$$

Вы можете изучить свойства сложения векторов с помощью следующего апплета. (Этот апплет также показывает координаты векторов, о которых вы можете прочитать на другой странице.)

Сумма двух векторов. Сумма $\vc{a}+\vc{b}$ вектора $\vc{a}$ (синяя стрелка) и вектора $\vc{b}$ (красная стрелка) показана зеленой стрелкой .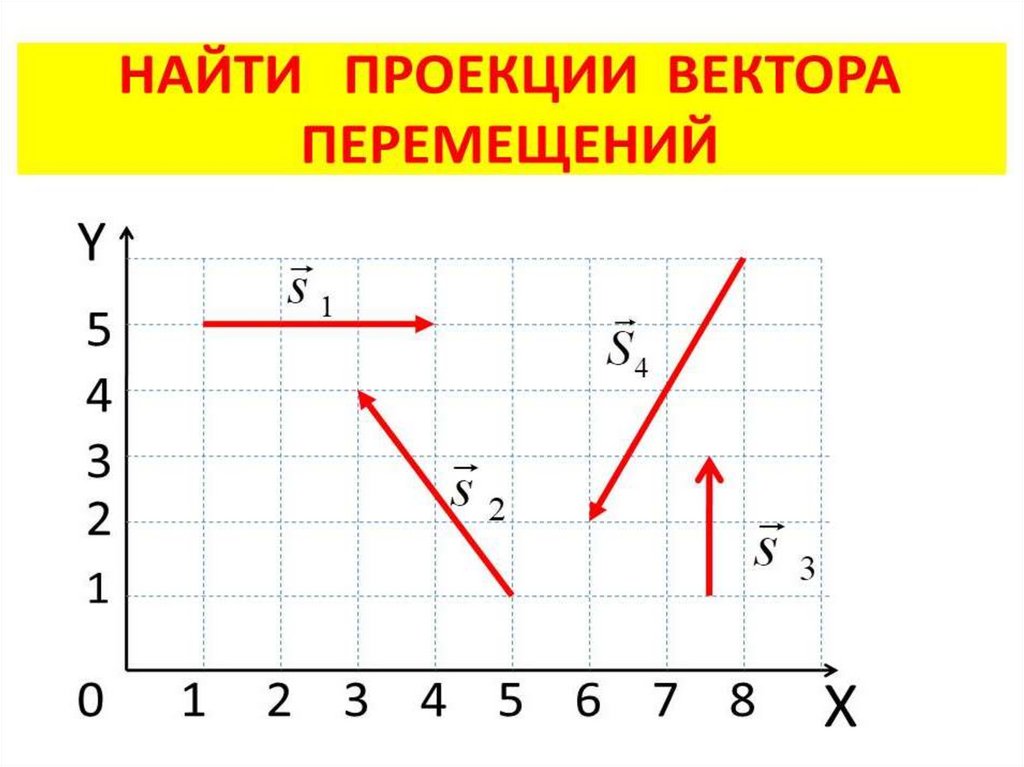 Поскольку векторы не зависят от их начального положения, обе синие стрелки представляют один и тот же вектор $\vc{a}$, а обе красные стрелки представляют один и тот же вектор $\vc{b}$. Сумму $\vc{a}+\vc{b}$ можно составить, поместив хвост вектора $\vc{b}$ в начало вектора $\vc{a}$. То же самое можно сделать, поместив хвост вектора $\vc{a}$ в начало вектора $\vc{b}$. Обе конструкции вместе образуют параллелограмм, сумма $\vc{a}+\vc{b}$ которого является диагональю. (По этой причине закон перестановки $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ иногда называют законом параллелограмма.) Вы можете изменить $\vc{a} $ и $\vc{b}$, перетаскивая желтые точки.

Дополнительная информация об апплете.

Вычитание вектора

Перед определением вычитания мы определяем вектор $-\vc{a}$, который является противоположностью $\vc{a}$. Вектор $-\vc{a}$ — это вектор с той же величиной, что и $\vc{a}$, но направленной в противоположном направлении.

Мы определяем вычитание как сложение с противоположным вектором: $$\vc{b}-\vc{a} = \vc{b} + (-\vc{a}).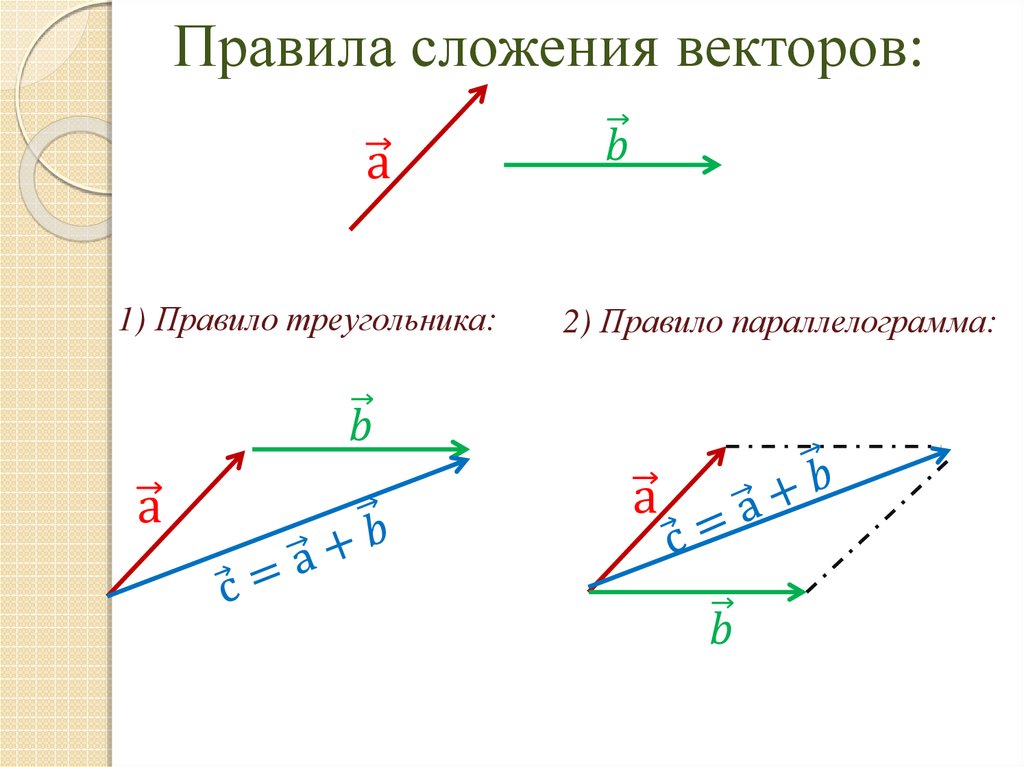 $$ Это эквивалентно переворачиванию вектора $\vc{a}$ при применении вышеуказанные правила добавления. Вы видите, как вектор $\vc{x}$ в ниже рисунок равен $\vc{b}-\vc{a}$? Обратите внимание, как это то же самое как утверждается, что $\vc{a}+\vc{x}=\vc{b}$, как и при вычитании скалярные числа.

Скалярное умножение

Имея вектор $\vc{a}$ и действительное число (скаляр) $\lambda$, мы можем сформировать вектор $\lambda\vc{a}$ следующим образом. Если $\lambda$ положительна, то $\lambda\vc{a}$ — это вектор, направление которого совпадает с направлением $\vc{a}$, а длина равна $\lambda$, умноженной на длину $ \vc{а}$. В этом случае умножение на $\lambda$ просто растягивает (если $\lambda>1$) или сжимает (если $0

Если, с другой стороны, $\lambda$ отрицательно, то мы должны взять напротив $\vc{a}$ перед его растяжением или сжатием. Другими словами, вектор $\lambda\vc{a}$ указывает направление, противоположное вектору $\vc{a}$, а длина $\lambda\vc{a}$ равна $|\lambda|$, умноженной на длину $\vc{a}$.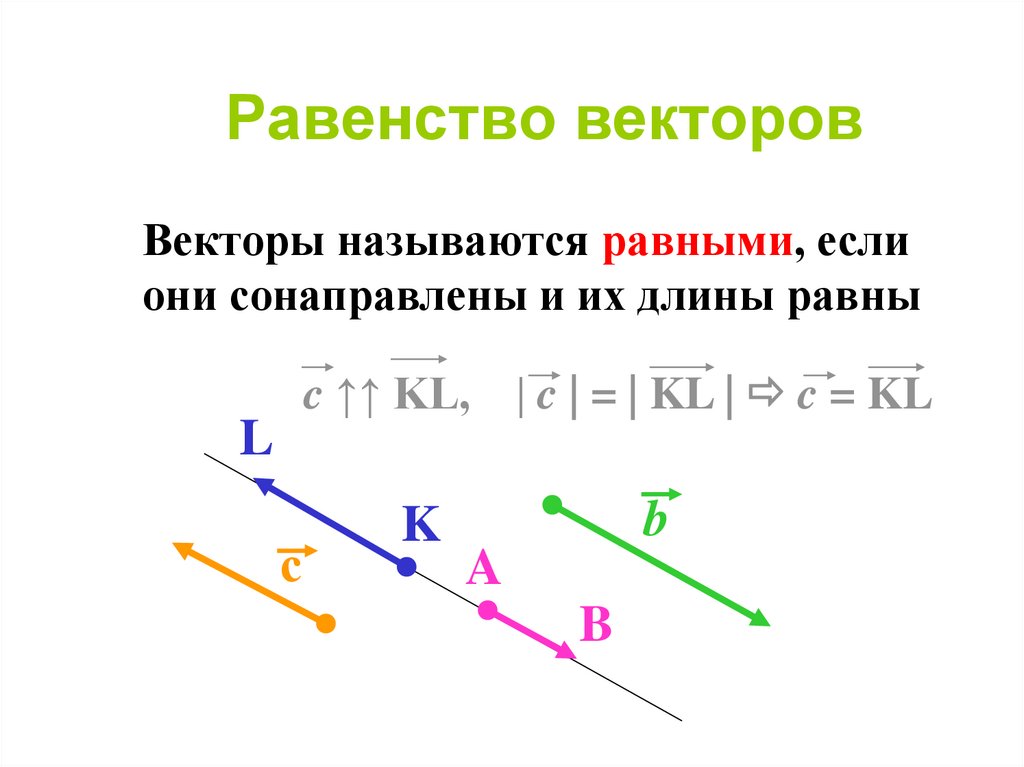 Независимо от знака $\lambda$, мы наблюдаем, что величина $\lambda\vc{a}$ в $|\lambda|$ умножается на величину $\vc{a}$: $\| \лямбда \vc{а}\| = |\лямбда| \|\vc{a}\|$.

Скалярные умножения удовлетворяют многим из тех же свойств, что и обычное умножение.

1. $s(\vc{a}+\vc{b}) = s\vc{a} + s\vc{b}$ (распределительный закон, форма 1)
2. $(s+t)\vc{a} = s\vc{a}+t\vc{a}$ (распределительный закон, форма 2)
3. $1\vc{а} = \vc{а}$
4. $(-1)\vc{a} = -\vc{a}$
5. $0\vc{a} = \vc{0}$

В последней формуле ноль слева — это число 0, а ноль справа — это вектор $\vc{0}$, уникальный вектор, длина которого равна нулю.

Если $\vc{a} = \lambda\vc{b}$ для некоторого скаляра $\lambda$, то мы говорим что векторы $\vc{a}$ и $\vc{b}$ параллельны. Если $\lambda$ отрицательно, некоторые люди говорят, что $\vc{a}$ и $\vc{b}$ антипараллельны, но мы не использовать этот язык.

Мы смогли описать векторы, сложение векторов, вычитание векторов и скалярное умножение без привязки к какой-либо системе координат.