Найти область сходимости ряда — примеры, решения
Пример 1:
Найти область сходимости ряда:
Решение от преподавателя:
Пример 2:
Найти область сходимости ряда:
Решение от преподавателя:
Пример 3:
Найти область сходимости ряда:
Решение от преподавателя:
Областью сходимости степенного ряда является интервал (-R;R), где:
R — радиус сходимости. Вычислим его:
x1 = 2 — 1 = 1
x2 = 2 + 1 = 3
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (1;3)
Теперь проверим сходимость ряда на концах этого интервала.
Пусть x = 1
Получаем ряд:
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
б) По второму признаку Лейбница предел ряда должен стремится к 0.
Второе условие Лейбница выполняется.
Ряд сходится, значит, x = 1 — точка сходимости.
При x = 3
получаем ряд:
числовой знакоположительный ряд.
Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:
Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, x = 3 — точка расходимости.
Таким образом, данный степенной ряд является сходящимся при x [1;3)
Пример 4:
Исследовать область сходимости функционального ряда:
Решение от преподавателя:
Пример 5:
Найти область сходимости степенного ряда:
Решение от преподавателя:
Пример 6:
Найти область сходимости ряда:
Решение от преподавателя:
: общий член ряда имеет вид , при этом члены ряда не определены при х=-3/11, а если х≠-3/11, то
при любом х – ряд расходится всюду.
Пример 7:
Найти область сходимости ряда:
Решение от преподавателя:
Областью сходимости степенного ряда является интервал (-R;R), где:
R — радиус сходимости. Вычислим его:
x1 = -1 — 2 = -3
x2 = -1 + 2 = 1
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-3;1)
Теперь проверим сходимость ряда на концах этого интервала.
Пусть x = -3
Получаем ряд:
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие не выполняется
1б) По второму признаку Лейбница предел ряда должен стремится к 0.
Второе условие Лейбница не выполняется.
Ряд расходится, значит, x = -3 — точка расходимости.
При x = 1
получаем ряд:
числовой знакоположительный ряд.
Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:
Рассмотрим несобственный интеграл:
Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, x = 1 — точка расходимости.
Таким образом, данный степенной ряд является сходящимся при x (-3;1)
Пример 8:
Найти область сходимости ряда:
Решение от преподавателя:
: общий член ряда имеет вид , при этом
Следовательно, ряд сходится, если
и расходится, если
Если x=4/9, то ряд принимает вид — знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница).
Если x=2/3, то ряд принимает вид — такой ряд расходится (по признаку сравнения, т.к. и ряд расходится (гармонический ряд)).
Окончательно получаем область сходимости исходного ряда: [4/9;2/3).
Пример 9:
Найдите множество абсолютной (условной) сходимости ряда:
Решение от преподавателя:
Пример 10:
Найти область сходимости ряда:
Решение от преподавателя:
: общий член ряда имеет вид , при этом
Следовательно, ряд сходится, если
и расходится, если
Если x=-3/7, то ряд принимает вид — знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница).
Такой ряд сходится (по теореме Лейбница).
Если x=-1/7, то ряд принимает вид — такой ряд также сходится (обобщенный гармонический ряд с параметром p=11>1).
Окончательно получаем область сходимости исходного ряда: [-3/7;-1/7].
Пример 11:
Найдите множества абсолютной (условной) сходимости ряда
Решение от преподавателя:
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
Проверяем выполнение признака Лейбница:
Если члены знакочередующегося ряда монотонно убывают по абсолютной величине и стремятся к нулю, то ряд сходится.
Ряд знакочередующийся. Составим ряд из абсолютных величин членов данного ряда
По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
Второе условие Лейбница выполняется.
Данный ряд сходится, так как удовлетворяет условиям признака Лейбница для знакочередующихся рядов.
Следовательно, ряд условно сходящийся.
Следовательно, сходится условно и исходный ряд.
Область сходимости ряда:(-∞; +∞)
Пример 12:
Найти область сходимости ряда:
Решение от преподавателя:
: общий член ряда имеет вид — обобщенный гармонический ряд с параметром .
Такой ряд сходится, если
Однако и поэтому при любом х – ряд всюду расходится.
Пример 13:
Найти область сходимости ряда:
Решение от преподавателя:
По признаку Лейбница ряд расходится
Т. о., область сходимости имеет вид (-1; 1)
Пример 14:
Найти область сходимости ряда:
Решение от преподавателя:
: общий член ряда имеет вид , при этом
Следовательно, ряд сходится, если
и расходится, если
Если x=1/6, то ряд принимает вид — такой ряд расходится (не выполнено необходимое условие сходимости).
Если x=3/2, то ряд принимает вид — такой ряд также расходится (также не выполнено необходимое условие сходимости). 2, {x, 1, 7}]
2, {x, 1, 7}]
| Out[1]= |
Некоторые известные последовательности уже встроены в язык:
| In[2]:= | ⨯ Table[Fibonacci[x], {x, 1, 7}] |
| Out[2]= |
Для задания рекурсивных последовательностей используем функцию RecurrenceTable:
| In[1]:= | ⨯ RecurrenceTable[{a[x] == 2 a[x - 1], a[1] == 1}, a, {x, 1, 8}] |
| Out[1]= |
Вычислим сумму всех элементов последовательности, используя функцию Total:
| In[2]:= | ⨯ Total[%] |
| Out[2]= |
Вычислим сумму элементов последовательности, используя функцию Sum и производящую функцию:
| In[1]:= | ⨯ Sum[i (i + 1), {i, 1, 10}] |
| Out[1]= |
Используйте ESCsumtESC для создания заполняемого шаблона:
| In[2]:= | ⨯ \!\( \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(10\)]\(i \((i + 1)\)\)\) |
| Out[2]= |
Существует возможность задания вложенных и неопределенных сумм:
| In[3]:= | ⨯ \!\( \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(n\)]\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 1\), \(n\)]i\ j\)\) |
| Out[3]= |
Найдем производящую функцию для последовательности:
| In[1]:= | ⨯ FindSequenceFunction[{2, 4, 6, 8}, n] |
| Out[1]= |
Сгенерируем степенной ряд для представления практически любой комбинации встроенных функций:
| In[1]:= | ⨯ Series[Exp[x^2], {x, 0, 8}] |
| Out[1]= |
O[x]9 представляет член высшего порядка; используем функцию Normal для того, чтобы отбросить его:
| In[2]:= | ⨯ Normal[%] |
| Out[2]= |
Если функции Series передать неизвестную или неопределенную функцию, то она вернет степенной ряд в терминах производных:
| In[3]:= | ⨯ Series[2 f[x] - 3, {x, 0, 3}] |
| Out[3]= |
Сходящийся ряд может упрощаться автоматически:
| In[1]:= | ⨯ \!\( \*UnderoverscriptBox[\(\[Sum]\), \(n = 0\), \(\[Infinity]\)] \*SuperscriptBox[\(0. |
| Out[1]= |
Справочная информация: Целочисленные последовательности »
Справочная информация: Разложение в ряд »
›
Пожалуйста, включите JavaScript для того, чтобы иметь возможность использования интерактивных элементов, а также для отправки форм на веб-сайтах компании Wolfram. Узнайте, как это сделать »
Калькулятор сходимости серии— Обмен файлами
Этот сценарий находит сходимость или расхождение бесконечных рядов, вычисляет сумму, предоставляет график частичной суммы и вычисляет радиус и интервал сходимости степенного ряда. Включены следующие тесты: тест дивергенции (тест n-го члена), интегральный тест (тест Маклорена-Коши), тест сравнения, тест предельного сравнения, тест отношения (тест отношения Даламбера), тест корня (тест корня Коши), тест чередующихся рядов. (критерий Лейбница), критерий абсолютной сходимости, критерий p-серии, критерий геометрического ряда, критерий Раабе, критерий Бертрана, критерий Ермакова, критерий конденсации Коши и критерий степенного ряда. Тест степенных рядов использует тест отношений, тест корня и теорему Коши-Адамара для расчета радиуса и интервала сходимости степенных рядов. Все тесты имеют графики частичной суммы, кроме теста Power Series. Этот сценарий поможет учащимся исчисления (II или III) с главой «Бесконечные ряды», учащимся, изучающим дифференциальные уравнения, с решениями для рядов и учащимся, изучающим реальный анализ, с расширенными тестами сходимости.
Тест степенных рядов использует тест отношений, тест корня и теорему Коши-Адамара для расчета радиуса и интервала сходимости степенных рядов. Все тесты имеют графики частичной суммы, кроме теста Power Series. Этот сценарий поможет учащимся исчисления (II или III) с главой «Бесконечные ряды», учащимся, изучающим дифференциальные уравнения, с решениями для рядов и учащимся, изучающим реальный анализ, с расширенными тестами сходимости.
В основном списке (упомянутом выше) 15 тестов сходимости. Тест абсолютной сходимости имеет второй список с 3 тестами сходимости: абсолютная сходимость с интегральным тестом, абсолютная сходимость с тестом сравнения и абсолютная сходимость с тестом предельного сравнения. Всего имеется 17 тестов сходимости. Все тесты на сходимость требуют ввода выражения бесконечной последовательности, выбранного номера теста (из 15) и начального k для 12 тестов — это все, что требуется для выполнения этих тестов. Тест абсолютной сходимости имеет дополнительные входные данные из списка Тест абсолютной сходимости (из 3): Абсолютная сходимость с интегральным тестом, Абсолютная сходимость с тестом сравнения и Абсолютная сходимость с тестом предельного сравнения.
Я написал этот скрипт, потому что никто другой этого не делал, и я предположил, что он может получить значительное количество загрузок. Я изучил и протестировал этот сценарий с помощью книг по бесконечным сериям, интернет-исследований и обширно с ~ 22 книгами по математическому анализу. Первоначально я предназначал этот сценарий для студентов, но он стал настолько мощным, точным, простым и надежным, что профессор скачал его. Если у кого-то есть вопросы или комментарии по этому сценарию, включая возможности трудоустройства, не стесняйтесь обращаться ко мне!
Цитировать как
Дэвид Казенав (2023). Калькулятор сходимости серий (https://www.mathworks.com/matlabcentral/fileexchange/72141-series-convergence-calculator), MATLAB Central File Exchange.
Проверено
Калькулятор сходимости серий (https://www.mathworks.com/matlabcentral/fileexchange/72141-series-convergence-calculator), MATLAB Central File Exchange.
Проверено
Исчисление II — Проверка соотношения
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 10.10: Проверка соотношения
В этом разделе мы рассмотрим тест, который мы можем использовать, чтобы увидеть, является ли ряд абсолютно сходящимся или нет. Напомним, что если ряд абсолютно сходится, то мы также будем знать, что он сходится, и поэтому мы будем часто использовать его, чтобы просто определить сходимость ряда.
Прежде чем приступить к тесту, давайте быстро напомним о факториалах. Этот тест будет особенно полезен для рядов, содержащих факториалы (и мы увидим некоторые из них в приложениях), поэтому давайте убедимся, что можем с ними справиться, прежде чем столкнемся с ними в примере.
Если \(n\) является целым числом таким, что \(n \ge 0\), то \(n\) факториал определяется как
\[\begin{выравнивание*}n! & = n\left( {n — 1} \right)\left( {n — 2} \right) \cdots \left( 3 \right)\left( 2 \right)\left( 1 \right) & \ hspace{0.15in} & {\mbox{if}}n \ge 1\\ 0! & = 1 & \hspace{0,15 дюйма} & {\mbox{по определению}}\end{align*}\]
Давайте быстро посчитаем пару.
\[\begin{выравнивание*}& 1! = 1\\ & 2! = 2\влево( 1\вправо) = 2\\ & 3! = 3\влево(2\вправо)\влево(1\вправо) = 6\\ & 4! = 4\влево(3\вправо)\влево(2\вправо)\влево(1\вправо) = 24\\ & 5! = 5\влево(4\вправо)\влево(3\вправо)\влево(2\вправо)\влево(1\вправо) = 120\конец{выравнивание*}\]
Обратите внимание, что в последнем вычислении выше мы могли бы переписать факториал несколькими способами. Например,
\[\begin{выравнивание*}5! & = 5 \ подкос {\ влево ( 4 \ вправо) \ влево ( 3 \ вправо) \ влево ( 2 \ вправо) \ влево ( 1 \ вправо)} _ {4!} = 5 \ cdot 4! \\ 5! & = 5 \ влево ( 4 \ вправо) \ подкос {\ влево ( 3 \ вправо) \ влево ( 2 \ вправо) \ влево ( 1 \ вправо)} _ {3!} = 5 \ влево ( 4 \ вправо) \ cdot 3!\end{выравнивание*}\]
В общем случае мы всегда можем «вырезать» члены из факториала следующим образом.
\[\begin{выравнивание*}n! & = n\left( {n — 1} \right)\left( {n — 2} \right) \cdots \left( {n — k} \right)\left( {n — \left( {k + 1} \right)} \right) \cdots \left( 3 \right)\left( 2 \right)\left( 1 \right)\\ & = n\left( {n — 1} \right)\left ( {n — 2} \right) \cdots \left( {n — k} \right) \cdot \left( {n — \left( {k + 1} \right)} \right)!\\ & = n\left( {n — 1} \right)\left( {n — 2} \right) \cdots \left( {n — k} \right) \cdot \left( {n — k — 1} \right )!\конец{выравнивание*}\]
Нам нужно будет делать это время от времени, так что не забывайте об этом.
Кроме того, при работе с факториалами нужно быть очень осторожным со скобками. Например, \(\left( {2n} \right)! \ne 2\,\,n!\), как мы увидим, выписав каждый из следующих факториалов.
\[\begin{align*}\left( {2n} \right)! & = \left( {2n} \right)\left( {2n — 1} \right)\left( {2n — 2} \right) \cdots \left( 3 \right)\left( 2 \right)\ влево( 1 \вправо)\\ 2\,\,n! & знак равно 2 \ влево [ {\ влево ( п \ вправо) \ влево ( {п — 1} \ вправо) \ влево ( {п — 2} \ вправо) \ cdots \ влево ( 3 \ вправо) \ влево ( 2 \ вправо)\влево( 1 \вправо)} \вправо]\конец{выравнивание*}\]
Опять же, мы столкнемся с факториалами со скобками, так что не опускайте их. Часто это одна из самых распространенных ошибок, которую допускают учащиеся, когда впервые сталкиваются с факториалами.
Итак, мы готовы к тесту.
Проверка соотношения
Предположим, у нас есть ряд \(\displaystyle \sum {{a_n}} \). Определить,
\[L = \mathop {\lim}\limits_{n \to \infty} \left| {\ frac {{{a_{n + 1}}}}{{{a_n}}}} \right|\]
Тогда
- , если \(L < 1\), ряд абсолютно сходится (и, следовательно, сходится).
 2} \ left ( {n + 2} \ right)}}} \ right | \\ & = \ frac {{10}}{{16}}\mathop {\lim}\limits_{n \to \infty} \frac{{n + 1}}{{n + 2}}\\ & = \frac{{10 }}{{16}} < 1\end{align*}\]
9n}}}{{n!}}} \right| = \mathop {\lim }\limits_{n \to \infty} \frac{{\left({n + 1} \right)!}}{{5\,\,n!}}\]
2} \ left ( {n + 2} \ right)}}} \ right | \\ & = \ frac {{10}}{{16}}\mathop {\lim}\limits_{n \to \infty} \frac{{n + 1}}{{n + 2}}\\ & = \frac{{10 }}{{16}} < 1\end{align*}\]
9n}}}{{n!}}} \right| = \mathop {\lim }\limits_{n \to \infty} \frac{{\left({n + 1} \right)!}}{{5\,\,n!}}\]Чтобы выполнить этот предел, нам нужно исключить факториалы. Мы просто не можем сделать предел с факториалами в нем. Чтобы исключить факториалы, мы вспомним из нашего обсуждения факториалов выше, что мы всегда можем «вырезать» термины из факториала. Если мы проделаем это с числителем (в данном случае потому, что он больший из двух), мы получим
\[L = \mathop {\lim}\limits_{n \to \infty} \frac{{\left({n + 1} \right)\,\,n!}}{{5\,\,n !}}\]
после чего мы можем отменить \(n\)! для числителя знаменатель получить,
\[L = \mathop {\lim}\limits_{n \to \infty} \frac{{\left({n + 1} \right)}}{5} = \infty > 1\]
Итак, по тесту отношений этот ряд расходится.
 2}}}{{\left({2n — 1} \right)!}}} \]
9n}}}} \right|\\ & = \mathop {\lim }\limits_{n \to \infty} \left| {\ frac {{9 \, n}} {{\ left ({ — 2} \ right) \, \ left ( {n + 1} \ right)}}} \ right | \\ & = \ frac {9 {2}\mathop {\lim }\limits_{n \to \infty} \frac{n}{{n + 1}}\\ & = \frac{9}{2} > 1\end{align* }\]
2}}}{{\left({2n — 1} \right)!}}} \]
9n}}}} \right|\\ & = \mathop {\lim }\limits_{n \to \infty} \left| {\ frac {{9 \, n}} {{\ left ({ — 2} \ right) \, \ left ( {n + 1} \ right)}}} \ right | \\ & = \ frac {9 {2}\mathop {\lim }\limits_{n \to \infty} \frac{n}{{n + 1}}\\ & = \frac{9}{2} > 1\end{align* }\]Следовательно, по тесту отношений этот ряд расходится.
В предыдущем примере для получения правильного ответа требовались полосы абсолютного значения. Если бы мы их не использовали, то получили бы \(L = — \frac{9{2} < 1\), что подразумевало бы сходящийся ряд!
Теперь давайте рассмотрим пару примеров, чтобы увидеть, что происходит, когда мы получаем \(L = 1\). Напомним, что тест отношения ничего не скажет нам о сходимости этих рядов. В обоих этих примерах мы сначала проверим, что получаем \(L = 1\), а затем используем другие тесты для определения сходимости.
Пример 5 Определите, является ли следующий ряд сходящимся или расходящимся.
 2} + 1}}} \ ]
9\ infty {\ гидроразрыва {{n + 2}} {{2n + 7}}} \]
2} + 1}}} \ ]
9\ infty {\ гидроразрыва {{n + 2}} {{2n + 7}}} \]Показать решение
Вот предел.
\[L = \mathop {\lim}\limits_{n \to \infty} \left| {\ frac {{n + 3}} {{2 \ left ( {n + 1} \ right) + 7}} \, \, \ frac {{2n + 7}} {{n + 2}}} \ правильно| знак равно \ mathop {\ lim} \ limit_ {n \ to \ infty} \ frac {{\ left ({n + 3} \ right) \ left ({2n + 7} \ right)}} {{\ left ({ 2n + 9} \right)\left( {n + 2} \right)}} = 1\]
Опять же, тест отношения ничего нам не говорит. Однако мы можем быстро использовать для этого тест на дивергенцию. На самом деле, это, вероятно, должно было быть нашим первым выбором в любом случае.
\[\ mathop {\lim }\limits_{n \to \infty} \frac{{n + 2}}{{2n + 7}} = \frac{1}{2} \ne 0\]
По критерию расходимости этот ряд расходится.

Итак, как мы видели в предыдущих двух примерах, если мы получаем \(L = 1\) из проверки отношений, ряд может быть либо сходящимся, либо расходящимся.
Прежде чем мы перейдем к следующему разделу, мы должны отметить еще одну вещь, связанную с тестом соотношения. Последняя серия представляла собой полином, деленный на полином, и мы увидели, что получили \(L = 1\) из теста отношения. Это всегда будет происходить с рациональным выражением, включающим только полиномы или полиномы под радикалами. Таким образом, в будущем не стоит даже пробовать тест отношения для таких задач, поскольку теперь мы знаем, что получим \(L = 1\).
Кроме того, в предпоследнем примере мы видели пример знакопеременного ряда, в котором положительный член был рациональным выражением, включающим полиномы, и снова мы всегда будем получать \(L = 1\) в этих случаях.
Давайте закончим этот раздел доказательством теста соотношения.
Доказательство соотношения
Во-первых, обратите внимание, что мы можем предположить без ограничения общности, что ряд будет начинаться с \(n = 1\), как мы делали для всех наших тестовых доказательств.
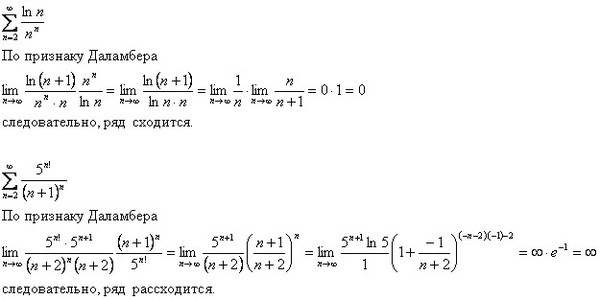
Давайте начнем доказательство здесь, предположив, что \(L < 1\), и нам нужно показать, что \(\sum {{a_n}} \) абсолютно сходится. Для этого сначала заметим, что, поскольку \(L < 1\), существует некоторое число \(r\) такое, что \(L < r < 1\).
Вспомните,
\[L = \mathop {\lim}\limits_{n \to \infty} \left| {\ frac {{{a_{n + 1}}}}{{{a_n}}}} \right|\]
и поскольку мы также выбрали \(r\) так, что \(L < r\) существует некоторое \(N\) такое, что если \(n \ge N\) мы будем иметь,
\[\слева| {\ frac {{{a_{n + 1}}}}{{{a_n}}}} \right| < r\hspace{0,5 дюйма} \Rightarrow \hspace{0,5 дюйма}\left| {{a_{n + 1}}} \right| < г \ влево | {{a_n}} \право|\] 9\infty {{a_n}} \) абсолютно сходится.
Далее нам нужно предположить, что \(L > 1\) и показать, что \(\sum {{a_n}} \) расходится. Напоминая,
\[L = \mathop {\lim}\limits_{n \to \infty} \left| {\ frac {{{a_{n + 1}}}}{{{a_n}}}} \right|\]
и поскольку \(L > 1\) мы знаем, что должно быть некоторое \(N\) такое, что если \(n \ge N\) мы будем иметь,
\[\слева| {\ frac {{{a_{n + 1}}}}{{{a_n}}}} \right| > 1\hspace{0,5 дюйма} \Rightarrow \hspace{0,5 дюйма}\left| {{a_{n + 1}}} \right| > \влево| {{a_n}} \право|\]
Однако, если \(\left| {{a_{n + 1}}} \right| > \left| {{a_n}} \right|\) для всех \(n \ge N\), то мы знаем то,
\[\ mathop {\lim }\limits_{n \to \infty} \left| {{a_n}} \право| \ne 0\]
, потому что члены становятся больше и гарантированно не будут отрицательными.

 5\), \(n\)]\)
5\), \(n\)]\)