Простые числа-близнецы | это… Что такое Простые числа-близнецы?
Простые числа-близнецы, или парные простые числа — пары простых чисел, отличающихся на 2.
Содержание
|
Общая информация
Все пары простых-близнецов, кроме (3, 5), имеют вид .
По модулю 30 все пары близнецов, кроме первых двух, имеют вид (11, 13), (17, 19) или (29, 31).
Первые простые числа-близнецы:
(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883)
На данный момент, наибольшими известными простыми-близнецами являются числа [1].
Они были найдены 24 декабря 2011 года в рамках проекта распределенных вычислений PrimeGrid[2].
Предполагается, что таких пар бесконечно много, но это не доказано. По гипотезе Харди-Литтлвуда, количество пар простых-близнецов, не превосходящих x, асимптотически приближается к
где — константа простых-близнецов:
Теорема Бруна
Вигго Брун в 1919 доказал, что и ряд обратных величин сходится
Это означает, что если простых близнецов и бесконечно много, то они все же расположены в натуральном ряду довольно редко.
Значение называется константой Бруна для простых-близнецов.
Впоследствии была доказана сходимость аналогичного ряда для обобщенных простых близнецов.
Списки
Самые большие известные простые близнецы
- (200700 цифр)
- (100355 цифр)
- (58711 цифр)
- (51780 цифр)
- (51780 цифр)
- (51779 цифр)
Простые числа-триплеты
Это тройка различных простых чисел, разность между наибольшим и наименьшим из которых минимальна.
Наименьшими простыми числами, отвечающими заданному условию, являются — (2, 3, 5) и (3, 5, 7). Данная пара триплетов исключительна, так как во всех остальных случаях разность между первым и третьим членом равна шести. Обобщёно, последовательность простых чисел (p, p+2, p+6) или (p, p+4, p+6) называется триплетом.
Первые простые числа-триплеты:
(5, 7, 11), (7, 11, 13), (11, 13, 17), (13, 17, 19), (17, 19, 23), (37, 41, 43), (41 , 43, 47), (67, 71, 73), (97, 101, 103), (101, 103, 107), (103, 107, 109), (107, 109, 113), (191, 193 , 197), (193, 197, 199), (223, 227, 229), (227, 229, 233), (277, 281, 283), (307, 311, 313), (311, 313, 317), (347, 349, 353), (457, 461, 463), (461, 463, 467), (613, 617, 619), (641, 643, 647), (821, 823, 827), (823, 827, 829), (853, 857, 859), (857, 859, 863), (877, 881, 883), (881, 883, 887)
На данный момент наибольшими известными простыми-триплетами являются числа:
(p, p+2, p+6), где p = 2072644824759 × 233333 − 1 (10047 цифр, ноябрь, 2008, Norman Luhn, François Morain, FastECPP)
Квадруплеты простых чисел
Четвёрки простых чисел вида (p, p+2, p+6, p+8) или сдвоенные близнецы или квадруплеты:
(5, 7, 11, 13), (11, 13, 17, 19), (101, 103, 107, 109), (191, 193, 197, 199), (821, 823, 827, 829), (1481, 1483, 1487, 1489), (1871, 1873, 1877, 1879), (2081, 2083, 2087, 2089), (3251, 3253, 3257, 3259), (3461, 3463, 3467, 3469), (5651, 5653, 5657, 5659), (9431, 9433, 9437, 9439), (13001, 13003, 13007, 13009), (15641, 15643, 15647, 15649), (15731, 15733, 15737, 15739), (16061, 16063, 16067, 16069), (18041, 18043, 18047, 18049), (18911, 18913, 18917, 18919), (19421, 19423, 19427, 19429), (21011, 21013, 21017, 21019), (22271, 22273, 22277, 22279), (25301, 25303, 25307, 25309),.
.. — последовательность A007530 в OEIS.
По модулю 30 все квадруплеты, кроме первого, имеют вид (11, 13, 17, 19).
По модулю 210 все квадруплеты, кроме первого, имеют вид либо (11, 13, 17, 19), либо (101, 103, 107, 109), либо (191, 193, 197, 199).
Секступлеты простых чисел
Шестёрки простых чисел вида (p, p+4, p+6, p+10, p+12, p+16):
(7, 11, 13, 17, 19, 23), (97, 101, 103, 107, 109, 113), (16057, 16061, 16063, 16067, 16069, 16073), (19417, 19421, 19423, 19427, 19429, 19433), (43777, 43781, 43783, 43787, 43789, 43793) … — последовательность A022008 в OEIS.
По модулю 210 все секступлеты, кроме первого, имеют вид (97, 101, 103, 107, 109, 113).
См. также
- Числа Софи Жермен
- Простые числа, отличающиеся на шесть
- Последовательности A001359 и A006512 из Энциклопедии числовых последовательностей.
- Арифметические прогрессии из простых чисел
- PrimeGrid
Примечания
- ↑ The Largest Known Primes
- ↑ World Record Twin Primes
В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. |
Простые числа-близнецы | это… Что такое Простые числа-близнецы?
Содержание
|
Общая информация
Все пары простых-близнецов, кроме (3, 5), имеют вид .
По модулю 30 все пары близнецов, кроме первых двух, имеют вид (11, 13), (17, 19) или (29, 31).
Первые простые числа-близнецы:
(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883)
На данный момент, наибольшими известными простыми-близнецами являются числа [1].
Они были найдены 24 декабря 2011 года в рамках проекта распределенных вычислений PrimeGrid[2].
Предполагается, что таких пар бесконечно много, но это не доказано. По гипотезе Харди-Литтлвуда, количество пар простых-близнецов, не превосходящих x, асимптотически приближается к
где — константа простых-близнецов:
Теорема Бруна
Вигго Брун в 1919 доказал, что и ряд обратных величин сходится
Это означает, что если простых близнецов и бесконечно много, то они все же расположены в натуральном ряду довольно редко.
Значение называется константой Бруна для простых-близнецов.
Впоследствии была доказана сходимость аналогичного ряда для обобщенных простых близнецов.
Списки
- (200700 цифр)
- (100355 цифр)
- (58711 цифр)
- (51780 цифр)
- (51780 цифр)
- (51779 цифр)
Простые числа-триплеты
Это тройка различных простых чисел, разность между наибольшим и наименьшим из которых минимальна.
Наименьшими простыми числами, отвечающими заданному условию, являются — (2, 3, 5) и (3, 5, 7). Данная пара триплетов исключительна, так как во всех остальных случаях разность между первым и третьим членом равна шести. Обобщёно, последовательность простых чисел (p, p+2, p+6) или (p, p+4, p+6) называется триплетом.
Первые простые числа-триплеты:
(5, 7, 11), (7, 11, 13), (11, 13, 17), (13, 17, 19), (17, 19, 23), (37, 41, 43), (41 , 43, 47), (67, 71, 73), (97, 101, 103), (101, 103, 107), (103, 107, 109), (107, 109, 113), (191, 193 , 197), (193, 197, 199), (223, 227, 229), (227, 229, 233), (277, 281, 283), (307, 311, 313), (311, 313, 317), (347, 349, 353), (457, 461, 463), (461, 463, 467), (613, 617, 619), (641, 643, 647), (821, 823, 827), (823, 827, 829), (853, 857, 859), (857, 859, 863), (877, 881, 883), (881, 883, 887)
На данный момент наибольшими известными простыми-триплетами являются числа:
(p, p+2, p+6), где p = 2072644824759 × 233333 − 1 (10047 цифр, ноябрь, 2008, Norman Luhn, François Morain, FastECPP)
Квадруплеты простых чисел
Четвёрки простых чисел вида (p, p+2, p+6, p+8) или сдвоенные близнецы или квадруплеты:
(5, 7, 11, 13), (11, 13, 17, 19), (101, 103, 107, 109), (191, 193, 197, 199), (821, 823, 827, 829), (1481, 1483, 1487, 1489), (1871, 1873, 1877, 1879), (2081, 2083, 2087, 2089), (3251, 3253, 3257, 3259), (3461, 3463, 3467, 3469), (5651, 5653, 5657, 5659), (9431, 9433, 9437, 9439), (13001, 13003, 13007, 13009), (15641, 15643, 15647, 15649), (15731, 15733, 15737, 15739), (16061, 16063, 16067, 16069), (18041, 18043, 18047, 18049), (18911, 18913, 18917, 18919), (19421, 19423, 19427, 19429), (21011, 21013, 21017, 21019), (22271, 22273, 22277, 22279), (25301, 25303, 25307, 25309),.
.. — последовательность A007530 в OEIS.
По модулю 30 все квадруплеты, кроме первого, имеют вид (11, 13, 17, 19).
По модулю 210 все квадруплеты, кроме первого, имеют вид либо (11, 13, 17, 19), либо (101, 103, 107, 109), либо (191, 193, 197, 199).
Секступлеты простых чисел
Шестёрки простых чисел вида (p, p+4, p+6, p+10, p+12, p+16):
(7, 11, 13, 17, 19, 23), (97, 101, 103, 107, 109, 113), (16057, 16061, 16063, 16067, 16069, 16073), (19417, 19421, 19423, 19427, 19429, 19433), (43777, 43781, 43783, 43787, 43789, 43793) … — последовательность A022008 в OEIS.
По модулю 210 все секступлеты, кроме первого, имеют вид (97, 101, 103, 107, 109, 113).
См. также
- Числа Софи Жермен
- Простые числа, отличающиеся на шесть
- Последовательности A001359 и A006512 из Энциклопедии числовых последовательностей.
- Арифметические прогрессии из простых чисел
- PrimeGrid
Примечания
- ↑ The Largest Known Primes
- ↑ World Record Twin Primes
В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. |
Нахождение простых чисел-близнецов до N (гипотеза о простых числах-близнецах)
Получить эту книгу -> Задачи на массив: для интервью и конкурентного программирования
В этой статье мы узнаем о простых числах и гипотезе о простых числах-близнецах . Мы также рассмотрим эффективный алгоритм для нахождения первых пар простых чисел-близнецов от до числа N.
Содержание:
- Введение в простые числа
- Гипотеза о простых числах-близнецах
- Нахождение простых чисел-близнецов до числа N
- Сложность пространства и времени
Начнем с поиска простых чисел-близнецов до N (гипотеза о простых числах-близнецах).
Простое число — это натуральное число, которое делится только на единицу и само на себя, что означает, что его можно представить только как произведение единицы и самого себя
Любое число, не являющееся простым, называется составным числом, что означает, можно составить как произведение меньших чисел. Например, 11 — это простое число, поскольку оно может быть представлено только как 11 * 1, а 8 — составное число, поскольку оно может быть представлено как 2 * 4, а также как 8 * 1.
Простые числа играют важную роль в информатике. Одной из областей, где они широко используются, является криптография.
Двойная простая пара — это пара простых чисел (a,b), такая, что a меньше или больше b на 2. Другими словами, это пары простых чисел, разница между которыми точно равна двум .
Гипотеза о простых числах-близнецах утверждает, что существует бесконечно много простых чисел-близнецов . Это называется гипотезой, потому что, хотя утверждение может быть верным, его истинность еще не доказана.
Алгоритм
Шаги для поиска простых чисел-близнецов до числа N:
- Определение первых простых чисел до N
- Определите пары простых чисел-близнецов среди идентифицированных простых чисел
- Показать результат
Шаг 1
Чтобы идентифицировать первые простые числа до N, мы будем использовать алгоритм, известный как решето Эратосфена. Это алгоритм, который находит все простые числа до числа N, так что это именно то, что мы ищем.
Решето Эратосфена работает, сначала создавая экземпляры всех чисел от 2 до N в списке или сетке. Начиная с двух, он итеративно помечает все кратные каждого встречающегося ему простого числа как составные. В конце концов, все числа, которые не были отмечены, являются в точности простыми числами до N.
Мы можем представить это на примере.
Приведенная выше сетка содержит 50 чисел, что означает, что мы хотим найти первые простые числа до 50.
Следуя алгоритму и начиная с двух.
Мы помечаем все числа, кратные двум, в сетке, поскольку они не являются простыми.
Переходим к следующему непомеченному числу 3, которое, как мы знаем, будет простым, отмечаем его кратные. Будет перекрытие, но нам нужно беспокоиться только о еще не отмеченных множителях.
Следующее неотмеченное число — 5. Мы отмечаем числа, кратные 5, которые еще не были отмечены. Возможно, вы заметили тенденцию: следующее простое число всегда в конечном итоге отмечает меньшее число кратных, потому что некоторые из его кратных уже покрыты предыдущими меньшими простыми числами.
Наконец, мы отмечаем числа, кратные семи. После этого мы можем завершить алгоритм. Мы знаем, что можем закончить, потому что квадрат следующего непомеченного числа 11 равен 121, что больше 50. Все другие меньшие числа, кратные 11, уже были бы покрыты меньшими простыми числами. и поскольку 11 — это наименьшее немаркированное число с квадратом больше 50, мы можем быть уверены в своем решении прекратить.
После завершения мы можем быть уверены, что все непомеченные числа являются правильными простыми числами.
Реализация Python
def findPrimes(N):
"""
Использует решето Эратосфена, чтобы найти первые простые числа до N.
ввод: N, натуральное число
возвращает: набор первых простых чисел до N
"""
# Инициализировать логический массив, в котором индекс соответствует числу до n
# Все числа сначала инициализируются как True
# В конце концов, после запуска сита, isPrime[i] будет False, если i
# составной
isPrime = [Истинно для x в диапазоне (N + 1)]
кандидат = 2
# начиная со 2 повторяем и отмечаем все кратные
в то время как кандидат ** 2 <= N:
если isPrime[кандидат]:
для k в диапазоне (кандидат * 2, n + 1, кандидат):
isPrime[k] = Ложь
кандидат += 1
# Используйте логический массив для фильтрации только простых чисел в новый список
onlyprimes = [i для i в диапазоне (2, len (isPrime)) if isPrime [i]]
# Преобразование в набор для постоянных операций поиска и возврата
возвращаемый набор (только простые числа)
Шаг 2
Теперь нам нужно определить простые числа-близнецы.
На самом деле это легко сделать. Все, что нам нужно, находится в определении. Нам просто нужно перебрать простые числа и выбрать пары простых чисел, разница которых равна 2.
Реализация Python
def findTwinPrimes(primes):
"""
берет набор простых чисел и находит все простые числа-близнецы
ввод: набор простых чисел
возвращает: список кортежей twinprime
"""
твинПраймс = []
для простых чисел:
если простое + 2 в простых числах:
twinPrimes.append((простое, простое + 2))
вернуть TwinPrimes
Шаг 3
Мы можем связать все вместе и отобразить наши результаты.
по умолчанию printPrimePairs(n):
"""
Выводит первые пары простых чисел до n
"""
простые числа = найти простые числа (n)
twinprimes = найтиTwinPrimes(простые числа)
# вывести результаты в консоль
для пары в twinprimes:
печать (пара)
Наконец, давайте проверим наш метод с фактическим значением
printPrimePairs(50)
(3, 5)
(5, 7)
(11, 13)
(17, 19)
(29, 31)
(41, 43)
Решето Эратосфена имеет временную сложность O(n log log n) и пространственную сложность O(n).
FindPrimes, который его реализует, также имеет такую же временную и пространственную сложность.
FindTwinPrimes имеет временную сложность O(d), где d < n, он также имеет пространственную сложность O(d) n log log n) и пространственной сложностью O(n).
С помощью этой статьи на OpenGenus вы должны иметь полное представление о поиске простых чисел-близнецов до числа N и гипотезе о простых числах-близнецах.
Что такое простые числа-близнецы? – Объяснение, свойства, типы
Простые числа-близнецы – это пара простых чисел, разница между которыми равна 2. Например, 3 и 5, 41 и 43 — две распространенные пары простых чисел-близнецов.
В качестве альтернативы вы также можете определить простые числа-близнецы, имеющие пробел между простыми числами, равный 2. Теперь, что подразумевается под простым интервалом?
Изучим подробно!
Простые числа-близнецы составляют основу математики, эта концепция преподается очень рано в школах, и учащиеся должны получить глубокие знания о простых числах-близнецах, поскольку они могут помочь учащимся критически понять язык чисел и могут помочь им получить хорошие знания.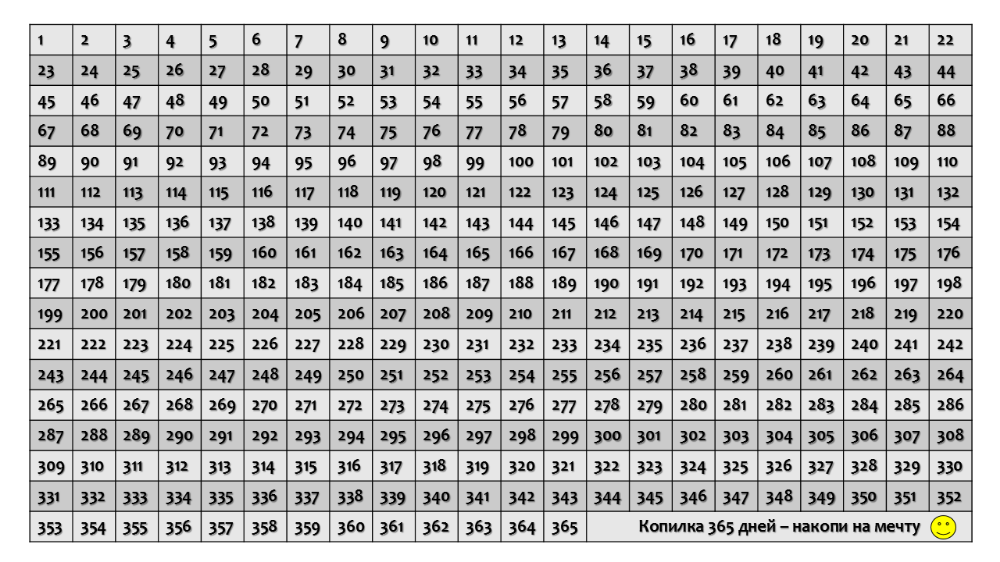
оценка на экзамене.
Двойные простые числа можно определить как набор из двух чисел, между которыми находится только одно составное число. Другое определение простых чисел-близнецов: пара чисел с разницей в два также называется простыми числами-близнецами. Термин «прайм-близнец» был введен Стэклом в 1919 г.16. Говоря простым языком, простые числа-близнецы — это числа, в которых два числа имеют разность в два.
Первые несколько простых чисел-близнецов равны n+/-1 для n=4, 6, 12, 18, 30, 42, 60, 72, 102, 108, 138, 150, 180, 192, 198 и т. д. Явно, эти являются (3, 5), (5, 7), (11, 13), (17, 19) и т. д.
Свойства простых чисел-близнецов
которые имеют разницу в два. Вот некоторые свойства простых чисел-близнецов:
5 — единственная простая цифра, которая имеет положительную и отрицательную разность простых чисел 2.
Следовательно, 5 имеет две пары простых чисел — (3,5) и (5,7).И 2, и 3 не являются парой простых чисел-близнецов, так как между ними нет составного числа.
Основная форма, в которой представлены простые числа, это {6n-1, 6n+1}, 3 и 5 являются исключением.
Пары простых чисел при сложении, их сумма всегда делится на 12, за исключением 3 и 5.
Следовательно, 5 имеет две пары простых чисел — (3,5) и (5,7).Гипотеза о простых числах-близнецах
Гипотеза о простых числах-близнецах также называется гипотезой Полиньяка в терминах теории чисел. Определение гипотезы о простых числах-близнецах гласит, что существует бесконечное число пар простых чисел-близнецов с разницей в два. Гипотеза утверждает, что положительное четное число m имеет бесконечные пары двух последовательных простых чисел с разностью n.
Гипотеза о простых числах-близнецах в основном говорит о том, что существует бесконечное количество простых чисел-близнецов.
Это означает, что чем больше число, тем реже встречаются простые числа, и поэтому простые числа-близнецы встречаются реже. Гипотеза Полиньяка названа в честь Альфонса де Полиньяка в 1849 году.как он это представил. Альфонс обнаружил, что любое четное число можно представить бесконечным числом способов как разность между двумя последовательными простыми числами. Она также известна как гипотеза Евклида о простых числах-близнецах.
Понятия, связанные с простыми числами-близнецами, которые помогут лучше понять концепцию, следующие:
Свойства простых чисел-близнецов
Теорема Бруна
Гипотеза о простых числах-близнецах
- гипотеза о простых числах близнецов
Гипотезы
Первая гипотеза Харди–Литтлвуда
Гипотеза Полиньяка
Разность между двумя простыми числами
9 Ничто иное, как разность между двумя простыми числами.
В математической форме это может быть выражено следующим образом:
Разрыв между простыми числами = простое число + 1 – простое число
Что такое свойства простых чисел-близнецов?
Единственная простая цифра, имеющая как положительные, так и отрицательные простые разности двух, — это 5. Следовательно, она встречается в двух простых парах — (3, 5) и (5, 7).
Поскольку между 2 и 3 не существует составного числа, эти две последовательные цифры не являются парой простых чисел-близнецов.
Все остальные пары простых чисел-близнецов остаются в виде {6n – 1, 6n + 1}, кроме пары (3, 5).
Если сложить два числа из пары простых чисел, результат будет делиться на 12. Опять же, в этом случае пара (3, 5) является исключением.
Что такое гипотеза простых чисел-близнецов?
Французский математик Альфонс де Полиньяк в 1846 году выдвинул первое утверждение о простых числах-близнецах.
Он заявил, что любое четное число можно представить бесконечным числом способов. Примером того же является разница между двумя простыми числами (13 – 11 = 5 – 3 = 2).
Эту теорию иногда называют гипотезой Евклида о простых числах-близнецах, но было доказано, что может существовать бесконечное число простых чисел. Однако это не относится к простым числам-близнецам.
Первая гипотеза Харди-Литтлвуда
Эта гипотеза названа в честь двух английских математиков, а именно Г. Х. Харди и Джона Литтлвуда. Эта гипотеза, связанная с распределением созвездий простых чисел, включающих простые числа-близнецы, обобщает гипотезу о близнецах.
Считайте π2(x) числом простых цифр при условии, что p меньше, чем равно x, так что p + 2 также дает простое число. Следовательно, константа простого числа-близнеца C2 может быть представлена следующим образом: 9{2}} \right ) \right )\]
Здесь p — простое число, больше равное 3.
Приблизительный ответ: 0,660161815846869573927812110014….
Кроме того, уникальность исходной гипотезы Харди-Литтлвуда можно проиллюстрировать следующим образом: «2» — единственное четное простое число.
Как гипотеза Полиньяка утверждала, что существует много пар простых чисел-близнецов с разницей в 2, но Итан Чжан доказал, что существует бесконечное число пар простых чисел, которые содержат разрыв не менее 70 миллионов.
Различные другие типы простых чисел
Двоюродные простые числа
Когда разница между двумя простыми числами равна 4, они называются двоюродными простыми числами.
Тройка простых чисел
Набор троек простых чисел содержит три числа, разница между наибольшим и наименьшим числом которых равна 6. Два исключения: (2, 3, 5) и (3, 5, 7).
Решено Численное на простых числах-близнецах
Раствор.