Программа pascal: Курсы на Stepik

Содержание

Free Pascal — Скачать

Официальные версии

Это готовые пакеты вместе с программой установки, получить вас и работает в кратчайшие сроки. Все пакеты содержат файл README, который вы должны прочитать для получения инструкций по установке и последних новостей.

Последний выпуск — 3.2.2 .

Из-за отсутствия сборщиков релизов и тестировщиков версия 3.2.2 доступна только для ограниченного числа пользователей. количество платформ и не во всех форматах пакетов. Если вы хотите изменить это и построить и протестировать будущее релизы, свяжитесь с нами через списки рассылки.

Двоичные файлы

Вы можете загрузить версию 3.2.2 для следующих процессоров и операционных систем:

РУКА
- Линукс
- Андроид
- Windows СЕ
- Game Boy Advance
- Нинтендо ДС
- АРОС
ARM64 (aarch64)
- Линукс
- Андроид
- macOS
Intel x86/i386
- Windows 32-бит (и кросс-компилятор ARM/MIPS/i386-Android)
- Линукс
- Mac OS X/OS X/macOS (и кросс-компиляторы для ARM64, PowerPC(64), iOS и iPhoneSimulator, JVM/Java и JVM/Android).
- FreeBSD
- Солярис
- OS/2 (и eComStation)
- DOS (расширитель GO32v2)
- Хайку
- АРОС
AMD64/Intel 64/x86_64
- Windows 64-разрядная
- Линукс
- Mac OS X/OS X/macOS (и кросс-компиляторы для PowerPC(64)/Mac OS X, iOS и iPhoneSimulator, JVM/Java и JVM/Android).
- FreeBSD
- Солярис
Intel i8086
- МС-ДОС
PowerPC
- АмигаОС
- АIX
- Линукс
- Mac OS X
- МорфОС
- Нинтендо Wii
PowerPC64
- АIX
- Линукс
- Mac OS X
PowerPC64 с обратным порядком байтов
- Линукс
СПАРК
- Линукс
- Солярис
MIPS
- Линукс
МИПСЕЛЬ
- Linux (экспериментальный, не тестировался)
Моторола 68k
- Амига
- Линукс

Источник

Исходники можно скачать отдельно в виде zip файла или tar. gz с одного из сайтов загрузки.

Документация

Документацию можно загрузить в нескольких форматах с одного из наших скачать сайты.

Снимки

В дополнение к официальным релизам мы также предлагаем так называемые «снимки» компилятора, RTL, IDE и несколько других пакетов на странице разработки. Эти представляют собой скомпилированные версии текущих исходников со всеми исправлениями и улучшениями с момента последней официальный релиз, поэтому, пожалуйста, попробуйте их, если у вас возникнут проблемы. Конечно, они также могут содержать новые ошибки.

Старые выпуски

Ссылки на некоторые старые выпуски (уже не поддерживаемые) FPC для платформ для лучшей альтернативы которой на данный момент не существует, можно найти здесь. Не трудитесь сообщать об ошибках с этими старыми релизами — исправлять не будем. Основная причина, по которой эти платформы больше не поддерживаются из-за отсутствия сопровождающих — если вы хотите обновить их, свяжитесь с нами (например, с помощью рассылки fpc-devel список).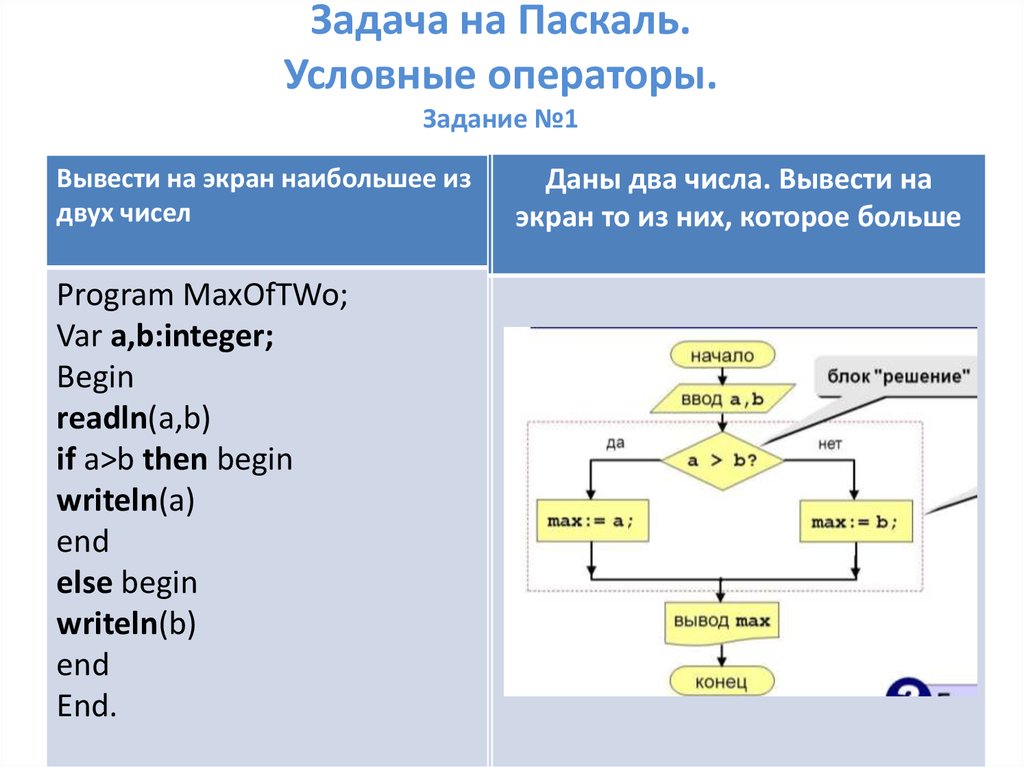

Программа на языке Turbo Pascal для расчета зависящих от масштаба коэффициентов ассоциации

Программа на языке Turbo Pascal для вычисления зависящих от масштаба коэффициентов ассоциации

Скачать PDF

Рефераты программ/алгоритмы
Опубликовано: Март 1996 г.

Стеф Декоэн ¹

Методы исследования поведения, инструменты и компьютеры том 28

, страницы 128–130 (1996 г.

)Процитировать эту статью

339 доступов
Детали показателей

Abstract

Описана программа на языке Turbo Pascal, которая вычисляет зависящие от масштаба коэффициенты ассоциации, принадлежащие общему семейству коэффициентов ассоциации Зегера. Члены этого семейства могут быть построены адаптированными к масштабному типу переменных в том смысле, что они нечувствительны к допустимым преобразованиям переменных, но чувствительны к недопустимым преобразованиям. Программа может вычислять (с поправкой на случайность) коэффициенты связи между переменными восьми различных типов шкалы и между переменными смешанного типа шкалы.

Скачайте, чтобы прочитать полный текст статьи

Ссылки

Aczel, J. , &Roberts, F. (1989). О возможных функциях слияния. Математические социальные науки , 17 , 205–243.
Артикул Google Scholar
Коэн, Дж. (1960). Коэффициент согласия для номинальных шкал. Образовательные и психологические измерения , 20 , 37–46.
Артикул Google Scholar
Янсон, С., и Вегелиус, Дж. (1982). Коэффициенты корреляции для более чем одного типа шкалы. Многомерное исследование поведения , 17

, 255–269.
Артикул Google Scholar
Кранц Д.Х., Люс Р.Д., Суппес П. и Тверски А. (1971). Основы измерения: Том. 1. Аддитивное и полиномиальное представление . Нью-Йорк: Академическая пресса.
Google Scholar
Наренс, Л., и Люс, Р. Д. (1993). Дальнейшие комментарии о «нереволюционности», вытекающей из аксиоматической теории измерения. Психологические науки , 4 , 127–130.
Артикул Google Scholar
Робертс, Ф. (1979). Теория измерений . Чтение, Массачусетс: Аддисон-Уэсли.
Google Scholar
Стайн, В. В. (1989). Соглашение об отношениях между наблюдателями. Психологический бюллетень , 106 , 341–347.

Артикул Google Scholar
Суен, Х.К., и Ари, Д. (1989). Анализ количественных данных наблюдения за поведением . Хиллсдейл, Нью-Джерси: Эрлбаум.
Google Scholar
Вегелиус, Дж. (1978). О полезности концепции коэффициента Е-корреляции в психологических исследованиях. Образовательные и психологические измерения , 38 , 605–611.
Артикул Google Scholar
Zegers, FE (1986a). Семейство коэффициентов ассоциации с поправкой на случайность для метрических шкал. Психометрика , 51 , 559–569.
Артикул Google Scholar
Зегерс, Ф. Э. (1986b). Общее семейство ассоциативных коэффициентов
. Гронинген: Бумкер.
Google Scholar
Зегерс, Ф. Э. (1991). Коэффициенты межведомственного согласия. Прикладные психологические измерения , 15 , 321–333.
Артикул Google Scholar
Зегерс, Ф. Э., и Тен Берге, Дж. М. Ф. (1985). Семейство коэффициентов ассоциации для метрических шкал. Психометрика , 50 , 17–24.
Артикул Google Scholar
Зегерс, Ф.Э., и Тен Берге, Дж.М.Ф. (1986). Коэффициенты корреляции для более чем одного типа шкалы: альтернатива подходу Янсона и Вегелиуса.