Демонстрационные примеры Simulink MatLab
RADIOMASTERЛучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
1763 0
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- Главная /
- База знаний /
- CAD / CAM /
ввести в командном окне команду simulink,
нажать кнопку на панели инструментов (кнопка указана на рис.
13),щелкнуть (двойной щелчок) пункт Library Browser в окне Launch Pad.
Чтобы открыть диалоговое окно Configuration Parameters, на вкладке Modeling в разделе Setup щелкните Model Settings .
Выберите панель Solver .
Установите Время остановки на
25.Щелкните стрелку рядом с Детали решателя , чтобы просмотреть дополнительные параметры решателя.
Под Варианты пересечения нуля , установите Алгоритм на
Неадаптивный.В Время моделирования , установите Время остановки на
25.Развернуть Детали решателя . В Параметры пересечения нуля установите для Алгоритм значение
Неадаптивный.- Просмотр данных в Инспекторе данных моделирования
Анимация в пространстве — аттрактор Лоренца
Встроенные фигуры
В паутине нейронных сетей
Просмотр текстов примеров и m-файлов
Справочная система MATLAB 6.0
Меню Help
Запуск справочной системы
Виды работы справочной системы
Работа с индексным каталогом
Поиск по всей справке
Новые функции системы MATLAB 6.0
Поиск функций по имени
Просмотр документации в формате PDF
Галерея примеров — MATLAB Demos
Вызов галереи демонстраций
Демонстрационные примеры Simulink
Копирование демонстрационных примеров
Что нового мы узнали?
Следующий
пример, показанный на рис. 4.16, иллюстрирует доступ к примерам пакета системного
моделирования Simulink — одного из самых мощных пакетов прикладных программ,
расширяющих возможности системы MATLAB. Этот пакет создан для моделирования
линейных и нелинейных динамических систем заданием их в виде системы функциональных
блоков с автоматическим составлением и решением матричной системы дифференциальных
уравнений состояния, описывающей работу созданной модели.
На рис. 4.17 приведен пример просмотра одного из простых примеров — моделирования динамической системы второго порядка, описываемой нелинейными дифференциальными уравнениями Ван-дер-Поля. Сверху показана блок-схема моделируемого объекта, а снизу — результат моделирования его работы. Для пуска моделирования в панели инструментов окна системы Simulink нажимается кнопка пуска с изображением треугольника.
Рис. 4.16. Доступ к примерам пакета Simulink
Окно MAT LAB
Demos дает возможность ознакомиться со многими десятками самых серьезных примеров
применения системы MATLAB и позволяет убедиться в высоком качестве визуализации
их решений. При необходимости всегда можно ознакомиться с файлом любого примера
и использовать его для решения схожих задач.
Рис. 4.17. Пример моделирования нелинейной динамической системы второго порядка средствами пакета моделирования Simulink
Нравится
Твитнуть
Теги MatLab САПР
Сюжеты MatLab
Знакомство с матричной лабораторией MATLAB MatLab
8268 0
Визуализация и графические средства MatLab
9818 0
Техническая документация по системе MatLab
6314 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
© 2005–2022 radiomaster.ru
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.8737 s
Демонстрационные примеры Simulink
Запустите
систему MATLAB,
используя приемы запуска программ в
Windows.
На экране появится окно, показанное на
рис. 13. В верхних строках окна имеются
привычное меню и панель инструментов.
Основное пространство окна делится на
части: Launch
Pad
(начальное меню), Command
Windows
(окно для ввода команд и вывода сообщений),
Command
History
(история работы с MATLAB
в командах и сообщениях), Current
Directory
(рабочая директория), Workspace
(сведения о текущем рабочем документе).
Вид экрана настраивается в пункте меню
Откройте пункт менюWiew и выделите пункты Launch Pad и Command Windows (выделенный пункт помечается галочкой), с остальных пунктов выделение снимите. И то и другое осуществляется щелчком мыши на соответствующем пункте. После этих действий вид окна должен соответствовать приведенному на рис. 13.
Запуск Simulink осуществляется запуском его библиотеки Library Browser. Запустить библиотеку можно разными способами:
13),В результате любого из этих действий раскрывается новое окно, дающее доступ к средствам Simulink.
Примечание: Все окна можно перемещать и изменять их размеры, используя обычные приемы системы Wiтdows.
Запустите Simulink. Рассмотрите окно Simulink Library Browser. Это окно − важная часть интерфейса Simulink. Оно открывает доступ к множеству других подобных окон для новых пакетов компонентов (Blocksets&Toolboxes) и примеров их применения (Demos). Это дает пользователю возможность постепенно знакомиться с новыми областями применения Simulink. Закройте окно Simulink Library Browser.
В
окне
Launch Pad MATLAB раскройте
пункт Simulink.
В раскрывшемся
меню дважды щелкните пункт Demos.
Появляется новое окно MATLAB Demo Window,
предназначенное для работы с встроенными
примерами, описаниями и демонстрациями.
В окне MATLAB Demo Window в меню Simulink щелкните пункт General, после чего раскроется список примеров (рис. 14). В этом списке найдите и выделите пример Spring—mass system simulation (щелчком мыши). Запустите пример, щелкнув кнопку Run Spring—mass system. Результатом описанных действий будет запуск демонстрационного примера. Открывается окно onecart (рис. 15), в котором представлена графическая модель, описывающая движение массы (в виде кубика) по плоскости с учетом трения.
На
массу воздействует сила пружины,
начальная деформация которой может
изменяться. Скачкообразное изменение
начальной деформации пружины моделирует
внешнее возмущение, воздействующее на
систему. Входное воздействие моделируется
перемещением опоры (вертикальная линия),
с которой соединен свободный конец
пружины.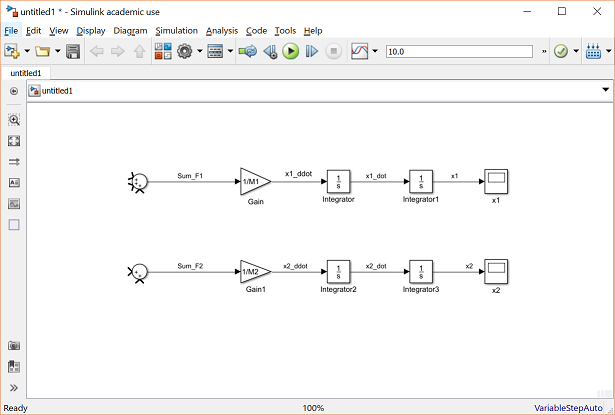
При возмущении системы с помощью скачкообразного перемещения опоры можно наблюдать характерные затухающие колебательные движения кубика. Таким образом, в этом примере решается типичная физическая задача о колебаниях реального механического маятника под действием внешней силы.
Модель в Simulink представляется в виде графической блок-схемы (рис. 15). Каждый блок выполняет определенные функции, преобразуя сигнал, поступающий на его вход, в выходной сигнал по некоторому алгоритму. Все блоки соединены между собой связями в порядке, определяемом последовательностью преобразования сигнала в моделируемой системе. На основе функций блоков с учетом последовательности их соединений Simulink автоматически составляет систему дифференциальных уравнений, решением которых является переходный процесс в системе.
Каждый
блок может иметь идентификатор и
настраиваемые параметры. Идентификаторы
блоков (или их названия) видны на схеме
модели. Доступ к настраиваемым параметрам
блоков осуществляется через контекстные
меню, которые вызываются двойным щелчком
мыши на изображении блока.
Рассмотрите модель Spring—mass system. На рис. 15 полужирным курсивом приведены дополнительные пояснения, которых нет в окне модели. Блок Input модели представляет собой генератор, создающий последовательность прямоугольных импульсов, которые моделируют скачкообразные возмущения на входе исследуемой системы. Блок Actual Position является универсальным индикатором (осциллографом), позволяющим наблюдать переходные процессы в графической форме. Блок Animation function позволяет вывести результат моделирования в виде анимации движений исследуемой системы.
Блок x1&x2 выполняет
функции мультиплексора для одновременного
наблюдения входного и выходного сигналов
модели. Остальные блоки реализуют
динамическую модель исследуемой системы,
представленной в виде структурной
схемы, в соответствии с методами теории
автоматического управления. Имеются
также текстовые комментарии и средства
для вывода
подсказок и открытия окон справочной
системы.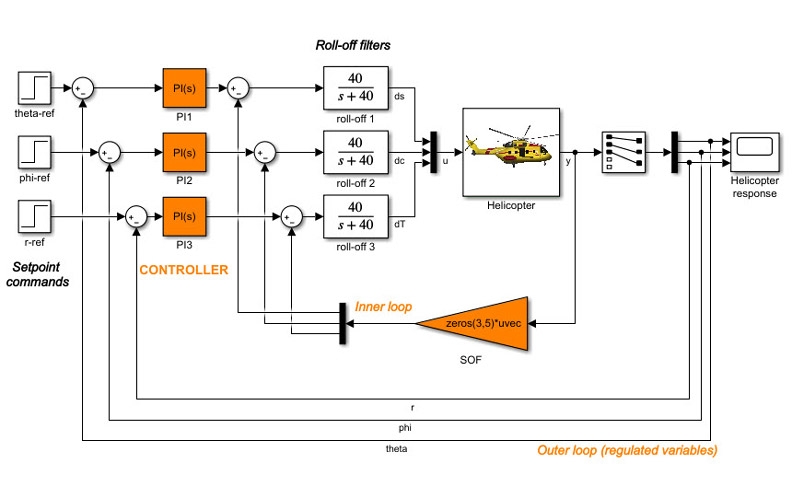
Дважды щелкните блок Input и изучите появившееся меню параметров блока. Для этого блока можно изменить форму выходного сигнала, его амплитуду и частоту. Закройте меню параметров, щелкнув кнопку Cancel.
Дважды щелкните квадрат со знаком вопроса (
Дважды щелкните прямоугольник с надписью Double click here for Simulink Help (Помощь по Simulink). Рассмотрите появившееся окно Information и закройте это окно.
Познакомьтесь с заданием параметров моделирования (расчета модели). Для этого в верхней строке меню щелкните пункт Simulation. Появляется новое меню, содержащее ряд пунктов:
Start – запуск моделирования (расчета),
Stop – останов моделирования (расчета),
Simulation parameters – задание
параметров расчета.
Щелкните пункт Simulation parameters – раскроется новое меню, содержащее несколько закладок. Основные параметры расчета задаются с использованием закладки Solver. Здесь можно задать время начала и конца процесса, способ решения дифференциальных уравнений, шаг решения, допускаемую погрешность и др. Познакомьтесь с установленными для изучаемой модели параметрами расчета и закройте окно.
Теперь, когда общие представления о модели получены, запустите модель, щелкнув значок треугольника на панели инструментов (вторая строка вверху окна). Инструменты Запуск моделирования и Останов моделирования показаны на рис. 15.
Система начинает расчет движений массы и результаты расчета выводит в виде анимационной картинки в отдельном окне onecart Animation. Изучите характер движений массы, выделите входное воздействие и выходную величину. Закройте окно анимации.
Дважды
щелкните значок осциллографа Actual Position в окне модели onecart.
Раскроется окно, содержащее экран
осциллографа, на котором отображаются
графики переходных процессов для
входного воздействия (деформация
пружины) и выходной величины – перемещения
кубика по плоскости. Это окно можно
масштабировать или раскрыть на весь
экран, используя приемы управления
окнами Windows.
Изучите графики переходных процессов,
сравните их с анимационной картинкой.
Закройте окно демонстрационного примера Spring—mass system simulation и окно MATLAB Demo Window, используя обычные приемы Windows.
Рассмотрение описанного примера позволяет получить общие представления об основных возможностях Simulink и приемах его использования. Полный набор возможностей Simulink существенно шире.
Моделирование прыгающего мяча — MATLAB и Simulink
Открытая модель
В этом примере используются две модели прыгающего мяча, чтобы продемонстрировать различные подходы к моделированию гибридных динамических систем с поведением Zeno.
Поведение Зенона неформально характеризуется бесконечным числом событий, происходящих за конечный интервал времени для определенных гибридных систем. По мере того, как мяч теряет энергию, мяч сталкивается с землей через все меньшие промежутки времени.
Гибридные динамические системы
Модель прыгающего мяча является примером гибридной динамической системы. Гибридная динамическая система — это система, которая включает в себя как непрерывную динамику, так и дискретные переходы, в которых динамика системы может меняться, а значения состояния могут скачком. Непрерывная динамика прыгающего мяча определяется следующими уравнениями:
где ускорение свободного падения, положение мяча и скорость. Система имеет два непрерывных состояния: положение и скорость.
Аспект гибридной системы модели происходит от моделирования столкновения мяча с землей. Если предположить частично упругое столкновение с землей, то скорость до столкновения и скорость после столкновения могут быть связаны коэффициентом восстановления мяча следующим образом:
Таким образом отображает скачок в непрерывном состоянии (скорости) при условии перехода, .
На изображении показан мяч, брошенный со скоростью 0 м/с с высоты 25 м.
Использование двух блоков интегратора для моделирования прыгающего мяча
Модель sldemo_bounce_two_integrators использует два блока интегратора для моделирования прыгающего мяча. Блок Integrator слева — это интегратор скорости, моделирующий первое уравнение. Блок Integrator справа является интегратором положения. Откройте диалоговое окно Block Parameters для интегратора положения, чтобы увидеть, что блок имеет нижний предел нуля. Это условие представляет собой ограничение, согласно которому мяч не может уйти под землю.
Порт состояния интегратора положения и соответствующий результат сравнения используются для определения момента удара мяча о землю и для сброса обоих интеграторов. Порт состояния интегратора скорости используется для вычисления .
Чтобы наблюдать за поведением системы Zeno, измените параметры конфигурации решателя.
Смоделируйте модель.
Поскольку мяч чаще ударяется о землю и теряет энергию, симуляция превышает значение по умолчанию Количество последовательных пересечений нуля предел 1000 .
В диалоговом окне «Параметры конфигурации» установите для параметра Алгоритм значение Адаптивный . Адаптивный алгоритм вводит сложную обработку болтливого поведения. Теперь вы можете смоделировать систему за пределами 20 секунд. Разброс состояний между 21 и 25 секундами по-прежнему велик, и программное обеспечение выдает предупреждение примерно через 20 секунд.
Используйте блок интегратора второго порядка, чтобы смоделировать прыгающий мяч
Модель sldemo_bounce использует один блок интегратора второго порядка для моделирования прыгающего мяча. В этой модели второе уравнение является внутренним по отношению к блоку Second-Order Integrator. Откройте диалоговое окно блока Second-Order Integrator и посмотрите, что имеет нижний предел нуля. На вкладке Атрибуты выберите Повторно инициализировать dx/dt, когда x достигнет насыщения . Этот параметр позволяет повторно инициализировать (в модели прыгающего мяча) до нового значения, когда достигает своего предела насыщения. Итак, в модели прыгающего мяча, когда мяч ударяется о землю, его скорость может быть установлена на другое значение, например, на скорость после удара. Обратите внимание на цикл расчета скорости после столкновения с землей. Чтобы зафиксировать скорость мяча непосредственно перед столкновением, используются выходной порт блока Second-Order Integrator и блока Memory.
затем используется для расчета скорости отскока.
В диалоговом окне «Параметры конфигурации» перейдите на панель Solver .
Смоделируйте модель.
Обратите внимание, что симуляция не вызывает проблем. Вы можете смоделировать модель, не испытывая чрезмерной вибрации через 20 секунд и без установки Алгоритм от до Адаптивный .
Сравните подходы к моделированию прыгающего мяча
Вы можете аналитически рассчитать точное время, когда мяч опускается на землю с нулевой скоростью, суммируя время, необходимое для каждого отскока. Это время представляет собой сумму бесконечного геометрического ряда, определяемого как:
, где и — начальные условия для положения и скорости соответственно.
Скорость и положение мяча должны быть тождественно нулевыми для . На рисунке показаны результаты обоих симуляций вблизи . Вертикальная красная линия на графике соответствует заданным параметрам модели. Для и вдали от обе модели дают точные и идентичные результаты. На графике видна только пурпурная линия от второй модели. Однако результаты моделирования по первой модели неточны после . График продолжает отображать чрезмерную болтовню для . Напротив, модель, которая использует блок Second-Order Integrator, устанавливается ровно на ноль для .
Модель, использующая блок Second-Order Integrator, имеет превосходящие числовые характеристики по сравнению с первой моделью, поскольку второе дифференциальное уравнение является внутренним для блока Second-Order Integrator. Алгоритмы блоков могут использовать эту взаимосвязь между двумя состояниями и использовать эвристику для подавления дребезга при определенных условиях. Эти эвристики становятся активными, когда два состояния перестают быть взаимно согласованными из-за ошибок интегрирования и вибраций.
Таким образом, вы можете использовать физические знания системы, чтобы предотвратить застревание симуляций в состоянии Zeno для определенных классов моделей Zeno.
См. также
Интегратор | Интегратор второго порядка | Память
См. также
Построение и моделирование простой модели Simulink | Начало работы с Simulink, часть 1 Видео
Из серии: Начало работы с Simulink
Узнайте, как начать работу с Simulink ®. Изучите стартовую страницу Simulink и узнайте, как использовать несколько основных блоков и компонентов моделирования. Пример показывает, как построить простую модель, которая принимает входной синусоидальный сигнал и усиливает его. В нем показано, как Simulink упрощает перетаскивание блоков в вашу модель. Он также показывает, как запустить симуляцию, чтобы убедиться, что ваша модель ведет себя так, как ожидалось.
Привет и добро пожаловать на вебинар Simulink для новых пользователей.
Меня зовут Приянка, я менеджер по маркетингу Simulink.
Привет, я Майкл, старший менеджер по маркетингу продуктов, также для Simulink.
И сегодня мы поговорим о том, как начать работу с Simulink. Здесь мы будем использовать эти четыре блока: моделирование, симуляция, по существу, три блока и совместная работа. И мы покажем вам, как использовать некоторые функции, начать работу с Simulink, приступить к созданию моделей.
Правильно. Поэтому я думаю, что мы хотим представить это с точки зрения того, как бы вы использовали Simulink. Обычно вы начинаете строить модель, проектируете систему, а затем моделируете модель, чтобы убедиться, что эта система ведет себя так, как вы ожидаете. А затем, когда вы довольны результатами и захотите поделиться своей моделью с другими — либо в своей команде, либо во всей организации — как лучше всего это сделать. Итак, мы как бы собираемся пройтись по всем этим разным вещам.
Ага. Итак, без дальнейших проволочек, мы можем начать с того, что покажем вам, как вы можете делать эти вещи в MATLAB.
Итак, позвольте мне поднять здесь MATLAB. И для тех, кто использовал MATLAB, интерфейс будет выглядеть примерно так. У нас есть это общее окно, где вы можете начать вводить команды. И чтобы начать работу с Simulink, сначала я начну вводить здесь Simulink. И если я нажму Enter, откроется стартовая страница Simulink. Давайте максимизировать его. Здесь у нас есть несколько шаблонов, которые позволяют новым пользователям начать работу. Например, у нас есть цифровой фильтр или контроллер обратной связи с некоторыми уже существующими блоками, поэтому вам не нужно открывать пустую модель Simulink.
И если у вас есть другие продукты, помимо Simulink, при прокрутке вниз вы увидите другие шаблоны отправной точки и для других продуктов. Но я думаю, что для нашей сегодняшней презентации мы просто начнем с пустой модели, верно?
Да, просто чтобы показать, как легко настроить модель, я хотел бы начать с пустой модели. А вот так будет выглядеть пустой представленный холст. В качестве первого шага я просто хочу сохранить свою модель.
Поэтому я просто последовал за своей моделью и сохранил ее в том же текущем каталоге, в котором я работаю.
Звучит хорошо. Итак, у нас есть пустая модель. И нам нужно поместить несколько блоков сюда, и лучший способ сделать это — вероятно, браузер библиотеки, верно?
Да. Итак, Simulink — это среда блок-схем. Все, что вам нужно сделать, это принести несколько блоков. Доступ к блокам можно получить из этого браузера библиотеки Simulink. Я просто щелкнул браузер библиотеки из меню здесь. И это вызывает этот браузер библиотек, в котором есть не только Simulink, но и все другие продукты и несколько блоков, которые вы можете просто перетаскивать. Таким образом, вам не нужно создавать некоторые из этих блоков самостоятельно, но вы можете использовать некоторые из уже существующих блоков.
Итак, какую модель, по вашему мнению, мы должны построить в качестве отправной точки?
Да, так что для первого примера давайте создадим очень простую модель, которая принимает синусоидальный сигнал, усиливает его в несколько раз и способ работы с сигналами.
Поэтому для этого я буду использовать библиотеку источников, в которой есть разные блоки, действующие как источник сигнала. Как видите, вы можете иметь постоянное значение в качестве источника сигнала.
Но вы ищете синусоиду.
Синусоида, да. Так что я просто принесу синусоидальный блок. Я просто перетащу его и брошу. И это внесет блок в мою модель. И когда я это сделал, это дало мне возможность выбора амплитуды синусоиды. Я могу просто проигнорировать его и использовать значение по умолчанию, равное 1, или я могу указать здесь другое значение.
Теперь давайте принесем другие блоки, позволяющие усилить эту волну. Один из приятных способов добавления блоков — это быстрая вставка, когда вы можете просто щелкнуть по холсту один раз. Это вызовет поисковое увеличительное стекло. И вы можете начать вводить названия блоков, если вы уже знаете, что использовать.
Итак, вы знаете, допустим, мы хотим добавить в модель блок усиления.
Обычно мы знаем, что коэффициент усиления используется для умножения определенного значения на коэффициент.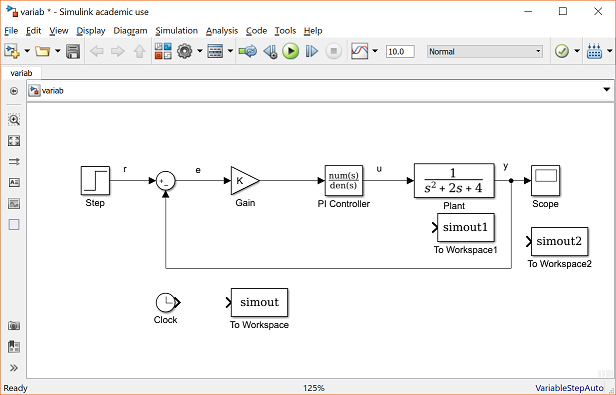
Итак, я напечатаю это. И это показало мне все результаты поиска из различных доступных библиотек. Опять же, просто просмотр и сопоставление с браузером библиотеки.
Таким образом, он говорит вам обо всем со словом «усиление» — о каждом блоке, в котором есть слово «усиление». И чтобы знать, какой из них выбрать, вы можете видеть, что под каждым именем указано название продукта, в котором существует этот блок, а затем подбиблиотека для…
Так что я просто использую библиотеку математических операций и приведу этот блок усиления. Допустим, вы хотите умножить его на коэффициент 3, я могу просто ввести 3 здесь, аналогично тому, что вы сделали для синусоиды. Но если вы пропустили это или просто выбрали значение по умолчанию, вы всегда можете дважды щелкнуть и изменить значение здесь. По мере того, как вы выполняете упражнение по моделированию, вы можете попробовать несколько значений, поскольку это работает для вас. Так что вы можете это сделать.
Так что эта небольшая подсказка, которая появляется, это просто удобство.
Да.
Таким образом, вам не нужно открывать это диалоговое окно, если вы этого не хотите.
Да, когда вы… когда вы хотите быстро что-то построить, вы можете использовать удобный механизм, который поставляется с быстрой вставкой, но в противном случае вы можете просто использовать диалоги блоков. Итак, когда у вас есть пара блоков, соединить их очень просто. Перетащите сигнал и присоедините его к следующему блоку рядом с ним.
Теперь, когда у нас есть ввод и мы усилили его значением, мы хотим его визуализировать. Теоретически мы знаем, что он должен умножить этот сигнал на 3. Итак, для визуализации…
Я сделаю это с помощью оптического прицела.
Да, масштаб — самый популярный способ визуализации сигналов в Simulink. Так что я просто искал его. Он находится в библиотеке стоков, и я добавляю его обратно в модель. Теперь я добавлю для этого два порта, потому что я хочу визуализировать выходной сигнал, а именно это. И вы видите это прекрасное руководство, которое позволяет подключать эти сигналы в любое время.
..
Да, каждый раз, когда вы выравниваете два блока, вы получаете индикатор выравнивания, который поможет вам создать красивую четкую диаграмму.
И хорошо, что ты не… Мне не пришлось тянуть сигнал. Это просто… щелчок по нему соединит его, соединит блок. Теперь, чтобы подключить этот блок, я просто перетаскиваю этот сигнал и добавляю его в блок осциллографа.
В этот раз вы не выполнили базовое перетаскивание левой кнопкой мыши. Вы сделали для этого перетаскивание правой кнопкой мыши, верно?
Да. Если бы я щелкнул левой кнопкой мыши, это просто переместило бы сигнал. Но если я щелкну правой кнопкой мыши, это разветвит сигнал. И когда у вас есть ветка, вы можете просто перетащить ее левой кнопкой мыши. Поэтому я просто выберу ветку и удалю ее на данный момент.
Затем я могу использовать некоторые сочетания клавиш, такие как пробел, чтобы подогнать всю модель для просмотра или использовать масштабирование и панорамирование с помощью колесика мыши, что позволяет вам смотреть на вашу модель.
Мы хотим максимально использовать пространство, верно?
Правильно.
Итак, мы готовы к моделированию, верно?
Да. Я закрою браузер библиотеки, открою наш блок прицела, чтобы мы могли увидеть результаты нашего моделирования. И просто запустите симуляцию. Как только я запускаю его, вы видите ввод, представляющий собой синусоидальную волну с амплитудой 2. Он усиливается в 3 раза. Здесь вы видите вывод.
Хорошо, это хорошо. Итак, вы запускаете симуляцию только для того, чтобы убедиться, что все ведет себя так, как мы ожидаем. Это так, так что мы очень счастливы. Итак, это довольно распространенный рабочий процесс, верно?
Да.
Вы строите свою модель. Каждый раз, когда вы вносите изменения, вы хотите как можно чаще нажимать кнопку воспроизведения, чтобы это в основном сохраняло вашу честность. И вы всегда проверяете, можно ли смоделировать здание.
Да. И в этом сила Simulink. Честно говоря, если бы я просто пошел сюда и изменил значение, просто нажмите кнопку Play и быстро визуализируйте его в блоке области видимости.