Позиция цифры в числе это: Как называется позиция цифры в числе?

сайт школы №127 — Системы счисления_1

Важно и полезно Информация Школа сегодня Общение Навигатор Детства Школьная группа ВК Большая перемена Засветись! Госуслуги Статистика

Системы счисления_1 Системы счисления. Формы записи чисел в позиционных системах счисления Система счисления или нумерация — это способ записи (обозначения) чисел. Символы, при помощи которых записываются числа, называются цифрами, а их совокупность — алфавитом системы счисления. Количество цифр, составляющих алфавит, называется его размерностью. Позиционная система счисления система счисления, у которой количественный эквивалент цифры зависит от ее положения в записи числа   ПРИМЕР: В привычной десятичной системе счисления значения числа образуется следующим способом: значения цифр умножаются на «веса» соответствующих разрядов и все полученные значения складываются 5034 = 5·1000+0·100+3·10+4·1   Непозиционная система счисления система счисления, у которой количественный эквивалент («вес») цифры не зависит от ее местоположения в записи числа   ПРИМЕР: Рассмотрим римское число VVV. В десятичной системе счисления это число 15. При записи числа VVV использовались одинаковые «цифры» — V. И если сравнить их между собой, то получим абсолютное равенство. Т.е. на каком бы месте не стояла цифра в записи числа, ее «вес» всегда один и тот же. В данном примере он равен 5. Позиционные системы счисления Основные достоинства любой позиционной системы счисления: Возможность записи произвольного числа при помощи ограниченного количества символов; Простота выполнений арифметических операций. Разряд — позиция цифры в числе. Основание (базис) позиционной системы счисления — это количество цифр или других знаков, используемых для записи чисел в данной системе счисления. Развернутая запись числа a=±(an-1Pn-1+an-2Pn-2+. ..+a0P0+a-1P-1+a-2P-2+…+a-mP-m) Здесь: a — само число; P — основание системы счисления; ai — цифры данной системы счисления; n — число разрядов целой части числа; m — число разрядов дробной части числа. Свернутая запись числа — запись числа в виде а=an-1an-2…a0,a-1а-2…a-mP-m Позиционных систем счисления очень много, так как за основание системы счисления можно принять любое число не меньшее 2. На уроках информатики мы подробно изучим 10-ю, 2-ю, 8-ю, 16-ю системы счисления. 10-я система счисления Основание: 10 Цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Пример: а10 = 2012 — свернутая форма записи а10 = 2·103+2·102+2·101+2·100 — развернутая форма записи 2-я система счисления Основание: 2 Цифры: 0, 1 Пример: а2 = 1011 — свернутая форма записи а2 = 1·23+0·22+1·21+1·20 — развернутая форма записи 8-я система счисления Основание: 8 Цифры: 0, 1, 2, 3, 4, 5, 6, 7 Пример: а8 = 3752 — свернутая форма записи а8 = 3·83+7·82+5·81+2·80 — развернутая форма записи 16-я система счисления Основание: 16 Цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Пример: а16 = 2A9E — свернутая форма записи а16 = 2·163+A·162+9·161+E·160 — развернутая форма записи

Простая информатика — Система счисления

Система счисления – это способ записи чисел.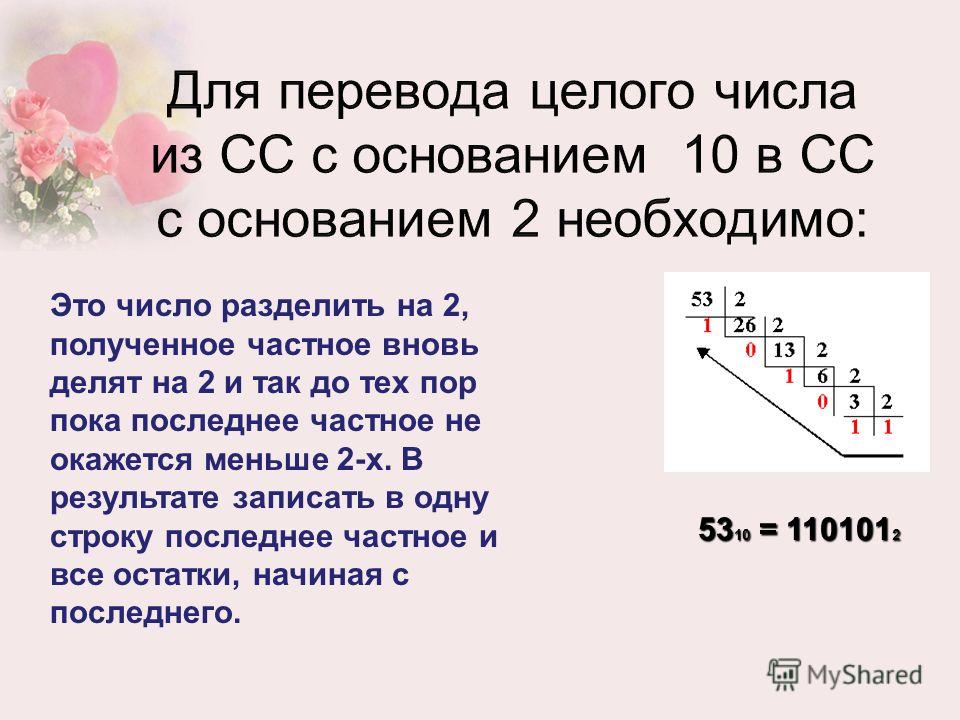 Обычно, числа записываются с помощью специальных знаков – цифр (хотя и не всегда). Если вы никогда не изучали данный вопрос, то, по крайней мере, вам должны быть известны две системы счисления – это арабская и римская. В первой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и это позиционная система счисления. А во второй – I, V, X, L, C, D, M и это непозиционная система счисления.

В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет. Например:

11 – здесь первая единица обозначает десять, а вторая – 1.
 II – здесь обе единицы обозначают единицу.

345, 259, 521 – здесь цифра 5 в первом случае обозначает 5, во втором – 50, а в третьем – 500.

XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.

Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т.

к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел). 

В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная.

Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.

Основание системы счисления – это количество знаков, которое используется для записи цифр.

Разряд — это позиция цифры в числе. Разрядность числа — количество цифр, из которых состоит число (например, 264 — трехразрядное число, 00010101 — восьмиразрядное число). Разряды нумеруются справа на лево (например, в числе 598 восьмерка занимает первый разряд, а пятерка — третий).

Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления. (придумать схему)

Одно и тоже число (значение) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.

Двоичная система счисления

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни. 

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Попробуем считать в двоичной системе:
 0 – это ноль
 1 – это один (и это предел разряда)
 10 – это два
 11 – это три (и это снова предел)
 100 – это четыре
 101 – пять
 110 – шесть
 111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные. 

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1476 = 1000 + 400 + 70 + 6

Можно пойти еще дальше и разложить так:

1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100

Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*2⁷ + 0*2

6 + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰ = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:

10001001₂ = 13710
Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.

Перевод десятичного числа в двоичное

Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:

77 / 2 = 38 (1 остаток)
 38 / 2 = 19 (0 остаток)
 19 / 2 = 9 (1 остаток)
 9 / 2 = 4 (1 остаток)
 4 / 2 = 2 (0 остаток)
 2 / 2 = 1 (0 остаток)
 1 / 2 = 0 (1 остаток)

Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:

1001101 = 1*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 1*2² + 0*2¹ + 1*2⁰ = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

Восьмеричная система счисления

Итак, современное «железо понимает» лишь двоичную систему счисления.

Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.

В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:

000 – 0
 001 – 1
 010 – 2
 011 – 3
 100 – 4
 101 – 5
 110 – 6
 111 – 7

Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:

1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135

Т. е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 1011101₂ = 1358.

Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.

100₈ = 1 0 0 = 001 000 000 = 001000000 = 10000002 

Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:

6728 = 6 * 8² + 7 * 8¹ + 2 * 8⁰ = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
 1008 = 1 * 8² + 0 * 8¹ + 0 * 8⁰ = 6410

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.

В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).  

При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:

Например:
 10001100101 = 0100 1100 0101 = 4 C 5 = 4C5

Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):

4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221

Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи — это FF.

FF = 15 * 161 + 15 * 160 = 240 + 15 = 255 

255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние

Разрядное значение — диаграммы с десятичными знаками

Разрядное значение в математике описывает значение каждой цифры в числе в зависимости от ее положения. Эти позиции начинаются с разряда единиц (единиц). Порядок разряда цифр в числе справа налево выражается единицами/единицами, десятками, сотнями, тысячами, десятками тысяч и так далее.

9Таблица стоимости места 0009

1.	Что такое разрядное значение?
2.
3.	Таблица разрядов с десятичными знаками
4.	Разрядная стоимость и номинальная стоимость
5.	Часто задаваемые вопросы о стоимости места

Что такое разрядное значение?

Разрядное значение — это значение каждой цифры в числе. Значение каждой цифры в числе зависит от ее положения. Число может иметь две одинаковые цифры, но разные значения, что определяется позицией, которую занимает цифра в числе.

Разрядное значение Значение

Разрядное значение — это значение цифры в соответствии с ее положением в числе, например единицы, десятки, сотни и т. д. Например, разрядное значение 5 в 3458 равно 5 десяткам или 50. Однако разрядное значение 5 в 5781 выражается как 5 тысяч или 5000. Важно понимать, что цифра может быть одной и той же, но ее значение зависит от ее положения в числе.

Пример: Запишите разрядность каждой цифры в числе 543.

Решение: Правильное значение разряда каждой цифры в числе может быть выражено следующим образом:

• 5 × 100 = 500 или 5 сотен
• 4 × 10 = 40 или 4 десятка
• 3 × 1 = 3 или 3 единицы

Таблица стоимости мест

Таблицы разрядов помогают нам убедиться, что цифры выровнены в правильных местах. Диаграмма разряда показывает правильное положение или место цифры в числе. Чтобы точно определить позиционные значения или ценность различных цифр в числе, мы сначала записываем данные цифры в диаграмму разрядности, чтобы проверить их положение. Чтобы упростить процесс, большие числа разбиты на точки, разделенные запятыми. Наиболее часто используются два типа диаграмм стоимости мест:

• Индийская таблица разрядности
• Таблица международных разрядов

Мы можем обратиться к международной или индийской диаграмме стоимости мест, основанной на системе счисления, которой следуют обе диаграммы. Индийская диаграмма стоимости места основана на индийской системе счисления, в то время как международная диаграмма стоимости места основана на международно принятой системе счисления. Основное различие между индийской и международной системами счисления заключается в размещении разделителей (запятых) и номенклатуре различных разрядных значений.

Индийская диаграмма разрядности

Индийская диаграмма разрядности представляет собой таблицу, которая используется для определения значения каждой цифры в числе в зависимости от ее положения в соответствии с индийской системой счисления.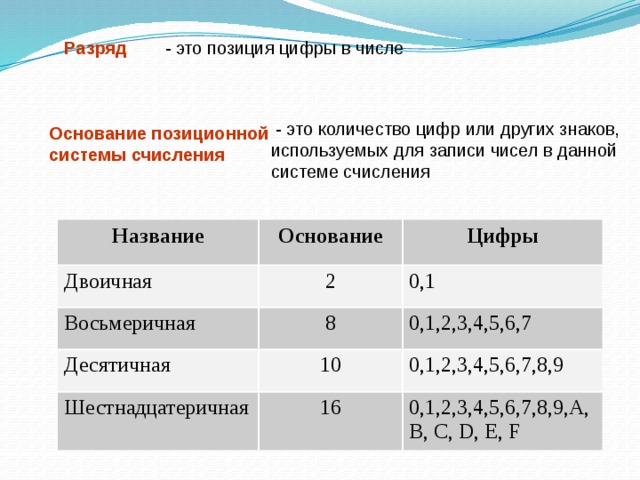 На этой диаграмме стоимости места 10-значное число сгруппировано в периоды единиц, тысяч, лакхов, крор и так далее. Эти числа разделяются запятыми по правилу 3:2:2. Это означает, что начиная справа первая запятая ставится после 3 цифр, затем следующие запятые ставятся после каждых 2 цифр. Например, обратите внимание на запятые в следующем числе: 5,43,13,62,283

Обратите внимание на приведенную ниже таблицу индийских разрядов, которая показывает разрядность цифр до десяти крор.

Международная таблица стоимостей мест

Международная система счисления используется во всем мире, в которой мы считаем в порядке единиц, десятков, сотен, тысяч, десятков тысяч, сотен тысяч, миллионов и так далее. В этой диаграмме разрядности числа сгруппированы в периоды единиц, тысяч, миллионов и т. д. и разделены запятой после каждых трех цифр, начиная справа. Например, обратите внимание на запятые в следующем числе: 135,912 332. Обратите внимание на приведенную ниже международную диаграмму разрядности, которая показывает разрядность цифр до сотен миллионов.

Пригодные для печати таблицы разрядной стоимости

Запоминание и решение задач по системам разрядной стоимости становится проще с помощью печатаемой таблицы разрядной стоимости. На этих диаграммах значения мест напечатаны в табличной форме через пробелы для каждой цифры в числе. Обращаясь к этим диаграммам для решения проблемы, мы можем напрямую поместить цифры в их соответствующие позиции в соответствии с цифрами в числе и соответственно оценить их позиционные значения.

Таблица разрядов с десятичными знаками

Таблица значений десятичных разрядов показывает разрядность цифр в десятичном числе. Десятичная система счисления используется для выражения целых чисел и дробей вместе с помощью десятичной точки. Эта десятичная точка находится между целой частью числа и дробной частью. В то время как целая числовая часть следует обычной таблице разрядов единиц, десятков, сотен и т. д., есть небольшая разница в разрядах чисел справа от десятичной точки. Если мы пойдем вправо после запятой, значения разрядов начнутся с десятых и продолжатся как сотые, тысячные и так далее. Первое место справа от запятой стоит на одной десятой (1/10 ^-й ), следующая 1/100 и так далее. Обратите внимание на следующую таблицу значений разрядов для десятичных чисел.

Разрядная стоимость и номинальная стоимость

Номинальная стоимость цифры в любом числе — это сама цифра. Независимо от того, является ли число однозначным, двузначным или любым числом, каждая цифра имеет свое номинальное значение. Давайте разберемся в этом на следующих примерах.

• Если задано число 4, то номинал 4 равен 4, а разряд 4 также равен 4 (4 единицы = 4 × 1 = 4).
• Для заданного числа 78 номинальная стоимость 7 равна 7, а разрядность равна 70 (7 десятков = 7 × 10 = 70).
• Для 52369 номинальная стоимость 3 равна 3, а разрядная стоимость равна 300 (3 сотни = 3 × 100 = 300).

Разница между разрядным значением и номиналом

Разрядное значение описывает позицию цифры в заданном числе. С другой стороны, номинал представляет собой само число. Возьмем в качестве примера число, скажем, 1437. Таблица, приведенная ниже, объясняет разницу между разрядным значением и номиналом цифр в этом числе.

Цифры в номере 1437	Место Значение	Номинальная стоимость
1	1 тысяча (1 × 1000 = 1000)	1
4	4 Сотни (4 × 100 = 400)	4
3	3 Десятки (3 × 10 = 30)	3
7	7 Единицы или единицы ( 7 × 1 = 7)	7

Разрядное значение в числах

Разрядное значение в числах может быть выражено двумя различными способами. Например, разрядное значение 4 в числе 2458 может быть выражено как 4 сотни или 400. В другом примере разрядное значение 4 в числе 4681 выражается как 4 тысячи или 4000.

Проще говоря, если нам нужно выразить значение разряда в числовой форме, мы просто умножаем число на имя столбца, к которому оно относится. Например, если нам нужно найти значение разряда 5 в 67538, мы сначала поместим данное число под таблицу значений разряда так, чтобы каждая цифра была правильно размещена в соответствующем столбце. В этом случае мы видим, что 5 находится в столбце сотен. Итак, мы можем сказать, что разрядное значение числа 5 равно 5 × 100 = 500. Следовательно, разрядное значение числа 5 равно 500 в данном числе.

☛ Статьи по теме

• Калькулятор стоимости места
• Разница между разрядной стоимостью и номинальной стоимостью

Часто задаваемые вопросы о стоимости места

Что такое разрядное значение в математике?

Разрядное значение — это значение каждой цифры в числе.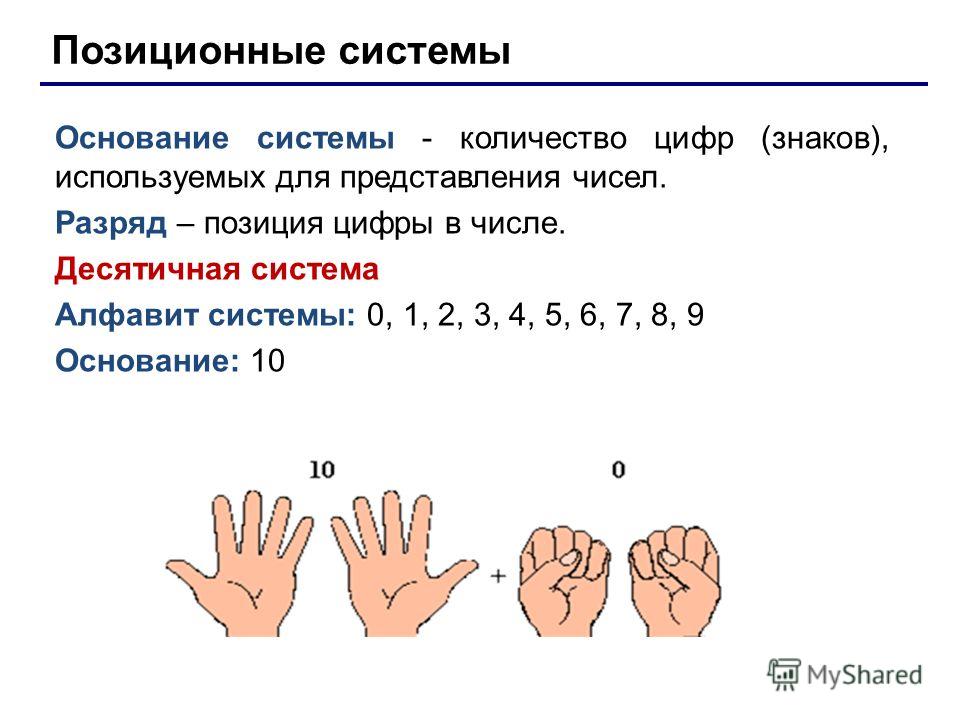 Значение каждой цифры в числе зависит от ее положения. Число может иметь две одинаковые цифры, но разные значения, что определяется позицией, которую занимает цифра в числе. Например, разрядное значение ‘9’ в числе 8934 будет 9 сотен или 900, потому что 9 стоит на разряде сотен.

Какое место занимает число 6 в 64?

Так как 6 стоит в разряде десятков, разрядное значение 6 в 64 равно 6 десяткам, т. е. 6 × 10 = 60.

Каков пример разрядного значения в числах?

Разрядное значение представляет ценность цифры в числе. Несколько примеров разрядных значений приведены ниже:

Каково разрядное значение числа 5 из 50?

Разрядное значение — это значение каждой цифры в числе. Порядковый номер цифры 5 в числе 50 равен 5 десяткам, т. е. 5 × 10 = 50,

Что такое разрядная стоимость и номинальная стоимость с примером?

Номинал цифры в любом числе — это сама цифра, а разрядность — это ее позиция в числе. Например, номинальная стоимость 7 в числе 2769 равна 7, а разрядная стоимость равна 7 сотням или 700.

Что такое таблица разрядов?

Таблица значений разрядов — это таблица, которая используется для определения значения каждой цифры в числе на основе ее положения в системе счисления. Чтобы точно определить ценность различных цифр в числе, мы помещаем данное число в таблицу разрядности так, чтобы было видно разрядность каждой цифры. Чтобы упростить процесс, большие числа разбиты на точки, разделенные запятыми. Наиболее часто используются два типа диаграмм места: индийская диаграмма места и международная диаграмма места.

Как составить таблицу стоимостей мест?

Чтобы составить диаграмму разрядности, мы можем использовать следующие шаги:

• Шаг 1: Нарисуйте столбцы, показывающие разные периоды в зависимости от типа системы счисления: единицы, десятки, сотни, тысячи и т. д.
• Шаг 2: Под каждым периодом нарисуйте подстолбцы, чтобы показать различные значения места.

Вы можете обратиться к индийской диаграмме разрядной стоимости и международной таблице разрядной стоимости в приведенных выше разделах для разных периодов и разрядных значений цифр в числе в соответствии с типом системы счисления.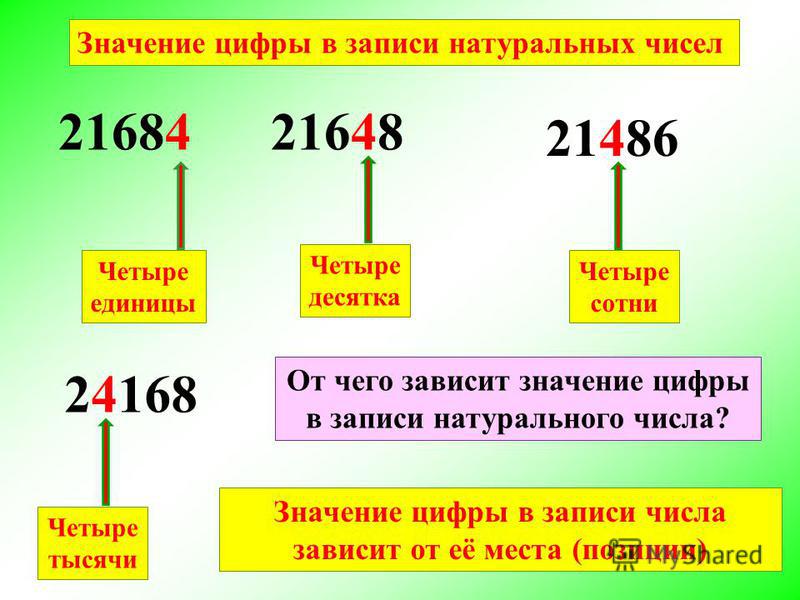

Почему значение разряда в числах важно?

Концепция разряда в числах важна, поскольку она дает значение каждой цифры в числе в соответствии с ее положением. Сущность чисел в целом можно понять только через знание разрядных значений.

Каково разрядное значение нуля?

Позиционное значение нуля всегда равно нулю. Например, в данном числе 4078 ноль стоит под разрядом сотен. Итак, это выражается как 0 сотен, то есть 0 × 100 = 0,9.0005

Как найти разрядное значение в десятичных числах?

В десятичных числах порядковый номер цифр после запятой выражается немного по-другому. Мы знаем, что десятичное число состоит из целого числа и дробной части, которая пишется после запятой. Целая числовая часть следует обычной таблице разрядов единиц, десятков, сотен. Теперь, если мы пойдем вправо после запятой, разрядные значения начинаются с десятых и продолжаются как сотые, тысячные и так далее. Например, запишем разрядное значение всех цифр в следующем десятичном числе: 578,43

• 5 находится в столбце сотен, следовательно, разрядное значение числа 5 равно 5 сотням, или 5 × 100 = 500
.
• 7 находится в столбце десятков, следовательно, разряд 7 равен 7 десяткам, или 7 × 10 = 70
• 8 находится в столбце единиц, следовательно, разрядное значение числа 8 равно 8 единицам, или 8 × 1 = 8
.
• 4 находится под столбцом десятых, поэтому разрядное значение 4 равно 4 десятым, или 4/10 = 0,4
• 3 находится под столбцом сотых, поэтому разрядное значение 3 равно 3 сотым, или 3/100 = 0,03

терминология — Какой правильный термин для обозначения положения цифры в числе?

Задавать вопрос

спросил 5 лет, 9 месяцев назад

Изменено 5 лет, 9 месяцев назад

Просмотрено 1к раз

Я пишу документацию для базы кода и хочу, чтобы моя документация была максимально ясной и недвусмысленной. Я ищу правильный термин для обозначения положения цифры в числе.

Возьмите число 00100000, и я хочу сослаться на позицию 1. До сих пор я придумал бит «размещение»; однако неясно, в каком направлении увеличивается размещение бит, без дополнительных объяснений. Я знаю, что начальный бит называется «самым значащим битом», а самый правый — «младшим значащим битом»; следовательно, имеет ли смысл использовать термин «значение бита» или существует математический термин для его описания?

Пример того, как я планирую использовать этот термин: размещение 1 равно 5, или значение 1 равно 5. 6

В позиционной системе счисления вес каждой цифры определяется ее позицией в числе .

1

Это вопрос как по информатике, так и по английскому языку. Битовые позиции в числовом слове имеют запутанные аспекты. Мы читаем слева направо, но биты нумеруются справа налево. Кроме того, младший бит называется «бит 0», а не «бит 1». Таким образом, , а не изначально ясно для носителей английского языка в целом, является ли «пятый» бит 5-м справа или 5-м слева. Даже программисты могут запутаться, особенно новые «дети», которых часто учат языкам высокого уровня без базовых знаний об оборудовании или даже языке ассемблера.

Теперь к самому вопросу. Я бы подошел к этому одним из двух способов. Если бы я знал, что документацию следует читать от начала до конца, я бы включил в начало короткий раздел с рисунком числового слова и его битов и объяснил, что бит 0 находится справа, а бит 1 — рядом с ним. и т.д. На чертеже можно было бы все это показать. Затем в остальной части документа просто укажите «бит 7» или «бит 23», как если бы читатель понял, что вы имеете в виду. Другой распространенной технической формой является то, что «бит 0» — это 9.0311 1-битный , «бит 1» — это 2-битный , «бит 4» — это 16-битный и т.