Системы счисления. Позиционная и непозиционная системы счисления
Систему счисления можно определить как способ записи чисел как количественной характеристики (отвечает на вопрос «сколько») чего-либо. Синонимом понятию «система счисления» является слово «нумерация».
В любой системе счисления числа записываются с помощью специальных, используемых в данной системе знаков-символов, которые все вместе формируют алфавит этой системы счисления. Пользуясь десятичной системой счисления мы привыкли называть символы ее алфавита цифрами.
Одно и тоже число (значение, количество) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.
Широко известны две системы счисления – арабская и римская.
Алфавит арабской системы счисления:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Арабская система счисления – это позиционная система счисления.
Алфавит римской системы счисления:
I, V, X, L, C, D, M
Римская система счисления относится к непозиционным.
В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, в непозиционных такой однозначной зависимости нет. Например:
11– здесь первая единица обозначает десять количественных единиц, вторая – только одну единицу.II– здесь обе единицы обозначают одну единицу.345,259,521– здесь цифра 5 в первом случае обозначает 5 единиц, во втором – 50, в третьем – 500.XXV,XVI,VII– здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.
Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, так как они легко описываются с помощью универсальных алгоритмов. Например, умножение в столбик или поразрядное сравнение двух чисел.
Например, умножение в столбик или поразрядное сравнение двух чисел.
В связи с этим позиционные системы счисления нашли более широкое распространение. Помимо всем известной десятичной, в которой используются десять цифр от 0 до 9, в вычислительных технике и технологиях нашли применение такие системы как двоичная (алфавит состоит из цифр 0 и 1), восьмеричная (алфавит: 0, 1, 2, 3, 4, 5, 6, 7) и шестнадцатеричная (алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Следует отметить, важную роль нуля. Открытие этой цифры в истории человечества сыграло большое значение в формировании позиционных систем счисления.
Основание системы счисления
Основание системы счисления равно размерности алфавита системы счисления. Размерность алфавита – это количество цифр, составляющих алфавит.
Размерность алфавита – это количество цифр, составляющих алфавит.
Разряд – это позиция цифры в числе. От того, в каком месте числа находится цифра, зависит обозначаемое ею количество, то есть то, что она значит.
Разрядность числа – количество цифр, из которых состоит число. Например, 264 – трехразрядное число в десятичной системе счисления, 00010101 – восьмиразрядное число в двоичной системе счисления. Разряды нумеруются справа налево. Например, в числе 598 восьмерка занимает первый разряд, а пятерка – третий.
В позиционных системах счисления числа записываются таким образом, что каждый следующий при движении справа налево разряд больше другого на одну степень основания системы счисления.
Другими словами, у каждого разряда есть свой вес, представляющий собой основание системы счисления, возведенное в степень, соответствующую данному разряду. Показатель степени соотносится с разрядом как разряд-1.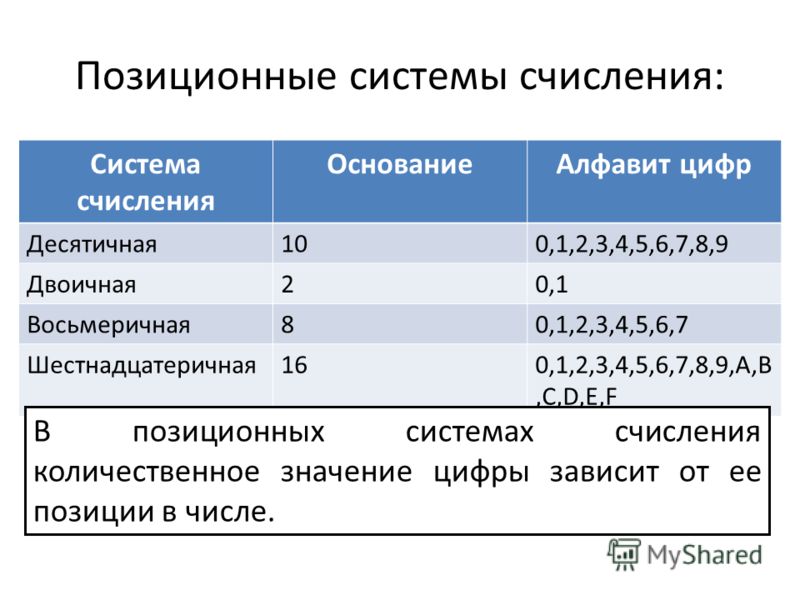 Например, в примере десятичного числа ниже цифра 8 находится в четвертом разряде числа. Значит, обозначаемое ею количество вычисляется вычисляется как произведение числа 8 на основание системы счисления (здесь 10) в степени 3.
Например, в примере десятичного числа ниже цифра 8 находится в четвертом разряде числа. Значит, обозначаемое ею количество вычисляется вычисляется как произведение числа 8 на основание системы счисления (здесь 10) в степени 3.
8325 = 8 * 1000 + 3 * 100 + 2 * 10 + 5
8325 = 8 * 103 + 3 * 102 + 2 * 101 + 5 * 100
Перевод чисел в позиционных системах счисления_8 класс_Урок информатики
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Невероятная позиционная система | plus.maths.org
Сентябрь 2008 г.
Символы 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 настолько распространены, что мы редко осознаем, насколько уникальна наша система счисления. . Полторы тысячи лет развития дали нам чрезвычайно лаконичный метод записи даже очень больших чисел. Наши числительные произошли от системы, разработанной индуистскими учеными Индии в середине первого тысячелетия нашей эры. Их система была, в свою очередь, принята арабами, которые в конце концов передали ее Европе в двенадцатом веке. По этой причине эти цифры, как правило, обозначаются как 9.0006 индо-арабские цифры .
Ключом к успеху этой системы является ее позиционный характер. В нашем распоряжении всего десять символов, но мы, конечно, не ограничены записью десяти различных значений. Одна из первых вещей, которую мы все узнаём в школе, это то, что наши числа расположены в столбцах. Читая справа налево, мы сначала имеем столбец единиц, затем десятки, сотни, тысячи и так далее.
Важно не только то, какие символы мы записываем, но и где мы размещаем их в таком расположении. Это то, что мы подразумеваем под позиционной системой счисления. Но почему вообще должна возникнуть позиционная система?
Одна из первых вещей, которую мы все узнаём в школе, это то, что наши числа расположены в столбцах. Читая справа налево, мы сначала имеем столбец единиц, затем десятки, сотни, тысячи и так далее.
Важно не только то, какие символы мы записываем, но и где мы размещаем их в таком расположении. Это то, что мы подразумеваем под позиционной системой счисления. Но почему вообще должна возникнуть позиционная система?
Начало нумерации
Карта MapMaster, воспроизведенная под лицензией свободной документации GNU.
Самые ранние системы счисления возникли из желания человека считать. Самой примитивной и основной из всех таких систем является система учетных меток , в которой мы размещаем одну метку на странице для каждого подсчитываемого элемента. Но даже если мы посчитаем до числа среднего размера, мы получим растянутую коллекцию счетных меток на странице, которые не очень приятны для глаз. Поэтому мы вводим доп.
шагов, например, если диагональная линия, проходящая через четыре вертикальные отметки, обозначает пять, — это означает введение в нашу систему совершенно новой цифры.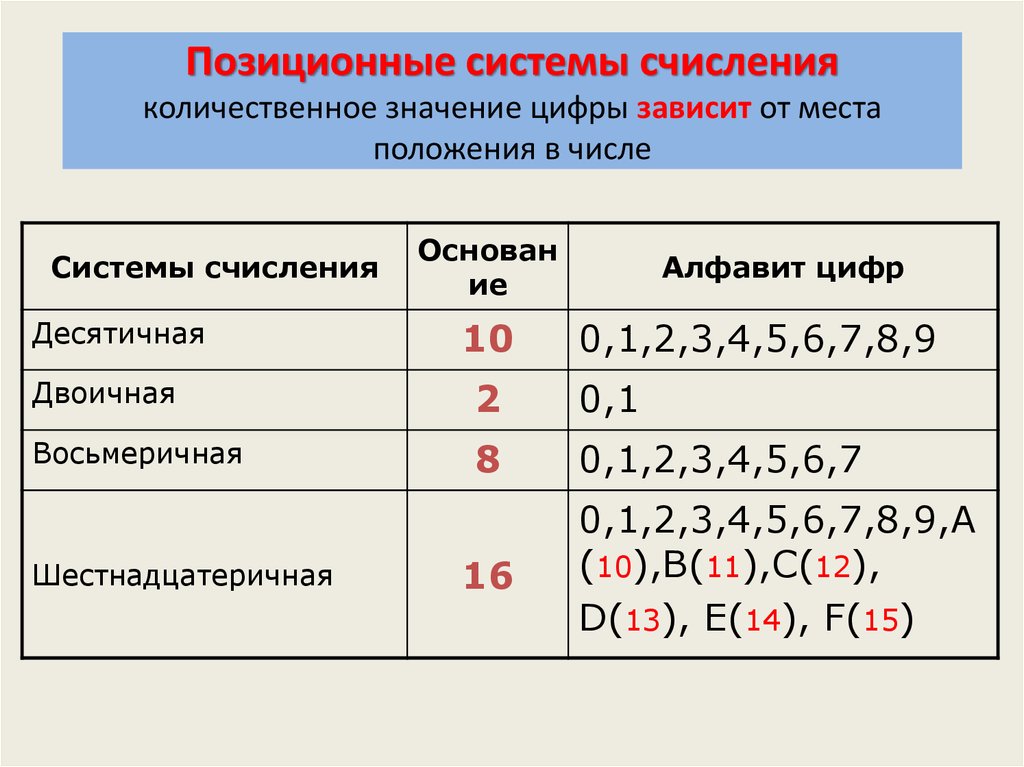 Теперь мы можем записывать числа, которые гораздо легче воспринимать с первого взгляда. Но по мере того, как мы записываем все большие и большие числа, мы обнаруживаем, что обозначения снова становятся громоздкими. Одним из решений этой проблемы является введение новых символов. Это
именно так исторически развивались системы счисления. В качестве примера системы с различными символами рассмотрим древнюю вавилонскую систему. Первые четыре символа даны на рисунке 1:
Теперь мы можем записывать числа, которые гораздо легче воспринимать с первого взгляда. Но по мере того, как мы записываем все большие и большие числа, мы обнаруживаем, что обозначения снова становятся громоздкими. Одним из решений этой проблемы является введение новых символов. Это
именно так исторически развивались системы счисления. В качестве примера системы с различными символами рассмотрим древнюю вавилонскую систему. Первые четыре символа даны на рисунке 1:
Рисунок 1: Вавилонские цифры
Эта система была впервые разработана шумерами около 3500 г. до н.э., но обычно ассоциируется с вавилонянами. Сотня теперь представлена одним символом, что является значительным улучшением по сравнению с нашей первоначальной системой подсчета. Даже большие числа, форма подсчета которых была бы ужасной, теперь можно записать более кратко. Например, 3964 записывается следующим образом:
Рис. 2: Число 3964, записанное вавилонскими цифрами.
Обратите внимание, что благодаря размещению этих символов в столбцах, а не в ряд, можно сэкономить еще больше места:
Важно отметить одну важную вещь, касающуюся этих цифр, это то, что символ единицы всегда означает единицу, символ сотни всегда означает сотню и т. д. На самом деле не имеет значения, в каком порядке мы пишем символы. Число
д. На самом деле не имеет значения, в каком порядке мы пишем символы. Число
также представляет собой число 3964; порядок символов не имеет значения. Вавилоняне имели тенденцию использовать разумное расположение: они группировали подобные символы вместе и располагали группы в порядке возрастания, читая справа налево.
В отличие от индийско-арабских числительных, эта вавилонская система непозиционная . На рисунках 3 и 4 приведены дополнительные примеры непозиционных систем счисления.
Рис. 3: Египетские цифры, около 3000 г. до н.э.
Рисунок 4: Минойские (линейное письмо B) цифры, около 1500 г. до н.э.
Системы счисления, представленные на рисунках 3 и 4, кажутся более легкими для восприятия, чем вавилонская система. Причина этого, возможно, в том, что они используют только один знак для каждого из 100 и 1000, в отличие от составных вавилонских символов. Несмотря на это, мы продолжаем концентрироваться на вавилонской системе, потому что вавилоняне ввели новшество, которое никогда не приходило в голову
Египтяне или минойцы (насколько нам известно. ..!).
..!).
Займите позицию
Часы напоминают нам о римской непозиционной системе счисления и вавилонской шестидесятеричной системе счисления.
Вавилоняне предположительно осознавали недостатки своей непозиционной системы счисления. Используя символы, приведенные на рис. 1, они могли записать любое число до 9999 включительно, но не большее число. Если бы они хотели записывать все большие числа, они были бы вынуждены вводить все новые и новые символы. Это поставило бы перед ними две проблемы: громоздкие обозначения и необходимость запоминать большое количество символов. Вавилонянам нужен был другой подход к записи больших чисел. И новым подходом была, конечно же, позиционная система.
Первым шагом было удаление всех символов, кроме единиц и десяти. Затем, как и мы, они выстраивали комбинации этих символов в столбцы, читая справа налево. Однако, в отличие от нашей, вавилонская система счисления была не десятичной, а шестидесятеричной : последовательные столбцы представляли степени 60, а не 10. Мы унаследовали эту систему как для измерения времени, так и для измерения углов:
например 60 секунд в минуте.
Мы унаследовали эту систему как для измерения времени, так и для измерения углов:
например 60 секунд в минуте.
В следующем примере мы нарисуем границы вокруг столбцов для наглядности, хотя сами вавилоняне этого не делали. Столбец с наименьшим значением — это самый правый столбец, который может содержать любое число до 59 включительно.— это шестидесятеричная версия столбца единиц. Любое число, меньшее или равное 59, появится в этой системе, как это было в более ранней непозиционной системе. системы, например, 42 равно
. Чтобы выйти за пределы 59, мы должны добавить еще один столбец слева, который представляет числа, кратные 60. Например,
представляет (1 × 60) + (0 × 1) = 60, (символ в правом столбце указывает на пустой столбец — об этом чуть позже). Строка символов
представляет собой (11 × 60) + (24 × 1) = 684,9.0003
С одним столбцом наш предел 59; с двумя мы можем записать числа до (59 × 60) + (59 × 1) = 3599. Чтобы подняться выше, нам нужно только добавить дополнительные столбцы слева, представляющие кратные более высокой степени 60. Если мы добавим третий столбец, то введенное там значение представляет собой кратное 3600 = 60 × 60, а четвертый столбец будет представляют кратные 216 000 = 60 3 . С
в трех столбцах мы можем записывать числа до (59 × 3600) + (59 × 60) + (59× 1) = 215 999. В этой новой схеме наше любимое число 3964 становится:
Если мы добавим третий столбец, то введенное там значение представляет собой кратное 3600 = 60 × 60, а четвертый столбец будет представляют кратные 216 000 = 60 3 . С
в трех столбцах мы можем записывать числа до (59 × 3600) + (59 × 60) + (59× 1) = 215 999. В этой новой схеме наше любимое число 3964 становится:
, потому что 3964 = (1 × 3600) + (6 × 60) + (4 × 1).
Легко видеть, что мы можем бесконечно расширять эту систему, просто добавляя дополнительные столбцы слева. Больше нет необходимости в новых символах.
Несколько слов следует сказать о «-», используемом для обозначения пустого столбца в представлении числа 60. Во-первых, у вавилонян не было такого символа. Они либо оставляли пустое место для обозначения пустого столбца, либо вообще не отмечали столбец, что создавало большую вероятность двусмысленности в их числительных. Например
может означать (21 × 60) + (12 × 1) = 1 272, или (21 × 3 600) + (12 × 1) = 75 612, или (21 × 3 600) + (12 × 60) = 76 320 и т. д. Однако кажется, что у вавилонян здесь никогда не было проблем, поскольку из контекста всегда было ясно, какое число имелось в виду. Только когда персы унаследовали вавилонскую систему счисления около 400 г. до н.э., был введен знак для обозначения пустого столбца. Знак
было
д. Однако кажется, что у вавилонян здесь никогда не было проблем, поскольку из контекста всегда было ясно, какое число имелось в виду. Только когда персы унаследовали вавилонскую систему счисления около 400 г. до н.э., был введен знак для обозначения пустого столбца. Знак
было
поэтому 216001 записывается как
Окончательный вердикт
По сравнению с непозиционными системами позиционные системы относительно редки в истории. Однако преимущества использования позиционной системы очевидны: она более лаконична и проста в использовании. Наша собственная система доводит эту лаконичность до крайности: вместо комбинации цифр, составляющих значение в каждой позиции, мы имеем ровно один символ на позицию. Легко понять, почему
вавилоняне сами не использовали этот способ ведения дел: всего им потребовалось бы 60 символов, поэтому их система была бы довольно сложной для памяти. Наш «один символ на позицию» означает, что наши цифры настолько лаконичны, насколько это возможно. Просто сравните наш способ написания 9 876 543 210 с вавилонским аналогом
Просто сравните наш способ написания 9 876 543 210 с вавилонским аналогом
Однако у индийско-арабских цифр есть и обратная сторона. Все наши цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, являются абстрактными символами, которые имеют мало связи или не имеют никакой связи с величинами, которые они представляют, кроме той связи, которую мы им навязываем. Вавилонский способ записи «два» более явно связан с количеством два, чем с символом 2. Чтобы произвести арифметические действия с нашими числительными, мы должны
ознакомиться с правилами их работы. Мы должны знать, что когда мы добавляем символ 1 к символу 2, мы получаем символ 3 и так далее. Нам нужно знать нашу таблицу умножения. Нам нужно знать, что когда мы прибавляем 1 к 9в определенном столбце, то мы должны ввести 0 в этом столбце и добавить 1 в следующий столбец слева. При таком перечислении эти правила начинают казаться сложными.
для внешнего наблюдателя, который не имеет предварительных знаний о нашей системе счисления. У всех у нас есть определенная способность обращаться с этими цифрами, потому что она вбита в нас с раннего возраста. С другой стороны, арифметика вавилонских цифр гораздо более механическая. Мы по-прежнему можем использовать подход «столбец за столбцом», но теперь нам нужно только собрать вместе, как символы, а затем применить следующие два
правила:
С другой стороны, арифметика вавилонских цифр гораздо более механическая. Мы по-прежнему можем использовать подход «столбец за столбцом», но теперь нам нужно только собрать вместе, как символы, а затем применить следующие два
правила:
| 1) Заменять каждые десять вхождений | на один | . |
| 2) Если шесть из | встречаются в определенном столбце, затем удалите их и | |
| введите | в следующую колонку слева. |
Индуистско-арабские цифры: любимые и незаменимые.
Расхвалив сказочные позиционные системы, я никоим образом не хочу умалять значение наших собственных числительных. Дело в том, что мы находим их простыми в использовании — потому ли, что нас обучают их использованию с раннего возраста, или потому, что они изначально просты в использовании, не имеет значения, по крайней мере, с прагматической точки зрения. По правде говоря, эти числительные настолько вездесущи (тем более
чем когда-либо были вавилонские цифры), что нам было бы чрезвычайно трудно изменить их, даже если бы мы захотели. Похоже, они здесь, чтобы остаться! Поэтому в следующий раз, когда вы будете проверять свой банковский счет или набирать номер телефона, подумайте о столетиях развития, которые ушли на создание этих бесценных знаков.
По правде говоря, эти числительные настолько вездесущи (тем более
чем когда-либо были вавилонские цифры), что нам было бы чрезвычайно трудно изменить их, даже если бы мы захотели. Похоже, они здесь, чтобы остаться! Поэтому в следующий раз, когда вы будете проверять свой банковский счет или набирать номер телефона, подумайте о столетиях развития, которые ушли на создание этих бесценных знаков.
Об авторе
Кристофер Холлингс получил степень и докторскую степень по математике в Йоркском университете. В настоящее время он является постдокторантом Центра алгебры Лиссабонского университета. Основные области его интересов — теория полугрупп и история математики. Он любит писать, как по профессиональным причинам, так и для отдыха. Другие увлечения включают чтение и фотографию, а также трудно говорить по-португальски.
Позиционная система счисления и примеры » NetworkUstad
В позиционной системе счисления каждый символ представляет различное значение в зависимости от позиции, которую они занимают в числе, и каждая система имеет значение, которое относится к числу, непосредственно стоящему рядом с ним. Суммарное значение позиционного числа равно сумме результирующего значения всех позиций. Десятичная система счисления известна как позиционная система счисления , потому что значение числа зависит от положения цифр. Например, число 12345 имеет совсем другое значение, чем число 9.0134 54321 , хотя в обоих номерах используются одни и те же цифры. Позиция, в которой появляется цифра, влияет на значение этой цифры.
Суммарное значение позиционного числа равно сумме результирующего значения всех позиций. Десятичная система счисления известна как позиционная система счисления , потому что значение числа зависит от положения цифр. Например, число 12345 имеет совсем другое значение, чем число 9.0134 54321 , хотя в обоих номерах используются одни и те же цифры. Позиция, в которой появляется цифра, влияет на значение этой цифры.
В позиционной системе счисления значение каждой цифры определяется тем, на каком месте она стоит в полном числе. Наименьшее разрядное значение — это крайняя правая позиция , а каждая последующая позиция слева имеет на более высокое разрядное значение . Таким образом, крайняя правая позиция представляет столбец «единицы», следующая позиция представляет столбец «десятки», следующая позиция представляет «сотни», а следующая позиция представляет «тысячи», затем десять тысяч и т. д. Таким образом, число 54321 представляет 5 х десять тысяч, 4 х одна тысяча 3 х сто, 2 десятка и 1 х один, тогда как число 12345 представляет 1 х десять тысяч 2 х одна тысяча 3 сотни, 4 х десятки и 5 единиц. Двоичная, восьмеричная и шестнадцатеричная системы счисления являются примерами позиционной системы счисления.
Двоичная, восьмеричная и шестнадцатеричная системы счисления являются примерами позиционной системы счисления.
Десятичное позиционное представление
Десятичное позиционное представление работает, как описано в таблице на рисунке ниже. Чтобы использовать позиционную систему счисления, сопоставьте данное число с его позиционным значением. Стрелка с левой стороны показывает, что таблица может быть расширена в соответствии с позицией и может выполнять вычисления.
ОснованиеТермин Основание используется для описания количества цифр, используемых в позиционной системе счисления, или для обозначения основания позиционной системы счисления. Десятичная система счисления основана на 10, поэтому основание равно 10.
Позиция в Показывает позицию десятичного числа. Позиция начинается справа налево. Таким образом, 0 — это 1-я позиция, 1 — 2-я позиция, 2 — 3-я позиция и так далее. Числа также представляют экспоненциальное значение, которое будет использоваться для вычисления позиционного значения 4-й строки.
3-я строка вычисляет позиционное значение, беря систему счисления и повышая ее на экспоненциальное значение его позиции. Важно то, что n 0 всегда = 1.
Позиция ЗначениеПервая строка показывает систему счисления или систему счисления. Таким образом, указанное значение слева направо представляет единицы тысяч, сотен, десятков и единиц.
Пример – 12345 и 54321
Двоичное позиционное представлениеДвоичное позиционное представление также работает аналогично десятичной системе счисления, как показано на рисунке ниже. У него также есть Radix, Position, то есть справа налево; Расчет и позиционное значение, как описано для десятичного числа. Основание для двоичного кода равно 2. Пример также показан ниже 9.0003
Примеры
Преобразование десятичных и двоичных чисел Преобразование двоичных чисел в десятичные (с основанием 2 в основание 10) и обратно является важной концепцией для понимания двоичной системы счисления. Двоичная система счисления является основой для всех компьютеров, цифровых систем, языков программирования, а также важна для понимания IP-адреса и подсети IP-адреса.
Двоичная система счисления является основой для всех компьютеров, цифровых систем, языков программирования, а также важна для понимания IP-адреса и подсети IP-адреса.
Для понимания IP-адресации и подсетей сетевой техник должен понимать, как преобразовывать двоичные числа в десятичные и обратно. Существует несколько способов преобразования двоичного числа в десятичное. Здесь мы поймем преобразование из двоичного в десятичное, а затем из десятичного в двоичное.
Двоичное представление в десятичное с использованием позиционного представленияПозиционное представление является одним из наиболее часто используемых методов преобразования между двоичным и десятичным числом. Итак, если у нас есть двоичное число 11000110 2 и мы хотим преобразовать это число в десятичную систему с основанием 10, используя позиционную систему записи.
На рисунке ниже показано преобразование двоичного числа в десятичное, запишите позиционное значение справа налево и справа вниз двоичного числа в следующей строке под позиционными значениями. Затем умножьте двоичные числа во второй строке на соответствующее позиционное значение в первой строке и сложите их, чтобы получить десятичное число, равное 19.9.
Затем умножьте двоичные числа во второй строке на соответствующее позиционное значение в первой строке и сложите их, чтобы получить десятичное число, равное 19.9.
Позиционное значение удваивается справа налево. Например, справа налево первое позиционное значение равно 1, следующее позиционное значение равно 2, что удваивает 1 (значение первой позиции), третье позиционное значение равно 4, что также удваивает 2 -й -й позиции. ценность. Мы можем записать позиционное значение этим методом в соответствии с цифрами двоичного кода.
Следующее двоичное значение: 10111100 Итак, запишите позиционное значение в соответствии с количеством цифр в двоичном значении. А затем напишите двоичные числа под позиционными значениями и сопоставьте их. Теперь, если цифра равна 1, напишите соответствующее позиционное значение под линией, под цифрой. Если цифра равна 0, напишите 0 под чертой, под цифрой и сложите числа, написанные под чертой. Это десятичный эквивалент двоичного числа. См. рисунок ниже.
См. рисунок ниже.
Теперь мы разобрались с основным преобразованием из двоичного в десятичное, поэтому мы можем попытаться преобразовать двоичный IPv4-адрес в его десятичный эквивалент с точками. Сначала разделите 32 бита адреса IPv4 на четыре 8-битных октета. Затем вычислите двоичное позиционное значение для первого двоичного числа октета и вычислите все остальные.
Например, предположим, что 11110110.10111111.11101011.11011011 — это двоичный адрес IPv4. Вам нужно преобразовать двоичный адрес в десятичный, просто начните с первого октета, как показано на рисунке ниже. Введите 8-битное двоичное число под позиционным значением строки 1, а затем вычислите, чтобы получить десятичное число для первого октета десятичной записи с точками. Затем преобразуйте оставшиеся октеты. И запишите полный IP-адрес в десятичной записи с точками.
Преобразование десятичного числа в двоичное Преобразование десятичного числа в двоичное также важно понимать, нам может потребоваться преобразовать десятичный IPv4-адрес с точками в двоичный. Для преобразования из десятичной в двоичную мы также можем использовать таблицу позиционных значений. На рисунке ниже показан процесс преобразования десятичной системы в двоичную. Например, мы хотим преобразовать цифру 246 в двоичную. Шаги преобразования десятичной системы в двоичную следующие:
Для преобразования из десятичной в двоичную мы также можем использовать таблицу позиционных значений. На рисунке ниже показан процесс преобразования десятичной системы в двоичную. Например, мы хотим преобразовать цифру 246 в двоичную. Шаги преобразования десятичной системы в двоичную следующие:
Шаг-1
Запишите позиционное значение слева направо, как показано на рисунке ниже. Если десятичное число ( 242 в нашем случае ) равно или больше старшего бита (128). Если да, добавьте двоичную единицу под позиционным значением 128 и вычтите 128 из десятичного числа (в нашем случае 242 -128 = 114). Если нет, введите двоичный 0 ниже позиционного значения 128.
Шаг 2
Сравните, равен ли остаток ( 114 ) следующему старшему биту (64) или больше. Если да, добавьте двоичную единицу под позиционным значением 64 и вычтите позиционное значение 64 из десятичного числа (в нашем случае 114 -64 = 50 ). Если нет, введите двоичный 0 под позиционным значением 64.
Шаг 3
Сравните, равен ли остаток (50) следующему старшему биту (32) или больше. Если да, добавьте двоичную единицу под позиционным значением 32 и вычтите позиционное значение 32 из десятичного числа (в нашем случае 50 -32 = 18 ). Если нет, введите двоичный 0 под позиционным значением 64.
Шаг 4
Сравните, равен ли остаток (18) следующему старшему биту (16) или больше. Если да, добавьте двоичную единицу под позиционным значением 16 и вычтите позиционное значение 16 из десятичного числа (в нашем случае 18 -16 = 2 ). Если нет, введите двоичный 0 ниже 16-позиционного значения.
Шаг-5
Сравните напоминание (2) со следующим старшим битом, вы увидите, что остаток меньше значимого значения (80), поэтому добавьте двоичный 0 в 8-позиционный значение и шаг вперед к следующему позиционному значению, которое равно (4), напоминание также меньше, чем это позиционное значение, поэтому добавьте 0 ниже этого значения позиции и сделайте шаг вперед к следующему значению.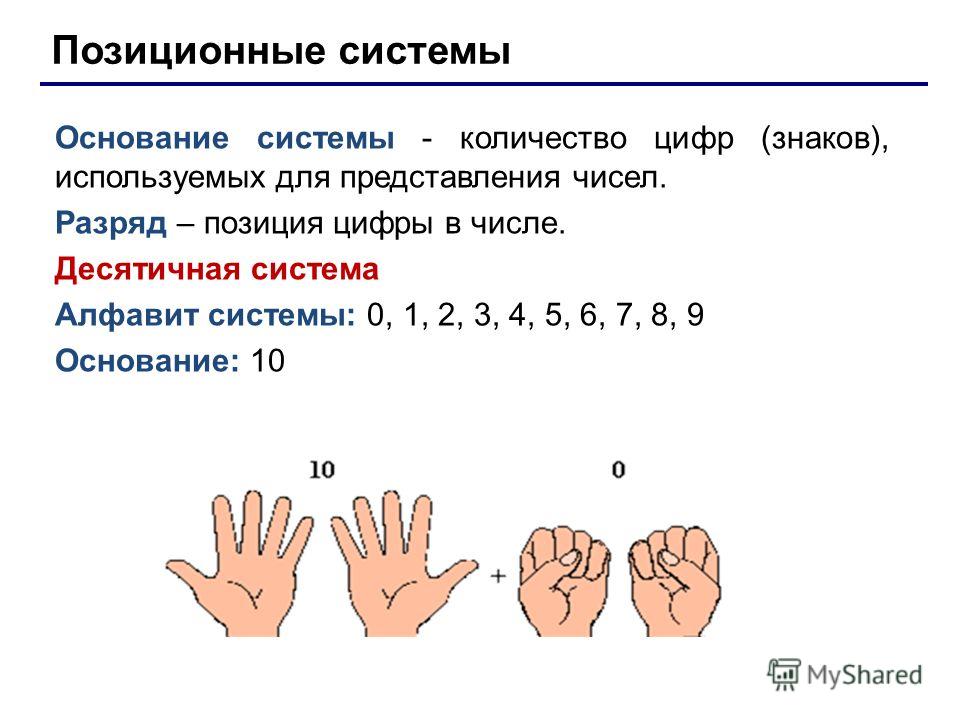


 (В числе 252 – первая двойка означает
количество сотен, последняя – количество
единиц)
(В числе 252 – первая двойка означает
количество сотен, последняя – количество
единиц) В качестве цифр используются
следующие латинские буквы:
В качестве цифр используются
следующие латинские буквы: Разряды
возрастают справа налево (единицы, десятки,
сотни и т.д.).
Разряды
возрастают справа налево (единицы, десятки,
сотни и т.д.).




