Поворот матрицы: О матрице поворота простыми словами / Хабр

Поворот матриц MatLab

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

1672 0

Курсы программирования kotlin курсы программирования kotlin ievetrov.ru

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

• Главная
/
• org/Breadcrumb»>База знаний
/
• CAD / CAM
/
• MatLab

Урок 10. Операции с векторами и матрицами
Создание матриц с заданными свойствами
Создание единичной матрицы
Создание матрицы с единичными элементами
Создание матрицы с нулевыми элементами
Создание линейного массива равноотстоящих точек
Создание вектора равноотстоящих в логарифмическом масштабе точек
Создание массивов со случайными элементами
Конкатенация матриц
Создание матриц с заданной диагональю
Перестановки элементов матриц
Вычисление произведений
Суммирование элементов
Функции формирования матриц
Поворот матриц
Выделение треугольных частей матриц
Вычисление сопровождающей матрицы
Вычисление тестовых матриц
Матрицы Адамара

Матрицы Ганкеля
Матрицы Гильберта
Вычисление магического квадрата
Матрицы Паскаля
Матрицы Теплица
Матрицы Уилкинсона
Матричные функции
s Что нового мы узнали?

Следующая функция обеспечивает поворот матрицы (по расположению элементов): О rot90(A) — осуществляет поворот матрицы А на 90° против часовой стрелки;

rot90(A,k) — осуществляет поворот матрицы А на величину 90*k градусов, где k — целое число.

Пример:

» М=[3.2,7;3.3.2:1.1.1]

	м=
		3	2	7
		3	3	2
		1	1	1
	» rot90(M)
	ans	=
		7	2	1
		2	3	1
		3	3	1

 

Теги MatLab САПР

Сюжеты MatLab

Знакомство с матричной лабораторией MATLAB MatLab

8252 0

Визуализация и графические средства MatLab

9768 0

Техническая документация по системе MatLab

6283 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2334 s

Матрица преобразований

Матрица преобразований применяется для вычисления новых координат объекта при его трансформации. Изменяя значения элементов матрицы преобразования, к объектам можно применять любые трансформации (например: масштабирование, зеркальное отражение, поворот, перемещение и т. п.). При любой трансформации сохраняется параллельность линий объекта.

Координаты в PDF выражаются в терминах двумерного пространства. Точка (x, y) в пространстве может быть выражена в векторной форме

[x y 1]. Постоянный третий элемент этого вектора (1) нужен для использования вектора с матрицами 3х3 в вычислениях, описанных ниже.

Преобразование между двумя системами координат представлено, как матрица 3х3 и записывается следующим образом:

Координатные преобразования выражаются в виде матричных умножений:

Так как последняя колонка не оказывает ни какого влияния на результаты расчета, то она в вычислениях не принимает участия. Координаты трансформации высчитываются по следующим формулам:

Единичная матрица

Единичной матрицей называется, та у которой значения матрицы a и d равны

1, а остальные равны 0. Такая матрица применяется по умолчанию, так как не приводит к трансформации. Поэтому единичную матрицу используют как основу.

Масштабирование

Для увеличения или уменьшения размера объекта по горизонтали/вертикали следует изменить значение a или d соответственно, а остальные применить из единичной матрицы.

Например: Для увеличения размера объекта в два раза по горизонтали, значение a необходимо принять равным 2, а остальные оставить такими как в единичной матрице.

Высчитываем новые координаты объекта:

Отражение

Чтобы получить зеркальное отображение объекта по горизонтали следует установить значение a = -1, по вертикали d = -1. Изменение обеих значений применяется для одновременного отображения по горизонтали и вертикали.

Наклон

Наклон объекта по вертикали/горизонтали обеспечивается изменением значений b и c соответственно. Изменение значения b/-b — наклон вверх/вниз, c/-c – вправо/влево.

Например: Для наклона объекта по вертикали вверх установим значение b = 1

Высчитываем новые координаты объекта:

В итоге к наклону объекта приводит только координата y, которая увеличивается на значение x.

Поворот

Поворот — это комбинация масштабирования и наклона, но для сохранения начальных пропорций объекта, преобразования должны проводится с точными вычислениями при использовании синусов и косинусов.

Сам поворот происходит против часовой стрелки, α задаёт угол поворота в градусах.

Перемещение

Перемещение осуществляется изменением значений e (по горизонтали) и f (по вертикали). Значения задаются в пикселях.

Например: Перемещение с использованием матрицы применяется редко из-за того, что эту операцию можно проделать другими методами, например, изменить положение объекта во вкладке Геометрия.

Поскольку матрица трансформации имеет только шесть элементов, которые могут быть изменены, визуально она отображается в PDF [a b c d e f]. Такая матрица может представлять любое линейное преобразование из одной координатной системы в другую. Матрицы преобразований образуются следующим образом:

• Перемещения указываются как [1 0 0 1 t_x t_y], где t_x и t_y — расстояния от оси системы координат по горизонтали и вертикали, соответственно.
• Масштабирование указывается как [s_x 0 0 s_y 0 0]. Это масштабирует координаты так, что 1 единица в горизонтальном и вертикальном измерениях в новой координатной системе такого же размера, как и s_x и s_y единиц в старой координатной системе соответственно.
• Повороты производятся матрицей [cosθ sinθ −sinθ cosθ 0 0], что соответствует повороту осей координатной системы на θ градусов против часовой стрелки.
• Наклон указывается как [1 tanα tanβ 1 0 0], что соответствует наклону оси x на угол α и оси y на угол β.

На рисунке ниже показаны примеры трансформации. Направления перемещения, угол поворота и наклона, показанные на рисунке, соответствуют положительным значениям элементов матрицы.

Умножения матрицы не коммутативны — порядок, в котором перемножаются матрицы, имеет значение.

В таблице ниже приведены допустимые преобразования и значения матрицы.

Исходный рисунок	Трансформированный рисунок	Матрица	Описание
		1       0 0       2 0       0	Масштаб по вертикали. Если значение матрицы больше 1, объект расширяется, меньше 1 — сжимается.
		2       0 0       1 0       0	Масштаб по горизонтали. Если значение матрицы больше 1, объект расширяется, меньше 1 — сжимается.
		-1      0 0       1 0       0	Отражение по горизонтали.
		1       0 0      -1 0       0	Отражение по вертикали.
		1       1 0       1 0       0	Наклон по вертикали вверх.
		1      -1 0       1 0       0	Наклон по вертикали вниз.
		1       0 1       1 0       0	Наклон по горизонтали вправо.
		1       0 -1      1 0       0	Наклон по горизонтали влево.
		1       0 0       1 0       1	Смещение по вертикали вверх в пикселях.
		1       0 0       1 0      -1	Смещение по вертикали вниз в пикселях.
		1       0 0       1 1       0	Смещение по горизонтали вправо в пикселях.
		1       0 0       1 -1      0	Смещение по горизонтали влево в пикселях.

Несмотря на все выше сказанное, матрица преобразований очень простой и эффективный инструмент для трансформации. Конечно, применять ее, например, для поворота нецелесообразно, так как во вкладке Геометрия имеется функция Поворот, но для отражения объекта она просто необходима.

Матрица вращения для вращения вокруг оси x

Матрицы вращения используются для вращения вектора в новое направление.

При преобразовании векторов в трехмерном пространстве часто встречаются матрицы вращения. Матрицы вращения используются в двух смыслах: их можно использовать для поворота вектора в новый положение или их можно использовать для поворота базы координат (или системы координат) в новую один. В этом случае вектор остается в покое, но его компоненты в новом базисе будут отличается от исходной базы. В евклидовом пространстве есть три основных вращения: по одному вокруг осей x, y и z. Каждое вращение определяется углом вращение. Угол поворота определяется как положительный для поворота, который против часовой стрелки, если смотреть наблюдателем, смотрящим вдоль оси вращения в сторону источник. Любое произвольное вращение может быть составлено из комбинации этих трех (теорема Эйлера о вращении) . Например, вы можете повернуть вектор в в любом направлении, используя последовательность из трех вращений: v′=Av=Rz(γ)Ry(β)Rx(α)v.

Матрицы вращения, которые вращают вектор вокруг x, y, и оси z задаются как:

• Вращение против часовой стрелки вокруг оси x

  Rx(α)=[1000cosα−sinα0sinαcosα]

• Вращение против часовой стрелки вокруг оси Y

  Ry(β)=[cosβ0sinβ010−sinβ0cosβ]

• Вращение против часовой стрелки вокруг оси Z

  Rz(γ)=[cosγ−sinγ0sinγcosγ0001]

Следующие три рисунка показывают, как выглядят положительные вращения например, для каждой оси вращения:

Для любого вращения существует обратное вращение, удовлетворяющее A−1A=1. Например, обратная матрица вращения по оси X получается как изменение знака угла:

Rx−1(α)=Rx(−α)=[1000cosαsinα0−sinαcosα]=Rx′(α)

Этот пример иллюстрирует основное свойство: обратную матрицу вращения является транспонированием оригинала.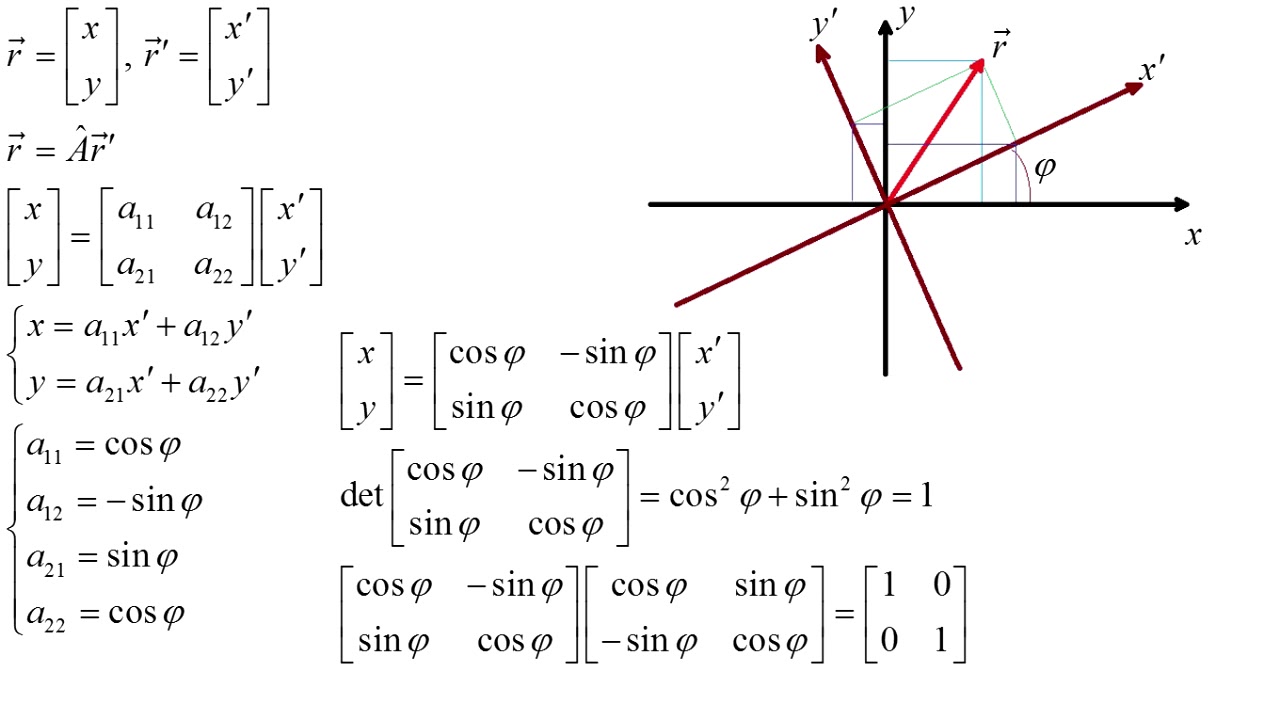 Матрицы вращения удовлетворяют А’А = 1 и следовательно, det(A) = 1 . При поворотах длины векторов сохраняются как а также углы между векторами.

Мы можем думать о вращениях по-другому. Рассмотрим исходный набор базисных векторов i,j,k и поверните их все, используя матрицу вращения A . Этот создает новый набор базисных векторов i’,j,’k’, связанных с исходным соотношением:

i’=Aij’=Ajk’=Ak

Используя транспонирование, вы можете записать новые базисные векторы в виде линейного комбинаций старых базисных векторов:

[i′j′k′]=A′[ijk]

Теперь любой вектор можно представить в виде линейной комбинации любого набора базисных векторов:

v=vxi+vyj+vzk=v′xi′+ v′yj′+v′zk′

Используя алгебраические вычисления, вы можете вывести преобразование компоненты для фиксированного вектора, когда базис (или система координат) вращается. Этот Преобразование использует транспонирование матрицы вращения.

[v′xv′yv′z]=A−1[vxvyvz]=A′[vxvyvz]

На следующем рисунке показано, как вектор преобразуется в координату система вращается вокруг оси x. На следующем рисунке показано, как это преобразование может быть реализовано. интерпретируется как вращение вектора наоборот направление.

Матрица вращения

Матрицы вращения осей Вращение осей и векторное вращение

Матрицы вращения осей

Рисунок 1

Компоненты свободного вектора изменяются по мере меняется перспектива (система отсчета). На рис. 1 показаны два различные системы отсчета: система XY и система X’Y’ . Вектор против на рисунке 1 можно выразить как ( x , y ) в в системе XY или ( x ‘, y ‘) в системе X’Y’ . отношения между x и y и x ‘и y ‘ могут быть получено из геометрических соотношений:

  [1]

Расширение [1] до 3 размеры:

   [2]

[2] является матрица вращения оси за вращение вокруг оси Z . Применяя тот же метод к вращениям вокруг оси X и Y соответственно:

    [3]

    [4]

Эти матрицы для поворотов осей вокруг конкретных координатные оси важны при разработке концепции Эйлера/Кардана. углы . См. Эйлеровы углы для подробности. Матрицы вращения удовлетворяют требованиям матрицы преобразования. Подробную информацию о требованиях см. в Матрице трансформации.

Топ

Вращение оси против векторного вращения

На рис. 2 показано Ситуация немного отличается от той, что на рисунке 1. На этот раз вектор, а не оси, повернулся вокруг оси Z на f . Это называется вращением вектора . Другими словами, вектор v ₁ был повернут на v ₂ по углу f .

Рисунок 2

Опять же, можно получить следующее отношения:

[5]

с

[6]

, где r = длина вектора, а a = угол v ₁ делает с осью X .