Пересечение поверхностей. Метод секущих плоскостей — Студопедия
Пересечение поверхностей. Метод секущих сфер.
Для определения линии пересечения двух произвольных поверхностей вращения целесообразно воспользоваться одним свойством, присущим поверхностям вращения, которое состоит в том, что две любые соосные поверхности вращения пересекаются по окружностям, проходящим через точки пересечения меридианов поверхностей.
В частном случае, если одна из поверхностей вращения – сфера, приведенное выше предложение может быть сформулировано иначе: если центр секущей сферы находится на оси поверхности вращения, то сфера пересечет данную поверхность по окружностям, число которых равно числу точек пересечения главных меридианов поверхностей.
Построить линии пересечения поверхностей с помощью вспомогательных секущих сфер можно двумя способами:
1. Способом концентрических сфер;
2. Способом эксцентрических сфер.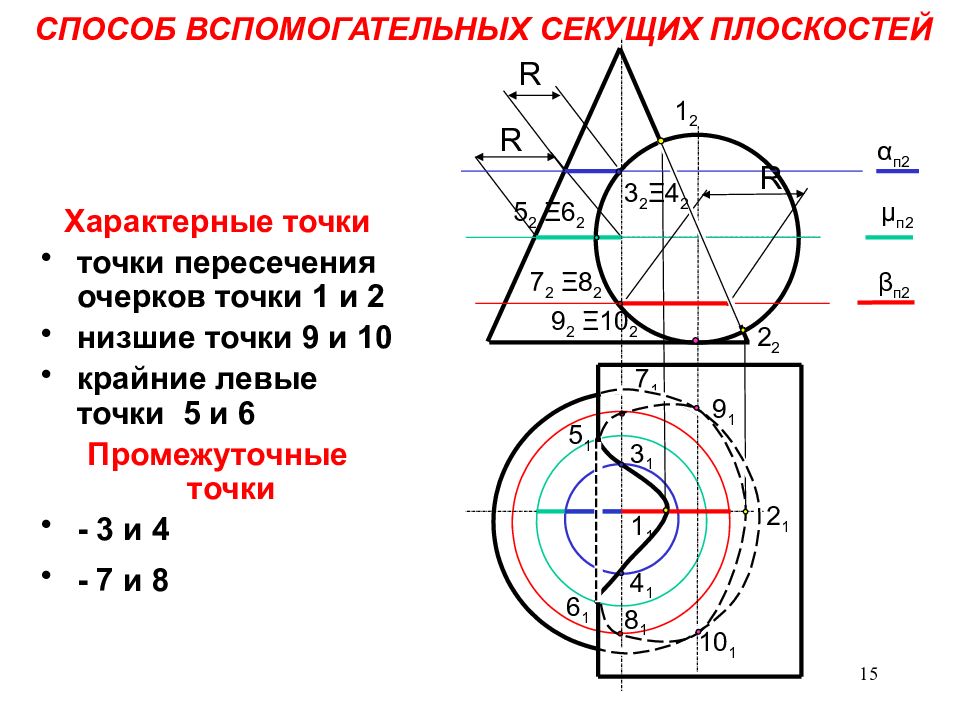
Способ концентрических сфер.
Этот способ применяется для построения линии пересечения двух поверхностей вращения, оси которых пересекаются. Для упрощения графического решения необходимо, чтобы плоскость, определяемая осями поверхностей вращения, была параллельной какой0либо плоскости проекции.
Способ эксцентрических сфер.
Способ эксцентрических сфер может быть использован для построения линии пересечения двух поверхностей, имеющих общую плоскость симметрии. При этом каждая поверхность, имеющих общую плоскость симметрии. При этом каждая поверхность должна иметь семейство окружностей. Как и в способе концентрических сфер, плоскость симметрии должна быть параллельна одной из плоскостей проекции.
Способ эксцентрических сфер можно применять и в тех случаях, когда из пересекающихся поверхностей не является поверхностью вращения. Необходимым условием является наличие на этой поверхности семейства окружностей, которые можно рассматривать как результат пересечения поверхности со сферой.
Пересечение поверхностей. Метод секущих плоскостей.
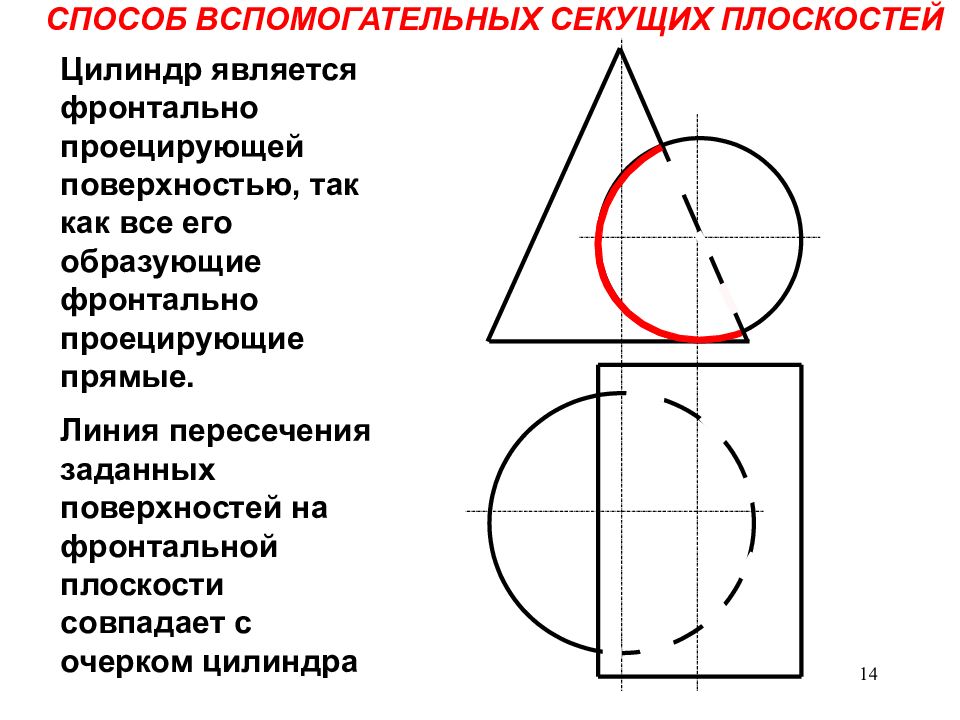
В качестве поверхностей-посредников используют секущие плоскости. Этот способ применяется в тех случаях, когда можно найти в качестве поверхностей-посредников такие плоскости, которые пересекали бы обе заданные поверхности по геометрически простым линиям — окружностям и прямым (рис. 21). Чаще всего в качестве вспомогательных секущих плоскостей выбираются плоскости уровня, то есть плоскости, параллельные плоскостям проекций. Следует отметить, что способ вспомогательных секущих плоскостей применяется во всех случаях, то есть каждая из пересекающихся поверхностей может быть как гранной, так и поверхностью вращения.
Рис. 21.
На чертеже (рис. 21, 22) прямой конус вращения пересекается с полусферой.
Построение проекций линии взаимного пересечения поверхностей осуществляется в следующей последовательности:
Определяют на чертеже положения опорных точек кривой пересечения. Фронтальная проекция A2 самой высшей точки кривой пересечения определяется на пересечении главных меридианов пересекающихся поверхностей: для конуса главным меридианом является очерковый треугольник, а для полусферы — очерковая полуокружность во фронтальной плоскости проекций.
Фронтальная проекция A2 самой высшей точки кривой пересечения определяется на пересечении главных меридианов пересекающихся поверхностей: для конуса главным меридианом является очерковый треугольник, а для полусферы — очерковая полуокружность во фронтальной плоскости проекций.
Рис. 22.
Проведя линию связи из точки A2 до пересечения с горизонтальной проекций главных меридианов, получаем горизонтальную проекцию A1 самой высшей точки кривой пересечения. То обстоятельство, что основания фигур располагаются непосредственно в горизонтальной плоскости проекций (рис. 22) позволяет выявить положения самых низших точек 1 и 2 кривой пересечения.
Действительно, точки 11 и 21 пересечения проекций оснований фигур являются горизонтальными проекциями самых низших точек 1 и 2 кривой персечения. Их фронтальные проекции 12 и 22 располагаются на оси ОХ и определяются пересечением оси ОХ с линиями связи, проведенными из точек 11 и 21. В тоже время по отношению к наблюдателю точки 1(11;12) и 2(21;22) являются самой близкой и самой дальней точками кривой пересечения соответственно.
Все точки, кроме A, 1 и 2 являются регулярными точками кривой пересечения. Для определения на чертеже положения их проекций используют способ вспомогательных секущих плоскостей. При этом необходимо удачно выбрать положение секущей плоскости. Это положение выбирают таким образом, чтобы в сечении каждой из заданных поверхностей вращения получались графически простые линии — прямые или окружности.
В данной задаче в качестве вспомогательных секущих плоскостей выбирают горизонтальные плоскости уровня, так как они пересекают обе поверхности: конус и полусферу, по графически простым линиям — окружностям. На чертеже проводят одну секущую плоскость α1, задав ее фронтальным следом α21. Далее строят проекции параллелей — окружностей сечения секущей плоскостью α1 конуса и полусферы. На чертеже фронтальные проекции этих параллелей l2 и m2 располагаются на следе α21 секущей плоскости α1.
Горизонтальные проекции l1 и m1 этих параллелей представляют собой окружности с центрами S1 и O1, радиусами R и R′ соответственно. В пересечении горизонтальных проекций l1 и m1 параллелей получают горизонтальные проекции 41 и 51 регулярных точек кривой пересечения. Проведя линии связи из точек 41 и 51 до пересечения со следом α21 секущей плоскости α1, получают фронтальные проекции 42 и 52 кривой пересечения. Построенные точки 4(41; 42) и 5(51; 52) являются регулярными точками кривой пересечения. Аналогичным образом проводят несколько ниже секущие плоскости α2 — α6, задав их на чертеже фронтальными следами α22 — α26, и строят регулярные точки 6(61; 62) — 15(151; 152) кривой пересечения поверхностей.
В пересечении горизонтальных проекций l1 и m1 параллелей получают горизонтальные проекции 41 и 51 регулярных точек кривой пересечения. Проведя линии связи из точек 41 и 51 до пересечения со следом α21 секущей плоскости α1, получают фронтальные проекции 42 и 52 кривой пересечения. Построенные точки 4(41; 42) и 5(51; 52) являются регулярными точками кривой пересечения. Аналогичным образом проводят несколько ниже секущие плоскости α2 — α6, задав их на чертеже фронтальными следами α22 — α26, и строят регулярные точки 6(61; 62) — 15(151; 152) кривой пересечения поверхностей.
После построения на чертеже проекций опорных и регулярных точек кривой соединяют их одноименные проекции плавной кривой (при помощи лекала) и получают горизонтальную и фронтальную проекции кривой взаимного пересечения заданных поверхностей. По чертежу устанавливают, что конус и полусфера имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций. Тогда горизонтальные проекции точек кривой пересечения окажутся расположенными симметрично относительно горизонтального следа главной меридианальной плоскости, являющейся общей для обеих фигур.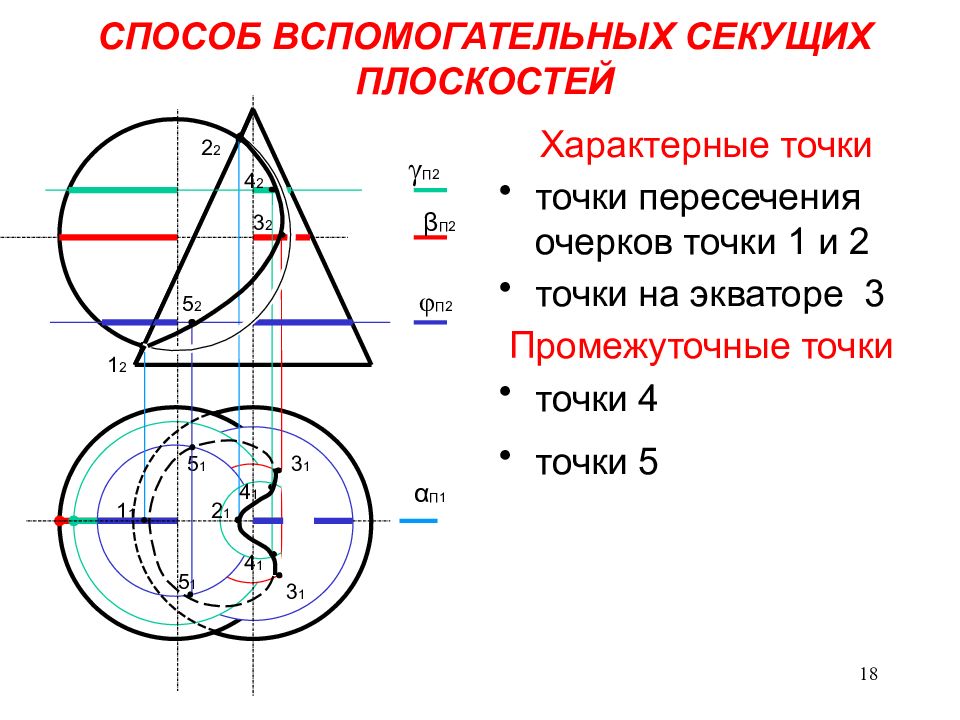
Фронтальные проекции точек кривой пересечения будут совпадать, так как в этом случае они являются конкурирующими по отношению к фронтальной плоскости проекций. Причем проекции точек, расположенных перед главной меридианальной плоскостью фигур, будут видимыми на фронтальной плоскости проекций, а расположенных за ней — невидимыми. Горизонтальные проекции точек кривой пересечения являются видимыми, поэтому горизонтальная проекция кривой пересечения проводится на чертеже сплошной линией.
В заключение отметим, что способ вспомогательных секущих плоскостей уровня используется тогда, когда оси вращения обеих поверхностей (если обе поверхности являются поверхностями вращения) располагаются перпендикулярно одной из плоскостей проекций.
В том случае, когда при пересечении обеих поверхностей одной секущей плоскостью невозможно получить в сечениях графически простые линии — прямые или окружности применяется способ вспомогательных секущих сфер.
Метод секущих плоскостей, AutoCAD, Начертательная геометрия
В этом уроке рассмотрим одну из самых распространенных задач начертательной геометрии – построение пересечения поверхностей методом секущих плоскостей и способ ее решения средствами AutoСАD.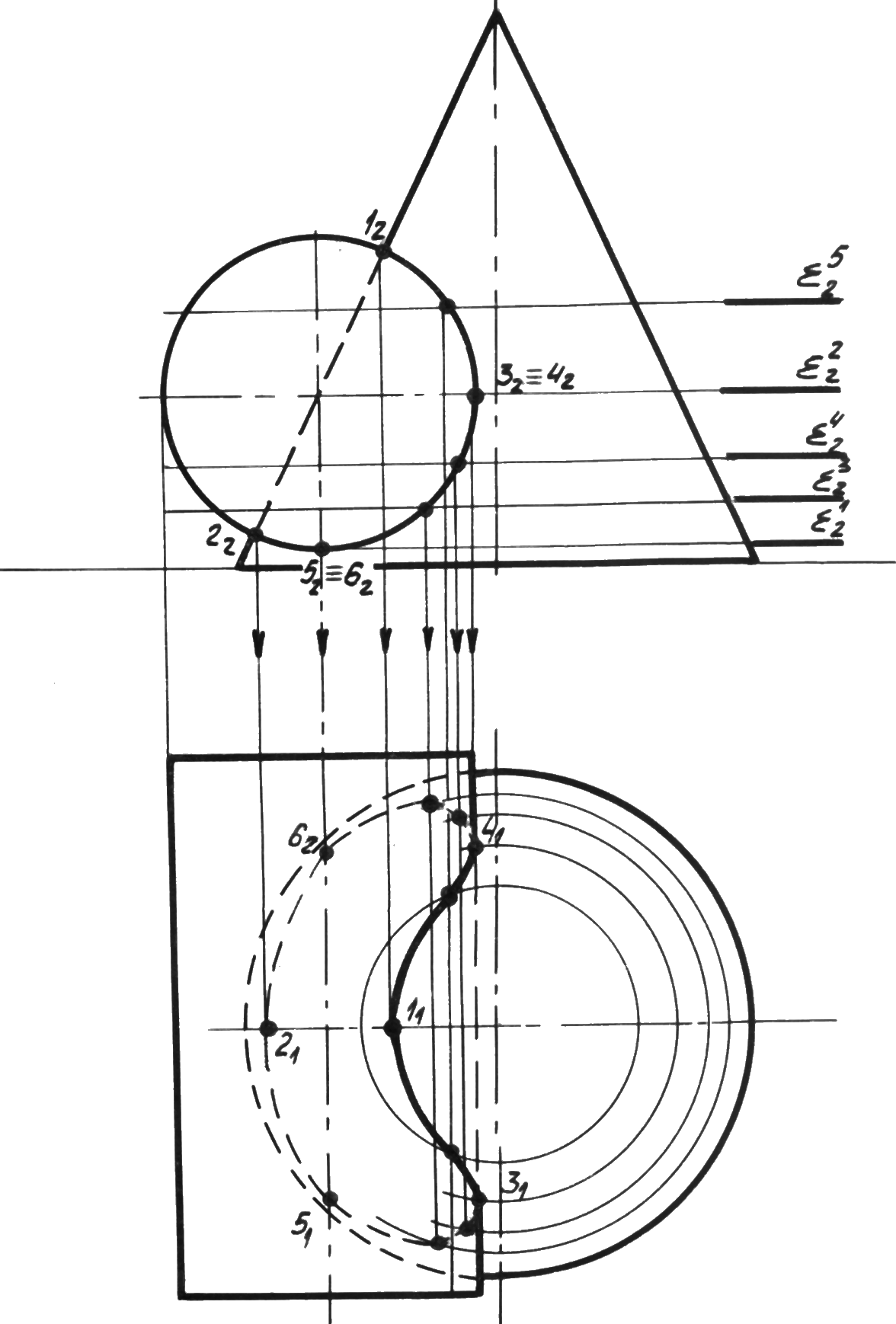
Метод секущих плоскостей, немного теории
Вкратце суть метода секущих плоскостей состоит в том, что для построения линии пересечения двух поверхностей строятся вспомогательные плоскости (обычно – параллельные одной из плоскостей проекций), которые пересекают заданные поверхности, образуя при этом простые геометрические фигуры.
Точки взаимного пересечения заданных поверхностей будут общими точками двух кривых, образованных пересечением секущей плоскости с каждой из поверхностей.
Условия задачи
Зададим условия: пусть необходимо построить пересечение полусферы и конуса, расположенных таким образом:
Размеры показаны для наглядности, проставлять их на чертеже не нужно.
Решение
Строим секущие плоскости, вид с боку
Очевидно, что для тел вращения удобно использовать плоскости, перпендикулярные осям этих тел. В нашем случае вспомогательные плоскости будут параллельными горизонтальной плоскости. Изобразим их на фронтальном виде (в нашем случае верхняя из плоскостей проходит через явно видимую верхнюю точку пересечения конуса и полусферы, в других случаях для нахождения этой точки потребуются дополнительные построения):
Секущие плоскости, вид сверху
Теперь перенесем линии пересечения секущих плоскостей с каждой из поверхностей на вид сверху.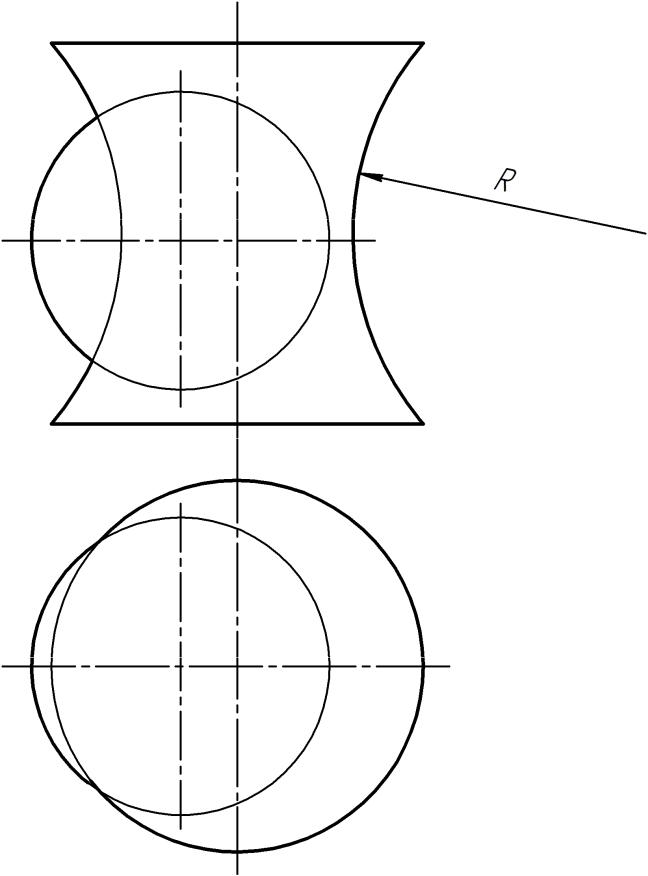 Очевидно, что горизонтальные плоскости пересекают каждое из тел по окружностям, центры которых находятся на одной вертикали с центрами тел. Радиусы этих окружностей легко переносятся на вид сверху с образующих каждой поверхности. Вот эти окружности для полусферы:
Очевидно, что горизонтальные плоскости пересекают каждое из тел по окружностям, центры которых находятся на одной вертикали с центрами тел. Радиусы этих окружностей легко переносятся на вид сверху с образующих каждой поверхности. Вот эти окружности для полусферы:
И для конуса:
Точки пересечения секущих плоскостей
Отметим для наглядности общие точки для каждой из пар окружностей, образованных одной плоскостью:
Видно, что в районе верхней точки построение недостаточно «информативно», т.е. будет полезным построить еще одну секущую плоскость:
Вот еще две точки, заданные этой плоскостью:
Линия пересечения
Соединив на виде сверху полученные точки сплайном (команда Сплайн), мы получим приближенную линию пересечения двух поверхностей:
Остается перенести линию на фронтальный вид. Сделать это совсем несложно: нужно перенести каждую из точек с вида сверху на соответствующую секущую плоскость на фронтальном виде.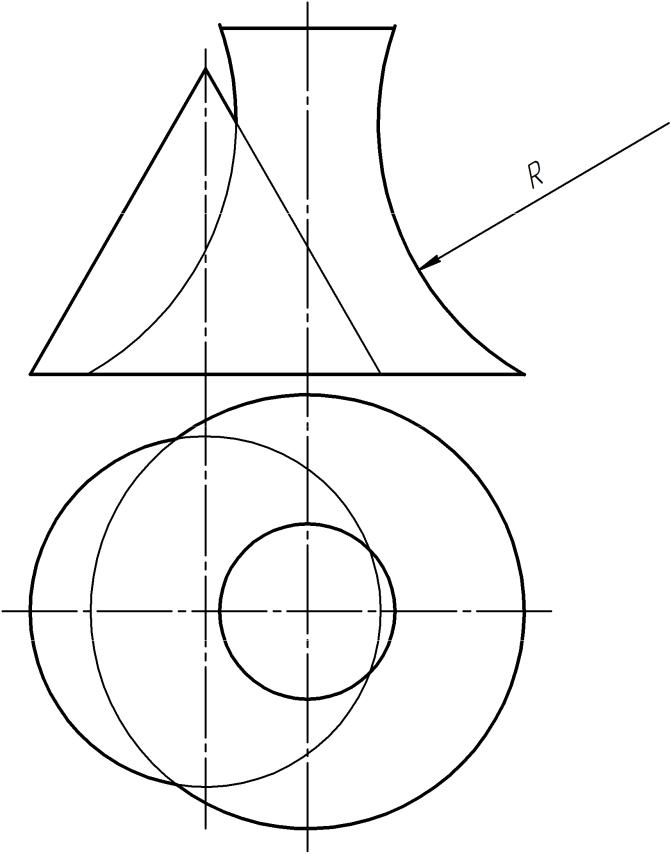 Линии построения выделены желтым цветом:
Линии построения выделены желтым цветом:
Поскольку исходные поверхности (и, соответственно, линия их пересечения) симметричны относительно плоскости, параллельной фронтальной плоскости проекции, достаточно перенести только половину точек. В нашем частном случае невидимая на фронтальном виде часть кривой «спрятана» за видимой, а верхняя точка является точкой разделения видимой и невидимой частей.
Проверка вида линии пересечения
Полезно проверить правильность наших построений средствами 3D-моделирования. Построим соответствующие фигуры, перейдя предварительно к интерфейсу 3D- моделирование , и сравним полученную модель с построением (для этого удобнее объединить объекты командой Объединить).
Резюме
Как видим, наше построение довольно точно передает реальную линию пересечения поверхностей вращения. И хотя современные средства моделирования позволяют строить такие пересечения гораздо быстрее, рассмотренные нами принципы очень полезны для понимания «механики» геометрических построений, без которого любой, даже самый современный инструмент 3D-моделирования превращается в сложную и непонятную игрушку.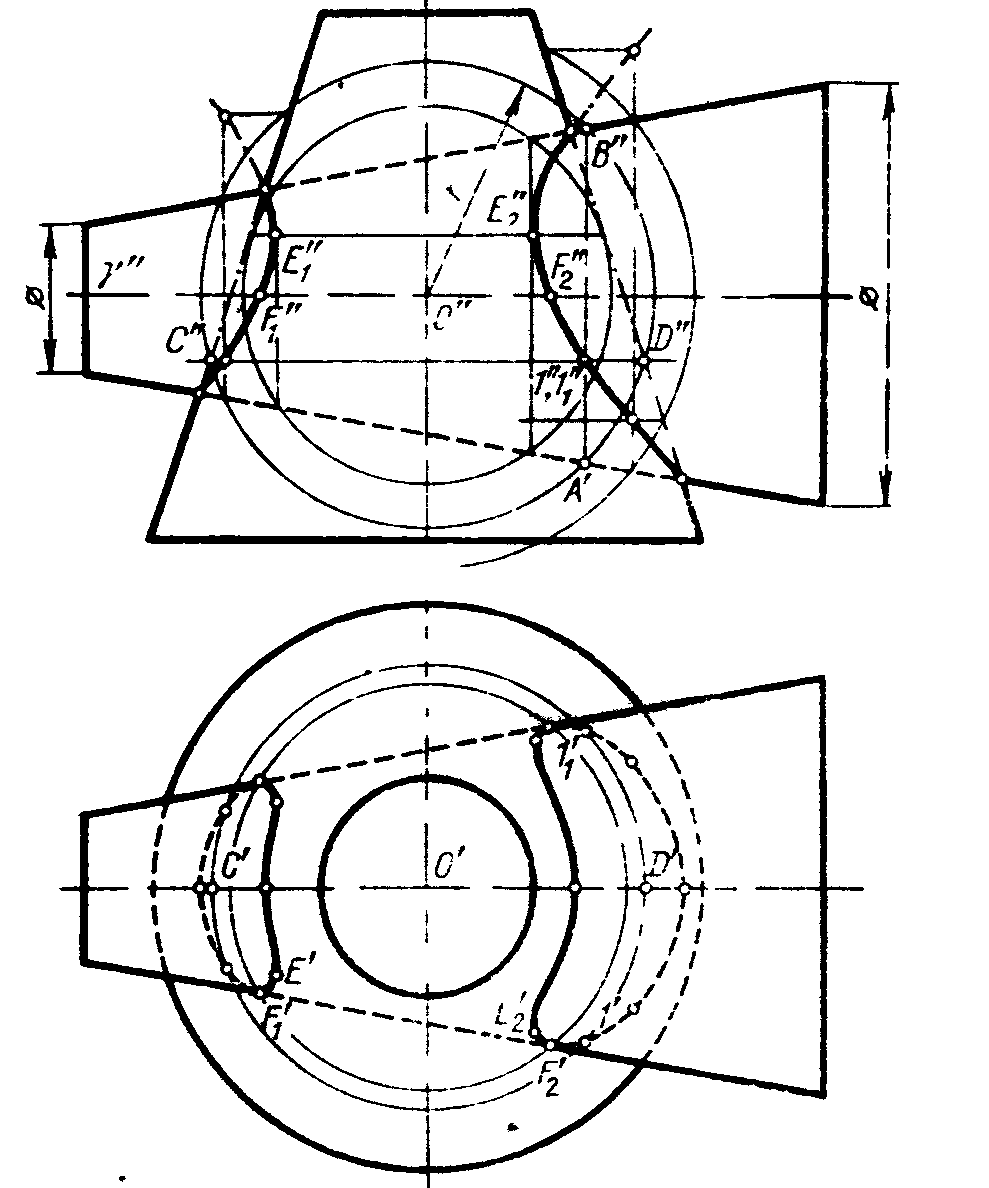
Компания «Студия Vertex» с 2009 года специализируется на выпуске образовательных курсов посвященных использованию популярных современных САПР.
|
ЗНАЕТЕ ЛИ ВЫ? |
Выдается на тринадцатой неделе после проведения практического занятия 15 и лекции 8 [1, 2, 11]. Для решения задач необходимо усвоить следующий теоретический материал: а) построение линии пересечения поверхностей вращения и многогранников с помощью вспомогательных секущих плоскостей; б) построение линии пересечения поверхностей вращения методом вспомогательных секущих сфер.
11.1 Способ вспомогательных секущих плоскостей частного положения
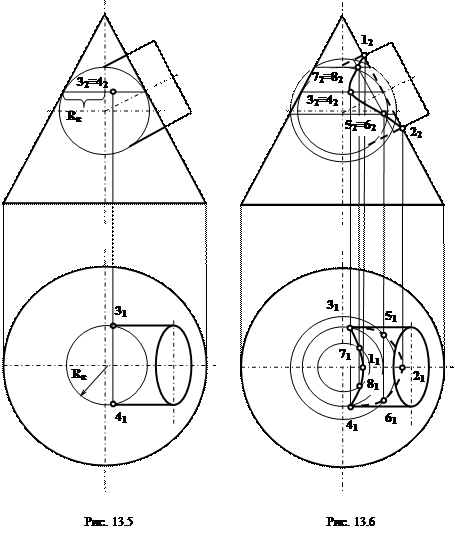
Основное требование при выборе положения вспомогательных секущих плоскостей: плоскости должны пересекать каждую поверхность по простым для построения фигурам. Задача 1. Построить линию пересечения конуса и призмы (рисунок 67). Вспомогательные секущие плоскости пересекают призму по прямоугольникам, конус – по окружностям. Призма является фронтально-проецирующей поверхностью, состоящей из трех проецирующих плоскостей. Горизонтальная грань рассекает конус по окружности. Две других дают в сечении эллипсы. Для построения точек выбраны несколько секущих плоскостей: Q1, Q2 и Q3. Плоскость Q1 рассекает конус по окружности, радиус которой определяется по чертежу, и дает точку 1 и две точки2.Плоскости Q2 и Q3выбраны случайным образом для более точного построения участков эллипса. Эти плоскости пересекают призму по прямоугольникам, а конус по окружностям.
Рисунок 67 ‑ Пересечение призмы с конусом Задача 2. В первую очередь найдены характерные точки линии пересечения: высшая и низшая точки 1 и 3 и точки 2 и 2, разделяющие горизонтальную проекцию кривой на видимую и невидимую части. Точки 1 и 3 определены при помощи вспомогательных фронтальных плоскостей Q1 и Q3, которые пересекают поверхность цилиндра по крайним (верхней и нижней) образующим, а поверхность конуса по окружностям, радиус которых измеряют прямо по чертежу на фронтальной проекции. Горизонтальные проекции точек находятся на горизонтальной проекции в точках пересечения окружности от конуса с образующими цилиндра. Точки 2 и 2 найдены при помощи фронтальной плоскости Q2, проведенной через ось цилиндра.
Рисунок 68 – Пересечение цилиндра с конусом
Задача 3. Построить линию пересечения конуса и сферы (рисунок 69). Для конуса и сферы подходят в качестве вспомогательных секущих плоскостей горизонтальные плоскости уровня, которые пересекают обе поверхности по окружностям Q2, Q3 и Q4. Первую секущую плоскость Q1(для определения высшей и низшей точек сечения 1 и 2) проведем на горизонтальной проекции. Плоскость Q2 нужна для построения крайней левой точки сечения 3 на фронтальной плоскости проекций. Она является также крайней точкой видимости для горизонтальной проекции. При сечении вспомогательной плоскостью Q2 конус и сфера рассекаются по окружностям, радиус которых измеряют прямо по чертежу на фронтальной проекции. Строим на горизонтальной проекции эти окружности. Они пересекаются по точкам 31и 31. По линиям связи строим проекцию точек 32 на фронтальной плоскости. Секущие плоскости Q3 и Q4 являются промежуточными (случайными), т.е. их можно проводить в удобном для построения кривой месте. Напоминаем: положение секущих плоскостей Q1 и Q2 является строго определенным, так как выявляет положение опорных точек кривой пересечения данных поверхностей.
Рисунок 69 ‑ Пересечение конуса и сферы
11.2 Способ вспомогательных концентрических сфер
Выдается на четырнадцатой неделе после проведения практического занятия 14 [1, 2, 11]. Для решения задач необходимо усвоить следующий теоретический материал: а) пересечение поверхностей; б) построение линии пересечения поверхностей с помощью вспомогательных секущих сфер, концентрических сфер и качающихся плоскостей. При построении линии пересечения двух поверхностей вращения часто целесообразно применять в качестве вспомогательных секущих поверхностей концентрические сферы, т.е. построенные из одного центра. Это обусловлено тем, что всякая сфера с центром на оси поверхности вращения пересекает любую поверхность вращения по окружности, т.е. по линии, построение которой не вызывает затруднений (рисунок 70). Если при этом оси двух пересекающихся поверхностей вращения пересекаются и параллельны одной из плоскостей проекций, то всякая сфера с центром в точке пересечения осей пересечет каждую из поверхностей по окружностям, которые проецируются на одну из плоскостей проекций в виде отрезков прямых.
Рисунок 70 – Пересечение сферы с цилиндром и конусом
Задача 1. Построить линию пересечения двух цилиндров вращения (рисунок 71). Оси заданных поверхностей вращения пересекаются и параллельны плоскости проекций V, следовательно, необходимые для применения способа сфер условия имеются. Точки 12и 22 ‑ фронтальные проекции точек пересечения крайних образующих двух цилиндров – отмечаются на эпюре непосредственно, без каких бы то ни было построений.
Рисунок 71 ‑ Пересечение двух цилиндров вращения
Задача 2. Построить линию пересечения конуса вращения и цилиндра вращения (рисунок 73). При таком положении поверхностей точки 12 и 22 ‑ фронтальные проекции точек пересечения крайних образующих конуса и цилиндра – отмечаются на эпюре непосредственно, без каких бы то ни было построений. Для нахождения промежуточных точек из точки О описана сферическая поверхность Сф.I наименьшего диаметра. Она только касается поверхности конуса в точках а и b и, следовательно, пересекает ее по окружности, фронтальная проекция которой ‑ прямая аb. Поверхность цилиндра Сф.I пересекает также по окружностям, фронтальная проекция которых ‑ прямая сd. Пересечение этих прямых ‑ точки 32‑ есть фронтальная проекция крайних левой и правой точек искомой линии пересечения (рисунок 72).
Рисунок 72 ‑ Построение касательной к конусу сферы Сф.I
Рисунок 73 ‑ Пересечения конуса и цилиндра вращения Задача 3. Построить линию пересечения конуса вращения и цилиндра вращения (рисунок 75). От предыдущей эта задача отличается размерами цилиндра. При увеличении диаметра цилиндра вид линии пересечения полностью меняется. При таком положении поверхностей точки 12 и 32 ‑ фронтальные проекции точек пересечения крайних образующих конуса и цилиндра – отмечаются на эпюре непосредственно, без каких бы то ни было построений. Решение начинаем с построения Сф.I, касательной к цилиндру. Она касается поверхности цилиндра в точках с и d и, следовательно, пересекает ее по окружности, фронтальная проекция которой ‑ прямая сd. Поверхность конуса Сф.I пересекает также по окружностям, фронтальные проекции которых ‑ прямые аb. В пересечении этих прямых находятся точки 22 и 42. Это фронтальные проекции опорных точек искомой линии пересечения (рисунок 69). Точка 22– это нижняя точка для верхней линии пересечения, а 42 – верхняя для нижней линии пересечения (рисунок 74). Аналогично при помощи Сф.II построена фронтальная проекция точек 52(еще двух точек, принадлежащих линии пересечения). Горизонтальные проекции найденных точек могут быть построены как проекции точек, лежащих на поверхности конуса (рисунок 75).
Рисунок 74 ‑ Построение касательной Сф.
Рисунок 75 ‑ Пересечение конуса вращения и цилиндра вращения Подготовка к контрольной работе № 2. Контрольная работа № 2 проводится на пятнадцатой неделе. Для подготовки к контрольной работе следует повторить задачи из тем 5, 6, 7, 8.
Приложение А
Таблица А1 – Содержание лекций по начертательной геометрии
Таблица А.
ЛИТЕРАТУРА
1. Гордон, В.О. Курс начертательной геометрии: Учеб. пособие / В.О. Гордон, М.А. Семинцов-Огиевский; под ред. Ю.Б. Иванова.-23-е изд., перераб. – М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 2000. 2. Чекмарев, А.А. Начертательная геометрия и черчение: учебное пособие для вузов / А.А. Чекмарев; 2-е изд. перераб. и доп. ‑ М.: ВААДОС. 1999. 3. Алексеева, Э.А. Комплексный чертеж точки и прямой: методические рекомендации по курсу начертательной геометрии для студентов специальностей 230100, 171500, 340100, 130400, 120100 всех форм обучения / Э. 4. Алексеева, Э.А. Взаимное положение прямой и плоскости: методические указания по изучению курса начертательной геометрии для студентов специальностей 230100, 171500, 340100, 130400, 120100 всех форм обучения / Э.А. Алексеева, С.В. Левин; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2005. – 26 с. 5. Куничан, Г.И. Способы задания плоскости. Положение прямой относительно плоскости. Взаимное положение плоскостей: методические рекомендации по изучению курса начертательной геометрии для студентов специальностей 190603, 170104, 220501, 160302, 151001 дневной, вечерней и заочной форм обучения / Г.И. Куничан; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. тех. ун-та, 2007. – 30 с. 6. Куничан, Г.И. Перпендикуляр к плоскости. Взаимно перпендикулярные плоскости. Перпендикуляр к прямой: методические рекомендации по курсу начертательной геометрии для самостоятельной работы студентов механических специальностей 171200, 120100, 171500, 170600 / Г. 7. Светлова, О.Р. Способы преобразования чертежа: способ замены плоскостей проекций, способы вращения: методические рекомендации по начертательной геометрии для студентов всех специальностей, изучающих дисциплину «Начертательная геометрия и инженерная графика» / О.Р. Светлова, Э.А. Алексеева, Г.Д. Леонова, Г.И. Куничан; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2008. – 36 с. 8. Куничан, Г.И. Сечение поверхностей плоскостями общего положения: методические рекомендации по курсу начертательной геометрии для самостоятельной работы студентов механических специальностей 171200, 120100, 171500, 170600 / Г.И. Куничан, Л.И. Идт; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2005. – 28 с. 9. Куничан, Г.И. Построение разверток поверхностей: методические рекомендации по курсу начертательной геометрии для самостоятельной работы студентов механических специальностей 171200, 120100, 171500, 170600 / Г. 10. Столлер, А.В. Пересечение прямой с поверхностью: методические рекомендации по изучению курса начертательной геометрии для самостоятельной работы студентов специальностей 230100, 171500, 130400, 120100, 171200, 170600 всех форм обучения / А.В. Столлер; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2005. – 15 с. 11. Леонова, Г.Д. Взаимное пересечение поверхностей. Взаимное пересечение кривой поверхности с поверхностью многогранника. Взаимное пересечение многогранников: методические рекомендации по изучению курса начертательной геометрии для студентов специальностей 230100, 171500, 340100, 130400, 120100 дневной, вечерней и заочной форм обучения / Г.Д. Леонова, Н.Ю. Афанасьева; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2003. – 29 с. 12. Светлова, О.Р. Определение углов наклона прямых и плоскостей общего положения к плоскостям проекций: методические рекомендации к решению задач по начертательной геометрии для студентов всех специальностей, изучающих дисциплину «Начертательная геометрия и инженерная графика» / О. 13. Светлова, О.Р. Перпендикулярность. Контрольная работа № 1: методические рекомендации по начертательной геометрии для студентов всех специальностей, изучающих дисциплину «Начертательная геометрия и инженерная графика» / О.Р. Светлова, Г.И. Куничан, Н.С. Левина, Э.А. Алексеева; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2010. – 24 с.
Читайте также: |
Метод посредников (секущие плоскости) при построении проекций линий пересечения поверхностей.
В качестве вспомогательных секущих плоскостей чаще всего используют плоскости, параллельные одной из плоскостей проекций. Положение их выбирают такое, чтобы они пересекали заданные поверхности по простейшим линиям – прямым или окружностям.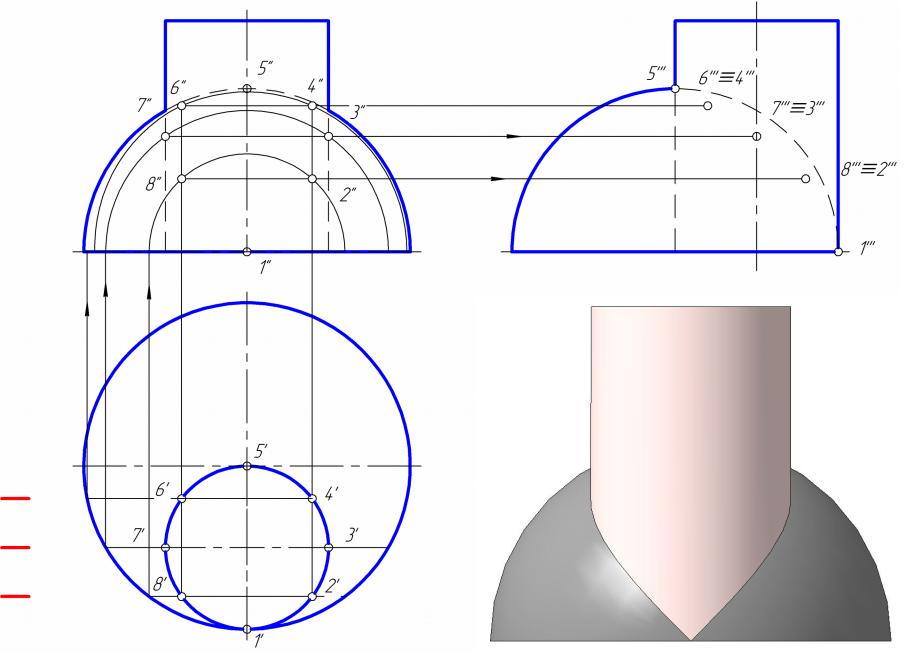
Если одна из поверхностей является цилиндрической проецирующей поверхностью, то построение линии пересечения упрощается, так как в этом случае одна проекция линии пересечения совпадает с окружностью – проекцией цилиндра на перпендикулярную плоскость проекций.
Линией пересечения указанных тел является пространственная кривая, фронтальная проекция которой совпадает с окружностью – фронтальной проекцией цилиндра.
Отметим на этой окружности точки линии пересечения: опорные (1, 2, 3, 4, 5, 6) и промежуточные (7, 8, 9). Точки обозначены только на одной симметричной части линии пересечения. Горизонтальные проекции точек 1 и 2, лежащие на правой очерковой образующей конуса, определим с помощью линий связи. Для построения горизонтальных проекций точек 3 и 4 использованы вспомогательные плоскости a и b.
Способ секущих плоскостей. Этот способ выбирается в том случае, если осевые линии двух поверхностей параллельны между собой. Секущая плоскость выбирается так, чтобы она пересекала заданные поверхности по наиболее простым для построения линиям – прямым или окружностям.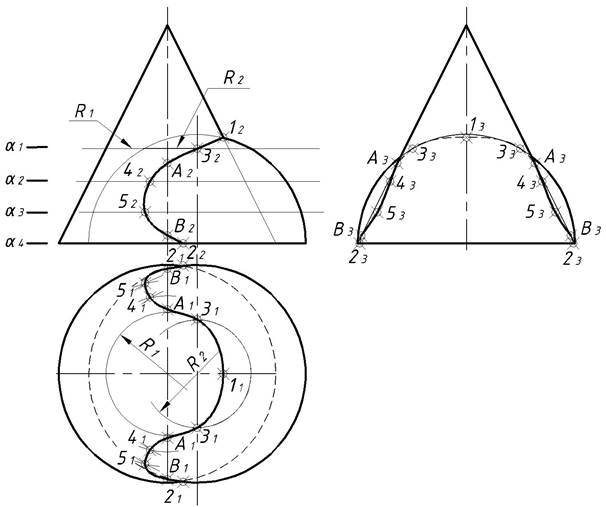 Чаще всего секущая плоскость является плоскостью уровня. Для того, чтобы найти произвольную точку линии пересечения, пользуются алгоритмом :
Чаще всего секущая плоскость является плоскостью уровня. Для того, чтобы найти произвольную точку линии пересечения, пользуются алгоритмом :
1) вводят вспомогательную секущую плоскость; 2) находят линию пересечения этой плоскости с каждой из заданных поверхностей 3) на пересечении найденных линий находят искомые точки.
Последовательно вводя ряд вспомогательных плоскостей, можно найти необходимое число точек.
Построение линий пересечения двух плоскостей общего положения. См 4
Линией пересечения двух плоскостей является прямая, для построения которой достаточно определить две точки, принадлежащие обеим плоскостям одновременно.
Образование конической поверхности. Сечения конической поверхности плоскостями.
КОНИЧЕСКИЕ СЕЧЕНИЯ — линия пересечения кругового конуса с плоскостями, не проходящими через его вершину. Конические сечения могут быть трех типов:
а) — секущая плоскость пересекает все образующие конуса в точках одной его полости; линия пересечения — замкнутая овальная кривая — эллипс, в частности, когда плоскость перпендикулярна оси конуса, — окружность;
б) — секущая плоскость параллельна одной из касательных плоскостей конуса; в сечении получается незамкнутая, уходящая в бесконечность кривая — парабола, целиком лежащая в одной полости;
в) — секущая плоскость пересекает обе полости конуса; линия пересечения гипербола — состоит из двух одинаковых незамкнутых, простирающихся в бесконечность ветвей, лежащих на обеих полостях конуса.
Эллипс Парабола Гипербола
Читайте также:
Пересечение поверхностей • ChertimVam.Ru
Из линейной алгебры (многомерной геометрии) хорошо известно, что в расширенном евклидовом пространстве Еn+ размерность пересечения геометрических объектов может быть определена из соотношения
p = m1 + m2 — n,
где p — размерность объекта получаемого в пересечении,
m1 — размерность первого объекта (m1 — поверхности),
m2 — размерность второго объекта (m2 — поверхности),
n — размерность рассматриваемого пространства.
В соответствии с выше приведенной формулой пересечение двух поверхностей (двумерных m1 = m1 = 2) в трехмерном евклидовом пространстве Е3+ должно привести к появлению одномерного объекта p = 2+2-3=1 — пространственной кривой (p = 1), все точки которой являются общими для обеих поверхностей.
При построении линии пересечения наиболее характерны два случая:
— одна из проекций линии пересечения известна и задача сводится к отысканию недостающих проекций точек по принадлежности одной из поверхностей;
— проекции линии пересечения не известны.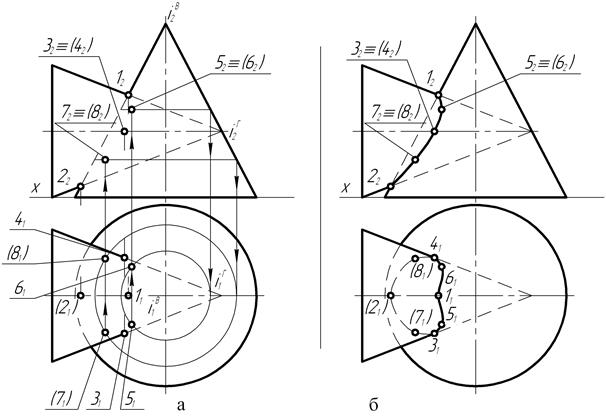
И в том и другом случае задача решается введением дополнительных секущих поверхностей, позволяющих находить точки, принадлежащие одновременно трем геометрическим объектам. В качестве дополнительных поверхностей берутся плоскости, цилиндры и сферы, дающие наиболее простые (заранее известные) линии при пересечении с заданными поверхностями.
Метод секущих плоскостей
Этот метод применяют для построения линии пересечения поверхностей, позволяющих получать (одновременно) во вводимых секущих плоскостях, графически простые линии (прямые или окружности). Это утверждение может быть проиллюстрировано на примере пересечения призмы ? и конуса Ф (см. рисунок 1, Метод секущих плоскостей).
Здесь в качестве вспомогательных секущих плоскостей выступают горизонтальные плоскости уровня Si. На поверхности конуса (в силу того, что они перпендикулярны оси вращения) эти плоскости выделяют окружности, а на поверхности призмы — параллельные прямые (образующие).
Характерные точки 1, 5 линии пересечения определяют в пересечении фронтальных очерков. Текущие точки линии пересечения определятся как результат пересечения соответствующих окружностей и прямых в секущих плоскостях Si.
Текущие точки линии пересечения определятся как результат пересечения соответствующих окружностей и прямых в секущих плоскостях Si.
Метод секущих сфер
Линия пересечения двух цилиндров Ф и ? (RФ > R?) может быть определена с помощью метода секущих сфер. Это определяется тем, что рассматриваемые поверхности являются поверхностями вращения и оси вращения пересекаются.
Линия пересечения распадается на две ветви, нижнюю и верхнюю, построение которых аналогично (см. рисунок 2, Метод секущих сфер).
Фронтальные проекции характерных точек линии пересечения 12 и 22 определятся в результате пересечения фронтальных очерков Ф2 и ?2 ,а горизонтальные — определятся по принадлежности этих точек цилиндру ?.
Низшая точка линии пересечения (3)определяется введением сферы RФ, которая пересечет цилиндр Ф по окружности l(фронтальная проекция этой окружности совпадет с фронтальной проекцией оси вращения цилиндра ?).
С цилиндром ? эта же сфера пересечется по окружностиm.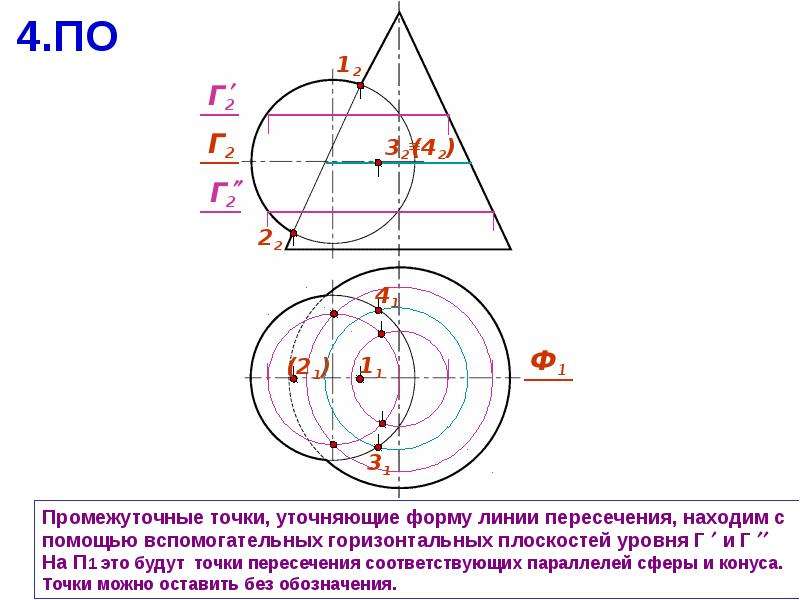 Точка 3 и есть результат пересечения окружностей lи m. Промежуточные точки определятся аналогично, как пересечение окружностей, получающихся в пересечении произвольных сфер RФ < Ri < О212 с цилиндрами Ф и ?. Фронтальные проекции точек линии пересечения определяются как пересечения отрезков прямых, в которые вырождаются окружности, перпендикулярные оси вращения, а горизонтальные проекции находятся по принадлежности одной из поверхностей. В данном случае — поверхности ?.
Точка 3 и есть результат пересечения окружностей lи m. Промежуточные точки определятся аналогично, как пересечение окружностей, получающихся в пересечении произвольных сфер RФ < Ri < О212 с цилиндрами Ф и ?. Фронтальные проекции точек линии пересечения определяются как пересечения отрезков прямых, в которые вырождаются окружности, перпендикулярные оси вращения, а горизонтальные проекции находятся по принадлежности одной из поверхностей. В данном случае — поверхности ?.
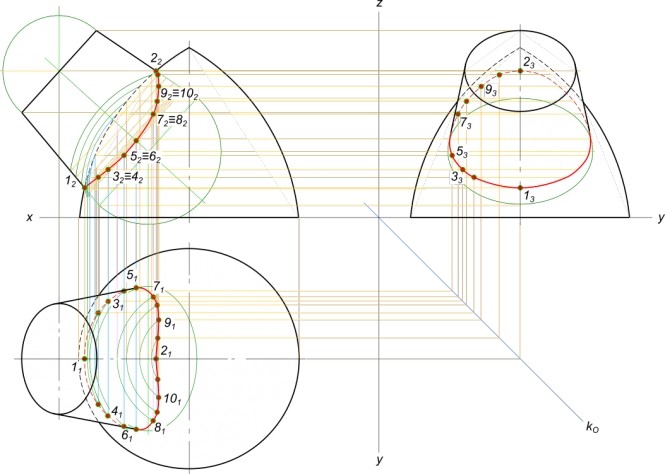
Пошаговый алгоритм решения задачи №8 — построение линии пересечения поверхностей конуса и цилиндра
Пошаговый алгоритм решения задачи №8 — построение линии пересечения поверхностей конуса и цилиндра
Необходимо построить линию пересечения поверхностей вращения — конуса с цилиндром вращения. Оси вращения данных поверхностей расположены взаимно перпендикулярно и являются проецирующими соответственно плоскостей проекций.
Для решения такой задачи по начертательной геометрии необходимо знать:
— построение поверхностей вращения на комплексном чертеже
по заданным координатам точек;
— частные случаи пересечений конуса и цилиндра вращения проецирующей плоскостью;
— метод секущей плоскости для построения линии пересечения
поверхностей.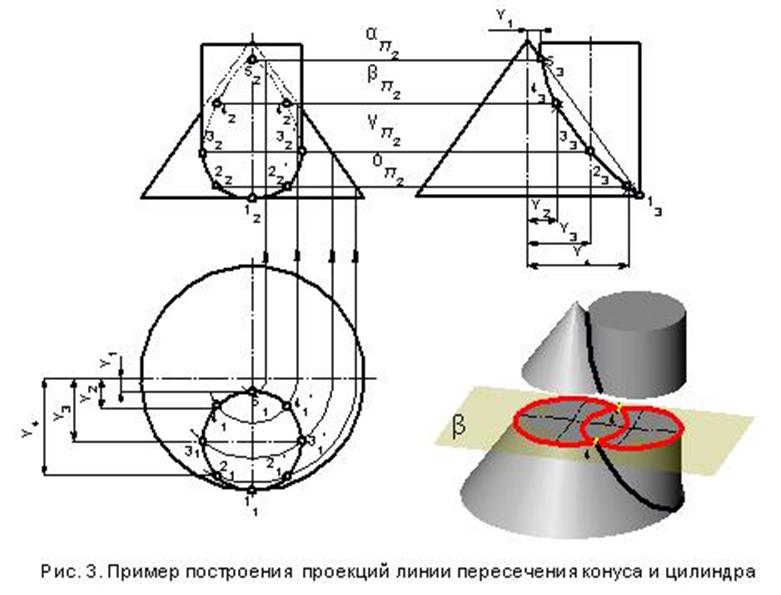
Порядок решения Задачи
1. В правой части листа бумаги формата A3 согласно варианту задания строятся очерки поверхностей конуса и цилиндра вращения в горизонтальной и фронтальной проекциях.
Рис.8.1
Рассматривая полученный чертеж, нетрудно заметить, что линия пересечения данных поверхностей уже имеется во фронтальной плоскости проекций, т.е. она задана исходным чертежом, выделяем ее красным цветом (искомая линия). Таким образом, для решения задачи остается спроецировать (перенести) ее на горизонтальную плоскость.
2. Построение линии пересечения начинаем с отметки опорных точек. Это точки, выше (ниже) которых правее (левее) нет линии пересечения, заметим, кстати, что линия пересечения может располагаться только в местах, одновременно принадлежащих обоим поверхностям.
Опорными точками на фронтальной проекции будут 1’ и 6’. Нахождение их на горизонтальной проекции не представляет затруднений.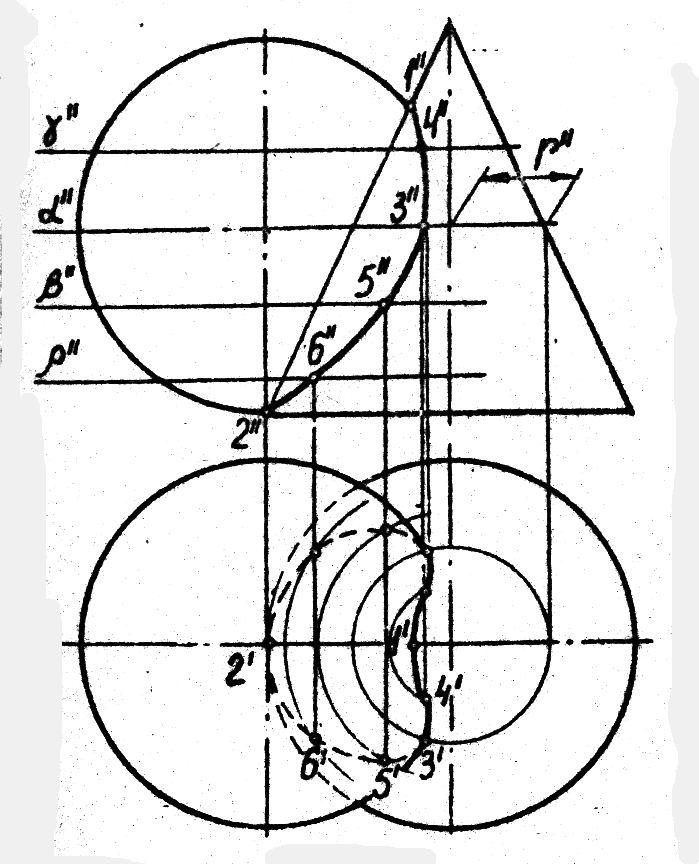 Они будут находиться на крайних образующих конуса, которые проецируется на эту плоскость прямой линией Sb. Перенеся их по линиям связи, получаем 1 и 5 (рис.8.2.а).
Они будут находиться на крайних образующих конуса, которые проецируется на эту плоскость прямой линией Sb. Перенеся их по линиям связи, получаем 1 и 5 (рис.8.2.а).
Рис.8.2
3. Далее, применяем метод секущей плоскости, которую можно проводить через определенный интервал или через характерные точки линии пересечения, проводим первую секущую плоскость ’ через точку 2’. Из частных случаев известно, что если секущая плоскость во фронтальной проекции пересекает конус перпендикулярно оси вращения, то в горизонтальной плоскости сечение будет в виде окружности с радиусом, взятым от оси вращения до очерка поверхности (крайней правой или левой образующих). Проводим указанную окружность данного радиуса Ra в горизонтальной плоскости, ставя ножку циркуля в центр конической поверхности. Поскольку точка 2 одновременно принадлежит конической и цилиндрической поверхности и находится в секущей плоскости, то ее горизонтальная проекция должна находиться в пересечении горизонтальных проекций от секущей плоскости по конусу и цилиндру.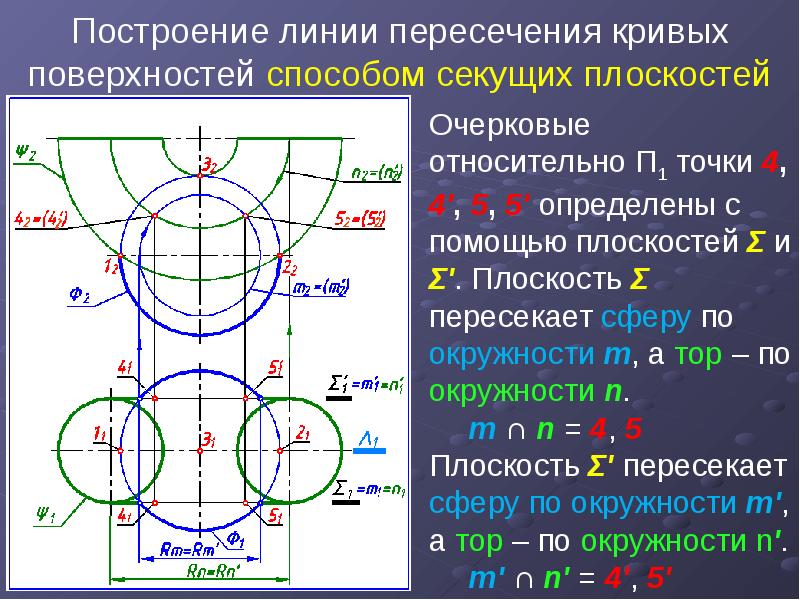
Уже отмечалось, что горизонтальная проекция от секущей плоскости, по конусу — окружность; а по цилиндру — прямая линия, т.к. секущая плоскость проходит параллельно оси вращения цилиндра.
Тогда из проекции точки 2’ проводим линию связи (прямую линию сечения цилиндра) пересечения ее с окружностью и получаем горизонтальные проекции точки 2. Очевидно, что проекций точки будут две: одна — на лицевой стороне конуса 2 (нижняя точка в горизонтальной плоскости проекций), вторая — на тыльной стороне поверхности конуса 21 (верхняя точка в горизонтальной плоскости проекций) (рис.8.2.б).
4. Точно таким же способом находим горизонтальные проекции остальных точек 4 и 5, т.е. через их фронтальные проекции проводим секущие плоскости, в горизонтальной плоскости проекций — соответствующие окружности, на которые проецируем указанные точки (рис.8.3 — б).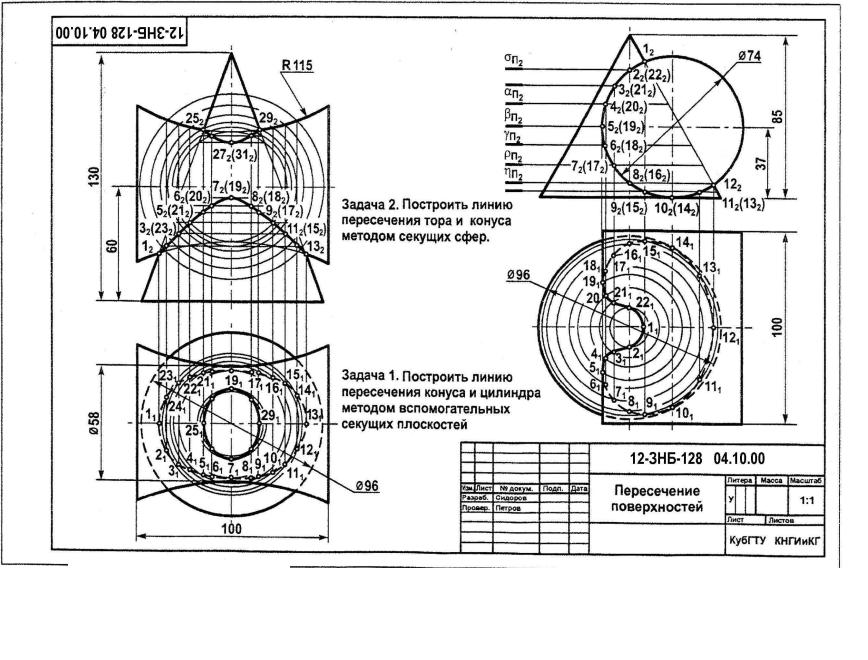
5. Полученные горизонтальные проекции точек соединяем последовательно плавной линией с учетом видимости, которая определяется относительно обоих поверхностей. Видимость по конусу будет полной, поскольку в горизонтальной проекции любая точка, лежащая на ее поверхности будет видимой. Видимость по цилиндру определяется таким образом, что все точки, находящиеся выше диаметра цилиндра на фронтальной проекции, будут видимыми на горизонтальной проекции, а все точки, находящиеся ниже диаметра цилиндра на фронтальной проекции — на горизонтальной будут невидимыми (рис.8.3 -б).
Итак, в горизонтальной плоскости точки 1, 2, 3 будут видимыми, а точки 4, 5, 6 будут невидимыми, в точке 3 (3; 31) происходит смена видимости. Соединяя видимые точки контурной линией, а невидимые пунктирной, получаем искомую линию пересечения заданных поверхностей.
Рис.8.3
В заключение отметим два замечания:
1. В практике и в вариантах заданий встречаются так называемые полные и неполные пересечения поверхностей. При неполном пересечении, когда одна поверхность не полностью пересекает другую ( в нашем случае) линия пересечения есть одна замкнутая петля; при полном пересечении, когда одна поверхность полностью пересекает другую, линия пересечения распадается на несколько замкнутых ветвей и их будет столько, сколько полных пересечений участков заданных поверхностей. В предлагаемых вариантах заданий рассматриваются задачи с 2-3 петлями линии пересечений. Построение их такое же, как и рассмотренное построение (рис.8.4)
Рис.8.4
2. Предлагаемые задачи на пересечение поверхностей могут быть решены методом образующих, когда через заданную линию пересечения поверхностей проводится ряд образующих, отмечаются точки пересечения этих образующих с заданной линией пересечения, затем эти образующие вместе с точками на них проецируются на сопряженную плоскость проекций.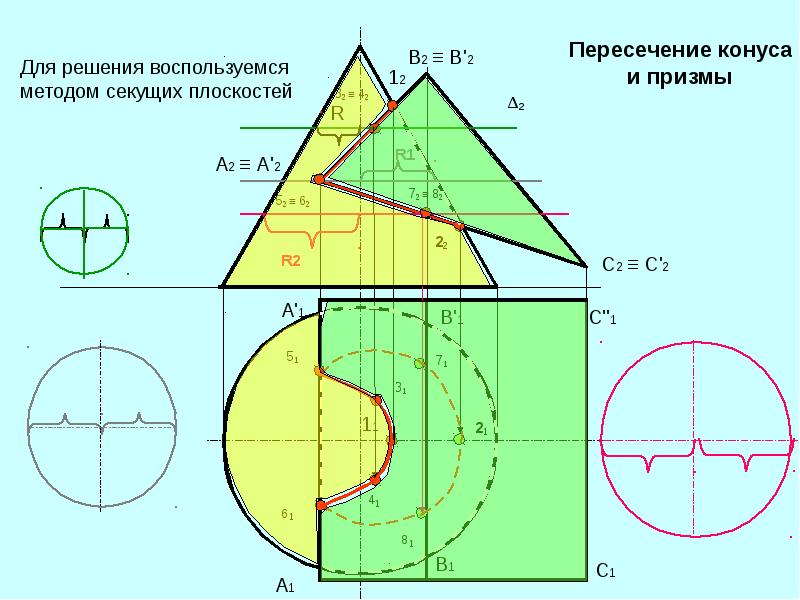
- Рекомендуем
- Комментарии
- Наши товары
Пересечение криволинейных поверхностей, Общие сведения о пересечении криволинейных поверхностей, Применение вспомогательных пересекающихся плоскостей
Пересечение кривых поверхности
Общие сведения о пересечении криволинейных поверхностей
Общая информация. Форма большинства наиболее сложных и ответственных оригинальных деталей устройств и машин формируется сочетанием различных элементарных тел, расположенных в пространстве таким образом, чтобы их поверхности пересекались друг с другом.Поэтому важным этапом построения таких деталей является определение границ элементарных исходных поверхностей, которые представляют собой линии их взаимного пересечения.
Мы уже обсуждали построение линий пересечения некоторых поверхностей и тел друг с другом: двух плоскостей (пп.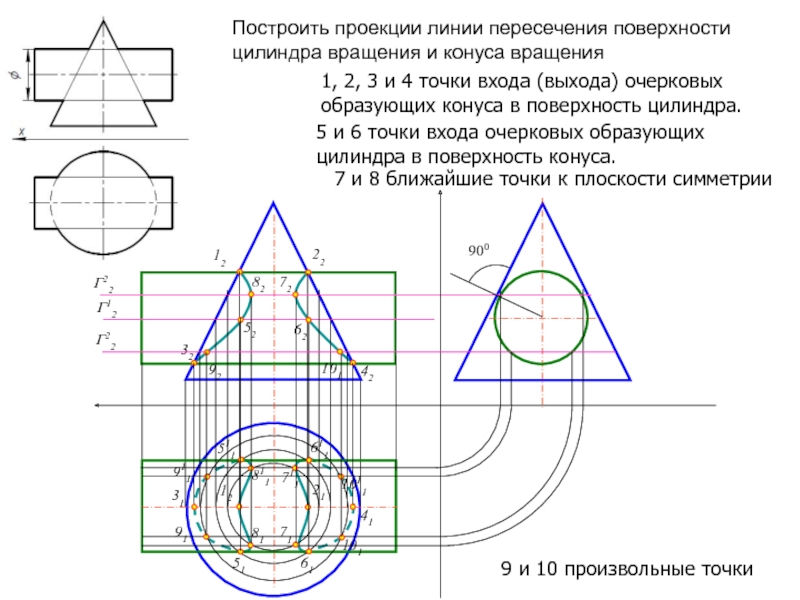 4.2, 4.4), многогранников (п. 6.6).
4.2, 4.4), многогранников (п. 6.6).
В этой главе мы рассмотрим общий способ построения линии пересечения двух криволинейных поверхностей друг с другом, а также некоторые частные случаи пересечения при различном взаимном расположении поверхностей и их положении относительно плоскостей проекций.
Общий способ построения линии пересечения двух криволинейных поверхностей друг с другом. В общем случае линия пересечения двух криволинейных поверхностей строится относительно точек, которые находятся с помощью вспомогательных секущих поверхностей.
Две криволинейные поверхности P1 и P2 (рисунок 10.1) пересекаются третьей секущей вспомогательной поверхностью p3. Найти линии пересечения KL и MN вспомогательной поверхности с каждой из заданных.Пересечение построенных линий пересечения KL и MN относится к линии пересечения данных поверхностей.
Многократное повторение таких построений с помощью других вспомогательных
Рис.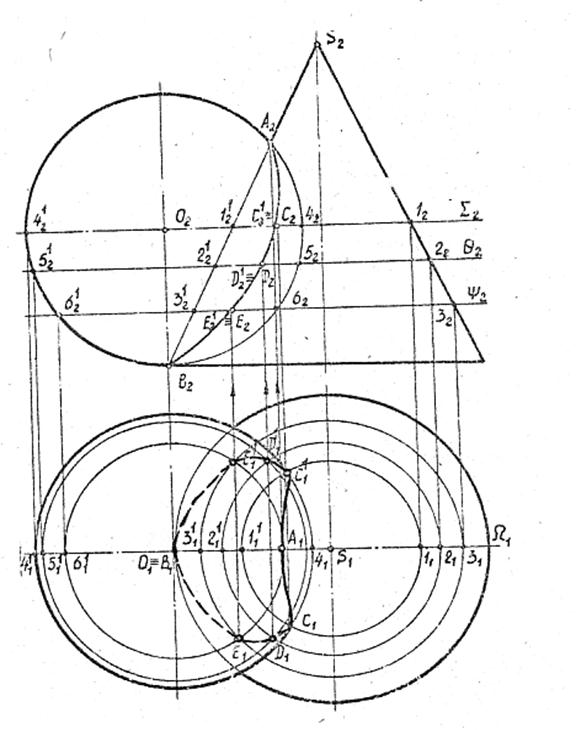 10.1
10.1
Соответствующие поверхности находят необходимое количество точек пересечения двух поверхностей на линии их пересечения.
Сформулируем общее правило построения линии пересечения поверхностей:
— выбрать вид вспомогательных поверхностей;
— строить линии пересечения вспомогательных поверхностей с заданными поверхностями;
— найдите точки пересечения построенных линий и соедините их вместе.
В качестве вспомогательных поверхностей выбираются те, линии пересечения которых с заданными поверхностями проецируются на чертеж в графически простые линии — прямые, окружности. В качестве вспомогательных поверхностей, например, можно использовать плоскости или сферы. Рассмотрим их применение.
Отметим, что если одна из исходных поверхностей линейчатая, то задача построения линии пересечения в этом случае сводится к построению точки пересечения прямой (образующей линейчатой поверхности) со второй заданной поверхность (см. § 9.5).
При построении применяются методы преобразования чертежей, если это упрощает и уточняет конструкцию.
При построении точек пересечения поверхностей сначала находят те точки, которые называются характеристическими или опорными точками.
Применение вспомогательных секущих плоскостей
Рассмотрите возможность использования вспомогательных секущих плоскостей, построив линию пересечения сферы с конусом вращения (рисунок 10.2).
Для построения линии пересечения заданных поверхностей в качестве вторичной поверхности удобно использовать ряд горизонтальных плоскостей, перпендикулярных оси конуса, которые пересекают сферу и конус по окружностям.На пересечении этих кругов найдите точки искомой линии пересечения.
Построение обычно начинается с нахождения проекций характерных точек. Выступы 1 верхней и 2 нижней точки являются точками пересечения фронтальных проекций эскизов, поскольку центр сферы и ось конуса лежат в плоскости, параллельной плоскости π2. Горизонтальные Г, 2 ‘ и профиль 7 2 выступов находятся в соединении выступов.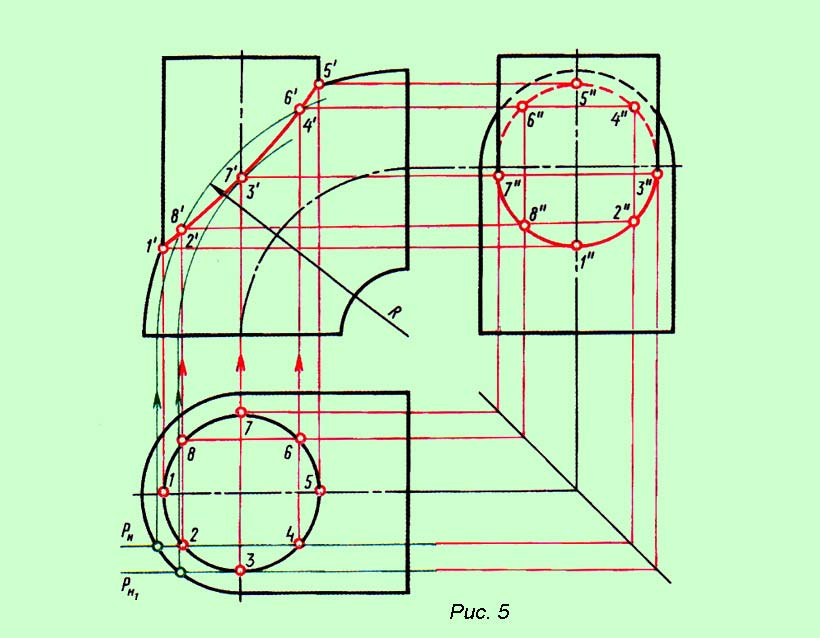 Проекции 3, «3 ‘, 3 и 4», 4′, 4 точек, лежащих на экваторе сферы, находятся с использованием горизонтальной плоскости β (β), проходящей через центр сфера O (O). Она пересекает сферу по формуле
Проекции 3, «3 ‘, 3 и 4», 4′, 4 точек, лежащих на экваторе сферы, находятся с использованием горизонтальной плоскости β (β), проходящей через центр сфера O (O). Она пересекает сферу по формуле
Рис.10.2
ротор и конус по окружности радиуса r 2, в пересечении горизонтальных выступов которого находятся горизонтальные выступы 3 ‘, 4’ точек требуемой линии пересечения.Горизонтальные проекции 3 ‘ и 4′ этих точек являются границами видимости участков линии пересечения на этой проекции. Проекции промежуточных точек, например 5, 5, 5, и 6, 6, 6 , находятся с использованием вспомогательной горизонтальной плоскости γ (y). Их конструкция понятна из рисунка. Аналогично строятся и другие точки. Профильные проекции точек линии пересечения нанесены по их фронтальной и горизонтальной проекциям.Точки с проекциями 7, V, 7 ‘и 8, 8, 8 являются границами видимости участков профиля проекции линии пересечения.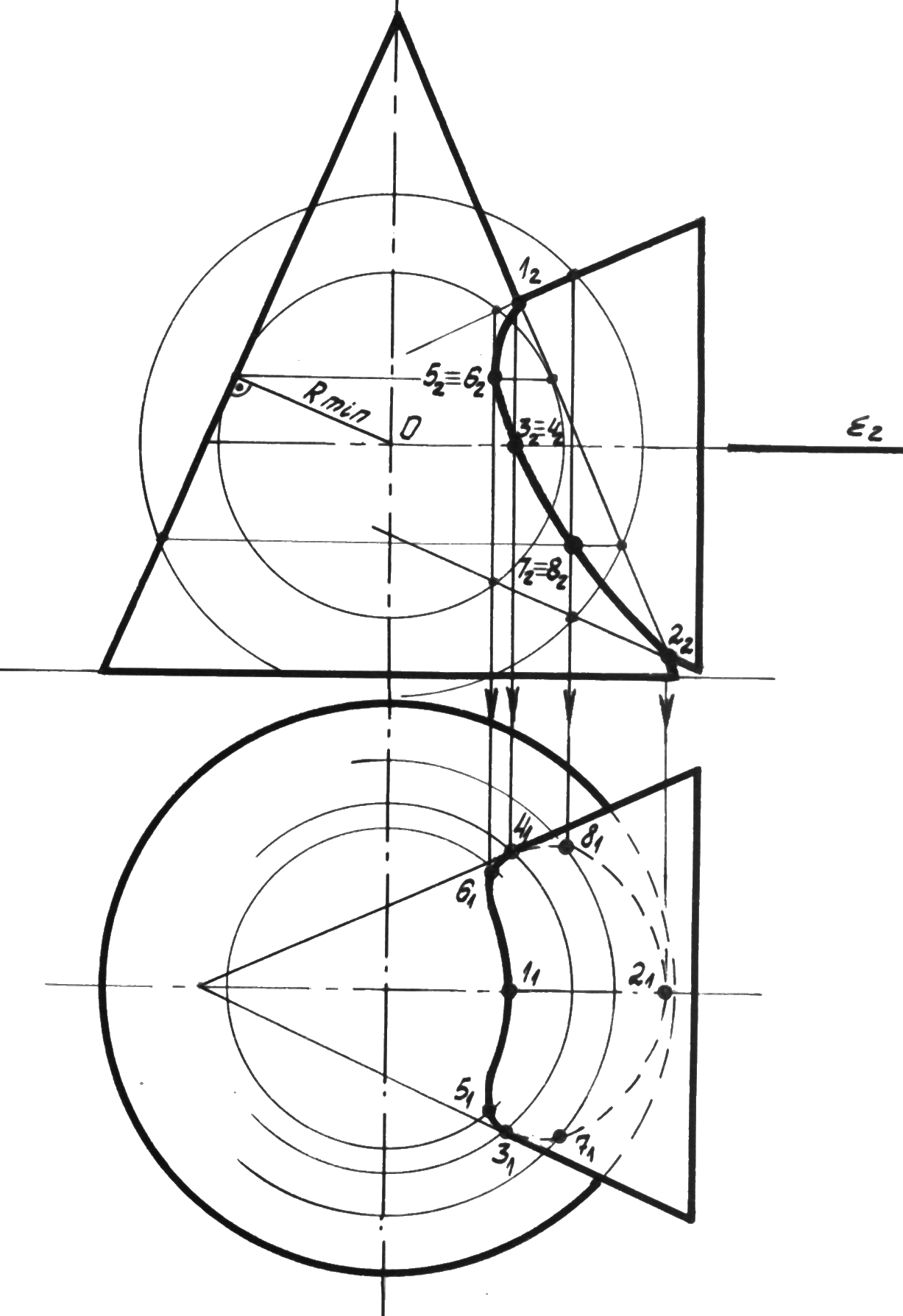 Ниже выступов 7 и , , 8, видна профильная проекция линии пересечения. Точное построение проекций этих точек рассмотрено на рис. 10.5.
Ниже выступов 7 и , , 8, видна профильная проекция линии пересечения. Точное построение проекций этих точек рассмотрено на рис. 10.5.
тематических картинок
Исчисление III — Касательные плоскости и линейные приближения
Онлайн-заметки ПавлаНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- «> Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Приложения частных производных Введение
- Вектор градиента, касательные плоскости и нормальные линии
- Глава
- Частные производные
- Несколько интегралов
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер для комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Заметки Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Полная книга — Только проблемы
- Полная книга — Решения
- Текущая глава — Только проблемы
- Текущая глава — Решения
- Текущий раздел — Только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Предварительные мероприятия
- Целые экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сводка
- Приложения квадратных уравнений
- Уравнения, сводимые к квадратичным в форме
- Уравнения с радикалами
- Линейные неравенства
- Полиномиальные неравенства
- Рациональное неравенство
- Уравнения абсолютных значений
- Неравенства абсолютных значений
- Графики и функции
- Графики
- Строки
- Круги
- Определение функции
- Графические функции
- Комбинирование функций
- Обратные функции
- Общие графы
- Прямые, окружности и кусочные функции
- Предварительные мероприятия
% PDF-1.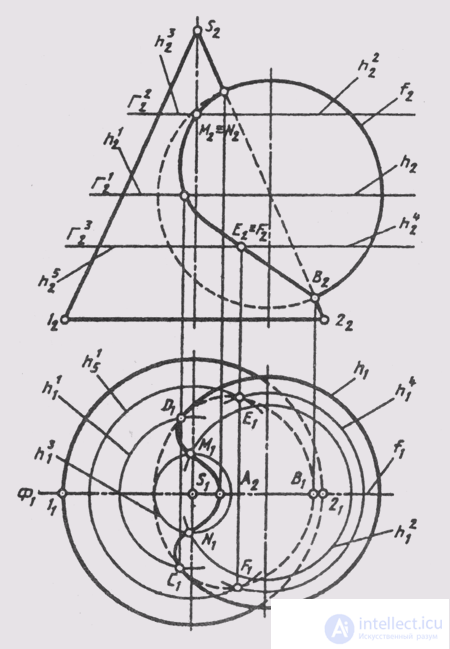 4
%
574 0 объект
>
endobj
xref
574 147
0000000016 00000 н.
0000003292 00000 н.
0000003526 00000 н.
0000003557 00000 н.
0000003622 00000 н.
0000004790 00000 н.
0000005288 00000 п.
0000005355 00000 п.
0000005507 00000 н.
0000005603 00000 п.
0000005698 00000 п.
0000005818 00000 н.
0000005929 00000 н.
0000006046 00000 н.
0000006187 00000 п.
0000006312 00000 н.
0000006484 00000 н.
0000006585 00000 н.
0000006733 00000 н.
0000006835 00000 н.
0000006951 00000 п.
0000007106 00000 н.
0000007235 00000 н.
0000007351 00000 н.
0000007505 00000 н.
0000007630 00000 н.
0000007746 00000 н.
0000007902 00000 н.
0000008019 00000 н.
0000008124 00000 н.
0000008255 00000 н.
0000008403 00000 п.
0000008536 00000 н.
0000008652 00000 п.
0000008775 00000 н.
0000008890 00000 н.
0000009005 00000 н.
0000009124 00000 н.
0000009264 00000 н.
0000009379 00000 п.
0000009513 00000 н.
0000009646 00000 п.
0000009785 00000 н.
0000009919 00000 н.
4
%
574 0 объект
>
endobj
xref
574 147
0000000016 00000 н.
0000003292 00000 н.
0000003526 00000 н.
0000003557 00000 н.
0000003622 00000 н.
0000004790 00000 н.
0000005288 00000 п.
0000005355 00000 п.
0000005507 00000 н.
0000005603 00000 п.
0000005698 00000 п.
0000005818 00000 н.
0000005929 00000 н.
0000006046 00000 н.
0000006187 00000 п.
0000006312 00000 н.
0000006484 00000 н.
0000006585 00000 н.
0000006733 00000 н.
0000006835 00000 н.
0000006951 00000 п.
0000007106 00000 н.
0000007235 00000 н.
0000007351 00000 н.
0000007505 00000 н.
0000007630 00000 н.
0000007746 00000 н.
0000007902 00000 н.
0000008019 00000 н.
0000008124 00000 н.
0000008255 00000 н.
0000008403 00000 п.
0000008536 00000 н.
0000008652 00000 п.
0000008775 00000 н.
0000008890 00000 н.
0000009005 00000 н.
0000009124 00000 н.
0000009264 00000 н.
0000009379 00000 п.
0000009513 00000 н.
0000009646 00000 п.
0000009785 00000 н.
0000009919 00000 н.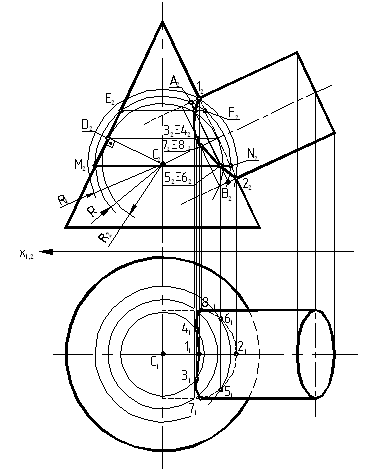 0000010058 00000 п.
0000010193 00000 п.
0000010330 00000 п.
0000010463 00000 п.
0000010598 00000 п.
0000010733 00000 п.
0000010870 00000 п.
0000011005 00000 п.
0000011138 00000 п.
0000011276 00000 п.
0000011411 00000 п.
0000011545 00000 п.
0000011678 00000 п.
0000011811 00000 п.
0000011944 00000 п.
0000012080 00000 п.
0000012258 00000 п.
0000012429 00000 п.
0000012591 00000 п.
0000012786 00000 п.
0000012976 00000 п.
0000013072 00000 п.
0000013168 00000 п.
0000013265 00000 п.
0000013361 00000 п.
0000013457 00000 п.
0000013552 00000 п.
0000013648 00000 п.
0000013743 00000 п.
0000013840 00000 п.
0000013936 00000 п.
0000014033 00000 п.
0000014129 00000 п.
0000014226 00000 п.
0000014322 00000 п.
0000014418 00000 п.
0000014513 00000 п.
0000014610 00000 п.
0000014706 00000 п.
0000014803 00000 п.
0000014899 00000 п.
0000014995 00000 н.
0000015090 00000 н.
0000015187 00000 п.
0000015283 00000 п.
0000015379 00000 п.
0000015474 00000 п.
0000015570 00000 п.
0000010058 00000 п.
0000010193 00000 п.
0000010330 00000 п.
0000010463 00000 п.
0000010598 00000 п.
0000010733 00000 п.
0000010870 00000 п.
0000011005 00000 п.
0000011138 00000 п.
0000011276 00000 п.
0000011411 00000 п.
0000011545 00000 п.
0000011678 00000 п.
0000011811 00000 п.
0000011944 00000 п.
0000012080 00000 п.
0000012258 00000 п.
0000012429 00000 п.
0000012591 00000 п.
0000012786 00000 п.
0000012976 00000 п.
0000013072 00000 п.
0000013168 00000 п.
0000013265 00000 п.
0000013361 00000 п.
0000013457 00000 п.
0000013552 00000 п.
0000013648 00000 п.
0000013743 00000 п.
0000013840 00000 п.
0000013936 00000 п.
0000014033 00000 п.
0000014129 00000 п.
0000014226 00000 п.
0000014322 00000 п.
0000014418 00000 п.
0000014513 00000 п.
0000014610 00000 п.
0000014706 00000 п.
0000014803 00000 п.
0000014899 00000 п.
0000014995 00000 н.
0000015090 00000 н.
0000015187 00000 п.
0000015283 00000 п.
0000015379 00000 п.
0000015474 00000 п.
0000015570 00000 п.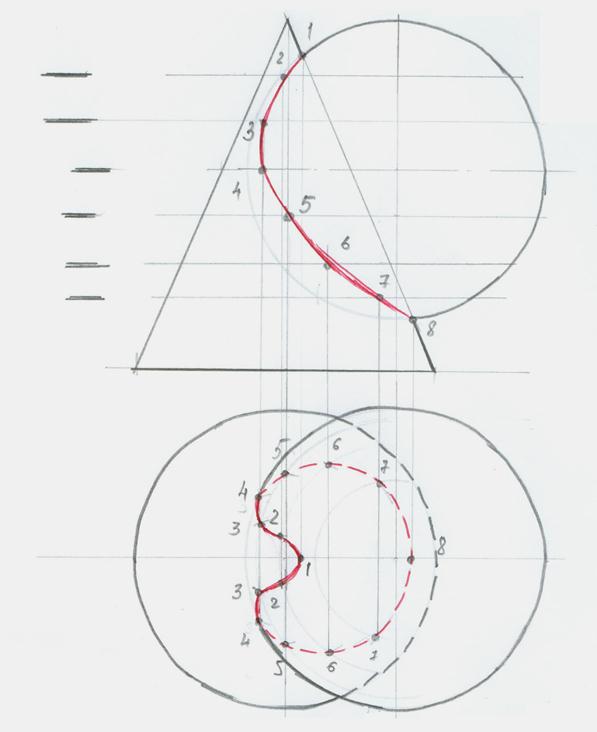 0000015665 00000 п.
0000015760 00000 п.
0000015854 00000 п.
0000015950 00000 п.
0000016045 00000 п.
0000016141 00000 п.
0000016236 00000 п.
0000016331 00000 п.
0000016425 00000 п.
0000016521 00000 п.
0000016757 00000 п.
0000017145 00000 п.
0000021400 00000 п.
0000022020 00000 н.
0000022413 00000 п.
0000022454 00000 п.
0000022865 00000 п.
0000023160 00000 п.
0000023607 00000 п.
0000024122 00000 п.
0000024707 00000 п.
0000031286 00000 п.
0000031657 00000 п.
0000032140 00000 п.
0000032534 00000 п.
0000033169 00000 п.
0000039209 00000 п.
0000039231 00000 п.
0000040235 00000 п.
0000040258 00000 п.
0000041456 00000 п.
0000041478 00000 п.
0000042524 00000 п.
0000042547 00000 п.
0000043629 00000 п.
0000043652 00000 п.
0000044766 00000 п.
0000044789 00000 п.
0000045944 00000 п.
0000046251 00000 п.
0000046633 00000 п.
0000046803 00000 п.
0000047099 00000 п.
0000047339 00000 п.
0000047407 00000 п.
0000047430 00000 п.
0000048550 00000 п.
0000048572 00000 н.
0000015665 00000 п.
0000015760 00000 п.
0000015854 00000 п.
0000015950 00000 п.
0000016045 00000 п.
0000016141 00000 п.
0000016236 00000 п.
0000016331 00000 п.
0000016425 00000 п.
0000016521 00000 п.
0000016757 00000 п.
0000017145 00000 п.
0000021400 00000 п.
0000022020 00000 н.
0000022413 00000 п.
0000022454 00000 п.
0000022865 00000 п.
0000023160 00000 п.
0000023607 00000 п.
0000024122 00000 п.
0000024707 00000 п.
0000031286 00000 п.
0000031657 00000 п.
0000032140 00000 п.
0000032534 00000 п.
0000033169 00000 п.
0000039209 00000 п.
0000039231 00000 п.
0000040235 00000 п.
0000040258 00000 п.
0000041456 00000 п.
0000041478 00000 п.
0000042524 00000 п.
0000042547 00000 п.
0000043629 00000 п.
0000043652 00000 п.
0000044766 00000 п.
0000044789 00000 п.
0000045944 00000 п.
0000046251 00000 п.
0000046633 00000 п.
0000046803 00000 п.
0000047099 00000 п.
0000047339 00000 п.
0000047407 00000 п.
0000047430 00000 п.
0000048550 00000 п.
0000048572 00000 н. 0000049483 00000 п.
0000049577 00000 п.
0000051394 00000 п.
0000054095 00000 п.
0000065616 00000 п.
0000003663 00000 н.
0000004768 00000 н.
трейлер
]
>>
startxref
0
%% EOF
575 0 объект
>
endobj
576 0 объект
[
577 0 руб.
]
endobj
577 0 объект
>
>>
endobj
578 0 объект
>
endobj
719 0 объект
>
поток
HToe? bBH0M>, u {-eRmfvn33KtPg / RZ_h | $ HMx.mlg; s \ ~
0000049483 00000 п.
0000049577 00000 п.
0000051394 00000 п.
0000054095 00000 п.
0000065616 00000 п.
0000003663 00000 н.
0000004768 00000 н.
трейлер
]
>>
startxref
0
%% EOF
575 0 объект
>
endobj
576 0 объект
[
577 0 руб.
]
endobj
577 0 объект
>
>>
endobj
578 0 объект
>
endobj
719 0 объект
>
поток
HToe? bBH0M>, u {-eRmfvn33KtPg / RZ_h | $ HMx.mlg; s \ ~
Планшетная съемка с методами и примерами
Что такое плоскостная съемка?
Планшетная съемка — это быстрый метод съемки. В этом виде съемки возможно одновременное построение плана и полевые наблюдения. При съемке на планшете Геометрические условия участка рукописи на листе карты с использованием планшетного стола и алидады, после чего на карте размещаются топографические детали.
Оборудование, используемое при обследовании на плоскости
Общее оборудование, используемое для проведения обследования планшетов —
- Плоский стол
- Алидада прицельная (телескопическая или простая)
- Отвес и вилка для отвеса
- Компас
- Уровень духа
- Цепь
- Стержни дальномерные
- Штатив
- Лист для рисования и инструменты для рисования
- Скрепки или винты
Планшетное оборудование для съемки размещено в 4 этапа следующим образом
Крепление плоского стола
Прикрепите планшет к штативу.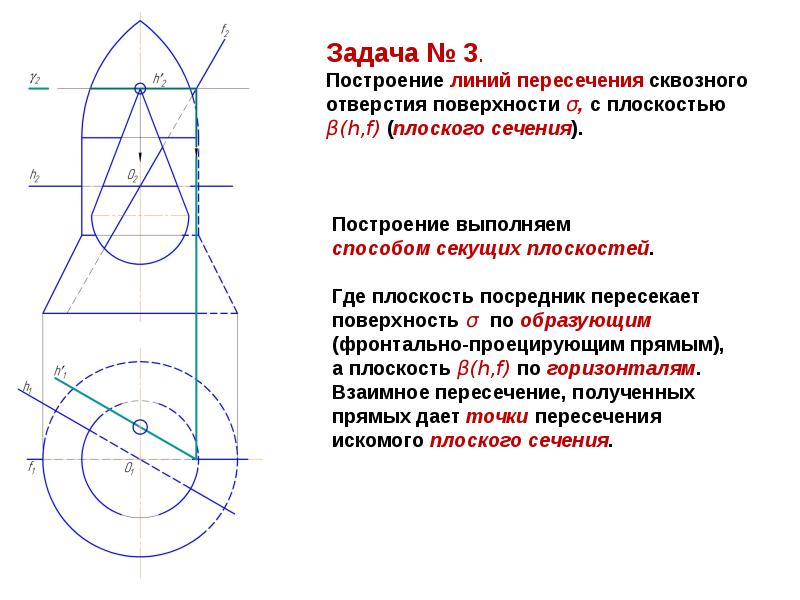 Разместите чертежный лист на плоском столе, используя канцелярские скрепки или винты с накатанной головкой. Лист должен быть в одном положении от первого до последнего.
Разместите чертежный лист на плоском столе, используя канцелярские скрепки или винты с накатанной головкой. Лист должен быть в одном положении от первого до последнего.
Выравнивание плоского стола
Плоский стол необходимо выровнять с помощью спиртового уровня. Для небольших работ подойдет оценка глаз.
Центрирование плоского стола
Отцентрируйте стол с помощью вилки. Благодаря чему мы можем расположить нанесенную точку точно над точкой земли.
Ориентация плоского стола
Когда мы используем более одной приборной станции, ориентация очень важна.Это можно сделать с помощью компаса или прицеливания. В этом случае плоский стол поворачивается так, что нанесенные линии на листе чертежа параллельны соответствующим линиям на земле.
Методы топографической съемки
Как правило, существует четыре метода для выполнения съемки на планшете. Их
- Радиация
- Перекресток
- Перемещение
- Резекция
Излучение
В этом методе плоский стол располагается в одной точке «o», как показано на рис. и выполнять все с этой точки. Из точки O наведите взгляд на точки A, B, C, D и E с помощью алидады, найдите и нанесите точки как a, b, c, d и e на лист чертежа.
и выполнять все с этой точки. Из точки O наведите взгляд на точки A, B, C, D и E с помощью алидады, найдите и нанесите точки как a, b, c, d и e на лист чертежа.
Перекресток
В этом методе мы можем найти точку, построив два луча от двух известных станций. Как показано на рисунке, P и Q — известные станции. Сначала оборудование размещается на P и наносится линия, наведенная на станции A, B и Q. Затем переместите оборудование на станцию Q и нанесите линии, наведя на нее станции A, B и P.Наконец, пересечение лучей A и B является требуемым местом пересечения.
Перемещение
Перемещение — это соединение серии прямых линий. В случае перемещения, плоский стол расположен в одной точке для предположения A, как показано ниже. С этой точки посмотрите в сторону B и измерьте расстояние AB. Затем переместите плоский стол в точку B, посмотрите в сторону A и измерьте BA. Среднее расстояние AB и Ba нанесено в масштабе на чертежном листе. Затем наведите взгляд на точку C из точки B, измерьте BC и повторите ту же процедуру до последней точки. Проведите несколько проверок в некоторых точках. Наконец, на чертежном листе наносятся линии хода.
Проведите несколько проверок в некоторых точках. Наконец, на чертежном листе наносятся линии хода.
Резекция
Обратная засечка — это метод съемки плоского стола, при котором местоположение плоского стола неизвестно и определяется путем его наведения на известные точки или точки на графике. Его также называют методом ориентации, и его можно проводить в двух полевых условиях следующим образом.
- Трехточечная задача
- Двухточечная задача
Задача трех точек
В этом состоянии известны три точки и их положение на поле.Плоский стол ставится на стыке, откуда видны все три точки. Итак, наблюдая за этими тремя точками, мы можем определить точку, в которой находится оборудование. Этого можно добиться многими следующими способами.
- Метод отслеживания
- Метод Лемана
- Аналитические методы
- Графический метод
Метод трассировки при съемке на плоскости
В методе трассировки плоский стол располагается в точке, откуда видны три точки. Таблица ориентирована по нанесенным линиям этих трех точек. Поместите кальку на лист чертежа и снова наведите взгляд на три точки и нанесите излучающие линии. Затем калька перемещается над чертежным листом до тех пор, пока три излучающие линии не пройдут через соответствующие точки, ранее нанесенные на карту. Наконец, отмечается положение плоского стола.
Таблица ориентирована по нанесенным линиям этих трех точек. Поместите кальку на лист чертежа и снова наведите взгляд на три точки и нанесите излучающие линии. Затем калька перемещается над чертежным листом до тех пор, пока три излучающие линии не пройдут через соответствующие точки, ранее нанесенные на карту. Наконец, отмечается положение плоского стола.
Метод Леманна
В этом методе плоскостной стол располагается в точке P и наводится на станции A, B и C и строит лучи Aa, Bb и Cc.Лучи образуют небольшой треугольник, который называется треугольником ошибки. Другая точка P1 выбрана для уменьшения ошибки и наведения на точку A из P1 аналогично B и C., что даст еще один треугольник ошибки. Повторяйте эту процедуру, пока ошибка не станет нулевой.
Аналитические методы
Существует множество аналитических методов, разработанных в условиях трехточечной задачи. В этом методе со станции P наблюдаются A, B и C и отмечаются значения углов и длин.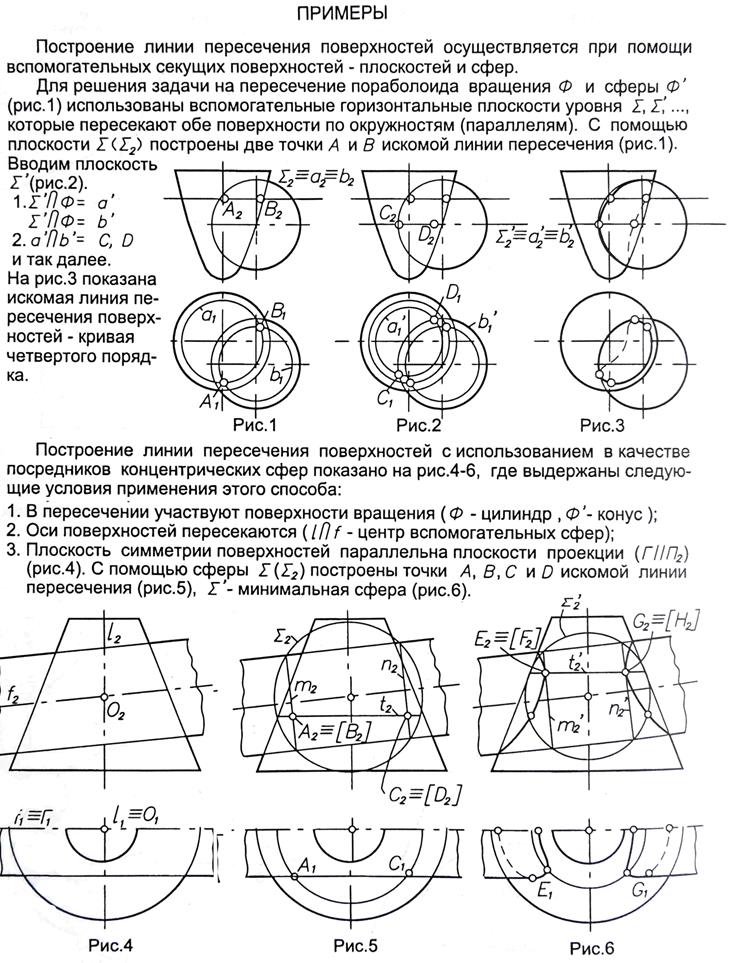 По этим значениям определите положение неизвестных точек с помощью аналитических формул.
По этим значениям определите положение неизвестных точек с помощью аналитических формул.
Графический метод
Графическим способом также определяются углы и длины, которые отображаются на графике и определяет положение плоского стола.
Задача двух точек
В двухточечной задаче две точки наблюдаются из другой точки, соответствующей точкам, указанным в листе плоской таблицы. Здесь следует обсудить два случая.
Случай 1: когда точки могут быть заняты плоским столом
Как показано на рис.A и B — две точки, соответствующие точкам a и b. Теперь плоскостной стол расположен в точке B и ориентирован по прицелу A. Прицел C из точки B и bx нанесен на лист. Затем переместите планшет в положение C, ориентируясь по задней визирной точке B по xb. Затем алидада помещается над точкой a и наведена на станцию A, затем линия Aa пересекает линию bx в каком-то месте, которое находится в точке c на станции C.
Случай 2: Когда плоский стол не может занимать управляющие станции
В этом случае вспомогательная точка D считается более близкой к C.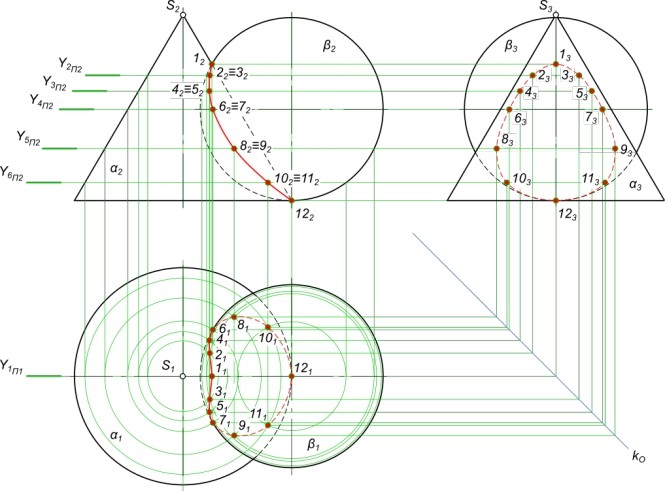 Расположите плоский стол в точке D по линии ab, параллельной AB. Затем найдите станции A и B, соответствующие точкам a и b. нарисованные лучи пересекаются в некоторой точке, отмеченной d. затем посмотрите на C, поместив алидаду на d. обозначьте расстояние Dc как c1. Переместите таблицу в положение C и заднюю точку в D относительно c1.
Расположите плоский стол в точке D по линии ab, параллельной AB. Затем найдите станции A и B, соответствующие точкам a и b. нарисованные лучи пересекаются в некоторой точке, отмеченной d. затем посмотрите на C, поместив алидаду на d. обозначьте расстояние Dc как c1. Переместите таблицу в положение C и заднюю точку в D относительно c1.
Затем прицел A, соответствующий a, нарисованный луч пересекает ранее нарисованный луч из D в c2. Из точки c2 нарисуйте луч, который пересекает точку db, и отметьте пересечение как b1.Стол ориентируется до тех пор, пока ab не окажется на одной линии с P. Из взгляда P и проведите лучи Aa и Ba. Пересечение этих двух лучей даст Местоположение точки C.
Подробнее:
Оборудование для осмотра стола и его применение
Детали теодолита и их функции для угловых измерений при геодезии
Оборудование, используемое для измерения углов и возвышений при геодезии
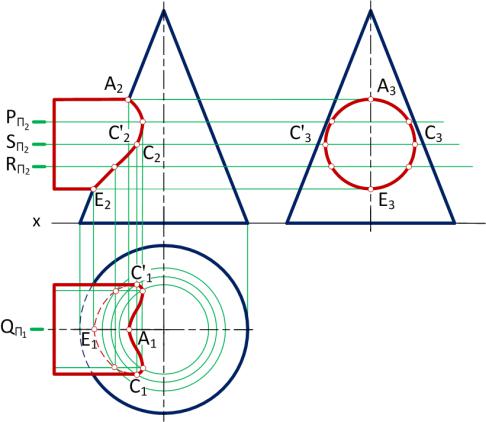
Пересечение трех плоскостей
Как найти связь между двумя плоскостями.
Дано трех самолетов:
Сформируйте систему из уравнений плоскостей и вычислите ранги.
r = ранг матрицы коэффициентов
r ‘= ранг расширенной матрицы
Связь между двумя плоскостями можно описать следующим образом:
Случай 1. Пересечение в точке | ||
Корпус 2.1. Каждая плоскость разрезает две другие по прямой Три плоскости образуют призматическую поверхность | Корпус 2. | |
Корпус 3.1. Три плоскости, пересекающиеся по прямой | Корпус 3.2. Две совпадающие плоскости и другие пересекающиеся их в линии | |
Корпус 4.1. Три параллельные плоскости | Корпус 4. | |
Случай 5. Три совпадающих плоскости |
Укажите взаимосвязь между тремя плоскостями:
Решение:
Сформируйте систему из уравнений плоскостей и вычислите ранги.
Каждая плоскость рассекает два других по прямой, и они образуют призматическую поверхность.
Укажите взаимосвязь между тремя плоскостями:
Решение:
Сформируйте систему из уравнений плоскостей и вычислите ранги.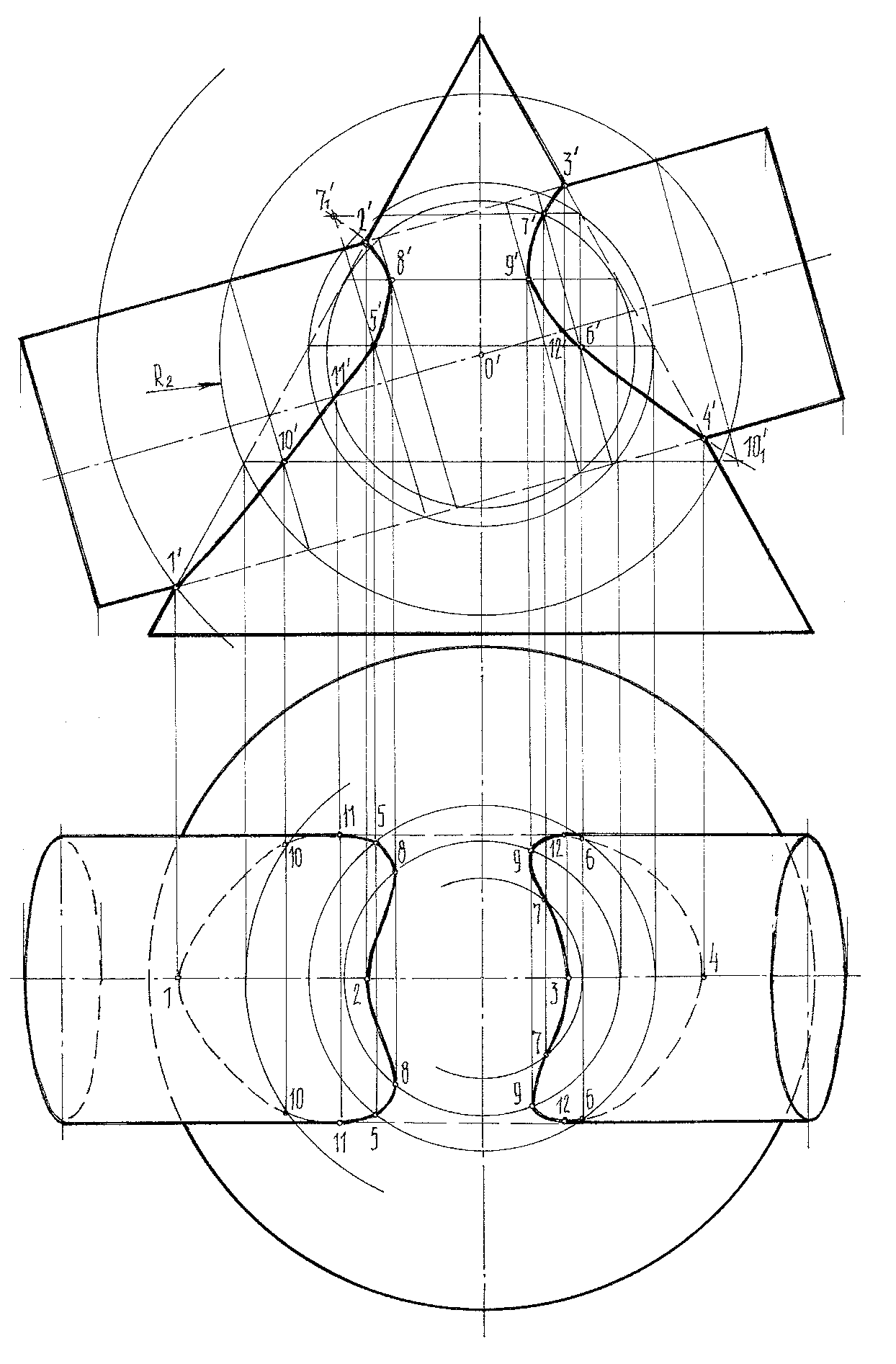
Каждая плоскость пересекает точку.
Укажите взаимосвязь между тремя плоскостями:
Решение:
Сформируйте систему из уравнений плоскостей и вычислите ранги.
Вторая и Третья плоскости совпадают, и первая пересекает их, поэтому три плоскости пересекаются по линии.
.
 Построить линию пересечения конуса и цилиндра вращения (рисунок 68). Вспомогательные секущие плоскости пересекают цилиндр по прямоугольникам, конус – по окружностям.
Построить линию пересечения конуса и цилиндра вращения (рисунок 68). Вспомогательные секущие плоскости пересекают цилиндр по прямоугольникам, конус – по окружностям.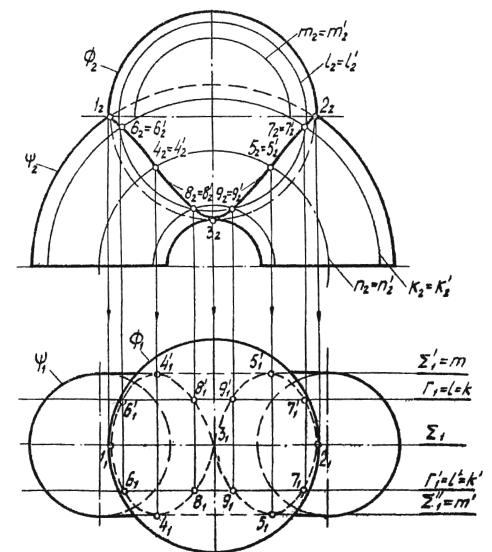 ПлоскостьQ2 пересекает поверхность цилиндра по крайним образующим (левой и правой), а поверхность конуса ‑ по окружности. Пересечения горизонтальных проекций крайних образующих и окружности дают точки 21 и 21 . Промежуточные точки 4 и 5 линии пересечения найдены при помощи фронтальных плоскостей Q4 и Q5.
ПлоскостьQ2 пересекает поверхность цилиндра по крайним образующим (левой и правой), а поверхность конуса ‑ по окружности. Пересечения горизонтальных проекций крайних образующих и окружности дают точки 21 и 21 . Промежуточные точки 4 и 5 линии пересечения найдены при помощи фронтальных плоскостей Q4 и Q5.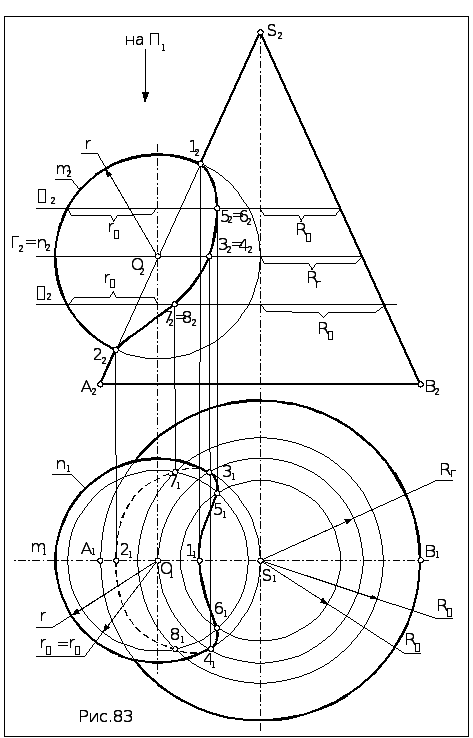 Эта плоскость рассечет конус по треугольнику, а сферу по окружности, диаметр которой равен диаметру сферы. Их пересечение дает на фронтальной плоскости проекции точек 12 и 22. По линиям связи перенесем их на горизонтальную плоскость проекций.
Эта плоскость рассечет конус по треугольнику, а сферу по окружности, диаметр которой равен диаметру сферы. Их пересечение дает на фронтальной плоскости проекции точек 12 и 22. По линиям связи перенесем их на горизонтальную плоскость проекций.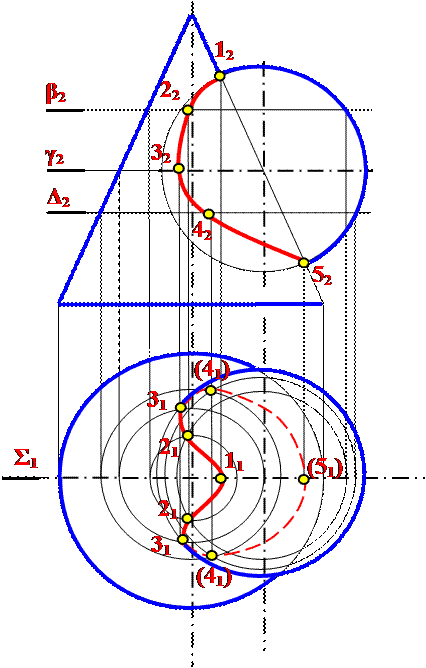
 Для нахождения опорных точек 3 из точки О описана сферическая поверхность Сф.I наименьшего диаметра. Она касается поверхности вертикального стоящего цилиндра, т.е. пересекает его по одной горизонтальной прямойав. А второй (горизонтальный) цилиндр Сф.I пересекает по окружностям, фронтальная проекция которых ‑ вертикальные прямые сd. Пересечение прямыхав и сd определяют положение опорных точек 3. Это крайние левая и правая точки. Аналогично при помощи вспомогательной Сф.II построена фронтальная проекция точек 4 и 5, принадлежащих линии пересечения цилиндров. Размер сферы Сф.II и полученные точки являются случайными, т.е. строятся для более точного определения положения линии пересечения. Горизонтальные проекции найденных точек могут быть построены по линиям связи, и они все лежат на окружности, т.к. цилиндр является горизонтально проецирующим образом.
Для нахождения опорных точек 3 из точки О описана сферическая поверхность Сф.I наименьшего диаметра. Она касается поверхности вертикального стоящего цилиндра, т.е. пересекает его по одной горизонтальной прямойав. А второй (горизонтальный) цилиндр Сф.I пересекает по окружностям, фронтальная проекция которых ‑ вертикальные прямые сd. Пересечение прямыхав и сd определяют положение опорных точек 3. Это крайние левая и правая точки. Аналогично при помощи вспомогательной Сф.II построена фронтальная проекция точек 4 и 5, принадлежащих линии пересечения цилиндров. Размер сферы Сф.II и полученные точки являются случайными, т.е. строятся для более точного определения положения линии пересечения. Горизонтальные проекции найденных точек могут быть построены по линиям связи, и они все лежат на окружности, т.к. цилиндр является горизонтально проецирующим образом.
 Аналогично при помощи Сф.II построена фронтальная проекция 42 еще двух точек, принадлежащих линии пересечения. Горизонтальные проекции найденных точек могут быть построены как проекции точек, лежащих на поверхности конуса (рисунок 73).
Аналогично при помощи Сф.II построена фронтальная проекция 42 еще двух точек, принадлежащих линии пересечения. Горизонтальные проекции найденных точек могут быть построены как проекции точек, лежащих на поверхности конуса (рисунок 73).
 I для нахождения точек 2 и 4
I для нахождения точек 2 и 4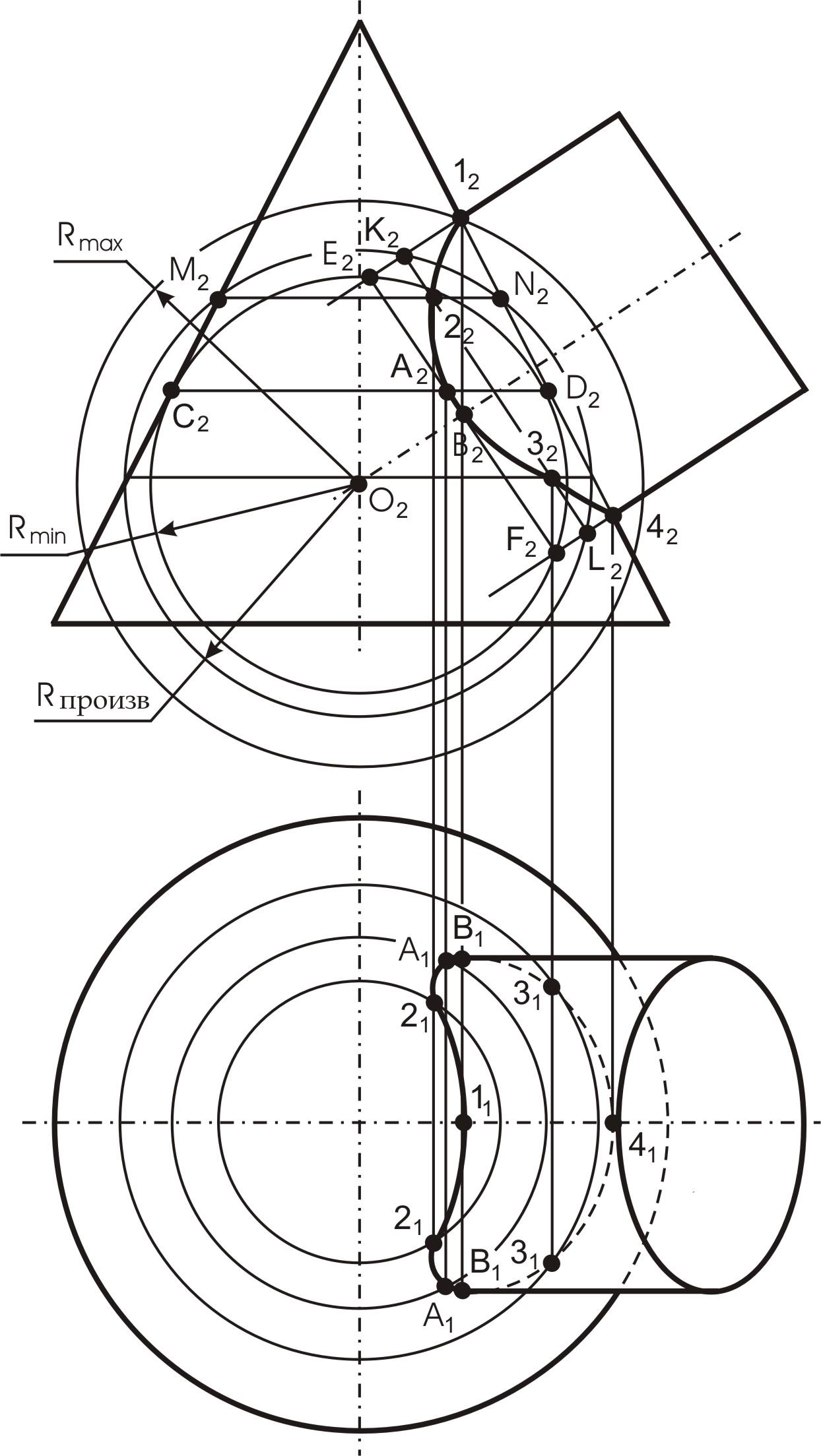 Проекции точки
Содержание и цель курса. Метод проекций (понятие о центральных проекциях, параллельных проекциях и ее свойстве, понятие о методе Г. Монжа). Система прямоугольных координат. Эпюры точки, расположенной в четвертях пространства. Построение 3-ей проекции точки по двум данным. [1, 2, 4, 5]
Проекции точки
Содержание и цель курса. Метод проекций (понятие о центральных проекциях, параллельных проекциях и ее свойстве, понятие о методе Г. Монжа). Система прямоугольных координат. Эпюры точки, расположенной в четвертях пространства. Построение 3-ей проекции точки по двум данным. [1, 2, 4, 5]
 О проекциях плоских углов. Особые прямые плоскости. [1, 2, 4, 5]
О проекциях плоских углов. Особые прямые плоскости. [1, 2, 4, 5]
 Плоскопараллельное перемещение. Решение четырех методических задач. Вращение вокруг линии уровня. Основные методические задачи. [1, 2, 7]
Плоскопараллельное перемещение. Решение четырех методических задач. Вращение вокруг линии уровня. Основные методические задачи. [1, 2, 7]
 Плоское сечение цилиндра, конуса, сферы. Плоское сечение наклонного цилиндра, поверхности вращения с криволинейной образующей. [1, 2, 8, 9]
Плоское сечение цилиндра, конуса, сферы. Плоское сечение наклонного цилиндра, поверхности вращения с криволинейной образующей. [1, 2, 8, 9]
 2 – Практические занятия (I семестр)
2 – Практические занятия (I семестр)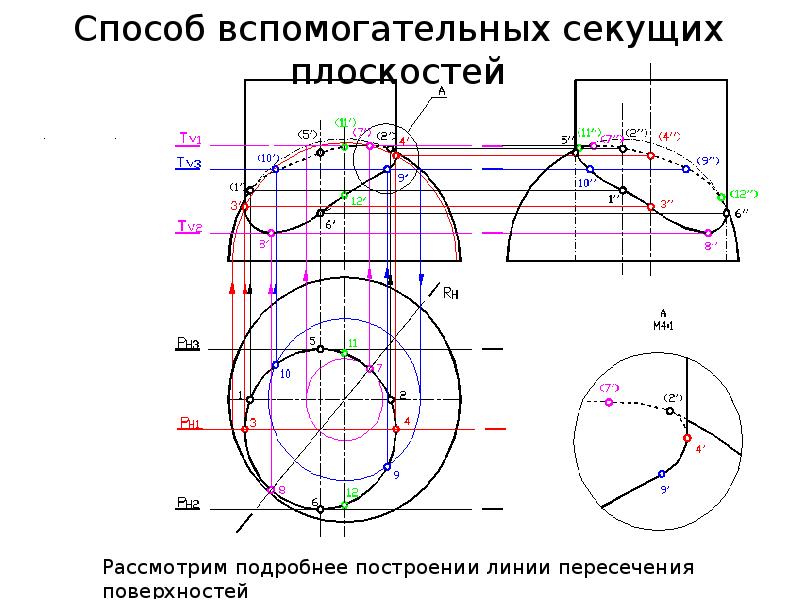 Точка и прямая в плоскости. Проведение проецирующей плоскости через прямую. Главные линии плоскости. На дом: задачи 2.1 и 2.2. Контроль по заданию № 1. [1, 3, 4, 5, 8]
Точка и прямая в плоскости. Проведение проецирующей плоскости через прямую. Главные линии плоскости. На дом: задачи 2.1 и 2.2. Контроль по заданию № 1. [1, 3, 4, 5, 8]
 Построение плоскости, перпендикулярной к прямой. Построение взаимно перпендикулярных прямых. Выдача задания № 4 [1, 3, 4, 5, 6, 12, 13]
Построение плоскости, перпендикулярной к прямой. Построение взаимно перпендикулярных прямых. Выдача задания № 4 [1, 3, 4, 5, 6, 12, 13]
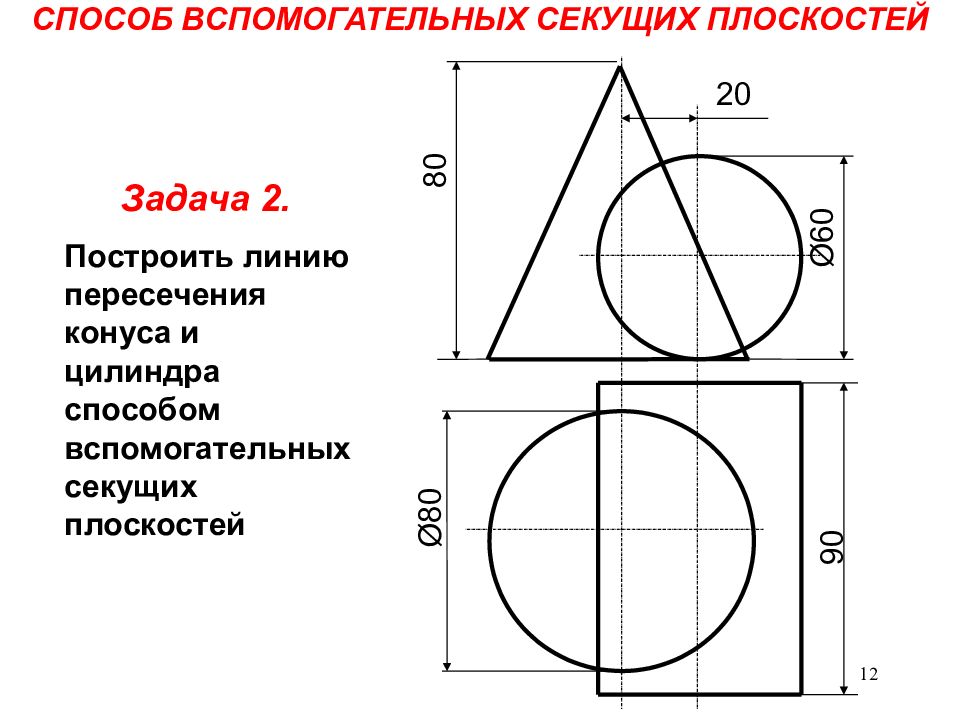 Выдача эпюра № 1. Контроль выполнения задания № 5[1, 2, 7]
Выдача эпюра № 1. Контроль выполнения задания № 5[1, 2, 7]
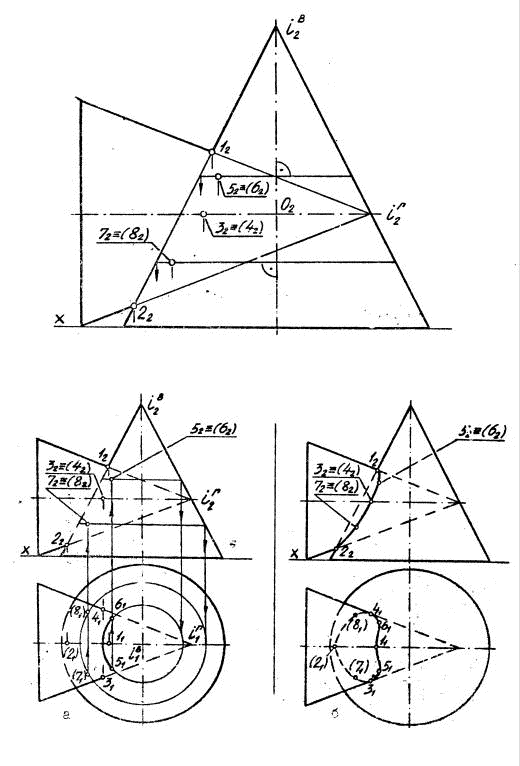 Выдача задания на эпюр № 2. Выдача задания № 8 на дом [1, 2, 8, 9]
Выдача задания на эпюр № 2. Выдача задания № 8 на дом [1, 2, 8, 9]
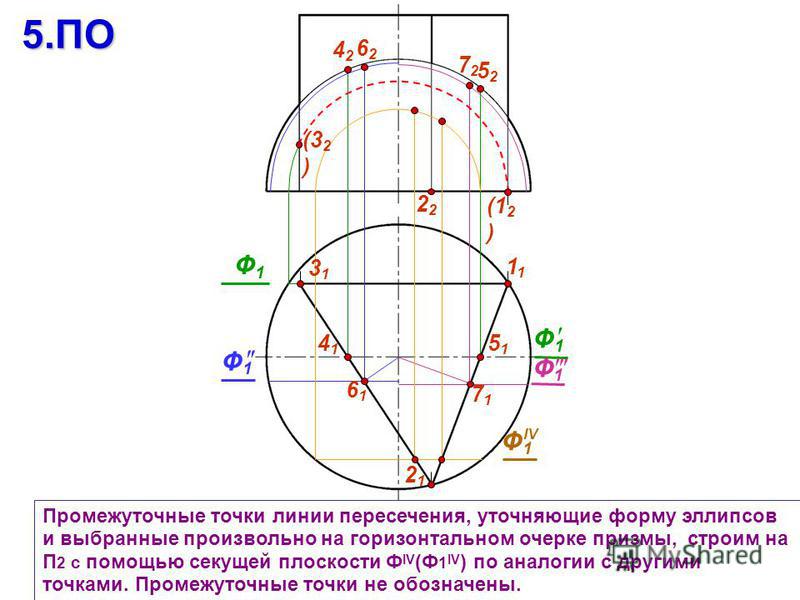 Пересечение поверхностей с применением вспомогательных секущих плоскостей. Выдача эпюра № 3 [1, 2, 11]
Пересечение поверхностей с применением вспомогательных секущих плоскостей. Выдача эпюра № 3 [1, 2, 11]
 А. Алексеева, С.В. Левин; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2005. ‑ 28 с.
А. Алексеева, С.В. Левин; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2005. ‑ 28 с. И. Куничан, Л.И. Идт; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2008. ‑ 16 с.
И. Куничан, Л.И. Идт; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2008. ‑ 16 с.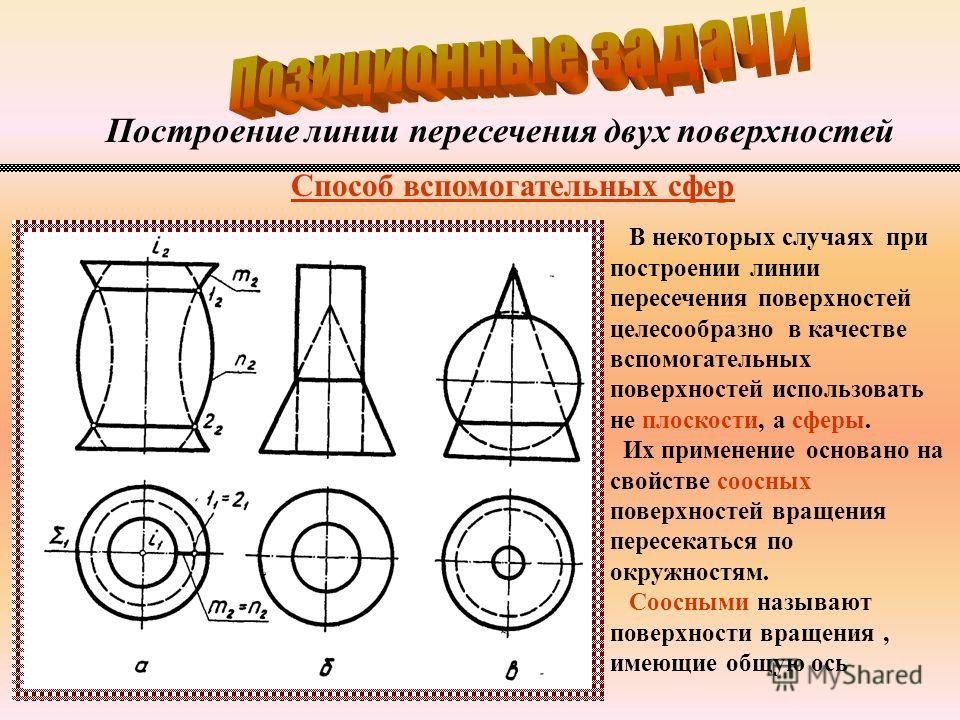 И. Куничан, Л.И. Идт; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2005. – 22 с.
И. Куничан, Л.И. Идт; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2005. – 22 с. Р. Светлова, Н.С. Левина; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2010. – 14 с.
Р. Светлова, Н.С. Левина; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2010. – 14 с.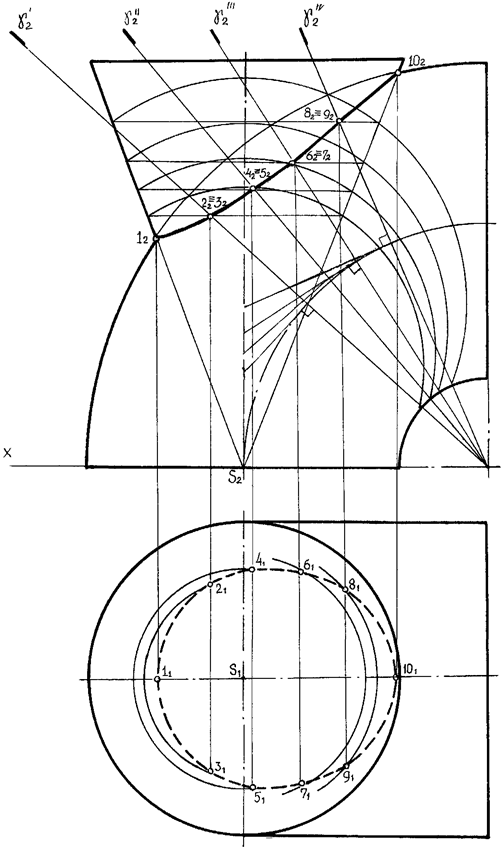 2. Две параллельные плоскости и другие разрезы по прямой
2. Две параллельные плоскости и другие разрезы по прямой  2. Две совпадающие плоскости и другая параллель
2. Две совпадающие плоскости и другая параллель