Дифференцирование функции, заданной параметрически
Примеры решенийРанг матрицы Умножение матриц Метод Гаусса Найти производную Найти интегралРешение СЛАУ методом Крамера Диф уравнения онлайнОпределитель матрицы Точки разрыва функции
В этом случае говорят, что функция y от x задана параметрически. Параметрическое задание функции удобно тем, что оно дает общую запись для прямой и обратной функций.
Предположим, что на некотором промежутке функции x=φ(t) и y=ψ(t) имеют производные, причем φ’(t)≠0. Кроме того, для x=φ(t) существует обратная функция x-1 = t(x) (производная обратной функции равна обратной величине производной прямой функции).
Пример 1. Найти производную функции y по x, заданной параметрически:
Решение.
.
Запишем функцию y’x в параметрической форме:В случае параметрического задания функции первую производную вычисляли по формуле:
(*)
и записывали y’x тоже в параметрической форме:К ней снова применим формулу (*) (при условии, что производные второго порядка существуют):
.
Результат тоже записываем в параметрической форме и берем третью производную и т.д. Так можно получить производную от y по x любого порядка.Пример 2. Найти y’’xx функции
Решение. Найдем y’x по формуле (*): .
Производную y’x
К этой функции снова применим формулу (*):
.
Пример 3. Для функции найти y’’’xxx.
Решение. тогда и
.
ПолучаемЕще раз применяем формулу (*):
.
Если требуется получить зависимость y’’’xxx от x, то выражаем x из соотношения x=e—t и подставляем в y’’’xxx.Для функций, заданных неявно, производные высших порядков можно находить тем же способом, что и первую производную, так как производная любого порядка сама является функцией, заданной неявно, если ее не разрешать относительно производной предыдущего порядка.
Пример 7. Найти производную первого и второго порядка функции, заданной параметрически:
Решение.
;
.
Далее будем искать y’’xx по формуле
.
Отсюда
.
Производную второго порядка также можно было найти по формуле.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Построить график функции, заданной параметрически
2. Вычислить пределы:
а)
б)
в)
г) Исследовать функцию на непрерывность в точке , если
3. Вычислить производные:
а)
б)
в)
г) Составить уравнение нормали к кривой, заданной параметрически
в точке, соответствующей параметру .
4.Исследовать функцию и построить ее график.
5. Вычислить интергалы:
а)
б)
в)
6.
Вычислить площадь фигуры, ограниченной параболой и прямой
Вариант №15
1. Построить в полярной системе координат
2. Вычислить пределы:
а)
б)
в)
г) Исследовать функцию на непрерывность в точке , если
3. Вычислить производные:
а)
б)
в)
г) Написать уравнение нормали к кривой в точке
4. Исследовать функцию и построить ее график.
5. Вычислить интегралы:
а)
б)
в)
6.Вычислить площадь фигуры, ограниченную кривой и прямой
Вариант №16
1.
Построить в полярной системе координат кривую
2. Вычислить пределы:
а)
б)
в)
г) Исследовать функцию в точке на непрерывность
3. Вычислить производные:
а)
б)
в)
г) Написать уравнение касательной к кривой в точке
4. Исследовать функцию и построить ее график.
5. Вычислить интегралы:
а)
б)
в)
6. Вычислить площадь фигуры, заключенной между кривыми и
Вариант №17
1.Построить график функции, заданной в полярной системе координат
2. Вычислить пределы:
а)
б)
в)
г) Исследовать на непрерывность функцию в точке
3.
Вычислить производные:
а)
б)
в)
г) Составить уравнение касательной к кривой, заданной параметрически
В точке
4.Исследовать функцию и построить ее график.
5. Вычислить интегралы:
а)
б)
в)
Вычислить площадь фигуры, заключенной между кривыми
и прямой .
Вариант №18
1. Построить график функции, заданной параметрически
2. Вычислить пределы:
а)
б)
в)
г) Исследовать функцию на непрерывность в точке если
3. Вычислить производные:
а)
б)
в)
г) Составить уравнение касательной к кривой в точке
4.
Исследовать функцию и построить ее график.
Вычислить интегралы
а)
б)
в)
6. Вычислить площадь, заключенную между параболой , осью ox и прямой .
Вариант №19
1. Построить кривую, заданную параметрически
2. Вычислить пределы:
а)
б)
в)
г) Исследовать функцию в точке на непрерывность.
3. Вычислить производные:
а)
б)
в)
г) Составить уравнение нормали к кривой в точке
4. Исследовать функцию и построить ее график
5.
Вычислить интегралы:
а)
б)
в)
6. Вычислить площадь между окружностью и параболой .
Вариант №20
1. Построить график кривой в полярной системе координат:
2. Вычислить пределы:
а)
б)
в)
г) Исследовать на непрерывность функцию в точке
3. Вычислить производные:
а)
б)
в)
г) Составить уравнение касательной к кривой в точке
4. Исследовать функцию и построить ее график.
Вычислить интегралы
а)
б)
в)
6.
Вычислить площадь между кривыми и
Вариант №21
1. Построить график функции, заданной параметрически
2. Вычислить пределы:
а)
б)
в)
г) Исследовать функцию на непрерывность в точке если
Вычислить производные
а)
б)
в)
г) Составить уравнение нормали в точке к кривой
4. Исследовать функцию и построить ее график.
Вычислить интегралы.
а)
б)
в)
6. Вычислить площадь между кривой , осью ox и прямой .
Вариант № 22
исчисление — изучить и построить график функции, заданной в параметрической форме
спросил
Изменено 5 лет, 8 месяцев назад
Просмотрено 94 раза
$\begingroup$
Мне трудно понять, как исследовать и построить график функции, заданной в параметрической форме.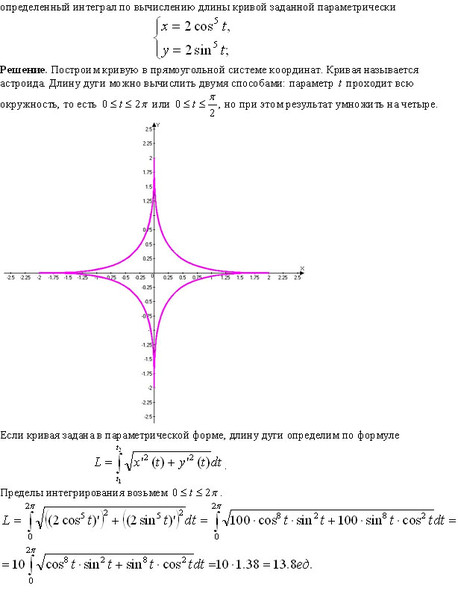
- вычисления
- графические функции
- параметрические
$\endgroup$
2
$\begingroup$
Не общий ответ, но каждый раз, когда вы видите пару уравнений вида \начать{выравнивать*} и &= а + Ь, \\ v &= а — б, \конец{выравнивание*} тихий голос в вашей голове должен спросить: «Что произойдет, если я сложу и вычту (т. е. решу $a$ и $b$ через $u$ и $v$)?» 9{2}$.
Теперь $(u, v)$ представляет собой повернутую и масштабированную декартову систему координат:
Ось $u$ имеет уравнение $v = 0$, т. е. $y = x$;
Ось $v$ имеет уравнение $u = 0$, т. е. $y = -x$;
Обе координаты увеличиваются на $y$;
Точка $(x, y) = (1, 1)$ удовлетворяет условию $(u, v) = (1, 0)$, поэтому одна единица длины в $(u, v)$ равна $\sqrt{ 2}$ единиц длины в $(x, y)$.
Следовательно, ваша парабола выглядит так: 92}$$ у нас была бы просто прямая линия с наклоном $1$. Это говорит нам о том, что когда $t$ становится большим (когда квадраты членов преобладают над линейными), график будет выглядеть как такая линия. Это дополнительно говорит нам о том, что график не является замкнутой кривой.
Какой же вклад вносят «антисимметричные» члены $\pm 2t$? Ну, $-2t$ для $x$ заставляет прямую линию расти медленнее в направлении $x$, и то же самое с $y$, только вместо этого с увеличением роста, поэтому график должен иметь наклон, который обычно больше $1$ в начале. 92-2x$). Однако с этого момента $x$ также всегда увеличивается. Зная это, а также тот факт, что через некоторое время график должен напоминать прямую линию, вы можете получить представление о том, как будет выглядеть весь график, а именно:
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
многомерное исчисление — по двум кривым найти параметрическую кривую
спросил
Изменено 7 лет, 5 месяцев назад
Просмотрено 300 раз
$\begingroup$
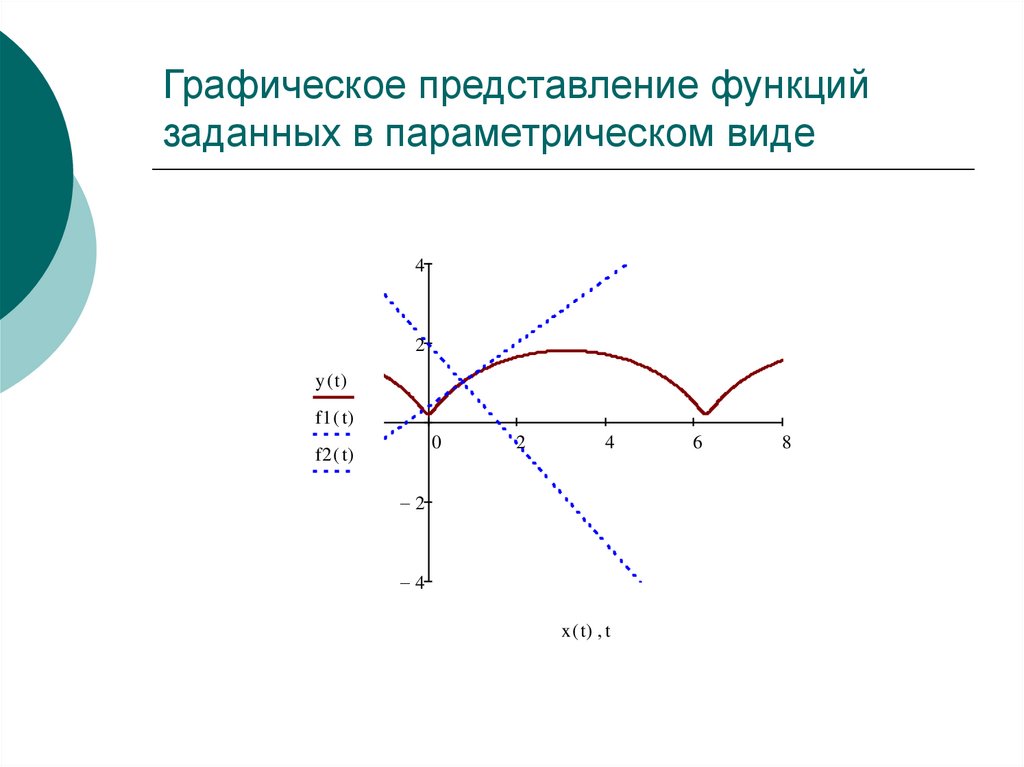
Мне даны два графика x в зависимости от t и y в зависимости от t, и я должен определить параметрическую кривую.
Два графика, которые мне даны:
Параметрическая кривая (это правильный ответ):
Таким образом, решения говорят, что: из первого графика значения x проходят через значения от -2 до 2 дважды. На втором графике значения y делают то же самое. Поэтому этот граф (то, что я показал выше) удовлетворяет этим условиям.
Итак, я не могу понять, что означает это решение. Что означает цикл? Есть ли другое решение, которое правдоподобно в этом вопросе?
- многомерное исчисление
- параметрическое
$\endgroup$
$\begingroup$
Параметрические кривые работают по принципу, согласно которому для каждого $t$ существуют значения $x(t)$ и $y(t)$, соответствующие точке на плоскости. Построив эти точки для всех $t$, мы получим кривую. У вас есть цикл, потому что $x(-2)=x(2)$ и $y(-2)=y(2)$. Для заданных функций $x(t)$ и $y(t)$ существует единственная параметрическая кривая, заданная выражением $c(t)=(x(t),y(t))$.