Сопряжения. Способы построения сопряжения — презентация онлайн
Похожие презентации:
Основы архитектуры и строительных конструкций. Основы проектирования
Конструктивные схемы многоэтажных зданий
Стадии проектирования зданий. Маркировка строительных чертежей (лекция №2)
Правила выполнения архитектурно-строительных чертежей
ЕСКД. Общие правила оформления чертежей. (Лекция 1.1)
задачи на построение (геометрия 7 класс)
Выполненный вариант контрольной работы по разделу «Техническое черчение». (Приложение 3)
Параллельность в пространстве. (Графическая работа 2)
Строительное черчение. Графическое оформление и чтение строительных чертежей
Правила оформления чертежей ЕСКД. Форматы, масштабы, линии, шрифты
1. Геометрические построения.
Сопряжения.Способы построения
сопряжения
Сопряжением называют плавный
переход одной линии в другую.
Что нужно для построения сопряжения?
Знать радиус сопряжения (Rc)
Найти центр сопряжения (Ос)
Найти точки сопряжения
3.
 Виды сопряжения:• Сопряжение двух пересекающихся
Виды сопряжения:• Сопряжение двух пересекающихсяпрямых дугой заданного радиуса.
• Сопряжение дуги и прямой линии дугой
заданного радиуса.
• Сопряжение двух дуг окружности дугой
заданного радиуса.
4. Сопряжение двух пересекающихся прямых дугой заданного радиуса
Даны пересекающиеся под прямым, острым и тупымуглами прямые линии.
Нужно построить сопряжения этих прямых дугой
заданного радиуса R.
5. Сопряжение двух пересекающихся прямых дугой заданного радиуса
Проводим вспомогательные прямыепараллельно заданным на расстоянии R от
заданных.
Точка пересечения этих прямых будет
центром О дуги сопряжения.
Перпендикуляры, опущенные из центра О
на заданные прямые, определят точки
касания A и B.
Сопряжения острого угла.
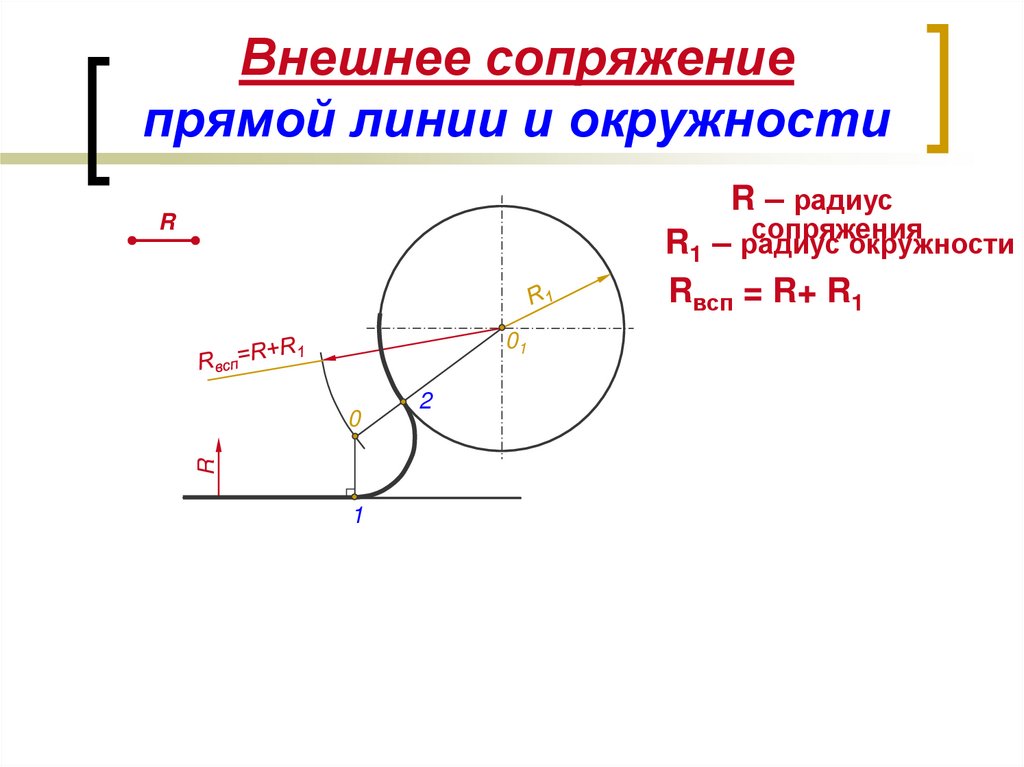
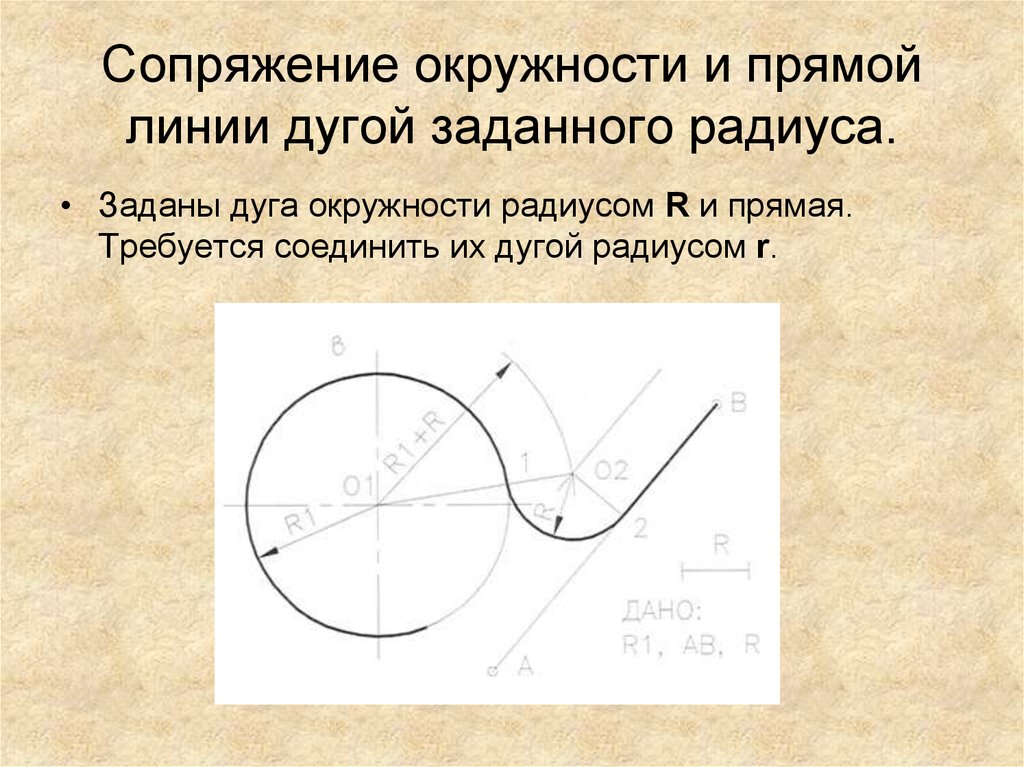
7. Сопряжение окружности и прямой линии дугой заданного радиуса.
• Заданы дуга окружности радиусом R и прямая.Требуется соединить их дугой радиусом r.
8. Сопряжение дуги и прямой линии дугой заданного радиуса.
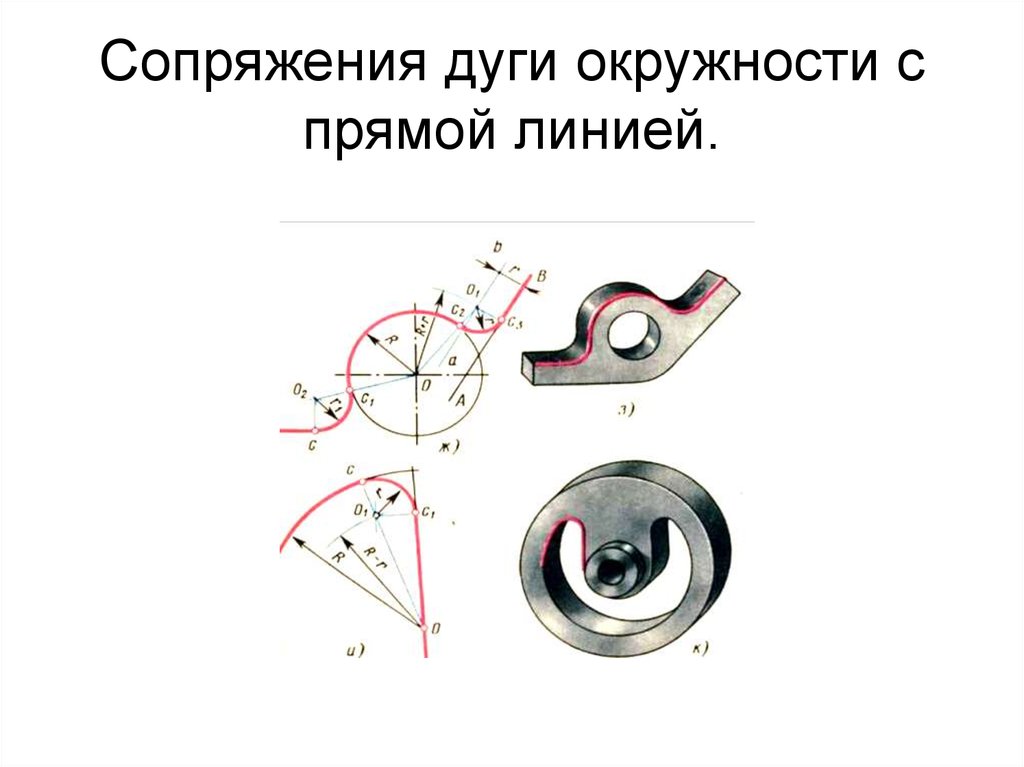 Проводим прямую параллельно заданной на
Проводим прямую параллельно заданной нарасстоянии r.
Из центра О данной окружности проводим дугу
вспомогательной окружности радиусом R+r.
Пересечение прямой и вспомогательной дуги даст
точку центра дуги сопряжения О1.
Точка касания дуги и линии D лежит на
пересечении перпендикуляра из точки О1 на прямую.
Точка касания дуг E лежит на линии ОО1.
Сопряжения прямой и окружности.
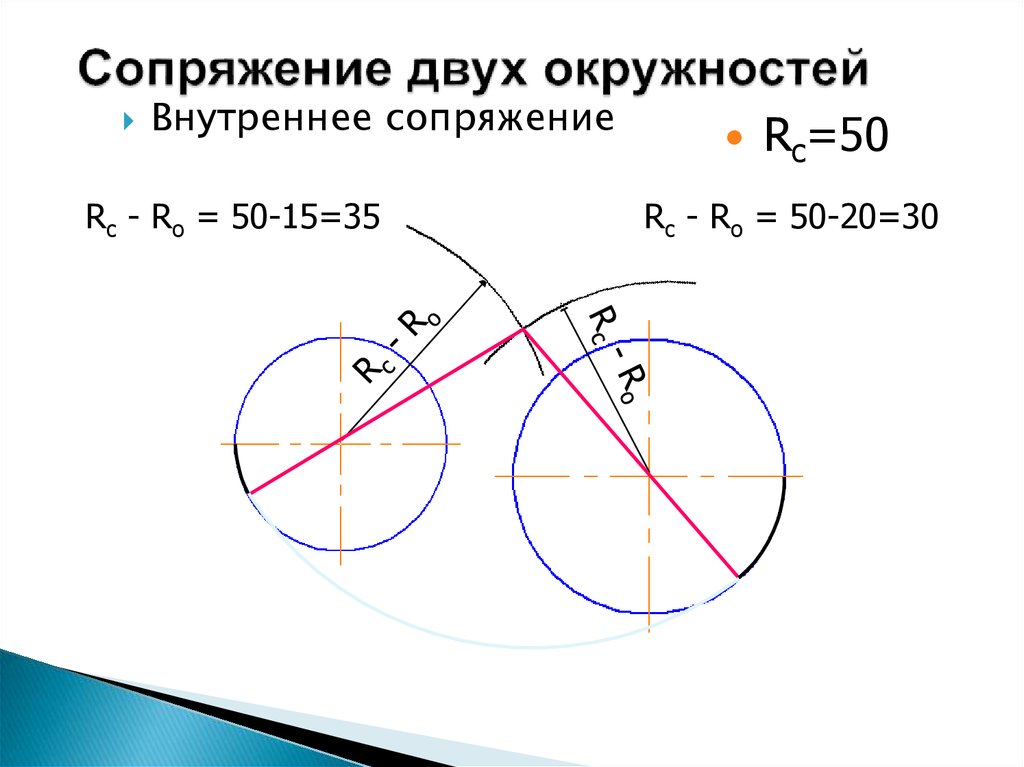
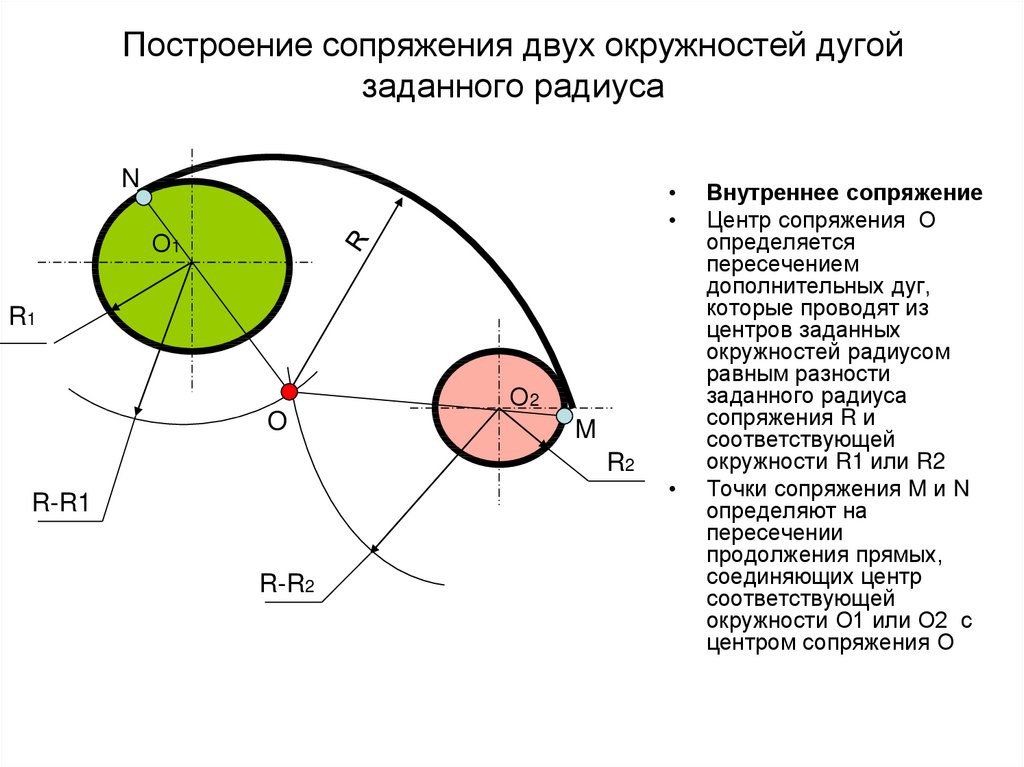
10. Сопряжение двух окружностей дугой заданного радиуса.
Заданы две дуги радиусами R1 и R2. Требуетсяпостроить сопряжение дугой, радиус которой задан R.
Различают два случая касания:
внешнее и внутреннее .
11. Сопряжение двух окружностей дугой заданного радиуса Внешнее касание.
Из центра окружности О1 описываем дугувспомогательной окружности радиусом R1+R.
Из центра окружности О2 описываем дугу
вспомогательной окружности радиусом R2+R.
Пересечение дуг вспомогательных окружностей
даст точку О, которая является центром дуги
сопряжения (окружности с радиусом R).
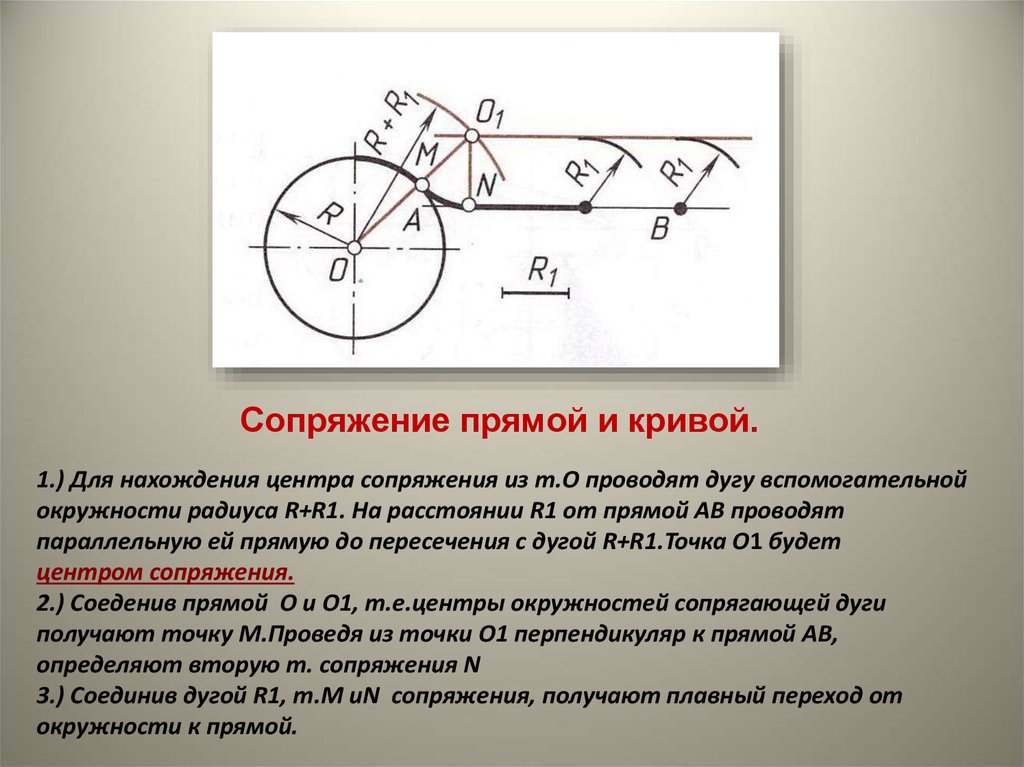
Точки касания A и B находятся на линиях ОO1 и
ОO2.
Внешнее сопряжение
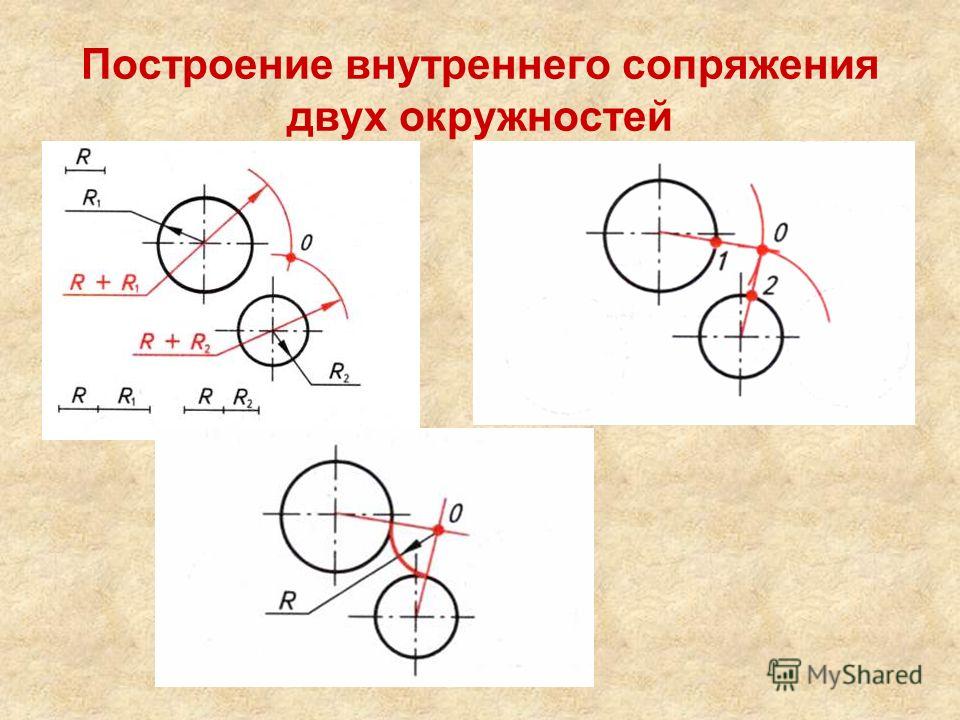
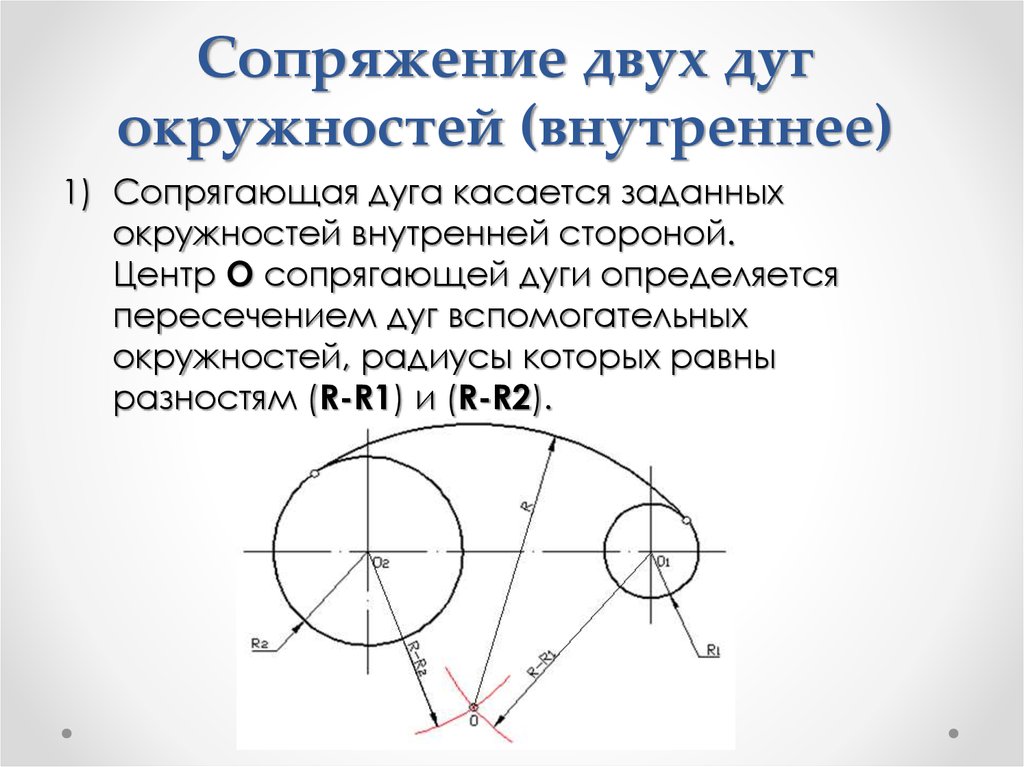
13. Сопряжение двух окружностей дугой заданного радиуса Внутреннее касание.
Из центра окружности О1 описываем дугувспомогательной окружности радиусом R-R1.
Из центра окружности О2 описываем дугу
вспомогательной окружности радиусом R-R2.
Пересечение дуг вспомогательных окружностей
даст точку О, которая является центром дуги
Точки сопряжения A и B лежат на продолжении
линий ОO1 и ОO2.
Внутренне сопряжения
50
А теперь для закрепления материала выполним практическое
задание:
R 25
Выполняется в тетради с предварительным разбором и
демонстрацией.
R 15
R 15
80
60
R 25
«Построить сопряжения в заданной фигуре».
English Русский Правила
Построение шрифтов 56
5. Построение прямоугольника в пропорциях стороны и диаго¬
нали квадрата (фиг. 5).
Первый вариант построения. На отрезке прямой AD, который
На отрезке прямой AD, который
является заданной шириной прямоугольника, в точке А восстанав¬
ливают перпендикуляр. На перпендикуляре откладывают радиусом
AD отрезок Am, после чего на противоположной стороне радиусом
Dm из центра D засекается в точке С высота прямоугольника ABDC.
В
Фиг. 5
Второй вариант построения (дан штрихпунктирными линиями).
Заданная высота прямоугольника AB делится пополам, и из точки
п проводится окружность диаметром AB, после чего из центра В
радиусом ВК, равным длине хорды, стягивающей четверть окружно¬
сти, на верхней (или нижней) линии прямоугольника засекается его
ширина ВС.
6. Проведение параллельных прямых на заданном расстоянии через
две заданные точки (фиг. 6).
Решение этой задачи применяется при построении наклонных
элементов букв.
Фиг. 6
Точки А и В соединяют прямой, и на отрезке AB, как на диа¬
метре, строят окружность. Из точек А и В, как из центров, радиу¬
сом, равным заданному расстоянию L, проводятся окружности, ко¬
торые, пересекаясь с окружностью, проведенной из центра О, дают
точки М и N, определяющие направление прямых AM и NB.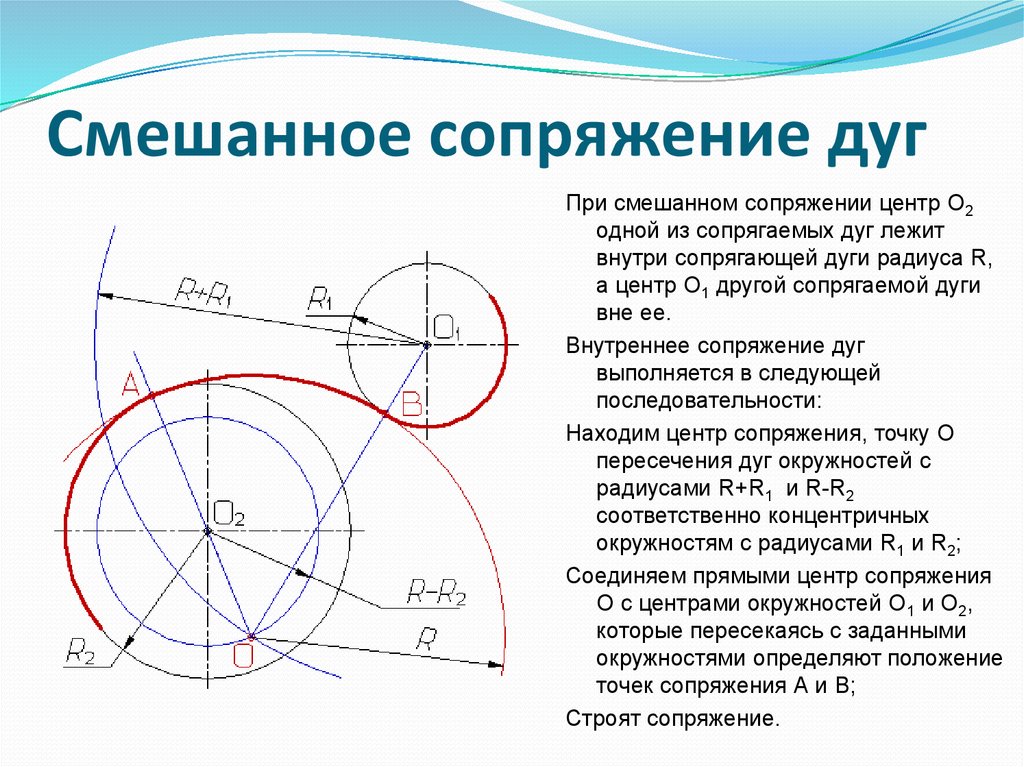
7. Проведение окружности через три точки (фиг. 7).
Эту задачу часто приходится решать при переходе от лекаль¬
ных кривых к циркульным.
Фиг. 7
Из точек А и В, как из центров, радиусами, большими, нежели
половина расстояния между этими точками, делаются засечки а и
Ь. Соединив точки а и Ь прямой, получим направление одного из
радиусов искомой окружности. Подобное же построение, сделанное
из точек В и С, дают засечки cud, определяющие направление
второго радиуса. Точка пересечения двух полученных прямых дает
центр О искомой окружности. Для построения можно брать лю¬
бые две пары из трех заданных точек.
8. Проведение прямой, проходящей через заданную точку, и ка¬
сательной к данной окружности (фиг. 8).
Фиг. 8
Точку А соединяем с центром О окружности. На отрезке ОА,
как на диаметре, строим окружность, которая при пересечении с
заданной окружностью дает точки касания М и N с искомой пря¬
9. Построение наружных касательных к двум окружностям
(фиг. 9).
9).
Фиг. 9
108
Из центра Ог большей окружности проводится вспомогательная
окружность радиусом, равным разности радиусов данных окруж¬
ностей. Центры О i и Ог соединяют прямой и на полученном отрезке,
как на диаметре, строят окружность (с центром Т). Эта окруж¬
ность пересекается с вспомогательной окружностью в точках А и
В. Пересечение прямых ОаА и ОаВ при их продолжении с заданной
окружностью определит точки касания М и N. Точки касания
К и L на малой окружности определяются при проведении из
центра Оі прямых, параллельных О2М и OaN.
10. Построение внутренних касательных к двум окружностям
(фиг. 10).
Фиг. 10
12. Построение окружности заданного радиуса, сопрягающей
прямую п окружность (фиг. 12).
Из центра Ог большей окружности проводится вспомогательная
окружность радиусом Ri~\~Ra (сумма радиусов данных окружностей).
На прямой, соединяющей центры Оі и Ог, как на диаметре, строит¬
ся окружность, которая пересекается в точках С и О с вспомога¬
тельной окружностью. Прямые, проведенные через эти точки и центр
Прямые, проведенные через эти точки и центр
Ог, определяют точки касания М и N искомой прямой на большой
окружности. Параллельно ОгС из центра Оі проводим прямую,
которая, пересекаясь с малой окружностью, даст точку касания Р
и соответственно, проводя прямую через Оі параллельно OaD, полу¬
чим точку касания R.
11. Построение окружности задапного радиуса, сопрягающей пе¬
ресекающиеся прямые (фиг. 11).
Сопряжение окружности с прямой сводится к нахождению то¬
чек их касания.
b
[о J
‘j
к
В
Фиг. 1 1
Между заданными прямыми АА и ВВ, пересекающимися под
некоторым углом, проводим биссектрису угла и прямую ЬЬ, парал¬
лельную одной из них на расстоянии R, равном заданному радиу¬
су сопряжения. Пересечение биссектрисы и параллельной прямой
ЬЬ дает центр О окружности, а перпендикуляры, опущенные из цент¬
ра О на заданные прямые АА и ВВ. определяют точки сопряжения
(касания) N и М окружности и заданных прямых. сде¬
сде¬
лать сопряжение этих окружностей радиусом R. Центр искомой ок¬
ружности определяется точкой О пересечения дуг, проведенных из
центра N i радиусом Л+П и из центра Na радиусом R+ra, то есть
суммой радиусов данной и искомой окружностей. Точки сопряже¬
ния Кі и Ка получаются как точки пересечения прямых OA’i и
ONa с заданными окружностями.
109
3.2: Геометрия Мебиуса — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 85717
- Дэвид В. Лайонс
- Ливан Вэлли Колледж
Геометрия Мёбиуса обеспечивает единую основу для изучения планарных геометрий. В частности, группы преобразований гиперболической и эллиптической геометрий в следующих разделах являются подгруппами группы преобразований Мёбиуса.
A Möbius transformation (also called a linear fractional transformation ) of the extended complex plane \(\hat{\mathbb{C}}\) is a функция формы
\begin{equation}
f(z)= \frac{az+b}{cz+d}\label{stdlinfractransf}\tag{3.2.1}
\end{equation}
где \(z\ ) – комплексная переменная, \(a,b,c,d\) – комплексные константы, а \(ad-bc\neq 0\text{.}\) для завершения определения мы выполняем присваивания \(f( -d/c)=\infty\) и \(f(\infty)=a/c\) if \(c\neq 0\text{.}\) If \(c=0\text{,}\ ) мы присваиваем \(f(\infty)=\infty\text{.}\)
Примечание об условном обозначении: Обычно используются заглавные буквы, такие как \(S,T,U\), обозначают преобразования Мёбиуса. Также принято опускать скобки и писать \(Tz\) вместо \(T(z)\) для обозначения значения преобразования Мёбиуса.
- КПП 3.
 2.1.
2.1. Пусть \(f(x)=(ax+b)/(cx+d)\) будет функцией действительной переменной \(x\) с вещественными константами \(a,b,c,d \) с \(ad-bc\neq 0\) и \(c\neq 0\text{.}\)
- Показать, что \(\displaystyle \lim_{x\to -d/c}|f(x)|=\infty\text{.}\)
- Показать, что \(\displaystyle \lim_{x\to \infty}f(x)=a/c\text{.}\)
- КПП 3.2.2.
Покажите, что условие \(ad-bc\neq 0\) необходимо и достаточно для обратимости. Найдите формулу, обратную выражению \(z\to (az+b)/(cz+d)\text{.}\)
- КПП 3.2.3.
Покажите, что композиция двух преобразований Мёбиуса является преобразованием Мёбиуса. Предложение: Сначала покажите, что композиция имеет вид \(z\to \frac{rz+s}{tz+u}\text{.}\) Далее вместо грубого вычисления проверьте, что \(ru-ts \neq 0\text{,}\) используйте Контрольно-пропускной пункт 3.
 2.2 .
2.2 .
Определение 3.2.4.
Набор всех преобразований Мёбиуса образует группу \(\mathbf{M}\text{,}\), называемую группой Мёбиуса , при выполнении операции композиции функций. Геометрия Мёбиуса является парой \((\hat{\mathbb{C}},\mathbf{M})\text{.}\)
Существует естественная связь между групповыми операциями Мёбиуса и матричными групповыми операциями. Карта \({\mathcal T}\colon
GL(2,\mathbb{C})\to \mathbf{M}\) задается как
\begin{equation}
\left[
\begin{array}{cc}a& b\\ c& d\ конец {массив}\право]\к
\влево[г\к \фрак{аз+б}{ч+д}\право]\метка{gl2tomobgp}\тег{3.2.2}
\конец{уравнение}
является групповым гомоморфизмом. Ядром \({\mathcal T}\) является группа ненулевых скалярных матриц.
\begin{equation*}
\ker{\mathcal T}=\left\{\left[
\begin{array}{cc}k& 0\\ 0& k\end{array}\right],
 }
} \end{уравнение*}
Фактор-группа \(GL(2,\mathbb{C})/\ker{\mathcal T}\) называется проективной линейной группой \(PGL(2,\mathbb{C})\ text{.}\) Таким образом, мы имеем групповой изоморфизм 3.2.5.
Покажите, что отображение \({\mathcal T}\) является гомоморфизмом групп. Покажите, что ядро \({\mathcal T}\) равно
\begin{equation*}
\ker{\mathcal T}=\left\{\left[
\begin{array}{cc}k& 0\\ 0& k\end{массив}\right],
k\ neq 0\right\}\text{.}
\end{уравнение*}
Гомотетии, повороты, переносы и инверсии (см. Таблицу 3.1.4 в Разделе 3.1) являются частными случаями преобразований Мёбиуса. Эти основные преобразования можно рассматривать как строительные блоки для общих преобразований Мёбиуса следующим образом.
Предложение 3.2.6.
Каждое преобразование Мёбиуса представляет собой композицию гомотетий, вращений, переводов и инверсий.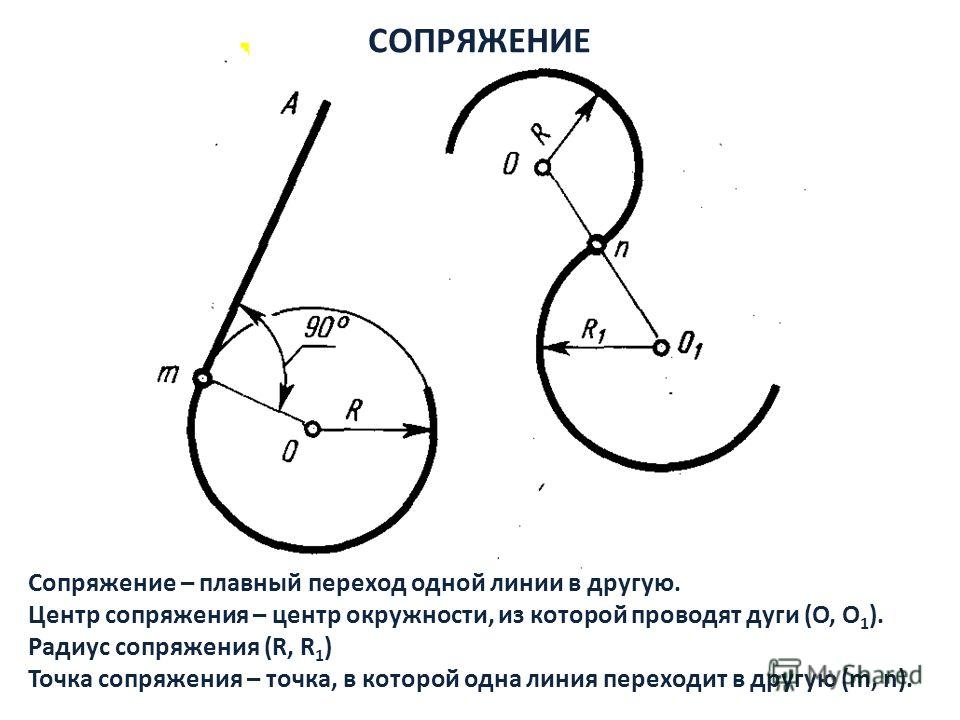
- Доказательство.
См. Упражнение 3.2.6.1
- КПП 3.2.7.
- Определите значения коэффициентов \(a,b,c,d\) в преобразовании Мёбиуса \(z\to \frac{az+b}{cz+d}\), который является гомотетией, вращением, сдвигом , и инверсия соответственно.
- Напишите преобразование Мёбиуса, которое выполняет «вращение по часовой стрелке на четверть оборота вокруг точки \(2-i\)».
Следствие 3.2.8.
Преобразования Мёбиуса конформны.
- Доказательство.
Применить Предложение 3.2.6 и Группа упражнений 3.1.4.2–5 .
Далее простое наблюдение в виде следующей леммы приводит к результату, называемому основной теоремой геометрии Мёбиуса.
Лемма 3.2.9.
Если преобразование Мёбиуса имеет более двух неподвижных точек, то это тождественное преобразование.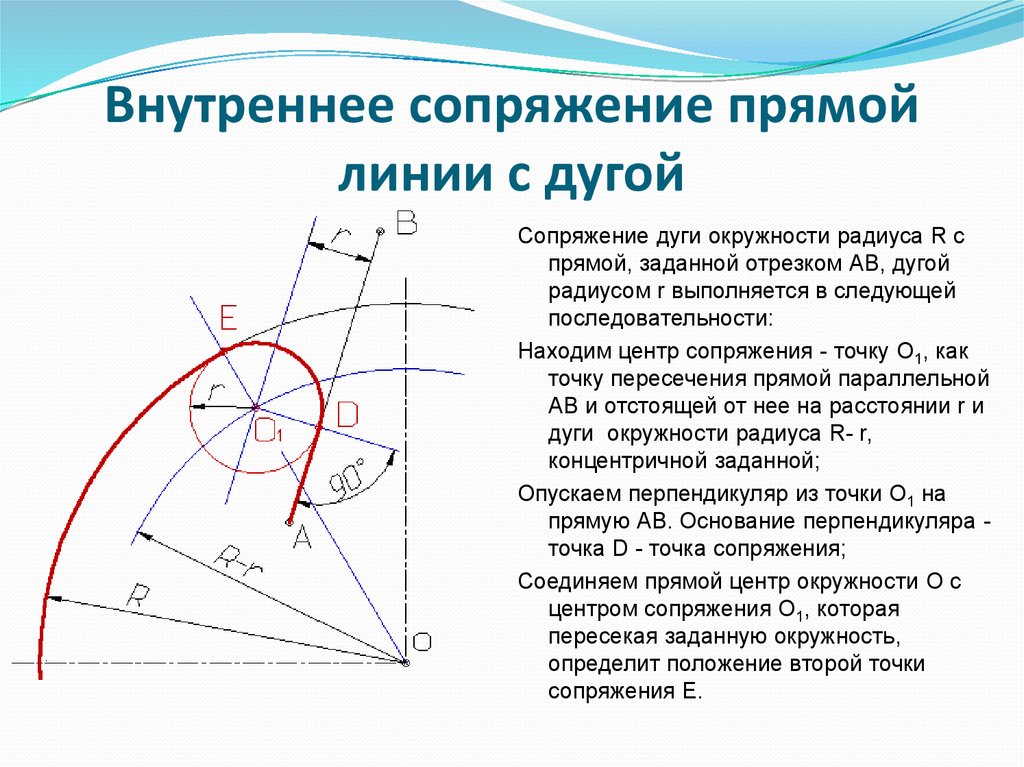
- Доказательство.
Подсказка: просто решите \(z=\frac{az+b}{cz+d}\text{.}\) Вам нужно будет рассмотреть случаи.
Предложение 3.2.10. Основная теорема геометрии Мёбиуса.
Преобразование Мёбиуса полностью определяется любыми тремя парами вход-выход. Это означает, что для любой тройки различных входных значений \(z_1,z_2,z_3\) в \(\hat{\mathbb{C}}\) и любой тройки различных выходных значений \(w_1,w_2,w_3\) в \(\hat{\mathbb{C}}\text{,}\) существует единственный \(T\in \mathbf{M}\) такой, что \(Tz_i=w_i\) для \(i=1, 2,3\текст{.}\) 9{-1}\) исправляет три точки. Теперь применим предыдущую лемму.
Кросс-коэффициент Далее мы рассматриваем частный случай выходной тройки \(w_1=1\text{,}\) \(w_2=0\text{,}\) \(w_3=\ infty\text{.}\) Для трех различных точек \(z_1,z_2,z_3\) в \(\hat{\mathbb{C}}\text{,}\) мы пишем \((\cdot,z_1, z_2,z_3)\) для обозначения уникального преобразования Мебиуса, которое удовлетворяет \(z_1\to
1\text{,}\) \(z_2\to 0\text{,}\) и \(z_3\to \infty\ text{.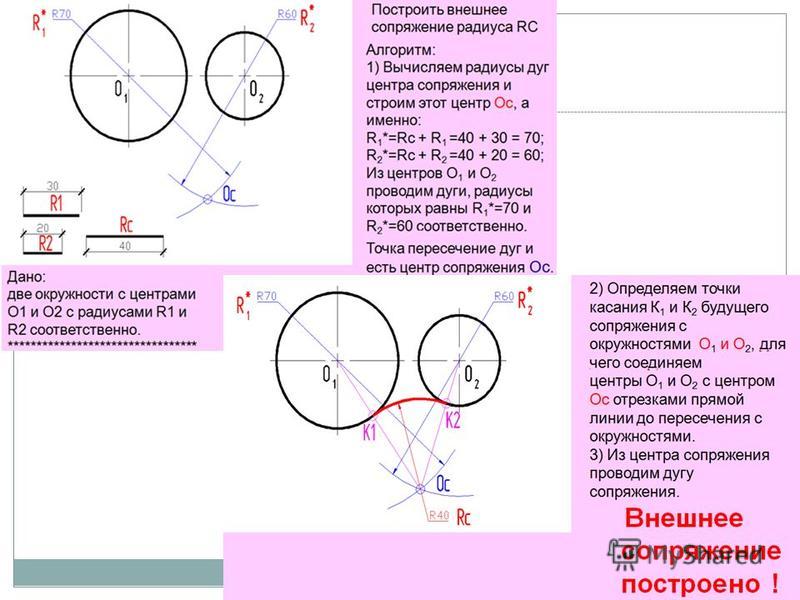 }\) Мы пишем \((z_0,z_1,z_2,z_3)\) для обозначения образа \(z_0\) под \((\cdot,z_1,z_2,z_3)\text{.}\ ) Выражение \((z_0,z_1,z_2,z_3)\) называется0038 перекрестное отношение кортежа \(4\)\(z_0,z_1,z_2,z_3\text{.}\) Следующие два предложения дают важные свойства перекрестного отношения.
}\) Мы пишем \((z_0,z_1,z_2,z_3)\) для обозначения образа \(z_0\) под \((\cdot,z_1,z_2,z_3)\text{.}\ ) Выражение \((z_0,z_1,z_2,z_3)\) называется0038 перекрестное отношение кортежа \(4\)\(z_0,z_1,z_2,z_3\text{.}\) Следующие два предложения дают важные свойства перекрестного отношения.
Предложение 3.2.11. Кросс-отношение является инвариантным.
Пусть \(z_1,z_2,z_3\) – различные точки в \(\hat{\mathbb{C}}\text{,}\) пусть \(z_0\in \hat{\mathbb{C}}\ text{,}\) и пусть \(T\) – любое преобразование Мёбиуса. Тогда у нас есть
\begin{equation*}
(z_0,z_1,z_2,z_3)= (Tz_0,Tz_1,Tz_2,Tz_3).
\end{уравнение*}
- Доказательство.
Преобразования \((\cdot,z_1,z_2,z_3)\) и \((\cdot,Tz_1,Tz_2,Tz_3)\circ T\) отправляют \(z_1\to 1\text{,}\) \(z_2\to 0\text{,}\) и \(z_3\to \infty\text{,}\) , поэтому они должны быть равны по основной теореме. Теперь примените оба преобразования к \(z_0\text{.
 {-1}\left(\hat{\mathbb{R}}\right)\) – прообраз расширенной вещественной прямой \(\hat{\ mathbb{R}}=\mathbb{R}\cup \{\infty\}\) под \(T\text{.}\) Тогда \(C_T\) – евклидова окружность или прямая. Кроме того, \(C_T\) – это уникальная евклидова окружность или прямая линия, содержащая точки \(z_1,z_2,z_3\text{.}\)
{-1}\left(\hat{\mathbb{R}}\right)\) – прообраз расширенной вещественной прямой \(\hat{\ mathbb{R}}=\mathbb{R}\cup \{\infty\}\) под \(T\text{.}\) Тогда \(C_T\) – евклидова окружность или прямая. Кроме того, \(C_T\) – это уникальная евклидова окружность или прямая линия, содержащая точки \(z_1,z_2,z_3\text{.}\)- Доказательство.
См. Упражнение 3.2.6.4
Следствие 3.2.13.
Кросс-отношение \((z_0,z_1,z_2,z_3)\) действительно тогда и только тогда, когда \(z_0,z_1,z_2,z_3\) лежит на евклидовой окружности или прямой.
Следствие 3.2.14.
Пусть \(C\) – евклидова окружность или прямая линия в \(\hat{\mathbb{C}}\), и пусть \(T\) – любое преобразование Мёбиуса. Тогда \(T(C)\) – евклидова окружность или прямая. 9{\ast C}\) относительно окружности \(C\)
Определение симметричной точки зависит только от окружности \(C\text{,}\) , а не от трех точек \(z_1,z_2, z_3\text{.}\) Этот факт является следствием следующего предложения.
Предложение 3.2.16.
Пусть \(C\) – клин, а \(S\) – преобразование Мёбиуса. Если \(z,z’\) – пара точек, симметричных относительно \(C\text{,}\), то \(Sz,Sz’\) симметричны относительно клины \(S( C)\text{.}\) То есть имеем 9{\ast C}\) зависит только от окружности \(C\text{,}\) а не от трех точек \(z_1,z_2,z_3\), используемых в определении (3.2.3) .
- Доказательство.
См. Упражнение 3.2.6.6 .
Мы завершаем этот раздел, посвященный геометрии Мёбиуса, обсуждением нормальной формы преобразования Мёбиуса. Начнем с леммы.
Лемма 3.2.18.
Если преобразование Мёбиуса имеет ровно две неподвижные точки \(0\) и \(\infty\text{,}\) , то оно имеет вид \(z\to \alpha z\) для некоторого ненулевого \(\alpha \in
\mathbb{C}\text{.}\) Если преобразование Мёбиуса имеет единственную фиксированную точку в \(\infty\text{,}\), тогда оно имеет вид \(z\to z+\beta\ ) для некоторых ненулевых \(\beta\in \mathbb{C}\text{.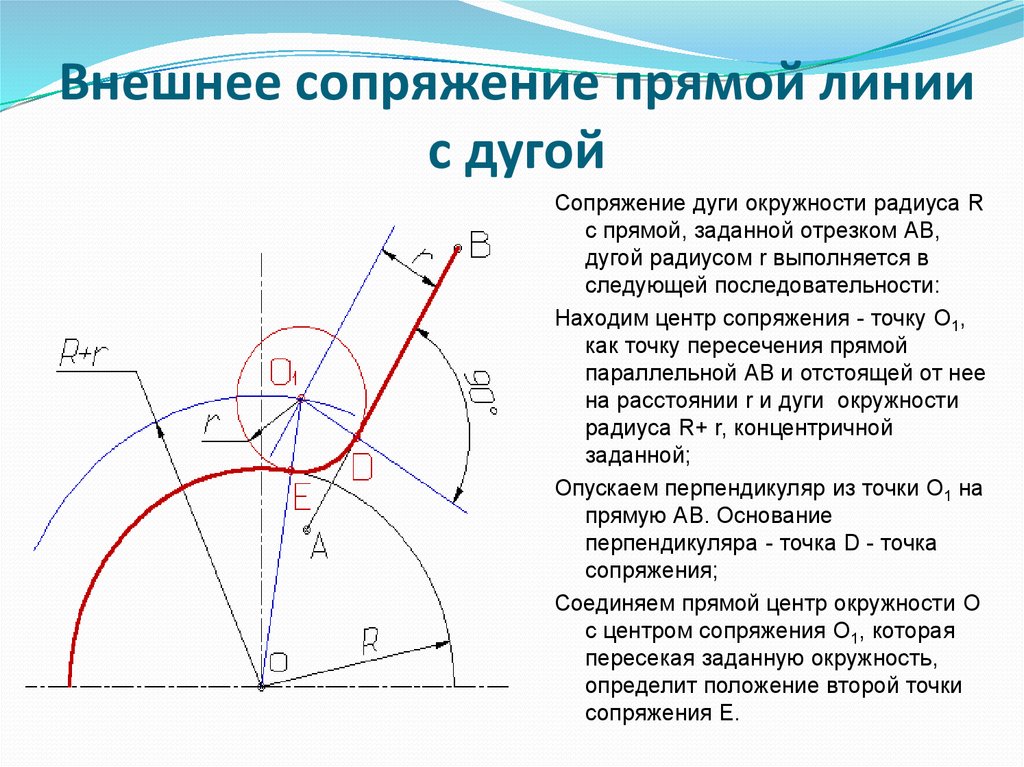 }\)
}\)- Доказательство.
См. Упражнение 3.2.6.5 .
9{-1}\) – преобразование \(w\)-плоскости, сопряженной с \(T\) через \(S\) (см. Группа упражнений 1.3.3.3–6 ). Легко проверить, что \(U\) имеет ровно две неподвижные точки \(0\) и \(\infty\text{.}\) Применяя предыдущую лемму, мы имеем \(Uw=\alpha w\) для некоторые ненулевые \(\alpha\in - Объясните, почему преобразование вида \(z\to az\text{,}\) с любой ненулевой комплексной константой является композицией гомотетии и поворота.
- Явно идентифицируйте каждую гомотетию, поворот, перевод и инверсию в (3.2.6) до (3.2.9) в приведенном ниже выводе для случая \(c\neq 0\text{.}\)
\begin{align}
z & \to cz+d\label{mobiusdecompfirst}\tag{3.2.6}\\
&\to \frac{1}{cz+d}\tag{3.2.7}\ \
&\to \frac{bc-ad}{cz+d} + a\tag{3.2.8}\\
&\to
\frac{1}{c}\left(\frac{bc-ad }{cz+d} + a\right)\label{mobiusdecomplast}\tag{3.2.9}\\
& = \frac{az+b}{cz+d}\tag{3.2.10}
\конец{выравнивание} - Напишите собственную декомпозицию для случая \(c=0\text{.}\)
- Покажите, что для особого случая, когда \(z_1,z_2,z_3\) комплексны (то есть ни одна из трех точек не является \(\infty\)), мы имеем следующее.

\begin{align}
(\cdot,z_1,z_2,z_3) &=
\left[z\to \frac{z-z_2}{z-z_3}\frac{z_1-z_3}{z_1-z_2} \right]\label{mob10inftyform}\tag{3.2.11}\\
(z_0,z_1,z_2,z_3) &= \frac{z_0-z_2}{z_0-z_3}\frac{z_1-z_3}{z_1-z_2}\label{crossratiofracform}\tag{3.2.12}
\ конец{выравнивание} - Найдите явные формулы для \((\cdot,z_1,z_2,z_3)\) когда \(z_1=\infty\text{,}\), затем сделайте то же самое для \(z_2=\infty\) и \(z_3 =\infty\текст{.}\)
- \(\displaystyle 1\to a, 0\to b, \infty\to c\) 9{\ast C}\) – это отражение \(z\) через \(C\text{.}\)
- \(\displaystyle z\to \frac{1}{z}\)
- \(\displaystyle z\to \frac{3z-1}{z+1}\)
\mathbb{C}\text{.}\) Применяя обе части \(S\circ T=U\circ S\) к \(z\text{,}\) мы иметь следующую нормальную форму для \(T\text{.}\)\begin{equation}
\frac{Tz-p}{Tz-q}= \alpha
\frac{z-p}{z-q}\label{normalform2fixedpts}\tag{3.2.4}
\end{equation}Преобразование \(T \) Называется Elliptic , Hyperbolic , или loxodromic , если \ (u \) — это Rottation \ (| \ alpha | \ alpha | \ alpha | \ alpha | \ alpha \ (| \ alation \ (| \ alpha | \ alpha | гомотетия \((\alpha >0)\) или ни то, ни другое соответственно.
 {-1}\text{.}\) На этот раз \(U\ ) имеет ровно одну неподвижную точку в \(\infty\text{.}\) Применяя лемму, мы имеем \(Uw=w+\beta\) для некоторого ненулевого \(\beta\in
{-1}\text{.}\) На этот раз \(U\ ) имеет ровно одну неподвижную точку в \(\infty\text{.}\) Применяя лемму, мы имеем \(Uw=w+\beta\) для некоторого ненулевого \(\beta\in
\mathbb{C}\text{.}\) Применив обе стороны от \(S\circ T=U\circ S\) к \(z\text{,}\), мы получим следующую нормальную форму для \(T\text{.}\)\begin{equation}
\frac{1}{Tz-p}=
\frac{1}{z-p}+\beta\label{normalformfixedpt}\tag {3.2.5}
\end{equation}Преобразование Мёбиуса этого типа называется параболическим . Вот краткое изложение терминологии классификации, связанной с нормальными формами.
Таблица 3.2.19. Сводка нормальных форм \(T\in \mathbf{M}\)
Круги Штейнераобычная форма нормальная форма тип сопряженного преобразования эллиптический \(\frac{Tz-p}{Tz-q}= \alpha \frac{z-p}{z-q}, |\alpha|=1\) вращение гиперболический \(\frac{Tz-p}{Tz-q}= \alpha \frac{zp}{zq},
\alpha\gt 0\)гомотетия локсодромный \(\frac{Tz-p}{Tz-q}= \alpha \frac{z-p}{z-q},
\alpha\neq 0\)\(|\alpha |\neq 1, \alpha\not\gt 0\)
композиция гомотетии с поворотом параболический \(\frac{1}{Tz-p}= \frac{1}{z-p} + \beta,
\beta\neq 0\)перевод Рисунок 3.
 2.20. Сетка полярных координат и координатная сетка круга Штейнера
2.20. Сетка полярных координат и координатная сетка круга ШтейнераРисунок 3.2.21. Вырожденные линии координатной сетки и вырожденные окружности Штейнера
Обсуждение нормальных форм показывает, что любое нетождественное преобразование Мёбиуса сопряжено с одной из двух основных форм: \(w\to \alpha w\) или \(w\to w+\beta\text{.}\) естественной системой координат для изображения действия \(w\to
\alpha w\) являются стандартные полярные координаты. См. Рисунок 3.2.20 . Гомотетия — это поток по радиальным линиям, а вращение — это поток по полярным кругам. Естественная «вырожденная» система координат для изображения переноса \(w\to w+\beta\) – это семейство прямых, параллельных линии, содержащей начало координат и \(\beta\text{.}\) перенос на \ (\beta\) – это поток вдоль этих параллельных линий. См. 9{-1}\) сопоставляет линии в \(w\)-плоскости, которые параллельны линии, проходящей через \(0\) и \(\beta\), с клинами в \(z\)-плоскости, которые содержат \ (p\text{.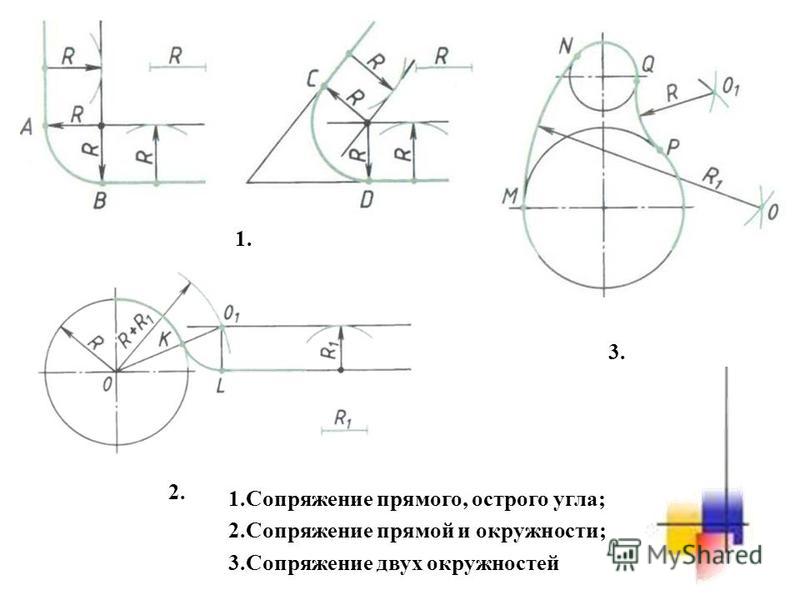 }\) Каждая клин в этом семействе касается любой другой клин в этом семействе ровно в одной точке \(p\text{.}\) Клайны в этом семействе называются вырожденными окружностями Штейнера . См. Рисунок 3.2.21 . В таблице 3.2.22 обобщается графическое изображение преобразований Мёбиуса.
}\) Каждая клин в этом семействе касается любой другой клин в этом семействе ровно в одной точке \(p\text{.}\) Клайны в этом семействе называются вырожденными окружностями Штейнера . См. Рисунок 3.2.21 . В таблице 3.2.22 обобщается графическое изображение преобразований Мёбиуса.Таблица 3.2.22. Сводная информация о кругах Штейнера с изображениями преобразований Мёбиуса
Упражненияобычная форма графический динамический эллиптический течение по кругам Штейнера второго рода гиперболический течение по кругам Штейнера первого рода локсодромный композиция эллиптических и гиперболических течений параболический течение по вырожденным кругам Штейнера Упражнение 1
Разложение преобразований Мёбиуса на четыре основных типа.
Упражнение 2
Явная форма преобразования \(\) (⋅,z1,z2,z3).Упражнение 3
Найдите преобразования Мёбиуса, которые выполняют следующие назначения.
Упражнение 7
Найдите нормальную форму и нарисуйте график, используя круги Штейнера для следующих преобразований.
Упражнение 8
Пусть \(p\) – единственная неподвижная точка преобразования Мебиуса, сопряженного с \(w\to w+\beta\) через \(Sz=\frac{1}{z-p}\text {.
 \ast\text{.}\) 9\аст\текст{.}\)
\ast\text{.}\) 9\аст\текст{.}\)
Упражнение 9
Покажите, что (обобщенная) окружность Аполлония (окружность Штейнера второго рода) характеризуется множеством точек вида
\begin{equation*}
C=\left\{P\ in \mathbb{C}\colon \frac{d(P,A)}{d(P,B)}=k\right\}
\end{equation*}
для некоторых \(A,B\in \mathbb{C}\) и некоторая вещественная константа \(k\gt 0\text{.}\)
Эта страница под названием 3.2: Геометрия Мебиуса распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Дэвидом В. Лайонсом посредством исходного контента, отредактированного в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Дэвид В.
 Лайонс
Лайонс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Теги
- Геометрия Мебиуса
- источник@https://mathvista.org/algeom_text_files/frontmatter.html
комплексный анализ — Каждая линия или окружность в $\mathbb{C}$ являются наборами решений уравнения…
Задай вопрос
спросил
Изменено 8 лет, 3 месяца назад
Просмотрено 2к раз
$\begingroup$
Вот сложная домашняя задача по анализу, которую я не могу понять:
Докажите, что каждая линия или окружность в $\mathbb{C}$ является множеством решений уравнения вида $a|z|^2+\bar{w}z+w\bar{z}+b=0 $, где $a,b\in\mathbb{R}$ и $w,z\in\mathbb{C}$.
И наоборот, покажите, что каждое уравнение этой формы имеет линию, окружность, точку или пустое множество в качестве множества решений. 92$ в виде $y=mx+b$ в $\mathbb{C}$, где $m$ вещественные, а $x,b$ комплексные. Я знаю, что окружность на комплексной плоскости задается как $|z-a|=r$, где $a$ — центр, а $r$ — радиус.
Я также заметил, что $\bar{w}z+w\bar{z}=2\text{Re}(\bar{w}z)$. Я просто не уверен, как все эти части сочетаются друг с другом, отвечая на вопрос. Любая помощь будет принята с благодарностью.
- комплексный анализ
- комплексные числа
$\endgroup$
3 92\right)$ дает общий вид уравнения окружности на комплексной плоскости. Это уравнение также описывает линии, которые можно рассматривать как круги с бесконечным радиусом.
$$ Az\overline{z} + \overline{z\alpha} + z\alpha + B = 0 $$
Когда $A = 0$ представляет собой линию,
$$ \overline{z\alpha} + z\alpha + B = 0 $$
Вы можете убедиться, что это уравнение описывает прямую, положив $z = x + iy$ и $\alpha = p + iq$.
