Изометрическая проекция — Википедия
Материал из Википедии — свободной энциклопедии
 Стол в прямоугольной изометрической проекции
Стол в прямоугольной изометрической проекции 
Изометри́ческая прое́кция (др.-греч. ἴσος «равный» + μετρέω «измеряю») — это разновидность аксонометрической проекции, при которой в отображении трёхмерного объекта на плоскость коэффициент искажения (отношение длины спроецированного на плоскость отрезка, параллельного координатной оси, к действительной длине отрезка) по всем трём осям один и тот же. Слово «изометрическая» в названии проекции пришло из греческого языка и означает «равный размер», отражая тот факт, что в этой проекции масштабы по всем осям равны. В других видах проекций это не так.
Изометрическая проекция используется в машиностроительном черчении и САПР для построения наглядного изображения детали на чертеже, а также в компьютерных играх для трёхмерных объектов и панорам.
Необходимо отметить, что параллельные проекции, разновидностью которых являются аксонометрические и, в том числе, изометрические проекции, делятся также на ортогональные (перпендикулярные), с направлением проекции перпендикулярным к плоскости проекции, и косоугольные, с углом между направлением и плоскостью, отличным от прямого. По советским стандартам (см. ниже) аксонометрические проекции могут быть и ортогональными, и косоугольными[1]. В результате, по западным стандартам изометрическая проекция определяется более узко и, помимо равенства масштабов по осям, включает условие равенства 120° углов между проекциями любой пары осей. Во избежание путаницы далее, если не указано иное, под изометрической проекцией будет подразумеваться только прямоугольная изометрическая проекция.
ru.wikipedia.org
Прямоугольная изометрия — Мегаобучалка
Положение аксонометрических осей приведено на Рис. 24, а.
Коэффициенты искажения по осям x, y, z равны 0,82.
Изометрическую проекцию, как правило, выполняют без искажения по осям, используя так называемый приведенный коэффициент искажения равный 1 (при этом изображение получается увеличенным в 1,22 раза).
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в изометрии в равновеликие эллипсы. Ориентация эллипсов в различных плоскостях показана на Рис. 24а большая ось эллипса, лежащего в плоскости x,z перпендикулярна оси y; большая ось эллипса, лежащего в плоскости x, y перпендикулярна оси z; большая ось эллипса, лежащего в плоскости z, y перпендикулярна оси x.
Если изометрическую проекцию выполняют без искажения по осям x, y, z, то большие оси эллипсов равны 1,22 диаметра окружности, а малые оси – 0,71 диметра окружности.
Пример построения предмета в прямоугольной изометрии с вырезом передней четверти показан на Рис. 17 (штриховка фигур производится параллельно диагоналям квадратов, построенных в соответствующих аксонометрических плоскостях).
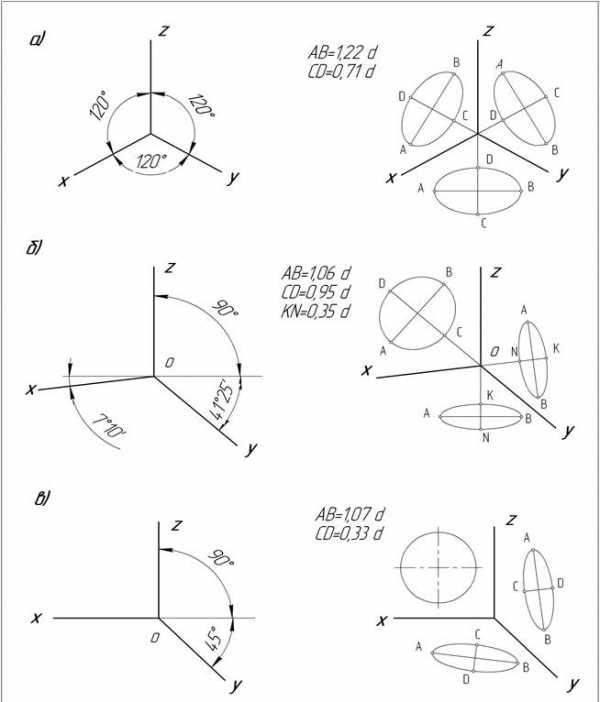
Рисунок 24 (а, б, в) – Аксонометрические проекции (а – прямоугольная изометрия, б – прямоугольная диметрия, в – косоугольная фронтальная диметрия)
Прямоугольная диметрия
Положение аксонометрических осей приведено на Рис. 24, б.
Коэффициенты искажения по осям x, z равны 0,94, а по оси y — 0,47.
Диметрическую проекцию, как правило, выполняют без искажения по осям x, z и с коэффициентом искажения 0,5 по оси y (в этом случае изображение получается увеличенным в 1,06 раза).
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрические плоскости проекций эллипсами. Ориентация эллипсов в различных плоскостях показана на Рис. 24, б: большая ось эллипса, лежащего в плоскости x,z перпендикулярна оси y; большая ось эллипса, лежащего в плоскости x, y перпендикулярна оси z; большая ось эллипса, лежащего в плоскости z, y перпендикулярна оси x.
Величины осей эллипсов даны на Рис. 24, б.
Косоугольная фронтальная диметрия
Положение аксонометрических осей приведено на Рис. 24, в.
Коэффициенты искажения по осям x, z равны 1, а по оси y — 0,5.
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрические плоскости проекций в окружности.
Окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, проецируются на аксонометрические плоскости проекций эллипсами.
Величины осей эллипсов приведены на Рис. 24, в.
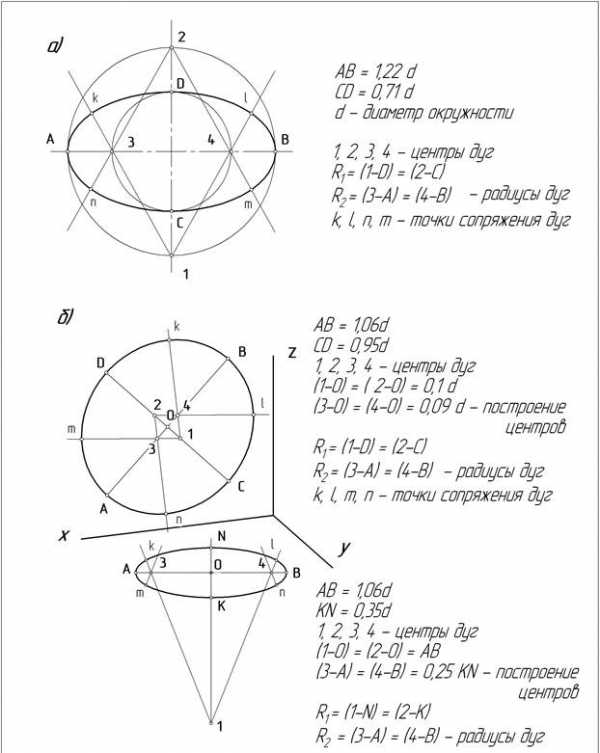
Рисунок 25 (а, б) – Построение овалов в аксонометрии (а – прямоугольная изометрия, б – прямоугольная диметрия)
Содержание заданий
Методическое руководство содержит варианты для трех графических заданий.
Количество заданий, входящих в контрольную работу, зависит от специальности обучающегося и определяется преподавателем на установочной лекции.
Номер варианта, который должен быть выполнен студентом, определяется по последней цифре учебного шифра. Всего вариантов 20.
Например, если учебный шифр 13 – СМТ – 7, студент выполняет вариант № 7.
Если учебный шифр 13 – СМТ – 32, номер варианта получится 32 – 20 = 12.
Если учебный шифр 13 – СМТ – 41, номер варианта получится 41 – 2 х20 = 1 и т. д.
Задание 1.
Формат А3, масштаб 1:1.Перечертить два вида предмета, построить вид слева, выполнить рациональные разрезы. Проставить размеры. Выполнить аксонометрию с вырезом передней четверти.
Пример выполнения задания приведен на Рис. 17, варианты задания в Приложении А.
Задание 2. Формат А3, масштаб 1:1.
Перечертить два вида предмета, построить вид слева, выполнить ступенчатый разрез указанными плоскостями. Проставить размеры.
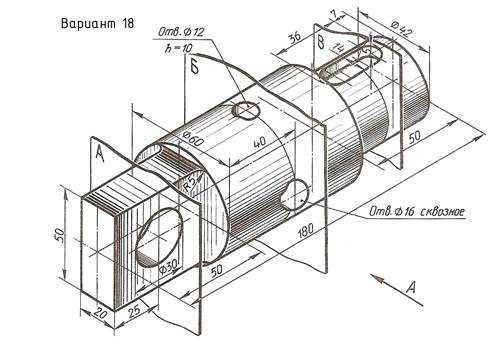
Пример выполнения задания приведен на Рис. 18 варианты задания в Приложении Б
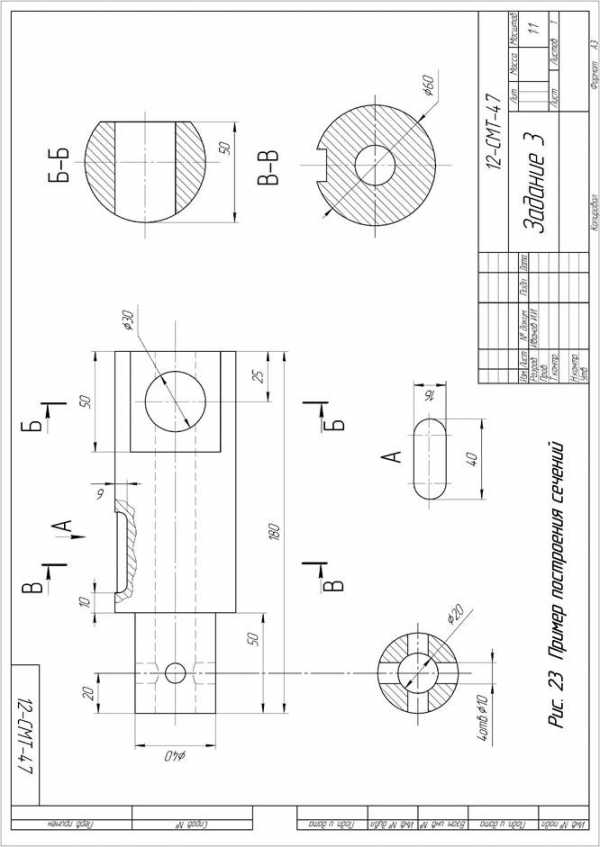
Задание 3. Формат А3, масштаб 1:1
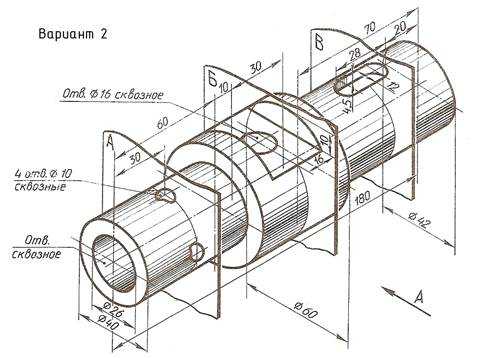
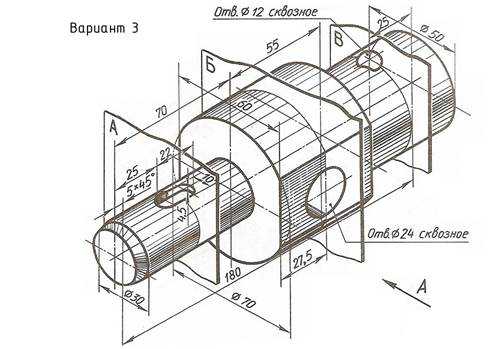
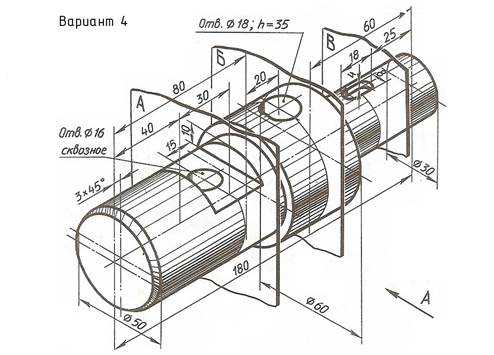
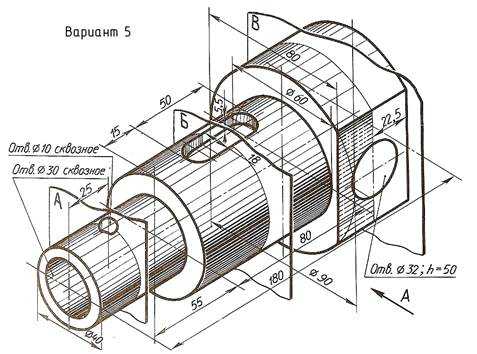
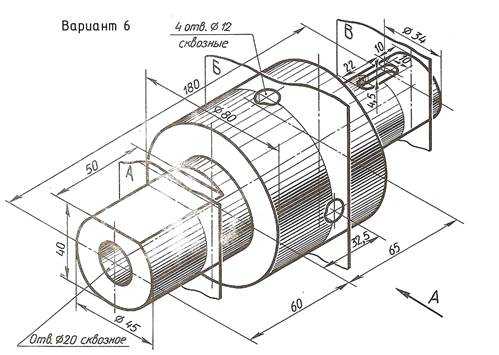
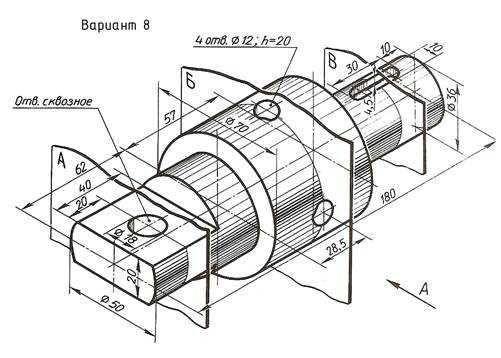
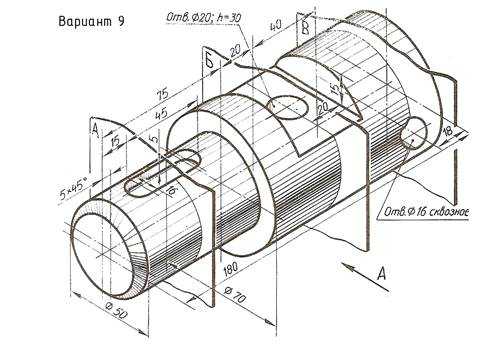
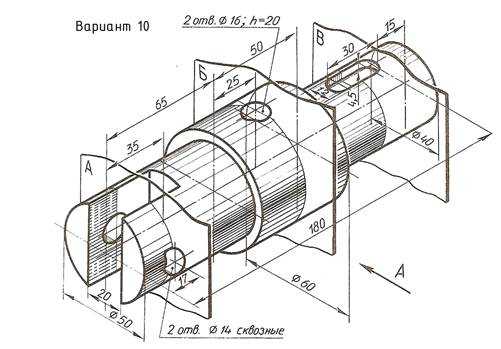
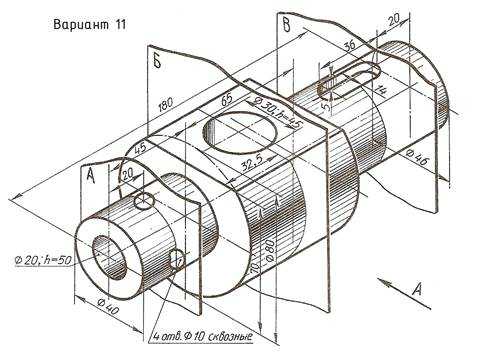
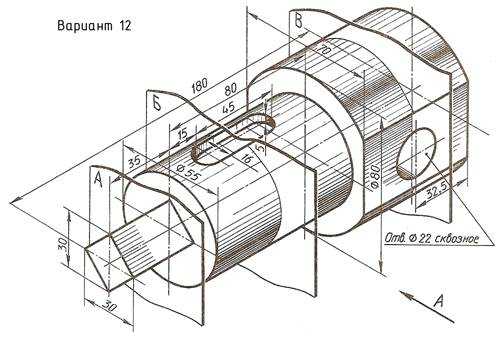
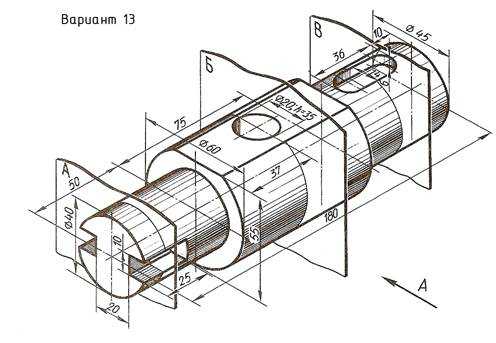
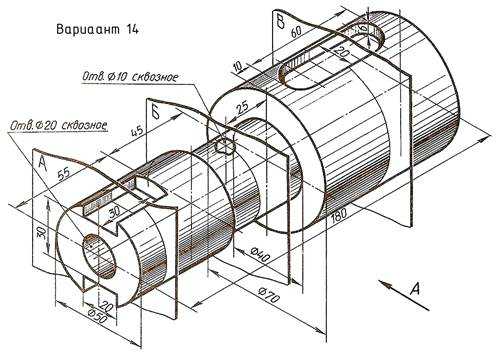
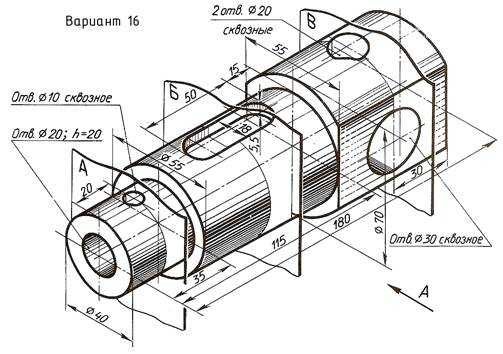
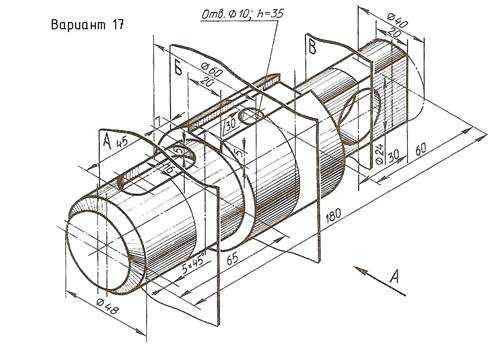
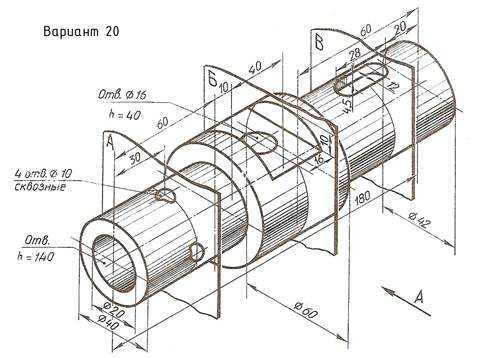
По наглядному изображению вала выполнить его чертеж, который должен содержать главный вид (направление взгляда показано стрелкой А), три сечения указанными плоскостями и другие изображения, необходимые для прочтения конструкции вала. Нанести размеры.
Пример выполнения задания приведен на Рис. 23,
ПРИЛОЖЕНИЯ
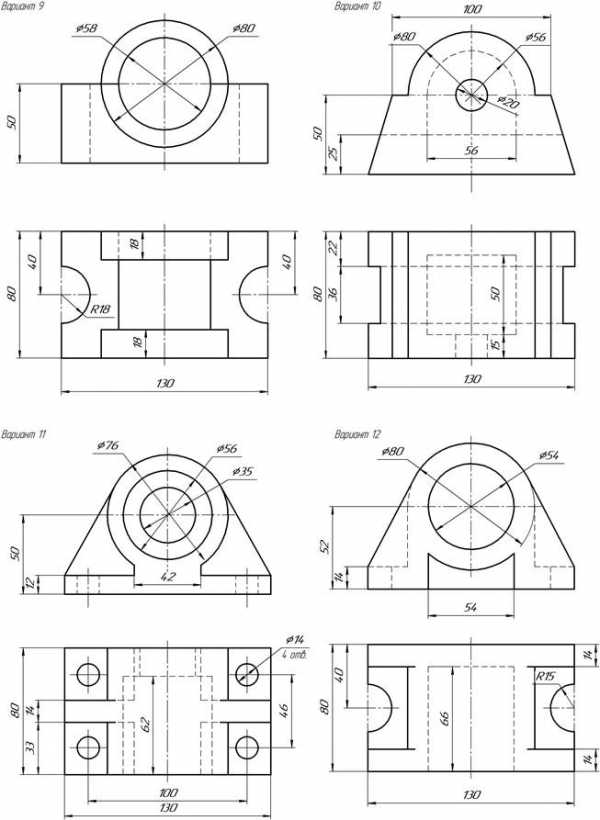
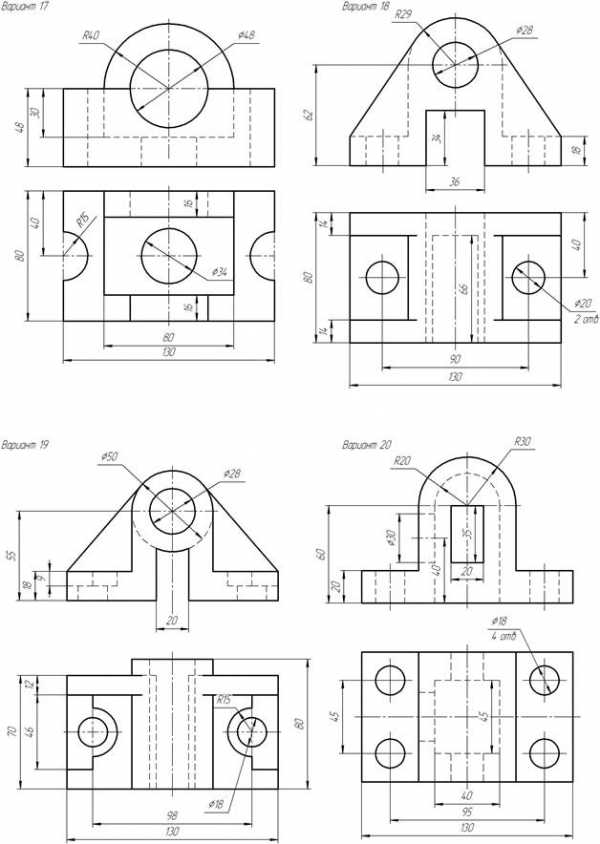
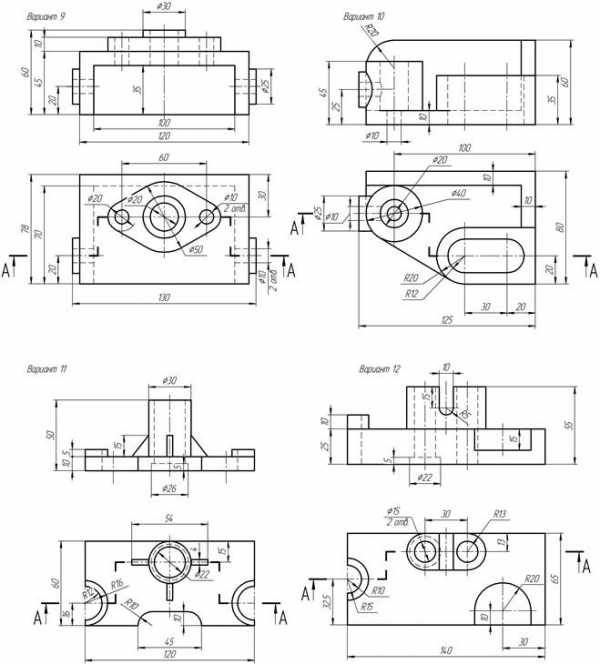
Приложение А Варианты задания «Простые разрезы»
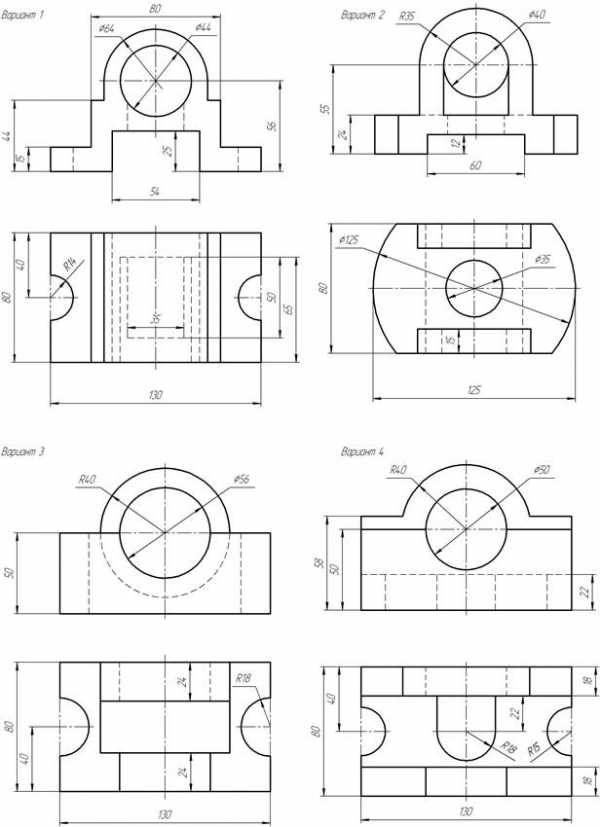


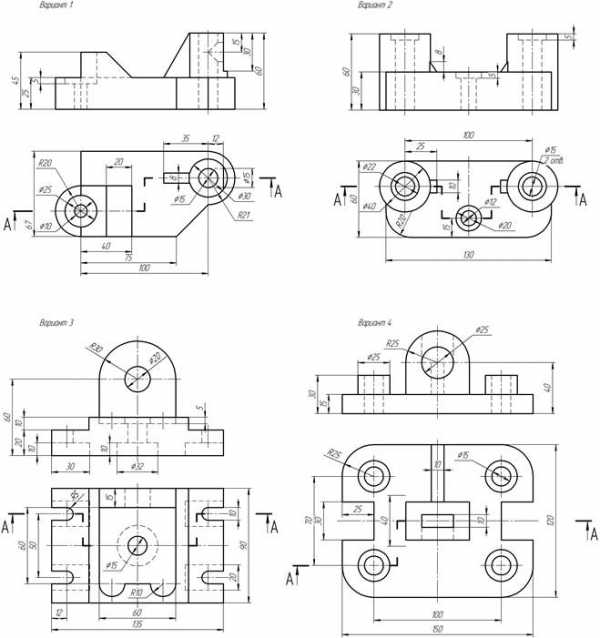
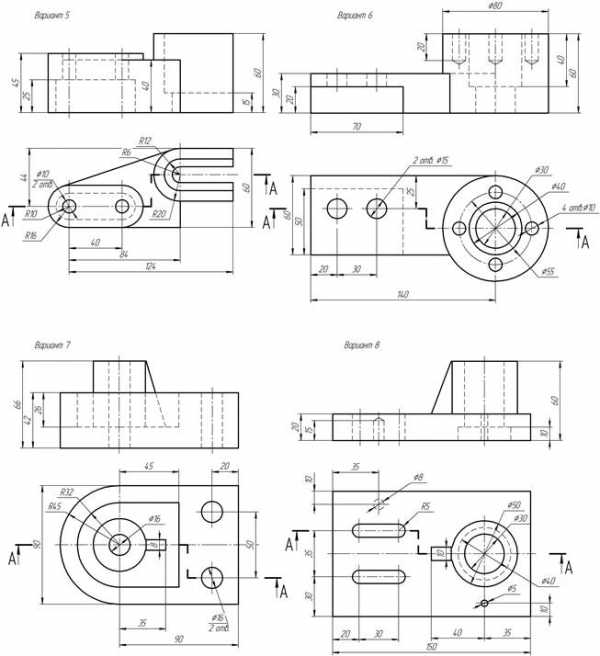
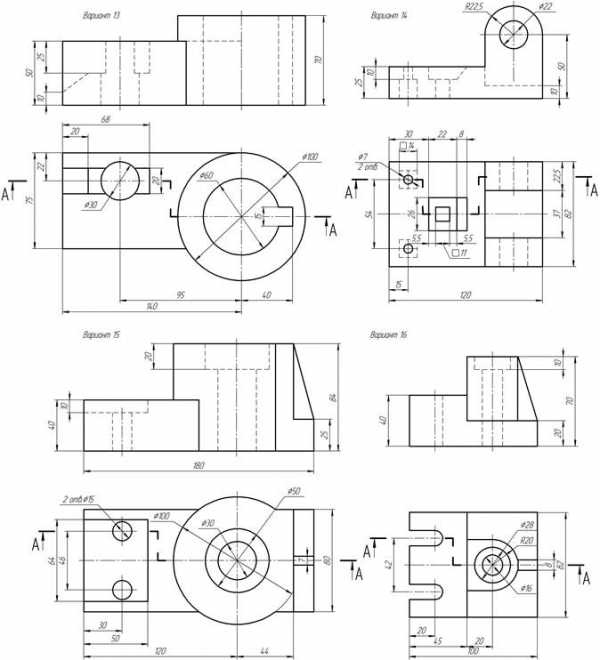
Приложение Б Варианты задания «Сложные разрезы»

Приложение Д Варианты задания «Сечения»




Литература
1. ЕСКД. Общие правила выполнения чертежей. ГОСТ 2.301-68-2.321-84. – М., 1991. –237 с.
2. Инженерная графика: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений /Фролов С.А., Бубенников А.В., Левицкий В.С., Овчинникова И.С. – М.: Высшая школа, 1982. – 80 с.
3. Окунцова Е.А. Проекционное черчение: Учебное пособие. – Новосибирск: Западно-Сибирское книжное издательство, 1965. – 119 с.
4. Миронов Б.Г. Сборник заданий по инженерной графике с примерами выполнения чертежей на компьютере: Учебное пособие /Б.Г. Миронов, Д.А.Пяткина, А.А.Пузиков. – 3-е изд., испр. и доп.- М.: Высшая школа, 2004. – 355 с.: ил.
5. Практикум по черчению (Геометрическое и проекционное черчение). Учеб.пособие для студентов пед. институтов по спец. «Черчение и труд» / Е.А. Василенко, Е.П. Гордеева, М.А. Косолапов и др.; Под общ. ред. Е.А. Василенко. – М.: Просвещение, 1982. – 175 с.
Оглавление
1. Изображения в ортогональных проекциях. Основные положения. 3
2 Виды.. 6
2.1 Основные виды.. 6
2.2 Дополнительные виды.. 8
2.3 Местные виды.. 9
3. Разрезы.. 10
3.1 Классификация разрезов. Основные определения. 12
3.2 Обозначение разрезов. 13
3.3 Расположение разрезов на чертеже. 14
3.4 Соединение части разреза и части соответствующего вида. 17
3.5 Когда разрезы не обозначаются. 19
3.6 Выбор рациональных разрезов. Примеры выполнения разрезов. 20
4. Сечения. 24
4.1 Классификация сечений. Основные определения. 26
4.2 Симметричные сечения. 26
4.3 Несимметричные сечения. 27
4.4 Особенности выполнения сечений. 28
5. Аксонометрические проекции. 31
5.1 Прямоугольная изометрия. 32
5.2 Прямоугольная диметрия. 34
5.3 Косоугольная фронтальная диметрия. 34
6. Содержание заданий. 36
ПРИЛОЖЕНИЯ. 38
Приложение А Варианты задания «Простые разрезы». 38
Приложение Б Варианты задания «Сложные разрезы». 43
Приложение Д Варианты задания «Сечения». 48
megaobuchalka.ru
Аксонометрия, диметрия, изометрия — ИЗО
Просмотр содержимого документа
«Аксонометрия, диметрия, изометрия»

ОБЩИЕ ПОНЯТИЯ

ЦЕЛЬ УРОКА: дать новые понятия:
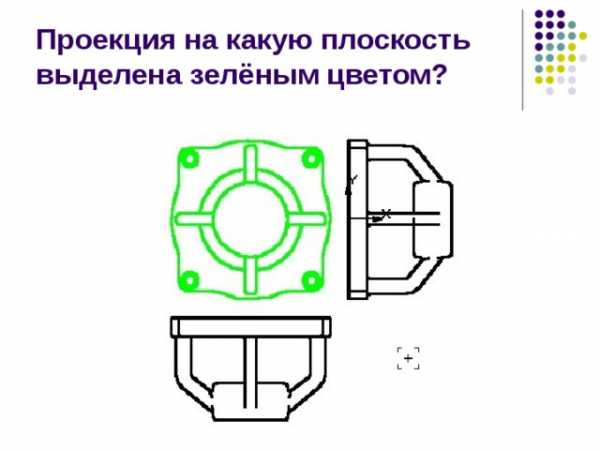
Проекция на какую плоскость выделена зелёным цветом?

Проекция на какую плоскость выделена зелёным цветом?
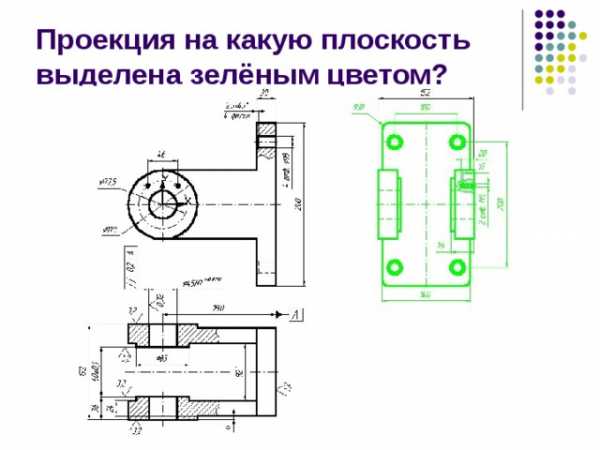
Проекция на какую плоскость выделена зелёным цветом?

В переводе с греческого это слово означает- измерение по осям
В зависимости от расположения осей ( x y z ) аксонометрические проекции могут быть прямоугольными (углы между осями равны между собой) и
косоугольными (один из углов между осями отличается от остальных).
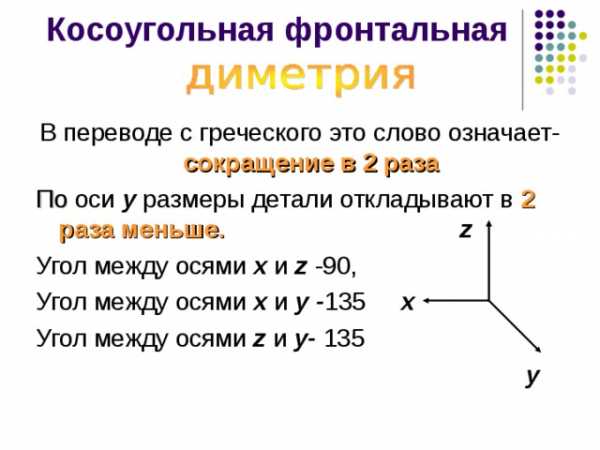
Косоугольная фронтальная
В переводе с греческого это слово означает- сокращение в 2 раза
По оси y размеры детали откладывают в 2 раза меньше. z
Угол между осями х и z -90,
Угол между осями х и у — 135 х
Угол между осями z и у- 135
у
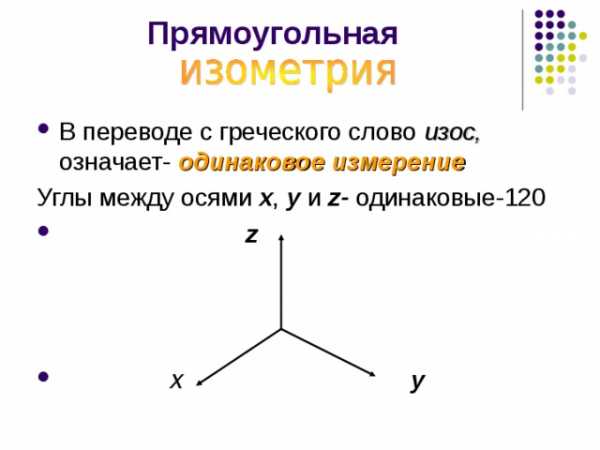
Прямоугольная
- В переводе с греческого слово изос, означает- одинаковое измерение
Углы между осями х , у и z — одинаковые-120
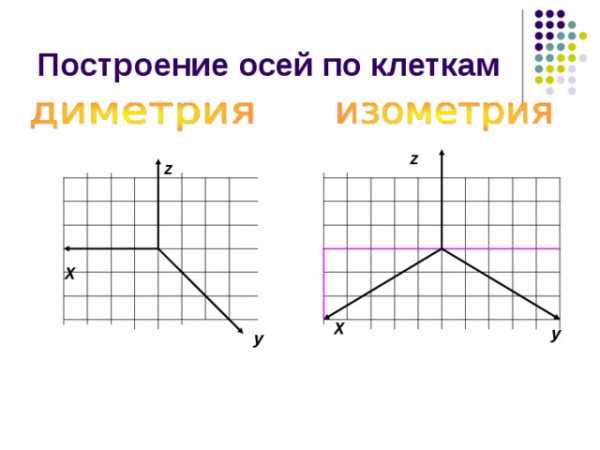
Построение осей по клеткам
z
z
Х
Х
у
у
у
у
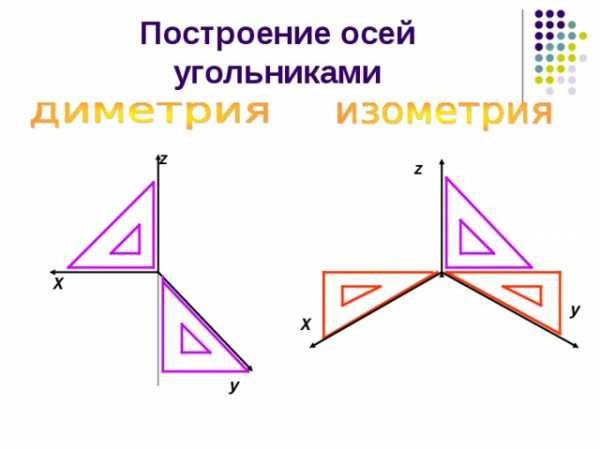
Построение осей угольниками
z
z
Х
Х
у
у
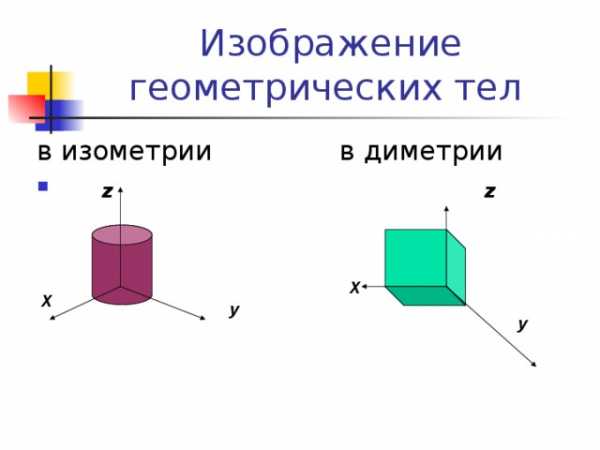
Изображение геометрических тел
в изометрии в диметрии
Х
Х

Закрепление новой темы :
V
Какие оси и под каким углом
диметрия
H
Какие оси и под каким углом
изометрия
W
Какие оси и под каким углом

Домашнее задание:
- Стр. 77 , пар. 27 Начертить куб в изометрии.
multiurok.ru
Способ построения овалов в изометрии.
На рис. 6 дан пример построения проекции окружности — овала, плоскость которой параллельно плоскости H(П1).
а) Строим изометрические оси X, Y и направление осей эллипса овала (рис. 7). Направление осей эллипса показано на рис. 5.
б) Из точки О проводим окружность заданного размера;
в) Отмечаем точки пересечения изометрических осей и осей эллипса с проведённой окружностью: A,B,C,D,B1,E.
г) Из точек В и В1 (точки пересечения малой оси эллипса с окружностью) проводим дуги окружности радиусом ВD и В1А. Точки пресечения этих дуг с малой осью эллипса обозначим К и К1.
д) Проводим дуги окружности радиусом ОК и отмечаем точки F1 и F2 на большой оси эллипса.
е) Соединяем точки В1F1 и В1F2. Отмечаем точки Р и Р1 (точки пересечения прямых В1F1 и В1F2 с большими дугами овала). Отрезок F1Р = F2Р1 является малым радиусом овала.
ж) Проводим дуги окружностей радиусами F1Р и F2Р1.
Полученное изображение овала принимаем за проекцию окружности на аксонометрической плоскости, у которого большая ось эллипса равна 1.22d, а длина малой оси эллипса – 0,71d: где d – заданный диаметр окружности. Если плоскость окружности параллельна плоскости проекций V или W, то построения аналогичны (рис. 6), направление же осей эллипса показано ранее (рис. 5).
1.3. Построение изометрической проекции многогранника
На рис. 7, а задана призма в ортогональных проекциях. Требуется построить изометрию данной призмы. Приведённое построение выполняется в
4 этапа.
Первый этап. Строим наружные очертания призмы рис. 7, б. Для этого проводим изометрические оси и наносим на осях Х и Y вершины углов верхнего и нижнего оснований. Для нахождения вершин углов, расположенных на оси Х, откладываем размер 58 мм (по 29 мм по обе стороны от центра О).
Аналогично этому для нахождения вершин углов, расположенных на оси Y, откладываем размер 46 мм (по 23 мм). Найденные таким образом точки вершин соединяем прямыми.
Второй этап. Намечаем на верхнем основании призмы и внутри её линии выреза шириной 30 мм. Определяем глубину выреза, для чего, из концов линий выреза на верхнем основании проводим вертикальные прямые и на них откладываем равный глубине выреза отрезок длиной 17 мм. Полученные точки соединяем между собой (рис. 7, в).
Третий этап. Удаляем ненужные линии (рис. 7, г)
Четвёртый этап. Обводим чертёж сплошными толстыми линиями (рис. 7, д).

Рис. 7 Построение изометрической проекции многогранника
2. Прямоугольная диметрическая проекция
Прямоугольной диметрией называется аксонометрическая проекция с равными показателями искажения по двум осям. По ГОСТу 2.317- 2011 принята прямоугольная диметрия с равными показателями искажения по осям Х и Z. В стандарте предусмотрено упрощение, заключающееся в том, что по осям Х и Z, или параллельно им откладываются действительные величины отрезков, а по направлению оси Y коэффициент искажения равен 0,5.

а) б)
Рис. 8. Диметрические оси:
а) точное построение; б) упрощённое построение
В прямоугольной диметрии ось X наклонена к горизонтальной линии под углом 7°10, ось Y — под углом 41°25(рис. 8, а), ось Z остаётся в вертикальном положении. Для построения осей X и Y (под углами 7° и 41°) используют ранее представленный метод построения с помощью отрезков. Соотношения отрезков показано на рис. 8, б. Изображение фигуры в диметрии получают, как и в изометрии увеличенным, причём увеличение по каждой оси равно 1,06.
На рис. 9 приведён пример изображения детали в прямоугольной диметрической проекции.
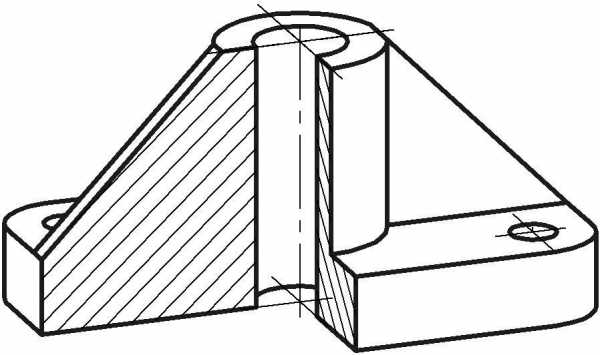
Рис. 9 Диметрия детали
studfiles.net
Начертательная геометрия
13.3. Прямоугольная изометрическая и диметрическая проекции
Поскольку в изометрии все три показателя искажения одинаковы, то из соотношения u2+v2+w2=2 получается, что u=v=w=0.82. Треугольник следов в этом случае равносторонний, поэтому аксонометрические оси как высоты равностороннего треугольника образуют углы 120°.
На практике пользуются приведенными показателями: т.е. принимают U=V=W=1. Построение приведенной изометрии значительно проще, нежели построение точной, так как аксонометрические координаты равны соответствующим натуральным. При использовании приведенных показателей искажения изображения получаются увеличенными в 1/0.82=1.22 раза.
В прямоугольной диметрии два показателя искажения равны u=w , а третий принимают равным u/2 , тогда из соотношения u2+v2+w2=2 следует, что u=w≈0.94 , а v≈0.47. Треугольник следов в этом случае равнобедренный. Если аксонометрическую ось O’z’ расположить на чертеже вертикально, то аксонометрическая ось O’x’ образует с горизонтальной линией угол 7°10′, а ось O’y’ — угол 41°25′, тангенсы этих углов равны 1/8 и 1/7 соответственно.
Показатели искажения по аксонометрическим осям O’x’ и O’z’ равны U=V=1, а V=0,5. Изображения в этом случае увеличиваются в 1/0.94=1.06 .
На рис. 166 углы между аксонометрическими осями показаны на примере треугольников осей в соответствии с ГОСТ 2.317-68. На чертеже аксонометрические оси наносят штрихпунктирной линией в соответствии с ГОСТ 2.303-68. Треугольники осей всегда изображают рядом с соответствующей аксонометрической проекцией.
Рис. 166. Углы между аксонометрическими осями в прямоугольной: а – изометрии; б – диметрии
Для построения осей прямоугольной изометрии (рис. 167, а) строят окружность произвольного радиуса r, затем из нижней точки пересечения ее с вертикальной осью строят дугу того же радиуса.
Через центр окружности и полученные точки пересечения проводят оси x и y.
Углы между аксонометрическими осями в прямоугольной диметрии можно построить следующим образом (рис.167, б): для построения оси O’x’ откладывают от начала координат O’ по линии горизонта восемь отрезков и на конце последнего отрезка перпендикулярно к нему – один такой отрезок. Для проведения оси O’y’ – по линии горизонта восемь равных отрезков и от конца последнего отрезка перпендикулярно ему семь таких отрезков.
Рис. 167. Построение осей графически: а – прямоугольной изометрии; б – прямоугольной диметрии
Пример построения приведенной прямоугольной изометрической и диметрической проекций пирамиды и точек на ее поверхности
Данная пирамида связывается с натуральной прямоугольной системой координат Oxyz, для чего на комплексном чертеже наносятся проекции координатных осей (рис. 168).
Построение приведенной прямоугольной изометрии пирамиды:
1. Построить изометрические оси.
2. Построить изометрические проекции вершин пирамиды:
Точка A лежит на оси Ox, поэтому для построения ее проекции достаточно отложить натуральную координату xA=O2A2=O1A1 в положительном направлении изометрической оси x. Для точки C сначала строят вспомогательную точку 1 на оси x, причем расстояние O111=O’1′ откладывается в отрицательном направлении оси x, затем в положительном направлении оси y откладывают натуральную координату yc=11C1. Остальные вершины строятся аналогично.
3. Соединить построенные вершины и определить видимость ребер пирамиды.
4. Точка М лежит в грани ASB, следовательно, принадлежит прямой l, проходящей через вершину S и пересекающей ребро основания BC в точке 2. Для получения изометрической проекции точки M достаточно построить проекцию прямой l’ и по координате zm построить M’∈l’ .
5. Прямоугольная приведенная диметрия строится аналогично, с учетом коэффициента искажения по оси y 0,5.
Рис. 168. Аксонометрические проекции пирамиды: а – ортогональный чертеж; б – прямоугольная изометрия; в – прямоугольная диметрия
cdot-nntu.ru
78. Прямоугольная диметрия | Техническая библиотека lib.qrz.ru
Прямоугольная диметрия характеризуется тем, что коэффициенты искажения, определенные из выражения (1), и = w = 0,94, a v = 0,47. Определяют их следующим образом:
u2+(u/2)2+u2=2;
u2 =8/9; u = w = (8/9)1/2=0,94; v = 0,47.
В соответствии с ГОСТ 2.317—69 практические построения в прямоугольной диметрии следует выполнять пользуясь приведенными коэффициентами искажения: u = w=1 и v = 0,5.
Расположение осей стандартной прямоугольной диметрии показано на рис. 162. Аксонометрический масштаб для прямоугольной диметрии будет МA1,06 : 1.
В прямоугольной диметрии равные окружности диаметра d, лежащие в координатных плоскостях хОу и уО, проецируются в равные эллипсы, большая ось которых 2а = 1,06d, а малая — 2b = 0,35d, если пользуемся приведенными коэффициентами искажения. Окружность, расположенная в плоскости xOz, проецируется в эллипс с осями: большая ось которых 2а1 = 1,066d, малая ось — 2b1= 0,95d (рис. 163). Диаметры.окруж-
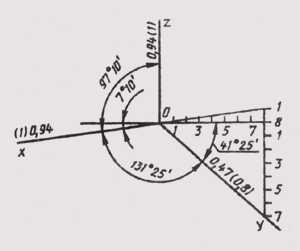
Рис. 162
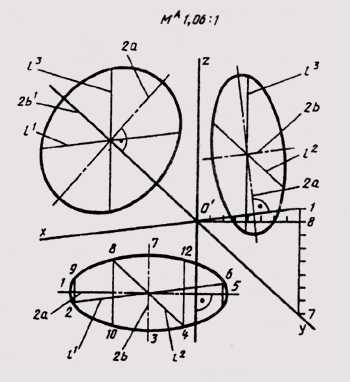
Рис. 163

Рис. 164
ности, параллельные координатным осям, спроецируются в отрезки, параллельные осям диаметрии l1 = l2 = d; l = 0,5d, при этом || Ох; l2|| Оу; l3|| Oz.
Можно построить кроме указанных точек еще четыре точки, симметричные точкам, ограничивающим проекции диаметров, параллельных координатным осям. Тогда эллипс, как диметрию окружности, можно построить по его двенадцати точкам.
Изображение геометрических поверхностей в прямоугольной ди-метрии рассмотрим на примере построения стандартной прямоугольной диметрии прямого кругового цилиндра. На рис. 164 приведен пример комплексного чертежа полого цилиндра высотой Н c наружным d и внутренним d1диаметрами. Цилиндр расположим в натуральную величину в натуральной системе координат Oxyz, относительно которой построим диметрическую его проекцию. Как и в случае построения окружностей в изометрии, в диметрии также начнем построение фигуры с эллипсов верхнего и нижнего оснований цилиндра, которые являются изометрическими проекциями окружностей этих оснований. Окружности основания расположены в плоскостях, параллельных горизонтальной плоскости проекций, поэтому, пользуясь приведенными ранее правилами, определим, что большие оси эллипсов будут перпендикулярны оси Oz. Малые оси эллипсов совпадут с направлением оси Oz. Центры осей эллипсов нижнего и верхнего оснований расположены на расстоянии Я. Величины осей определяем в зависимости от величины наружного и внутреннего диаметров цилиндров. Построив эллипсы, приведем очерковые линии, касательные к внешним эллипсам.
Для наглядности построим вырез четверти цилиндра, построение которого видно из рис. 164. Направление штриховки выреза выберем, как показано на рис. 200. Невидимые линии покажем штриховыми линиями. Для наглядности такими же линиями покажем линии вырезанной части цилиндра. Видимые контурные линии наводят нужной толщиной.
lib.qrz.ru
Урок 15. Плоские фигуры в аксонометрии
Лист 1. Для построения геометрических тел в аксонометрии мы должны научиться строить в аксонометрии плоские фигуры. На экране мы видим три фигуры. Ученики называют их: квадрат, треугольник, шестиугольник.
Лист 2. Даны размеры квадрата, равнобедренного треугольника, шестиугольника. Учащиеся записывают в тетрадь размеры плоских фигур. Заготовка для работы раздается на каждого ученика. Лист разделен пополам вертикально, в одной части которого начерчены три раза оси в диметрии, в другой части – три в изометрии (см. приложение 7).
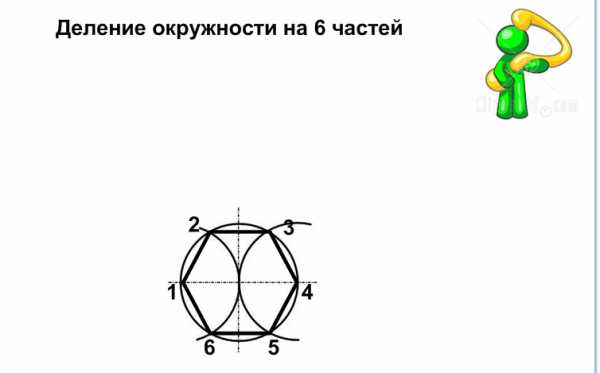
Лист 3-6. Деление окружности на 6 частей. Любая окружность делится ее радиусом на 6 частей. Перемещаем влево картинку, появится правило.
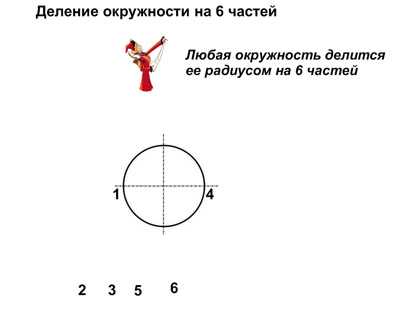
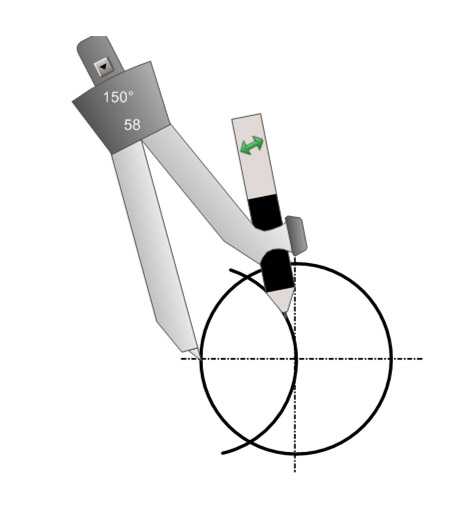
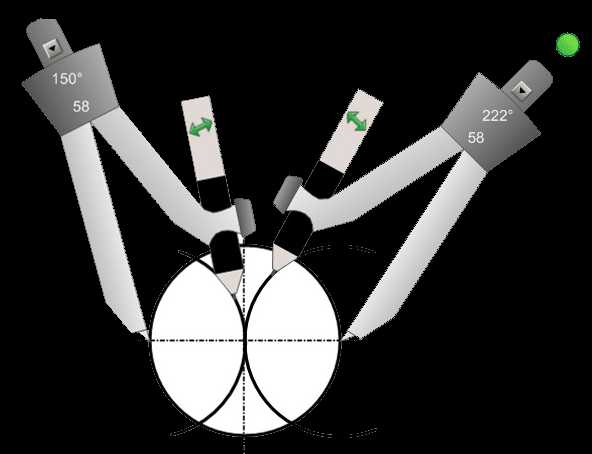
Рис. 15. 2 Рис. 15.3 Рис. 15.4
Обозначаем точки 1 и 4 (см. рис. 15.2).
Из точки 1 проводим дугу, радиусом, равным радиусу окружности (см. рис. 15.3). Из точки 4 проводим дугу, радиусом, равным радиусу окружности (см. рис. 15.4).
Обозначаем точки 2, 3, 5 и 6. Соединяем точки и получаем правильный шестиугольник. В правом верхнем углу картинка человечка — гиперссылка на лист построения шестиугольника в диметрии и изометрии (см. рис. 15.5).
Лист 7. Построение квадрата в диметрии и изометрии. При построении проекций квадрата его стороны расположены параллельно осям, в плоскости XZ (фронтальная) нет искажения, в плоскостях XY(горизонтальная) и ZY(профильная) по оси Y размер стороны квадрата уменьшаем в два раза. Вытаскиваем слева заготовки проекций квадрата (см. рис. 15.6) и расставляем на плоскости проекции в диметрии и справа спрятаны заготовки для изометрии (см. рис. 15.7).
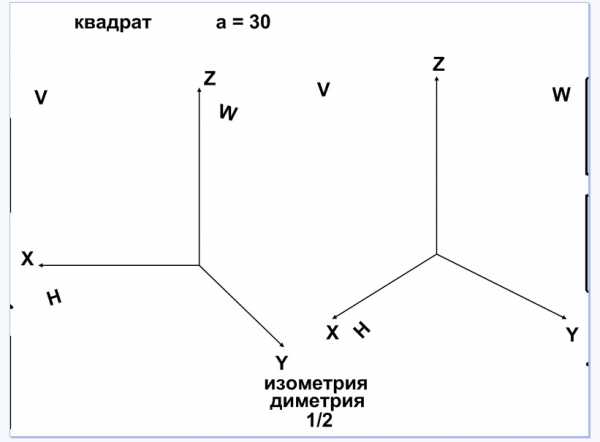
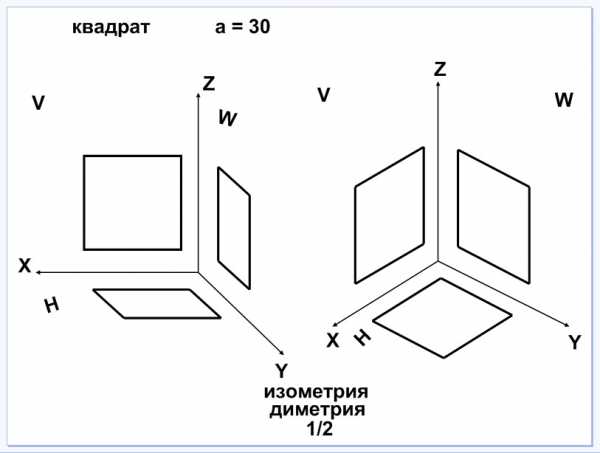
Рис. 15.6 Рис. 15.7
Лист 8. Построение равнобедренного треугольника в диметрии и изометрии. При построении проекции равнобедренного треугольника в плоскости XZ (фронтальная) его основание параллельно оси X, а высота треугольника параллельна оси Z, в плоскостях XY(горизонтальная) и ZY(профильная) по оси Y размер основания и высоты равнобедренного треугольника уменьшаем в два раза. Вытаскиваем слева заготовки проекций равнобедренного треугольника (см. рис 15.8) и расставляем на плоскости проекции в диметрии и справа спрятаны заготовки для изометрии (см. рис. 15.9).
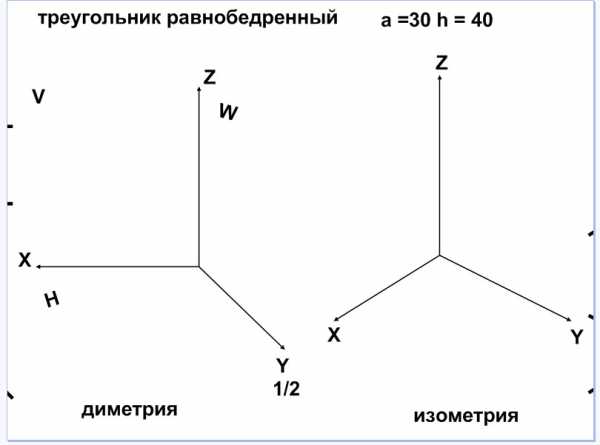
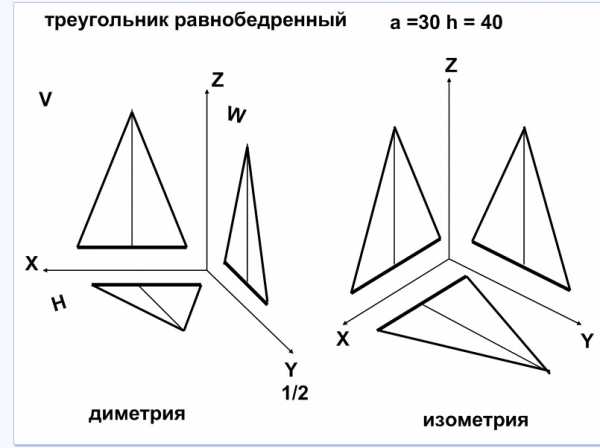
Рис. 15.8 Рис. 15.9
Лист 9. Построение шестиугольника в диметрии и изометрии.
Листы 10 -12.
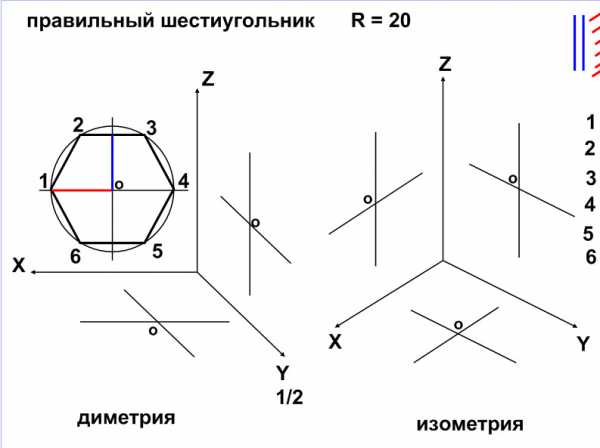
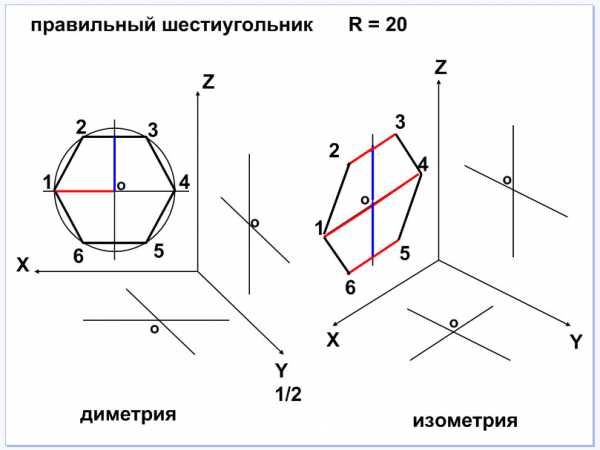
Рис. 15.10 Рис. 15.11
При построении в диметрии проекции шестиугольника в плоскости XZ (фронтальная) сначала строим окружность заданным радиусом, делим ее на 6 равных частей – получаем шестиугольник. На нем отмечаю радиус (красный цвет) и половина размера «под ключ» (синий цвет см. рис. 15.10). Затем строим шестиугольник в изометрии в плоскости XZ. Для этого втаскиваем заготовки справа и расставляем: параллельно оси Z – синий цвет, параллельно оси Х – красный цвет (точки 1 и 4). Чтобы построить точки 2 и 3 из верхнего конца синего отрезка откладываем половинки радиусов параллельно оси Х, и для построения точек 5 и 6 из нижнего конца синего отрезка – откладываем половинки радиусов параллельно оси Х. Соединяем полученные точки – получаем шестиугольник (см. рис. 15. 11).
Листы 13-14. Построение шестиугольника в горизонтальной плоскости в диметрии и в изометрии (см. рис. 15.12).

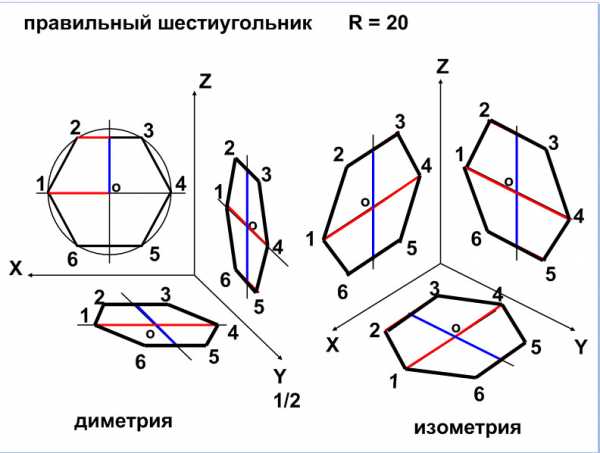
Рис. 15.12 Рис.15.13
Лист 15-18. Построение шестиугольника во фронтальной плоскости в диметрии и в изометрии (см. рис. 15 13).
Лист 19. Домашнее задание (см рис. 15.14).
Рис. 15.14
Лист 20. Дополнительный материал. Деление окружности на 3 части.
Лист 21. Деление окружности на 12 частей.
Лист 22. Деление окружности на 5 частей.
Лист 23. Деление окружности на 10 частей.
Файл проекта урока для интерактивной доски MIMIO Скачать
Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…
verysold.wordpress.com