Построение графиков вольфрам альфа: Графики функций одной переменной в Wolfram|Alpha

Использование Wolfram Alpha для решения задач курса высшей математики технического вуза

Байбисенова Асия Армановна,студентка 2 курса факультeта «Нефтегазовая и строительная техника», ФГБОУ ВО «Сибирский государственный автомобильнодорожный университет (СибАДИ)», г.Омск[email protected]

Гамалий Дмитрий Алексеевич,студент 2 курса факультeта «Нефтегазовая и строительная техника», ФГБОУ ВО «Сибирский государственный автомобильнодорожный университет (СибАДИ)», г.Омск[email protected]

Рождественская Елена Александровна,кандидат педагогических наук, доцент кафедры «Высшая математика» ФГБОУ ВО «Сибирский государственный автомобильнодорожный университет (СибАДИ)», г.Омск[email protected]

Использование Wolfram Alpha для решения задач курса высшей математики технического вуза

Аннотация.В статье описаны возможности программы Wolfram Alpha для поиска информации и решения математических задач применительно к различным разделам высшей математики технического вуза. Ключевые слова:Высшая математика, решение задач, графики функций и поверхностей, дифференцирование, интегрирование, численные методы, дифференциальные уравнения, технический вуз.

Wolfram Alpha –онлайнпрограмма, которую можно использовать для решения различных математических, инженерных и научных задач. Автором Wolfram Alpha является английский математик и программист Стивен Вольфрам.Впервые программа была представлена в мае 2009 года. Вскоре было выпущено мобильное приложение для Android.Поддержку сервиса Wolfram Alpha для мобильных устройств осуществляет виртуальный ассистент Siri, использующий технологии обработки речи;виртуальная клавиатура программы адаптирована для ввода математических формул.Wolfram Alpha представляет собой вычислительную машину знаний. Кроме вычислительных возможностей, в программе заложен поиск информации с последующей обработкой математическими методами, способность выдавать выкладки в виде готового результата, а не ссылок, этим программа отличается от поисковиков, подобныхGoogle.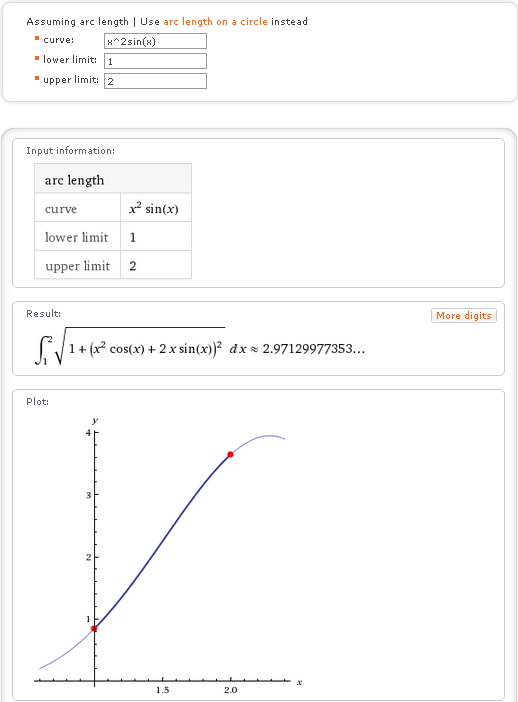

2), или график функции и график производной этой функции. Систему Wolfram Alpha можно спросить о том, кто такой «Эйлер» («Euler»), или вывести сведения и формулировку великой теоремы Ферма, или, например, перевести число из одной системы счисления в другую, перечислить проблемы современной математики и т.п.Начать работу с программой предельно просто, для этого необходимо зайти на сайт разработчиков и в поисковое окно ввести вопрос или задание на английском языке [1]. Системаприветствуетвасподсказкой«Enter what you want to calculate or know about». При наборе первых символов появляются похожие запросы, и можно выбрать уже готовый шаблон, который можно изменить с помощью своих данных. Даже непродвинутого пользователя заинтересует возможность построить объемные геометрические тела и графики поверхностей. На рисунке1 по нашему запросу «plot violet icosahedron» программа построила икосаэдр фиолетового цвета.

Рис. 1 ИкосаэдрвWolfram Alpha

Для построения графиков функций и поверхностей в Wolfram Alphaможно использовать функцию «рlot», можно также добавить параметры построения, указав границы по оси Ох; даже если вы не укажете функцию «рlot»,система распознает и построит функцию, автоматически подобрав масштабирование. Многие возможности программы представлены бесплатно, пошаговое решение и более подробные выкладки держатели программы предлагают оплатить покупкой доступа на определенный период, причем доступны приложения для студентов, так и разработки продвинутого уровня для инженеров и научных работников. На рисунке2 показан результат запроса на построение двуполостного гиперболоида по его уравнению. Заменяя некоторые знаки сложения и вычитания, мы мгновенно получим другую поверхность. Варьируя знаки и числовые параметры в данном примере, можно получить представление о различных поверхностях второго порядка, выполнив небольшое исследование «онлайн» даже в бесплатной версии. Например, читателя статьи может заинтересовать поверхность, называемая «сердце Тобина», для этого в браузер программы необходимо ввести запрос «Red Taubin’s heart surface»).

Рис.2 Построение двуполостного гиперболоида вWolfram Alpha

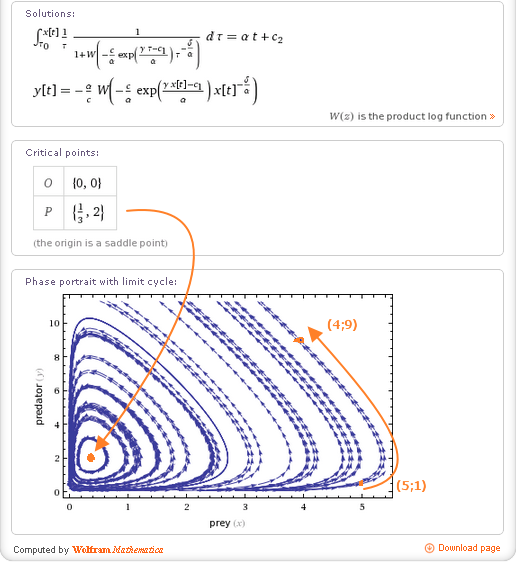
Эти возможности графической визуализации можно использовать в процессе обучения, например, при создании презентаций, а лучше, если есть доступ в интернет, интересно выполнять построения в режиме «онлайн». Возможности программы быстро генерировать ответ можно также использовать для быстрой самопроверки решения.Студентам, знакомым с математическим анализом, будет интересно узнать, что система позволяет дифференцировать и интегрировать, решать дифференциальные уравнения и многое другое, то есть охватывает курс высшей математики технического вуза вместе с различными специальными разделами, многие из которых не изучаются в стандартном курсе. Вопрос, каким образом это делается системой, представляет отдельный интерес. Знакомить студентов с возможностями программы целесообразно в конце изучения курса «Высшая математика».На рисунке3 представлено решение обыкновенного дифференциального уравнения, которое ранее «вручную» решалось в курсе математического анализа, система решила его, определила тип –линейное дифференциальное уравнение первого порядка, а также было построено семейство решений. Полноценное пошаговое решение («steр bystepsolution») недоступно, но доступ к данному функционалу можно купить, что для студента необязательно.

Рис. 3 Решение дифференциального уравнения в Wolfram Alpha

Таким образом, огромные математические возможности программы заключены в наборе функционала, с помощью которого можно получать решения алгебраических, дифференциальных, рекуррентных и функциональных уравнений и неравенств, использовать различные численные методы для нахождения корней уравнений и систем уравнений; возможность решать задачи дифференциального и интегрального исчислений, проводить анализ рядов и анализ Фурье, кластерный анализ и многое другое, то есть решать любые задачи курса математики технического вуза. Фактически, это та же математическая среда, но, в отличии от программных пакетов Maple, Mathcad, Matlab и других специализированных математических программ, адаптированная для использования среднестатистическим пользователем сети Интернет, не требующая предварительной установки. Применительно к курсу математики технического вуза, система Wolfram Alpha может работать с заданиями из линейной алгебры: совершать действия над матрицами, вычислять определители и решать системы линейных алгебраических уравнений.

Применительно к аналитической геометрии и векторной алгебре, программа позволяет строить уравнения прямых, плоскостей, кривых и поверхностей второго и высших порядков, решать задачи на нахождение скалярного, векторного и смешанного произведений и т.п. Wolfram Alpha также может работать с доказательствами теорем, с логическими функциями и операторами. Wolfram Alpha может работать с кривыми Безье, Bсплайнами, кривыми и поверхностями, проводить интерполяцию и аппроксимацию данных. Особенно важна возможность получать численные решения задач, которые не имеют аналитических решений вообще или аналитически простых решений. Широкий набор основных операций и алгоритмов на графах. Доступны математические константы любой точности, например,πили e.Встроена математическая статистика, включая автоматическую оценку параметров и проверку гипотез, анализ и построение статистических моделей с возможностью экспорта и импорта данных. Применительно к разделу математического анализа Wolfram Alpha позволяет находить производные, неопределенные и определенные интегралы, криволинейные интегралы, решать прикладные задачи. 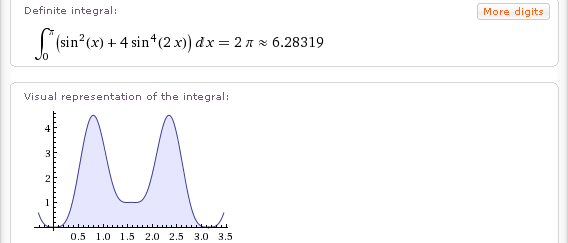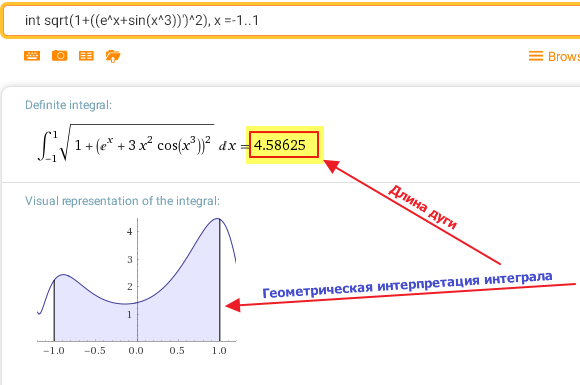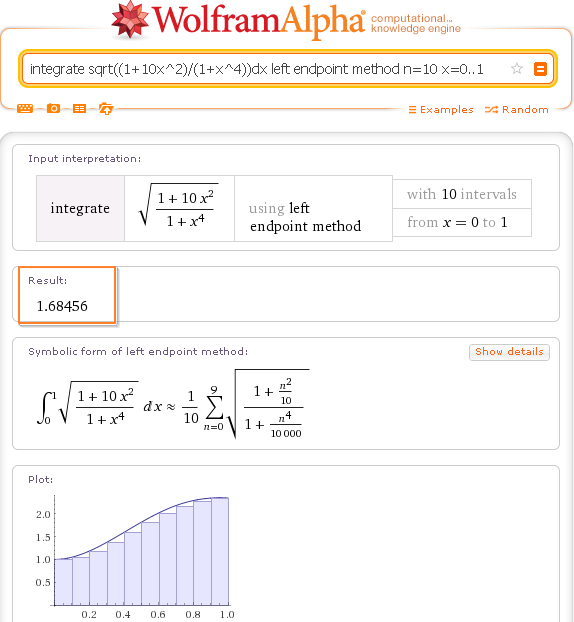Программа поддерживает различные форматы для импорта и экспорта, включая электронные таблицы, двумерные и трехмерные графические форматы,мультимедиафайлы, документы, архивные файлы и т.п. Встроены функции для вывода графиков из точек, линий и поверхностей, гистограмм, двумерных и трехмерных диаграмм разного вида.В продвинутых версиях программы многими параметрами математической задачи можно управлять интерактивно, изменяя их с помощью кнопок«ползунков», либо с помощью калькулятора с окнами для ввода различных параметров, что представляет огромные возможности для математического исследования. Проиллюстрируем применение методов численного интегрирования для вычисления «неберущихся» интегралов. На рисунке 4 показано решение интеграла Гаусса в Wolfram Alpha.

Рис.4 Вычисление «неберущегося» интеграла вWolfram Alpha

Некоторые операции из курса математики представлены в таблице 1. Отметим, что сам запрос может быть оформлен различными способами, и система отлично распознает его.Таблица 1Операторы для решения задач курса высшей математики

Название операцииОператорНахождение производной (дифференцирование)d/dxНахождение пределаlimitРешение различных уравненийsolveПостроение графиков и поверхностейplotНахождение неопределенного интегралаintegrateВычисление длины дугиarc lengthПолиномиальная интерполяция interpolating polynomial

Пользователь Wolfram Alphaможет обратиться к сайту русскоязычной поддержки программы[2], на котором представлены примеры из различных разделов курса математики,также к сайтам, содержащим синтаксис программы [3], либо к учебникам по Wolfram Alpha.

Можно воспользоваться сайтами поддержки с готовыми примерами.Галерея встроенных примеров доступна на сайте разработчиков во вкладке «Visual Gallery of Examples». Многие приложенияWolfram Alpha весьма интересны. В своем докладе Стивен Вольфрам [4] показывает пример работы одного из приложений программы: с помощью теории графов, позволяет анализировать связи между вашими друзьями в фейсбуке и проводить различные операции, например, визуализировать кластеры сообществ. По нашему мнению, решение стандартных и прикладных математических задач, которые можно осуществлять с помощью программы совместно с традиционным решением вручную, обогащает методику обучения математике, позволяет поддерживать интерес студентов к изучению математики и исследованиям, которые позволяют осуществить понимание математики и использование современных программных средств [5, 6]. Отметим важную мысль о том, что умение работать с программой не может заменять фундаментальных знаний, получаемых студентами технического вуза из курса высшей математики и специальных дисциплин. Знакомство сразличными программными средствами и интернетсервисами гармонично дополняет курс математики, делая инженерное образование отвечающим современным научным реалиям, способствует формированию информационнокомпьютерной компетентности преподавателя и математической компетентности студента [7, 8]. Особое внимание при преподавании математики должно быть уделено задаче выработки у студентов навыков математического исследования прикладных вопросов и умений перевести профессиональную задачу на математический язык [9], работа в программе Wolfram Alphaпоказывает студенту необходимость освоения данной компетенции, а также предоставляет огромные возможности для исследования и анализа решений прикладной задачи.Таким образом, Wolfram Alpha представляет собой мощную вычислительную и информационную среду, которая, несомненно, обладает тем преимуществом, что использовать ее может даже школьник и студент и доступ к ней осуществляется через интернет, посредством запроса на естественном языке. Для студентов же программа полезна и интересна даже в бесплатном ее варианте. Wolfram Alpha отлично справляется с заданиями курса математики технического вуза, в том числе с прикладными и с нестандартными, является прекрасным дополнением к изучению курса. Wolfram Alpha не требует глубоких знаний от начинающего пользователя. В то же время, чем лучше ваши математические познания, тем эффективнее вы сможете ее использовать, ведь система не ограничивается простой демонстрацией решения и визуализацией, она выдает описание множество свойств вызываемых математических объектов и относящихся к решению задач, не ограничиваясь ответом. Отметим, что преимуществом перед другими программами является ее простота использования и получение ответа и решения за счет действий с окном браузера в «в один клик».Прикладные возможности и исследовательские инструменты, предоставляемые ею, огромны как для студента, так и для инженера и ученого. Wolfram Alpha – это действительно современный и удобный инструмент для науки нового типа. Учитывая факт, что система совместима с различными устройствами, работает с облачными сервисами и различными технологиями, а также темпы расширения ее функционала и применения своих разработок все к большему числу областей, можно заключить, что возможности данной системы безграничны.

Ссылки на источники1.1.Wolfram Alpha/ Сайт разработчиков Wolfram Alpha. –URL:http://www.wolframalpha.com/.2.Синтаксис Wolfram Alpha // Викиучебник.–URL:https://ru.wikibooks.org/wiki/Синтаксис_Wolfram_Alpha.3.Вольфрам Альфа порусски / Сайт. –URL: wolframalpharu.com.4.ВольфрамС. Внедряя вычисления повсюду.–URL: https://habrahabr.ru/company/wolfram/blog/221487/.5.Рождественская Е. А., Болдовская Т. Е. Реализация прикладной направленности обучения высшей математике посредством рассмотрения алгоритмов решениязадач в интернетсервисах // Научнометодический электронный журнал «Концепт». –2015. –Т. 13. –С. 366–370. –URL: http://ekoncept.ru/2015/85074.htm.6.Болдовская Т. Е., Полякова Т. А., Рождественская Е. А. Реализация прикладной направленности обучения математике в учебных пособиях и задачниках по математике // Научнометодический электронный журнал «Концепт». –2016. –№ 10 (октябрь). –С. 120–126. –URL: http://ekoncept.ru/2016/16220.htm.7.Рождественская Е. А., Болдовская Т. Е. Информационнокомпьютерная компетентность преподавателя математики в высшей школе // Научнометодический электронный журнал «Концепт». –2016. –№ 4 (апрель). –С. 23–28. –URL:http://ekoncept.ru/2016/16064.htm.8.Болдовская Т. Е., Полякова Т. А., Рождественская Е. А. Методика формирования математической компетентности студента инженерного вуза: цели и перспективы // Научнометодический электронный журнал «Концепт». –2016. –№ 3 (март). –С. 76–80. –URL: http://ekoncept.ru/2016/16054.htm.9.Иванова О. В. Использование крупномодульных опор при изучении математических разделов в вузе // Научнометодический электронный журнал «Концепт». –2016. –№ 8 (август). –С. 79–85. –URL: http://ekoncept.ru/2016/16167.htm.

Аналоги Wolfram Alpha — 5 похожих программ и сервисов для замены

Аналоги Wolfram Alpha — 5 похожих программ и сервисов для замены

• 186

• SpeedCrunch

  SpeedCrunch — бесплатный, быстрый и высокоточный алгебраический калькулятор.

  • Бесплатная
  • Windows
  • Mac OS

  SpeedCrunch — это бесплатный, быстрый и высокоточный алгебраический калькулятор, находящийся в свободном доступе, с интуитивно понятным интерфейсом и широким списком функций, в том числе:

• 60

• fxSolver

  Программа для решения математических задач онлайн, уравнений и построения графиков.

  • Бесплатная
  • Онлайн сервис

  Онлайн программа для решения математических задач, библиотека уравнений, калькулятор для построения графиков, а также помощник в вопросах науки и техники.

• 37

• Calculator

  Калькулятор предоставляет простые и сложные математические функции в красиво оформленном приложении.

  • Бесплатная
  • Android
  • Онлайн сервис

  Калькулятор предоставляет простые и сложные математические функции в красиво оформленном приложении.

• 19

• Soulver

  Умный блокнот со встроенным калькулятором.

  • Платная
  • iPhone
  • Mac OS

  Soulver — это умный блокнот со встроенным калькулятором. Он дает мгновенные ответы на любые вычисления, которые он находит в вашем тексте. Это лучший способ для работы, чем с традиционным калькулятором, и более легкий инструмент для быстрых вычислений, чем электронная таблица.

• 9

• Grapher

  С Grapher вы можете составить график уравнений и наборов данных и визуализировать результаты на вашем Mac в реальном времени.

  • Бесплатная
  • Mac OS

  С Grapher вы можете составлять графики уравнений и наборов данных и визуализировать результаты на своем Mac в режиме реального времени. Grapher отображает алгебраические отношения, как явные, так и неявные, в 2D и 3D. Вы можете использовать различные системы координат и выбирать из широкого спектра математических функций, включая дифференциальные уравнения, параметрические кривые и многое другое. Когда вы закончите, вы можете экспортировать свою графику в виде анимации, которую можно воспроизвести в QuickTime Player.

Обнаружение естественного альфа-распада вольфрама — arXiv Vanity

К. Коццини1, ¹ , Г. Англохер2, К. Буччи3, Ф. фон Фейлиц5, Д. Хауф2, С. Генри1,
тыс. руб. Ягеманн4, Ю. Йохум5, Х. Краус1, Б. Майоровиц1, В. Михайлик1, Ю. Нинкович2,
Ф. Петричка2, В. Потцель4, Ф. Пребст2, Ю. Рамахерс1, ² , В. Рау4, М. Разети4,
В. Зайдель2, М. Старк4, Л. Стодольский2, А.Дж.Б. Толхерст1, В. Вестфал4, Х. Вуландари4 1Кафедра физики, Оксфордский университет, Оксфорд OX1 3RH, Великобритания
2MPI für Physik, Föhringer Ring 6, 80805 Мюнхен, Германия
3Laboratori Nazionali del Gran Sasso, 67010 Assergi, Италия
4Physikdepartment E-15, TU München, James-Franck-Str. , 85748 Гархинг, Германия
5Эберхард-Карлс-Университет Тюбинген, D-72076 Тюбинген, Германия

¹ 1 Автор, ответственный за переписку. Электронная почта адрес:

² 2 Текущий адрес: Уорикский университет, Ковентри CV4 7AL, Великобритания

12 июня 2022 г.

Аннотация

Естественный α-распад 180 Вт был однозначно обнаружены впервые. Пик α обнаруживается на фоне, не содержащем (γ,β и нейтронов) спектр. Это достигается одновременным измерением фононные и световые сигналы криогенными детекторами CRESST. А период полураспада T1/2=(1,8±0,2)×1018 лет и энергия релиз Q = (2516,4 ± 1,1 (стат.) ± 1,2 (сис.)) кэВ. измерено. Также установлены новые ограничения на периоды полураспада других природные изотопы вольфрама.

упак:

23.60.+e, 07.20.Mc, 29.40.Mc

I Введение

α-распад встречающихся в природе изотопов вольфрама (W) является предметом экспериментальных поисков на протяжении многих десятилетий. Вольфрам — интересный элемент, потому что α-распад энергетически допускается для всех пяти встречающихся в природе изотопы. масса избыточные измерения wapstra показывают, что доступная энергия распада Q для всех этих изотопов низкое (<3 МэВ) и что значения Q лежат в одной и той же энергии диапазоне по мере распада β и γ из-за естественных цепей (см. Таблицу 1). Поэтому подавление фона и, возможно, событие за событием дискриминация γ и β, которые могут скрывать сигнал α, являются критические вопросы для обнаружения таких редких событий.

Таблица 1: Репрезентативный изотопный состав согласно IUPAC, лучший сингл измерения содержания изотопов по отдельным эталонам и энергии распада изотопов из природного вольфрама.

Пока Ожидается, что модели 182 Вт, 183 Вт, 184 Вт и 186 Вт будут иметь период полураспада значительно превышает 1032 лет, ожидается, что период полураспада изотопа 180W будет около 1018 лет, и он близок к наблюдаемому с нынешние методики. Совсем недавно Киев-Флоренция Сотрудничество, эксплуатация сцинтилляционных детекторов CdWO4 на шахте Солотвина сообщил о «первых признаках возможного α-распада 180 Вт» с периодом полураспада Т1/2=1,1+0,8-0,4(стат.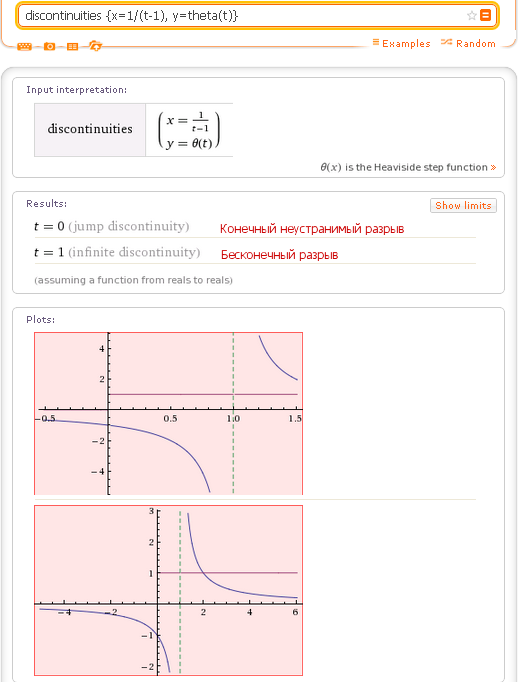 )±0,3(сис.)×1018 лет киев . Это хорошо известно birks , что выход сцинтилляций для α-частиц равен ниже, чем у β- или γ-частиц того же энергия. После анализа формы импульса α-пик при ∼300 кэВ был интерпретирован как 180Вт α-распад. Из-за низкого энергетического разрешения (FWHM = 110 кэВ) невозможно было исключить альтернативу объяснения пика, следовательно, результат был трактуется как указание. Они также установить 90% C.L. нижний предел T1/2≥0,7×1018 годы. Также коллаборация ROSEBUD, работа со сцинтилляционным болометром CaWO4 массой 54 г в Канфранке Подземная лаборатория, получен предел T1/2≥1,7×1017 лет в 90% CL цебриан .

Рисунок 1: Амплитуда импульса в световом канале в зависимости от энергии в кристалл CaWO4 D из опыта 28. Три четко разделенных события появляются популяции. Сплошные линии ограничивают три разных полосы: верхняя полоса обусловлена ​​γ и β, нижняя нейтронам, а средний — α. Каждый пик в α полоса была идентифицирована (см. текст) и обозначена здесь соответствующим образом.

Высокая чувствительность и отличное энергетическое разрешение при низких температурах. детекторы (см. например кресс ; fiorini ) и большие усилия сделано для подавления и понимания радиоактивного фона в поисках темной материи и экспериментах с двойным бета-распадом сделать такой аппарат чувствительным к редким ядерные распады. Например, α-распад 209Bi (считается самым тяжелым стабильным изотопом) был недавно обнаружен французской группой, разрабатывающей низкотемпературные болометры для Dark Прямое обнаружение материи marcillac . CRESST (Криогенный поиск редких событий с помощью сверхпроводящих термометров) — криогенная установка с низким фоном. в первую очередь посвящен прямому обнаружению частиц темной материи вимпов посредством их рассеяния ядрами. Такие ядерные отдачи, возникающие в результате взаимодействия вимпов, могут отличить от электронного фона (вызванного фотонами или электроны) путем измерения фононов и сцинтилляционного света одновременно. Энергия, обнаруженная с помощью фононов в криогенном детекторе, составляет первого порядка, не зависящего от природы частицы. Однако существует значительная разница в выходе сцинтилляций для ядер и электроны той же энергии. доля энергии, выделяемой в канале ядерного взаимодействия, пренебрежимо мала для фотонов и электронов, становится важным для α и тяжелых ионов и является доминирующим для вимпов и нейтронов. В результате отдачи, вызванные вимпом и нейтронами, дают значительно меньше сцинтилляционного света, чем электроны той же энергии, в то время как α-частицы можно четко различать поскольку они частично взаимодействуют как с ядрами, так и с электронами. Это приводит к чистому α-спектру, т. е. без вкладов β,γ и нейтронные события как в средней полосе рис. 1. Наконец, отметим, что энергия, измеренная после внутреннего α-распада в криогенной детектор соответствует сумме энергий α-частицы и ядра отталкивания, т. е. полная энергия распада Q.

В этой статье мы представляем четкие доказательства α-распада 180 Вт от первых запусков детекторов темной материи CRESST II, ​​происходящих из вольфрам в кристаллах CaWO4, используемых в качестве мишени темной материи.

II Экспериментальная установка

Рисунок 2: Схема модуля детектора. Он состоит из сцинтилляционный кристалл CaWO4 массой 300 г (фононный канал) и кремниевая пластина (световой канал), оба считываются ППД. Установка окружена отражающая фольга

CRESST — установка со сверхнизким фоном, работающая в Гран-Сассо. подземные лаборатории. Подробные описания можно найти в кресс ; Кресс II . CRESST разработала очень чувствительные криогенные детекторы, состоящие из диэлектрический кристалл-мишень со сверхпроводящим фазовым переходом термометр (СПТ) испаряется на одну поверхность. Взаимодействия частиц в криогенном детекторе производят фононы, которые распространяются на поверхность, где они нагревают электронная система в СПД. Эти термометры, смещенные в середине их сверхпроводящего к нормальному переход вблизи температуры 10 милликельвинов, превращают повышение температуры их электронов в относительно большое увеличение сопротивления пленки. Изменение сопротивления Затем с помощью СКВИДа измеряют термометр с низким импедансом. Увеличение сопротивления является мерой выделенной энергии.

Установка для одновременного обнаружения сцинтилляционного света и фононы описаны в cresstII и схематично показаны на Рис. 2 для одного модуля абсорбера. Он состоит из двух независимые детекторы, каждый со своим СПД со СКВИДом считывания. Основной детектор состоит из цилиндрического кристалла CaWO4 весом около 300 г. (∅=40 мм, h=40 мм). CaWO4 — хорошо известный сцинтиллятор с высоким световым выходом. и очень широкий спектр излучения с максимумом при 420 нм. Он характеризуется высоким показателем преломления (n = 1,92) и время затухания 17 мкс при 77 К. Детектируется сцинтилляционный свет, создаваемый в каждом целевом кристалле. через связанный калориметр, состоящий из кремниевой пластины (30 ×30×0,45)мм3 объем с Слой SiO2 толщиной 20 нм на обеих поверхностях. В CaWO4 лишь несколько процентов поглощенной энергии преобразуется в свет. К свести к минимуму световые потери, таким образом, весь модуль заключен в очень отражающая фольга.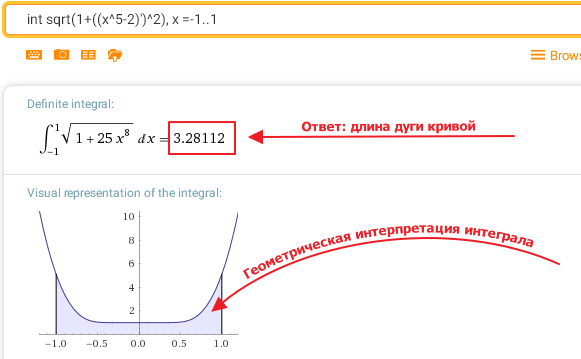

В представленных здесь данных три разных кристалла CaWO4 (называемые кристаллами B, D и E) использовались в Гран Установка Sasso для четырех различных запусков CRESST (22, 23, 27, 28). Для работы детектора Температура термометра контролируется специальным нагревателем. Кроме того, нагреватель используется для подачи тестовых импульсов, которые контролируют долговременная стабильность детектора кресс II . В частности, в опытах 27 и 28 формировался большой импульс напряжения, достигавший насыщения области сверхпроводящего перехода специально для контроля отклика детектора выше 1 МэВ. Этот пульс отправлялся с частотой 0,5 Гц в течение всего периода измерения. Длина записи 4096 отсчетов и временная развертка 40 мкс, в результате временное окно 164 мс для записи события было выбраны для всех представленных прогонов.

III Автономный анализ

Рис. 3. Подгонка двух событий из кристалла D (прогон 28) с шаблон, полученный усреднением импульсов от пика 122 кэВ. Подгонка усечена на 0,7 V. Для импульсов с амплитудой ниже этого значения процедура подгонки выглядит следующим образом: стандарт (левый участок). Для импульсов с амплитудой, превышающей это значение, верхняя часть формы импульса (над горизонтальной пунктирной линией на правом графике) искажен из-за насыщения. Поэтому подгонка усечена, т.е. подгонка только к точкам данных ниже 0,7 В, а амплитуда импульса реконструируется по шаблону. 9Детекторы CRESST 0015 оптимизированы, чтобы быть наиболее чувствительными в энергетическом диапазоне. область, имеющая отношение к прямому обнаружению темной материи (<200 кэВ). В этом диапазоне энергий Отклик детектора отображается тестовыми импульсами электронагревателя, а Линия 122 кэВ от источника 57Co обеспечивает калибровку теста импульсов в пересчете на эквивалентную энергию γ cressI . Форма импульса шаблон получен усреднением импульсов с линии 122 кэВ. Этот шаблон используется в подгонка к фактическим сигнальным импульсам для того, чтобы точно определить амплитуду сигнала.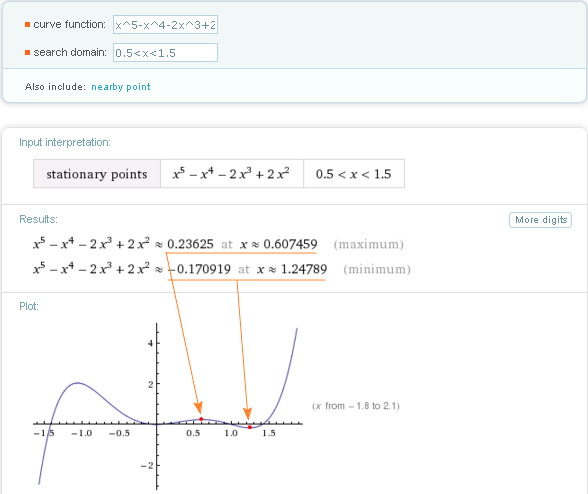 Это справедливо до тех пор, пока отклик детектора находится в линейный режим. Если отклик становится нелинейным, форма импульса изменения, и один и тот же шаблон нельзя использовать во всем диапазоне энергий.

Обычно форму импульса для детекторов CaWO4 можно описать как τ нарастание = 1,1 мс и τ спад = 30 мс. Однако повышение температуры вызванный α-распадами, обычно выходит за пределы динамического диапазона SPT и для точного определения энергии сигнала следует использовать длительность, а не высоту импульса. Поэтому два новых анализа методы, описанные в методы , были разработаны для реконструкции более высокие энергии (область МэВ), для которых отклик детектора нелинейный.

В первом методе (Метод А) шаблон из импульсов в линейная область (например, шаблон 122 кэВ из калибровки) используется для соответствия всем измеренные импульсы с амплитудой ниже напряжения, при котором отклик становится нелинейным. Для всех импульсов с амплитудой, превышающей это напряжение, подгонка обрезается, а верхняя часть восстанавливается по шаблону. Это показано в Рис. 3. Результирующий амплитудный спектр линейен по формуле строительство.

Если длительность импульса слишком велика, информация от затухающей части импульса находится за пределами окно времени записи, и метод не работает. Чтобы преодолеть это ограничения был разработан второй метод (метод B). Шаблон из линейной области снабжается функцией по модели описано в пробст . Это предполагает экспоненциальный рост и две компоненты экспоненциального затухания. После определения параметров модельной функции для линейная область, а математическое описание изменений пульса нужна форма в нелинейном диапазоне. При более высоких энергиях форма импульса меняется в зависимости от нелинейности сверхпроводящий фазовый переход. Эти изменения можно описать через последовательное приближение к модельной функции. Поправочные коэффициенты более высокого порядка извлекаются путем подгонки шаблоны различных энергий до 2,31 МэВ (см. методы ), включение энергии спектр, который необходимо восстановить до самого высокого зарегистрированного α-сигнала (α-α-каскад при ∼15 МэВ).

IV Фон

Благодаря мощному метод дискриминации, предлагаемый детекторами CRESST II, ​​загрязнения от естественного распада цепи и другие α-нестабильные изотопы были идентифицированы их α-распады с чувствительностью ~1 мкБк/кг. Результаты этого анализа показали очень хорошее совпадение с результаты, полученные с использованием различных методов, обычно используемых для определения наличие примесей в кристаллах. К ним относятся ИКПМС ^{4 4} 4 Лаборатория Гран Сассо и Даремский университет Дарем (масс-спектрометрия с индуктивно связанной плазмой), HPGe ^{5 5} 5 Modane Подземная лаборатория и Гран Подземная лаборатория Сассо arpesella (высокая чистота γ-спектроскопия германия) и рентгенолюминесцентные ^{6 6} 6Даремский университет Виталий методы.

Таблица 2: Результаты анализа редкоземельных элементов, гафния, и осмий. Для полуколичественный анализ калибровочная кривая определяется с многоэлементный стандарт, который может отличаться от один для анализа. На некоторых элементах, в частности на самарии, проведен количественный анализ. В этом случае калибровка полученные с использованием известных стандартов анализируемого элемента. Все образцы растворяют в растворе HNO3 в микроволновой печи при различные экспозиции для образцов I и II.

Доказательства загрязнения из-за α-нестабильного редкоземельного элемента элементы были обнаружены во всех измеренных детекторах. Кристаллы, легированные редкоземельными элементами обычно производятся для лазерных применений, поэтому эти примеси, вероятно, были введены во время производства кристаллов. В частности, был обнаружен α-пик при 2,31 МэВ. идентифицирован как α-распад 147Sm. Этот изотоп встречается в природе с содержанием изотопов 15% и известен как чистый альфа-нестабильный радионуклид с T1/2=1,06×1011 лет. интенсивность этого пика различается для разных детекторов, что означает различные уровни загрязнения в каждом кристалле. Кристалл B показал скорость счета (1,7 ± 0,1) имп/ч, что соответствует (13 ± 1) ppb природного самария в кристалле. Ставка на том же пик, измеренный кристаллом E, соответствует загрязнению (5,5 ± 0,4) частей на миллиард натуральный самарий.

анализов ICPMS было выполнено на установке Gran Sasso на кристаллах. Б и Е дающие результаты, показанные в таблице 2, в соответствии с нашими анализ интенсивностей α-пиков. Доказательства 144Nd (Q = 1905,1 кэВ, изотопный численность (i.a.) = 23,8%, T1/2=2,29×1015 лет) и 152Gd (Q = 2205 кэВ, м.кв. = 0,2%, T1/2=1,08×1014 у) изотоп α-распад также наблюдался, и результаты согласуются с ICPMS-анализ. Кроме того, рентгенолюминесцентный анализ кристалла В показал наличие характерный эмиссионный пик Gd и Er нинкович , два наиболее распространенных редкоземельных примеси (см. Таблицу 2).

Наконец, альтернативные кандидаты, такие как 174Hf (Q = 2496 кэВ, т.е. = 0,162%, T1/2=2,0×1015 лет) и 186Os (Q = 2822 кэВ, т.е. = 1,58%, T1/2=2,0×1015 лет) изотоп считались причиной пика 2,31 МэВ. Они были отбрасывается, однако, из-за необоснованно высокой концентрации атомов, необходимой для получения обнаруженной скорости.

Калибровка

Рис. 4: Вверху: подобранное положение пика в зависимости от известной энергии. энергетическая шкала по оси ординат фиксируется пиком 147Sm, а положение пики 232Th и 238U являются результатом простой линейной экстраполяция калибровки для обоих методов A и B. Внизу: остатки установленное положение от ожидаемого положения. Для метода А Результаты пика 232Th при (4081,3 ± 1,7) кэВ (ΔE = (28 ± 4) кэВ (FWHM)) и 238У в (4269.4 ± 2,2) кэВ. Для метода B пики лежат при (4076,3 ± 0,8) кэВ (ΔE = (14,1 ± 1,7) кэВ (FWHM)) и (4265,9 ± 1,1) кэВ соответственно. Калибровка амплитуды спектр, полученный методом А, намного точнее; однако разрешение меньше по сравнению с методом B.

После однозначного определения 147Sm использовался для калибровки полный альфа-спектр. Это позволило точно идентифицировать U-Th пики, которые затем использовались для определения точности калибровка для обоих методов реконструкции A и B. На рис. 4 показана линейность функций отклика для метода A (верхний левый рисунок) и метода B (верхний правый рисунок) показаны для данных опыта 28. По оси абсцисс отложены центральные значения табличных энергий wapstra 147Sm (Q= 2310,5 ± 1,1 кэВ), 232Th (Q= 4082,8 ± 1,4 кэВ) и Приведены пики 238U (Q= 4270 ± 3 кэВ). По оси ординат они установлены наносится положение пика. Энергия шкала по оси ординат зафиксирована на пике 147Sm при 2310,5 кэВ, а положение пики 232Th и 238U являются результатом простой линейной экстраполяция калибровки. В В нижней части рисунка показаны остатки установленного положения по отношению к ожидаемому положению. Калибровка амплитудного спектра, полученного методом А, гораздо точнее, но меньше информации может быть использовано для восстановления амплитуды сигнала по сравнению с методом B. Это приводит к несколько худшему энергетическому разрешению ΔE = (12,9± 0,3) кэВ (FWHM) на 147Sm пик, и это не удается полностью восстановить верхнюю часть α-спектра U-Th. Метод B, с другой стороны, использует больший объем информации от импульсов, чем метод А, дает гораздо лучшее разрешение (ΔE = (6,7 ± 0,1) кэВ (FWHM) на пике 147Sm), но аппроксимация описания формы импульса вводит более высокая систематическая ошибка при линейной экстраполяции калибровки. В дальнейшем метод B использовался для полной реконструкции и идентифицировать весь α-спектр, а метод А применялся как независимая проверка пикового положения доказательства 180 Вт. В частности, метод А используется для извлечения измеренной энергии для 180 Вт Q-значение.

Vi Результаты

Crystal D показал наилучшие характеристики в качестве детектор (энергетическое разрешение: ΔE = 1,8 кэВ (FWHM) для 122 кэВ гамма и ΔE = (6,7 ± 0,1) кэВ для 2,31 МэВ альфа, используя метод Б) и имеет самый длинный экспозиция (11,745 кг-сутки в 27-м заезде и 12,268 кг-дней в 28-м заходе). В пробеге 28 производительность модуля была улучшена заменой Ag отражающая фольга, использованная в опыте 27, который показал загрязнение 210Pb, высокоотражающей (99% при 420 нм) сцинтилляционной полимерной фольгой. Это эти данные, которые мы обсуждаем во всех подробностях. Пик был наблюдается при 2512,8 ± 0,4 (стат.) ± 4,3 (син.) кэВ с разрешение ΔE = (6,5 ± 0,7) кэВ (FWHM). Это показано в Рис. 5.

Рисунок 5: Альфа-события, измеренные в прогоне 28. На верхнем рисунке энергетический спектр между 1,7 и 2,7 МэВ показан с 3 кэВ бункеры. По вертикальной оси отображается количество отсчетов на логарифмическая шкала. На нижнем рисунке подгонка к 180 Вт α-распаду Показано. В широком интервале энергий вокруг пика фоновые отсчеты отсутствуют.

Позиция по энергии, полученная путем восстановления спектра методом А составляет (2516,5 ± 1,4) кэВ. Период полураспада T1/2=(1,7±0,2)×1018 лет. Это последовательно со значением из прогона 27 на том же кристалле и на кристаллах B и E, как показано в таблице 3. Согласованность результатов для разных кристаллов, как правило, подтверждает, что сигнал возникает из-за распада 180 Вт, а не из-за неизвестных примесей, которые могут для каждого отдельного кристалла, как показано в разделе 4, будет варьироваться. Кроме того, ICPMS измерения, проведенные на этих двух кристаллах, представлены в таблице 2. исключить альтернативные объяснения пика вольфрама, такие как 174Hf.

Кристалл	Выполнить	Воздействие	Номер	Период полураспада
	номер	[кг сут]	из подсчетов	[г]
Д	28	12. 268	35± 4,3	Т1/2=(1,7±0,2)×1018
Д	27	11.745	28,5 ± 5,6	Т1/2=(1,9±0,4)×1018
Е	23	3,467	9	Т1/2≥1,1×1018 (90% л.)
Б	22	1,14	4	Т1/2≥6,8×1017 (90% л.)
Все кристаллы		28,62	75,5±8,7	Т1/2=(1,8±0,2)×1018

Таблица 3: Период полураспада для α-распада 180 Вт получен из настоящей работы. Результаты предоставляются независимо для четыре разных прогона и за общую экспозицию. Для пробегов 27, 28, и общей экспозиции, количество отсчетов определяется Гауссовская подгонка к пику. Ошибки даны при 1σ. Для пробега 22 и 23 из-за малого количества отсчетов, общее количество событий, содержащихся в пределах ±3σ от дается ожидаемая энергетическая позиция.

Наконец, были добавлены четыре измерения, в результате чего был получен спектр для общая экспозиция 28,62 кг сутки. Данные каждого прогона были проанализированы методом А, откалиброваны индивидуально, а затем суммированы. Это приводит к увеличению периода полураспада T1/2=(1,8±0,2)×1018y, что согласуется с ранее опубликованные лимиты. С учетом неопределенности положения линии 147Sm пик энергии (2516,4 ± 1,1 (стат.) ± 1,2 (сис.)) кэВ. разрешение ΔE = (18 ± 2) кэВ (FWHM), как показано на Рис. 6. Этот результат согласуется с ожиданиями, основанными на разница масс 180W и 176Hf от Ссылка wapstra , но находится на расстоянии 2σ от последнего обновление wapstra03 (см. Таблицу 1). Заметим однако, что большая часть входных данных используется для оценки атомных масс состоят из относительных измерений, которые устанавливают отношение массы или энергии между двумя или более ядрами. На диаграмме показывая отношения между входными данными (рис. 1 Ref. wapstra03 ), 180W и 176Hf только слабо связаны и недооценка ошибок правдоподобный. Наш результат представляет собой отсутствие прямой связи между 180 Вт и 176 Гц.

Рисунок 6: Сумма четырех разных прогонов, каждый из которых проанализирован независимо с помощью метода A. Полученный пик аппроксимируется, давая энергию (2516,4 ± 1,1) кэВ с разрешение FWHM = (18 ± 2) кэВ. Несколько фоновых событий из-за поверхности загрязнение фольги Ag, используемой в пробег 27 видны. Блестящая фольга используемые в прогонах 22, 23 и 28 эффективно налагают вето на все эти события (см. текст).

Пределы периодов полураспада для ненаблюдаемых α-распадов также были рассчитаны другие четыре встречающихся в природе изотопа вольфрама. Для этого данные из прогон 27 не может быть использован. В этом опыте для окружения использовалась фольга Ag. кристалл, в то время как в трех других работает сцинтилляционный полимерный использовалась фольга. Любой загрязнение α-нестабильными изотопами, такими как 210Po, на поверхности фольги или на кристалле может привести к α-событиям деградации энергии от энергия цепочки U-Th снижается до ∼100 кэВ. Это наблюдалось в прогоне 27 с коэффициентом 0,087 отсчетов/100 кэВ/кг/день как в диапазоне ∼500 кэВ, так и в диапазоне 144 Nd пик 1,9МэВ, а также между пиками 180W и 232Th. Полимерная фольга использованный во всех других прогонах, не показал никакой поверхности загрязнение. Кроме того, если мерцающая сторона фольги обращена непосредственно к кристаллу, как в прогоне 28, он эффективно накладывает вето на все поверхностные события из-за свет, излучаемый самой полимерной фольгой. Пределы, полученные из суммы прогонов 22, 23 и 28, приведены в Таблица 4.

Таблица 4: Нижние пределы (90% CL) периодов полураспада ненаблюдаемых α-распадов другие четыре встречающихся в природе изотопа вольфрама, полученные при общем воздействии 16,875 кг дней. Для сравнения лучшие ранее также показаны опубликованные пределы киев ; Себриан .

VII Выводы

Мы наблюдали естественный α-распад 180 Вт с период полураспада T1/2 = (1,8 ± 0,2) × 1018 лет и значение Q (2516,4 ± 1,1 (стат.) ± 1,2 (сис.)) кэВ. Кроме того, отсутствие какого-либо сигнала от других изотопов вольфрама устанавливает новые пределы на период их полураспада. Эти результаты предлагают улучшение примерно в 50 раз выше лучших ранее опубликованных пределов. Напоследок хотелось бы отметить мощность и потенциал этого криогенного метод, который здесь позволил нам достичь очень высокой чувствительности в приложении к ядерной физике.

Благодарности

Мы хотели бы поблагодарить С. Ниси и М. Балата за измерения ICPMS и М. Лаубенштейн за анализ γ-спектроскопии в Гран Лаборатории Сассо. Спасибо также К. Гольдбаху для измерений Ge в Модане и Даремскому университету для ИСПМС и рентгенолюминесцентный анализ. Эта работа была поддержана PPARC, BMBF, сетью ЕС HPRN-CT-2002-00322 по прикладным криодетекторам, сеть ЕС по Криогенные детекторы (контракт ERBFMRXCT980167), DFG SFB 375 на Астрофизика элементарных частиц и две стипендии Марии Кюри ЕС.

Каталожные номера

• (1) Г. Ауди и А. Х. Вапстра, Ядерная физика A 595 (1995) 409-480.
• (2) А. Х. Вапстра Г. Ауди и К. Тибо, Ядерная физика A 729 (2003) 129-676.
• (3) К. Дж. Р. Росман и П. Д. П. Тейлор, Pure and Applied Химия 70 (1998) 217.
• (4) J. Völkening, M. Köppe and KG Heumann, International Journal of Mass Spectrometry and Ion Processes, 107 (1991) 361.
• (5) Ф. А. Даневич и др., Physical Review C 67 (2003) 014310.
• (6) Дж. Б. Биркс, Теория и практика сцинтилляций. Подсчет (1967), Пергамон, Нью-Йорк.
• (7) С. Себриан и др., Physics Letters B 556 (2003) 14-20.
• (8) Г. Англохер и др., Астрофизика частиц 18 (2002) 43-55.
• (9) G. Angloher et al., представлено Astroarticle Физика, астро-ф/0408006.
• (10) К. Арнабольди и др., Астрофизика частиц 20 (2003) 91-110.
• (11) П. де Марсильяк, Н. Корон, Г. Дамбье, Ж. Леблан, Дж. Моалик, Nature 422 (2003) 876.
• (12) F. Probst et al., которые будут представлены.
• (13) К.Дж.Оттли, Д.Г. Пирсон и Г.Дж. Ирвин в плазме Исходная масс-спектрометрия: приложения и новые технологии, под редакцией Дж. Г. Холланда и С. Д. Таннера, Королевское химическое общество, Кембридж (2003) 221-230.
• (14) C. Arpesella, Nucl. физ. B (Прокт. Приложение) 28 A (1992) 420.
• (15) В. Б. Михайлик, И. К. Пристав, Х. Краус, П. А. Rodnyi and J. Ninkovic, Radiation Measurements 38 (2004) 585-588.
• (16) F. Probst и др., J. Low Temp. физ. 100 (1995) 69.
• (17) J. Ninkovic et al., представленный Nucl. Инструм. и методы A Материалы конференции SCINT 2003.
• (18) Таблица изотопов под редакцией Р. Б. Файерстоуна и др. др., 8-е изд. (1996) Уайли, Нью-Йорк.

Экспериментальные энергии рентгеновского излучения K-альфа

Экспериментальные энергии рентгеновского излучения K-альфа

. Z Element Ka 2 eV(unc) Ka 1 eV(unc) 10 Ne 848. 61(26) 848.61(26) 11 Na 1040.98(12) 1040.98(12) 12 Mg 1253.437(13) 1253.688(11) 13 Ал 1486.295(10) 1486.708(10) 14 Si 1739.394(34) 1739.985(19) 15 P 2012.70(48) * 2013.68 (48) * 16 S 2306.700(38) 2307.885(34) 17 Cl 2620.846(39) 2622.440(39) 18 Ар 2955.566(16) 2957.682(16) 19 K 3311.1956(60) 3313.9476(50) 20 Ca 3688.128(49) 3691.719(49) 21 Sc 4085. 9526(85) 4090.735(19) 22 Ti 4504.9201(94) 4510.8991(94) 23 V 4944,671 (59) 4952.216(59) 24 Cr 5405.5384(71) 5414.8045(71) 25 Mn 5887.6859(84) 5898.8010(84) 26 Fe 6391.0264(99) 6404.0062(99) 27 Co 6915.5380(39) 6930.3780(39) 28 Ni 7461.0343(45 ) 7478.2521(45) 29 Cu 8027.8416(26) 8047.8227(26) 30 Zn 8615.823(73) 8638.906(73) 31 Ga 9224.835(27) 9251.674(66) 32 Ge 9855. 42(10) 9886.52(11) 33 As 10507.50(15) 10543.2674(81) 34 Se 11181.53(31) 11222.52(12) 35 Br 11877.75(34) 11924.36(34) 36 Kr 12595.424(56) 12648.002(52) 37 Rb 13335.88(21) 13395.49(19) 38 Sr 14098.03(24) 14165.20(24) 39 Y 14882.94(26) 14958.54(27) 40 Zr 15690.645(50) 15774.914(54) 41 Nb 16521.28( 33) 16615.16(33) 42 Mo 17374.29(29) 17479.372(10) 43 Tc 18250. 9(12) 18367.2(12) * 44 Ru 19150.49(18) 19279.16(18) 45 Rh 20073.67(20) 20216.12(20) 46 Pd 21020.15(22) 21177.08(17) 47 Ag 21990.30(10) 22162.917(30) 48 Cd 22984.05(20) 23173.98(20) 49 В 24002.03(28) 24209.75(22) 50 Sn 25044.04(23) 25271.36(23) 51 Sb 26110.78(25) 26358.86( 25) 52 Te 27201.99(26) 27472.57(27) 53 I 28317.52(67) 28612.32(49) 54 Xe 29458. 250(50) 29778.78(10) 55 Cs 30625.40(45) 30973.13(46) 56 Ba 31816.615(60) 32193.262(70) 57 La 33034.38(26) 33442.12(27) 58 Ce 34279.28(28) 34720.00(29) 59 Pr 35550,59(30) 36026.71(31) 60 Nd 37360.739(70) 37360.739(70) 61 Pm 38171.55(70) 38725.11(72) 62 Sm 39523.39(10) 40118.481(60) 63 Eu 40902.33(40) 41542.63(41) 64 Gd 42309.30 (43) 42996.72(44) 65 Tb 43744. 62(46) 44482.75(47) 66 Dy 45208.27(49) 45998.94(51) 67 Ho 46699.98(15) 47547.10(77) 68 Er 48221.61(20) 49127.24(12) 69 Tm 49772.67(12) 50741.475(92) 70 Yb 51354.60(63) 52389.48(66) 71 Lu 52965.57(67) 54070.39(70) 72 Hf 54612.0(11) # 55790.8(11) # 73 Ta 56277.6(15) 57533.2(16) 74 W 57981.77(14 ) 59318.847(50) 75 Re 59718.57(43) 61141.00(89) 76 Os 61487. 27(90) 63001.07(95) 77 Ir 63287.29(96) 64896.2(10) 78 Pt 65123.3(20) 66832.9(21) 79 Au 66990.73(22) 68804.50(18) 80 Hg 68895.1(17) 70819.5(18) 81 Tl 70832.5(12) 72872.5(13) 82 Pb 72805.42( 24) 74970.11(17) 83 Bi-209 74816.21(92) 77109.2(22) 84 Po-209 76864.4(71) * 79292.9 (75) * 85 AT-210 78 944 (15) * 81 514 (16) * 86 RN-222 86 RN-2229 81 86 81 86 86 81 86 86 86 86 81 86 86 86 86 86 86 86 81 81 86 86 87 Fr-223 83 232(25) * 86 105(27) * 88 Ra-226 85 436(12) 88 476(12) 89 Ac-227 87 676(18) * 90 884,8(79) * 90 Th-232 89 957.04(20) 93 347.38(25) 91 Pa-231 92 283.4(20) 95 866.4(20) 92 U-238 94 650.84(56) 98 431.58(28) 93 Np-237 97 068.4(30) * 94 Pu-239 99 523.2(12) * 94 Pu-244 99 529.4(20) * Энергии рентгеновского излучения представляют собой прямую линию при нанесении на график Мозли. * Интерполировано из близлежащих элементов. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт