Графики функций, построенные точками | Учебники
Графики функций, построенные точками
Показанный график полинома, построенный ромбиками, не означает, что полином представлен отдельными точками. В данном случае просто выбран стиль линии в виде точек. Однако часто возникает необходимость построения графиков функций, которые представлены просто совокупностями точек. Такая совокупность может быть создана искусственно, как, либо просто задаваться списком координат х и значений функции.
В данном случае переменная Р имеет вид списка, в котором попарно перечислены координаты точек функции sin(x). В этом нетрудно убедиться, заменив знак «:» после выражения, задающего Р, на знак «;». Далее по списку Р построен график точек в виде крестиков, которые отображают отдельные значения функции sin(x).
показано построение графиков функций по точкам при явном задании функции списком координат ее отдельных точек. В первом примере эти точки соединяются отрезками прямых, так что получается кусочно-линейный график.
Видно также, что указание типа точек после указания стиля линии игнорируется (а жаль, было бы неплохо, чтобы наряду с кусочно-линейной линией графика строились и выделенные окружностями точки).
Во втором примере показано построение только точек заданной функциональной зависимости. Они представлены маленькими кружками. Читателю предлагается самостоятельно совместить оба подхода к построению графиков по точкам и создать график в виде отрезков прямых, соединяющих заданные точки функции, представленные кружками или крестиками.
Графики функций, заданных своими именами
Способность Maple 15 к упрощению работы пользователя просто поразительна — жаль только, что многие возможности этого становятся ясными после основательного изучения программы, на что уходят, увы, не дни, а месяцы, а то и годы. Применительно к графикам одной из таких возможностей является построение графиков функций, заданных только их функциональными именами — даже без указания параметров в круглых скобках.
Такую возможность наглядно демонстрирует 11.9.
Этот пример показывает, что возможно построение графиков функций даже без указания в команде plot диапазонов. При этом диапазон по горизонтальной оси устанавливается равным по умолчанию -10.. 10, а по вертикальной оси выбирается автоматически в соответствии с экстремальными значениями функций в указанном диапазоне изменения независимой переменной (условно х).
Графики функций с ординатами, заданными вектором
Часто возникает необходимость построения графика точек, ординаты которых являются элементами некоторого вектора. Обычно при этом предполагается равномерное расположение точек по горизонтальной оси. Пример построения такого графика дан.
Из этого примера нетрудно заметить, что данная задача решается составлением списка парных значений координат исходных точек — к значениям ординат точек, взятых из вектора, добавляются значения абсцисс. Они задаются чисто условно, поскольку никакой информации об абсциссах точек в исходном векторе нет, так что фактически строится график зависимости ординат точек от их порядкового номера n.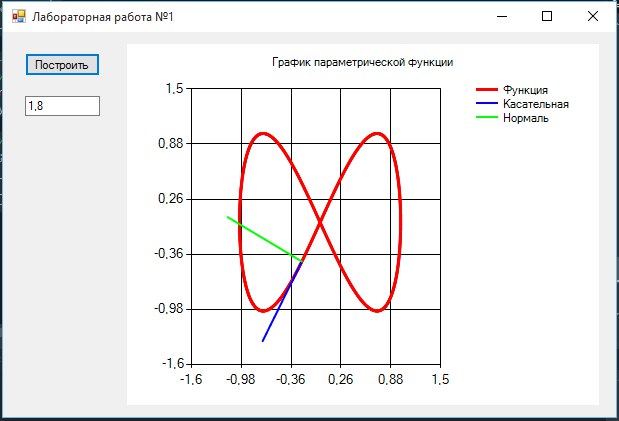
Графики функций, заданных процедурами
Некоторые виды функций, например кусочные, удобно задавать процедурами. Построение графиков функций, заданных процедурами, не вызывает никаких трудностей и иллюстрируется.
Здесь, пожалуй, полезно обратить внимание на то, что в функции plot указывается имя процедуры без списка ее параметров.
Графики функций, заданных функциональными операторами
Еще одна «экзотическая» возможность функции plot — построение графиков функций, заданных функциональными операторами. Она иллюстрируется.
Имена функций (без указания списка параметров в круглых скобках) тоже, по существу, являются функциональными операторами. Так что они также могут использоваться при построении графиков упрощенными способами.
Графики функций, заданных параметрически
В ряде случаев для задания функциональных зависимостей используются заданные параметрически уравнения, например х = f1(t) и у =f2(t) при изменении переменной t в некоторых пределах.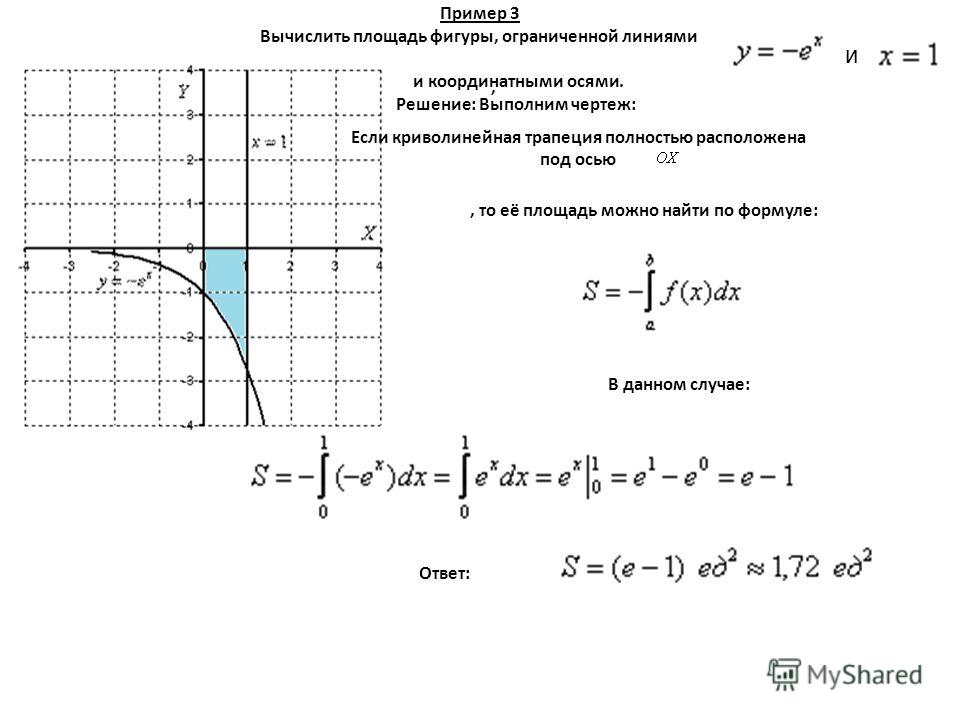
Точки(х, у) наносятся на график в декартовой системе координат и соединяются отрезками прямых. Для этого используется функция plot в следующей форме:
plot([fl(t),f2(t),t-tmin..tmax].h,v.p)
Если функции f1(?) и f2(0 содержат периодические функции (например, тригонометрические), то для получения замкнутых фигур диапазон изменения переменной t обычно задается равным 0. .2*Pi или -Pi..Pi. К примеру, если задать в качестве функций f1(t) и f2(t) функции sin(t) и cos(t), то будет получен график окружности. Рисунок показывает другие, чуть менее тривиальные примеры построения графиков такого рода.
Задание диапазонов для изменений h и v, а также параметров р не обязательно. Но, как и ранее, они позволяют получить вид графика, удовлетворяющий всем требованиям пользователя.
Глава 3. Использование KmPlot
Содержание
- Типы функций
- Функции в декартовой системе координат
- Параметрические функции
- Функции в полярной системе координат
- Неявно заданные функции
- Дифференциальные функции
- Комбинирование функций
- Настройка отображения графиков
- Контекстное меню
KmPlot работает с несколькими разными типами функций, которые возможно указывать как в виде функции, так и в виде уравнения:
Функции для построения графиков в декартовой системе координат возможно записывать в виде «y = x^2», где x используется как переменная; или в виде «f(a) = a^2», где название переменной является обязательным.
Определения функций, заданных параметрически, похожи на определений функций в декартовых координатах. Координаты x и y можно ввести в виде уравнений относительно переменной t, например «x = sin(t)», «y = cos(t)», или в виде функций, например «f_x(s) = sin(s)», «f_y(s) = cos(s)».
Определения функций, заданных в полярных координатах, также похожи на определения функций в декартовых координатах. Их возможно ввести либо в виде уравнения в θ, например «r = θ», либо в виде функции, например «f(x) = x».
Название функции, заданной неявно, следует вводить отдельно от выражения, связывающего между собой координаты x и y. Если переменные x и y указаны с помощью названия функции (например, если как название функции указано выражение «f(a,b)»), будут использованы эти переменные. В ином случае для обозначения переменных будут использоваться буквы x и y.
Функции, задаваемые дифференциальным уравнением, описываются в виде дифференциального уравнения, разрешённого относительно старшей производной.
Дифференцирование обозначается штрихом (‘). В виде функции уравнение будет выглядеть следующим образом: «f»(x) = f’ − f». В виде уравнения это будет что-то вроде «y» = y’ − y». Обратите внимание, что в обоих случаях часть «(x)» не следует добавлять в члены низшего порядка (то есть следует вводить «f'(x) = −f», а не «f'(x) = −f(x)»).
Дифференцирование обозначается штрихом (‘). В виде функции уравнение будет выглядеть следующим образом: «f»(x) = f’ − f». В виде уравнения это будет что-то вроде «y» = y’ − y». Обратите внимание, что в обоих случаях часть «(x)» не следует добавлять в члены низшего порядка (то есть следует вводить «f'(x) = −f», а не «f'(x) = −f(x)»).Справа от всех полей ввода уравнений имеется кнопка. При её нажатии откроется диалоговое окно Редактор выражений, в котором находится:
Ряд отсутствующих на обычной клавиатуре математических символов, которые можно использовать в уравнениях.
Список определённых пользователем постоянных и кнопка для их редактирования.
Список предустановленных функций. Обратите внимание, что если фрагмент текста уже выбран, то при вставке функции он будет использован в качестве её аргумента. Например, если в уравнении «y = 1 + x» выбран текст «1 + x», а затем указана функция синуса, то уравнение примет вид « y = sin(1+x)».
Функции в декартовой системе координат
Для указания явно заданной функции (например, функции вида y=f(x)) просто введите её в следующем виде:
f(x) = выражение, где:
f— имя функции, определяемое в виде строки с буквами и цифрами.x— горизонтальная координата для использования в выражении после знака равенства. Это мнимая переменная, поэтому можно использовать любое название переменной, результат останется таким же.выражение— выражение для построения графика, записанное согласно синтаксису, принятому в KmPlot. Подробнее: «Математический синтаксис».
Параметрические функции
Параметрическими функциями называются функции, в которых координаты x и y определяются отдельными функциями от другой переменной, обычно называемой t.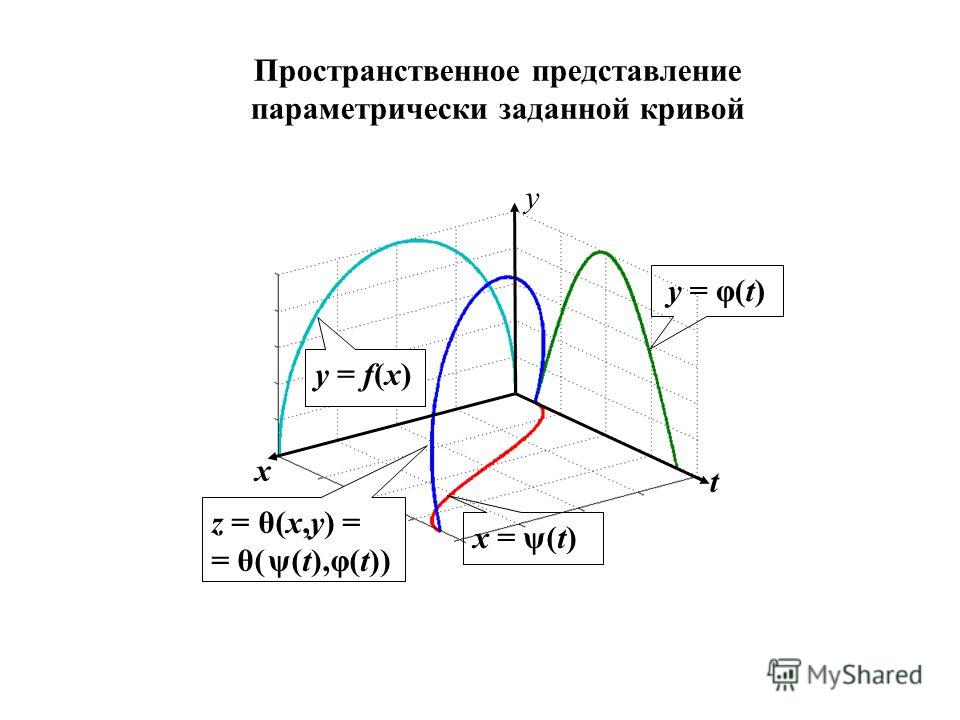
Чтобы задать параметрическую функцию, выполните для функций x и y те же действия, что и для функции в декартовых координатах. Как и в случае функций в декартовых координатах, для параметра возможно использовать любое название переменной.
Например, требуется нарисовать круг с параметрическими уравнениями x = sin(t), y = cos(t). После создания параметрического графика укажите соответствующие уравнения в полях для x и y, например f_x(t)=sin(t) и f_y(t)=cos(t).
В редакторе функций возможно установить некоторые дополнительные параметры графика:
- Мин.:, Макс.:
Эти параметры управляют диапазоном параметра t, для которого строится график функции.
Функции в полярной системе координат
Полярная система координат представляет точку по её расстоянию от начала координат (обычно называемому r) и углу между прямой, проходящей через точку и начало координат, и осью абсцисс (обычно представляемому греческой буквой «тета» — θ).
2 = 25
Дифференциальные функции
KmPlot позволяет строить графики явных дифференциальных функций. Они заданы уравнениями вида y(n) = F(x,y’,y»,…,y(n−1)), где yk — k-я производная функции y(x). KmPlot может устанавливать порядок производной только по количествуштрихов, записанных после названия функции. Например, для построения синусоидальной кривой можно использовать дифференциальное уравнение y'' = − y или f''(x) = −f.
Тем не менее, самого дифференциального уравнения недостаточно для построения кривой-решения. Каждая кривая в области построения генерируется комбинацией дифференциального уравнения и начальных условий. Чтобы изменить начальные условия, перейдите на вкладку Начальные условия после задания самого дифференциального уравнения. Количество столбцов доступных для редактирования начальных условий зависит от порядка дифференциального уравнения.
В редакторе функций возможно установить некоторые дополнительные параметры графика:
- Шаг:
Параметр шага в поле точности используется при численном решении дифференциального уравнения (с помощью метода Рунге — Кутты). Его значение — максимальный используемый размер шага; возможно использовать меньшее значение шага при достаточном увеличении части графика.
Справка онлайн — Справка Origin
Все книгиКниги, не связанные с программированием Руководство пользователя Учебники Быстрая справка Справка OriginКниги по программированию X-Function Origin C LabTalk Programming Python Python (внешний) Automation Server LabVIEW VI Приложения Разработка приложений Code Builder Лицензия Orlab 9 gMOCA0012 | ||||||||
Содержание
ПараметрПараметрУкажите параметр. ОчкиУкажите количество точек данных для отображения на графике функции. От и доУкажите начало и конец диапазона параметров. X(t) и Y(t)Введите здесь формулу параметров X и Y. Общие математические и статистические функции распределения доступны при нажатии кнопки треугольника справа от текстовых полей X(t) и Y(t) . Подробную информацию об этих функциях см. во встроенных функциях LabTalk. Кроме того, вы можете ввести функцию прямо в текстовое поле, используя любые операторы, распознаваемые Origin. Для умножения необходимо включить оператор умножения (*). Если нажать кнопку «Показать в отдельном окне» под треугольной кнопкой, откроется новое диалоговое окно Y(x)= с более широким полем ввода и панелью предварительного просмотра. На панели предварительного просмотра отображается столбец, рассчитанный по заданной вами формуле. Вы можете проверить результат и при необходимости отредактировать формулу в поле ввода. ОпределениеОпределите имена и значения переменных. Эти переменные можно использовать в определении функции. Если переменная еще не определена, но используется в теле функции, она будет выделена красным цветом. Показать сценарий LabTalkУстановите этот флажок, чтобы определить переменные с помощью сценариев LabTalk. Если вы уже определили некоторые переменные в таблице  В дополнение к встроенным функциям или функциям, определяемым пользователем, здесь поддерживаются любые сценарии LabTalk. Вы можете использовать переменные диапазона, строковые переменные, циклы и X-функции, доступные в LabTalk. Сценарии, введенные здесь, будут выполняться перед определением формулы.
График выходной функции Раскрывающийся список параметров в левом нижнем углу используется для указания способа вывода кривой графика функции, Создать новый график , Добавить в активный график или Добавить в активный график и изменить масштаб .
| ||||||||
Английский | немецкий |日本語
Wolfram|Alpha Примеры: чертежи и графика
Ого! Wolfram|Alpha не работает без JavaScript.
Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.