Плоскопараллельное перемещение треугольника: 7.3 Плоскопараллельное перемещение

Метод плоскопараллельного перемещения

В начертательной геометрии метод плоскопараллельного перемещения используется, как правило, для определения натуральных величин плоских фигур, отрезков и углов.

Свойства плоскопараллельного перемещения:

1. При перемещении любой фигуры параллельно плоскости проекции, проекция фигуры на эту плоскость остается неизменной.
2. При перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. На рисунке ниже точки C» и D», следуя этому свойству, заняли положение C»₁ и D»₁.
3. При перемещении точки параллельно фронтальной плоскости проекции, её горизонтальная проекция движется по прямой, параллельной оси X.

Пример 1

Рассмотрим перевод произвольно расположенного отрезка CD в положение, параллельное горизонтальной плоскости проекций П₂.

• Используя первое свойство параллельного перемещения, на любом свободном месте чертежа строим отрезок C’ ₁D’₁ = C’D’.
• По линиям связи определяем недостающие проекции C»₁ и D»₁. Стрелками показано перемещение точек C» и D» параллельно оси X в соответствии со вторым свойством рассматриваемого метода.

Пример 2

Следующий рисунок иллюстрирует перевод отрезка MN в проецирующее положение по отношению к фронтальной плоскости проекций П₂. В общем случае для решения подобной задачи необходимо дважды воспользоваться методом плоскопараллельного перемещения.

• После первого преобразования отрезок MN займет положение параллельно плоскости П₁. Сначала строится M»₁N»₁ = M»N» на произвольном месте чертежа, после чего по линиям связи находятся недостающие проекции M’₁ и N’₁.
• Второе преобразование заключается в параллельном переносе горизонтальной проекции отрезка M’₁N’
  1 в положение M’₂N’₂, перпендикулярное оси X. После этого точки M»₂ = N»₂ определяются по линиям связи.

Определение натуральной величины треугольника

Рассмотрим порядок плоскопараллельного перемещения треугольника ABC с целью определения его натуральной величины.

1. Через точку С треугольника ABC проводим горизонталь CD. Находим её недостающие проекции.
2. Переводим ABC в положение, перпендикулярное фронтальной плоскости проекций. Для этого строим C’₁D’₁ = C’D’ перпендикулярно оси X. В соответствии с первым свойством плоскопараллельного перемещения достраиваем треугольник A’₁B’₁C’₁ = A’B’C’. По линиям связи определяем точки A»₁, B»₁, C»₁.
3. Перемещаем проекцию A»₁B»₁C»₁ треугольника ABC в положение A» ₂B»₂C»₂, параллельное оси X, соблюдая равенство A»₂B»₂C»₂ = A»₁B»₁C»₁. По линиям связи определяем точки A’₂, B’₂, C’₂. Теперь треугольник ABC расположен параллельно горизонтальной плоскости проекций и проецируется на неё в натуральную величину A’₂B’₂C’₂.

Определение расстояния между параллельными прямыми

Расстояние между двумя параллельными прямыми равно длине перпендикуляра, опущенного из произвольной точки первой прямой на вторую прямую. Рассмотрим, как указанное расстояние определяется на практике с помощью метода плоскопараллельного перемещения.

Путем двух последовательных преобразований прямые a и b переводятся в положение, перпендикулярное горизонтальной плоскости. Таким образом, они проецируются на неё в точки A’

2 и B’₂, расстояние между которыми является искомым. Показанные на рисунке величины d₁ и d₂ являются вспомогательными для выполнения построений согласно свойствам плоскопараллельного перемещения.

---

Заказать чертеж

Способ плоскопараллельного перемещения

Положения:

Плоскопараллельным перемещением называется такое перемещение,    при    котором    все    точки    перемещаются    в

параллельных плоскостях. При таком перемещении движется сам предмет, плоскости  проекций остаются неподвижными.

Способ   вращения без указания осей, радиусов и центров вращения (при этом соблюдаются все свойства и правила) можно рассматривать     как     частный     случай     плоскопараллельного

перемещения.

План решения и построения:

1. Переместим плоскость, заданную треугольником АВС, из общего  положения в  частное  проецирующее положение, чтобы

одна из ее проекций стала прямой линией.

2. Вторым перемещением плоскость треугольника приведем в положение  плоскости  уровня,  тогда  одна  из  проекций треугольника будет в натуральную величину.

Построение:

1. В проекциях  ∆   АВС через вершину С проводим проекции

горизонтали H (h3, h2) (рис.6, этап 1).

2. Перемещаем проекцию  ∆    А1В1С1  в новое положение так,

чтобы h2 расположилась вертикально, при этом размеры проекции

остаются   неизменными.   При   таком   положении   горизонтали

заданная  плоскость  стала  фронтально  проецирующей  и  на  π2

спроецировалась отрезком прямой – В2С2 А2 (рис.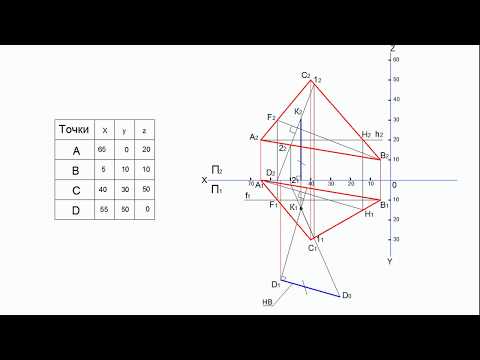 6, этап 2).

3. Перемещаем В2С2 А2 параллельно оси Х В2С2А2 (рис. 6, этап

3).

4. После          перемещения плоскость       треугольника

стала горизонтальной плоскостью уровня и проекция ∆   А1В1С1  

натуральная величина ∆   АВС (рис. 6, этап 3).

Алгоритм решения:

Рис. 6.

1.   Через вершину С ∆   АВС проводим H (h3, h2).

2.   Перемещаем ∆   А1В1С1   в положение, когда h2  ⊥  оси Х ∆   А

В С ⊥ π2  ⇒ В2С2 А2 прямая линия.

3.   Перемещаем | В2С2 А 2 | В2С2 А2 ║ оси Х. ∆   А1 В1 С1  н.в.

Задачу можно решить по аналогии, если начать с построения фронтали  F  и  перемещать фронтальную проекцию  ∆    АВС  до

горизонтально проецирующего положения.

СПИСОК ЛИТЕРАТУРЫ

1.  Гордон, В.О. Курс начертательной геометрии : учебное пособие для вузов / В.О. Гордон, М.А. СеменцовОгиевский; под. ред. В.О.  Гордона, Ю.Б. Иванова. – М. : Высшая школа, 1998. – 272 с.

2.  Кузнецов, Н.С. Начертательная геометрия : учебник для вузов / Н.С. Кузнецов. М. : Высшая школа, 1981. – 262 с.

3.   Павлова,  А.А.  Начертательная  геометрия  :  учебник  для вузов / А.А. Павлова. – М. :, 2001. – 304 с.

4. Расчетно-графические    работы    по    начертательной геометрии. Эпюр №2 : методические указания / Р.К. Низамов, Д.Н. Латыпов, Г.Ф. Гайсина. Казань : Изд-во Казан. гос. технол. ун-та, 1991. 12 с.

5.   Чекмарев,  А.А.  Начертательная  геометрия  и  черчение  :

учебник  для  студентов  вузов  /  А.А.  Чекмарев.   М.  :

ВЛАДОС, 1999. – 471 с.

6.   Эпюр №1 : методические указания / Г.Ф. Гайсина, Д.Н.

Латыпов,  Р.К.  Низамов.  –  Казань  :  Изд-во  Казан.  гос.

технол. ун-та, 1989. — 12 с.

Материал взят из книги Начертательная геометрия.

Натуральная величина плоской фигуры (Маркова О.А.)

дифференциальная геометрия — уравнения параллельного переноса

спросил 5 лет, 8 месяцев назад

Изменено 5 лет, 8 месяцев назад

Просмотрено 4к раз

$\begingroup$

У меня есть вопрос о параллельном транспорте, в котором я очень запутался, и был бы признателен за помощь. Вопрос звучит так: 93$ вращается вокруг оси $z$ как потоки? Орбиты этих потоков были бы линиями широты. Решите уравнения параллельного переноса $\nabla_X(V_i)=0$, для $V_1, V_2$ элементов базиса касательной плоскости, вдоль кривой широты 45 градусов. К чему возвращаются $V_i$ после того, как их перевезли по всему кругу?

Меня смущает, о каком векторном поле идет речь в вопросе. Будет ли это поле просто сферой, параметризованной как:

$$(x,y,z) = (r\cos(\theta)\sin(\varphi), r\sin(\theta)\sin(\varphi), r\cos(\varphi))$$ Где $\varphi$ постоянна?

• дифференциальная геометрия
• векторные поля
• сферическая геометрия
• градиентные потоки

$\endgroup$

13

$\begingroup$

Это не прямой ответ на ваш вопрос об уравнениях параллельного переноса, а стандартное геометрическое решение. Предполагая единичную сферу, параллельный перенос вокруг широты $L_{\varphi}$, составляющий угол $\varphi$ с экватором, можно найти, построив касательный к сфере конус вдоль $L_{\varphi}$, а затем разрезав конус вдоль генератора, прокатывая его по плоскости и выполняя параллельный перенос касательного вектора по дуге окружности.

Элементарная геометрия показывает, что развернутый конус представляет собой сектор круга радиуса $\cot\varphi$, центральный угол которого равен $2\pi\sin\varphi$. Параллельный перенос вокруг $L_{\varphi}$ в северном полушарии поворачивает вектор по часовой стрелке (смотрящий «вниз» на касательную плоскость, к центру сферы) на угол $2\pi\sin\varphi$. Анимация представляет собой панорамирование сферы по полному кругу.

$\endgroup$

1

$\begingroup$

Для точек на экваторе. вы можете обнаружить, что все эллипсоиды, присутствующие в северном полушарии, проявляют одинаковую интегральную сумму векторного ускорения вокруг регулярной поверхности. их транспорт должен быть похож на круговой транспорт на экваторе. это тот случай, когда транспорт с некоторым местоположением a (t)i что интегральная сумма ускорений больше, чем расстояние вокруг мира на экваторе, поэтому он не похож.

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

векторов — Расстояние от начала координат до плоскости.

спросил 6 лет, 9 месяцев назад

Изменено 1 месяц назад

Просмотрено 54к раз

$\begingroup$

Вопрос, на котором я застрял, заключается в следующем.

Предположим, что плоскость имеет декартово уравнение $3x+ 2y-6z=12$. Найдите расстояние от начала координат до плоскости. 9{\circ}$, но я не знаю, как это сделать.

$\textbf{Если бы я использовал угол, который я вычислил}$, чтобы найти расстояние, кто-нибудь мог бы посоветовать мне, как это сделать?

Заранее большое спасибо за любые идеи и извините за тривиальный вопрос или любые ошибки в маркировке тегов.