Перенос точек на чертеже: 1.4. Точка на комплексном чертеже

1.4. Точка на комплексном чертеже

Поскольку положение точки в пространстве однозначно определяется тремя координатами, а каждая из проекций задает значение двух координат, то легко сделать вывод, что положение точки в пространстве однозначно определяется двумя любыми проекциями.

Кроме того, каждая пара проекций связана какой либо координатой. Так, проекции A'(x,y) и A»(x,z) связаны координатой x, проекции A»(x,z) и A»‘(y,z) – координатой z, а A'(x,y) и A»‘(y,z) – координатой y.

Таким образом, можно отметить, что при любых значениях координат точки (как положительных, так и отрицательных) справедливо следующее утверждение:

а) горизонтальная и фронтальная проекции точки однозначно определяют положение точки в пространстве и, поскольку связаны координатой x, лежат на одной прямой (линии проекционной связи), перпендикулярной оси X (рис. 1.14).

б) фронтальная и профильная проекции точки однозначно определяют положение точки в пространстве и, поскольку связаны координатой z, лежат на одной прямой (линии проекционной связи), перпендикулярной оси Z (рис.

1.15).

в) горизонтальная и профильная проекции точки однозначно определяют положение точки в пространстве и, поскольку связаны координатой y, лежат на одной прямой (линии проекционной связи), перпендикулярной раздвоенной оси Y (рис. 1.16).

На рис. 1.17 построены проекции точки М, у которой координата z равна нулю. Это означает, что, поскольку координата z задает удаление точки от горизонтальной плоскости проекций, заданная точка М лежит в горизонтальной плоскости проекций. В этом случае на чертеже могут быть указаны не только проекции точки, но и сама точка, совпадающая со своей горизонтальной проекцией.

Рис. 1.18 иллюстрирует проекции точки N, находящейся на оси X, так как ее координаты y и z имеютнулевыезначения. Здесьсовпадаютгоризонтальная, фронтальнаяпроекцииточкиисаматочкаN.

И, наконец, отметим, что рассмотренный комплексный чертеж является обратимым, так как позволяет решать как прямую задачу (по заданным координатам построить проекции точки), так и обратную (по заданным проекциям определить координаты точки).

Исходными данными для прямой задачи являются координаты точки, заданные в виде последовательности трех чисел (координат x, y и z), заключенных в скобки.

Например, необходимо построить проекции точки A(20,15,25) (рис. 1.19,а). Рекомендуется следующий порядок построения. Сначала строится фронтальная проекция точки по координатам x=20, z=25 (рис. 1.19,б), затем по координатам x=20, y=15 – горизонтальная проекция точки (рис. 1.19,в). Обратите внимание, что для горизонтальной проекции ось Y направлена вниз.

Профильная проекция точки строится по координатам y=15, z=25, при этом ось Y направлена вправо (рис. 1.19,г). На рис. 1.20 приведены результаты построения проекций точки B, находящейся во II октанте, а на рис. 1.21 – точки C, которая находится в VI октанте.

Обратная задача – по заданным проекциям определить координаты точки. Для этого обычно задают две проекции точки, а задачу дополняют требованием построить недостающую проекцию. Рассмотрим такую задачу на примере точки D, две проекции которой заданы на рис. 1.22,а. По фронтальной проекции точки определяются координаты x и z (рис. 1.22,б), а по горизонтальной проекции – координата y (рис. 1.22,в), которая указывается вдоль оси yπ1 . У точки D координата

x > 0, y < 0, z < 0 – точка лежит в III октанте. Для построения недостающей профильной проекции необходимо координату y отложить на оси yπ3 и построить D′′′ по координатам y и z (рис. 1.22,г).

Одним из этапов построения чертежа является перенос координаты y между осями yπ1 и yπ3 (мы помним, что в пространстве ось Y всего одна). В рассмотренных выше примерах этот пе-

ренос осуществлялся с помощью дуги окружности, центр которой находится в начале координат. На рис. 1.23 вместо дуги использовалась ее хорда. На рис. 1.24,а для переноса координаты y использовалась прямая k0, называемая постоянной прямой эпюра Монжа. Эта прямая проходит через начало координат под углом 45°.

Обратите внимание, что линии проекционной связи на чертеже, где использована постоянная прямая эпюра Монжа, образуют в общем случае прямоугольник (рис. 1.24,б), причем в ряде случаев оси системы координат не изображаются, образуя безосный чертеж (рис. 1.24,в). Такие чертежи используют, когда нет необходимости задавать точное положение геометрического объекта относительно плоскостей проекций. Если при работе с безосным чертежом возникнет необходимость провести ось, то это можно сделать где угодно, помня о направлении.

При использовании на безосном чертеже постоянной прямой эпюра Монжа необходимо иметь в виду, что такая прямая на чертеже может быть только одна (рис. 1.25).

6.2.2. Задание поверхности вращения на чертеже. Точки и линии на поверхности

На чертеже поверхность изображают очеркомпроекций поверхности или её отдельных частей.

Задать поверхность на чертеже – значит указать условия, позволяющие построить каждую точку этой поверхности.

Точка принадлежит поверхности, если она находится на линии, принадлежащей данной поверхности.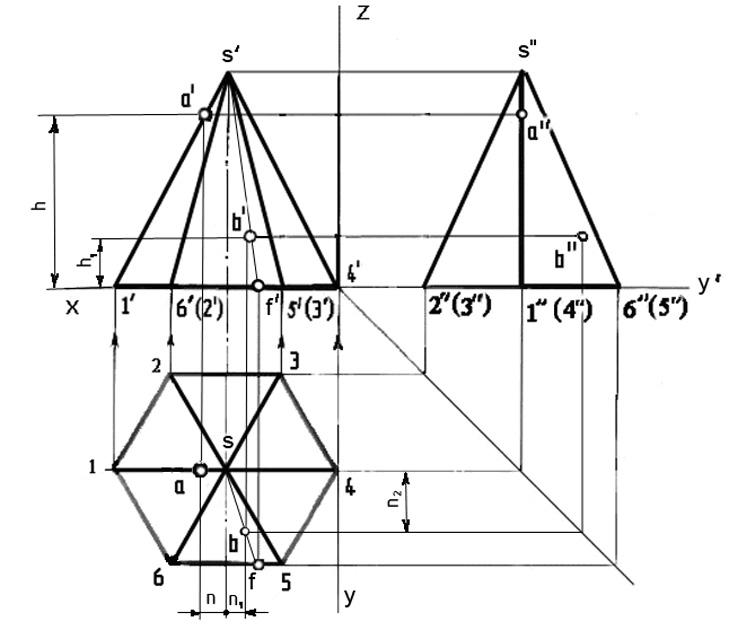 Рассмотрим чертёж конуса и точки, принадлежащие его поверхности (рис. 6.6). Фронтальная проекция конуса задана очерковыми образующими, определяющими границы поверхности, а горизонтальная – проекцией основания конуса. Каркас конуса – это совокупность образующих прямых линий, соединяющих их вершинуSи основание конуса и совокупность параллелей – окружностей различного радиуса, плоскость которых перпендикулярна оси конуса.

Рис. 6.6.

Рассмотрим ряд точек на боковой поверхности конуса. Точка Арасположена на очерковой образующей конуса, её горизонтальная проекция находится на линии связи, на оси конуса. Обратим внимание, что очерковая образующая является фронталью, т.е. её фронтальная проекция натуральная величина образующей конуса.

Принадлежность точек ВиСповерхности конуса определяется соответственно с помощью параллели радиусаRили образующей конуса (S₁).

6.2.3. Позиционные задачи на пересечение поверхности с прямой линией и плоскостью

В общем случае пересечения поверхности с плоскостью является кривая линия.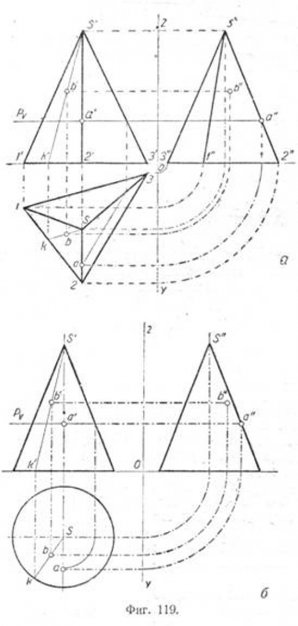

Рассмотрим конические сечения фронтально проецирующимися плоскостями и горизонтальной плоскостью уровня (рис. 6.7) Обозначим угол наклона образующей к оси конуса - а угол наклона следа плоскости -. В зависимости от угла наклона плоскости линией сечения может быть окружность, эллипс, парабола, гипербола. Если:

 = 90, линия сечения — окружность,

 > - эллипс,

 = - парабола,

 < - гипербола.

Если секущая плоскость проходит через вершину конуса, то сечением является треугольник.

Задача: Построить линию сечения конуса фронтально проецирующей плоскостью(рис. 6.8).

Решение: Линией сечения в данном случае будет неполны эллипс т.к. угол наклона плоскости  к оси конуса больше угла наклона образующей. Фронтальная проекция линии сечения совпадает со следом плоскости, т.к. секущая плоскость является фронтально проецирующей. Определим горизонтальную проекцию сечения. Первоначально отметим опорные точки – точка 1 на очерковой образующей является высшей точкой сечения, точки 2 и 3 на основании конуса – низшие точки.

Ряд промежуточных точек 4, 5, 6, 7 определяем с помощью параллелей конуса, проведённых через эти точки. Точки 8, 9 определены через образующую конуса. Полученные точки плавно соединяем с учётом видимости.

Рис. 6.7. Сечение конуса.

Рис. 6.8.

Задача:Определить точки пересечения прямойас конусом (рис. 6.9).

Решение:Для решения задачи выгоднее всего использовать вспомогательную плоскость, проходящую через вершину конуса. Для этого дополним прямуюадо плоскости прямойb,

Рис. 6.9. Пересечение прямой с конусом.

пересекающейся с ней в точке 1 (рис. 6.9). Определим горизонтальный след вспомогательной плоскости (аb). Для этого найдём следы прямыхаиb–МиМ¹. Отметим точки пересечения основания конуса с горизонтальным следом₁– точкиАиВ. Определилась линия сечения конуса со вспомогательной плоскостью – это треугольник

АВS.

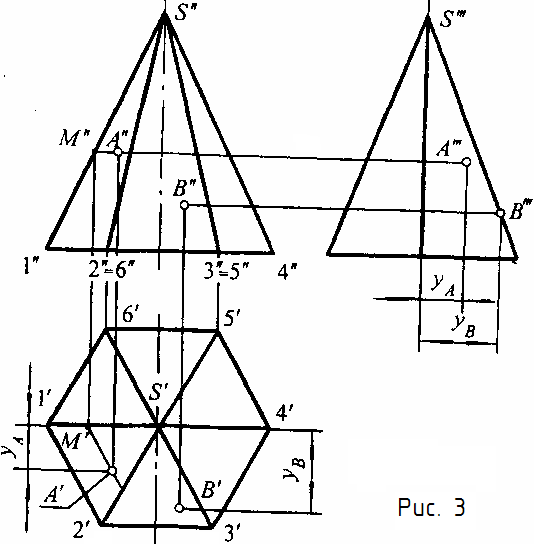
На пересечении линии сечения A₁B₁S₁и проекции прямойа₁находим искомые точкиK₁иL₁, по линиям связи —K₂иL₂. Затем определяем видимость прямой относительно точек пересечения.

ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ И ОСНОВНЫЕ ВИДЫ ЧЕРТЕЖА — Мегаобучалка

 

Рассмотрим основные принципы прямоугольного проецирования и способ получения ортогонального чертежа в системе трех плоскостей проекций. На рис. 4.8, а показано расположение трех плоскостей проекций, с помощью которых получают ортогональный чертеж. Плоскости располагаются под углом 90° друг к другу.

Плоскость H — горизонтальная плоскость проекций, плоскость V — фронтальная плоскость проекций, плоскость W — профильная плоскость проекций.

Рис. 4.8.

 

Линии пересечения плоскостей проекций называются осями проекций, или осями координат и обозначаются Ox, Оу, Oz.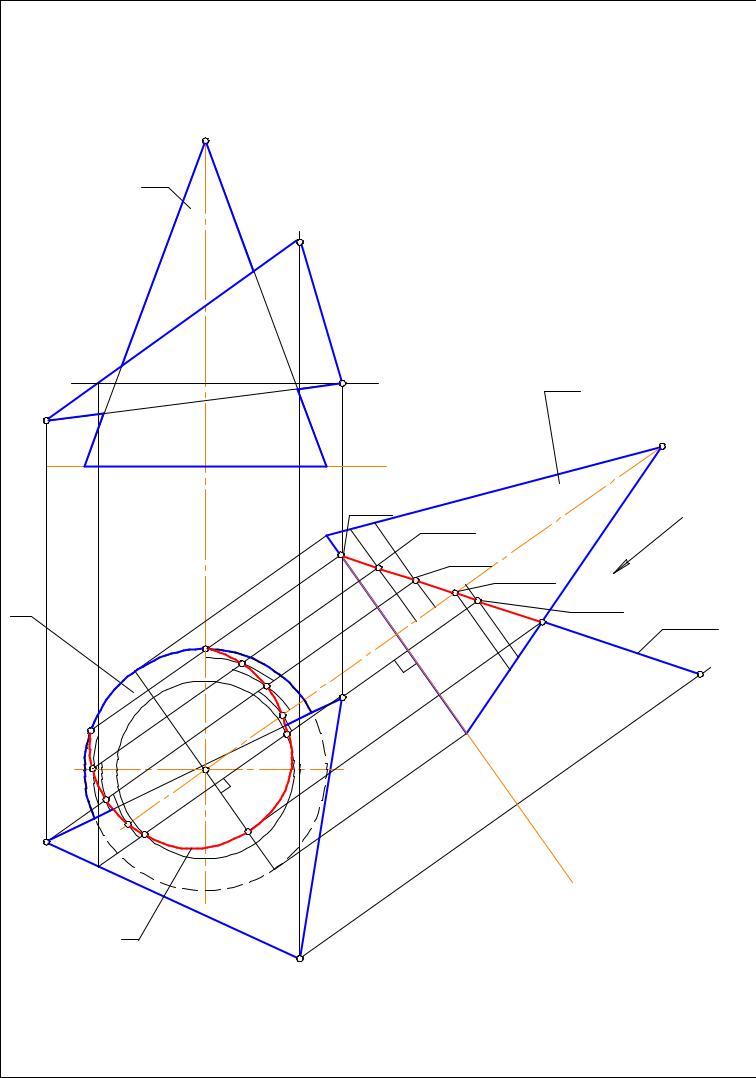 Точка пересечения трех осей координат (точка О) является началом координат, т.е. точкой, от которой ведется отсчет координат по осям Ox, Qy, Oz. Угол, образованный тремя плоскостями проекций, называют координатным у г л о м, так как плоскости проекций являются базами отсчета расстояний (координат) и ограничивают пространство плоскостями проекций, в котором располагают проецируемые предметы.

 

 

Помещая изображаемый (проецируемый) предмет (геометрическая фигура, модель, деталь и т.п.) в определенное положение относительно плоскостей проекций V. Н и W, фиксируют его положение относительно этих плоскостей, что дает возможность получить взаимосвязанные изображения данного предмета, по которым легко представить его положение в пространстве, его форму. Каждое изображение (проекция) предмета на плоскость отображает то, что мы видим при взгляде на предмет в определенном направлении. Чтобы получить представление о форме предмета, обычно недостаточно рассмотреть предмет с какой-то одной стороны.

Проецируя предмет в системе трех плоскостей проекций, его рассматривают с трех сторон, в направлениях, перпендикулярных трем плоскостям проекций.

Получив проекции предмета на трех плоскостях проекций, плоскости координатного угла развертывают в одну плоскость, как показано на рис. 4.8,б. При этом плоскости H и W условно разрезают по оси Оу, плоскость H поворачивают вокруг оси Ох, а плоскость W — вокруг оси Oz, получают одну общую плоскость — плоскость чертежа. При этом ось Оу как бы разрезаемся пополам. Одна ее «половина» оказывается в плоскости H и располагается перпендикулярно оси Ох, а другая — в плоскости W и располагается перпендикулярно оси Oz. Совмещенные плоскости проекций разделяются взаимно перпендикулярными осями, которые определяют на чертеже рабочее поле для построения проекций предмета. Каждая плоскость проекций имеет два измерения по взаимно перпендикулярным направлениям. Для плоскости Н — это оси Ох и Оу, для плоскости V — оси Oz и Оx:, для плоскости W -оси Oz и Оу.

Изображения, полученные на плоскостях координатного угла и совмещенные в одну плоскость, называют эпюром или ортогональным чертежом.

Проекции изделия на различные плоскости прямоугольной проекции представлены на Рис. 4.9 и 4.10

 

Рис. 4.9

 

Рис. 4.10

 

Основными видами чертежа изделия являются изображения его проекций на фронтальную (1 – главный вид спереди), горизонтальную (2 – вид сверху) и профильную (3 – вид с боку — слева) плоскости прямоугольной проекции. Изображение детали в этих плоскостях представлено на рис. 4.11.

Рис. 4.11.

 

Рассмотрим построение эпюры точки.

ПРОЕКЦИИ ТОЧКИ

Проецирование точки на три плоскости проекций координатного угла начинают с получения ее изображения на плоскости H — горизонтальной плоскости проекций. Для этого через точку А (рис. 4.12, а) проводят проецирующий луч перпендикулярно плоскости H.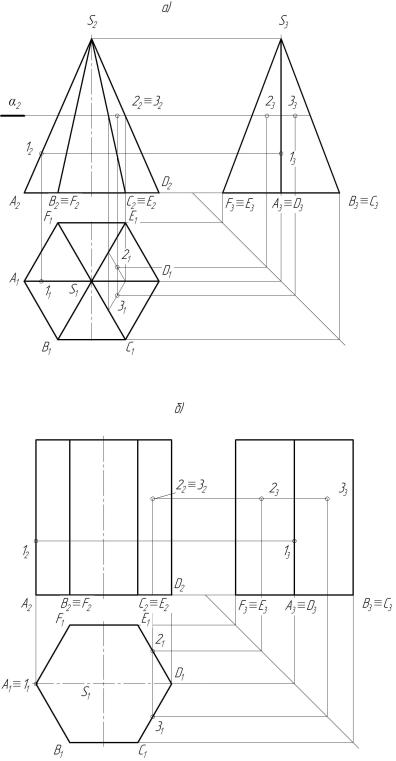

На рисунке перпендикуляр к плоскости Н параллелен оси Oz. Точку пересечения луча с плоскостью Н (точку а) выбирают произ­вольно. Отрезок Аа определяет, на каком расстоянии находится точка А от плоскости Н, указывая тем самым однозначно положение точки А на рисунке по отношению к плоскостям проекций. Точка а является прямоугольной проекцией точки А на плоскость Н и называется горизонтальной проекцией точки А (рис. 4.12, а).

 

в)

Рис. 4.12.

 

Для получения изображения точки А на плоскости V (рис. 4.12,б) через точку А проводят проецирующий луч перпендикулярно фронтальной плоскости проекций V. На рисунке перпендикуляр к плоскости V параллелен оси Оу. На плоскости Н расстояние от точки А до плоскости V изобразится отрезком аа_х, параллельным оси Оу и перпендикулярным оси Ох. Если представить себе, что проецирующий луч и его изображение проводят одновременно в направлении плоскости V, то когда изображение луча пересечет ось Ох в точке а_х, луч пересечет плоскость V в точке а’. Проведя из точки а_х в плоскости V перпендикуляр к оси Ох, который является изображением проецирующего луча Аа на плоскости V, в пересечении с проецирующим лучом получают точку а’. Точка а’ является фронтальной проекцией точки А, т. е. ее изображением на плоскости V.

Изображение точки А на профильной плоскости проекций (рис. 4.12, в) строят с помощью проецирующего луча, перпендикулярного плоскости W. На рисунке перпендикуляр к плоскости W параллелен оси Ох. Проецирующий луч от точки А до плоскости W на плоскости Н изобразится отрезком аа_у, параллельным оси Ох и перпендикулярным оси Оу. Из точки Оу параллельно оси Oz и перпендикулярно оси Оу строят изображение проецирующего луча аА и в пересечении с проецирующим лучом получают точку а». Точка а» является профильной проекцией точки А, т. е. изображением точки А на плоскости W.

Точку а» можно построить, проведя от точки а’ отрезок а’а_z (изображение проецирующего луча Аа» на плоскости V) параллельно оси Ох, а от точки а_z — отрезок а»а_z параллельно оси Оу до пересечения с проецирующим лучом.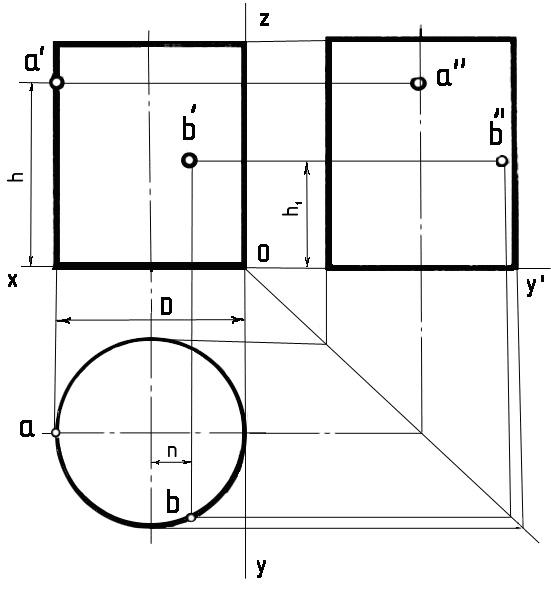

Получив три проекции точки А на плоскостях проекций, координатный угол развертывают в одну плоскость, как показано на рис. 4.11,б, вместе с проекциями точки А и проецирующих лучей, а точку А и проецирующие лучи Аа, Аа’ и Аа» убирают. Края совмещенных плоскостей проекций не проводят, а проводят только оси проекций Oz, Оу и Ох, Оу₁ (рис. 4.13).

Анализ ортогонального чертежа точки показывает, что три расстояния — Аа’, Аа и Аа» (рис. 4.12, в), характеризующие положение точки А в пространстве, можно определить, отбросив сам объект проецирования — точку А, на развернутом в одну плоскость координатном угле (рис. 4.13). Отрезки а’а_z, аа_y и Оа_х равны Аа» как противоположные стороны соответствующих прямоугольников (рис. 4.12,в и 4.13). Они определяют расстояние, на котором находится точка А от профильной плоскости проекций. Отрезки а’а_х, а»а_у1 и Оа_у равны отрезку Аа, определяют расстояние от точки А до горизонтальной плоскости проекций, отрезки аа_х, а»а_z и Оа_y1 равны отрезку Аа’, определяющему расстояние от точки А до фронтальной плоскости проекций.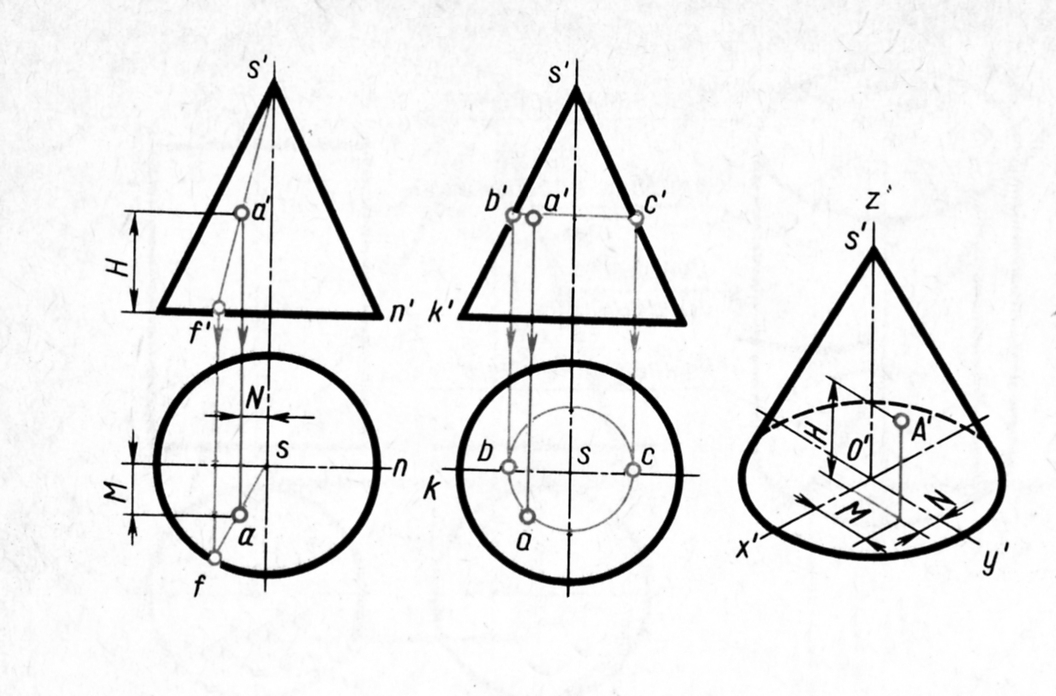

Рис. 4.13.

 

Отрезки Оа_х, Оа_у и Оа_z, расположенные на осях проекций, являются графическим выражением размеров координат X, Y и Z точки А. Координаты точки обозначают с индексом соответствующей буквы. Измерив величину этих отрезков, можно определить положение точки в пространстве, т. е. задать координаты точки.

На эпюре отрезки а’а_х и аа_х располагаются как одна линия, перпендикулярная к оси Ох а отрезки а’а_z и a»a_z — к оси Оz. Эти лини называются линиями проекционной связи. Они пересекают оси проекций в точках а_х и а_z соответственно. Линия проекционной связи, соединяющая горизонтальную проекцию точки А с профильной, оказалась «разрезанной» в точке а_у.

Две проекции одной и той же точки всегда располагаются на одной линии проекционной связи, перпендикулярной к оси проекций.

Для представления положения точки в пространстве достаточно двух ее проекций и заданного начала координат (точка О) На рис. 4.14, б две проекции точки полностью определяют ее положение в пространстве По этим двум проекциям можно построит профильную проекцию точки А. Поэтому в дальнейшем, если не будет необходимости в профильной проекции, эпюры будут построены на двух плоскостях проекций: V и Н.

Рис. 4.14. Рис. 4.15.

 

Рассмотрим несколько примеров построения и чтения чертежа точки.

Пример 1. Определение координат точки J заданной на эпюре двумя проекциях (рис. 4.14). Измеряются три отрезка: отрезок Ов_Х (координата X), отрезок b_Хb (координата Y) и отрезок b_Хb’ (координата Z). Координаты записывают в следующем п рядке: X, Y и Z, после буквенного обозначения точки, например, В20; 30; 15.

Пример 2. Построение точки по заданным координатам. Точка С задана координатами С30; 10; 40. На оси Ох (рис. 4.15) находят точку с_х, в которой линия проекционной связи пересекает ось проекций. Для этого по оси Ох от начала координат (точка О) откладывают координату X (размер 30) и получают точку с_х. Через эту точку перпендикулярно оси Ох проводят линию проекционной связи и от точки вниз откладывают координату У (размер 10), получают точку с — горизонтальную проекцию точки С. Вверх от точки с_х по линии проекционной связи откладывают координату Z (размер 40), получают точку с’ — фронтальную проекцию точки С.

 

Рис. 4.16.

Пример 3. Построение профильной проекции точки по заданным проекциям. Заданы проекции точки D — d и d’. Через точку О проводят оси проекций Oz, Oy и Оу₁ (рис. 4.16, а). Для построения профильной проекции точки D отточки d’ проводят линию проекционной связи, перпендикулярную оси Oz, и продолжают ее вправо за ось Oz. На этой линии будет располагаться профильная проекция точки D. Она будет находиться на таком расстоянии от оси Oz, на каком горизонтальная проекция точки d располагается: от оси Ох, т. е. на расстоянии dd_x. Отрезки d_zd» и dd_x одинаковы, так как определяют одно и то же расстояние — расстояние от точки D до фронтальной плоскости проекций. Это расстояние является координатой У точки D.

Графически отрезок d_zd» строят перенесением отрезка dd_x с горизонтальной плоскости проекций на профильную. Для этого проводят линию проекционной связи параллельно оси Ох, получают на оси Оу точку d_y (рис. 4.16,б). Затем переносят размер отрезка Od_y на ось Оу₁, проведя из точки О дугу радиусом, равным отрезку Od_y, до пересечения с осью Оу₁ (рис. 4.16,б), получают точку dy₁. Эту точку можно построить и как показано на рис. 4.16, в, проведя прямую под углом 45° к оси Оу из точки d_y. Из точки d_y1 проводят линию проекционной связи параллельно оси Oz и на ней откладывают отрезок, равный отрезку d’d_x, получают точку d».

Перенос величины отрезка d_xd на профильную плоскость проекций можно осуществить с помощью постоянной прямой чертежа (рис. 4.16, г). В этом случае линию проекционной связи dd_y проводят через горизонтальную проекцию точки параллельно оси Оу₁ до пересечения с постоянной прямой, а затем параллельно оси Оу до пересечения с продолжением линии проекционной связи d’d_z.

Частные случаи расположения точек относительно плоскостей проекций

Положение точки относительно плоскости проекций определяется соответствующей координатой, т. е. величиной отрезка линии проекционной связи от оси Ох до соответствующей проекции. На рис. 4.17 координата У точки А определяется отрезком аа_х — расстояние от точки А до плоскости V. Координата Z точки А определяется отрезком а’а_х — расстояние от точки А до плоскости Н. Если одна из координат равна нулю, то точка расположена на плоскости проекций. На рис. 4.17 приведены примеры различного расположения точек относительно плоскостей проекций. Координата Z точки В равна нулю, точка находится в плоскости Н. Ее фронтальная проекция находится на оси Ох и совпадает с точкой b_х. Координата У точки С равна нулю, точка располагается на плоскости V, ее горизонтальная проекция с находится на оси Ох и совпадает с точкой с_х.

Следовательно, если точка находится на плоскости проекций, то одна из проекций этой точки лежит на оси проекций.

Рис. 4.17.

 

На рис. 4.17 координаты Z и Y точки D равны нулю, следовательно, точка D находится на оси проекций Ох и две ее проекции совпадают.

ПРОЕКЦИИ ПРЯМОЙ

 

При проецировании прямой на какую-либо плоскость проекций проецирующие лучи, проходящие через точки прямой, образуют проецирующую плоскость, которая пересекает плоскость проекции по прямой (рис. 4.18). Следовательно, проекцией отрезка будет отрезок прямой. Чаще всего проекция отрезка меньше самого отрезка, так как его проекция (ab) является частью катета прямоугольной: треугольника (ВbМ), а отрезок (АВ) — частью гипотенузы. Так как Mb < MB, то и ab<AB. Отношение проекции отрезка к его натуральной величине называют коэффициентом искажения.

Рис. 4.17.

Коэффициент искажения обозначают буквой К,

К= аb/AB ≤1

Если отрезок прямой параллелен плоскости проекций, при проецировании образуется прямоугольник, в котором сам отрезок и его проекция являются противоположными сторонами этого прямоугольника. Следовательно ВС=bс. В этом случае коэффициент искажения К= аb/AB =1, т. е. отрезок проецируется без искажения.

Положение прямой в пространстве можно определить двумя ее точками, поэтому, чтобы задать прямую на эпюре, достаточно задать проекции двух ее точек (рис. 4.18), т.е. проекции отрезка этой прямой. Данные проекции отрезка прямой полностью определяют положение прямой в пространстве.

 

Рис. 4.18.

Сравнивая координаты точек А и В, являющихся концами отрезка, можно представить себе, как располагается отрезок в пространстве. Точка В находится выше точки А относительно плоскости Н, так как b’b_х>а’а_х, т. е. ZB>ZA, и точка В ближе к плоскости V, чем точка А, так как bb_x<aa_x, т. е. YB<YA.

Различные случаи расположения прямых относительно плоскостей проекций

Прямая общего положения — прямая, не параллельная ни одной из плоскостей проекций (рис. 4.18), т.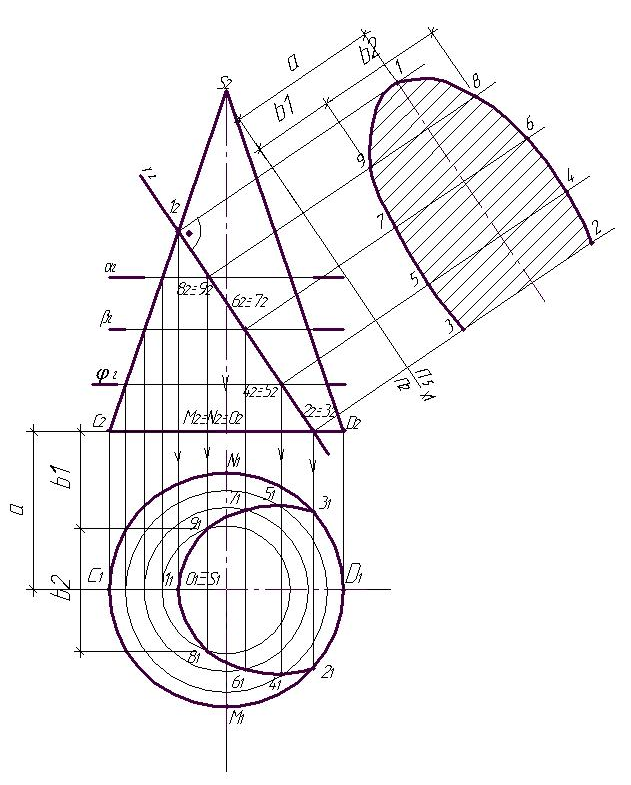 е. ни одна из проекций этой прямой не параллельна какой-либо оси проекций.

Горизонтальная прямая — прямая, параллельная плоскости Н. Все точки прямой находятся на одинаковом расстоянии от плоскости Н (рис. 4.19, а), т. е. координаты Z всех точек отрезка ВС равны между собой, ВЬ= = Сс — b’bx—c’cx — ZH = Zc- Фронтальная проекция горизонтальной прямой параллельна оси Ох (рис. 4.19,б). Положение второй проекции относительно оси Ох определяется положением самой прямой, Угол наклона горизонтальной прямой к плоскости V — р. На плос­кость Н отрезок горизонтальной прямой проецируется в натуральную величину.

Рис. 4.19.

 

Фронтальная прямая — прямая, параллельная плоскости V. Все точки прямой находятся на одинаковом расстоянии от плоскости V (рис. 4.20, а), т. е. координаты Y всех точек отрезка CD равны между собой. Горизонтальная проекция фронтальной прямой параллельна оси Ох (рис. 4.20,б). Положение второй проекции относительно оси Ох опреде­ляется положением самой прямой. Угол наклона фронтальной прямой к горизонтальной плоскости H равен α. На плоскость V отрезок фронтальной прямой проецируется в натуральную величину.

Рис. 4.20.

 

Профильная прямая — прямая, параллельная плоскости H. Все точки прямой находятся на одинаковом расстоянии от плоскости W (рис. 4.21,а), т. е. координаты X всех точек отрезка DE равны между собой. Фронтальная проекция профильной прямой параллельна оси Oz, а горизонтальная проекция — оси Оу (рис. 4.21,б). Положение профильной проекции определяется положением самой профильной прямой. Угол наклона профильной прямой к плоскости Н — α, к плоскости V — β. На плоскость W отрезок профильной прямой проецируется в натуральную величину.

 

Рис. 4.21.

Прямые, перпендикулярные одной из плоскостей проекций, называют проецирующими прямыми.

Горизонтально-проецирующая прямая перпендикулярна плоскости H. Проекция такой прямой на плоскости Н является точкой, а ее фронтальная проекция перпендикулярна оси Ох и параллельна оси Оz (рис. 4.22). На плоскость V прямая проецируется в натуральную величину.

Фронтально-проецирующая прямая перпендикулярна плоскости V. Проекция этой прямой на плоскость V является точкой, а ее горизонтальная проекция перпендикулярна оси Ох и параллельна оси Оу (рис. 4.23). На плоскость Н прямая проецируется в натуральную величину.

Профильно-проецирующая прямая перпендикулярна плоскости W. Проекция этой прямой на плоскость W является точкой. Ее горизонтальная проекция перпендикулярна оси Оу и параллельна оси Ох, а фронтальная — перпендикулярна оси Oz и параллельна оси Ох (рис. 4.24). На плоскости Н и V прямая проецируется в натуральную величину.

 

Рис. 4.22.

Рис. 4.23.

Рис. 4.24.

 

Точка, принадлежащая прямой. Если точка лежит на прямой, то ее проекции лежат на одноименных проекциях этой прямой и на одной линии проекционной связи. На рис. 4.25,а точка М лежит на прямой CD. Ее горизонтальная проекция т (рис. 4.25,б) лежит на горизонтальной проекции прямой cd, а фронтальная проекция т’ — на фронтальной проекции прямой c’d’.

Обычно по двум проекциям можно определить взаимное расположение точки и прямой. Точка 5 принадлежит прямой CD (рис. 4.25,б), так как ее проекции лежат на про­должении одноименных проекций прямой и на одной линии проекционной связи. Только одна проекция точки F (горизонтальная) лежит на одноименной проекции прямой ей, поэтому точка F не принадлежит прямой CD (рис. 4.25, а и б).

Рис. 4.25.

Если прямая параллельна одной из плоскостей проекций, о взаимном расположении прямой и точки можно получить представление на плоскости проекций, параллельной данной прямой. Для горизонтальной прямой — на плоскости, для фронтальной прямой — на плоскости V, для профильной прямой — на плоскости W.

На рис. 4.25, в и г показаны частные случаи расположения точки и прямой, когда только две проекции точки F лежат на одноименных проекциях прямой CD, и сама точка F не принадлежит прямой CD, так как третья проекция точки не лежит на проекции прямой.

 

Комплексный чертеж плоскости — Технология Jimdo-Page!

           В зависимости от положения относительно плоскостей проекций различают плоскости общего положения и плоскости частного положения.

 

Плоскость общего положения – плоскость, наклоненная под произвольными углами к плоскостям проекций (рис.1).

Плоскости частного положения можно разделить на две группы – проецирующие плоскости и плоскости уровня. Плоскости частного положения чаще всего задаются следами.

Плоскости, параллельные одной из плоскостей проекций, называются плоскостями уровня. Все объекты, лежащие в плоскости уровня, проецируются на параллельную плоскость проекций в натуральную величину.

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (рис. 2).

Треугольник ABC, лежащий в горизонтальной плоскости уровня, проецируется на П1 в натуральную величину.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (рис. 3).

Треугольник ABC, лежащий во фронтальной плоскости уровня, проецируется на П2 в натуральную величину.

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (рис. 4).

Треугольник ABC, лежащий в профильной плоскости уровня, проецируется на плоскость П3 в натуральную величину.

    Плоскости, перпендикулярные одной из плоскостей проекций, называются проецирующими.

     Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций П1 (рис.5).

Горизонтально-проецирующая плоскость задается горизонтальным следом плоскости ∑1

Углы наклона горизонтально-проецирующей плоскости к П2 и П3 проецируются на горизонтальную плоскость проекций в натуральную величину.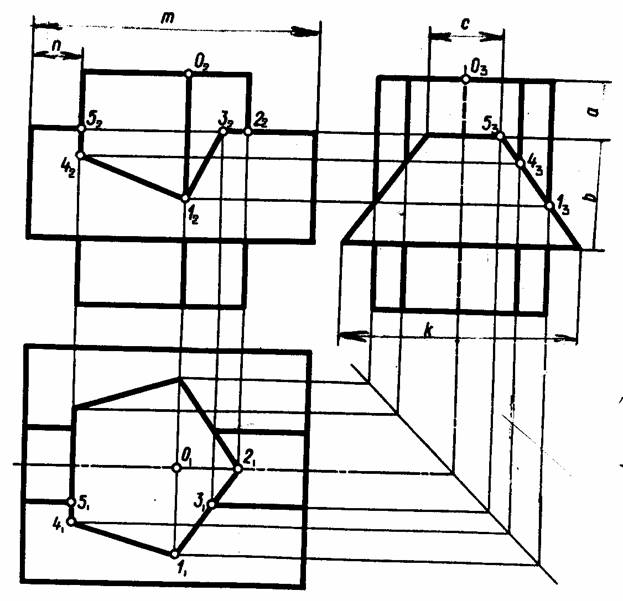

    Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций П2, задается фронтальным следом плоскости ∆2 (рис.6).

      Проекции всех линий и точек, лежащих во фронтально-проецирующей плоскости, совпадают с фронтальным следом этой плоскости. Углы наклона фронтально-проецирующей плоскости к П1 и П3 проецируются на фронтальную плоскость проекций в натуральную величину.

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций П3 , задается профильным следом плоскости Г3 (рис. 7).

Как правильно понимать термин «линия перехода воображаемая»? — Чертежи, спецификации

ГОСТ 2. 303 очень непонятно трактует видимые и воображаемые линии перехода. Можно понять двояко.

1.

Видимые линии перехода это линии пересечения двух граней не по касательной. Сплошная основная линия.

Воображаемые линии перехода это линии пересечения двух граней по касательной. Сплошная тонкая линия.

2.

Видимые линии перехода это это линии пересечения двух граней по касательной. Сплошная основная линия

Воображаемые линии перехода это линии, которые можно вообразить на пересечении двух скруглённых граней. То есть это линии, которые были до скругления. Сплошная тонкая линия.

Переход по касательной не дает видимого угла в детали, который, обычно и изображается основной линией. Поэтому на чертеже этот угол-линию-касания можно только вообразить. Понятно, что иногда имеет смысл показать касательный переход на чертеже. Что и осуществляют линии перехода воображаемые.

Эти линии предназначены для показа скругления на детали на том виде, на котором это скргление не очевидно. Их можно показывать две (по одной на каждом конце радиуса), а можно показывать и одну между концами радиуса, для упрощения. Причем расположение этой одной линии условное, примерное. Так учил НК в советское время и так сделаны рисунки в ГОСТах ЕСКД.

Далее. Если бы действительно было то, что

Видимые линии перехода это это линии пересечения двух граней по касательной. Сплошная основная линия

, то читать чертежи было бы не возможно, поскольку все касательные линии должны быть обязательно изображены и должны быть изображены основной линией и мы были бы обязаны все каксательные линии выполнять толстой основной линией. Поскольку иного в ГОСТ не предусмотрено.

Я пока не видел ни одного чертежа, в котором касательныя линия выполнялась толстой основной.

Но я видел тучу чертежей, в которых показывается тонкой линией именно скругление. Иногда на каждом конце радиуса, а чаще одной линией между концами.

Вот как по ГОСТу показывается канавка для выхода резьбы на вале. Линия перехода тонкая и находится на воображаемом пересечении двух скруглённых отрезков. Значит правильный вариант №2 ???

Вообще-то, надо давать ссылки на ГОСТ, номер пункта, номер рисунка, если приводится цитата или рисунок. Чтоб и другие смогли убедится в верности цитаты.

Скорее всего из прилагаемого рисунка не следует, что тонкой линией изображен угол между поверхностями до скругления. И сам русунок поясняет какой-то другой текст в ГОСТ. Однако, рисунок хорошо вписывается в те объяснения, что тонкой линией просто подтвержается наличие скругления на обозначаемом участке и больше ничего.

В теле детали, в под скруглением воображаемые поверхности могут идти как угодно и не факт что они обязаны продолжаться, например, линейно. Там теоретически может быть даже несколько ступенек!

То есть, если бы линии перехода воображаемые показывали бы отсутствующий угол в детали (до скругления), то тогда должны имет место правила, по которым эти линии должны строиться. Однако, в ЕСКД об этом не сказано ни слова.

Вывод. Линии перехода воображаемые — это линии, показывающие наличие скругления (начала другого радиуса), вознкающего на линии касания (пересечения) поверхностей детали.

Начертательная геометрия. Теория.

Краткий курс начертательной геометрии

---

Лекции предназначены для студентов инженерно–технических специальностей

Введение
Тема 1. Проецирование точки
Тема 2. Проецирование прямой
Тема 3. Положение прямой относительно плоскостей проекций. Следы прямой
Тема 4. Плоскость. Способы задания плоскостей
Тема 5. Положение плоскости. Следы плоскости
Тема 6. Взаимное положение прямой и плоскости
Тема 7. Взаимное положение плоскостей
Тема 8. Плоскопараллельное перемещение. Вращение. Замена плоскостей проекций

Начертательная геометрия входит в состав учебной дисциплины федерального значения, название которой в зависимости от специальности: «Начертательная геометрия и инженерная графика», «Инженерная и машинная графика» или просто «Инженерная графика». Инженерная графика – это единственная дисциплина целью, которой является непосредственно обучение студентов работе с различной по виду и содержанию графической информацией, основам графического представления информации, методам графического моделирования геометрических объектов, правилам разработки и оформления конструкторской документации, графических моделей явлений и процессов.

Тема 1. Проецирование точки

Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Г. Монжем.
Изложенный Монжем метод — метод ортогонального проецирования, причем берутся две проекции на две взаимно перпендикулярные плоскости проекций, — обеспечивая выразительность, точность и удобоизмеримость изображений предметов на плоскости, был и остается основным методом составления технических чертежей

Рисунок 1. 1 Точка в системе трех плоскостей проекций

Модель трех плоскостей проекций показана на рисунке 1.1. Третья плоскость, перпендикулярная и П1, и П2, обозначается буквой П3 и называется профильной. Проекции точек на эту плоскость обозначаются заглавными буквами или цифрами с индексом 3. Плоскости проекций, попарно пересекаясь, определяют три оси 0x, 0y и 0z, которые можно рассматривать как систему декартовых координат в пространстве с началом в точке 0. Три плоскости проекций делят пространство на восемь трехгранных углов — октантов. Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте. Для получения эпюра точки в системе трех плоскостей проекций плоскости П1 и П3 вращают до совмещения с плоскостью П2. При обозначении осей на эпюре отрицательные полуоси обычно не указывают. Если существенно только само изображение предмета, а не его положение относительно плоскостей проекций, то оси на эпюре не показывают. Координатами называют числа, которые ставят в соответствие точке для определения ее положения в пространстве или на поверхности. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x , y и z (абсцисса, ордината и аппликата).

К началу страницы

Тема 2. Проецирование прямой

Для определения положения прямой в пространстве существуют следующие методы: 1.Двумя точками ( А и В ). Рассмотрим две точки в пространстве А и В (рис. 2.1). Через эти точки можно провести прямую линию получим отрезок [AB]. Для того чтобы найти проекции этого отрезка на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка: [A1B1]<[AB]; [A2B2]<[AB]; [A3B3]<[AB].

Рисунок 2.1 Определение положения прямой по двум точкам

2.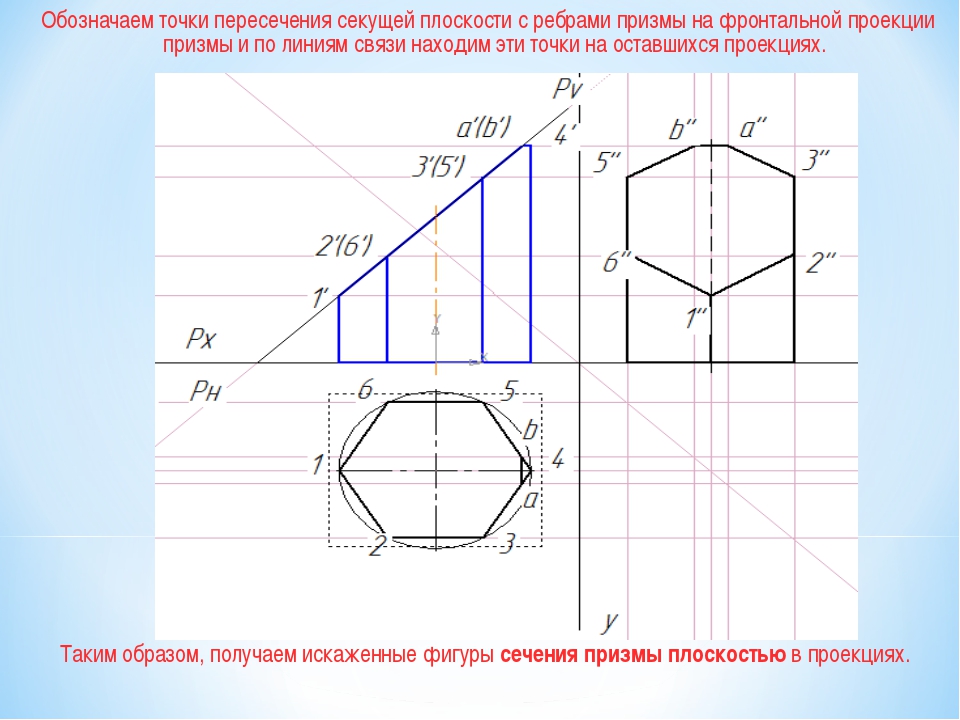 Двумя плоскостями (a; b). Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).

3. Точкой и углами наклона к плоскостям проекций. Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве.

К началу страницы

Тема 3. Положение прямой относительно плоскостей проекций. Следы прямой

В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения. 1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.3.1).

Рисунок 3.1 Прямая общего положения

2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня.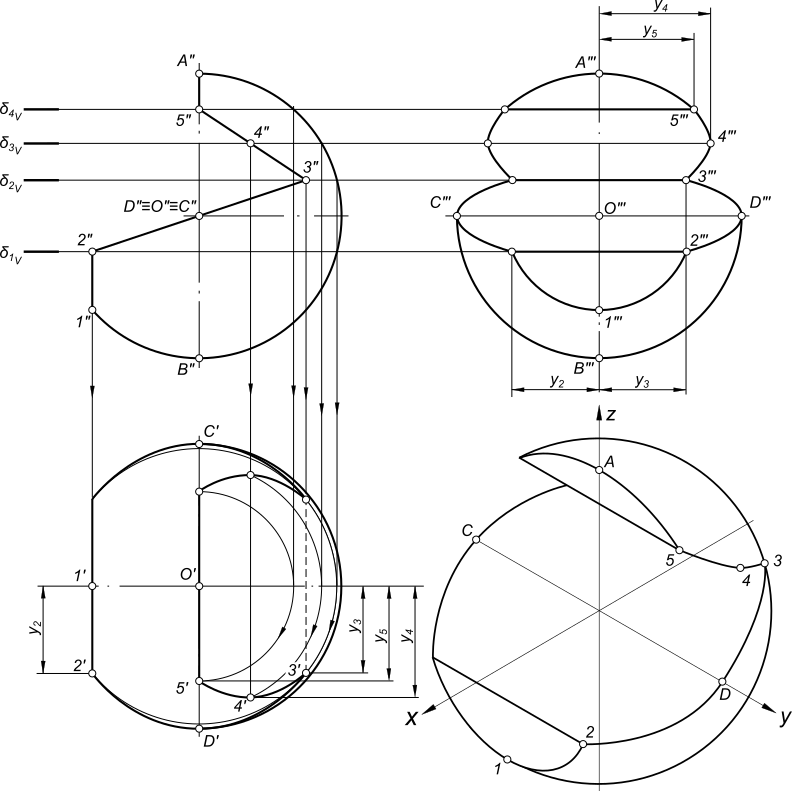 В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:

2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.3.2).

Рисунок 3.2 Горизонтальная прямая

2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями(рис.3.3).

Рисунок 3.3 Фронтальная прямая

2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 3.4).

Рисунок 3.4 Профильная прямая

3. Прямые, перпендикулярные плоскостям проекций, называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:

3.1. Фронтально-проецирующая прямая — АВ (рис.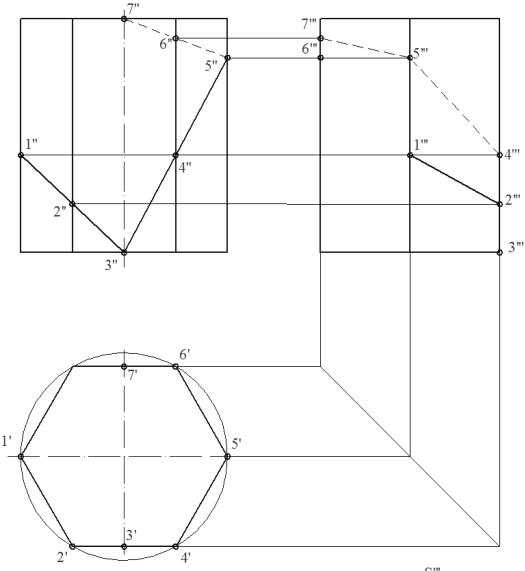 3.5).

Рисунок 3.5 Фронтально-проецирующая прямая

3.2. Профильно проецирующая прямая — АВ (рис.3.6).

Рисунок 3.6 Профильно-проецирующая прямая

3.3. Горизонтально-проецирующая прямая — АВ (рис.3.7).

Рисунок 3.7 Горизонтально-проецирующая прямая

К началу страницы

Тема 4. Плоскость. Способы задания плоскостей

Плоскость – одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскость обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Некоторые характеристические свойства плоскости: 1. Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки; 2. Плоскость есть множество точек, равноотстоящих от двух заданных точек.

Способы графического задания плоскостей Положение плоскости в пространстве можно определить:

1. Тремя точками, не лежащими на одной прямой линии (рис.4.1).

Рисунок 4.1 Плоскость заданная тремя точками, не лежащими на одной прямой

2. Прямой линией и точкой, не принадлежащей этой прямой (рис.4.2).

Рисунок 4.2 Плоскость заданная прямой линией и точкой, не принадлежащей этой линии

3. Двумя пересекающимися прямыми (рис.4.3).

Рисунок 4.3 Плоскость заданная двумя пересекающимися прямыми линиями

4. Двумя параллельными прямыми (рис.4.4).

Рисунок 4.4 Плоскость заданная двумя параллельными прямыми линиями

Тема 5. Положение плоскости. Следы плоскости

К началу страницы

Различное положение плоскости относительно плоскостей проекций

В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения. П2). Любая фигура в этой плоскости проецируется на плоскость П3 без искажения, а на плоскости П1 и П2 в прямые — следы плоскости S1 и S2 (рис.5.7).

Рисунок 5.7 Профильная плоскость

Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная, различают: горизонтальный, фронтальный и профильный следы плоскости.

Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой( как для построения любой прямой). На рисунке 5.8 показано нахождение следов плоскости S (АВС). Фронтальный след плоскости S2, построен, как прямая соединяющая две точки 12 и 22, являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости S. Горизонтальный следS1 – прямая, проходящая через горизонтальный след прямой АВ и Sx. Профильный следS3 – прямая соединяющая точки (Sy и Sz) пересечения горизонтального и фронтального следов с осями.

Рисунок 5.8 Построение следов плоскости

К началу страницы

Тема 6. Взаимное положение прямой и плоскости, точки и плоскости

Определение взаимного положения прямой и плоскости — позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость Q и установим относительное положение двух прямых a и b, последняя из которых является линией пересечения вспомогательной секущей плоскости Q и данной плоскости T(рис.6.1).

Рисунок 6.1 Метод вспомогательных секущих плоскостей

Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямая а лежит в плоскости T, параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю когда прямая а пересекает плоскость T. Таким образом возможны три случая относительного расположения прямой и плоскости: Прямая принадлежит плоскости; Прямая параллельна плоскости; Прямая пересекает плоскость, частный случай – прямая перпендикулярна плоскости. Рассмотрим каждый случай.

Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат той же плоскости (рис.6.2).

Задача. Дана плоскость (n,k) и одна проекция прямой m2. Требуется найти недостающие проекции прямой m если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k. Проекция прямой m2 пересекает прямые n и k в точках В2 и С2, для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек лежащих на прямых соответственно n и k. Таким образом точки В и С принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит согласно аксиоме прямая принадлежит этой плоскости.

Рисунок 6.2 Прямая и плоскость имеют две общие точки

Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости (рис.6.3).

Задача. Через точку В провести прямую m если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k. Пусть В принадлежит прямой n лежащей в плоскости заданной пересекающимися прямыми n и k. Через проекцию В2 проведем проекцию прямой m2 параллельно прямой k2, для нахождения недостающих проекций прямой необходимо построить проекцию точки В1, как точки лежащей на проекции прямой n1 и через неё провести проекцию прямой m1 параллельно проекции k1. Таким образом точки В принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k, значит согласно аксиоме прямая принадлежит этой плоскости.

Рисунок 6.3 Прямая имеет с плоскостью одну общую точку и параллельна прямой расположенной в этой плоскости

 

Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:

1. Горизонтали h — прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (h//П1)(рис.6.4).

Рисунок 6.4 Горизонталь

2. Фронтали f — прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (f//П2)(рис.6.5).

Рисунок 6.5 Фронталь

3. Профильные прямые р — прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (р//П3) (рис.6.6). Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след — это горизонталь плоскости, фронтальный — фронталь и профильный — профильная линия плоскости.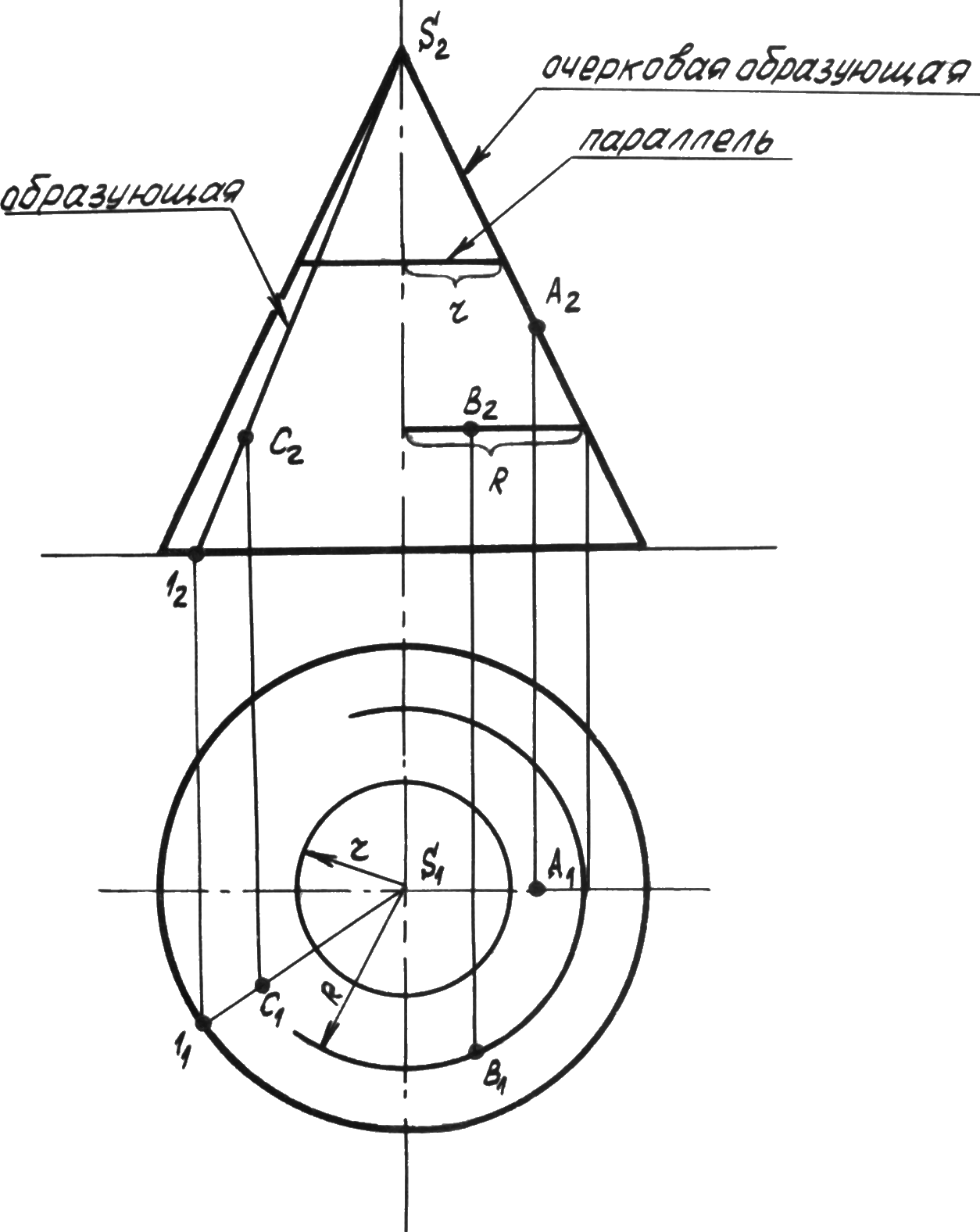

Рисунок 6.6 Профильная прямая

4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.6.7). Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.

Рисунок 6.7 Линия наибольшего ската

 

Возможны два варианта взаимного расположения точки и плоскости: либо точка принадлежит плоскости, либо нет. Если точка принадлежит плоскости то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну. Рассмотрим пример (рис.6.8): Построение проекции точки А принадлежащей плоскости общего положения заданной двумя параллельными прямыми a(a//b).

Задача. Дано: плоскость T(а,в) и проекция точки А2.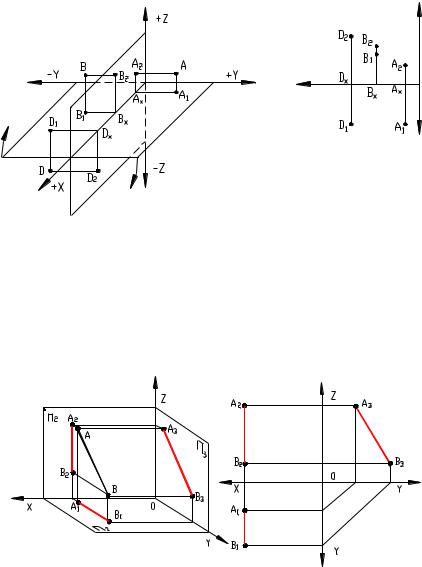 Требуется построить проекцию А1 если известно, что точка А лежит в плоскости в,а. Через точку А2 проведем проекцию прямой m2, пересекающую проекции прямых a2 и b2 в точках С2 и В2. Построив проекции точек С1 и В1, определяющие положение m1, находим горизонтальную проекцию точки А.

Рисунок 6.8. Точка, принадлежащая плоскости

К началу страницы

Тема 7. Взаимное положение плоскостей

Две плоскости в пространстве могут быть либо взаимно параллельны, в частном случае совпадая друг с другом, либо пересекаться. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей.

1. Параллельные плоскости. Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Это определение хорошо иллюстрируется задачей, через точку В провести плоскость параллельную плоскости, заданной двумя пересекающимися прямыми ab (рис. 7.1). Задача. Дано: плоскость общего положения, заданную двумя пересекающимися прямыми ab и точка В. Требуется через точку В провести плоскость, параллельную плоскости ab и задать её двумя пересекающимися прямыми c и d. Согласно определения если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости то эти плоскости параллельны между собой. Для того чтобы провести на эпюре параллельные прямые необходимо воспользоваться свойством параллельного проецирования — проекции параллельных прямых — параллельны между собой d||a, с||b; d1||a1,с1||b1; d2||a2 ,с2||b2; d3||a3,с3||b3.

Рисунок 7.1. Параллельные плоскости

2. Пересекающиеся плоскости, частный случай – взаимно перпендикулярные плоскости. Линия пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.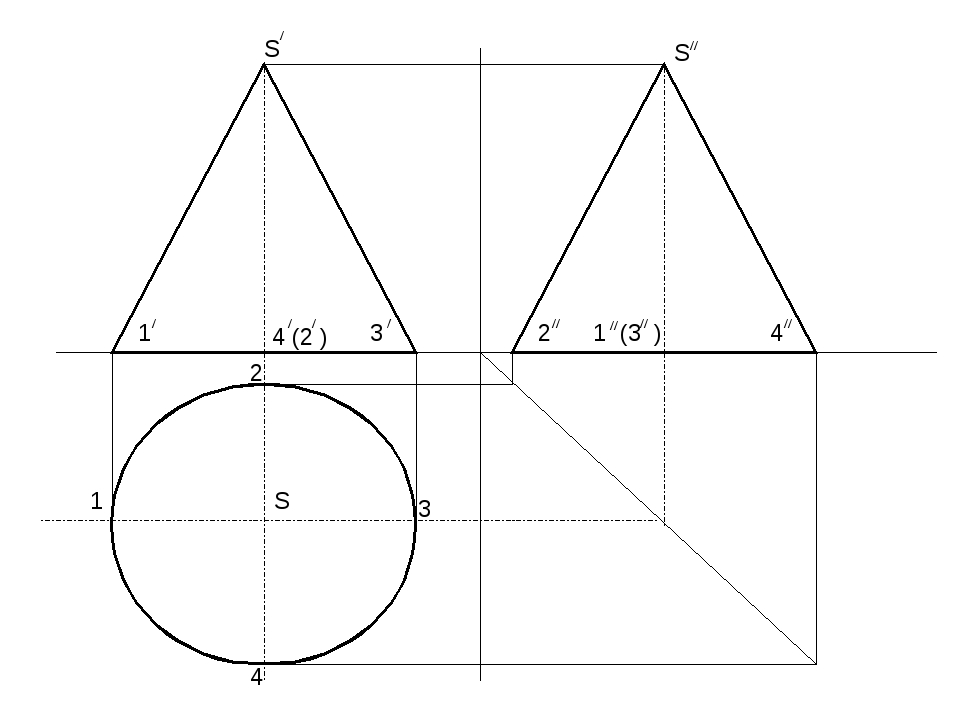 Рассмотрим построение линии пересечения двух плоскостей, когда одна из них проецирующая (рис.7.2).

Задача. Дано: плоскость общего положения задана треугольником АВС, а вторая плоскость — горизонтально проецирующая T. Требуется построить линию пересечения плоскостей. Решение задачи заключается в нахождении двух точек общих для данных плоскостей, через которые можно провести прямую линию. Плоскость, заданная треугольником АВС можно представить, как прямые линии (АВ), (АС), (ВС). Точка пересечения прямой (АВ) с плоскостью T — точка D, прямой (AС) -F. Отрезок [DF] определяет линию пересечения плоскостей. Так как T — горизонтально проецирующая плоскость, то проекция D1F1 совпадает со следом плоскости T1, таким образом остается только построить недостающие проекции [DF] на П2 и П3.

Рисунок 7.2. Пересечение плоскости общего положения с горизонтально проецирующей плоскостью

Перейдем к общему случаю. Пусть в пространстве заданы две плоскости общего положения a(m,n) и b (ABC) (рис.7.3).

Рисунок 7.3. Пересечение плоскостей общего положения

Рассмотрим последовательность построения линии пересечения плоскостей a(m//n) и b(АВС). По аналогии с предыдущей задачей для нахождения линии пересечения данных плоскостей проведем вспомогательные секущие плоскости g и d. Найдем линии пересечения этих плоскостей с рассматриваемыми плоскостями. Плоскость g пересекает плоскость a по прямой (12), а плоскость b — по прямой (34). Точка К — точка пересечения этих прямых одновременно принадлежит трем плоскостям a, b и g, являясь таким образом точкой принадлежащей линии пересечения плоскостей a и b. Плоскость d пересекает плоскости a и b по прямым (56) и (7C) соответственно, точка их пересечения М расположена одновременно в трех плоскостях a, b, d и принадлежит прямой линии пересечения плоскостей a и b. Таким образом найдены две точки принадлежащие линии пересечения плоскостей a и b — прямая (КМ).

Некоторого упрощения при построении линии пересечения плоскостей можно достичь, если вспомогательные секущие плоскости проводить через прямые, задающие плоскость.

Взаимно перпендикулярные плоскости. Из стереометрии известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Через точку А можно провести множество плоскостей перпендикулярных данной плоскости a(f,h). Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр опущенный из точки А на плоскость a . Для того чтобы из точки А провести плоскость перпендикулярную плоскости заданной двумя пересекающимися прямыми hf необходимо из точки А провести прямую n перпендикулярную плоскости hf (горизонтальная проекция n перпендикулярна горизонтальной проекции горизонтали h, фронтальная проекция n перпендикулярна фронтальной проекции фронтали f). Любая плоскость проходящая через прямую n будет перпендикулярна плоскости hf, поэтому для задания плоскости через точки А проводим произвольную прямую m.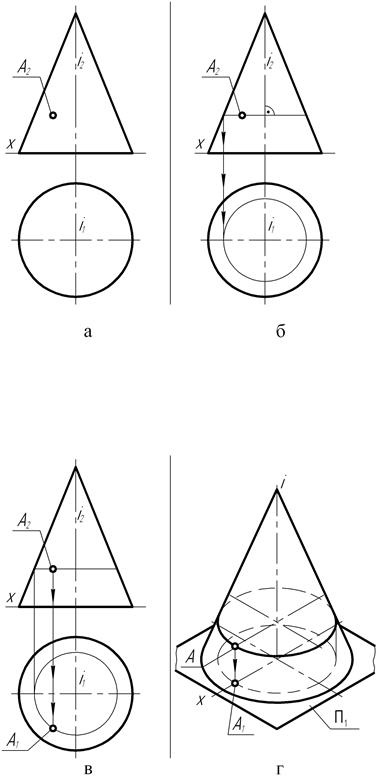 Плоскость заданная двумя пересекающимися прямыми mn будет перпендикулярна плоскости hf (рис.7.4).

Рисунок 7.4. Взаимно перпендикулярные плоскости

К началу страницы

Тема 8. Плоскопараллельное перемещение. Вращение. Замена плоскостей проекций

Изменение взаимного положения проецируемого объекта и плоскостей проекций методом плоскопараллельного перемещения осуществляется путем изменения положения геометрического объекта так, чтобы траектория движения её точек находилась в параллельных плоскостях. Плоскости носители траекторий перемещения точек параллельны какой-либо плоскости проекций (рис. 8.1). Траектория произвольная линия. При параллельном переносе геометрического объекта относительно плоскостей проекций, проекция фигуры хотя и меняет свое положение, но остается конгруэнтной проекции фигуры в ее исходном положении.

Рисунок 8. 1 Определение натуральной величины отрезка методом плоскопараллельного перемещения

Свойства плоскопараллельного перемещения:

1. При всяком перемещении точек в плоскости параллельной плоскости П1, её фронтальная проекция перемещается по прямой линии, параллельной оси х.

2. В случае произвольного перемещения точки в плоскости параллельной П2, её горизонтальная проекция перемещается по прямой параллельной оси х.

 

Плоскости носитель траекторий перемещения точек параллельны плоскости проекций. Траектория — дуга окружности, центр которой находится на оси перпендикулярной плоскости проекций. Для определения натуральной величины отрезка прямой общего положения АВ (рис. 8.2), выберем ось вращения (i) перпендикулярную горизонтальной плоскости проекций и проходящую через В1. Повернем отрезок так, чтобы он стал параллелен фронтальной плоскости проекций (горизонтальная проекция отрезка параллельна оси x). При этом точка А1 переместиться в А’1, а точка В не изменит своего положения. Положение точки А’2 находится на пересечении фронтальной проекции траектории перемещения точки А (прямая линия параллельная оси x) и линии связи проведенной из А’1. Полученная проекция В2 А’2 определяет натуральную величину самого отрезка.

Рисунок 8.2 Определение натуральной величины отрезка методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций

Рассмотрим этот способ на примере определения угла между пересекающимися прямыми (рис.8.3). Рассмотрим две проекции пересекающихся прямых а и в которые пересекаются в точке К. Для то чтобы определить натуральную величину угла между этими прямыми необходимо произвести преобразование ортогональных проекций так, чтобы прямые стали параллельны плоскости проекций. Воспользуемся способом вращения вокруг линии уровня — горизонтали. Проведем произвольно фронтальную проекцию горизонтали h3 параллельно оси Ох, которая пересекает прямые в точках 12 и 22 . Определив проекции 11 и 11, построим горизонтальную проекцию горизонтали h2 . Траектория движения всех точек при вращении вокруг горизонтали — окружность, которая проецируется на плоскость П1 в виде прямой линии перпендикулярной горизонтальной проекции горизонтали.

Рисунок 8.3 Определение угла между пересекающимися прямыми, вращением вокруг оси параллельной горизонтальной плоскости проекций

Таким образом, траектория движения точки К1 определена прямой К1О1, точка О -центр окружности — траектории движения точки К. Чтобы найти радиус этой окружности найдем методом треугольника натуральную величину отрезка КО .Продолжим прямую К1О1 так чтобы |О1К’1|=|КО| . Точка К’1 соответствует точке К , когда прямые а и в лежат в плоскости параллельной П1 и проведенной через горизонталь — ось вращения. С учетом этого через точку К’1 и точки 11 и 21 проведем прямые, которые лежат теперь в плоскости параллельной П1, а следовательно и угол фи — натуральная величина угла между прямыми а и в.

 

Изменение взаимного положения проецируемой фигуры и плоскостей проекций методом перемены плоскостей проекций, достигается путем замены плоскостей П1 и П2 новыми плоскостями П4 (рис. 8.4). Новые плоскости выбираются перпендикулярно старым. Некоторые преобразования проекций требуют двойной замены плоскостей проекций (рис. 8.5). Последовательный переход от одной системы плоскостей проекций другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.

Задача 1: Определить натуральную величину отрезка АВ прямой общего положений (рис. 8.4). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости. Выберем новую плоскость проекций П4, параллельно отрезку АВ и перпендикулярно плоскости П1. Введением новой плоскости, переходим из системы плоскостей П1П2 в систему П1П4 , причем в новой системе плоскостей проекция отрезка А4В4 будет натуральной величиной отрезка АВ.

Рисунок 8.4. Определение натуральной величины отрезка прямой методом замены плоскостей проекций

Задача 2: Определить расстояние от точки C до прямой общего положения, заданной отрезком АВ (рис. 8.5).

Рисунок 8.5. Определение натуральной величины отрезка прямой методом замены плоскостей проекций

 

К началу страницы

Перенос чертежей Silverpoint — Академия рисования

Вопрос от Райана

Как лучше всего перенести набросок на подготовленную бумагу для Silverpoint?

Ответ Владимира Лондона, преподавателя Академии рисования

Дорогой Райан,

Вы абсолютно правы, что рисунок нужно переносить на подготовленную подставку silverpoint, а не рисовать прямо на заземленной поверхности.Заземление Silverpoint следует защищать от стирания, перерисовки и контакта с кожей руки.

Существуют различные способы переноса чертежей для Silverpoint. Мне больше всего подходит калька.

Сначала сделайте подготовительный рисунок в натуральную величину графитным карандашом на бумаге. На этом этапе легко внести коррективы в композицию и изменить пропорции, размеры и расположение любых объектов. Вы можете стирать и перерисовывать свой набросок сколько угодно раз.

Когда эскиз вас устраивает, перенесите его на кусок кальки, обрезанный по размеру подготовленной подставки для серебра. Имейте в виду, что обведенное изображение будет зеркально отражено, если на этом этапе вы перенесете изображение на серебряную поверхность.

Чтобы исходная композиция не отражалась, переверните кальку и еще раз обведите рисунок графитным карандашом. После можно перевернуть кальку и стереть первый контур.Стирать необязательно, но это поможет вам увидеть любые недостающие части при перемещении на землю silverpoint.

Теперь вы готовы перенести рисунок на подготовленную поверхность silverpoint.

Прикрепите кальку к опоре silverpoint с помощью куска бумажной ленты так, чтобы контур рисунка был обращен к земле. Не приклеивайте ленту к земле; вместо этого оберните кальку вокруг спинки и приклейте ее к противоположной стороне подставки. Таким образом вы сохраните землю чистой и неповрежденной.Возьмите хорошо заточенный карандаш h3 и аккуратно пройдитесь по всем контурам. Во время этого процесса часто поднимайте кальку, чтобы проверить отметки на земле; вам может потребоваться уменьшить давление карандаша, если отметки слишком жирные.

Использование кальки для переноса изображения дает несколько преимуществ:

• Это очень точный инструмент, который дополняет характер техники серебряной иглы.
• Дает полный контроль над процессом перевода; вы можете поднять кальку и по ходу проверить свои результаты.
• Многоразовая. Если у вас есть калька с контуром, вы можете использовать ее для нескольких копий одного рисунка.
• Чисто и аккуратно. Калька защитит землю silverpoint от контакта с кожей руки при переносе рисунка.

Разумеется, при рисовании металлическим острием всегда следует держать под рукой чистый лист бумаги.

Если кто-либо использует различные методы переноса рисунков, которые одинаково чисты, точны и подходят для оснований silverpoint, поделитесь своими знаниями и опытом, оставив комментарий на этой странице.

Большое спасибо,

Владимир Лондон
Репетитор Академии рисования

Записаться на курс Академии рисования:

Оплатите курс в 3 простых платежа

• Получайте 15 новых видео ежемесячно (всего 45)
• Невероятная скидка — 4164 доллара
• Бонусы — Электронные книги и видео по искусству
• Диплом отличия Академии рисования после завершения курса за 3 месяца
• Персональное обучение преподавателей Академии рисования
• Пожизненное членство.Бесплатно после 3-го месяца

Общая стоимость: 291 долларов (три части по 97 долларов)

Получите все видео уроки за единовременный платеж

• Мгновенный доступ ко всем 45 видеоурокам
• Невероятная скидка — 4198 долларов
• Бонусы — Электронные книги и видео по искусству
• Диплом отличия Академии рисования после завершения курса за 3 месяца
• Персональное обучение преподавателей Академии рисования
• Пожизненное членство.Больше никаких платежей

Общая стоимость — всего 257 долларов

Категория: Задавайте вопросы репетиторам

Рисуйте прямые линии или выравнивайте объекты по линейке в PowerPoint

Вы можете управлять линейкой с помощью пальцев, мыши или нажатия клавиш.

Эта функция доступна в PowerPoint для Microsoft 365 и PowerPoint 2019.Если вы не видите линейку на ленте, см. Дополнительные сведения в разделе «Требования» ниже.

Включите вкладку Draw, чтобы увидеть линейку

1. Открыть файл > Параметры .

2. Коснитесь вкладки Настроить ленту в диалоговом окне Параметры .

3. В поле в правой части диалогового окна установите флажок с именем Draw .

4. Нажмите ОК , чтобы закрыть диалоговое окно Параметры .

5. Коснитесь вкладки Draw , и вы увидите линейку на ленте.

Нарисуйте линию или выровняйте элементы

1. Выберите слайд, на котором вы хотите использовать линейку.

2. Нажмите на линейку на вкладке Draw , чтобы она отображалась на поверхности для рисования слайда.

3. Расположите линейку под нужным углом.

   • Используйте одним пальцем для перемещения линейки вверх / вниз или влево / вправо.

   • Используйте двумя пальцами , чтобы повернуть линейку на нужный угол.

   • Используйте тремя пальцами , чтобы повернуть линейку с шагом в пять градусов.

4. Чтобы нарисовать линию Коснитесь ручки или маркера на вкладке Draw и начните рисовать.

   Выравнивание отдельных элементов Выделите каждый из них по очереди и перетащите объект, пока его маркер выбора не зафиксируется на линейке.

   Для одновременного выравнивания группы элементов Выделите несколько элементов, нажав Ctrl, одновременно касаясь каждого элемента по очереди. Перетащите набор объектов, пока он не прикрепится к линейке.

   Фигура выравнивается по линейке на ее краю, тогда как объект, такой как значок, рисунок или текстовое поле, выравнивается по линейке на ее ограничивающей рамке.

Управляйте линейкой с помощью мыши

Перемещайте линейку, щелкая и перетаскивая мышью.Чтобы прекратить перемещение линейки, отпустите кнопку мыши.

Поворачивайте линейку с шагом в один градус, поворачивая колесо прокрутки мыши. Линейка поворачивается туда, куда указывает указатель мыши. (Для вращения требуется колесо прокрутки мыши; оно не работает с трекпадами ноутбуков.)

Управление линейкой с клавиатуры

Если у вас нет сенсорного экрана или если вы предпочитаете использовать клавиатуру, используйте эти комбинации клавиш для управления линейкой после того, как вы нажали кнопку линейки, чтобы активировать ее на поверхности слайда.

Для управления линейкой с клавиатуры:

1. Нажмите на линейку на вкладке Draw , чтобы она отображалась на поверхности для рисования слайда.

2. Щелкните линейку мышью.

3. Нажмите Shift + F6, чтобы войти в режим управления линейкой.

4. Используйте сочетание клавиш для управления линейкой:

   Действие	Клавиши
   Перемещение линейки вверх, вниз, влево или вправо	Стрелка вверх, стрелка вниз, стрелка влево, стрелка вправо
   Поверните линейку с шагом 15 градусов	Удерживая нажатой клавишу Alt, нажмите стрелку влево или вправо один раз для каждого приращения Левая стрелка вращает линейку против часовой стрелки; стрелка вправо вращает его по часовой стрелке.
   Поверните линейку с шагом в один градус	Удерживая Alt + Ctrl, коснитесь стрелки влево или вправо один раз для каждого приращения * Левая стрелка вращает линейку против часовой стрелки; стрелка вправо вращает его по часовой стрелке.

   (Темно-серая граница появляется по краям линейки, когда вы перемещаете ее, чтобы указать, что включен режим управления линейкой.)

   * Комбинация клавиш Alt + Ctrl + стрелка также может использоваться Windows для поворота монитора. Функция поворота монитора контролируется видеокартой компьютера. Если эта функция включена для вашего компьютера, она будет иметь приоритет над сочетанием клавиш линейки, и в результате дисплей вашего монитора будет повернут на 90 градусов, когда вы нажмете Alt + Ctrl + стрелка вправо или влево. Вы можете сбросить поворот монитора, нажав Alt + Ctrl + стрелка вверх.

   Если вы хотите использовать комбинацию клавиш управления линейкой, отключите функцию поворота монитора, щелкнув правой кнопкой мыши на рабочем столе компьютера и выбрав команду, например, Свойства графики или Параметры графики . Найдите команду Hot Keys и установите для нее значение Disabled . (Точное расположение и названия этих команд зависят от производителя.) После того, как вы отключили функцию поворота монитора, комбинации клавиш Alt + Ctrl + стрелка могут использоваться как на линейке, так и на фигурах, которые были вставлены на слайды в PowerPoint.

Скрыть линейку

Требования к линейке

Эта функция работает на планшетах Windows, но не на телефонах Windows. См. Требования ниже для более подробной информации.

Нарисуйте линию или выровняйте элементы

1. Коснитесь слайда, на котором вы хотите использовать линейку.

2. Нажмите на линейку на вкладке Draw , чтобы она отображалась на поверхности для рисования слайда.

3. Расположите линейку под нужным углом:

   • Используйте одним пальцем для перемещения линейки вверх / вниз или влево / вправо.

   • Используйте двумя пальцами , чтобы повернуть линейку на нужный угол.

   • Используйте тремя пальцами , чтобы повернуть линейку с шагом в пять градусов.

4. Чтобы нарисовать линию Коснитесь ручки или маркера на вкладке Draw и начните рисовать.

   Выравнивание отдельных элементов Выделите каждый из них по очереди и перетащите объект, пока его маркер выбора не зафиксируется на линейке.

   Одновременное выравнивание группы элементов Выделите несколько элементов, выбрав один, а затем нажав и удерживая его, последовательно касаясь других элементов другим пальцем. Перетащите набор объектов, пока он не прикрепится к линейке.

   Форма выравнивается по линейке по краю, тогда как объект, такой как значок , изображение , изображение или текстовое поле , выравнивается по линейке на его ограничивающей рамке.

Скрыть линейку

Требования к линейке

	Эта функция предназначена для всех пользователей планшетов Windows.
Применимо к:	PowerPoint Mobile: Версия 17.9330.20541
Операционная система:	Windows 10, версия 1709 или более поздняя Найдите свою версию Windows

См. Также

Нарисуйте прямые линии или измерьте линейкой в ​​OneNote

OpenCV: функции рисования

img & pt1, Point & pt2)

void	cv :: arrowedLine (InputOutputArray img, Point pt1, Point pt2, const Scalar & color, int width = 1, int line_type = 8, int shift = 0, double tipLength = 0.1)
	Рисует сегмент стрелки, указывающий от первой точки ко второй. Подробнее …
void	cv :: circle (InputOutputArray img, Point center, int radius, const Scalar & color, int width = 1, int lineType = LINE_8, int shift = 0)
	Рисует круг. Подробнее …
bool	cv :: clipLine (Size imgSize, Point & pt1, Point & pt2)
	Обрезает линию по прямоугольнику изображения.Подробнее …
bool	cv :: clipLine (Size2l imgSize, Point2l & pt1, Point2l & pt2)
bool :: clip
void	cv :: drawContours (изображение InputOutputArray, контуры InputArrayOfArrays, int contourIdx, const Scalar & color, int width = 1, intray_line_Type = no InputArINE_erir (no) , int maxLevel = INT_MAX, Point offset = Point ())
	Рисует контуры контуров или контуры с заливкой.Подробнее …
void	cv :: drawMarker (Mat & img, Point position, const Scalar & color, int markerType = MARKER_CROSS, int markerSize = 20, int толщина = 1, int line_type = 8 )
	Рисует маркер в заранее заданной позиции на изображении. Подробнее …
void	cv :: ellipse (InputOutputArray img,

OpenCV: функции рисования

img img & pt1, Point & pt2)3131 void

Функции рисования работают с матрицами / изображениями произвольной глубины. Границы фигур можно визуализировать с помощью сглаживания (пока что реализовано только для 8-битных изображений). Все функции включают параметр color, который использует значение RGB (которое может быть создано с помощью конструктора Scalar) для цветных изображений и яркость для изображений в оттенках серого.Для цветных изображений порядок каналов обычно: Синий, Зеленый, Красный . Это то, чего ожидают imshow, imread и imwrite. Итак, если вы формируете цвет с помощью конструктора Scalar, он должен выглядеть так:

\ [\ texttt {Скаляр} (синий \ _ компонент, зеленый \ _ компонент, красный \ _ компонент [, альфа \ _ компонент]) \]

Если вы используете свои собственные функции рендеринга изображений и ввода-вывода, вы можете использовать любой порядок каналов. Функции рисования обрабатывают каждый канал независимо и не зависят от порядка каналов или даже от используемого цветового пространства.Все изображение можно преобразовать из BGR в RGB или в другое цветовое пространство с помощью cvtColor. {- shift}) \).Эта функция особенно эффективна при рендеринге фигур со сглаживанием.

Loidine cv , Point pt1, Point pt2, const Scalar & color, int width = 1, int line_type = 8, int shift = 0, double tipLength = 0.1)
	Рисует сегмент стрелки, указывающий от первой точки ко второй. Подробнее …
void	cv :: circle (InputOutputArray img, Point center, int radius, const Scalar & color, int width = 1, int lineType = LINE_8, int shift = 0)
	Рисует круг. Подробнее …
bool	cv :: clipLine (Size imgSize, Point & pt1, Point & pt2)
	Обрезает линию по прямоугольнику изображения.Подробнее …
bool	cv :: clipLine (Size2l imgSize, Point2l & pt1, Point2l & pt2)
bool :: clip
void	cv :: drawContours (изображение InputOutputArray, контуры InputArrayOfArrays, int contourIdx, const Scalar & color, int width = 1, intray_line_Type = no InputArINE_erir (no) , int maxLevel = INT_MAX, Point offset = Point ())
	Рисует контуры контуров или контуры с заливкой.Подробнее …
void	cv :: drawMarker (Mat & img, Point position, const Scalar & color, int markerType = MARKER_CROSS, int markerSize = 20, int толщина = 1, int line_type = 8 )
	Рисует маркер в заранее заданной позиции на изображении. Подробнее …
void	cv :: ellipse (InputOutputArray img, Point center, Size Axes, double angle, double startAngle, double endAngle, const Scalar & color, int width = 1, int lineType = LINE_8, int shift = 0)
	Рисует простую или толстую дугу эллипса или заполняет сектор эллипса.Подробнее …
void	cv :: ellipse (InputOutputArray img, const RotatedRect & box, const Scalar & color, int толщина = 1, int lineType = LINE_8)
cv :: ellipse2Poly (Point center, Size Axes, int angle, int arcStart, int arcEnd, int delta, std :: vector & pts)
	Приближает эллиптическую дугу к полилинии.Подробнее …
void	cv :: ellipse2Poly (Point2d center, Size2d axes, int angle, int arcStart, int arcEnd, int delta, std :: vector & pts)
void	cv :: fillConvexPoly (Mat & img, const Point * pts, int npts, const Scalar & color, int lineType = LINE_8, int shift = 0)
void cv :: fillConvexPoly (InputOutputArray img, InputArray points, const Scalar & color, int lineType = LINE_8, int shift = 0)
	Заполняет выпуклый многоугольник.Подробнее …
void	cv :: fillPoly (Mat & img, const Point ** pts, const int * npts, int ncontours, const Scalar & color, int lineType = LINE_8, int shift = 0, смещение точки = Point ())
void	cv :: fillPoly (InputOutputArray img, InputArrayOfArrays pts, const Scalar & color, int lineType = LINE_8, int shift (0, Point offset = Point ))
	Заполняет область, ограниченную одним или несколькими полигонами.Подробнее …
double	cv :: getFontScaleFromHeight (const int fontFace, const int pixelHeight, const int width = 1)
	Вычисляет размер шрифта для использования в достичь заданной высоты в пикселях. Подробнее …
Размер	cv :: getTextSize (const String & text, int fontFace, double fontScale, int width, int * baseLine)
	Вычисляет ширину и высоту текстовая строка.Подробнее …
void	cv :: line (InputOutputArray img, Point pt1, Point pt2, const Scalar & color, int width = 1, int lineType = LINE_8, int shift = 0)
	Рисует отрезок линии, соединяющий две точки. Подробнее …
void	cv :: polylines (Mat & img, const Point * const * pts, const int * npts, int ncontours, bool isClosed, const Scalar & color, int width = 1 , int lineType = LINE_8, int shift = 0)
void	cv :: polylines (InputOutputArray img, InputArrayOfArrays pts, bool isClosed, const Scalar & color line_Type = 1, int8 int shift = 0)
	Рисует несколько многоугольных кривых.Подробнее …
void	cv :: putText (InputOutputArray img, const String & text, Point org, int fontFace, double fontScale, Scalar color, int width = 1, int lineType = LINE_8, bool bottomLeftOrigin = false)
	Рисует текстовую строку. Подробнее …
void	cv :: rectangle (InputOutputArray img, Point pt1, Point pt2, const Scalar & color, int width = 1, int lineType = LINE_8, int shift = 0)
	Рисует простой, толстый или закрашенный прямоугольник с правой стороны.Подробнее …
void	cv :: rectangle (Mat & img, Rect rec, const Scalar & color, int толщина = 1, int lineType = LINE_8, int shift = 0)

Как перенести рисунок углем в энкаустике

В последнее время я рисовал серию птиц энкаустическим воском. Попутно я публиковал примеры своей незавершенной работы на Facebook. Несколько моих последователей спрашивали меня, как нанести древесный уголь на энкаустический воск.

Это очень просто…
Вот что вам понадобится:

• Фотография или рисунок объекта, который вы хотите перенести.
• Доска для энкаустики «грунтованная».
  • Доска должна быть загрунтована слоем воска, нанесенного на поверхность. Перед переносом изображения убедитесь, что воск расплавлен и остыл на ощупь.
• Угольный карандаш или виноградный уголь.
• Калька.
• Инструмент для втирания / полирования изображения на доску. Ниже я использую костяную папку. Вы также можете попробовать обратную сторону ложки.

Вот как я это делаю:

1. Углем я обрисовываю объект, который нужно передать — в данном случае это сова.
2. Затем я кладу рисунок углем лицевой стороной вниз на загрунтованную поверхность из энкаустического воска. Лицом вниз означает, что рисунок углем касается поверхности воска. Имейте в виду, что теперь изображение будет отображаться в противоположном направлении, чем ваш исходный рисунок.
3. Когда рисунок на месте, я использую папку для костей (или ложку), чтобы аккуратно протирать линии рисунка. Будьте внимательны, чтобы не надавить слишком сильно и не повредить восковую поверхность.
4. Наконец, я осторожно отделяю кальку, чтобы открыть рисунок, нанесенный углем.В этот момент я смотрю на переданное изображение, не поднимая полностью кальку. Если изображение слишком бледное, я могу легко заменить бумагу, совместить линии и повторить описанный выше процесс.
5. Когда я доволен переводом углем, я осторожно расплавляю рисунок перед добавлением энкаустического пигмента.

Эта техника передачи углем очень полезна и помогает мне в моем реалистичном подходе к рисованию энкаустикой. Надеюсь, вы поэкспериментируете с угольным переводом и дадите волю своему воображению!
* Давайте также встретимся в Twitter , и Google Plus , Pinterest, и присоединяйтесь к веселью на фан-странице Fine Art Tips в Facebook! Пожалуйста, посмотрите и мое искусство, LoriMcNee.com, или найдите меня в Instagram lorimcneeartist.

AutoCAD Precise Input: определение координаты точки

Вы узнали, как использовать инструменты рисования AutoCAD. Когда вы активируете инструмент рисования AutoCAD, AutoCAD запрашивает у вас две возможности: параметры или указание точек. Некоторые инструменты AutoCAD запрашивают у вас подтверждение настроек, прежде чем запрашивать у вас балл. В конце концов вам нужно будет определить точки. В этом руководстве мы обсудим, как мы можем дать точные данные, когда AutoCAD запрашивает у нас местоположение точки.

Объект чертежа по сравнению с AutoCAD Scale

Во-первых, давайте обсудим, как мы должны рисовать на вашем чертеже AutoCAD в соответствии с вашим масштабом. Рисуем наш объект в реальном размере. Если у вас есть объект длиной 5 футов, проведите линию длиной 5 футов. Если у вас есть объект длиной 100 см, нарисуйте его длиной 100 см. Я должен это подчеркнуть, потому что я обнаружил, что некоторые люди так не работают. У них есть объект длиной 100 см, и, поскольку они планируют построить его в масштабе 1: 100, они рисуют его длиной 1 см. Нет-нет.

Мы всегда рисуем объекты в их реальном размере в CAD… любых приложениях CAD. Мы используем масштаб только для построения графика. Мы рисуем в безграничном пространстве. Я знаю, что это неправда. Но большинство приложений САПР могут справиться с размером вашего дизайна.

AutoCAD по умолчанию имеет только 2 единицы: дюйм (британская) и мм (метрическая) для печати. Поэтому нам лучше использовать эти две единицы, чтобы избежать путаницы при построении графика (позже об этом). Итак, если вы работаете в метрической системе и хотите провести линию длиной 1 м, нарисуйте ее на 1000 мм.

Значит, AutoCAD распознает только миллиметры и дюймы? Нет. Только для сюжета. Мы можем использовать другие единицы измерения, такие как футы, см или м, но я рекомендую вам использовать дюйм или мм в первый раз.

«Классический» против динамического ввода

Начиная с AutoCAD 2006 (поправьте меня, если я ошибаюсь) Autodesk представляет пользователям AutoCAD «динамический ввод». Если вы только что установили AutoCAD, эта функция по умолчанию включена. Если вы или кто-то выключил его, попробуйте включить. Сначала попробуйте. Позже, если он вам не понравится, вы можете выключить его.Нажмите кнопку динамического ввода в группе настроек черчения.

Метод определения координат с использованием динамического ввода или «классического» ввода немного отличается. Однако у них та же концепция.

Относительная координата

Активировать инструмент линии. Мы попробуем этот базовый инструмент, чтобы понять, как мы можем говорить с AutoCAD о координатах точки.

AutoCAD спросит вас о первой точке. Поскольку в нашем чертеже еще ничего нет, просто щелкните в любом месте, чтобы определить начальную точку.

Полярные координаты

После того, как вы разместите первую точку, AutoCAD покажет вам динамический ввод, как показано на рисунке ниже. По умолчанию динамический ввод запрашивает ввод полярных координат.

Описание чертежа

1. Длина линии
2. Угол линии относительно положительной оси X
3. Инструмент опция

Вы можете просто ввести длину линии, нажать вкладку, чтобы перейти в поле угла, ввести значение угла и нажать [ввод].

При использовании более сложного инструмента AutoCAD вам, вероятно, потребуется изменить параметры инструмента. Вы можете нажать стрелку вниз, чтобы увидеть доступные параметры. Для инструмента AutoCAD Line есть только опция «отменить». Это отменит последний сегмент линии.

Значение, отображаемое динамическим вводом, является относительной координатой. Это означает, что он показывает расстояние между указателем и предыдущей точкой. Итак, если вы хотите нарисовать горизонтальную линию длиной 100: после того, как вы щелкнете по первой точке, введите 100 для длины, нажмите [tab], чтобы перейти к типу поля угла 0, затем [enter].Он создаст линию длиной 100 единиц, параллельную положительной оси X.

Что произойдет, если вы введете 100 для длины и 180 для угла? Попытайся!

Совет: вы также можете определить длину и угол, набрав расстояние <угол. Например 100 <30.

Декартова координата

Другой распространенной координатой, которую мы используем, является декартова координата, определяющая значения X и Y. Мы можем сделать это, набрав X, Y, когда динамический ввод запрашивает следующую точку. После того, как мы нажмем запятую, динамический ввод покажет вам значения X и Y, как это.

25,50 означает 25 единиц вправо, затем 50 единиц вверх.

Если ввести положительное значение, следующая точка будет на положительной оси X / Y. Но если вы введете отрицательное значение, оно будет находиться на отрицательной оси ОТ вашей последней точки. Попытайся!

Глобальная координата

Если вы работаете в сфере землеустройства, вам понадобится то, что мы называем глобальными координатами. Вы можете захотеть точно рисовать точки или объекты из контрольной точки. Точка пересечения осей AutoCAD X и Y — координата 0,0.

Помните: по умолчанию положительная ось X направлена ​​вправо, а положительная ось Y — вверху.

Мы можем ввести глобальную координату, добавив префиксный хэш-тег # перед вводом значения XY. Если вы добавите префикс #, AutoCAD проигнорирует предыдущую точку и будет измерять вашу точку от глобальной координаты 0,0 AutoCAD. Попробуйте!

Использование «классического» ввода AutoCAD

Все вышеперечисленные режимы ввода — если у вас включен динамический ввод. Если его выключить, то ввод координат немного отличается.Вы, вероятно, увидите, что многие опытные пользователи AutoCAD все еще используют этот способ. Основная причина, по которой люди не любят использовать динамический ввод, заключается в том, что они чувствуют, что это мешает их обзору.

Если отключить динамический ввод, то:

1. Когда вы вводите значение X, Y, вы определяете глобальную координату.
2. Для определения относительной координаты вам нужно добавить префикс @ перед вводом X, Y. Это будет @ X, Y.
3. Это также относится к полярным координатам. Вы должны ввести @distance <угол для относительной координаты.

Какой из них вы будете использовать, решать только вам. Однако я рекомендую вам использовать динамический ввод, потому что это обычный способ определения координат в других приложениях САПР.

Теперь у нас будет упражнение.

Об Эдвине Пракосо

Я работаю старшим техническим консультантом в компании Tech Data Advanced Solutions Indonesia.