Основы статистической обработки данных кривая гаусса: Нормальное распределение (Гаусса) в Excel

Закон нормального распределения

Значение для исследований в области физической культуры и спорта (ФКиС)

Нормальное распределение случайной величины (гауссово распределение, распределение Гаусса, распределение Гаусса-Лапласа) – одно из непрерывных распределений, имеющее основополагающую роль в математической статистике. Причинами это являются:

1. Многие эмпирические распределения можно успешно описать с помощью нормального закона распределения. Это чаще всего происходит в тех случаях, когда на показатель оказывает влияние большое число случайных факторов. При этом действие каждого фактора незначительно. Примерами показателей, которые распределяются по нормальному закону являются: рост, сила мышц, результаты в беге, прыжках, метаниях и др.
2. Нормальное распределение обладает рядом благоприятных математических свойств, обеспечивших его широкое применение в статистике.
3. Корректное использование критериев проверки статистических гипотез предполагает знание закона распределения экспериментальных данных. Так, например, использование t – критерия Стьюдента и  F-критерия Фишера требует нормального распределения экспериментальных данных.
4. Большинство экспериментальных распределений, полученных при исследованиях в области физической культуры и спорта может быть описано с помощью нормального распределения.

Однако в природе и в области ФКиС встречаются экспериментальные распределения, для описания которых модель нормального распределения малопригодна.

Более подробно о методах статистической обработки данных рассказано в книгах:

• Факторный анализ в педагогических исследованиях в области физической культуры и спорта
• Компьютерная обработка данных экспериментальных исследований
• Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта

История изучения нормального распределения

Блез Паскаль и Пьер Ферма

Первые исследования по теории вероятностей проводили математик, механик, физик Блез Паскаль и математик Пьер Ферма в середине XVII века. Эти исследования выполнялись по  просьбе Шевалье де Мере, азартного игрока в кости, который пытался понять природу выигрыша. В дальнейшем эти исследования заложили основы теории вероятностей (Дж. Гласс, Дж. Стэнли, 1976).

Якоб Бернулли

Дальнейшее развитие теория вероятностей получила в XVIII веке. В 1713 году была опубликована  книга швейцарского математика Якоба Бернулли «Искусство предположений». В этой книге был рассмотрен ряд вопросов теории вероятностей.  Якоб Бернулли ввёл значительную часть современных понятий теории вероятностей, а также  изложил правила подсчёта вероятности для сложных событий и дал первый вариант «закона больших чисел», разъясняющего, почему частота события в серии испытаний не меняется хаотично, а в некотором смысле стремится к своему предельному теоретическому значению (то есть вероятности).

Джеймс Стирлинг

В последствии (в 1730 г.) шотландский математик Джеймс Стирлинг опубликовал формулу, аппроксимирующую произведение первых n чисел. Это позволило упростить решение ряда задач, которые встречаются в теории вероятностей. Однако все еще эти задачи оставались трудно разрешимыми.

Абрахам де Муавр

Эту задачу решил английский математик Абрахам де Муавр. В работе «Доктрина случайностей», которая была издана в 1738 году он привел формулу, аппроксимирующую  биномиальное распределение события, вероятность которого была равна 0,5  (рис.1).  То есть он нашел уравнение кривой, проходящей через точки графика, изображенного на рис. 1. Эта была формула, которую впоследствии стали называть формулой нормального распределения вероятностей. Появление  формулы нормального распределения значительно упростило расчеты вероятностей событий.

Пьер-Симон де Лаплас

В начале XIX века (в 1812 г.) французский математик, механик, физик и астроном Пьер-Симон де Лаплас  обобщил результаты А. Муавра для произвольного биномиального распределения.

Рис.1. Биномиальное распределение

Карл Фридрих Гаусс

Одновременно с П. Лапласом в 1809 году немецкий математик, механик, физик и астроном Карл Фридрих Гаусс в сочинении «Теория движения небесных тел» использовал формулу нормального распределения для описания случайных ошибок, возникающих в результате многократных измерений  движений небесных тел. К.Ф. Гаусс внес настолько большой вклад в разработку теории нормального распределения, что впоследствии это распределение стали назвать гауссово распределение или распределение Гаусса-Лапласса.

Адольф Кетле

В начале ХХ века бельгийский математик, астроном и социолог Адольф Кетле  одним из первых применил  нормальный закон распределения случайной величины к анализу биологических и социальных процессов. Изучая распределение солдат американской армии по росту, Адольф Кетле  обратил внимание, что распределение роста подчиняется нормальному закону. Он писал: «…Человеческий рост, изменяющийся, по-видимому, самым случайным образом, тем не менее подчиняется самым точным законам, и эта особенность свойственна не только росту, она проявляется также в весе, силе, быстроте передвижений человека, во всех его физических … и нравственных способностях. Этот великий принцип… разнообразящий проявление человеческих способностей…кажется нам одним из самых удивительных законов мира» (А.Кетле, 1911).

В настоящее время нормальное распределение широко используется в биологии, медицине, экономике и других областях науки.

Формула нормального распределения

Формула, описывающая нормальный закон распределения случайной величины, имеет следующий вид:

где: μ — генеральное среднее арифметическое; σ — генеральное стандартное отклонение, е — основание натуральных логарифмов, приблизительно равное 2,719, π — число, приблизительно равное 3,142; xi — конкретное значение признака.

Пусть Вас не пугает эта формула. Сейчас мы с ней разберемся. Для начала давайте посмотрим, как выглядит график, построенный на основе этой формулы. Зададим значения μ=0  и σ=1.  Хочу заметить, что μ и σ — это просто числа. Их еще называют параметрами распределения. Поэтому критерии, в формулу расчета которых входят параметры распределения называют параметрическими. Например, параметрическим критерием является t-критерий Стьюдента. В формулу расчета критерия Стьюдента входят параметры μ и σ. Кривая нормального распределения вероятностей имеет вид (рис.2).

Рис.2. График плотности вероятностей нормального распределения при μ=0  и σ=1.

 

Если мы поменяем параметры, то получим следующее. Изменение параметра μ будет сдвигать график вдоль оси Х. Например при  μ=3 график сместится вправо вдоль оси Х  (рис.3).

Рис.3. График плотности вероятностей нормального распределения при μ=3  и σ=1.

Если мы оставим μ=0 , а изменим параметр σ, например σ=3, то получим распределение с большим размахом (рис.4).

Рис.4. График плотности вероятностей нормального распределения при μ=0  и σ=3.

Свойства нормального распределения

1. Нормальная кривая имеет колокообразную форму, симметричную относительно точки x=µ, с точками перегиба, абсциссы которых отстоят от µ на ± σ.
2. Нормальное распределение полностью определятся двумя параметрами: значением генерального среднего (µ) и генерального стандартного отклонения (σ).
3. Медиана и мода нормального распределения совпадают и равны µ.
4. Коэффициенты асимметрии и эксцесса нормального распределения равны нулю.

Нормированное отклонение

В области математической статистики важное место занимает нормированное отклонение (t) – показатель, представляющий отклонение той или иной варианты от средней величины, отнесенное к значению стандартного отклонения. Нормированное отклонение рассчитывает по формуле:

Нормированное отклонение позволяет установить, на сколько «сигм» отклоняются варианты от среднего значения. Например, необходимо определить насколько «сигм» отклоняется значение роста человека, равное 180 см от среднего, если среднее арифметическое равно 170 см, а «сигма», то есть стандартное отклонение равно 10 см. Подставив эти значения в формулу, получим: t= (180-170)/10 = 1.

Ответ: значение роста человека, равное 180 см отклоняется от среднего на одну «сигму».

Нормированное нормальное распределение

Рис. 5. Нормированное нормальное распределение роста мужчин с параметрами: µ=0; σ = 1.

Формула нормального распределения описывает целое семейство кривых, зависящих от двух параметров μ и σ, которые могут принимать любые значения. Поэтому возможно бесконечно много нормально распределенных совокупностей.

Чтобы избежать неудобств, связанных с расчетами для каждого конкретного случая в до компьютерную эпоху было предложено использовать нормированное (стандартное) нормальное распределение, для которого были составлены подробные таблицы. Нормированное нормальное распределение имеет параметры:   µ=0; σ = 1 (рис.1, 5). Это распределение получается, если пронормировать нормально распределенную величину Х по формуле: U= (X-μ)/σ.

Для нормированного нормального распределения характерно, что в интервал µ±σ попадают 68 % всех результатов, в интервал µ±2σ попадают 95% всех результатов, в интервал µ±3σ попадают 99 % всех результатов.

В области физической культуры и спорта эти закономерности используют для разработки системы оценок. Так, В.М. Зациорским (рис. 6) предложено использовать следующую систему оценок результатов.  Если результат, показанный спортсменом, попал в интервал от -2σ до -1σ — он получает низкую оценку (Рассчитать, в какой интервал попадает результат можно при помощи нормированного отклонения. Это описано выше). Если результат попал в интервал от -1σ до -0,5σ — оценка ниже средней. Средний результат соответствует интервалу от -0,5σ до -0,5σ, результат, получивший оценку выше среднего — от 0,5 до 1σ. Высокий результат попадает в интервал от 1σ до 2σ.

Рис.6. Использование нормального распределения для разработки системы оценок результатов

Критерии согласия

Чтобы проверить, соответствует ли распределение нормальному закону, существует много методов.

Можно использовать свойства нормального распределения (равенство среднего, моды и медианы).

Однако более точные результаты дают критерии согласия. В зависимости от объема выборки (n) следует использовать различные критерии:

• если объем выборки небольшой (n = 10) – критерий Шапиро – Уилки;
• если объем выборки более 40 — критерий хи-квадрат и критерий Колмогорова-Смирнова.
• в статистическом пакете Statgraphics Centurion существует специальная опция — критерии проверки нормальности распределения. В этой опции есть 4 критерия, посредством которых можно сделать вывод о соответствии эмпирического распределения нормальному закону.

Литература

1. Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
2. Гласс Дж., Стенли Дж. Статистические методы в педагогике и психологии.- М.: Прогресс, 1976.-495 с.
3. Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
4. Кетле А. (1835) Социальная физика, или опыт исследования о развитии человеческих способностей.  Т.1, 1911.- С. 38-39.
5. Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.

Статистические методы обработки медико-биологической информации

30

КРАТКАЯ ТЕОРИЯ

В медицине необходимо вести учет, анализ и прогноз различных массовых явлений. В целом, массовым явлениям присущи свои особые закономерности. К доктору обращаются пациенты с различными заболеваниями. Болезнь конкретного человека — случайное событие для врача. Но случайные события предсказуемы, например, в период эпидемии гриппа наиболее часто встречаются заболевания гриппом. Закономерности массовых случайных событий — статистических данных, отражающих эти события, — изучаются с помощью математической статистики. Математическая статистика использует основные понятия и положения теории вероятностей.

Типичная задача математической статистики — это приближенная оценка неизвестной вероятности случайного события по результатам наблюдений, экспериментов, когда событие может происходить или не осуществляться. Поэтому необходимо вычислять различные вероятности и сравнивать их между собой. Такие задачи необходимо решать специалистам по генетике, экологии, демографии, в различных областях медицины. Подробно практическое применение в медицине статистических методов рассматривается в курсе социальной гигиены и организации здравоохранения.

Случайной величиной называется переменная величина, значение которой зависит от исхода некоторого испытания.

Дискретной называется случайная величина, которая может принимать значения некоторой конечной или бесконечной числовой последовательности (число таблеток в упаковке, больных в палате, студентов в аудитории …).

Непрерывной называется случайная величина, которая может принимать любые значения внутри некоторого интервала (масса, температура, рост

. .).

Распределение дискретной случайной величины

Дискретная случайная величина считается заданной, если указаны ее возможные значения и соответствующие им вероятности:

Дискретные случайные величины X j	Xi	Х2	Хз	х4	Х5
Вероятность Р;	Pi	р2	Рз	р4	р5. …

Совокупность X, и Pj называется распределением дискретной случайной величины.

Поскольку всс возможные значения дискретной случайной величины представляют полную систему, то сумма вероятностей равна 1:

п

i=l

условие нормировки

Различные распределения

1. Биномиальное распределение (позволяет определить вероятность того, что событие А произойдет i раз при п испытаниях).

2. Распределение Максвелла (распределение газовых молекул по скоростям, кинетическим энергиям. График — кривая Максвелла).

На рисунке показано распределение молекул газа по скоростям- распределение Максвелла, которое строго верно для газа, находящегося в покое

3. Распределение Больцмана (распределение частиц по потенциальным

энергиям в силовых полях

гравитационном, электрическом.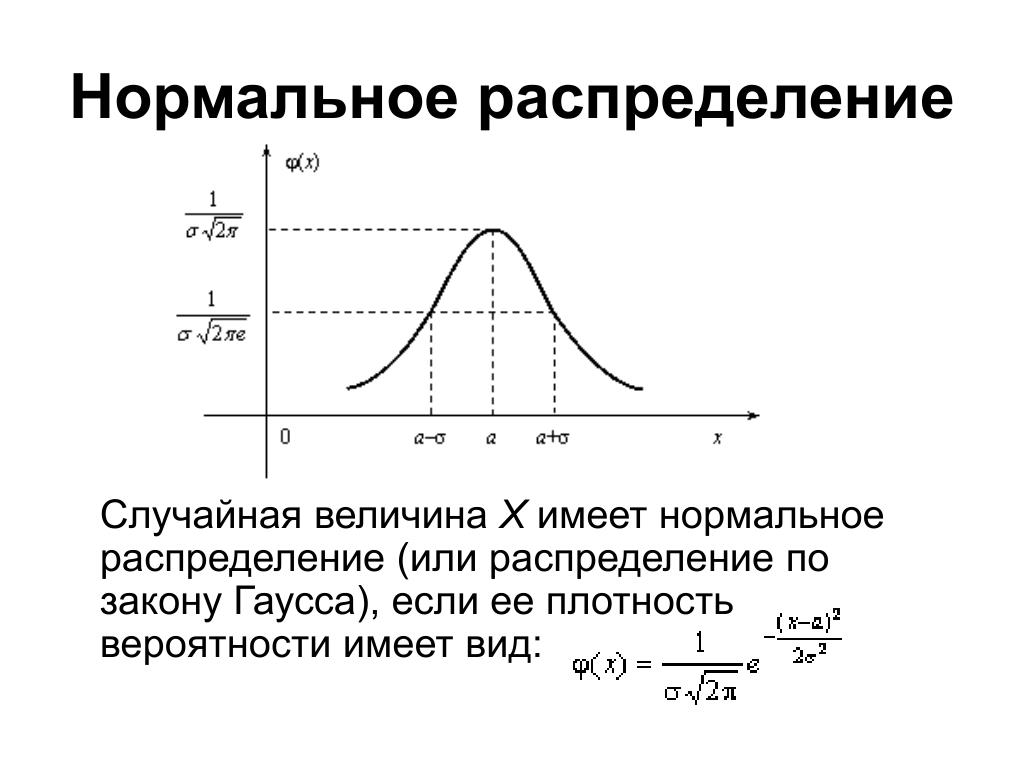 График — экспонента).

Это распределение приемлемо к частицам, находящимся в состоянии хаотического теплового движения.

4. Нормальное распределение (график — кривая Гаусса).

5. Распределение Пуассона (вероятностная модель редких событий — эпидемии, космические лучи, аварии, распределение изюминок в булочке) и др.

Нормальный закон распределения имеет важное практическое значение в естественных науках. Оказывается, распределение роста, массы новорожденных, параметров частоты сердечных сокращений, давления, жизненной ёмкости лёгких, частоты дыхания и много других случайных событий физической и биологической природы описываются нормальным законом распределения и графически иллюстрируется кривой Гаусса. Для понимания этого закона необходимо изучить терминологию и освоить новые понятия числовых характеристик дискретных и непрерывных случайных величин.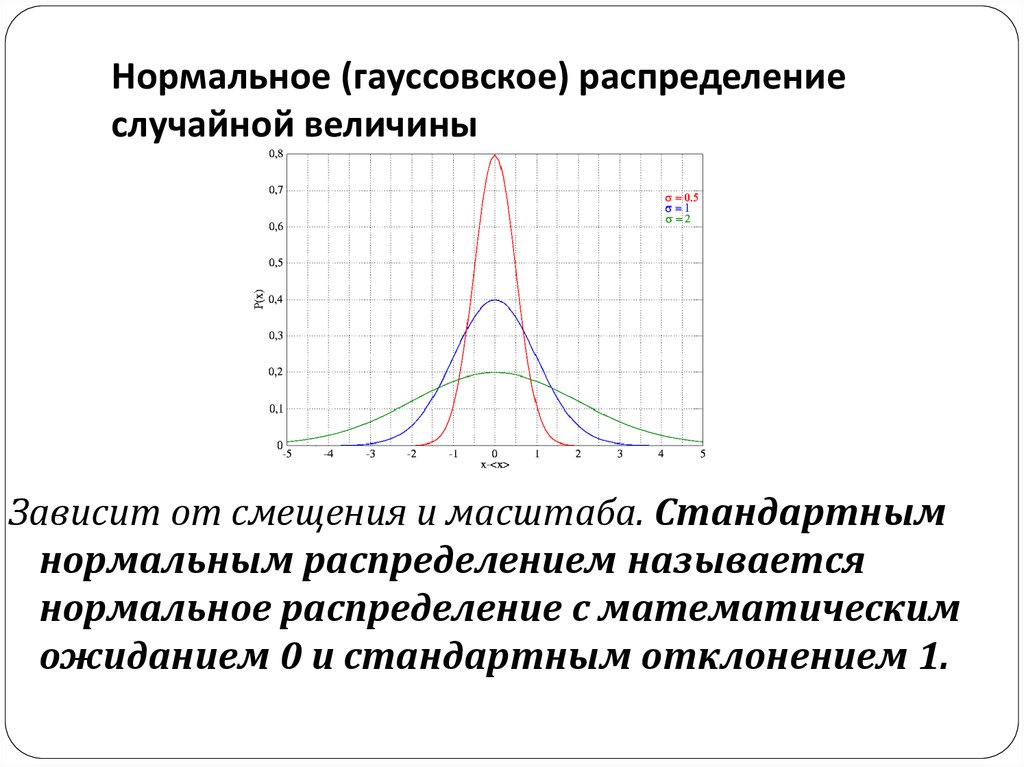

Что это такое, свойства, применение и формула

Что такое нормальное распределение?

Нормальное распределение, также известное как распределение Гаусса, представляет собой распределение вероятностей, симметричное относительно среднего значения, показывающее, что данные, близкие к среднему, встречаются чаще, чем данные, далекие от среднего.

В графической форме нормальное распределение выглядит как «гауссова кривая».

Основные выводы

• Нормальное распределение — это правильный термин для колоколообразной кривой вероятности.
• В нормальном распределении среднее значение равно нулю, а стандартное отклонение равно 1. Оно имеет нулевую асимметрию и эксцесс 3.
• Нормальные распределения симметричны, но не все симметричные распределения являются нормальными.
• Многие естественные явления имеют тенденцию приближаться к нормальному распределению.
• Однако в финансах большинство распределений цен не являются совершенно нормальными.

Нормальное распределение

Понимание нормального распределения

Нормальное распределение является наиболее распространенным типом распределения, используемым в техническом анализе фондового рынка и в других видах статистического анализа. Стандартное нормальное распределение имеет два параметра: среднее значение и стандартное отклонение.

Модель нормального распределения важна в статистике и является ключом к Центральной предельной теореме (ЦПТ). Эта теория утверждает, что средние значения, рассчитанные для независимых, одинаково распределенных случайных величин, имеют приблизительно нормальное распределение, независимо от типа распределения, из которого взяты переменные (при условии, что оно имеет конечную дисперсию).

Нормальное распределение является одним из видов симметричного распределения. Симметричные распределения возникают, когда разделительная линия дает два зеркальных изображения. Не все симметричные распределения являются нормальными, поскольку некоторые данные могут выглядеть как два горба или ряд холмов в дополнение к кривой нормального распределения, указывающей на нормальное распределение.

Свойства нормального распределения

Нормальное распределение имеет несколько ключевых особенностей и свойств, которые его определяют.

Во-первых, его среднее (среднее), медиана (средняя точка) и мода (наиболее частое наблюдение) равны друг другу. Более того, все эти значения представляют собой пик или наивысшую точку распределения. Затем распределение падает симметрично вокруг среднего значения, ширина которого определяется стандартным отклонением.

Все нормальные распределения можно описать всего двумя параметрами: средним значением и стандартным отклонением.

Эмпирическое правило

Для всех нормальных распределений 68,2% наблюдений будут находиться в пределах плюс-минус одно стандартное отклонение от среднего значения; 95,4% наблюдений будут находиться в пределах +/- двух стандартных отклонений; и 99,7% в пределах +/- трех стандартных отклонений. Этот факт иногда называют «эмпирическим правилом» — эвристикой, описывающей, где будет появляться большая часть данных в нормальном распределении.

Это означает, что данные, выходящие за пределы трех стандартных отклонений («3-сигма»), будут означать редкие случаи.

Инвестопедия / Сабрина Цзян

Асимметрия

Асимметрия измеряет степень симметрии распределения. Нормальное распределение симметрично и имеет нулевую асимметрию.

Если вместо этого распределение набора данных имеет асимметрию меньше нуля или отрицательную асимметрию (асимметрию влево), то левый хвост распределения длиннее правого; положительная асимметрия (правая асимметрия) означает, что правый хвост распределения длиннее левого.

Эксцесс

Эксцесс измеряет толщину хвостов распределения по отношению к хвостам распределения. Нормальное распределение имеет эксцесс, равный 3,0.

Распределения с большим эксцессом более 3,0 демонстрируют хвостовые данные, превышающие хвосты нормального распределения (например, пять или более стандартных отклонений от среднего). Этот избыточный эксцесс известен в статистике как лептокуртик, но в просторечии он известен как «толстые хвосты». Возникновение толстых хвостов на финансовых рынках описывает так называемый хвостовой риск.

Распределения с низким эксцессом менее 3,0 (платикуртик) демонстрируют хвосты, которые обычно менее экстремальны («более тонкие»), чем хвосты нормального распределения.

Формула нормального распределения

Нормальное распределение подчиняется следующей формуле. Обратите внимание, что необходимы только значения среднего (μ) и стандартного отклонения (σ).

Формула нормального распределения.

где:

• x  = значение исследуемой переменной или данных и f(x) функция вероятности
• μ = среднее значение
• σ = стандартное отклонение

Как нормальное распределение используется в финансах

Предположение о нормальном распределении применяется как к ценам активов, так и к ценовому действию. Трейдеры могут отображать ценовые точки с течением времени, чтобы подогнать недавнее ценовое движение к нормальному распределению. Чем дальше цена движется от среднего значения, в этом случае тем выше вероятность того, что актив переоценен или недооценен. Трейдеры могут использовать стандартные отклонения, чтобы предлагать потенциальные сделки. Этот тип торговли, как правило, осуществляется на очень коротких временных интервалах, поскольку большие временные масштабы затрудняют выбор точек входа и выхода.

Точно так же многие статистические теории пытаются моделировать цены на активы в предположении, что они подчиняются нормальному распределению. В действительности, ценовые распределения, как правило, имеют толстые хвосты и, следовательно, имеют эксцесс больше трех. Цены на такие активы превышали среднее значение более чем на три стандартных отклонения чаще, чем можно было бы ожидать, исходя из предположения о нормальном распределении. Даже если актив прошел через длительный период, в течение которого он соответствует нормальному распределению, нет никакой гарантии, что прошлые результаты действительно влияют на будущие перспективы.

Пример нормального распределения

Многие естественные явления кажутся нормально распределенными. Возьмем, к примеру, распределение роста людей. Средний рост составляет примерно 175 см (5 футов 9 дюймов), считая как мужчин, так и женщин.

Как показано на приведенной ниже диаграмме, большинство людей соответствуют этому среднему показателю. Между тем, более высокие и низкие люди существуют, но их частота в популяции снижается. Согласно эмпирическому правилу, 99,7 % всех людей упадут с +/- тремя стандартными отклонениями от среднего или между 154 см (5 футов 0 дюймов) и 19 см.6 см (6 футов 5 дюймов). Те, кто выше и ниже, были бы довольно редки (всего 0,15% населения каждый).

Что подразумевается под нормальным распределением?

Нормальное распределение описывает симметричный график данных относительно среднего значения, где ширина кривой определяется стандартным отклонением. Визуально это изображается как «гауссовая кривая».

Почему нормальное распределение называется «нормальным»?

Нормальное распределение технически известно как распределение Гаусса, однако оно получило терминологию «нормальный» после научных публикаций в 19^-й -й век, показывающий, что многие природные явления, по-видимому, «нормально отклоняются» от среднего значения. Эта идея «нормальной изменчивости» стала популярной как «нормальная кривая» натуралиста сэра Фрэнсиса Гальтона в его работе 1889 года « Natural Inheritance».

Каковы ограничения нормального распределения в финансах?

Хотя нормальное распределение является чрезвычайно важным статистическим понятием, его применение в финансах может быть ограничено, поскольку финансовые явления, такие как ожидаемая доходность фондового рынка, не подпадают под нормальное распределение. На самом деле цены, как правило, следуют логарифмически нормальному распределению, которое смещено вправо и имеет более толстые хвосты. Следовательно, слишком сильно полагаться на кривую нормального распределения при прогнозировании этих событий может привести к ненадежным результатам. Хотя большинству аналитиков хорошо известно об этом ограничении, преодолеть этот недостаток довольно сложно, поскольку часто неясно, какое статистическое распределение использовать в качестве альтернативы.

Что такое нормальное распределение и стандартное отклонение в статистике

Данные, которые вы хотите проанализировать, могут иметь любое распределение, а графики распределения вероятностей могут принимать очень четкие и узнаваемые формы. Распознавание этих графиков и распределений может помочь вам найти определенные характеристики ваших данных и выполнить с ними определенные вычисления.

Что такое нормальное распределение?

Нормальное распределение — это непрерывное распределение вероятностей с функцией плотности вероятности, которая дает вам симметричную кривую нормального распределения. Проще говоря, это график функции вероятности переменной, в которой максимальные данные сосредоточены вокруг одной точки, а несколько точек симметрично сужаются к двум противоположным концам.

В этом определении нормального распределения вы изучите следующие термины:

1. Непрерывное распределение вероятностей: Распределение вероятностей, при котором случайная величина X может принимать любое заданное значение, например количество осадков. Вы можете записать количество осадков, полученных в определенное время, как 9 дюймов. Но это не точное значение. Фактическое значение может быть 9,001234 дюйма или бесконечное количество других чисел. В этом случае нет определенного способа нанести точку, и вместо этого вы используете непрерывное значение.
2. Функция плотности вероятности: выражение, используемое для определения диапазона значений, которые может принимать непрерывная случайная величина.

Нормальное распределение имеет распределение вероятностей, сосредоточенное вокруг среднего значения. Это означает, что распределение имеет больше данных вокруг среднего значения. Распределение данных уменьшается по мере удаления от центра. Полученная кривая симметрична относительно среднего значения и образует колоколообразную форму распределения. Рассмотрим приведенный ниже график, который показывает вероятностное распределение роста в классе:

Рисунок 1: Нормальное распределение

На приведенном выше графике видно, что распределение в основном соответствует среднему или среднему значению всех высот. Помимо этого, большинство данных находится около среднего значения. По мере удаления плотность вероятности также уменьшается. Такая кривая называется кривой Белла, и она является общей чертой нормального распределения.

Что такое стандартное отклонение?

Стандартное отклонение — это мера того, насколько значения в ваших данных отличаются друг от друга или насколько разбросаны ваши данные.

Стандартное отклонение измеряет, насколько далеко друг от друга находятся точки данных в ваших наблюдениях. Вы можете рассчитать его, вычитая каждую точку данных из среднего значения, а затем находя квадрат среднего значения разностей; это называется дисперсией. Квадратный корень из дисперсии дает вам стандартное отклонение.

Подобно тому, как среднее значение говорит вам, где центрируются данные, стандартное отклонение дает вам ширину кривой нормального распределения. Он говорит вам, насколько узкой или широкой является кривая нормального распределения. Рассмотрим пример доходов в сельской и городской местности.

 

Рисунок 2: Стандартное отклонение

В сельской местности, скажем, в фермерском поселке, большинство людей занимаются одной и той же профессией – земледелием. Все они зарабатывают более или менее одинаково, причем заминдар зарабатывает больше всего. Большинство людей здесь получают одинаковый средний доход, о чем свидетельствует высокий пик среднего значения. В наших данных нет большого отклонения. Следовательно, кривая относительно узкая.

В городском городе население больше. Есть также больше людей, выполняющих разные работы, которые оплачиваются на очень разном уровне. Некоторые люди могут быть бизнесменами, а другие могут даже не иметь фиксированного дохода. Это приводит к большему разбросу данных, и, следовательно, кривая становится более разбросанной или имеет более высокое стандартное отклонение.

Теперь разберем стандартное отклонение на примере.

Рассмотрим пример роста собак, приведенный ниже:

 

Рисунок 3: Высота собаки

Сначала вы найдете среднее или среднее значение всех этих значений, сложив их все и разделив полученную сумму на количество точек данных.

Рисунок 4: Средняя высота

Это означает, что средний рост собаки составляет 394 мм. Теперь вычтите все точки данных из среднего значения.

Рисунок 5: Разница между ростом и средним значением

Отрицательные значения означают, что значение находится ниже среднего, а положительные значения говорят о том, что точка данных находится выше среднего. Значение 0 означает, что точка данных совпадает со средним значением. Теперь давайте возведем каждое значение в квадрат и найдем их среднее значение, чтобы получить дисперсию.

Рисунок 6: Стандартное отклонение данных о росте собак

Нахождение квадратного корня из дисперсии дает вам стандартное отклонение. В данном случае это 147 мм. Это означает, что кривая скорее высокая, чем широкая, имеет небольшой разброс и является узкой. В данных не так много отклонений.

Что такое стандартное нормальное распределение?

Стандартное нормальное распределение — это тип нормального распределения со средним значением 0 и стандартным отклонением 1. Это означает, что центр нормального распределения находится в 0, а интервалы увеличиваются на 1.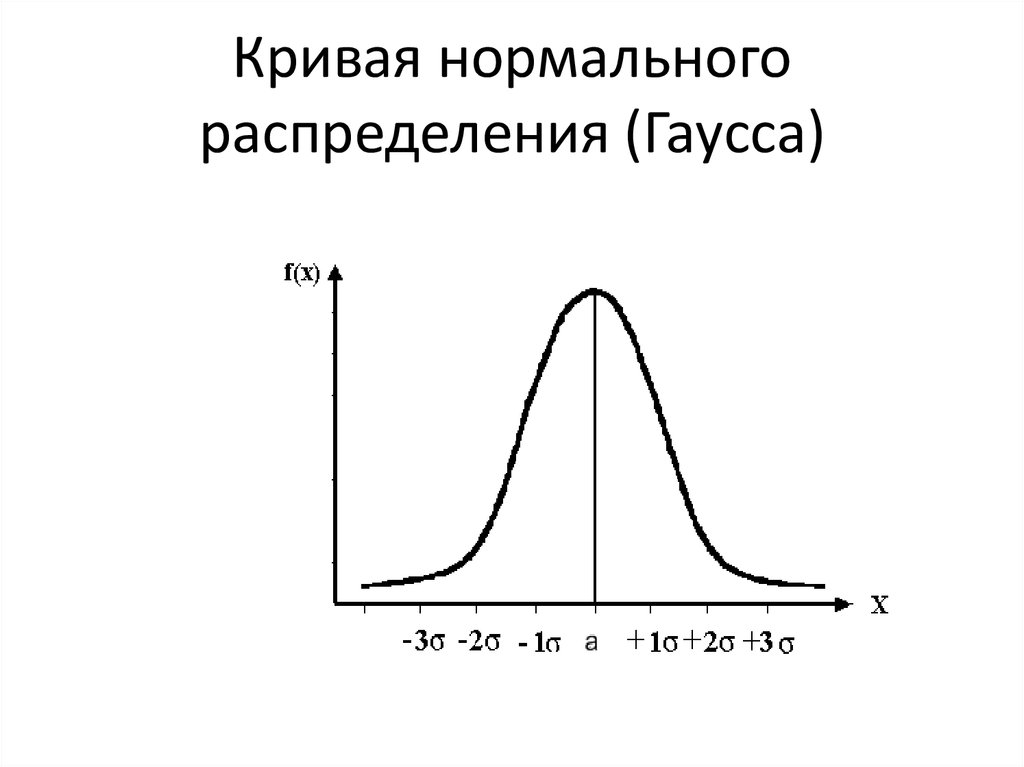

Среднее значение и стандартное отклонение в нормальном распределении не фиксированы. Они могут принимать любое значение. Однако при стандартизации нормального распределения среднее значение и стандартное отклонение остаются фиксированными и одинаковыми для всех стандартных нормальных распределений. Рассмотрим приведенный ниже пример весов учеников в классе:

Рисунок 7: Стандартное нормальное распределение

Отображает фактический вес учащихся над осью x. Но из графика видно, что точки данных отличаются на 5 баллов. Найдя среднее значение, вы получите его как 50, поэтому вы можете принять это как 0-ю точку. Остальные точки расположены на одинаковом расстоянии друг от друга и при стандартизации отличаются на 1, поэтому вы можете переписать шкалу так, чтобы центрировать ее вокруг 0 ​​и увеличивать на 1. Точки выше среднего попадают в положительные значения, а ниже среднего — в отрицательные. .

Когда вы стандартизируете свои данные, вычисление вероятностей на вашем графике становится проще. Вы также можете легко сравнивать разные графики друг с другом, так как все они имеют одинаковый масштаб. Некоторые характеристики стандартного нормального распределения приведены ниже:

Рисунок 8: Характеристики стандартного нормального распределения

Что такое Z-показатель?

Z-оценка используется, чтобы сообщить вам, насколько далека точка данных от среднего значения. Вы вычисляете его, используя среднее значение и стандартное отклонение, поэтому также можно сказать, что Z-показатель — это то, на сколько стандартных отклонений ниже среднего значение данных.

Z-оценка используется для стандартизации вашего нормального распределения. Используя z-оценку, вы можете преобразовать каждую точку данных в значение с точки зрения среднего значения и стандартного отклонения, эффективно преобразовав график в уменьшенную версию. Z-оценка показывает, насколько далеко каждая точка данных от среднего значения в шагах стандартного отклонения. Итак, со средним значением и стандартным отклонением вы можете нанести все точки на наш график.

Z-оценка определяется как:

Рисунок 9: Z-оценка

Давайте представим каждую точку данных как «x», тогда формула для z-показателя станет следующей:

Рисунок 10: Формула Z-показателя

Теперь разберемся с z-показателем на примере. Ниже приводится сводная информация о ежедневном времени в пути человека, который едет с работы. Значения указаны в минутах. Рассчитайте среднее значение, стандартное отклонение и Z-показатель.

Рисунок 11: Время в пути

Среднее значение — это среднее всех значений:

Рисунок 12: Среднее время в пути

Теперь вычтите среднее из каждой точки данных и найдите дисперсию и стандартное отклонение.

Рисунок 13: Различное время в пути

Рисунок 14: Разница во времени в пути

Рисунок 15: Стандартное отклонение времени в пути

Z-показатель сообщает нам, где находится точка данных относительно других точек. Z-оценка покажет вам, насколько далеко от среднего находится точка в шагах вашего стандартного отклонения. Теперь вычислите z-оценку для каждой точки:

Рисунок 16: Z-показатель времени в пути

Отрицательные значения говорят о том, что точка находится ниже среднего, а положительные значения означают, что точка находится выше среднего. Умножение каждого значения на стандартное отклонение даст разницу между средним значением и точкой данных.

В целом, он стандартизировал каждое значение. Вы можете построить новый график со средним значением в центре.

Ждете карьеры в области аналитики данных? Посетите учебный курс по аналитике данных и пройдите сертификацию уже сегодня.

Заключение

В этом учебном пособии «Все, что вам нужно знать о нормальном распределении» вы рассмотрели нормальное распределение и то, как его распознать. Затем вы посмотрели на стандартное отклонение и поняли важность стандартизации нашего нормального распределения.