2. Системы счисления
Можно считать, что любое число имеет значение (содержание) и форму представления.
Значение числа задает его отношение к значениям других чисел («больше», «меньше», «равно») и, следовательно, порядок расположения чисел на числовой оси. Форма представления, как следует из названия, определяет порядок записи числа с помощью предназначенных для этого знаков. При этом значение числа является инвариантом, т.е. не зависит от способа его представления. Это означает также, что число с одним и тем же значением может быть записано по-разному, т.е. отсутствует взаимнооднозначное соответствие между представлением числа и его значением.
В связи с этим возникают вопросы, во-первых, о формах представления чисел и, во-вторых, о возможности и способах перехода от одной формы к другой.
Способ представления числа определяется системой счисления.
Система счисления – это правило записи чисел с помощью
заданного набора специальных знаков –
цифр.
Людьми использовались различные способы записи чисел, которые можно объединить в несколько групп: унарная, непозиционные и позиционные.
Унарная – это система счисления, в которой для записи чисел используется только один знак – | (вертикальная черта, палочка). Следующее число получается из предыдущего добавлением новой палочки: их количество (сумма) равно самому числу. Унарная система важна в теоретическом отношении, поскольку в ней число представляется наиболее простым способом и, следовательно, просты операции с ним. Кроме того, именно унарная система определяет значение целого числа количеством содержащихся в нем единиц, которое не зависит от формы представления.
Из непозиционных наиболее распространенной можно считать римскую систему счисления. В ней некоторые базовые числа обозначены заглавными латинскими буквами: 1 — I, 5 — V, 10 — X, 50 — L 100 — С, 500 — D, 1000 — М. Все другие числа строятся комбинаций базовых в соответствии со следующими правилами:
если цифра меньшего значения стоит справа от большей цифры, то их значения суммируются; если слева — то меньшее значение вычитается из большего;
цифры I, X, С и М могут следовать подряд не более трех раз каждая;
цифры V, L и D могут использоваться в записи числа не более одного раза.

Например, запись XIX соответствует числу 19, МDХLIХ — числу 1549. Запись чисел в такой системе громоздка и неудобна, но еще более неудобным оказывается выполнение в ней даже самых простых арифметических операций. Отсутствие нуля и знаков для чисел больше М не позволяют римскими цифрами записать любое число (хотя бы натуральное). По указанным причинам теперь римская система используется лишь для нумерации.
В настоящее время для представления чисел применяют, в основном, позиционные системы счисления.
Позиционными называются системы счисления, в которых значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр.
Наиболее
распространенной и привычной является
система счисления, в которой для записи
чисел используется 10 цифр: 0, 1, 2, 3, 4, 5, 6,
7, 8 и 9. Число представляет собой краткую
запись многочлена, в который входят
степени некоторого другого числа —
основания системы счисления. Например:
Например:
В данном числе цифра 5 встречается трижды, однако значение этих цифр различно и определяется их положением (позицией) в числе. Количество цифр для построения чисел, очевидно, равно основанию системы счисления. Также очевидно, что максимальная цифра на 1 меньше основания. Причина широкого распространения именно десятичной системы счисления понятна — она происходит от унарной системы с пальцами рук в качестве «палочек».
Однако в истории человечества имеются свидетельства использования и других систем счисления — пятеричной, шестеричной, двенадцатеричной, двадцатеричной и даже шестидесятеричной. Общим для унарной и римской систем счисления является то, что значение числа в них определяется посредством операций сложения и вычитания базисных цифр, из которых составлено число, независимо от их позиции в числе. Такие системы получили название аддитивных.
В
отличие от них позиционное представление
следует считать аддитивно-мультипликативным, поскольку
значение числа определяется операциями
умножения и сложения.
По принципу, положенному в основу десятичной системы счисления, очевидно, можно построить системы с иным основанием. Пусть р — основание системы счисления. Тогда любое число Z (пока ограничимся только целыми числами), удовлетворяющее условию (, целое), может быть представлено в виде многочлена со степенями (при этом, очевидно, максимальный показатель степени будет равен ):
(1)
Из коэффициентов при степенях основания строится сокращенная запись числа:
Индекс р числа Z указывает,
что оно записано в системе счисления с
основанием р,
общее число цифр числа равно k.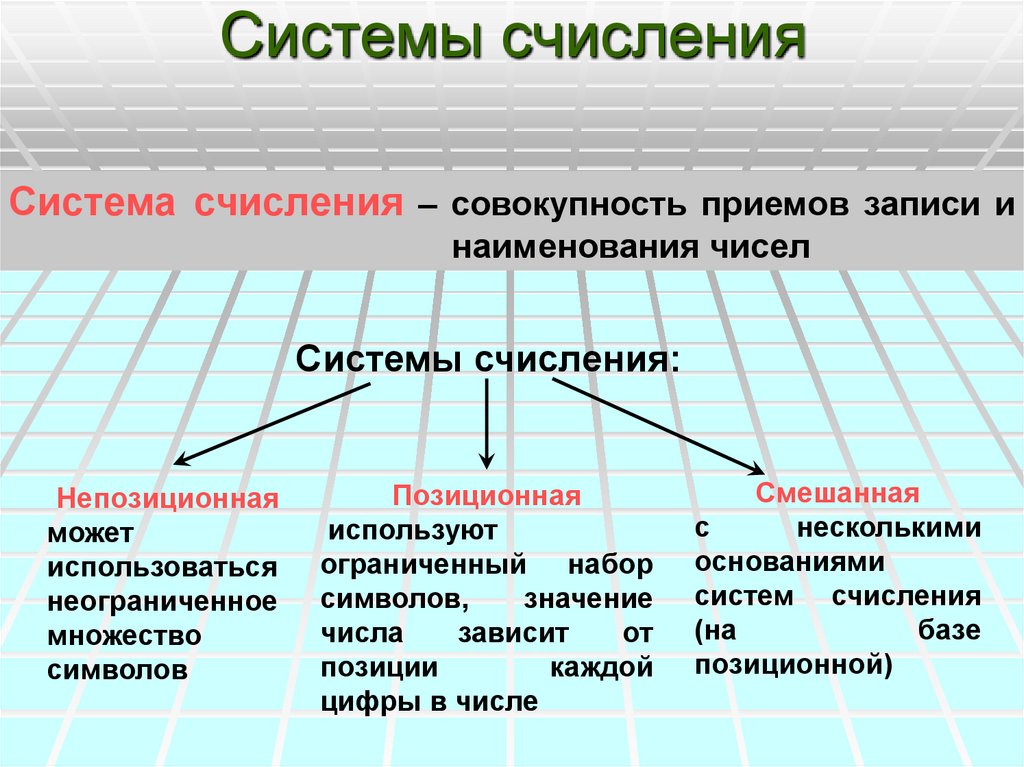 Все
коэффициенты — целые числа, удовлетворяющие условию: .
Все
коэффициенты — целые числа, удовлетворяющие условию: .
Уместно задаться вопросом: каково минимальное значение р? Очевидно, невозможно, поскольку тогда все и форма (1) теряет смысл. Первое допустимое значение — оно и является минимальным для позиционных систем.
Система счисления с основанием 2 называется двоичной. Цифрами двоичной системы являются 0 и 1, а форма (1) строится по степеням 2. Интерес именно к этой системе счисления связан с тем, что любая информация в компьютерах представляется с помощью двух состояний — 0 и 1, которые легко реализуются технически.
Наряду с двоичной в компьютерах используются восьмеричная и шестнадцатеричная системы счисления.
Представление чисел в различных системах счисления
Очевидно,
что значение целого числа, т. е. общее
количество входящих в него единиц, не
зависит от способа его представления
и остается одинаковым во всех системах
счисления; различаются только формы
представления с
одного и того же количественного
содержания числа.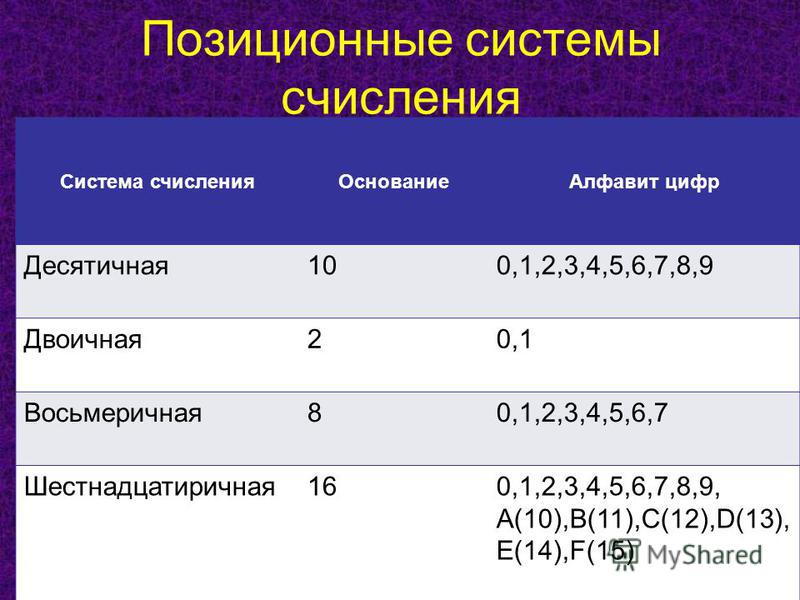
Например: |||||1= 510 = 1012 = 516.
Поскольку одно и то же число может быть записано в различных системах счисления, встает вопрос о переводе представления числа из одной системы в другую.
Перевод целых чисел из одной системы счисления в другую
Обозначим преобразование числа Z, представленного в p-ричной системе счисления в представление в q-ричной системе как . Теоретически возможно произвести его при любых q и р. Однако подобный прямой перевод будет затруднен тем, что придется выполнять операции по правилам арифметики недесятичных систем счисления (полагая в общем случае, что ).
По
этой причине более удобными с практической
точки зрения оказываются варианты
преобразования с промежуточным переводом с основанием r, для
которого арифметические операции
выполнить легко. Таким удобным основанием
является r = 10, т.е. перевод осуществляется через
десятичную систему счисления.
Таким удобным основанием
является r = 10, т.е. перевод осуществляется через
десятичную систему счисления.
Преобразование
Идея алгоритма перевода предельно проста: положим начальное значение ; из числа вычтем 1 по правилам вычитания системы р, т.e. , и добавим ее к по правилам сложения системы q, т.е. . Будем повторять эту последовательность действий, пока не достигнем .
Промежуточный переход к унарной системе счисления в данном случае осуществляется неявно — используется упоминавшееся выше свойство независимости значения числа от формы его представления. Рассмотренный алгоритм перевода может быть легко реализован программным путем.
Преобразование
Очевидно, первая и вторая части преобразования не связаны друг с другом, что дает основание рассматривать их по отдельности. Алгоритмы перевода вытекают из следующих соображений. Многочлен (1) для может быть представлен в виде:
(2)
где т — число разрядов в записи, а — цифры числа .
Разделим число на две части по разряду номер i. Число, включающее разрядов с -го по i-й, обозначим , а число с i разрядами с -го по 0-й — . Очевидно, .
.
Позаимствуем из языка VBA обозначение двух операций: \ — результат целочисленного деления двух целых чисел и mod— остаток от целочисленного деления 13 \ 4 = 3; 13 mod 4 = 1.
Теперь если принять , то в (2) усматривается следующее рекуррентное соотношение: из которого, в свою очередь, получаются выражения:
; . (3)
Аналогично, если принять , то для правой части числа будет справедливо другое рекуррентное соотношение: , из которого следуют:
; . (4)
Из
соотношений (3) и (4) непосредственно
вытекают два способа перевода целых
чисел из десятичной системы счисления
в систему с произвольным основанием q.
Способ 1 является следствием соотношений (3), предполагающий следующий алгоритм перевода:
Целочисленно разделить исходное число (Z10) на основании новой системы счисления (q) и найти остаток от деления — это будет цифра 0-го разряда числа Zq.
Частное от деления снова целочисленно разделить на q с выделением остатка; процедуру продолжать до тех пор, пока частное от деления не окажется меньше q.
Образовавшиеся остатки от деления, поставленные в порядке, обратном порядку их получения, и представляют Zq.
Пример. Выполнить преобразование
Остатки
от деления (3, 4) и результат последнего
целочисленного деления (4) образуют
обратный порядок цифр нового числа. Следовательно,
.
Следовательно,
.
Способ 2 вытекает из соотношения (4), действия производятся в соответствии со следующим алгоритмом:
Определить — максимальный показатель степени в представлении числа по форме (2) для основания q.
Целочисленно разделить исходное число (Z10) на основание новой системы счисления в степени (т.е. qm-1) и найти остаток от деления; результат деления определит первую цифру числа Zq.
Остаток от деления целочисленно разделить на gm-2, результат деления принять за вторую цифру нового числа; найти остаток; продолжать эту последовательность действий, пока показатель степени q не достигнет значения 0.
Продемонстрируем
действие алгоритма на той же задаче,
что была рассмотрена выше.
Определить можно либо путем подбора (50 = 1 < 123; 51 = 5 < 123; 52 = 25 < 123; 53 = 125 > 123, следовательно, ), либо логарифмированием с оставлением целой части логарифма (1оg5123 = 2,99, т.е. ). Далее:
Алгоритмы перевода явно вытекают из представлений (1) или (2): необходимо Zp представить в форме многочлена и выполнить все операции по правилам десятичной арифметики.
Пример. Выполнить преобразование .
Решение: .
Необходимо
еще раз подчеркнуть, что приведенными
алгоритмами удобно пользоваться при
переводе числа из десятичной системы
в какую-то иную или наоборот. Они работают
и для перевода между любыми иными
системами счисления, однако преобразование
будет затруднено тем, что все арифметические
операции необходимо осуществлять по
правилам исходной (в
первых алгоритмах) или конечной (в
последнем алгоритме) системы счисления.
По этой причине переход, например, проще осуществить через промежуточное преобразование к десятичной системе . Ситуация, однако, значительно упрощается, если основания исходной и конечной систем счисления оказываются связанными соотношением , где r — целое число (естественно, большее 1) или (, целое).
Контрольный тест №2:
Результат вычисления выражения имеет в двоичной системе счисления вид …
10010100
70040001
20020001
10010001
Результат вычисления выражения имеет в двоичной системе счисления вид …
112001
122001
10010001
10011001
Если числа в двоичной системе счисления имеют вид 10012 и 1012, то их разность в десятичной системе счисления равна …
8
2
4
900
Последняя цифра суммы чисел 578 и 568 в восьмеричной системе счисления равна
6
3
5
С
Последняя цифра суммы чисел 5516 и 5616 в шестнадцатеричной системе счисления равна
1
6
3
В
Укажите упорядоченную по возрастанию последовательность значений
5516 558 557
558 557 5516
557 558 5516
558 5516 557
В записи числа в двоичной системе счисления могут присутствовать
цифры от 1 до 5
шесть нечетных цифр
цифры 0 и 1
буквы от А до Е
СИСТЕМЫ СЧИСЛЕНИЯ: ТЕОРИЯ
ТЕОРИЯ
Система счисления(СС)-это совокупность приёмов и правил записи чисел с помощью определенного набора символов.
- Алфавит СС — набор символов(цифр), используемых для записи числа.
- Все системы счисления делятся на позиционные и непозиционные. Непозиционная система счисления — это система, в которой количественный эквивалент каждой цифры не зависит от ее положения (места, позиции) в записи числа.
Основание СС (мощность алфавита СС) — количество символов(цифр) алфавита СС.
Итак, в непозиционных системах счисления позиция, которую цифра занимает в записи числа, роли не играет. Так, например, римская система счисления непозиционная. В числах XI и IX «вес” обоих цифр одинаков, несмотря на их месторасположение.
Позиционные системы счисления
Позиционная система счисления это система, в которой значение цифры зависит от ее места (позиции) в записи числа. Основание системы счисления количество знаков или символов, используемых для изображения числа в данной системе счисленияОснование системы счисления определяет её название: основание p — p-ая система счисления.

Например, система счисления в основном, применяемая в современной математике, является позиционной десятичной системой, её основание равно десяти. Для записи любых чисел в ней используется десять всем хорошо известных цифр (0,1,2,3,4,5,6,7,8,9).
Итак, мы сказали, что в позиционных системах счислениях имеет значение позиция, которую цифра занимает в записи числа. Так, запись 23 означает, что это число можно составить из 3 единиц и 2 десятков. Если мы поменяем позиции цифр, то получим совсем другое число – 32. Это число содержит 3 десятка и 2 единицы. «Вес» двойки уменьшился в десять раз, а «вес» тройки в десять раз возрос.
- Развернутая запись числа
- Алгоритм перевода целых десятичных чисел
- Для того, чтобы перевести целое десятичное число в другую систему счисления,
необходимо осуществлять последовательное деление десятичного числа и затем
получаемых частных на основание той системы, в которую оно переводится, до тех
пор, пока не получится частное, меньшее делителя.

Число в новой системе счисления записывается в виде остатков от деления, в обратном порядке их получения, начиная с последнего полученного частного. - Алгоритм перевода правильных десятичных дробей Для того, чтобы перевести правильную десятичную дробь из десятичной системы счисления в другую, необходимо последовательно умножать эту дробь, а затем получаемые дробные части на основание той системы, в которую она переводится.
- Перевод A2—A8
- Для того, чтобы перевести число из двоичной системы счисления в
восьмеричную, необходимо: двигаясь от запятой влево и вправо, разбить двоичное
число на группы по три разряда, дополняя при необходимости нулями крайние левую
и правую группу.
 Затем триаду заменить соответствующей восьмеричной цифрой (см. таблицу триад выше)
Затем триаду заменить соответствующей восьмеричной цифрой (см. таблицу триад выше) - Перевод A2—A16
- Для того, чтобы перевести число из двоичной системы счисления в шестнадцатеричную, необходимо: двигаясь от запятой влево и вправо, разбить двоичное число на группы по четыре разряда, дополняя при необходимости нулями крайние левую и правую группу. Затем тетраду заменить соответствующей шестнадцатеричной цифрой (см. таблицу триад выше)
- Перевод A8—A2
- Для того, чтобы перевести число из восьмеричной системы счисления в двоичную достаточно заменить каждую цифру этого числа соответствующей триадой (см. таблицу триад выше), при этом отбрасывают незначащие нули в старших и младших (после запятой) разрядах.
- Перевод A16—A2
- Для того, чтобы перевести число из шестнадцатеричной системы счисления в
двоичную достаточно заменить каждую цифру этого числа соответствующей тетрадой
(см.
 таблицу триад выше), при этом отбрасывают незначащие
нули в старших и младших (после запятой) разрядах.
таблицу триад выше), при этом отбрасывают незначащие
нули в старших и младших (после запятой) разрядах. Двоичная арифметика
Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным правилам.Сложение
Рассмотрим сложение чисел в двоичной системе счисления. В основе лежит таблица сложения одноразрядных двоичных чисел:0+0=0
Важно обратить внимание на то, что при сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или больше основания системы счисления. Для двоичной системы счисления эта величина равна двум.
0+1=1
1+0=1
1+1=10
1+1+1=11
Сложение многоразрядных двоичных чисел происходит в соответствие с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов с старшие.Вычитание
Рассмотрим вычитание двоичных чисел. В основе лежит таблица вычитания
одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1)
производится заем из старшего разряда. В таблице заем обозначается 1 с чертой.
В основе лежит таблица вычитания
одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1)
производится заем из старшего разряда. В таблице заем обозначается 1 с чертой.0-0=_0
Сложение и вычитание одноразрядных двоичных чисел
0-1=11
1-0=1
1-1=0
Сложение и вычитание многоразрядных двоичных чисел (примеры)Умножение
В основе умножения лежит таблица умножения одноразрядных двоичных чисел:0*0=0
Умножение многоразрядных двоичных чисел происходит в соответствии с приведенной таблицей умножения по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя.
0*1=0
1*0=0
1*1=1Деление
Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.
Умножение и деление двоичных чисел
Любое число N в позиционной системе счисления с основанием p может быть представлено в виде многочлена от p:
N=ak pk + ak-1 pk-1+ak-2 pk-2+…+a1 p1+a0 p0+a-1 p-1+a-2 p-2+.
 ..,
.., где N — число, p — основание системы счисления (p>1), ai — цифры числа (коэффициенты при степени p).
Числа в p-ой системе счисления записываются в виде последовательности цифр:
N=ak ak-1 ak-2 …a1 a0 ,a-1 a-2…
Запятая в последовательности отделяет целую часть числа от дробной.
3210 -1-2
N=4567,1210=4*103+5*102+6*101+7*100+1*10-1+2*10-2
Двоичная система счисления
Для записи чисел используются только две цифры – 0 и 1. Выбор двоичной системы для использования в компьютере объясняется тем, что электронные элементы, из которых строятся ЭВМ, могут находиться только в двух хорошо различимых состояниях. По существу эти элементы представляют собой выключатели. Как известно выключатель либо включен, либо выключен. Третьего не дано. Одно из состояний обозначается цифрой 1, другое – 0. Благодаря таким особенностям
двоичная система стала стандартом при построении ЭВМ.
Благодаря таким особенностям
двоичная система стала стандартом при построении ЭВМ. В этой системе счисления любое число может быть представлено в виде:
N=ak 2k + ak-1 2k-1+ak-2 2k-2+…+a1 21+a0 20+a-1 2-1+a-2 2-2+….
Например:11001,012=1*24+1*23+0*22+0*21+1*20+0*2-1+1*2-2(развернутая запись числа в двоичной системе счисления)
Восьмеричная система счисления
| Цифра | Триада |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
 Это система счисления в ЭВМ используется как
вспомогательная для записи информации в сокращенном виде. Для представления
одной цифры восьмеричной системы используют три двоичных разряда (триада : см.
таблицу
Это система счисления в ЭВМ используется как
вспомогательная для записи информации в сокращенном виде. Для представления
одной цифры восьмеричной системы используют три двоичных разряда (триада : см.
таблицуРазвернутая запись числа в восьмеричной системе счисления:
5378=5*82+3*81+7*80
Шестнадцатеричная система счисления
| Символ | Тетрада |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
 Эта система счисления,
так же, как и восьмеричная система, используется в ЭВМ как вспомогательная для
записи информации в сокращенном виде. Для представления одного символа
шестнадцатеричной системы используют четыре двоичных разряда (тетрада): см.
таблицу
Эта система счисления,
так же, как и восьмеричная система, используется в ЭВМ как вспомогательная для
записи информации в сокращенном виде. Для представления одного символа
шестнадцатеричной системы используют четыре двоичных разряда (тетрада): см.
таблицу Развернутая запись числа в восьмеричной системе счисления:
A2F,416=A*162+2*161+F*160+4*16-1
Перевод чисел в десятичную систему счисления.
Алгоритм перевода Ap—A10.
Представьте число в развернутой форме. Вычислите сумму ряда. Полученное число является значением числа в десятичной системе счисления.
24
16 = 2 * 161 + 4 * 160 = 32 + 4 = 36Перевод чисел из десятичной системы счисления
Умножение производится до тех пор, пока дробная часть не станет равной нулю, или будет достигнута требуемая точность.
В новой системе дробь записывается в виде целых частей произведений, начиная с первого.
перевод десятичных дробей
Перевод чисел из двоичной системы счисления восьмеричную, шестнадцатеричную и обратно
Главная страница
Подписаться на: Сообщения (Atom)
Десятичная система | Определение, пример и факты
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Обзор недели
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
- Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
- Студенческий портал
Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
- Britannica Beyond
Мы создали новое место, где вопросы находятся в центре обучения. Вперед, продолжать. Просить. Мы не будем возражать. - Спасение Земли
Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать! - SpaceNext50
Britannica представляет SpaceNext50. От полёта на Луну до управления космосом — мы исследуем широкий спектр тем, которые подпитывают наше любопытство к космосу!
Содержание
- Введение
Краткие факты
- Факты и сопутствующий контент
номеров в разных основаниях
числа в разных основаниях- около
- Статистические данные
- Теория номеров
- Java
- .
 база 90$$
база 90$$
Обратите внимание, «цифры» нашего числа соответствуют коэффициентам при степенях десяти, которые складываются вместе, чтобы получить значение нашего числа.Аналогичным образом мы можем указать числа в других «основаниях» (помимо 10), используя разные цифры, соответствующие коэффициентам при степенях (данного основания), которые нужно сложить, чтобы получить значение нашего числа.
Например, число «основание 8» (или « восьмеричное «) (как указано в нижнем индексе) 90$$
Чтобы каждое число имело представление по основанию b, но ни одно число не имеет более одного такого представления, мы должны использовать только цифры от 0 до (b-1) в любом заданном числе по основанию b.
Это согласуется с числами с основанием 10, где мы используем цифры 0-9.
Для меньших баз мы используем подмножество этих цифр. Например, в базе 5 мы используем только цифры 0-4; в базе 2 (которую также называют двоичной ) мы используем только цифры 0 и 1.

Для больших оснований нам нужно иметь однозначные числа для значений после 9.0 = 23288$$
( Примечание. Как показано выше, нижний индекс, указывающий на используемую базу, часто не используется в случае шестнадцатеричных и/или двоичных чисел. В этих случаях контекст их использования обычно проясняет базу. )
Переход с базы 10 на другую базу
Один (прямой, но неэффективный) способ преобразования базы 10 в другую:
- Определите наибольшую степень основания, которое входит в число ненулевое число раз.
- Определите, сколько раз эту степень можно вычесть из числа, чтобы результат не был отрицательным (т. е. разделить число на степень). Запишите эту цифру.
- Переопределить число как наименьший положительный остаток от деления на рассматриваемую степень
- Переопределите мощность как мощность, деленную на основание.
- Вернитесь к шагу 2, если сила теперь не меньше единицы — в этом случае все готово.

Например, чтобы преобразовать 1073 в основание 5, мы вспоминаем, что:
5 0 = 1 5 1 = 5 5 2 = 25 5 3 = 125 5 4 = 625 5 5 = 3125
Затем мы замечаем, что 5 4 = 625 — это наивысшая степень числа 5 меньше 1073.
1073 = 1 * 625 + 448 448 = 3 * 125 + 73 73 = 2 * 25 + 23 23 = 4 * 5 + 3 3 = 3 * 1 + 0
Красные цифры 13243 показывают представление числа 1073 по основанию 5.
Этот процесс, однако, неэффективен, поскольку необходимо знать и использовать различные способности желаемого основания.
Есть более простой способ!
Рассмотрим остатки при делении следующих чисел на 5:
1073 = 214 * 5 + 3 214 = 42 * 5 + 4 42 = 8 * 5 + 2 8 = 1 * 5 + 3 1 = 0 * 5 + 1
Примечание: представление по основанию 5 происходит от считывания остатков (выделено красным) снизу вверх! На каждом шаге выше мы просто делим на 5 и смотрим как на частное, так и на остаток — никаких знаний о высших степенях числа 5 не требуется!
Удивительно, но эта техника работает на любой базе.
 ( Можете ли вы объяснить почему? )
( Можете ли вы объяснить почему? )Так, например, если мы хотим найти двоичное (с основанием 2) представление числа 1000, мы просто вычисляем следующее:
1000 = 500 * 2 + 0 500 = 250 * 2 + 0 250 = 125 * 2 + 0 125 = 62 * 2 + 1 62 = 31 * 2 + 0 31 = 15 * 2 + 1 15 = 7 * 2 + 1 7 = 3 * 2 + 1 3 = 1 * 2 + 1 1 = 0 * 2 + 1
Таким образом, 1000 в двоичном формате равно 1111101000 .
Подсчет в другой базе
Счет по другим основаниям не слишком отличается от счета по основанию 10. Чтобы увидеть сходство, давайте посчитаем до 41 по основанию 10 и 3 (как показано в таблице ниже).
Обратите особое внимание на то, что «2» в системе счисления 3 играет ту же роль, что и «9» в базе 10. Она представляет собой последнюю цифру, которую вы можете использовать перед увеличением цифры слева.
База 10 База 3 База 10 База 3 0 0 21 210 1 1 22 211 2 2 23 212 3 10 24 220 4 11 25 221 5 12 26 222 6 20 27 1000 7 21 28 1001 8 22 29 1002 9 100 30 1010 10 101 31 1011 11 102 32 1012 12 110 33 1020 13 111 34 1021 14 112 35 1022 15 120 36 1100 16 121 37 1101 17 122 38 1102 18 200 39 1110 19 201 40 1111 20 202 41 1112 Добавление в другую базу
Вы можете добавить другое основание (без преобразования в основание 10), если вы помните, что вы «переносите», когда у вас есть сумма, которая больше или равна вашему основанию (вместо того, чтобы быть больше или равна 10), и что то, что вы «несете», — это количество раз, которое вы можете вытащить из своей суммы.

Лучше всего это иллюстрируется примером. Предположим, вы хотите добавить шестнадцатеричные числа 4EF5A и 6ACF7:
1111 <---- Это "несущие" цифры 4EF5A +6ACF7 ------ B9C51
Давайте рассмотрим пример. Заметить, что
А + 7 = 11 (шестнадцатеричные вычисления) 10 + 7 = 17 = 1 * 16 + 1 (десятичные вычисления)
Итак, мы записываем 1 в столбце «единицы» и переносим 1. Затем
1 + 5 + F = 15 (шестнадцатеричные вычисления) 1 + 5 + 15 = 21 = 1 * 16 + 5 (десятичные вычисления)
Итак, мы записываем 5 в колонке «десятки/шестнадцать» и переносим 1. Затем
1 + F + C = 1C (шестнадцатеричные вычисления) 1 + 15 + 12 = 28 = 1 * 16 + 12 (десятичные вычисления)
Итак, мы записываем C в следующем столбце и переносим 1. Затем
1 + E + A = 19 (шестнадцатеричные вычисления) 1 + 14 + 10 = 25 = 1 * 16 + 9 (десятичные вычисления)
Итак, мы записываем 9 в следующем столбце и переносим 1.
