Основание системы это: Основание системы счисления

Основание позиционной системы.

Системы счисления, используемые в компьютере. Представление чисел в памяти ЭВМ.

• Системы счисления.

С древних времен человечество использует различные системы счета. Люди предпочитают десятичную систему, вероятно, потому, что считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.

1	0	0	0	0	0	0	1	1
1	0	0	1	1	0	0	0	1

В процессах хранения, обработки и передачи различной информации в компьютере используется двоичная система счисления. Если «заглянуть» внутрь машинной памяти ее удобно представить в виде листа в клетку. В каждой такой «клетке» хранится только одно из двух значений: нуль или единица. Каждая «клетка» памяти компьютера называется битом. Цифры 0 и 1, хранящиеся в «клетках» памяти компьютера называют значениями битов. С помощью последовательности битов можно представить различную информацию. Такое представление информации называется цифровым или двоичным кодированием. Преимущество цифрового кодирования данных в том, что их можно хранить и передавать с использованием одних и тех методов, независимо от типов данных.

Двоичная система счисления (двоичное кодирование информации) имеет ряд преимуществ перед другими системами:

• для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;

• представление информации посредством только двух состояний надежно и помехоустойчиво;

• возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

• двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.

Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются.

Позиционные и непозиционные системы счисления.

В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.

Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.

Сама же запись числа 757,7₁₀ означает сокращенную запись выражения, которую можно разложит по позициям (разрядам): сотен, десятки, единицы и т. д. Нумерация разрядов целой части числа с право налево, от 0,1,2…

2 1 0 -1 разряды числа

757,7₁₀

700 + 50 + 7 + 0,7 = 7*10² + 5*10¹ + 7*10⁰ + 7*10^—1 = 757,7.

Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения

a_n-1*q^n-1 + a_n-2*q^n-2 + … + a₁*q¹ + a₀*q⁰ + a_-1*q^-1 + … + a_—m*q^—m,

где:

a_i – цифры числа;

q – основание системы счисления;

n – число целых разрядов;

m – число дробных разрядов;

Например:

Разряды 3210 -1

Число 1011,1₂= 1*2³+0*2²+1*2

1+1*2⁰+1*2^-1

Разряды 210 -1

Число 276,5₈= 2*8²+7*8¹+6*8⁰+5*8^-1

Основанием позиционной системы называется возводимое в степень целое число, которое равно количеству цифр, используемых для изображения чисел в данной системе (2¹, 2³, 2⁴).

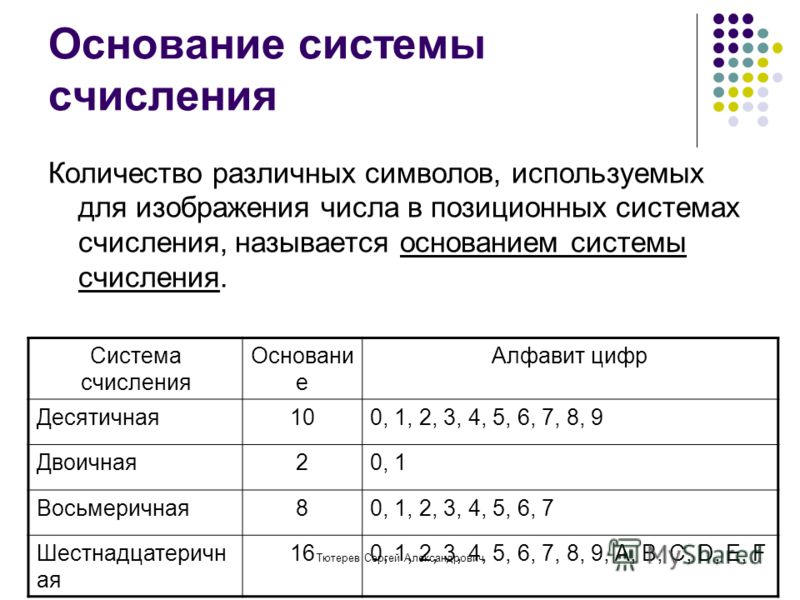
Основание позиционной системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления. Основание показывает также, во сколько раз изменяется количественное значение цифры при перемещении ее на соседнюю позицию.

Наименование системы счисления соответствует ее основанию (десятичная, двоичная, восьмеричная, шестнадцатеричная и так далее).

Система счисления	Алфавит цифр системы
десятичная	1 2, 3, 4, 5, 6, 7, 8, 9, 0
двоичная	0, 1
восьмеричная	1, 2, 3, 4, 5, 6, 7
шестнадцатеричная	1,2,3,4,5,6,7,8,9,A(10),B(11),C(12),D(13),E(14), F(15)

Для чисел, имеющих как целую, так и дробную части, перевод из одной системы счисления в другую, осуществляется отдельно для целой и дробной частей.

Перевод целых чисел из десятичной системы в другие системы счисления.

Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком («нацело») на q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения.

Пример:

Переведем число 75₁₀ из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Ответ: 75₁₀ = 1 001 011₂ = 113₈ = 4B₁₆.

Перевод чисел из двоичной (восьмеpичной, шестнадцатеpичной) системы в десятичную.

Перевод в десятичную систему числа x, записанного в q-ичной cистеме счисления (q = 2, 8 или 16), сводится к вычислению значения многочлена:

x₁₀ = a_n*qⁿ + a_n-1* q^n-1 + . . + a₀* q⁰ + a_-1* q ^-1 + a_-2*q^-2 + … + a_-m* q^-m

средствами десятичной арифметики.

Примеры:

Разряды 3210 -1

Число 1011,1₂= 1*2³+0*2²+1*2¹+1*2⁰+1*2^-1=8+0+2+1+0,5=11,5₁₀

Разряды 210 -1

Число 276,5₈= 2*8²+7*8¹+6*8⁰+5*8^-1=128+56+48+0,625=190,625₁₀

Разряды 210

Число 1F3₁₆= 1*16²+ 15*16

1+ 3*16⁰+ =256+240+3=499₁₀

2.Пеpевод пpавильных десятичных дpобей.

Для перевода правильной десятичной дроби F в систему счисления с основанием q необходимо F умножить на q , записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q, и т. д., до тех пор, пока дpобная часть очередного пpоизведения не станет pавной нулю, либо не будет достигнута требуемая точность изображения числа F в q-ичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой. Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется q ^-(k+1) / 2.

Пример.

Переведем число 0,36₁₀

из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

При умножении дроби на основание системы счисления q (2, 8, 16) в левой части остаются цифры алфавита этой системы счисления в (в двоичной – цифры 0,1 , в восьмеричной – цифры от 1 до 7, в шестнадцатеричной от 1 до 9,A-10,B-11,C-12.D-13,E-14,F-15).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, 2³ и 2⁴).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Например:

Перевод из двоичной системы счисления в восьмеричную или шестнадцатеричную.

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на «триады» (для восьмеричной) или «тетрады» (для шестнадцатеричной)  и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Например,

Сводная таблица переводов целых чисел.

Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления.

Сложение чисел в различных системах счисления.

Сложение проводится столбиком поразрядно, начиная с младшего нулевого разряда.

Если сумма двух чисел более основания системы(9₁₀+5₁₀=14₁₀> q=10), происходит переполнение нулевого разряда (14₁₀-10₁₀=4₁₀), тогда 4₁₀ остается в нулевом разряде, а 1 десяток суммируется с десятками (8+2+1=11>q=10).. 10 единиц переходят в виде 1в старший разряд числа.

Те же правила при сложении двоичных чисел (q=2 двоичное число, содержит цифры 0 и 1, нет 2). При сложении 1₂+1₂=0₂, т.к. в двоичной системе нет цифры 2, переполнение происходит, когда сумма чисел >2, в нулевом разряде пишем 0, две единицы нулевого разряда двоичного числа, суммируется в виде 1 с числами первого разряда (1₂+1₂+1₂=11₂) и т.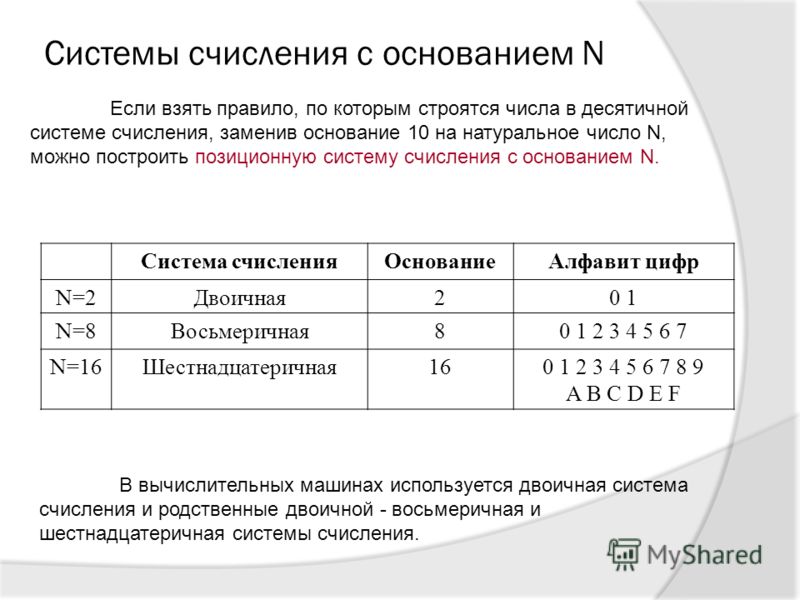 д.

При сложении восьмеричных чисел, основание системы q=8, алфавит цифр числа от 0 до 7 (нет числа больше 7). Переполнение происходит, когда сумма чисел >8 (т.е.5₈+4₈=9₈), тогда из суммы вычитается основание (q=8), т.е. 9₈ – 8₈=1₈, а восемь единиц нулевого разряда, суммируется в виде 1 с числами первого разряда (7₈+3₈+1₈=11₈) и т.д.

При сложении шестнадцатеричных чисел, основание системы q=16, алфавит цифр числа от 0 до 9, A(10), B(11), C(12), D(13), E(14), F(15) (нет чисел больше 15). Переполнение происходит, когда сумма чисел >15, (т.е.7₁₆+F(15)₁₆=22₁₆), тогда из суммы вычитается основание (q=16), т.е. 22₁₆ – 16₁₆=6₁₆, а 16 единиц нулевого разряда, суммируется в виде 1 с числами первого разряда (2₁₆+1₁₆+1₁₆=4₁₆) и т. д.

Вычитание чисел в различных системах счисления.

Если при вычитании чисел приходиться занимать единицу старшего разряда, она равна количеству единиц основания системы (q=2, 8, 16).

Например: Вычтем единицу из чисел 100₂, 100₈ и 100₁₆.

НОУ ИНТУИТ | Лекция | Арифметические основы

< Лекция 5 || Лекция 6: 1234 || Лекция 7 >

Аннотация: В лекции описаны системы счисления, представлена методика выбора системы счисления, даны правила перевода чисел из одной системы счисления в другую.

Ключевые слова: разряд, операции, система счисления, архитектура, множества, связь, место, вес, основание, запись, однородность, прямой, представление, обратный, перевод, вторая производная, минимум, отношение, анализ, функция, контроль, диагностика, произвольное, деление, остаток, умножение

В данном разделе курса рассматриваются способы представления чисел в ЭВМ, методы выполнения арифметических операций, которые отличны от методов, получивших широкое распространение на практике.

Как известно, еще в 19 веке производство операций над числами, содержащими много разрядов, представлялось сложной задачей, решить которую могли только профессионалы. В это время были уже разработаны основные правила выполнения операций над многозначными числами узбекским математиком Аль-Хорезми. Общие закономерности, по которым строились эти правила, впоследствии получили название АЛГОРИТМА. Они настолько широко вошли в жизнь, что, производя эти операции над многозначными числами, мы не задумываемся над тем, что выполняем строгую систему правил.

Система счисления.

Способ представления изображения произвольных чисел с помощью некоторого конечного множества символов назовем системой счисления .

В повседневной практике мы пользуемся, как правило, десятичной системой счисления. Ответ на вопрос: » Почему именно эта система счета получила наибольшее распространение? » — сейчас дать затруднительно. В литературе, как правило, в качестве обоснования приводится тот факт, что на руках человека — в сумме 10 пальцев. Вряд ли это обоснование можно принимать всерьез. На практике мы сталкиваемся и с более сложными, в частности, со смешанными системами. Например, система счета времени, где за единицу принята секунда, минута, час, сутки, неделя, месяц, год. Или система счета денег, до недавнего времени применявшаяся в Англии (пенс, шиллинг, фунт):

12п = 1ш, 20ш = 1ф.

Или еще более интересная — римская система счета, которая использует символы: I — 1, V — 5, X — 10, L — 50, C — 100, D — 500, M — 1000.

Эта система является особой и применяется редко (циферблат, архитектура, история и т.д.)

Системы счисления принято делить на:

• Позиционные.
• Непозиционные.
• Символические.

Начнем с последних. В этих системах каждому числу ставится в соответствие свой символ. Эти системы не находят широкого применения в силу естественной их ограниченности (алхимия, кодированные сообщения) -бесчисленного множества символов, которое требуется для изображения всех возможных чисел. Поэтому эти системы из рассмотрения опустим.

Позиционные системы счисления.

Само название этих систем указывает на связь значимости числа и его изображения от позиции.

Позиция — некоторое место, в котором может быть представлен лишь один символ.

Примером позиционной системы счисления является десятичная система.

В этой системе число представляется в виде полинома » n » степени, а изображается совокупностью некоторых символов, каждый из которых имеет различный вес в зависимости от позиции, которую он занимает.

a₄a₃a₂a₁ — число; a₁, a₂, a₃, a₄ — символы.

Всем позициям приписывается различный вес, который чаще всего выбирается как целая степень основания системы.

Основание системы счисления — число, которое является мощностью множества различных символов, допустимых в каждой позиции числа.

Так для десятичной системы допускаемыми являются символы: 0, 1, 2, 3,…, 9.

Обозначим через » p » основание системы счисления. Тогда веса позиций числа могут быть представлены так:

... p3 p2 p1 p0.

Само число, изображение которого имеет вид, например, a₃a₂a₁a₀ может быть представлено так:

intuit.ru/2010/edi»>a₀p⁰ + a₁p¹ + a₂p² + a₃p³ — это развернутая запись числа в позиционной системе.

Например:

97310 = 3*100 + 7*101 + 9*102 = 3 + 70 + 900.

В отличие от системы счета времени, десятичная система является однородной, т.е. одних и тех же десятичных символов достаточно, чтобы изобразить любое число. В то время как в смешанных системах нужно придумывать все новые и новые символы для того, чтобы изобразить следующее по величине число.

Таким образом, однородность — одно из важных свойств позиционных систем.

Любое число X в позиционной системе счисления можно представить в виде:

где

intuit.ru/2010/edi»>m — число позиций или разрядов, отведенное для изображения целой части числа.

n — общее число разрядов в числе.

a_i — любой допустимый символ в разряде, т.е. a_i = {0, 1, 2,…, p-1}.

p — основание системы счисления.

Например:

- 961,13 = - (9*102 + 6*101 + 1*100 + 1*10-1 + 3*10-2).

1. Заметим, что число, равное основанию системы счисления, т.е. » p «, в самой системе с основанием » p » записывается только в двух позициях ( разрядах ), а именно так:

   pp = 10p

2. Заметим также, что разделение числа на две части — дробную и целую — имеет смысл лишь в позиционных системах.
3. Заметим, что основание системы для представления числа мы можем выбрать произвольное. Такой же произвол мы можем допустить и в назначении весов разрядов. Однако наиболее целесообразно считать его, как и в десятичной системе, естественным, т.е. ввести в качестве степеней основания числа натурального ряда:

   ... +3, +2, +1, 0, -1, -2, -3 ...

Дальше >>

< Лекция 5 || Лекция 6: 1234 || Лекция 7 >

База и измерение

Цели

1. Понять определение базиса подпространства.
2. Поймите основную теорему.
3. Рецепты: основа для столбцового пространства, основа для нулевого пространства, основа для спана.
4. Рисунок: базис подпространства R2 или R3.
5. Теорема : базисная теорема .
6. Основные словарные слова: основа , измерение .

Как мы обсуждали в разделе 2. 6, подпространство — это то же самое, что и отрезок, за исключением того, что мы не имеем в виду набор остовных векторов. Существует бесконечно много вариантов остовных множеств для ненулевого подпространства; чтобы избежать избыточности, обычно удобнее всего выбирать остовный набор с минимальным числом векторов в нем. Это идея, лежащая в основе понятия базиса.

Определение

Пусть V — подпространство в Rn. Базис V — это набор векторов {v1,v2,…,vm} в V, таких что:

1. V=Span{v1,v2,…,vm} и
2. множество {v1,v2,…,vm} линейно независимо.

Напомним, что набор векторов является линейно независимым тогда и только тогда, когда при удалении любого вектора из набора отрезок уменьшается (теорема 2.5.12). Другими словами, если {v1,v2,…,vm} является базисом подпространства V, то никакое собственное подмножество {v1,v2,…,vm} не будет охватывать V: это минимальное охватный набор. Любое подпространство допускает базис по этой теореме из раздела 2. 6.

Ненулевое подпространство имеет бесконечно много различных оснований, но все они содержат одинаковое количество векторов.

Мы оставляем в качестве упражнения доказательство того, что любые два основания имеют одинаковое количество векторов; возможно, вы захотите подождать, пока не изучите теорему об обратимой матрице в разделе 3.5.

Определение

Пусть V — подпространство в Rn. Количество векторов в любом базисе V называется размерностью V и пишется dimV.

Пример (основа R2)

Пример (все базы R2)

Пример (Стандартный базис Rn)

Пример

Из предыдущего примера следует, что любой базис Rn содержит n векторов. Пусть v1,v2,…,vn — векторы в Rn, а A — матрица размера n×n со столбцами v1,v2,…,vn.

1. Утверждение, что {v1,v2,…,vn} охватывает Rn, означает, что A имеет точку поворота в каждой строке : см. эту теорему в разделе 2.3.
2. Сказать, что {v1,v2,. ..,vn} линейно независима, означает, что A имеет точку поворота в каждой 9-й точке.0010 столбец : см. это важное примечание в Разделе 2.5.

Поскольку матрица A является квадратной, она имеет точку опоры в каждой строке тогда и только тогда, когда она имеет точку опоры в каждом столбце. В разделе 3.5 мы увидим, что два приведенных выше условия эквивалентны обратимости матрицы A.

Пример

Теперь мы покажем, как найти основания для пространства столбцов матрицы и нулевого пространства матрицы. Чтобы найти основу для данного подпространства, обычно лучше всего сначала переписать подпространство как пространство столбца или нулевое пространство: см. это важное примечание в разделе 2.6.

Основа для пространства столбца

Сначала мы покажем, как вычислить базис для пространства столбцов матрицы.

Теорема

Опорные столбцы матрицы A образуют основу для Col(A).

Доказательство

Это переформулировка теоремы из раздела 2. 5.

Вышеупомянутая теорема относится к опорным столбцам в исходной матрице , а не к ее уменьшенной ступенчатой ​​форме строк. Действительно, матрица и ее сокращенная эшелонированная форма строк обычно имеют разные пространства столбцов. Например, в матрице A ниже:

A=120-1-2-345240-2FGRREF—→10-8-701430000FGpivotcolumns=basispivotcolumnsinRREF

сводными столбцами являются первые два столбца, поэтому базисом для Col(A) является

.

DB1-22C, B2-34CE.

Первые два столбца редуцированной эшелонированной формы строк определенно охватывают другое подпространство, так как

SpanDB100C, B010CE = DBab0CAAAa, binRE = (плоскость xy),

, но Col(A) содержит векторы, последняя координата которых отлична от нуля.

Следствие

Размерность Col(A) — это количество точек опоры A.

Основа пролета

Вычисление основы для диапазона выполняется так же, как вычисление основы для пространства столбца. В самом деле, длина конечного числа векторов v1,v2,. ..,vm равна пространству столбцов матрицы, а именно матрицы A, столбцами которой являются v1,v2,…,vm:

A=B|||v1v2···vm|||C.

Пример (основа пролета)

Пример (другая основа того же промежутка)

Основа для нулевого пространства

Чтобы вычислить базис нулевого пространства матрицы, нужно найти параметрическую векторную форму решений однородного уравнения Ax=0.

Теорема

Векторы, присоединенные к свободным переменным в параметрической векторной форме набора решений Ax=0, образуют основу Nul(A).

Доказательство теоремы состоит из двух частей. Первая часть заключается в том, что каждое решение лежит в промежутке заданных векторов. Это происходит автоматически: векторы выбираются точно так, чтобы каждое решение представляло собой линейную комбинацию этих векторов. Вторая часть состоит в том, что векторы линейно независимы. Эта часть обсуждалась в этом примере в Разделе 2.5.

Базис общего подпространства

Как упоминалось в начале этого подраздела, когда задано подпространство, записанное в другой форме, для вычисления базиса обычно лучше всего переписать его как пространство столбца или пустое пространство матрицы.

Пример (базис подпространства)

Напомним, что {v1,v2,…,vn} образует базис для Rn тогда и только тогда, когда матрица A со столбцами v1,v2,…,vn имеет центральную точку в каждой строке и столбце (см. этот пример ). Поскольку A представляет собой матрицу размера n × n, эти два условия эквивалентны: векторы охватывают тогда и только тогда, когда они линейно независимы. Базисная теорема — это абстрактная версия предыдущего утверждения, применимая к любому подпространству.

Основная теорема

Пусть V — подпространство размерности m. Тогда:

• Любые m линейно независимых векторов в V образуют базис для V.
• Любые m векторов, которые охватывают V, образуют основу для V.

Доказательство

Предположим, что B={v1,v2,…,vm} — набор линейно независимых векторов в V. Чтобы показать, что B является базисом для V, мы должны доказать, что V=Span{ v1,v2,…,vm}. Если нет, то существует некоторый вектор vm+1 в V, не содержащийся в Span{v1,v2,. ..,vm}. По возрастающему критерию размаха в разделе 2.5 множество {v1,v2,…,vm,vm+1} также линейно независимо. Продолжая в том же духе, мы продолжаем выбирать векторы, пока в конце концов не получим линейно независимый остовный набор: скажем, V=Span{v1,v2,…,vm,…,vm+k}. Тогда {v1,v2,…,vm+k} является базисом для V, откуда следует, что dim(V)=m+k>m. Но мы предполагали, что V имеет размерность m, поэтому B уже должна была быть базисом.

Теперь предположим, что B={v1,v2,…,vm} покрывает V. Если B не является линейно независимым, то по теореме из раздела 2.5 мы можем удалить некоторое количество векторов из B, не уменьшая его последовательность. После переупорядочения мы можем считать, что мы удалили последние k векторов, не уменьшая диапазон, и что мы не можем удалить больше. Теперь V=Span{v1,v2,…,vm-k}, и {v1,v2,…,vm-k} является базисом для V, поскольку он линейно независим. Отсюда следует, что dimV=m−k

Другими словами, если вы уже знаете, что dimV=m, и если у вас есть набор из m векторов B={v1,v2,…,vm} в V, то вам нужно проверить только один из:

1. B линейно независим, или
2. B пролеты V,

для того, чтобы B было основой V. Если вы еще не знали, что dimV=m, то вам нужно было бы проверить оба свойства .

Другими словами, предположим, что у нас есть набор векторов B={v1,v2,…,vm} в подпространстве V. Тогда, если любые два из следующих утверждений верны, третье также должно быть истинным :

1. B линейно независим,
2. B охватывает V, и
3. димВ=м.

Например, если V — плоскость, то любые два неколлинеарных вектора в V образуют базис.

Пример (Два неколлинеарных вектора образуют основу плоскости)

Пример (Нахождение основы путем проверки)

Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)

Основа для векторного пространства

Пусть V будет подпространством R ⁿ для некоторых n . Коллекция B = { V ₁ , V ₂ ,…, V _R } из векторов V IS AR vectors от v IS AS 9. A . A . A. . если B линейно независим и охватывает V . Если хотя бы один из этих критериев не выполняется, то коллекция не является основой для V . Если набор векторов охватывает V , то он содержит столько векторов, что каждый вектор в V может быть записан как линейная комбинация векторов в наборе. Если набор линейно независим, то он не содержит столько векторов, чтобы одни становились зависимыми от других. Таким образом, интуитивно понятно, что базис имеет правильный размер: он достаточно велик, чтобы охватывать пространство, но не настолько велик, чтобы быть зависимым.

Пример 1 : Коллекция { i, j } является основой для R ² , поскольку он охватывает R ² , а векторы i и j линейно независимы (поскольку ни один из них не кратен другому). Это называется стандартным основанием для R ² . Аналогично набор { i, j, k } называется стандартным базисом для R ³ и вообще

является стандартной основой для R ⁿ .

Пример 2 : Набор { i, i+j , 2 j } не является основой для R ² . Хотя он охватывает R ² , он не является линейно независимым. Никакая коллекция из 3 или более векторов из R ² не может быть независимой.

Пример 3 : Набор { i+j, j+k } не является основой для R ³ . Хотя он линейно независим, он не охватывает все Р ³ . Например, не существует линейной комбинации i + j и j + k , равной i + j + k .

Пример 4 : Набор { i + j, i − j } является основой для R ² . Во-первых, оно линейно независимо, поскольку ни i + j , ни i − j не кратны другим. Во-вторых, он охватывает все R ² , потому что каждый вектор в R ² может быть выражено как линейная комбинация i + j и i − j . В частности, если A I + B J — любой вектор в R ² , тогда IF K ₁ = ½ ( A + B925252525252525221 1 = ½ ( K ) ₁ = ½ ( A + B) ₁ = ½ ( K ₁ = ½ ( K ₁ = ½ (. = ½( а — б ).

Пространство может иметь много разных подставок. Например, как { i, j }, так и { i + j, i − j } являются основаниями для Р ² . Фактически, любой набор , содержащий ровно два линейно независимых вектора из R ² , является основой для R ² . Точно так же любой набор, содержащий ровно три линейно независимых вектора из R ³ , является основой для R ³ и так далее. Хотя ни одно нетривиальное подпространство R ⁿ не имеет уникальной базы, есть нечто такое, что должно быть общим для всех баз данного пространства.

Пусть V будет подпространством R ⁿ для некоторого n . Если V имеет базис, содержащий ровно r векторов, то каждый базис для V содержит ровно r векторов. То есть выбор базисных векторов для данного пространства не уникален, но число базисных векторов является уникальным. Этот факт позволяет четко определить следующее понятие: число векторов в базисе векторного пространства V ⊆ R ⁿ называется размером из V , обозначаемым dim V .

Пример 5 : Так как стандартный базис для R ² , { i, j } содержит ровно 2 вектора, каждый базис для R ² содержит ровно 2 вектора, так что di5m R2 содержит ровно 2 вектора ² = 2. Аналогично, поскольку { i, j, k } является основой для R ³ that contains exactly 3 vectors, every basis for R ³ contains exactly 3 vectors, so dim R ³ = 3. In general, dim R ⁿ = n для каждого натурального числа n .

Пример 6 : В R ³ векторы i и k охватывают подпространство размерности 2. Это плоскость x−z , как показано на рисунке .

Рисунок 1

Пример 7: Одноэлементный набор { i + j = (1, 1)} является основой для одномерного подпространства V of R ² , состоящего из строки y = х . См. рис.

Рисунок 2

Пример 8 : Тривиальное подпространство { 0 } в R ⁿ имеет размерность 0. Следовательно, чтобы соответствовать определению размерности, основание для { 0 } должна быть коллекцией, не содержащей элементов; это пустой набор, ø.

Подпространства R ¹ , R ² и R ³ , некоторые из которых были проиллюстрированы в предыдущих примерах, можно обобщить следующим образом:

  

Пример 9 : Найдите размерность подпространства V из R ⁴ , натянутого на векторы

 

The collection { v ₁ , v ₂ , v ₃ , v ₄ } is not a basis for V —and dim V is not 4— потому что { v ₁ , v ₂ , v ₃ , v ₄ } не является линейно независимым; см.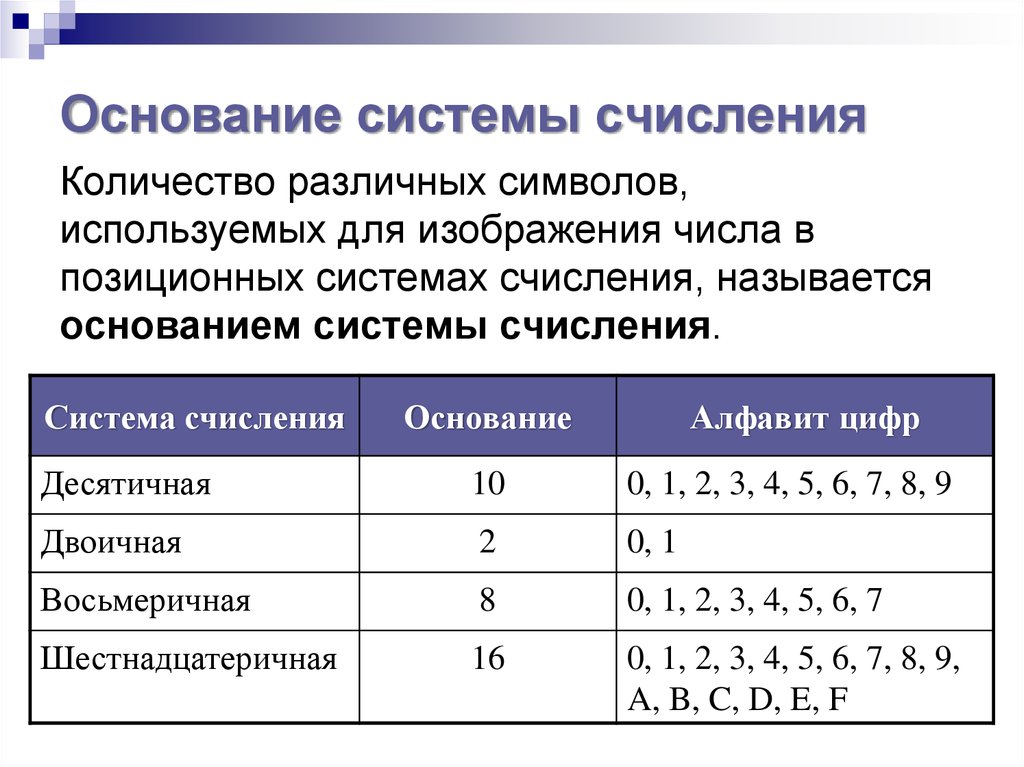 расчет, предшествующий приведенному выше примеру. Исключение v ₃ и v ₄ из этой коллекции не уменьшает пролет { V ₁ , V ₂ , V ₃ , V 1 4 ₃ , V 1 40221 3 , V 1 40221 3 , V _{3 3 , V 9 3 , . 1 , v 2 }, линейно независима. Таким образом, { v 1 , v 2 } является основой для V , поэтому dim V = 2,}

Пример 10 : Найдите размер промежутка векторов

 

Поскольку эти векторы находятся в R ⁵ , их диапазон S является подпространством R ⁵ . Однако это не трехмерное подпространство R ⁵ , поскольку три вектора w ₁ , w ₂ и w 3 не являются линейно независимыми 2 . Фактически, поскольку w ₃ = 3w ₁ + 2w ₂ вектор w ₃ можно исключить из коллекции без уменьшения диапазона. Поскольку векторы w ₁ и w ₂ независимы — ни один из них не является скалярным кратным другого, набор { w ₁ , w ₁ , w 2 служит базисом для 2 } S , поэтому его размерность равна 2.

Наиболее важным атрибутом базиса является возможность записать каждый вектор в пространстве в виде уникальный способ с точки зрения базисных векторов. Чтобы понять, почему это так, пусть B = { v ₁ , v ₂ , …, v _r } пространство будет базисом a 10 90 11 }. Поскольку базис должен охватывать V , каждый вектор v в V может быть записан по крайней мере одним способом как линейная комбинация векторов в B . То есть существуют скаляры k ₁ , k ₂ , …, k _r такой, что

Чтобы показать, что никакой другой выбор скалярных множителей не может дать v , предположим, что

также является линейной комбинацией базисных векторов, равной v .

Вычитание (*) из (**) дает

 

Это выражение представляет собой линейную комбинацию базисных векторов, которая дает нулевой вектор. Поскольку базисные векторы должны быть линейно независимыми, каждый из скаляров в (***) должен быть равен нулю:

 

Therefore, k′ ₁ = k ₁ , k′ ₂ = k ₂ ,…, and k′ _r = k _r , so the representation in ( *) действительно уникален. Когда v записывается как линейная комбинация (*) базисных векторов v ₁ , v ₂ , …, v _r скалярно определяемый коэффициент0010 k ₁ , k ₂ , …, k _r называются компонентами v относительно основы B. The row vector ( k ₁ , k ₂ , …, k _r ) is called the component vector of v relative to B and is denoted ( v ) _Б . Иногда удобно записать вектор компонентов в виде столбец вектор; В этом случае вектор компонента ( K ₁ , K ₂ ,…, K _R ) ^T — обозначено [ V ] ^{1111111111111111111111111111111111111111111111111111111н.}

Пример 11 : Рассмотрим набор C = { i, i + j , 2 j } векторов в R ² . Заметим, что вектор v = 3 i + 4 j может быть записан как линейная комбинация векторов в С следующим образом:

   

и

Тот факт, что существует более одного способа выразить вектор v в R ² в виде линейной комбинации векторов в C , еще раз указывает на то, что C не может быть основой для R ² . Если бы C были базисом, то вектор v можно было бы записать как линейную комбинацию векторов из C в одной девятке.0010 и только один способ .

Пример 12 : Рассмотрим базис B = { i + j , 2 i − j } числа R ² . Определить компоненты вектора v = 2 i − 7 j относительно B .

Составляющими v относительно B являются скалярные коэффициенты k ₁ и k ₂ которые удовлетворяют уравнению

 

Это уравнение эквивалентно системе

 

Решение этой системы: k ₁ = −4 и k ₂ = 3, поэтому

 

Example 13 : Relative to the standard basis { i, j, k } = { ê ₁ , ê ₂ , ê ₃ } for R ³ , компонентный вектор любого вектора v в R ³ равен самому v : ( v ) _B = v . . Тот же результат справедлив для стандартного базиса { ê ₁ , ê ₂ ,…, ê _n } для каждого R ^}

Ортонормированные базисы . Если В = { v ₁ , v ₂ , …, v _n } является основой для векторного пространства V , то каждый вектор v может быть записан как линейная комбинация V . базисных векторов одним и только одним способом:

 

Нахождение компонент v относительно базиса B — скалярные коэффициенты0011 в приведенном выше представлении — обычно включает решение системы уравнений. Однако, если базисные векторы являются ортонормированными , то есть взаимно ортогональными единичными векторами, то вычисление компонентов особенно легко. Вот почему. Предположим, что B = {vˆ ₁ ,vˆ ₂ ,…,vˆ _n } является ортонормированным базисом. Начиная с приведенного выше уравнения, где vˆ ₁ , vˆ ₂ ,…, vˆ _n вместо v ₁ , v ₂ , …, v _n , чтобы подчеркнуть, что базисные векторы теперь предполагаются единичными — возьмите скалярное произведение обеих сторон с vˆ ^{3 :} 4

 

В силу линейности скалярного произведения левая часть становится равной

.

 

Теперь, в силу ортогональности базисных векторов, vˆ _i · vˆ ₁ = 0 для i = 2 через n . Кроме того, поскольку vˆ — единичный вектор, vˆ ₁ · vˆ ₁ = ‖vˆ ₁ ‖1 ² = 1 ² = 1. Следовательно, приведенное выше уравнение упрощается до утверждения

В целом, если B = { Vˆ ₁ , Vˆ ₂ ,…, Vˆ _N 2} — это Orthonormal Presear для A -opect. k _i , любого вектора v относительно B находятся по простой формуле

 

Пример 14 : Рассмотрим векторы

из R ³ . These vectors are mutually orthogonal, as you may easily verify by checking that v ₁ · v ₂ = v ₁ · v ₃ = v ₂ · v ₃ = 0. Нормализуем эти векторы, тем самым получив ортонормированный базис для R ³ и затем найти компоненты вектора v = (1, 2, 3) относительно этого базиса.

Ненулевой вектор нормализуется — преобразуется в единичный вектор — путем деления его на длину. Следовательно,

 

С B = { Vˆ ₁ , Vˆ ₂ , Vˆ ₃ 2} — это ортонормальная база.0251 v относительно B можно найти, просто взяв следующие скалярные произведения:

Следовательно, ( v ) _B = (5/3, 11/(3√2),3/√2), что означает, что единственное представление v в виде линейной комбинации базиса векторы читаются как v = 5/3 vˆ ₁ + 11/(3√2) vˆ ₂ + 3/√2 vˆ _{2 902, как вы можете проверить.}

Пример 15 : Докажите, что набор взаимно ортогональных ненулевых векторов линейно независим.

Доказательство . Let { v ₁ , v ₂ , …, v _r } be a set of nonzero vectors from some R ⁿ which are mutually orthogonal, which means что нет v _i = 0 и v _i · v _j = 0 для i ≠ j . Пусть

   

— линейная комбинация векторов в этом наборе, дающая нулевой вектор. Цель состоит в том, чтобы показать, что k ₁ = k ₂ = … = k _r = 0. Для этого возьмем скалярное произведение обеих частей уравнения с v ₂ 1 :

Второе уравнение следует из первого в силу линейности скалярного произведения, третье уравнение следует из второго в силу ортогональности векторов, а итоговое уравнение является следствием того, что ‖ v ₁ ‖ ² ≠ 0 (начиная с v ₁ ≠ 0 ).