Основание систем счисления: Page Not Found | Glassdoor

Системы счисления | Статья в журнале «Юный ученый»

 

Мысль выражать все числа немногими знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна.

Пьер-Симон Лаплас (1749–1827)

 

Десятичная система счисления, которой мы пользуемся, кажется нам единственно удобной и пригодной для вычислений. Но так ли это? Попробуем выяснить какие системы счисления существуют, и какое применение находят различные системы счисления в практической деятельности человека.

Система счисления — способ изображения чисел при помощи ограниченного набора символов (цифр), и правила выполнения действий над этими числами.

Различают позиционные и непозиционные системы. В непозиционной системе счисления значение цифры не зависит от её положения в записи числа.

Примером непозиционной системы счисления, достаточно широко применяющейся в наше время, может служить так называемая римская нумерация (римская система, римские цифры), в которой для записи чисел используют лишь семь цифр I − 1, V − 5, X − 10, L − 50, C − 100, D −500, M — 1000. С помощью этих цифр можно записать любое число, используя принцип прибавления и вычитания. Отнимать можно, как правило, не больше одного знака, а прибавлять не больше трех одинаковых знаков. Знак, стоящий слева от другого знака, уменьшает значение старшего знака. Знак, стоящий справа от другого (старшего) знака, увеличивает значение старшего знака. Например, запись римскими цифрами числа 88: LXXXVIII.

Записи даже не очень больших чисел в римской нумерации длинные, умножение и деление письменно выполнять практически невозможно. Даже для того, чтобы прочитать число нужно сначала выполнить действия сложения и вычитания устно. Именно поэтому римская система счисления в математике практически не применяется.

Римские цифры используются редко, в основном в хронологии для нумерации столетий, для нумерации разделов книг, иногда они встречаются на циферблатах часов и т. д.

Общие недостатки всех непозиционных систем:

–                    существует постоянная потребность введения новых знаков для записи больших чисел;

–                    невозможно представлять дробные и отрицательные числа.

–                    сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения.

В позиционных системах счисления знаки, с помощью которых записываются числа называются цифрами, всё множество используемых знаков (цифр) − алфавитом, а их количество в алфавите − основанием системы счисления. Значение каждой цифры меняется в зависимости от её положения (позиции) в последовательности цифр, изображающих число.

Достоинства позиционных систем

–                    простота выполнения арифметических операций;

–                    ограниченное количество символов, необходимых для записи любого числа;

–                    удобство для механического представления чисел.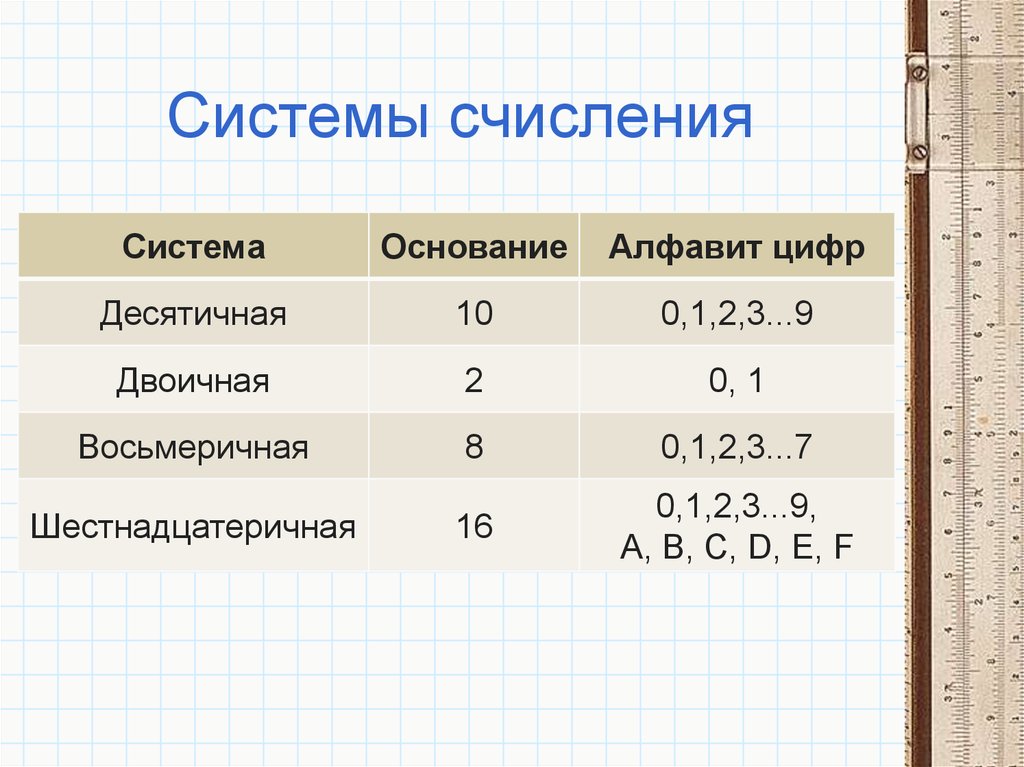

Первой известной нам системой счисления была шестидесятеричная система вавилонян, возникшая примерно за 2200–2000 лет до н. э. Вавилоняне записывали все числа от 1 до 59 по десятичной системе, применяя принцип сложения и используя всего два знака − вертикальный и горизонтальный клинья. Их получали при надавливании по сырой глиняной дощечке острием треугольной палочки. Счёт в пределах разрядов они вели по десятичной системе, а при переходе от одного разряда к другому − по шестидесятеричной. Однако у шумеро-вавилонских математиков не было знака нуля, а когда он появился, его ставили лишь при отсутствии разрядов внутри числа и никогда не писали в конце числа. Поэтому записи чисел 12, 120, 1200 и т. д. ничем не отличались. Их можно было определить только из условия задачи или каким-либо другим способом. Поэтому вавилонская система счисления считается позиционной, но непоследовательной. Мы и сейчас пользуемся этой системой при измерении времени и углов.

В V-XII веках н.  э. на полуострове Юкатан (Центральная Америка) племена индейцев майя создали двадцатеричную систему счисления (позиционную). В ней использовались три знака: единицы обозначались точками, пятерки − горизонтальными чертами и нуль — в форме ракушки. Однако бесценные творения удивительной культуры майя уничтожили огнем и мечом испанские конкистадоры.

Некогда у разных народов получила распространение двенадцатеричная система счисления. До сих пор мы делим год на 12 месяцев, сутки на часа (день и ночь). Согласно некоторым традициям и правилам этикета предметы интерьера (стулья), посуда и столовые приборы (тарелки, ножи, ложки) считают не десятками, а дюжинами (по 12 штук).

Двоичную систему счисления, возможно, как самую простую, использовали на определённом этапе все народы. Считают, что она была изобретена в IV тысячелетии до н. э. Она фактически заменила иероглифическую позиционную систему счисления египтян.

Различают анатомические (десятичная, пятеричная, двенадцатеричная, двадцатеричная) и машинные (двоичная, восьмеричная, десятичная, шестнадцатеричная) системы счисления.

Жизнь в современном мире невозможно представить без компьютеров. Для того чтобы оценить пригодность той или иной системы счисления в качестве основы для конструирования ЭВМ, нужно учитывать два главных фактора: простота осуществления математических операций и экономичность системы. Экономичность системы определяется тем количеством чисел, которые можно записать в данной системе с помощью определенного числа знаков.

Например, давайте сравним десятичную и двоичную системы счисления. Для того, чтобы в десятичной системе записать 1000 чисел (от 0 до 999), необходимо 30 знаков (3 разряда, по 10 цифр для каждого разряда). А в двоичной системе с помощью 30 знаков можно записать различных чисел. Для каждого двоичного разряда нужны только две цифры − 0 и 1. Очевидно, что , поэтому имея всего 15 двоичных разрядов, можно записать гораздо больше различных чисел, при чем 3-х разрядных десятичных. Таким образом мы убедились, что двоичная система счисления выгоднее, а значит экономичнее, чем десятичная система.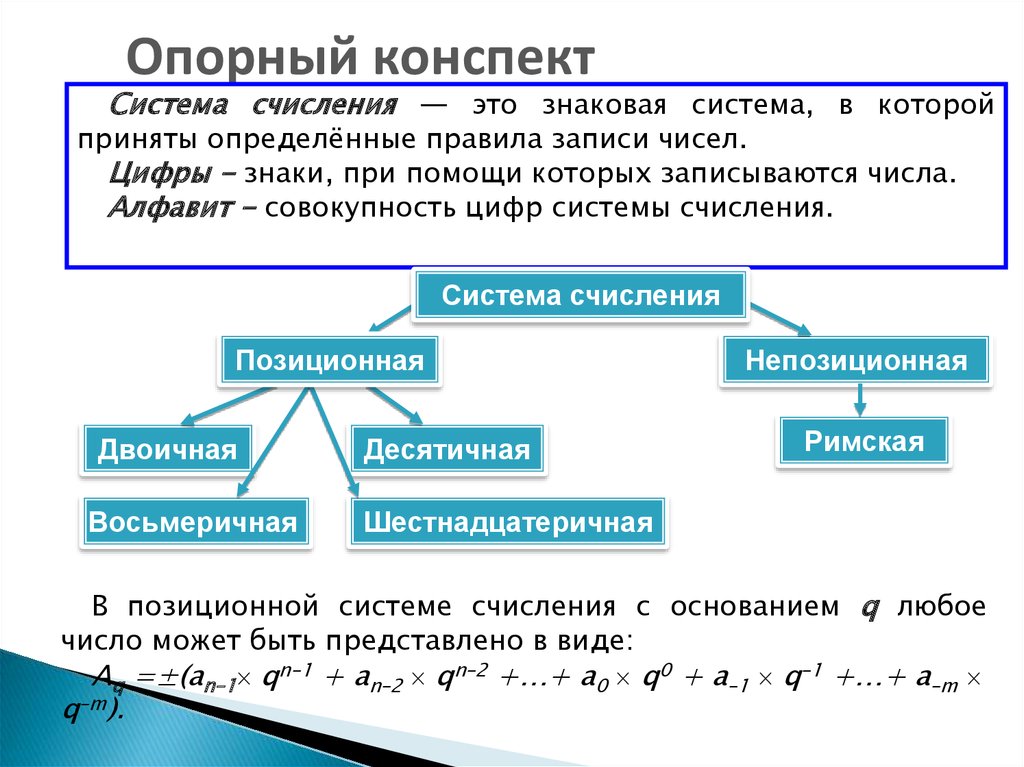

Какая же система счисления самая экономичная? Пусть в нашем распоряжении имеется знаков для записи чисел. Если за основание системы счисления взять некоторое число , то получится разрядов числа. Тогда количество чисел, которые при этом можно составить, будет равно .

Рассмотрим полученное выражение как функцию от переменной , принимающей любые положительные значения (целые, дробные, иррациональные). . Тогда задача будет формулироваться следующим образом: найти значение переменной , при котором эта функция достигает максимума.

Необходимое условие того, что в данной точке функция достигает максимума, состоит в обращении в нуль её первой производной в этой точке. В нашем случае:  — показательно-степенная функция. Для нахождения производной этой функции мы применим логарифмическое дифференцирование.

,

,

,

, ,

где е − иррациональное число, которое является основанием натуральной системы логарифмов. е =2,7182818284599045…

Ближайшим к e целым числом является 3. Это число и будет основанием наиболее экономичной системы счисления. Применение троичной системы счисления влечет за собой конструктивные трудности применительно к ЭВМ (при этом нужно пользоваться элементами, каждый из которых может находиться не в двух, а в трех устойчивых состояниях). Поэтому приоритет относительно применения в ЭВМ пока что остается за двоичной системой счисления.

Наряду с изучением давно известных систем ученые разрабатывают альтернативные системы счисления, у которых алфавит и основание не обязательно натуральные числа, они могут быть целыми отрицательными или комплексными числами. Рассмотрим несколько примеров таких систем счисления.

Уравновешенная троичная система счисления. Такую систему называют еще системой с симметричным основанием. Это система с основанием , но вместо традиционных цифр 0, 1, 2 в ней в качестве базисных используют цифры 1, 0, , где .

Примеры записи чисел в такой системе:

,

.

Особенности этой системы:

–                    если число, записанное в уравновешенной системе, начинается цифрой , то оно отрицательное, а если цифрой 1, то оно положительное;

–                    при выполнении арифметических действий над числами не требуется использовать правила знаков.

Нега-позиционная система счисления. Это система с целым отрицательным основанием. Если то система называется нега-двоичной; если − нега-четверичной и т. д.

Формула числа в такой системе:

Основным достоинством нега-позиционных систем с любым основанием является отсутствие знака перед отрицательными числами, а, следовательно, и отсутствие правила знаков.

Системы счисления с основанием, содержащим мнимую единицу .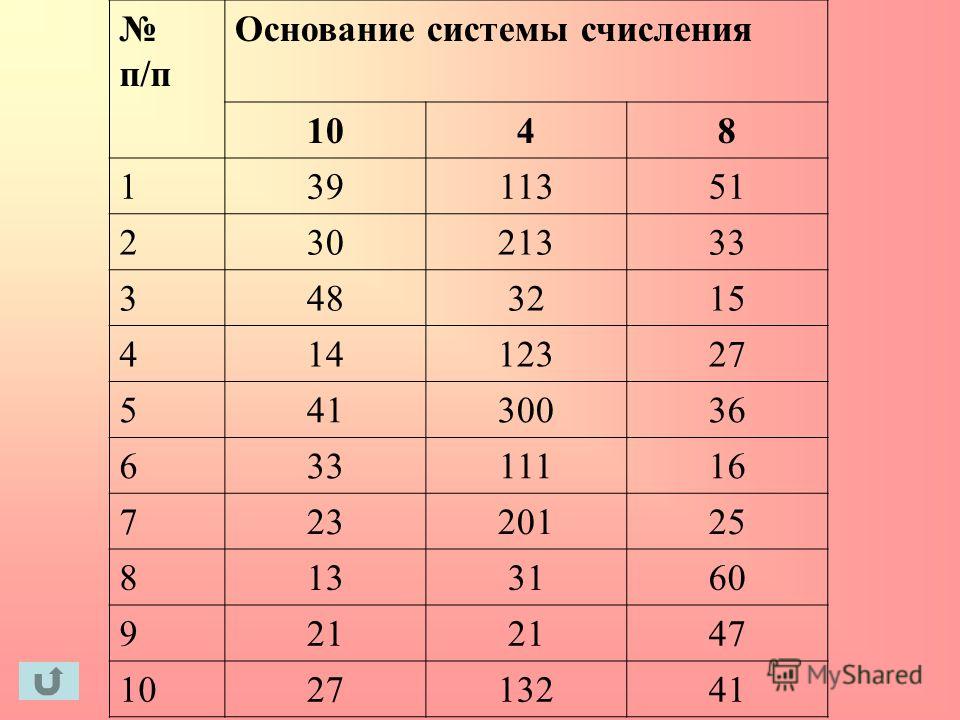 Из таких оснований больше всего для реализации на ЭВМ подходит основание . Такая система называется мнимо-четверичная. Формула числа в ней записывается так:

, где , .

Пример:

.

Оказывается, что очень легко осуществляется переход от мнимо-четверичной системы к десятичному комплексному числу и к нега-четверичной системе по формулам:

,

.

Достоинство записи комплексного числа в цифровой форме: арифметические действия над числами, записанными в цифровой форме, выполняются проще.

Факториальная система счисления. Форма записи числа в факториальной системе имеет вид:

.

Пример:

,

.

Чтобы перейти от десятичной системы к факториальной, нужно начинать делить число не на основание, а на 2, затем І частное делить на 3, ІІ частное на 4 и т.  д.

Пример:

_1236	2
1236	_618	3
0	618	_206	4
	0	204	_51	5
		2	50	_10	6
			1	6	_1	7
				4	0	0
					1
					1

 

.

Таким образом, мы видим, что развитие вычислительной техники, появление быстродействующих программно-управляемых электронно-вычислительных машин, возникновение искусства программирования − всё это требует глубокого и целенаправленного изучения особенностей различных позиционных систем счисления и разработки новых альтернативных систем счисления, на основе которых могут быть построены вычислительные системы для ЭВМ.

 

Литература:

 

1.                  Гашков С. Б. Системы счисления и их применение / С. Б. Гашков:2-е изд., испр. и доп. — М.: изд-во МЦНМО, 2012. — 68 с.

2.                  Фомин С. В. Системы счисления / С. В. Фомин: 5-е изд., − М.: Наука, Гл. ред. Физ.-мат лит., 1987. — 48 с.

О системах счисления

А.Д. Смирнов

Со школьной скамьи мы привыкли пользоваться как для счета, так и для вычислений позиционной десятичной системой счисления. Нуль и первые девять целых чисел обозначены знаками: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемыми цифрами. Десять обозначается двумя цифрами: единицей и нулем, и называется основанием системы.

Каждая цифра в числе имеет свой вес в зависимости от той позиции (места), на которой она стоит. Вес единицы в каждой позиции является степенью числа — основания системы. Действительно, 100 — это 10²; 10=10¹; 1=10⁰; 0,1=10^-1 и т. д. Веса всех позиций мы помним на память, поэтому просто пишем 251,9, а не 2в10²+5в10¹+1в10⁰+ 9в10^-1. Чтобы производить арифметические действия над числами, мы должны знать таблицу сложения и таблицу умножения для первых девяти чисел.

Десятичная позиционная система очень удобна для вычислений, производимых вручную, поэтому она вытеснила другие системы и содействовала успешному развитию математики. Следы других, ранее применявшихся систем остались в некоторых мерах веса, длины, в измерении времени, углов и для обозначения часов суток или летоисчисления.

Но попробуйте произвести арифметические действия в этих системах счисления, — например сложить 37 и 97 в римской системе вычисления: XXXVII+XCVII, или из 1 версты 457 сажен 1 аршина 1 вершка вычесть 490 сажен 2 аршина 15 вершков, — как вы сразу почувствуете всю непригодность непозиционных систем или систем с разными основаниями для проведения арифметических действий.

Хотя для ручного счета и вычислений с помощью механических счетных машин десятичная позиционная система оказалась наилучшей, ее применение в электронных машинах вызывает много трудностей.

Дело в том, что в ней слишком много цифр. Каждый разряд счетчика или запоминающего устройства, независимо от того, построены ли они на механическом принципе действия, на электромагнитном или на электронном, должен принимать 10 различных состояний для изображения цифр от 0 до 9.

В механическом счетчике дело обстояло просто: цифровое колесо делилось по окружности на 10 частей и каждой цифре соответствовал угол поворота цифрового колеса. В электронных и электромагнитных устройствах это осуществить труднее.

Но ведь основание десять не единственное возможное основание для позиционной системы счисления. Меньше всего цифр потребуется в системе счисления, за основание которой принято число два.

В двоичной позиционной системе счисления потребуются только две цифры, 0 и 1, вместо 10 цифр в десятичной системе. Каждая цифра в числе в зависимости от ее положения (позиции) будет умножаться на определенную степень двух, подобно тому как в десятичной системе каждая цифра умножалась на определенную степень десяти (одну десятую, десять, сто, тысячу и т. п.). Запись в двоичной системе числа 10110,1 означает (для отличия чисел двоичной системы от десятичной первые будем давать жирным шрифтом): 1в24+0в23 + 1в22+1в21+0в20+1в2-1=16+4+2+1/2=22, 5; число 5, которое можно представить в виде 5 =4+1 = 1в22+1в20, записывается, следовательно, как 101.

Запись чисел в двоичной системе легко представить себе следующим образом. Возьмем счеты, у которых в каждом разряде вместо десяти костяшек всего две. Будем откладывать на этих счетах подряд целые числа, начиная с единицы. Единица отложится как обычно. Отложив два, мы уже используем две костяшки, следовательно, их нужно сбросить и сделать перенос, отложив 1 в следующем втором разряде. Число два будет записано как 10, число три — как 11, и т. д. Приведем для примера несколько чисел, записанных в двоичной системе:

1 — один

1011 — одиннадцать

10 — два

1100 — двенадцать

11 — три

1101 — тринадцать

100 — четыре

1110 — четырнадцать

101 — пять

1111 — пятнадцать

110 — шесть

10000 — шестнадцать

111 — семь

0,1 — половина

1000 — восемь

0,01 — четверть

1001 — девять

0,001 — восьмая

1010 — десять

0,11 — три четверти

Основное преимущество применения двоичной системы в математических машинах состоит в том, что довольно легко создать счетчик, имеющий всего два фиксированных состояния в каждом разряде. Кроме того, оказалось очень просто изображать двоичные цифры при помощи импульсов. Наличие импульса соответствует 1, отсутствие импульса — 0. Запоминать двоичные цифры также легко, например: намагничен участок магнитофонной ленты — это значит, что запоминается 1, не намагничен этот участок — запоминается 0.

Арифметические действия в двоичной системе счисления очень просты.

Таблица умножения выглядит так:

0в0 = 0; 1в0 = 0; 0в1 = 0; 1в1 = 1.

А таблица сложения так:

0 + 0 = 0; 1+0=1; 0+1 = 1; 1 + 1 = 10.

Сложим, например, 2 и 3, для чего запишем числа одно под другим:

 10
+
 11
----
101

Начнем сложение с младших разрядов. 1+0=1; 1+1=2, но два — это единица в следующем старшем разряде, поэтому запишем нуль и перенесем 1 в старший разряд, подобно тому как при сложении 8 и 2 мы пишем 0, а десять переносим в виде единицы в старший разряд. Получилось число 101, т. е. 5.

Умножить одно число на другое тоже просто. Когда в разряде множителя стоит 1, множимое переписывается без изменения, когда 0 — умножения вообще не происходит и нужно переходить к следующему разряду множителя, не забывая сдвигать частичные произведения влево на соответствующее число разрядов.

Умножим, например, 6-5. Шесть в двоичной записи — это 110, а 5 — 101.

  110 
* 101
  110
110
------
11110

Следовательно, умножение свелось к переписи множимого в соответствующих разрядах и сложению. Получилось число, которое мы сможем расшифровать так:

1в24+1в23+1в22+1в21+1в20=16+8+4+2=30.

Деление сведется к последовательному вычитанию делителя из делимого и анализу остатка. Если остаток положителен, в частном записывается единица, а делитель сдвигается вправо; если остаток отрицателен, в частном записывается нуль, восстанавливается уменьшаемое, делитель опять же двигается вправо.

Проследим это на примере: 15:3. Изображение пятнадцати в двоичной системе — это 1111, а трех — 11.

 1111|11
-    |---
 1100|101
-----
0011
-
11
-----
–0011 – отрицательный остаток
 0011 – восстанавливаем предыдущее значение
-
   11
-----
 0000

Следовательно, деление свелось к вычитанию делителя из соответствующих разрядов делимого и обратному прибавлению его, если получается отрицательный результат.

А как же учесть знаки чисел при умножении и делении? Сделать это, оказывается, просто. Возьмем для учета знаков одноразрядный счетчик. Минус обозначим через 1, а плюс — через 0. Для определения знака произведения или частного достаточно сложить знаки сомножителей или знаки делимого и делителя. Проверим результаты:

+ на + дает + 0+0 = 0, т. е. +

+ на — дает — 0+1 = 1, т.  е. —

— на + дает — 1+0 = 1, т. е. —

Более подробно рассмотрим случай, когда оба сомножителя или и делимое и делитель имеют знак “-”. Будем складывать 1+1. В двоичной записи это будет 10, но так как счетчик знака имеет всего один разряд, то в нем окажется цифра младшего разряда, т. е. 0, а единица переноса в старший разряд пропадет. Следовательно, и в этом случае получается правильный результат:

— на — дает + 1 + 1 = 1, т. е. +.

Мы убедились, что все четыре действия арифметики в двоичной системе свелись в конечном итоге к сложению и вычитанию. А нельзя ли и вычитание заменить сложением?

Оказывается можно, но только в том случае, если отрицательные числа записывать в специальном виде: вместо единиц писать нули, а вместо нулей — единицы. Такая форма записи называется обратным кодом.

Если ввести некоторые дополнительные элементы в арифметическое устройство и представлять отрицательные числа в обратном коде, то вычитание двух положительных чисел можно заменить их сложением, записав вычитаемое в обратном коде.

Все действия в двоичной системе нам удалось в конечном итоге свести к сложению и замене кодов на обратные. Простота арифметических действий в двоичной системе и наличие в ней всего двух цифр, 0 и 1, делают ее наиболее удобной для применения в электронной машине.

Но мы привыкли иметь дело с десятичными числами. Перевод их в двоичную систему весьма трудоемок, точно так же как и обратный перевод результатов из двоичной системы в десятичную. Выполнение этой задачи возложили на саму машину. По специальной программе она выполняет эти переводы, а чтобы десятичные числа можно было ввести в машину, каждую цифру десятичного разряда изображают четырьмя двоичными разрядами.

Число 15 запишется в такой десятично-двоичной форме как 0001 0101, а уже в машине оно переведется в чисто двоичную форму 1111. Результат вычислений сначала переводится в десятично-двоичную форму, а потом печатается в чисто десятичной системе.

Некоторые машины считают прямо с числами, представленными в десятично-двоичной форме. Арифметическое устройство таких машин значительно сложнее, зато не требуется перевода чисел в двоичную систему и обратно.

Глава из книги “Современные математические машины”, М., 1959 г., стр. 58.
Перепечатывается с разрешения автора.

Система счисления 2 (стр. 1 из 2)

Содержание

Что такое система счисления?

Как порождаются целые числа в позиционных системах счисления?

Почему люди пользуются десятичной системой, а компьютеры — двоичной?

Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?

Перевод чисел из одной системы счисления в другую

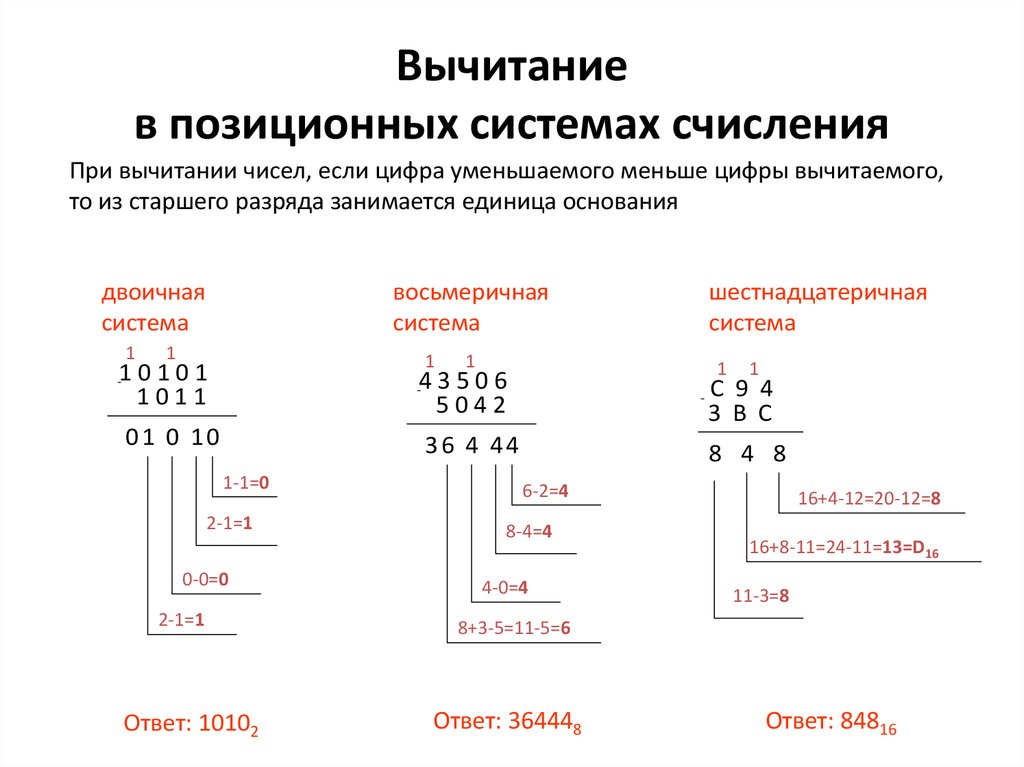
Сложение в различных системах счисления

Вычитание в различных системах счисления

Умножение в различных системах счисления

Деление в различных системах счисления

Что такое система счисления?

Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются.

Существуют позиционные и непозиционные системы счисления.

В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.

Сама же запись числа 757,7 означает сокращенную запись выражения:

Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления.

За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т. д.

Как порождаются целые числа в позиционных системах счисления?

В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.

Продвижениемцифры называют замену её следующей по величине.

Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры — 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 — замену её на 0.

Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.

Применяя это правило, запишем первые десять целых чисел

· в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;

· в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;

· в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;

· в восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.

Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:

Двоичная система	Четверичная система	Восьмеричная система	Десятичная система	Шестнадцатиричная система
1	1	1	1	1
10	2	2	2	2
11	3	3	3	3
100	10	4	4	4
101	11	5	5	5
110	12	6	6	6
111	13	7	7	7
1000	20	10	8	8
1001	21	11	9	9
1010	22	12	10	A
1011	23	13	11	B
1100	30	14	12	C
1101	31	15	13	D
1110	32	16	14	E
1111	33	17	15	F
10000	40	20	16	10

Почему люди пользуются десятичной системой, а компьютеры — двоичной?

Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.

А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:

· для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;

· представление информации посредством только двух состояний надежно и помехоустойчиво;

· возможно применениеаппарата булевой алгебры для выполнения логических преобразований информации;

· двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.

Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?

Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).

Перевод чисел из одной системы счисления в другую

Количество p различных цифр, употребляемых в позиционной системе определяет название системы счисления и называется основанием системы счисления – «p«. Любое число N в позиционной системе счисления с основанием p может быть представлено в виде полинома от основания p:

N = a_npⁿ+a_n-1p^n-1+ … +a₁p+a₀+a_-1p^-1+a_-2p^-2+ . .. (1.1)

здесь N – число, a_j – коэффициенты (цифры числа), p – основание системы счисления (p>1). Принято представлять числа в виде последовательности цифр:

N = a_na_n-1… a₁a₀. a_-1a_-2…

Перевод чисел в десятичную систему осуществляется путем составления степенного ряда с основанием той системы (см. формулу 1.1), из которой число переводится. Затем подсчитывается значение суммы.

Перевод целых десятичных чисел в недесятичную систему счисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.

Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Ответ: 75₁₀ = 1 001 011₂ = 113₈ = 4B₁₆.

Перевод правильных дробей из десятичной системы счисления в недесятичную. Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.

Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную. Перевести 23.125₁₀

2 с. с.

Системы счисления называются кратными, если выполняется соотношение: S = R^N, где S, R – основания систем счисления, N – степень кратности (целое число: 2, 3 … ).

Для перевода числа из системы счисления R в кратную ей систему счисления Sпоступают следующим образом: двигаясь от точки влево и вправо, разбивают число на группы по N разрядов, дополняя при необходимости нулями крайние левую и правую группы. Затем группу заменяют соответствующей цифрой из системы счисления S.

Таблица

Для перевода числа из системы счисления S в кратную ей систему счисления Rдостаточно заменить каждую цифру этого числа соответствующим числом из системы счисления R, при этом отбрасывают незначащие нули в старших (00512) и младших (15,124000) разрядах.

Преобразование между основными системами счисления

Обновлено 25 апреля 2017 г.

Автор Mike Gamble

Двоичная система состоит из чисел, выраженных комбинациями цифр один и ноль. В 1937 году Клод Шеннон понял, что состояния включения/выключения электрических цепей могут соответствовать истинным/ложным состояниям логики. Он представил идею о том, что булева логика может быть объединена с двоичным представлением значений истинности для разработки схем. Даже с развитием современных компьютеров двоичная система является фундаментальной частью современной схемы. Двоичная система и связанные с ней восьмеричная и шестнадцатеричная системы широко распространены во многих компьютерных областях. Таким образом, преобразование между системами счисления является важным навыком для всех, кто работает с компьютерами.

Преобразование общего основания

Разделите число, которое необходимо преобразовать, на желаемое основание. Используя стандартную запись деления, запишите частное как целое число над делимым, а остаток справа от частного. Например, чтобы преобразовать число 12 в двоичное (по основанию 2), разделите 12 на 2, в результате чего получится частное 6 с остатком 0.

Добавьте еще один символ деления над частным и снова разделите на основание. Повторите этот процесс с каждым полученным частным, пока не получите частное 0. Например, продолжая делить 2 на 6, вы получите 3 с остатком 0, затем 1 с остатком 1, а затем 0 с остатком 1.

Перепишите каждый остаток, используя систему счисления, в которую вы конвертируете, если основание больше, чем та, из которой вы конвертируете. Если вы не пытаетесь выполнить преобразование из недесятичной системы счисления, это будет применяться только при преобразовании в систему счисления больше 10. Шестнадцатеричная система (основание 16) использует буквы A, B, C, D, E и F для представления чисел. 10, 11, 12, 13, 14 и 15 соответственно. Поэтому, если вы конвертируете в шестнадцатеричный формат, вы будете переписывать каждый остаток со значением 10 или выше, используя соответствующую букву.

Запишите остатки как цифры одного числа, начиная с последнего остатка и заканчивая первым. Это ваш конвертированный номер. В приведенном примере найдено четыре остатка: 1100. Это двоичный эквивалент числа 12.

Этот метод работает для преобразования из любого основания в любое другое основание. Однако преобразование из недесятичной системы счисления требует выполнения математических операций с недесятичной системой счисления. Например, 1100 можно преобразовать обратно в 12, если вы знаете, как выполнять двоичные вычисления. По этой причине удобно иметь другой метод преобразования недесятичных оснований в десятичные. 90.

Оцените каждую из перечисленных способностей. В приведенном примере степени равны 512, 64, 8 и 1.

Умножьте каждую цифру на соответствующую степень и найдите сумму этих произведений. Для оснований больше 10 преобразуйте цифры в их десятичные эквиваленты перед умножением. Полученная сумма представляет собой десятичное значение заданного числа. Например, восьмеричное число 2154 = 2_512 + 1_64 + 5_8 + 4_1 = 1132 в десятичном виде.

Преобразование двоичного в восьмеричное или шестнадцатеричное

Запишите двоичное число с пробелом после каждой третьей или четвертой цифры, в зависимости от того, преобразуете ли вы в восьмеричное или шестнадцатеричное число, начиная справа. При преобразовании в восьмеричное число ставьте пробел после каждой третьей цифры (для шестнадцатеричного числа ставьте пробел после каждой четвертой цифры). Это создает небольшие пакеты двоичных цифр. Например, чтобы преобразовать в шестнадцатеричное число, перепишите двоичное число 1101010 как 110 1010. Обратите внимание, что в первом пакете только три цифры, поскольку счет четырех цифр начинается справа.

Преобразование каждого пакета в его восьмеричный или шестнадцатеричный эквивалент. Три двоичных разряда имеют диапазон значений от 0 до 7, что является тем же диапазоном для восьмеричного разряда. Точно так же диапазон четырех двоичных цифр от 0 до 15 соответствует диапазону шестнадцатеричных цифр. Не забудьте использовать степени двойки при преобразовании из двоичного: 8, 4, 2 и 1. Например, первый пакет 110 равен 1_4 + 1_2 + 0_1 = 6. Второй пакет 1010 равен 1_8 + 0_4 + 1_2 + 0*1. = 10, что является шестнадцатеричным значением A.

Запишите шестнадцатеричные цифры как одно число. В приведенном примере 1101010 — это 6А в шестнадцатеричном формате. Преобразование из двоичного в шестнадцатеричное намного проще, чем преобразование из двоичного в десятичное, потому что нет размера двоичного пакета, соответствующего значениям от 0 до 9. По этой причине шестнадцатеричный формат очень удобен в качестве сокращенного способа записи очень длинных двоичных чисел.

Обратите внимание, что преобразование из восьмеричного или шестнадцатеричного числа прямо противоположно преобразованию в них. Запишите каждую цифру в виде трех- или четырехзначного двоичного пакета, а затем соедините их вместе как одно число. Например, восьмеричное число 2154 = 10 001 101 100. Сложив их вместе, мы получим двоичное число 10001101100.

CS101 — Системы счисления и двоичные числа

Вот некоторые неформальные заметки о системах счисления и двоичных числах. См. также разделы 3.1–3.2 учебника.

Наша обычная система счисления — это позиционная система, в которой позиция (столбец) цифры представляет ее значение. Начиная справа, у нас есть столбец единиц, столбец десятков, сотни, тысячи и так далее. Таким образом, число 3724 означает три ТЫСЯЧИ, СЕМЬСОТ, две ДЕСЯТКИ (называемые двадцатью) и четыре ЕДИНИЦЫ.

Значения этих столбцов получаются из степеней десяти, которые затем называются основанием системы счисления. Систему счисления с основанием десять также называют десятичной .

В десятичной системе счисления нет ничего особенного, за исключением того, что это то, чему вы научились с юных лет. Позиционная система счисления может использовать любое количество в качестве основы. Возьмем, к примеру, основание пять. В базе пять столбцы представляют количества (справа налево) один, пять, двадцать пять и сто двадцать пять. Нам нужно использовать пять символов для обозначения количества от нуля до четырех. Для простоты давайте сохраним те же цифры, которые мы знаем: 0, 1, 2, 3 и 4.

Число, показанное на этом рисунке, 3104 по основанию пять, представляет то же самое количество, которое мы обычно записываем как 404 по основанию десять. Это потому, что это три × сто двадцать пять (= 375), плюс один × двадцать пять (= 25) плюс четыре единицы (= 4), поэтому 375 + 25 + 4 = 404.

Вы можете посчитать прямо в основание пять; выглядит так: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30, 31, 32, 33, 34, 40, 41, 42 , 43, 44, 100. (Соответствуют количествам от нуля до двадцати пяти.)

Попробуйте считать и конвертировать между другими базами. Ниже представлен интересный видеообзор дюжинальной системы счисления (с основанием двенадцать).

Компьютерные системы используют двоичные числа — это просто означает, что они находятся в базе два. Использование двух в качестве основы действительно удобно и гибко, потому что нам нужны только два «символа», и существует так много способов их представления: ноль/единица, вкл/выкл, вверх/вниз, высокий/низкий, положительный/отрицательный. и т. д.

В двоичном формате столбцы (справа налево) 1, 2, 4, 8, 16, 32 и т. д. Использование нуля означает, что мы исключаем количество этого столбца, а единица означает, что мы его включаем.

Итак, двоичное число 10110 равно количеству 16 + 4 + 2 = 22. Каждая двоичная цифра (единица или ноль) называется битом. Самое большое пятиразрядное двоичное число, тогда 11111 = 16 + 8 + 4 + 2 + 1 = 31.

Стоит научиться считать в двоичном виде, хотя бы от нуля до пятнадцати:

 0000 = 0 0100 = 4 1000 = 8 1100 = 12
    0001 = 1 0101 = 5 1001 = 91101 = 13
    0010 = 2 0110 = 6 1010 = 10 1110 = 14
    0011 = 3 0111 = 7 1011 = 11 1111 = 15 

Сравнительно легко складывать числа непосредственно в двоичном виде. Выровняйте столбцы, а затем действуйте справа налево, как обычно. Возможны только четыре случая:

• Если в столбце нет единиц, ниже запишите ноль.
• Если в столбце есть один, напишите один ниже.
• Если в столбце две единицы, запишите ноль и перенесите единицу в следующий столбец (слева).
• Наконец, если в столбце три единицы (возможно, из-за входящего переноса), запишите единицу и перенесите единицу в следующий столбец.

Ниже приведен пример сложения 10110 плюс 11100. Результат равен 110010, и вы можете видеть биты переноса над исходными числами оранжевым цветом.

При сложении таким способом всегда полезно проверить свою работу, преобразовав числа в десятичные числа и проверив сложение. В этом случае мы добавляем 22 (10110) к 28 (11100), чтобы получить 50 (110010).

Обычно мы располагаем числа вдоль линии, уходящей в бесконечность. Действительно, в двоичном формате мы всегда можем продолжить счет, добавляя все больше и больше столбцов, которые являются степенями двойки.

Однако в большинстве компьютерных систем и программ мы используем фиксированных чисел . То есть мы заранее решаем, сколько битов будет использовано для представления числа. Например, 32-разрядный компьютер представляет большинство своих чисел и адресов с помощью 32-разрядных чисел. Наибольшее такое число 2³²–1 = 4,29.4 967 295.

Если ваши числа имеют фиксированное количество битов, то нет числовой линии, уходящей в бесконечность. Вместо этого мы расставляем числа по кругу, как часы. Ниже представлено числовое колесо для 3-битных целых чисел. Наименьшее 3-битное целое число равно нулю, а наибольшее — семи. Затем, если вы попытаетесь продолжить счет, он просто снова вернется к нулю.

Когда вы выполняете арифметические действия с числами фиксированного размера, вы отбрасываете все лишние биты переноса; результат не может превышать обозначенный размер. Например, посмотрите, что произойдет, если мы попытаемся сложить 110 + 011, используя 3-битные целые числа:

В 3-битной арифметике 6 плюс 3 равно 1. Вы можете понять это на числовом колесе. Дополнение соответствует обходу колеса по часовой стрелке. Итак, начните с 6 и пройдите по часовой стрелке на 3. Вы получите 1, то есть 6+3.

Ниже видео о двоичных числах фиксированного размера в старых видеоиграх.

Теперь мы рассмотрим числа со знаком , то есть числа, которые могут быть положительными или отрицательными. Существует два метода кодирования чисел со знаком. Первый называется величина со знаком. Сначала это кажется простым, но за этой простотой скрываются некоторые неуклюжие свойства.

Вот как это работает. Мы используем фиксированную ширину, а затем крайний левый бит представляет знак. Итак, 4-битная величина со знаком выглядит так:

 ___ ___ ___ ___
  sign 4 2 1 

, где бит знака, установленный в «1», означает, что величина интерпретируется как отрицательная. Таким образом, 0110 равно +6 , тогда как 1110 равно -6 . В этой системе наибольшее положительное число равно 9.0131 0111 = +7 и самое отрицательное число 1111 = -7 .

Одним из неприятных эффектов этого представления является то, что есть два способа записать ноль: 0000 и также 1000 . Нет такой вещи, как отрицательный ноль, так что это не имеет особого смысла.

Второй способ представления величин со знаком называется дополнением до двух. Хотя на первый взгляд это выглядит сложнее, на самом деле это работает очень хорошо. Ниже приведена интерпретация 4-битного дополнения до двух. Все, что нам нужно сделать по сравнению с обычными числами без знака, — это инвертировать значение самого левого бита.

 ___ ___ ___ ___
   -8 4 2 1 

Таким образом, +6 — это 0110 , как и прежде, но как насчет -6 ? Нам нужно включить минус 8, а затем добавить два: 1010 . Чтобы представить -1 , вы включаете все биты: 1111 , потому что это дает -8+4+2+1 = -8+7 = -1 .

Преимущество дополнения до двух заключается в том, что вы можете сложить эти числа, и все получится. Давайте попробуем добавить 7 и -3 :

 0 1 1 1 = 7
   1 1 0 1 = -3
  --------- ----
   0 1 0 0 = 4 

Также относительно легко инвертировать число, то есть перейти от +6 к -6 или от -3 к +3 . Вот шаги:

1. Сначала переверните все биты. То есть все нули становятся единицами, а все единицы становятся нулями.

2. Затем добавьте один.

Например, вот как мы производим -6 из +6 :

 0 1 1 0 = +6
   1 0 0 1 (перевернуть все биты)
       + 1 (добавить один)
  ---------
   1 0 1 0 = -6 

Вам даже не нужно выполнять эти шаги в обратном порядке, чтобы преобразовать обратно:

 1 0 1 0 = -6
   0 1 0 1 (перевернуть все биты)
       + 1 (добавить один)
  ---------
   0 1 1 0 = +6 

Вот мультфильм от XKCD о том, как считать овец с помощью дополнения до двух!

Сколько битов использует этот человек?

Наконец, я хочу представить две системы счисления, которые очень полезны как 9.0051 аббревиатура для двоичного кода. Они работают так хорошо, потому что их основания являются степенью двойки.

Восьмеричное число по основанию восемь, поэтому мы используем символы 0–7, а значения столбцов следующие:

 ___ ___ ___ ___
   512 64 8 1
    8³ 8² 8¹ 8⁰ 

Однако реальное значение восьмеричного числа состоит в том, что каждая восьмеричная цифра соответствует ровно трем двоичным цифрам. Таким образом, восьмеричное число, например 3714 , отображается следующим образом:

 3 7 1 4 восьмеричное число
  0 1 1 1 1 1 0 0 1 1 0 0 двоичное число
  
 (4 2 1 4 2 1 4 2 1 4 2 1) 

Шестнадцатеричное число — это основание шестнадцать, поэтому мы используем символы 0–9, а затем А для обозначения десяти, В для одиннадцати и так далее до F для пятнадцати. Значения столбцов:

 ____ ____ ____ ____
4096 256 16 1
 16³ 16² 16¹ 16⁰ 

Таким образом, шестнадцатеричное число, например 2A5C , имеет значение 2×4096 + 10×256 + 5×16 + 12×1 = 10844 с основанием десять.

В шестнадцатеричном формате каждая цифра соответствует ровно четырем битам. Вот то самое число в двоичном формате:

 2 А 5 С
  0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 0
  
 (8 4 2 1 8 4 2 1 8 4 2 1 8 4 2 1) 

Ниже приведены два отличных видеообзора шестнадцатеричных чисел. ( Обратите внимание на , когда вы смотрите это — британцы часто произносят ноль как «ноль». )

1. Преобразуйте следующие десятичные числа в двоичные числа.

   1. 6
   2. 18
   3. 51
   4. 63

2. Преобразуйте следующие двоичные числа без знака в десятичную систему счисления.

   1. 1010
   2. 1101
   3. 1000
   4. 10001

3. Что общего у всех нечетных чисел, записанных в двоичном формате? (Подсказка: попробуйте записать числа 3, 5, 7, 9, 11 в двоичном формате.)

4. Используя 7-битные знаковые (дополнение до двух) двоичные числа, какое наибольшее положительное число? Какое самое отрицательное число?

5. Преобразуйте следующие 5-битные знаковые (дополнение до двух) двоичные числа в основание десяти.

   1. 01101
   2. 01111
   3. 10011
   4. 11111

6. Преобразование следующего 16-разрядного двоичного числа в шестнадцатеричное, а затем в восьмеричное.

    0 1 1 1 1 1 1 1 0 0 1 1 1 0 1 0 

7. Преобразование следующих шестнадцатеричных чисел в двоичные:

   1. 9Д
   2. С4
   3. А17Е

8. Добавьте и проверьте следующие беззнаковые двоичных числа.

    1 0 1 1 1 1 1 1 0 1 1 1
   + 1 1 1 0 1 + 1 0 0 1 0 0
   ————————————— —————————————— 

Решения здесь

@jaffathecake в Твиттере

Введение в системы счисления — Digital Detective

Системы счисления используют разные базы счисления. Числовая база указывает, сколько различных цифр доступно при использовании определенной системы счисления. Например, десятичное число — это число с основанием 10, что означает, что оно использует десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.. Двоичная система счисления основана на 2, что означает, что в ней используются две цифры: 0 и 1. Для разных целей необходимы разные системы счисления. Люди используют систему счисления 10, тогда как компьютеры используют двоичную систему счисления.

Числовая база определяет, сколько цифр необходимо для представления числа. Например, число 78 в десятичном формате (с основанием 10) требует двух цифр. Двоичный эквивалент (с основанием 2) равен 1001110, что требует семи цифр. Как следствие этого, в вычислениях часто требуются очень длинные двоичные числа. Чтобы решить эту проблему, можно использовать другие системы счисления, которые требуют меньшего количества цифр для представления чисел. Например, в некоторых аспектах вычислений используется система счисления 16, которая называется шестнадцатеричной.

Принятый метод представления различных систем счисления (в технической документации) состоит в том, чтобы показать число с основанием в нижнем индексе. Например:

• 37 ₁₀ — это десятичное число
.
• 1101 ₂ является двоичным
• 12FF ₁₆ — шестнадцатеричное число
.

Вы часто будете видеть шестнадцатеричные числа, представленные с использованием синтаксиса программирования C, где к значению добавляется префикс 0x: 0x12FF.

Шестнадцатеричный (или Hex) формат особенно удобен для представления больших чисел, так как требуется меньше цифр. Hex используется несколькими способами. Адреса памяти отображаются в шестнадцатеричном формате, как и цветовые коды. Основное преимущество шестнадцатеричного формата состоит в том, что две цифры представляют один байт.

Рассмотрим число 10001001 ₂ . Это 8-битное число, которое при преобразовании в десятичное число равно 137 ₁₀ . То же число в шестнадцатеричном формате 89 ₁₆ . Этот базовый пример показывает, что 8-битное двоичное число может быть представлено как двузначное шестнадцатеричное число.

Так как это число с основанием 16, в шестнадцатеричном формате используется 16 различных цифр: от 0 до 9 и от A до F. На изображении ниже показано средство просмотра шестнадцатеричного представления, отображающее все значения байтов от 0 до 255 в десятичном виде или от 0 до FF в шестнадцатеричном формате.

 

При выполнении вычислений люди используют систему счисления 10, вероятно, потому, что у нас на руках 10 цифр. Обычно эта система известна как десятичная и использует 10 различных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Когда мы доходим до 9, мы добавляем дополнительную цифру слева и начинаем снова. . Когда мы доходим до 99, мы добавляем дополнительную цифру слева и так далее. Каждая цифра, которую мы добавляем, в десять раз превышает предыдущую цифру. Взвешенное значение для каждой позиции выглядит следующим образом:

 

Число 3265 легко понять в десятичном выражении. Он составляется следующим образом:

 (3 x 1000) + (2 x 100) + (6 x 10) + (5 x 1) 

При создании номера мы начинаем с единиц и при необходимости добавляем дополнительные цифры. чтобы создать номер, который мы хотим.

Двоичные числа используют числовую систему счисления 2 и работают по точно такому же принципу. На этот раз у нас есть только две цифры: 0 и 1. Она должна быть двоичной, потому что компьютеры работают либо с нулем, либо с единицей (выключается и включается). Следовательно, 1 — это наибольшее значение, которое мы можем получить с одним битом. Чтобы увеличить размер числа, мы добавляем больше битов. Каждый бит в два раза больше предыдущего бита, потому что мы используем основание 2. В таблице ниже показано 8-битное двоичное число 10010111. Значение каждого нового бита удваивается, поскольку двоичное число соответствует основанию 2.

 

Используя тот же принцип для вычисления числа, мы имеем:

 (1 x 128) + (1 x 16) + (1 x 4) + (1 x 2) + (1 x 1) = 151 

Двоичные числа можно преобразовать в десятичные целые числа следующим образом:

• Запишите двоичное число (например, 10010111).
• Над числом, начиная с младшего бита (LSB), напишите цифру 1.
• При перемещении влево от младшего бита к старшему биту (MSB) удваивайте значение предыдущего числа.

Везде, где есть 1, добавьте десятичное значение. Пример выше представляет:

 (1 x 128) + (1 x 16) + (1 x 4) + (1 x 2) + (1 x 1) = 151 

Следовательно, двоичное значение 1001011 равно 151 как десятичное целое число.

Чтобы преобразовать десятичное целое число в двоичное, используйте тот же метод, что и выше, но в обратном порядке. Например, чтобы преобразовать число 151, запишите последовательность в степени двойки следующим образом:

• Начиная со старшего бита, поместите 1 или 0 в каждый столбец по мере необходимости, чтобы гарантировать, что в сумме получится 151.
• 128 меньше 151, поэтому поместите 1 в первый столбец: 151 – 128 = 23
• 64 больше 23, поэтому поместите 0 во второй столбец
.
• 32 больше 23, поэтому поместите 0 в третий столбец
.
• 16 меньше 23, поэтому поместите 1 в четвертый столбец: 23 – 16 = 7
• 8 больше 7, поэтому поместите 0 в пятую колонку
• 4 меньше 7, поэтому поместите 1 в шестой столбец: 7 – 4 = 3
• 2 меньше 3, поэтому поместите 1 в седьмой столбец: 3 – 2 = 1
• 1 равно 1, поэтому поместите 1 в восьмой столбец. 1 – 1 = 0

Следовательно, 10010111 = 151

Альтернативный метод выполнения этого расчета состоит в повторном делении десятичного числа следующим образом:

• 151 разделить на 2 = 75 с остатком 1
• 75 разделить на 2 = 37 с остатком 1
• 37 разделить на 2 = 18 с остатком 1
• 18 разделить на 2 = 9 с остатком 0
• 9 разделить на 2 = 4 с остатком 1
• 4 разделить на 2 = 2 с остатком 0
• 2 разделить на 2 = 1 с остатком 0
• 1 разделить на 2 = 0 с остатком 1

Продолжайте делить на 2, пока не останется ничего, что можно было бы делить. Чтение снизу вверх дает нам 10010111, что равно 151.

Вы можете проверить ответ, действуя в обратном порядке:

 128 + 16 + 4 + 2 + 1 = 151 

Общий подход для преобразования десятичных целых чисел to hex означает сначала преобразовать десятичное число в двоичное, а затем преобразовать двоичное в шестнадцатеричное. Взяв в качестве примера десятичное число 211:

• Рассчитать двоичный эквивалент:

• Разделить двоичное число на две группы по четыре бита и преобразовать каждую группу в шестнадцатеричный эквивалент.

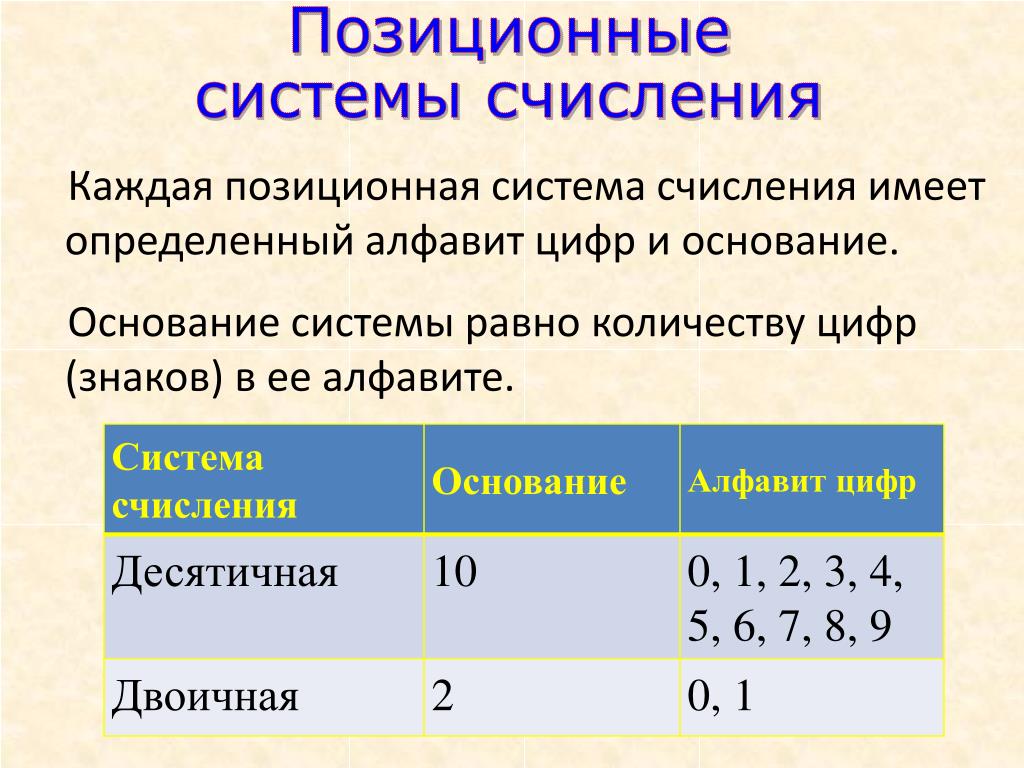
• 11010011 ₂ = 211 ₁₀
• Первая группа: 8 + 4 + 1 = 13 (или D в шестнадцатеричном формате)
• Вторая группа: 2 + 1 = 3

Следовательно, 11010011 ₂ = 211 ₁₀ = D3 ₁₆ (0xD3).

Самый простой способ преобразовать шестнадцатеричное число в десятичное — сначала преобразовать шестнадцатеричное в двоичное, а затем двоичное в десятичное. Преобразование шестнадцатеричных данных в двоичные представляет собой процесс, обратный описанному выше. Возьмите шестнадцатеричное значение, а затем преобразуйте каждую цифру по очереди в ее двоичный эквивалент, используя группы из четырех битов (обычно называемые полубайтами). Мы будем использовать 2А3 ₁₆ (0x02A3) например:

 2 = 0010, A = 1010, 3 = 0011 

Следовательно, 1010100011 ₂ является двоичным эквивалентом 2A3 1609.

Затем это двоичное значение можно преобразовать в десятичное с помощью описанного выше метода.