Оси х у z – Прямоугольная система координат — Википедия

4. Построение аксонометрических осей координат.

1. В прямоугольной изометрической проекции, или, сокращенно, изометрии, аксонометрические оси расположены под углом 120^о друг к другу (рис. 3.41) и коэффициенты искажения по осям х’, у’ и z’ равны между собой. Линии изображаемого предмета, расположенные параллельно осям, проецируются с искажениями истинной величины в 0,82 раза.

В практике пренебрегают этим показателем искажения и для простоты построения предметов в изометрической проекции вместо 0,82 истинной длины откладывают по осям единицу. Получающееся при этом изображение увеличено по отношению к истинному в 1:0,82 = 1,22 раза. На наглядность изображения такое увеличение не отражается.

Оси изометрической проекции можно построить с помощью циркуля (рис. 3.41, а). Для этого сначала проводят ось z’. Затем из точки 0′ произвольным радиусом В описывают дугу, пересекающую ось z’ в точке 1. Из этой точки тем же радиусом делают засечки на дуге в точках 2 и 3. Ось х’ проводят через точки 3 и 0′, а ось у’ — через точки 2 и 0′. Построение осей при помощи рейсшины и прямоугольного треугольника с углами 30

о и 60^о показано на рис. 3.41, б.

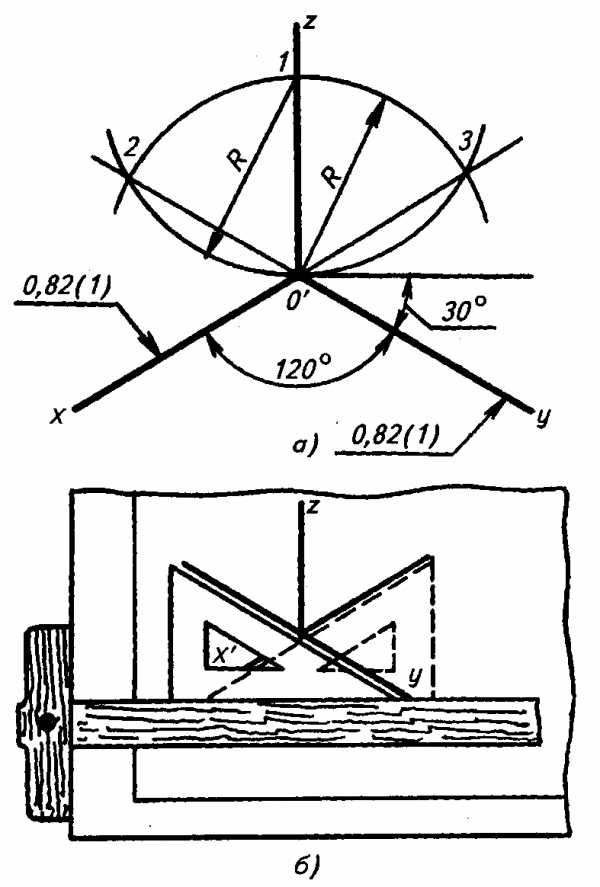
Рис. 3.41.

Построение аксонометрических осей прямоугольной изометрической проекции

2. В прямоугольной диметрической проекции, или сокращенно диметрии, ось z’ располагают вертикально, ось х’ наклонена под углом 7^o10′, а ось у’— под углом 41^o25′ к линии горизонта. Показатели искажения по осям х’ и z’ равны 0,94, а по оси у’ — 0,47 (рис. 3.42, а).

В практике применяют увеличенную диметрию с показателями по осям х и z или по направлениям, им параллельным, откладывают действительные размеры, то есть единицу, а по оси у размеры уменьшают в два раза (0,5).

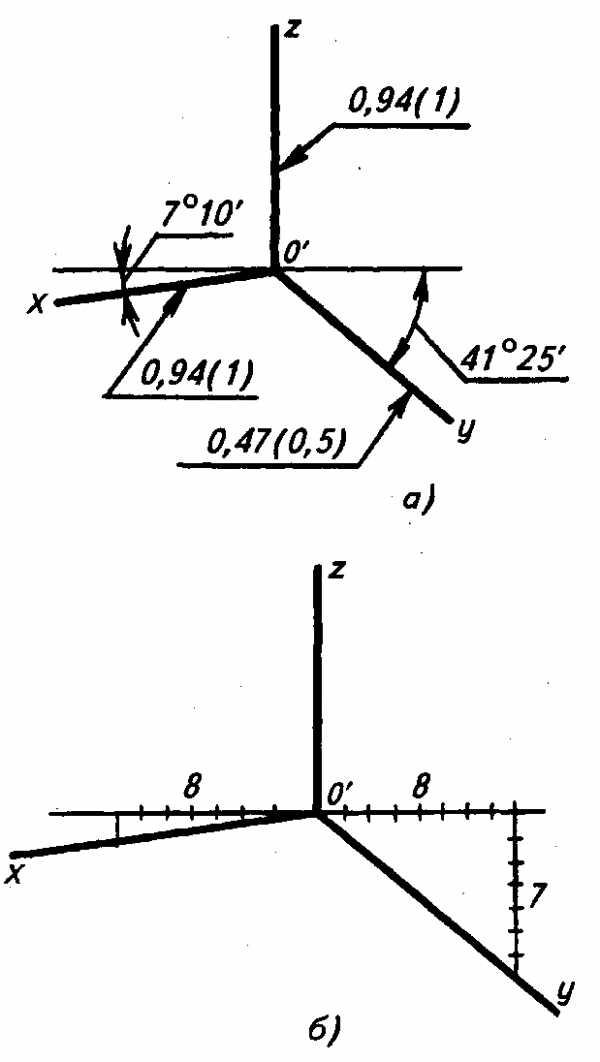
Рис. 3.42

Построение аксонометрических осей прямоугольной диметрической проекции

Наиболее простой способ построения осей диметрии (рис. 3.42, 6) заключается в том, что на горизонтальной прямой, проходящей через точку О, откладывают в обе стороны от точки 0′ восемь равных произвольных отрезков. Из конечных точек этих отрезков вниз по вертикали откладывают слева один такой же отрезок, а справа — семь. Полученные точки соединяют с точкой 0 и получают направления аксонометрических осей х и у.

3. В косоугольной фронтальной диметрической проекции, или, сокращено фронтальной диметрии, ось х’ — горизонтальная прямая; ось z’ перпендикулярна к оси х’, а ось у’ расположена под углом 45^о к горизонтальной оси (под углом 135^о к оси г’) (рис. 3.43, а). Коэффициент искажения по оси х и z равен единице, а по оси у’ — 0,5.

Обычно построение осей выполняют при помощи рейсшины и равнобедренного треугольника, как показано на рис. 3.43, б.

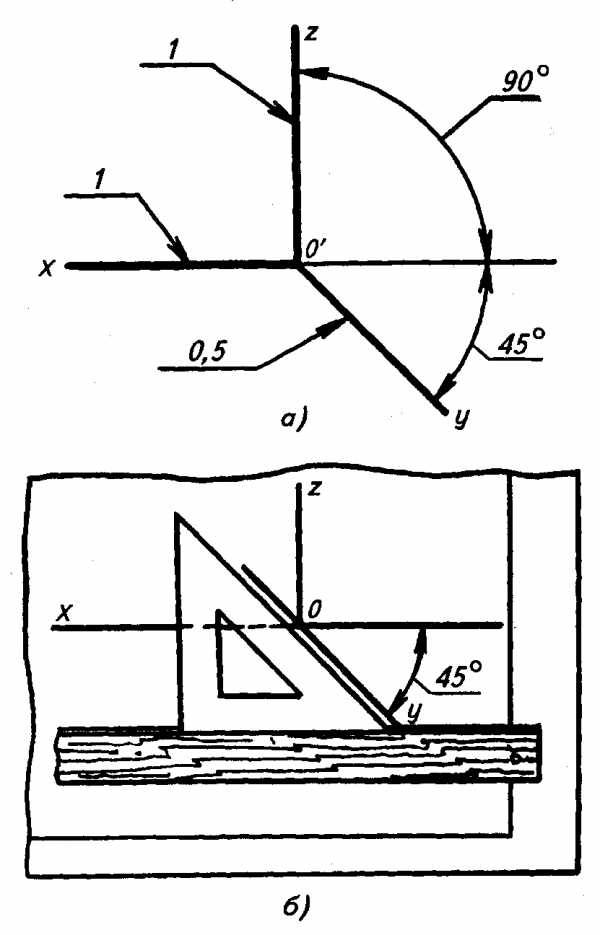
Рис. 3.43.

Построение аксонометрических осей фронтальной диметрической проекции

5. Построение аксонометрических проекций предметов призматической и пирамидальной формы.

Построение аксонометрических проекций начинают с изображения основания или характерной грани предмета, то есть плоских фигур, расположенных в одной из плоскостей: фронтальной, горизонтальной или профильной. Поэтому рассмотрим сначала изображение плоских фигур.

Пример 1. Построение аксонометрических проекций равностороннего треугольника (рис. 3.44 и рис. 3.45).

1) Треугольник расположен во фронтальной плоскости. По оси х’ откладывают по обе стороны от точки 0′, принадлежащей оси z’, отрезки b/2, равные в сумме d — стороне треугольника, а по оси z’ — его высоту h. Полученные точки соединяют отрезками прямых.

2) Треугольник расположен в горизонтальной плоскости. По оси х’ откладывают от точки 0′, принадлежащей оси z отрезки b/2, равные в сумме b— стороне треугольника, а по оси у’ — высоту h для изометрической (рис. 3.44) проекции и половину его высоты (h/2) — для фронтальной диметрической (рис. 3.45).

3) Треугольник расположен в профильной плоскости. По оси у откладывают половину стороны (b/2) для фронтальной диметрической проекции и сторону b для изометрической, а по оси z’ — его высоту h.

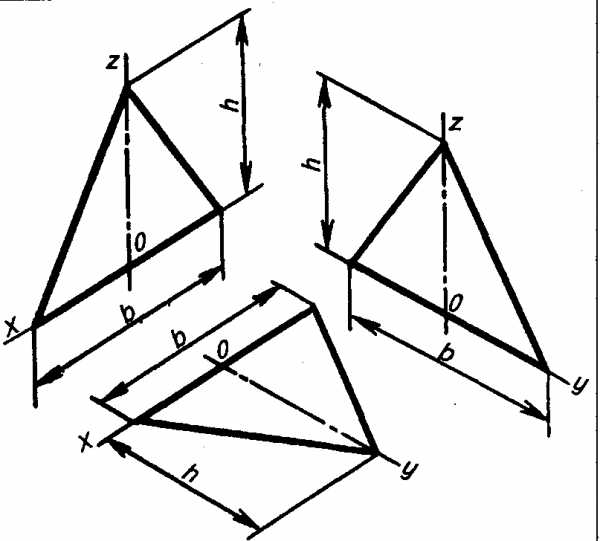
Рис. 3.44

Изображение равнобедренного треугольника в прямоугольной изометрической проекции

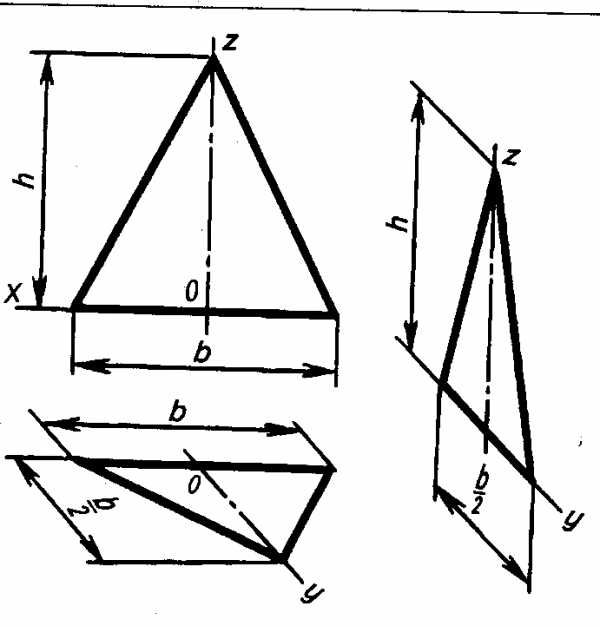
Рис.3.45

Изображение равнобедренного треугольника во фронтальной диметрической проекции

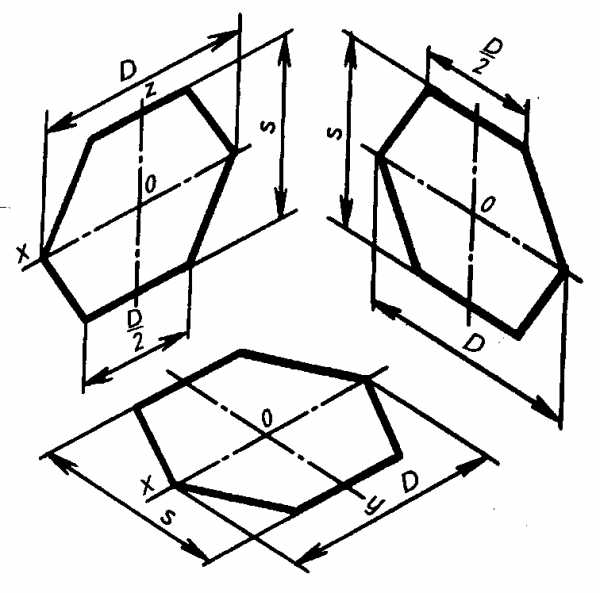
Рис. 3.46.

Изображение правильного шестиугольника в изометрической проекции

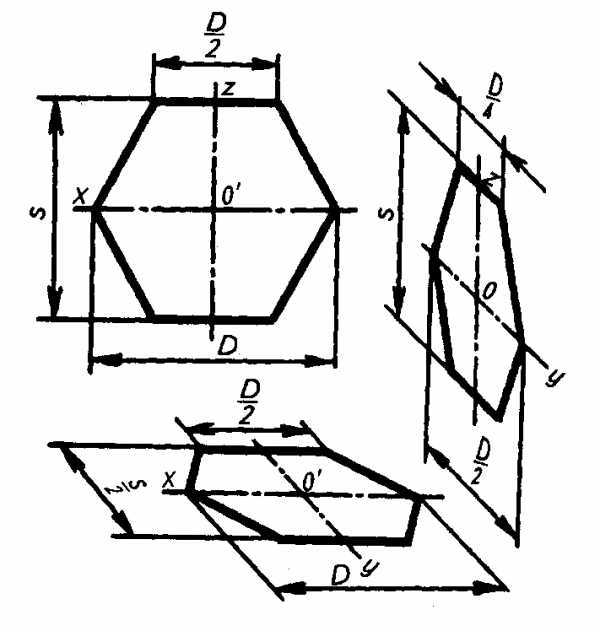
Рис. 3.47.

Изображение правильного шестиугольника во фронтальной диметрической проекции

Пример 2. Построение аксонометрических проекций правильного шестиугольника (рис. 3.46 и рис. 3.47).

1) Шестиугольник расположен во фронтальной плоскости. По оси х’ симметрично точке 0′ откладывают радиусы описанной окружности (d/2), равные размеру стороны шестиугольника, а по оси z, также симметрично точке 0 — отрезки S/2, равные половине расстояния между противоположными сторонами шестиугольника (их можно определить по формуле S = 0,866 В).

Через точки, полученные на оси z’, проводят прямые, параллельные оси х, и симметрично оси z’ откладывают на них отрезки, равные половине стороны шестиугольника (D/2). Полученные шесть точек соединяют отрезками прямых.

2) Шестиугольник расположен в горизонтальной плоскости. Построение выполняют, как было рассмотрено выше, с той лишь разницей, что расстояние S между противоположными сторонами (для фронтальной диметрической проекции S(2)) откладывают по оси у’.

3) Шестиугольник расположен в профильной плоскости. В этом случае размер В (для фронтальной диметрической проекции — D/2) откладывают по оси у, а размер S — по оси г. В этой проекции сокращаются в два раза также стороны шестиугольника, расположенные параллельно оси у (размер В/4).

Пример З. Построение аксонометрических проекций призм (рис. 3.48 и рис. 3.49).

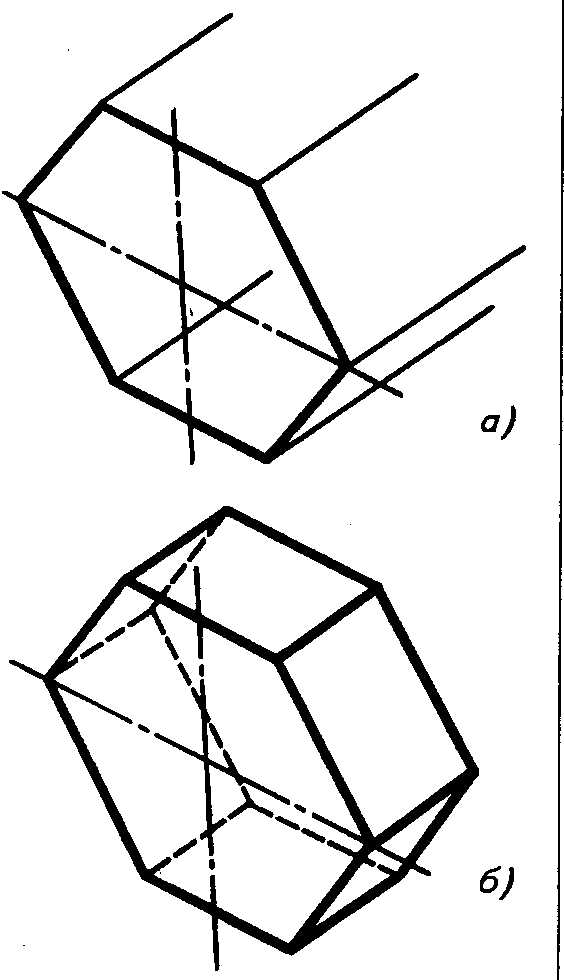
Рис. 3.48.

Изображение правильной шестиугольной призмы в изометрической проекции

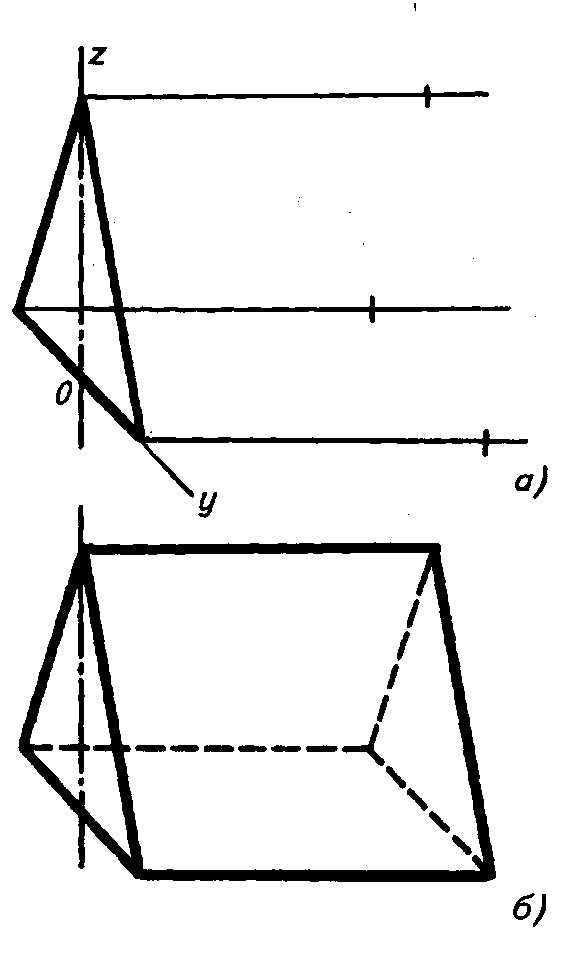
Рис. 3.49.

Изображение треугольной призмы во фронтальной диметрической проекции

Сначала строят проекции видимого основания, например, в плоскости у 0 z Через его вершины проводят прямые, параллельные оси х’, и отклады- вают на них высоту (длину) призмы (рис. 3.48, а и рис. 3.49, а).

Полученные точки соединяют отрезками прямых и обводят линии видимо- го и невидимого контура (рис. 3.48, б и рис. 3.49, б).

Пример 4. Построение аксонометрических проекций правильных пирамид (рис. 3.50 и рис. 3.51).

Сначала строят проекцию основания пирамиды и через точку 0′ — центр тяжести полученной на плоскости фигуры — проводят ось z’. От точки 0 по оси z’ откладывают высоту пирамиды (рис. 3.50, а и рис. 3.51, а).

Полученную точку (проекцию вершины пирамиды) соединяют с проекциями вершин основания. В заключение обводят линии видимого и невидимого контура (рис. 3.50, б и рис. 3.51, б).

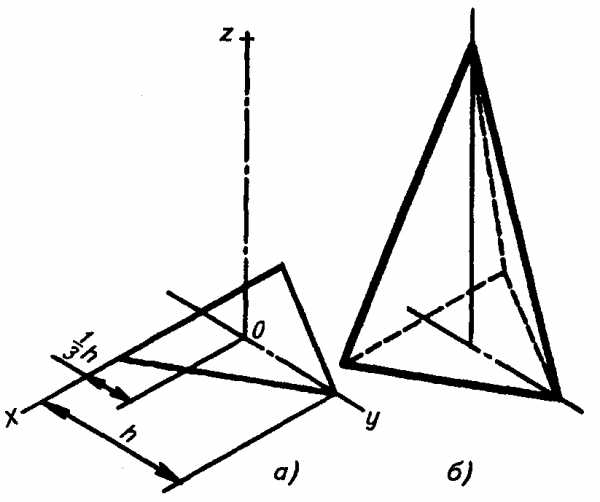
Рис. 3.50.

Изображение правильной треугольной пирамиды в изометрической проекции

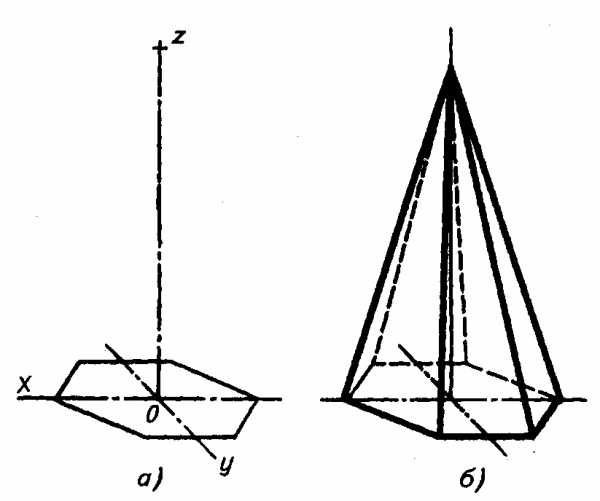
Рис. 3.51.

Изображение правильной шестиугольной пирамиды во фронтальной диметрической проекции

studfiles.net

3. Оси координат и направления движения в станках с чпу

Работа станка с ЧПУ тесно связана с системами координат.

Оси координат станка распалагают как правило параллельно направляющим, что позволяет при программировании обработки в УП непосредственно указывать направления и величины перемещения рабочих органов.

С целью облегчения эксплуатации станков с ЧПУ в них установлено единое направление координатных осей, обязательное для всех изготовителей.

В качестве единой системы координат для всех станков с ЧПУ в соответствии с ГОСТ 23597-79 (СТ СЭВ 3135-81) принята стандартная (правая) декартова система координат, при которой оси X,Y,Z (рис 4.5) указывают положительные перемещения инструментов относительно подвижных частей станка.

Положительные направления движения заготовки относительно неподвижных частей станка указывают оси X`,Y`,Z`, направленные противоположно осям X,Y,Z. Таким образом, положительным всегда является такое направление движения, при котором инструмент и заготовка удаляются друг от друга.

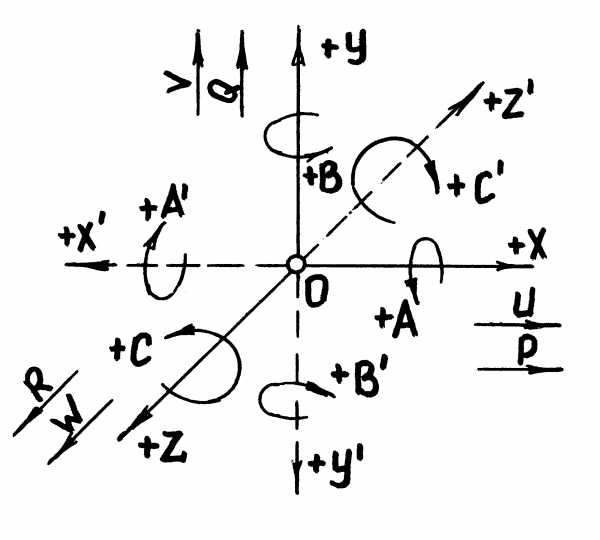
Рис.4.5. Стандартная система координат для станка с ЧПУ

Круговые перемещения инструмента (например, угловое смещение оси шпинделя фрезерного станка) обозначают буквами А (вокруг оси Х), В (вокруг оси Y), С (вокруг оси Z), а круговые перемещения заготовки (например, управляемый по программе поворот стола на расточном станке) — соответственно буквами A’,B’,C’. В понятие «круговые перемещения» не входит вращения шпинделя, несущего инструмент, или шпинделя токарного станка.

Для обозначения вторичных угловых движений вокруг специальных осей используют буквы Д и Е.

Для обозначения направления перемещения двух рабочих органов вдоль одной прямой используют так называемые вторичные оси: U (параллельно X), V (параллельно Y), W (параллельно Z). При трех перемещениях в одном направлении применяют еще и так называемые третичные оси: P,Q,R (см.рис.4.5).

У станков различных типов и моделей системы координат размещают по-разному, определяя при этом положительные направления осей и положение начала координат.

Систему координат станка, выбранную в соответствии с ре-комендациями ГОСТ 23597-79 (рис.4.5), принято называть стандартной. В этой системе положительные направления осей координат определяются по правилу правой руки. Большой палец (рис.4.6) указывает положительное направление оси абсцисс (X), указательный — оси ординат (Y), средний — оси аппликат (Z). Положительное направление вращений вокруг этих осей определяются другим правилом правой руки. Согласно этому правилу, если расположить большой палец по направлению оси, то остальные согнутые пальцы укажут положительное направление вращения.

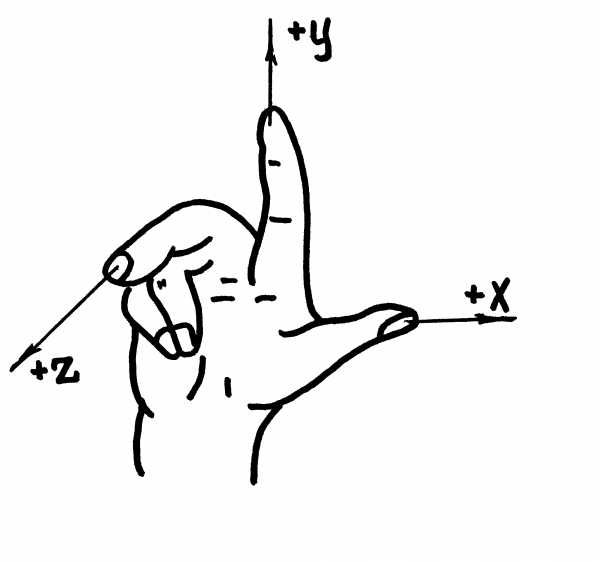
Рис.4.6. Правило правой руки для прямоугольной системы координат

Ориентация осей стандартной системы координат на станке связывается с направлением движения при сверлении на сверлильных, расточных, фрезерных и токарных станках. Направление вывода сверла из заготовки принято в качестве положительного для оси Z, т.е. ось Z всегда связывается с вращающемся элементом станка — шпинделем. Ось X перпендикулярна к оси Z и параллельна плоскости установки заготовки. Если такому определению соот- ветствуют две оси, то за ось X принимают ту, вдоль которой возможно большее перемещение узла станка. При известных осях X и Z ось Y однозначно определяется из условия расположения осей в правой прямоугольной системе координат.

studfiles.net

X, Y, Z.

Политика / JarRra 26.08.2010, источник

Не забудь рассказать друзьям

Поделиться на Facebook

После недавних событий мтинга мне все чаше приходят мысли о бесполеpности «правой игры».
Правые уже не горят, но еще воняют, как тухнувшие свечи
Весь политический спектр разбит на несколько отсеков по оси Х, Y и оси Z с точкой пересечения 0;0, где все эти три вектора приобретают целостное значение большого и толстого сочетания осей Х,У,Z
И если ось У — это вертикаль власти,которая возвышается над всеми и также уходит в невидимую глазу глубь, занимая собой всю плоскость, то ось Х принимает на свое значение и отрицательное и положительное, которое в любом положении спектра мы модем наблюдать. Здесь хоть и соблюдается баланс за счет перевешивания Правых и Левых , но из-за этого баланса присутствует и бессмысленное деление пространства, в чем ось Х проигрывает оси У, а т.ч. и горизонталью власти.
Но важно не забывать и о том, что мир мы видим в трехмерном пространстве. Вот тут-то и появляется раннее не замечаемая ось Й. Да-да именно Й, а не Z. Ибо об этой оси мы что-то знаем, а об оси У — ни по центру. Почему не замечаемая??? Вспомните как в детстве вы рисовали домики! Вспомнили? Вы даже и представления не имели о том, что может быть иначе. Тоже происходит и сейчас с нашим сознанием. Это некий старинный телевизор, который может показывать только в двухмерном изображении!!! К сожалению прогресс идет не так быстро, как хотелось бы.
Ее мы не замечаем из-за видимой оси Х и У, она расположена где-то между ними, она почти незаметна, но без нее не может строится весь облик политического спектра. сейчас эта ось застряла где-то перед осью У, прикрываясь ею и строя свою политику.
Поскольку по всей оси Х идут бесконечные междоусобицы и постоянно возникают какие-то новые объединения, то площадь влияния этих объединений постоянно уменьшается, на фоне этого все ярче выделяется ось У, направленная и стремящаяся вверх. Учитывая все это, ось Й может существовать в безопасности и покое, творя свои дела. Здесь получается просто иллюзия, в результате которой одно видно, другое нет.
Теперь нужно пояснить, что есть что на каждом фронте.
Ось У — центральная, ненавистная мне партия. Ее вектор стремится вверх — вертикаль власти. Начало вектора находится где-то глубоко внизу, но он может начинаться откуда угодно, в т.ч. и с ноля, потому он будет постоянно возрастать. Он рассчитан на «Верхи» общества и постоянно к ним тянется, с помощью чего его сила не увянет, ведь не кончатся никогда богатые, сильные люди.
Ось Х — все оппозиционные партии и движения. Но поскольку вектор стремится вправо, к положительным значениям, то в скором времени отрицательная сторона, а именно — левая часть вектора, исчезнет. Левая часть будет потихоньку тлеть, когда правая — ярко гореть. Но что ярко горит, то и быстро сгорает. Поскольку вектор стремится к положительному, то даже при сгорании его, пустое место заменится чем-либо, но не левой частью вектора, т.к. левая часть она может стать правой, она может либо тлеть, либо равняться нулю. А заместит это место ось Й.
Что же это за ось такая, которая прикрывается У и находится вне видимости и которая творит все невидимые дела? Ответ прост — это финансы и те, кто их создает — банки. Это война и те, кто ее создает — военные. Это новые технологии и те, кто их создает — ученые. А вот о значении медиа индустрии и говорить не приходится. Каждый из них в силах захватить власть, но им это не надо, т.к. они живут, творят под прикрытием оси У.
Эта ось находится в балансе между Х и У, но ее можно склонить на свою сторону, если развернуть под нужным углом всю конструкцию. Никогда не задумывались, почему в науку так мало денег вкладывают и боятся выпустить ее из-под контроля, или дают вознаграждения только за планы и модели и не дают развиваться дальше? Это всего лишь панический страх оси У за свою важность, за свою власть. Именно по этому вливаются большие деньги в обеспечение соц. условий в военную составляющую гос-ва. Ведь они в любой момент могут поднять бунт против гос-ва, если у них не будет нормальных условий. А вот без науки они — никто. Ну а про значимость банков в системе гос-ва уже была одна лекция.
Вывод. Ось Й — проститутка ,которую модно заманивать к себе. И она особо не задумывается над тем, с кем быть, по этому легко может менять свое положение. Главное — ею правильно воспользоваться.

Политика оппозиция X Y Z.

0

Не забудь рассказать друзьям

Поделиться на Facebook

rndnet.ru

Оси координат и структуры движений станков с ЧПУ.

Posted by Менеджер in Промышленность

Для всех станков с ЧПУ применяют единую систему обозначений координат, рекомендованную стандартом ISO 841:1974. Координатами обозначают положение оси вращения шпинделя станка или заготовки, а также прямолинейные либо круговые движения подачи инструмента или заготовки.

При этом обозначение осей координат и направление движений в станках устанавливаются так, чтобы программирование операций обработки не зависело от того, перемещается инструмент либо заготовка или нет. За основу принимается перемещение инструмента относительно системы координат неподвижной заготовки.

Стандартная система координат представляет собой правую прямоугольную систему, связанную с заготовкой, оси которой параллельны прямолинейным направляющим станка.

Все прямолинейные перемещения рассматриваются в системе координат X, Y, Z. Круговое движение по отношению к каждой из координатных осей обозначают прописными буквами латинского алфавита: А, В, С. Во всех станках ось Z совпадает с осью шпинделя главного движения, т.е. шпинделя, вращающего инструмент (в станках сверлильно-фрезерно-расточной группы), или шпинделя, вращающего заготовку (в станках токарной группы).

При наличии нескольких шпинделей в качестве основного выбирают один из них, предпочтительно перпендикулярный к рабочей поверхности стола, на котором крепится заготовка. При неповоротной оси основного шпинделя за ось Z принимают одну из трех осей стандартной трехкоординатной системы, параллельную оси шпинделя. Если ось основного шпинделя может находиться в нескольких положениях, параллельных различным осям стандартной трехкоординатной системы, за ось Z принимают стандартную ось, предпочтительно перпендикулярную к рабочей поверхности стола, на котором крепится заготовка.

Движение по оси Z в положительном направлении должно соответствовать направлению отвода инструмента от заготовки. Если станок применяется для сверления или растачивания с использованием только трех основных линейных перемещений, то обработка происходит при перемещении инструмента в отрицательном направлении оси Z.

Ось X должна располагаться предпочтительно горизонтально и параллельно поверхности крепления заготовки. На станках с вращающейся заготовкой, например токарных, движение по оси X направлено по радиусу заготовки и параллельно поперечным направляющим. Положительное движение по оси X происходит, когда инструмент, установленный на главном резцедержателе поперечных салазок, отходит от оси вращения заготовки.

На станках с вращающимся инструментом (например, фрезерных, сверлильных) при горизонтальном расположении оси Z положительное перемещение по оси X направлено вправо, если смотреть от основного инструментального шпинделя в сторону изделия. При вертикальном расположении оси Z положительное перемещение по оси X направлено вправо для одностоечных станков, если смотреть от основного инструментального шпинделя на стойку, а для двухстоеч-ных — от основного инструментального шпинделя на левую стойку.

Положительное направление движения по оси У следует выбирать так, чтобы ось У вместе с осями Z и X образовывала правую прямоугольную систему координат. Для этого пользуются правилом правой руки: большой палец — ось X, указательный — ось У, средний — ось Z . При определении координатных перемещений станка правую руку мысленно кладут тыльной стороной на обрабатываемую плоскость заготовки так, чтобы полусогнутый средний палец совпал с осью Z инструмента. Тогда большой палец покажет направление оси X, а указательный — У.

Направления движения рабочих органов, несущих инструмент, обозначаются буквами без штриха, а несущих заготовку — буквами со штрихом. При этом положительное направление движения, обозначаемое буквой со штрихом, противоположно направлению соответствующего движения, обозначенного той же буквой без штриха.

Вращательные движения вокруг осей, параллельных X, У и Z, обозначаются буквами Л, Б и С соответственно. Для определения знака кругового перемещения мысленно охватывают правой рукой одну из координатных осей так, чтобы большой палец показывал ее положительное направление. Тогда остальные пальцы покажут положительное направление вращения.

Если дополнительно к основным (первичным) прямолинейным движениям по осям X, Y и Z имеются вторичные движения, параллельные им, то вторичные движения обозначаются соответственно U, V, W. В случае, если имеются третичные движения, их обозначают Р, Q и Д.

Первичные, вторичные и третичные движения рабочих органов станка определяются в зависимости от удаленности этих органов от основного шпинделя.

Для станков с двумя функционально одинаковыми рабочими органами, управляемыми от двух независимых двухкоор-динатных устройств ЧПУ (например, для токарных станков с функционально одинаковыми шпинделями и суппортами), оси координат для обоих одинаково работающих органов (например, суппортов) обозначают одинаково: Z и X.

Вторичные вращательные движения, параллельные или не параллельные А, В и С, обозначаются D или Е.

trastcomp.ru

Отрицательные значения x, y и z на эпюре Монжа | Начертательная геометрия

Даны координаты точки A (30, -10, 40) или A (Ax, Ay, Az). Необходимо построить проекции A`, A», A»` и определить в каком октанте находится данная точка.

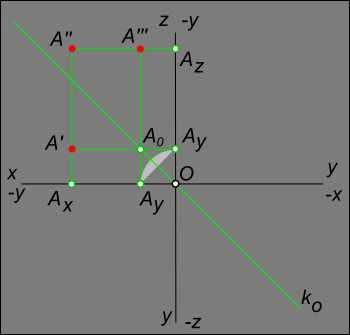
Отрицательные значения x, y и z на эпюре Монжа

Для построения проекций точки по координатам требуется знать где направления x, y, z положительные и где отрицательные значения x, y и z на эпюре Монжа. Значение координаты равное нулю принято относить к положительной полуоси. Эпюры точек и знаки координат точек в октантах левой половины пространственного макета

Эпюр точки
Положение	Октант I	Октант II	Октант III	Октант IV
x	+	+	+	+
y	+	—	—	+
z	+	+	—	—

Эпюры точек и знаки координат точек в октантах правой половины пространственного макета

Эпюр точки
Положение	Октант V	Октант VI	Октант VII	Октант VIII
x	—	—	—	—
y	+	—	—	+
z	+	+	—	—

По приведенным эпюрам точек в октантах выводится следующая последовательность построения эпюра точки:
— проводятся оси координат Oxyz;
— откладывается абсцисса точки от оси z;
— проводится линия проекционной связи ⊥ оси x;
— откладывается аппликата точки от оси x;
— откладывается ордината точки от оси x.

Для определения октанта в котором располагается точка A следует знать преобразование пространственного макета Эпюра Монжа путем совмещения плоскостей H и W с фронтальной плоскостью проекций V или воспользоваться таблицей. Положение точки A соответствует в таблице октанту №2.

+

ngeo.fxyz.ru

§ 5. Повороты вокруг оси х

Вы, пожалуй, подумаете: «Это становится смешным. Чему же нас теперь будут учить— поворотам на 47° вокруг оси у, потом на 33° вокруг x? Долго ли это будет продолжаться?» Нет, оказы­вается, я почти все рассказал. Зная только два преобразова­ния — на 90° вокруг оси у и на произвольный угол вокруг оси z (как вы помните, именно с этого мы начали),— мы уже способны производить любые повороты.

Для иллюстрации предположим, что нас интересует пово­рот на угол а вокруг оси х. Мы знаем, как быть с поворотом на угол а вокруг оси z, но нам нужен поворот вокруг оси х. Как его определить? Сперва повернем ось z вниз до оси х, а это есть поворот на +90° вокруг оси у (фиг. 4.8).

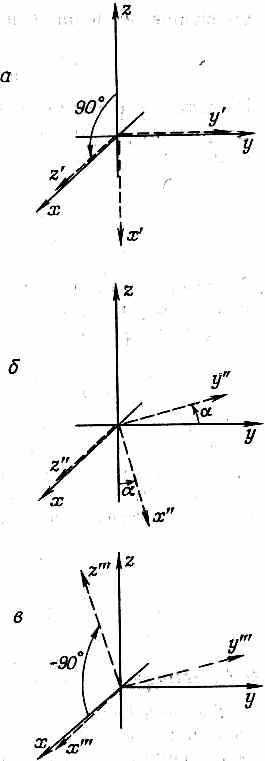
Фиг. 4.8. Поворот на угол  вокруг оси х равнозначен повороту на +90° вокруг оси у (а), за которым следует поворот ни а вокруг оси z’ (б), вслед за которым про­исходит поворот на -90° вокруг оси. у» (в).

Затем во­круг оси z’ повернемся на угол . А потом повернемся на -90° вокpуг оси у».

Итог этих трех поворотов тот же самый, что при повороте вокруг оси х на угол . Таково свойство пространства. (Все эти сочетания поворотов их результат очень трудно себе представить. Не правда ли, странно, что, живя в трех измерениях, мы все же с трудом воспринимаем, что произойдет, если сперва повернуться так, а потом еще как-нибудь. Вероятно, если бы мы были птицами или рыбами и если а мы на собственном опыте знали, что бывает, когда все время крутишь разные сальто в пространстве, нам было бы легче воспринимать подобные вещи.) Во всяком случае, давайте выведем преобразование для поворота на угол а вокруг оси х, пользуясь тем, что нам уже известно. При первом повороте на +90° вокруг оси у амплитуды следуют закону (4.32). Если повернутые оси обозначить х’, y’ и z’, то последующий поворот на угол а вокруг оси z переводит нас в систему отсчета х». у», z», для которой

Последний поворот на -90° вокруг оси у» переводит нас в систему х'», у'», z'»; из (4.33) следует

Сочетая эти два последних преобразования, получаем

Подставляя сюда вместо С’₊ и С’_— (4.32), придем к полному преобразованию

А если вспомнить, что

то эти формулы можно записать проще:

Это и есть наше искомое преобразование для поворота вокруг оси х на любой угол . Оно лишь чуть посложнее остальных,

§ 6. Произвольные повороты

Теперь уже понятно, как быть с произвольным поворотом. Во-первых, заметьте, что любая относительная ориентация двух систем координат может быть описана тремя углами (фиг. 4.9).

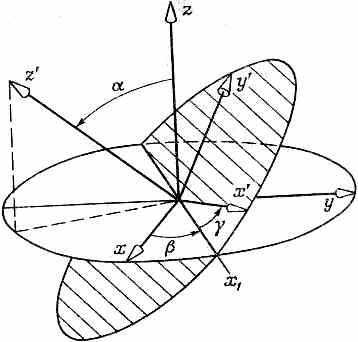
Фиг. 4.9. Ориентацию лю­бой системы координат х’, у’, г’ по отношению к другой системе х, у, z можно опре­делить с помощью углов Эйлера , , .

Если есть система осей х’, у’, z’, ориентированных относительно х, у, z как угодно, то соотношение между ними можно описать тремя углами Эйлера ,  и , определяющими три последовательных поворота, которые переводят систему х, у, z в систему х’, у’, z’ . Отправляясь от x, у, z, мы повора­чиваем нашу систему на угол bets вокруг оси z, перенося ось х на линию х’. Затем мы проводим поворот на угол а вокруг этой временной оси х₁, чтобы довести ось z до z‘. Наконец, по­ворот вокруг новой оси z (т. е. вокруг z’) на угол  переведет ось х₁ в х’, а ось у в у’. Мы знаем преобразования для каж­дого из трех поворотов — они даются формулами (4.19) и (4.34). Комбинируя их в нужном порядке, получаем

Итак, начав просто с некоторых предположений о свойст­вах пространства, мы вывели преобразование амплитуды при любом повороте. Это означает, что если нам известны ампли­туды того, что любое состояние частицы со спином ¹/₂ перейдет в один из двух пучков прибора Штерна — Герлаха S с осями х, у, z, то мы можем подсчитать, какая часть перейдет в каж­дый пучок в приборе Т с осями х’, у’ и z’. Иначе говоря, если имеется состояние  частицы со спином ¹/₂, у которого ам­плитуды пребывания вверху и внизу по отношению к оси z системы координат х, у, z равны С₊=<+|> и С_—=<-|>, то тем самым мы знаем амплитуды С₊ и C_— пребывания вверху и внизу по отношению к оси z’ любой другой системы х’, у», z’ , Четверка коэффициентов в (4.35) — это члены «матрицы преобразования», с помощью которой можно проецировать амплитуды частицы со спином ¹/₂ в другие системы ко­ординат.

Теперь решим несколько примеров, чтобы посмотреть, как все это работает. Возьмем следующий простой вопрос. Пустим атом со спином ¹/₂ через прибор Штерна — Герлаха, пропу­скающий только состояние (+z). Какова амплитуда того, что атом окажется в состоянии (+x)? Ось +х — это все равно, что ось +z’ системы, повернутой на 90° вокруг оси у. Поэтому в этой задаче проще воспользоваться выражением (4.32), хотя, конечно, можно применить и полное уравнение (4.35). По­скольку С₊=1 и С_—=0, то получится С’₊=1/2. Вероятности -это квадраты модулей этих амплитуд; таким образом, 50% шансов за то, что частица пройдет сквозь прибор, отбирающий состояние (+х). Если бы мы поинтересовались состоянием (-х), то амплитуда оказалась бы -1/2, что опять дало бы вероятность ¹/₂, чего и следовало ожидать из симметрии про­странства. Итак, если частица находится в состоянии (+z), то ей в равной степени вероятно побывать в состояниях (+x) и (-х). Но фазы противоположны.

Ось у тоже без претензий. Частица в состоянии (+z) имеет равные шансы быть в состоянии (+у) или (-у). Но теперь (согласно формуле для поворота на -90° вокруг оси х) амплитуды суть l/2 и —i/2. В этом случае разница в фа­зах двух амплитуд уже не 180°, как было для (+х) и (-х), а 90°. В этом-то и проявляется различие между х и у.

Вот еще пример. Пусть нам известно, что частица со спином ¹/₂ находится в состоянии , поляризованном вверх относи­тельно оси А, определяемой углами  и  (фиг. 4.10).

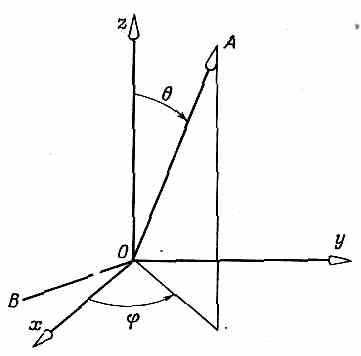
Фиг. 4.10. Ось А, определяе­мая полярными углами  и .

Мы хо­тим знать амплитуду <C₊|> того, что частица относительно оси z окажется в состоянии «вверх», и амплитуду <C_—|> того, что она окажется в состоянии «вниз» относительно той же оси z. Эти амплитуды мы можем найти, вообразив, что А есть ось z’ системы, у которой ось х’ направлена произвольно, ска­жем лежит в плоскости, образованной А и z. Тогда можно перевести систему А в систему х, у, z тремя поворотами. Во-первых, надо сделать поворот на -/2 вокруг оси A, что пере­ведет ось x в линию В на рисунке. Затем повернуть на — 0 вокруг линии В (вокруг новой оси х системы А), чтобы ось А попала на ось z. И, наконец, повернуть вокруг оси z на угол (/2-).

Вспоминая, что вначале было только одно состояние (+) по отношению к А, получаем

Мы хотели бы напоследок подытожить результаты этой главы в форме, которая окажется полезной для нашей даль­нейшей работы. Во-первых, напомним, что наш основной ре­зультат (4.35) может быть записан в других обозначениях. Заметьте, что (4.35)— это то же самое, что и (4.4) Иначе го­воря, в (4.35) коэффициенты при С₊=<+S|> и C’_—= <-S|> суть как раз амплитуды <jT|iS> в (4.4), амплитуды того, что частица в состоянии i по отношению к S окажется в состоя­нии j по отношению к Т (когда ориентация Т по отношению к S дается углами ,  и ). Мы их также называли R^TS_ji в выра­жении (4.6). (Чего-чего, а обозначений у нас хватало!) Например,— это коэффициент при С₊ в формуле для С_— , а именно isin(/2)exp[i(-)/2]. Поэтому сводку наших ре­зультатов мы можем дать в виде табл. 4.1.

Было бы удобно иметь эти амплитуды расписанными для некоторых особо важных случаев. Пусть R_z() — поворот на угол  вокруг оси z. Так же можно обозначить и соответ­ствующую матрицу поворота (опуская молчаливо подразу­меваемые индексы i и j). В том же смысле R_x() и R_y() будут обозначать повороты на угол  вокруг оси х и оси у,

В табл. 4.2 мы приводим матрицы — таблицы амплитуд <jT|iS>, которые проецируют амплитуды из системы S в систему Т, где Т получается из S указанным поворотом.

* Нетрудно показать, что систему х, у, z можно перевести в систему х’, у’, z’ следующими тремя поворотами вокруг первоначальных осей: 1) повернуть на угол  вокруг первоначальной оси z; 2) повернуть на угол а вокруг первоначальной оси х; 3) повернуть на угол  вокруг первоначальной оси z.

* Второе решение меняет все знаки у а, b, с, d и отвечает повороту на —270°.

* Заметим, что если последовательность малых поворотов приведет в конце концов к первоначальной ориентации предмета, то всегда есть возможность, проследив всю историю, отличить поворот на 360° от по­ворота на 0° (но интересно, что для поворота на 720° это неверно).

* Конечно, подошло бы и m=—¹/₂. Однако из (4.17) ясно, что изме­нение знака просто переопределит понятие «спин вверх».

* Можно посмотреть на это и иначе. Мы просто производим преоб­разование к «стандартной форме», описанное в § 2, используя формулу (4.15).

* Эта глава — не что иное, как весьма абстракт­ное и длинное отступление от основной линии расска­за; в ней нет каких-либо новых идей, которые бы не появлялись иным путем в дальнейших главах. Поэ­тому можете спокойно пропустить ее, а позже, если заинтересуетесь, вернуться.

studfiles.net

Декартова система координат — это… Что такое Декартова система координат?

Прямоугольная, или декартова система координат — наиболее распространённая система координат на плоскости и в пространстве.

Прямоугольная система координат на плоскости

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление.Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X’X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y’Y. Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y, называются координатными углами (см. Рис. 1).

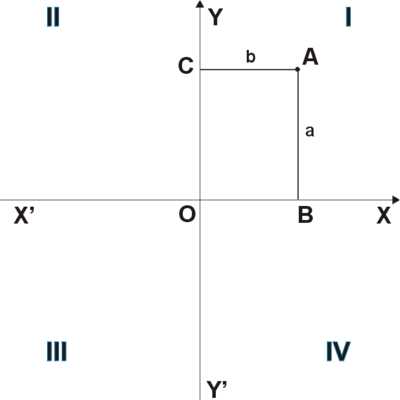
Рис. 1

Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(x, y).

Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.

Прямоугольная система координат в пространстве

Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для всех осей. OX — ось абсцисс, OY — ось ординат, OZ — ось апликат. Положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Такая система координат называется правой. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. Рис. 2).

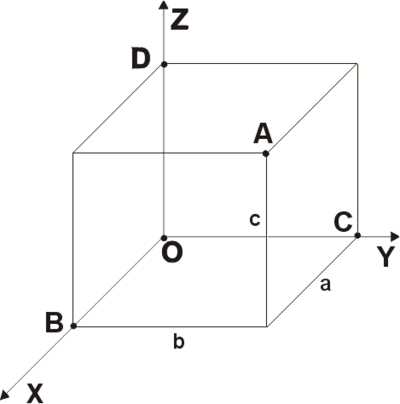
Рис. 2

Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: A(a, b, c).

Орты

Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.

В трёхмерном случае такие орты обычно обозначаются i j k или e_xe_ye_z . При этом в случае правой системы координат действительны следующие формулы с векторным произведением векторов:

• [i j]=k ;
• [j k]=i ;
• [k i]=j .

История

Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.

Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.

См. также

Ссылки

Wikimedia Foundation. 2010.

dic.academic.ru