Ось х и у: Ось абсцисс

§ Прямоугольная система координат. Ось абсцисс и ось ординат. Координатная четверть

Оси координат. Координатные четверти Как найти и записать координаты точки

В повседневной жизни часто можно услышать фразу: «Оставь мне свои координаты». В ответ человек обычно оставляет свой адрес или номер телефона, то есть данные, по которым его можно найти.

Координаты могут обозначаться самыми разными наборами цифр или букв.

Например, номер автомобиля — это координаты, потому что по номеру машины можно определить из какого она города и кто ёё владелец.

Важно!

Координаты — это набор данных, по которому определяется положение того или иного объекта.

Примерами координат являются: номер вагона и места в поезде, широта и долгота на географической карте, запись положения фигуры на шахматной доске, положение точки на числовой оси и т.д.

Всегда, когда мы по определенным правилам однозначно обозначаем какой-то объект набором букв, чисел или других символов, мы задаём координаты объекта.

Французкий математик Рене Декарт (1596–1650) предложил задавать положение точки на плоскости с помощью двух координат.

Для нахождения координат нужны ориентиры, от которых ведётся отсчёт.

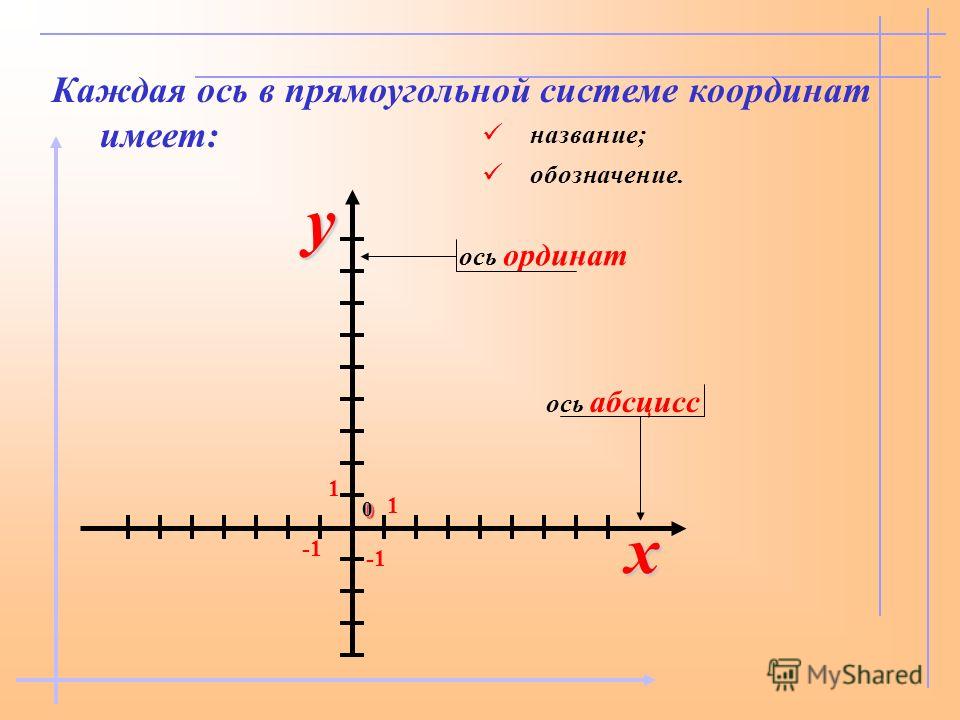
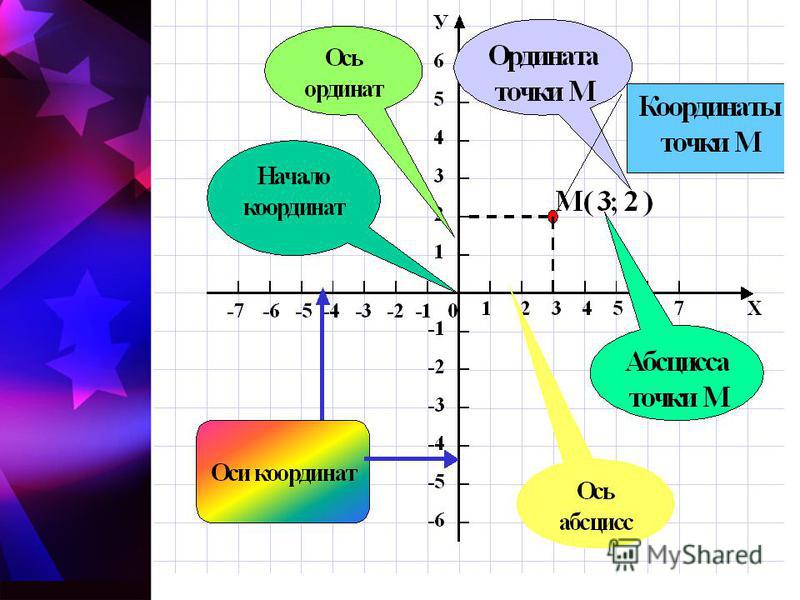
• На плоскости такими ориентирами будут служить две числовые оси. На чертеже обычно первую ось рисуют горизонтально, её называют осью АБСЦИСС и обозначают буквой «X», записывают ось «Ox». Положительное направление на оси абсцисс выбирают слева направо и показывают стрелкой.
• Вторую ось проводят вертикально, её называют осью ОРДИНАТ и обозначают буквой «Y», записывают ось «Oy». Положительное направление на оси ординат выбирают снизу вверх и показывают стрелкой.

Оси взаимно перпендикулярны (т.е. угол между ними равен 90°) и пересекаются в точке, которую обозначают «O». Точка «O» является началом отсчёта для каждой из осей.

Запомните!

Система координат — это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчёта для каждой из них.

Координатные оси — это прямые, образующие систему координат.

Ось абсцисс «Ox» — горизонтальная ось.

Ось ординат «Oy» — вертикальная ось.

Координатная плоскость — плоскость, в которой построена система координат. Обозначается плоскость как «x0y».

Обращаем ваше внимание на выбор длины единичных отрезков по осям.

Цифры, обозначающие числовые значения на осях можно располагать как справа, так и слева от оси «Oy». Цифры на оси «Ox», как правило, пишут внизу под осью.

Обычно единичный отрезок на оси «0y» равен единичному отрезку на оси «0x». Но бывают случаи, когда они не равны друг другу.

Оси координат делят плоскость на 4 угла, которые называют координатными четвертями. Четверть, образованная положительными полуосями (правый верхний угол), считают первой I.

Отсчитываем четверти (или координатные углы) против часовой стрелки.

Оси координат. Координатные четверти Как найти и записать координаты точки

Ось абсцисс – что такое?

4. 6

Средняя оценка: 4.6

Всего получено оценок: 111.

4.6

Средняя оценка: 4.6

Всего получено оценок: 111.

Оси абсцисс и ординат часто путают между собой. Это касается не только учеников, но и студентов и преподавателей нематематических дисциплин. Это знание ни на что особенно не влияет, но во многих теоремах пишут именно названия.

Системы координат

Название оси абсцисс относится к системам координат. На самом деле в мире используется две системы, хотя привычной для нас является декартова система координат.

Плоская декартова система координат состоит из двух взаимно перпендикулярных отрезков. Точка пересечения отрезков считается началом отчета. На каждом из отрезков обозначается единичный отрезок и направление движения.

Каждый из перпендикулярных отрезков называется осью. Единичный отрезок у каждой из осей может быть разным. Направления задаются, как правило, традиционно: вверх и вправо. Но иногда составители задач пытаются подловить учеников на этом и делают другие направления в системе. Поэтому, нужно быть крайне внимательным при работе с чужой системой координат.

Еще одной системой координат называется полярной. Если в декартовой системе для того, чтобы определить местоположение точки нужно знать две ее координаты, то в полярной системе нужно знать координату и угол подъема. Этой системой пользовались в древность, сегодня от нее почти отказались из-за излишней сложности.

Декартова система координат

Принцип работы с декартовой системой основан на понимании понятия проекции. Проекция в системе это перпендикуляр, опущенный на оси. Оси обозначаются как х и у. Ось х направлена вправо. Ось у направлена влево.

Представим себе точку на плоскости. Если нам нужно узнать ее координаты, то необходимо опустить два перпендикуляра: по одному на оси.

Так мы получим проекцию точки на ось х, это отрезок от начала отчета до точки пересечения оси с перпендикуляром. И проекцию отрезка на ось у: это расстояние на оси у от начала координат до точки пересечения оси с перпендикуляром.

Значение каждой из проекции и будет являться координатами точки на плоскости. По этим же координатам можно получить точку заново. Для этого нужно отложить требуемые значения на осях, после чего провести через отложенные точки прямые, перпендикулярные осям. Точка пересечения перпендикуляров и будет искомой прямой.

Оси декартовой системы

Вот мы и подошли к главному вопросу. Ось х имеет название оси абсцисс. Название это происходит от латинского «отрезок». Ось названа так потому, что отслеживает движение точки по горизонтали.

Вторая ось называется осью ординат, от латинского «порядок, движение по порядку». Имеется в виду, что эта координата отслеживает порядок движения вверх. Такая уж была логика у математиков древности.

Секрет в том, что названия осей можно менять как угодно, но оси все равно будут зваться осью абсцисс и осью ординат. Вне зависимости от буквенного обозначения осей, единичных отрезков и начала отсчета.

Что мы узнали?

Мы поговорили о системах координат.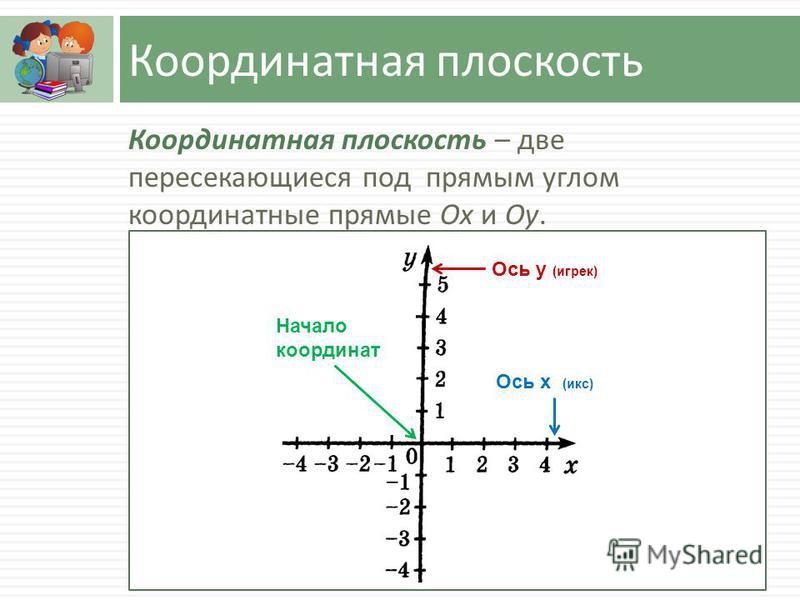 Выделили полярную и декартову систему. Отдельно обсудили декартову систему. Поговорили об обязательных характеристиках системы координат: единичный отрезок, направление осей, начало отсчета. Выяснили, что такое ось абсцисс. Поговорили о том, почему именно такое название получила каждая из осей.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 111.

---

А какая ваша оценка?

Графики X и Y — определение, различия, уравнение на графике X и Y, примеры

Графики x и y, также известные как оси x и y, являются двумя важными линиями, которые составляют график. График состоит из горизонтальной оси и вертикальной оси, на которых могут быть представлены данные. Точка может быть описана по горизонтали или по вертикали, что легко понять с помощью графика.

Эти горизонтальные и вертикальные линии или оси на графике являются осью x и осью y соответственно. Давайте узнаем больше о графике x и y в математике, таблице, диаграммах и решим несколько примеров, чтобы лучше понять концепцию.

1.	Определение графика X и Y
2.	Разница между графиками по осям X и Y
3.	График уравнения по осям X и Y График
4.	Уравнение оси Y
5.	Уравнение оси X
6.	Часто задаваемые вопросы по X и Y График

Определение графика X и Y

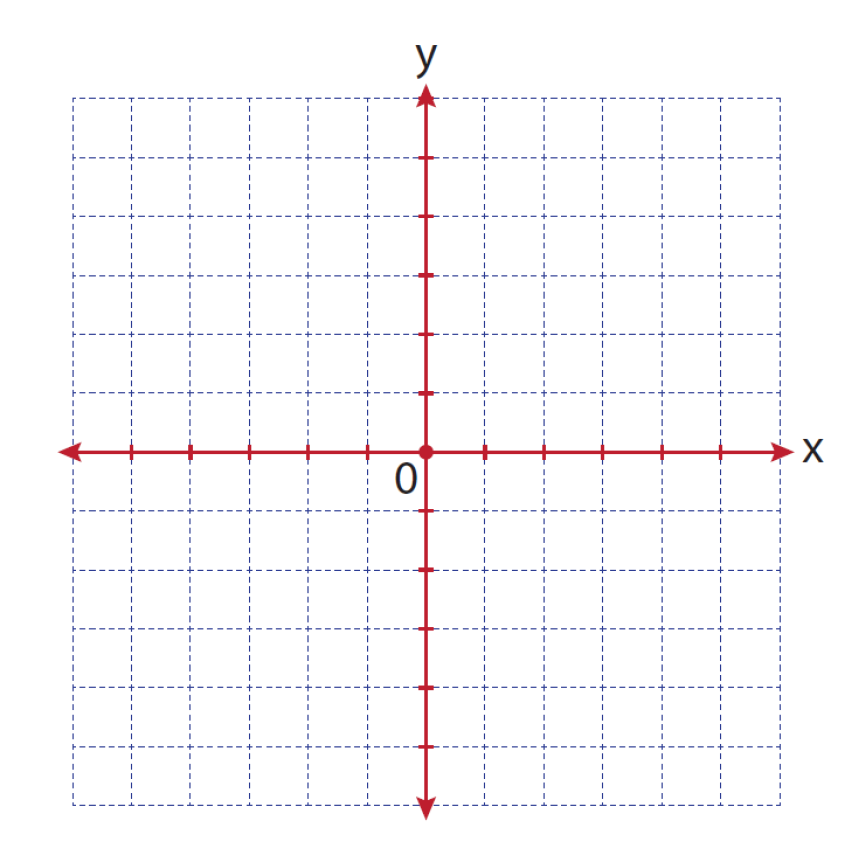
График x и y может быть определен двумя осями, т. е. осью x и осью y, которые образуют координатную плоскость для графика. Горизонтальная ось представлена ​​осью x, а вертикальная ось представлена ​​осью y. Точка пересечения осей x и y называется началом координат и используется в качестве опорной точки для плоскости.

На изображении ниже представлена ​​координатная плоскость с обеими осями.

Ось X на графике также известна как абсцисса. Ось Y на графике также известна как ордината. Любая точка на координатной плоскости хорошо определяется упорядоченной парой, где упорядоченная пара записывается как (координата x, координата y) или (x, y), где координата x представляет точку на оси x или перпендикулярно расстояние от оси y и координата y представляет собой точку на оси y или перпендикулярное расстояние от оси x. График x и y имеет 4 квадранта, то есть каждая перпендикулярная линия является одним квадрантом. Изображение ниже описывает график x и y как с положительными, так и с отрицательными координатами.

Например: Население города с 2015 по 2020 год указано в таблице X и Y как:

Годы	2015	2016	2017	2018	2019	2020
Люди в миллионах	1	1,5	2	2,5	3	3,5

Чтобы найти любую точку на координатной плоскости, мы используем упорядоченную пару, где упорядоченная пара записывается как (x-координата, y-координата) или (x, y), где x-координата представляет точку на координатной плоскости. ось x или перпендикулярное расстояние от оси y, а координата y представляет собой точку на оси y или перпендикулярное расстояние от оси x, поэтому сверху ясно, что ось x идет первой при записи упорядоченной пары в найти точку. Здесь мы видим, что расположение каждой точки на графике отмечено как упорядоченная пара, где ось x или координата x опережает ось y или координату y. Затем представить эти точки на диаграмме x и y, используя годы на оси x и соответствующее население на оси y как:

Разница между графиками по осям X и Y

График x и y состоит из осей x и y, которые образуют координатную плоскость графика, где числа представлены для сравнения или даже для формирования линейных уравнений. Есть много различий между осью X и осью Y, даже если они имеют одну и ту же точку начала координат. Давайте посмотрим на различия:

ось x графика	ось Y графика
Горизонтальная плоскость графика в декартовой системе координат, дающая числовое значение в каждой точке.	Это вертикальная плоскость графика в декартовой системе координат, дающая числовое значение в каждой точке.
Ось X называется абсциссой.	Ось Y называется ординатой.
Переменные на оси x представляют причину данных.	Переменные на оси Y представляют следствие данных.
Числа, размещенные на оси x, называются координатами x.	Числа, размещенные на оси Y, называются координатами Y.
Ось X представляет собой горизонтальную линию с 0 в начале координат, положительными числами справа и отрицательными числами слева.	Ось Y рисуется вертикально снизу вверх с тем же началом, что и ось X, с положительными числами вверху и отрицательными числами внизу.
Координаты относительно оси x записываются как (x, y).	Координаты относительно оси Y записываются как (y, x).

График уравнения по осям X и Y График

На графике x и y можно изобразить линейное уравнение, показывающее координаты как по оси x, так и по оси y. В геометрии линейное уравнение можно изобразить с помощью графика x и y, и оно представлено в виде прямой линии. Давайте посмотрим на пример, чтобы понять это лучше:

Рассмотрим линейное уравнение y = 2x + 1. Теперь, чтобы построить график этого уравнения, постройте таблицу с двумя столбцами для значений x и y. Выберем некоторые значения для переменной x и найдем соответствующие значения для y. Если x = 1, то y = 2 × 1 + 1 = 3. Если x = 2, то y = 2 × 2 + 1 = 5 и так далее. Здесь мы берем значения только трех точек, начиная с 0. Чтобы нарисовать график координат линейного уравнения по осям x и y, нам нужно нарисовать таблицу сетки осей x и y по крайней мере для двух точек.

х	г
0	1
1	3
2	5

Теперь нарисуйте точки на графике, где значения x лежат на оси x, а соответствующие значения y лежат на оси y. Затем соедините точки прямой линией, чтобы нарисовать график уравнения.

Уравнение оси Y

Ось Y — это линия, на которой значения координаты x равны нулю для всех значений y. Тогда точки данных для оси Y: (0, -1), (0, 0,5), (0, 1), (0, 1,5). Следовательно, уравнение оси y равно x = 0, и его график на графике x и y показан ниже. Если мы подставим значение x вместо 0 в общее уравнение y = mx + c, мы сможем найти координаты для y.

Уравнение оси X

Ось X — это линия, на которой значения координаты Y равны нулю для всех значений x. Тогда точки данных для оси x: (1,0), (-1,5, 0). Следовательно, уравнение оси x равно y = 0, и его график на графике x и y показан ниже. Если мы заменим значение y на 0 в общем уравнении y = mx + c, мы сможем найти координаты для x.

Связанные темы

Ниже перечислены несколько интересных тем, связанных с графиком x и y, посмотрите.

• Введение в графику
• Геометрия
• Полярные координаты

Часто задаваемые вопросы о графике X и Y

Что такое график X и Y?

График x и y — это визуальное представление данных, отображаемых на графике с осью x и y, образующими координатные плоскости. Ось X на графике также известна как абсцисса, тогда как ось Y известна как ордината. Любая точка на координатной плоскости хорошо определяется упорядоченной парой, где упорядоченная пара записывается как (координата x, координата y) или (x, y), где координата x представляет точку на оси x или перпендикулярно расстояние от оси y и координата y представляет собой точку на оси y или перпендикулярное расстояние от оси x. График x и y имеет 4 квадранта.

Как изобразить уравнение на графике X и Y?

Чтобы построить уравнение, сначала постройте таблицу с двумя столбцами для значений x и y, подставив значения x и y в уравнение, начиная с 0. Затем нарисуйте точки на графике, где значения x лежат на ось x и соответствующие значения y лежат на оси y. Затем соедините точки, чтобы нарисовать график уравнения. Обычно это прямая линия, диагональная, вертикальная или горизонтальная при построении линейного уравнения.

Какая точка находится на отрицательной оси Y на графике X и Y?

Точка с отрицательным значением координаты y находится на отрицательной оси y.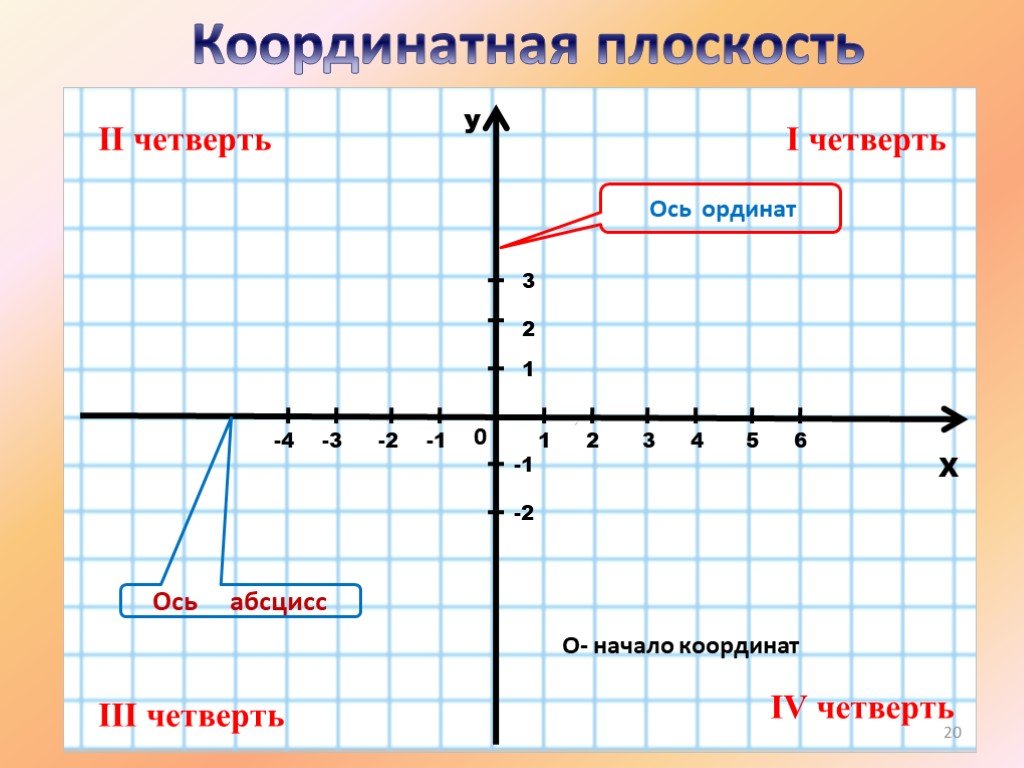 Поскольку ось Y представляет собой вертикальную линию, которая начинается снизу вверх, отрицательные числа лежат в нижней части области и охватывают 3-й и 4-й квадранты графика.

Что является осью X и что является осью Y на графике X и Y?

Горизонтальная ось известна как ось x, а вертикальная ось известна как ось y. Начало 0 является общим фактором для обеих осей. Ось X показывает причину данных, а ось Y показывает эффект данных. Например, при отображении температуры в Нью-Йорке ось X показывает недели, а ось Y показывает температуру. Каждая точка на обеих осях будет показывать предыдущее значение, начиная с 0,

Как построить график с осями X и Y?

Сначала мы рисуем и обозначаем оси x и y. Затем мы наносим координаты функции при различных значениях координат x и y. Затем соединяем координаты и строим график функции.

Как называются оси X и оси Y на графике X и Y?

Вертикальная ось, т. е. ось Y, известна как ось абсцисс. А ось x известна как ось ординат.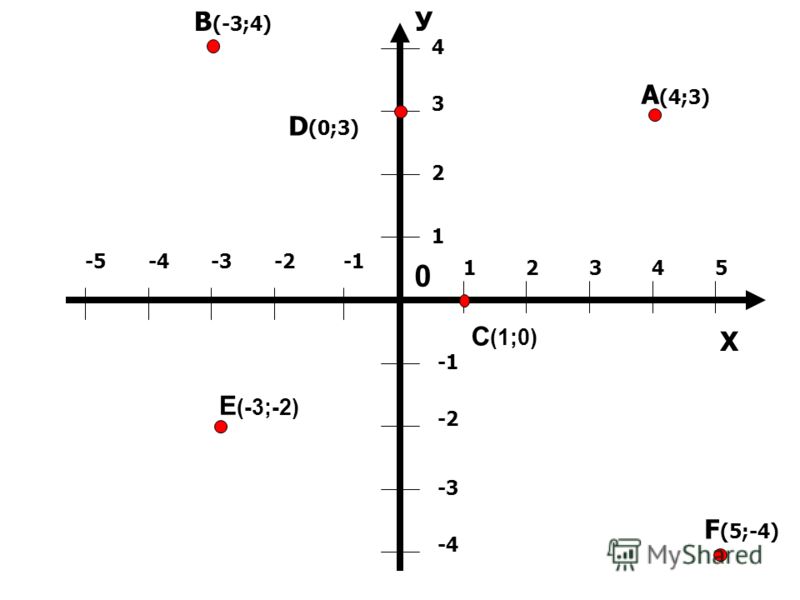

Что такое координаты x и y?

К

• Рахул Авати

Что такое координаты x и y?

Координаты X и y — это, соответственно, горизонтальный и вертикальный адреса точки в любом двумерном (2D) пространстве, таком как лист бумаги или экран дисплея компьютера. Вместе эти координаты помогают определить точное местоположение точки.

В декартовой системе координат координаты x и y являются частью осей x и y в 2D-пространстве. Для точки в пространстве координаты x и y записываются в виде упорядоченной пары (x, y). Первое число представляет положение точки на оси x, а второе число представляет ее положение на оси y. Координаты также могут быть записаны как (x,y) без пробела после запятой.

Координаты X и Y (оси) — это горизонтальные и вертикальные адреса в 2D-пространстве.

Порядок координат x и y в упорядоченной паре важен. Координата x всегда идет первой, за ней следует координата y. Вот почему (3, 4) не то же самое, что (4, 3).

(3, 4) относится к точке на три единицы справа от нуля и на четыре единицы выше нуля.

(4, 3) относится к точке на четыре единицы справа от нуля и на три единицы выше нуля.

Две оси пересекаются перпендикулярно в исходной или нулевой точке. Координаты x и y этого местоположения записываются как (0, 0) или (0,0).

Важные координаты x и y

Оси x и y, на которых нанесены координаты x и y, образуют координатную плоскость. Система была изобретена французским математиком Рене Декартом и известна как декартова система координат.

Координатная плоскость необходима для представления любой точки в заданном 2D-пространстве. Плоскость, образованная пересечением двух осей, является двухмерной, поскольку для определения местоположения любой точки на этой плоскости требуются две точки данных:

1. его расстояние по оси x
2. его расстояние по оси Y

Эти расстояния представлены координатами x и y соответственно.

Значение x точки (x, y) известно как абсцисса . Он представляет собой расстояние точки от начала координат или вдоль горизонтальной оси x. Значение y точки (x, y) известно как ордината . Он представляет собой вертикальное или перпендикулярное расстояние точки от начала координат или от оси x.

Точка, в которой линия пересекает ось x, называется x- пересечением , а точка, в которой она пересекает ось y, называется y-пересечением . Координата y точки пересечения x равна 0, а координата x точки пересечения y равна 0. Если доступно уравнение прямой (y = mx + b), подстановка x = 0 в уравнение дает y -перехват. Точно так же подстановка y = 0 дает точку пересечения по оси x.

Координатная плоскость разделена на четыре квадранта:

• Квадрант 1 находится вверху справа.
• Квадрант 2 находится вверху слева.
• Квадрант 3 находится внизу слева.
• Квадрант 4 находится внизу справа.

Представление координат x и y с примерами

Любая точка в 2D-пространстве представлена ​​координатами x и y в виде упорядоченной пары, любая из которых может быть нулевой, положительной или отрицательной.

Если одно из значений равно нулю, точка представлена ​​следующим образом:

• (0, y): координата x равна нулю, поэтому точка лежит на оси y.
  • (0, 10): точка находится на оси Y и на 10 единиц выше .
  • (0, -10): точка находится на оси Y и на 10 единиц ниже .
• (x, 0): координата y равна нулю, поэтому точка лежит на оси x.
  • (10, 0): точка находится на оси x и на 10 единиц вправо от нуля.
  • (-10, 0): точка находится на оси X и на 10 единицах по оси осталось нулей.

Если обе координаты x и y равны нулю (0, 0), точка находится в начале координат, где оси x и y пересекаются.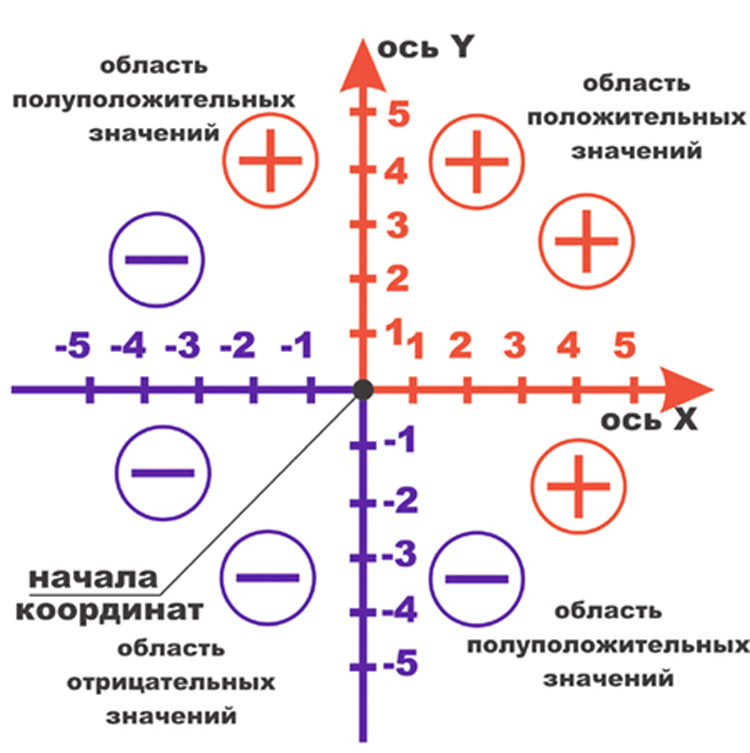

Если обе координаты x и y отличны от нуля, точка находится где-то на двумерной координатной плоскости в одном из ее четырех квадрантов.

Пример 1

Рассмотрим здесь точку M в координатной плоскости.

М лежит на одну единицу правее нуля и на две единицы выше нуля. Таким образом, его координата x равна (1), а его координата y равна (2). Вместе его координаты (x, y) представлены на двухмерной координатной плоскости следующим образом:

М = (1, 2)

Точка M находится в квадранте 1.

Пример 2

Здесь рассмотрим точку N в координатной плоскости.

N лежит на три единицы левее нуля и на четыре единицы ниже нуля. Итак, его координата x равна (-3), а координата y равна (-4). Вместе его координаты (x, y) представлены на двухмерной координатной плоскости следующим образом:

Н = (-3, -4)

Точка N находится в квадранте 3.

Положительные и отрицательные значения в 4 квадрантах

В зависимости от расположения точки в одном из четырех квадрантов координатной плоскости координаты x и y будут иметь положительные или отрицательные значения. Если координата x находится в левой части плоскости, она имеет отрицательное значение, а если в правой, то ее значение положительное.

Аналогично, если координата y находится в верхней части плоскости, ее значение положительно. Если он находится в нижней плоскости, он имеет отрицательное значение. Левая, правая, верхняя и нижняя части плоскости определяются положением точки от начала координат или нулевого значения.

Квадрант	Местоположение точки	Значение X (положительное/отрицательное)	Значение Y (положительное/отрицательное)	(х, у)
Квадрант 1	Вверху справа	Положительный	Положительный	(+, +)
Квадрант 2	Вверху слева	Отрицательный	Положительный	(-, +)
Квадрант 3	Внизу слева	Отрицательный	Отрицательный	(-, -)
Квадрант 4	Внизу справа	Положительный	Отрицательный	(+, -)

Пример 1

(2, 5): точка находится в квадранте 1, на две единицы правее нуля и на пять единиц выше нуля.

Пример 2

(-2, 5): точка находится в квадранте 2, две единицы до осталось нуля и пять единиц выше нуля.

Пример 3

(-2, -5): точка находится в квадранте 3, две единицы до слева от нуля и пять единиц ниже нуля.

Пример 4

(2, -5): точка находится в квадранте 4, на две единицы правее нуля и на пять единиц ниже нуля.

Использование координат x и y

Координаты x и y точки необходимы для определения расстояния этой точки от заявленного начала координат 2D-пространства. Координаты также используются для нахождения середины и наклона линии, а также для определения ее линейного уравнения.

Линейное уравнение прямой представляется как y = mx + b:

• м = уклон = изменение по у / изменение по х
• х = координата х, «как далеко»
• y = координата y, «как далеко вверх»
• b = значение y, когда x = 0

Вот как выглядит пара координат (x, y), если значение x известно и уравнение выражается как y = 2x + 2:

Координата X	Координата Y	Уклон (м)	у = 2х + 2	(х, у)
0	2	2	2	(0, 2)
1	4	2	4	(1, 4)
2	6	2	6	(2, 6)
3	8	2	8	(3, 8)
4	10	2	10	(4, 10)

Чтобы изобразить уравнение y = 2x + 2, каждая координата в каждой упорядоченной паре расположена на координатной сетке. Затем координаты x и y соединяются в прямую линию.

См. также: математические символы .

Последнее обновление: август 2022 г.

Продолжить чтение О координатах x и y

• Медицинская школа Kaiser Permanente для обучения студентов современным технологиям

• Как предприятия будут использовать еще не определенную метавселенную

• Чем CPU, GPU и DPU отличаются друг от друга?

• Как улучшение математических навыков может помочь в программировании

• Будущее науки о данных: карьерный рост и отраслевые тенденции

распознавание голоса

Распознавание голоса или говорящего — это способность машины или программы принимать и интерпретировать диктовку или понимать и выполнять голосовые команды.

Сеть

• система управления сетью

  Система управления сетью, или NMS, представляет собой приложение или набор приложений, которые позволяют сетевым инженерам управлять сетевыми . ..

• хост (в вычислениях)

  Хост — это компьютер или другое устройство, которое обменивается данными с другими хостами в сети.

• Сеть как услуга (NaaS)

  Сеть как услуга, или NaaS, представляет собой бизнес-модель для предоставления корпоративных услуг глобальной сети практически на основе подписки.

Безопасность

• API веб-аутентификации

  API веб-аутентификации (WebAuthn API) — это программный интерфейс приложения (API) для управления учетными данными, который позволяет веб-…

• Общая система оценки уязвимостей (CVSS)

  Общая система оценки уязвимостей (CVSS) — общедоступная система оценки серьезности уязвимостей безопасности в …

• Вредоносное ПО Dridex

  Dridex — это форма вредоносного ПО, нацеленное на банковскую информацию жертв с основной целью кражи учетных данных онлайн-аккаунта . ..

ИТ-директор

• программа аудита (план аудита)

  Программа аудита, также называемая планом аудита, представляет собой план действий, в котором документируются процедуры, которым аудитор будет следовать для подтверждения…

• децентрализация блокчейна

  Децентрализация — это распределение функций, контроля и информации вместо того, чтобы быть централизованным в едином учреждении.

• аутсорсинг

  Аутсорсинг — это деловая практика, при которой компания нанимает третью сторону для выполнения задач, управления операциями или предоставления услуг…

HRSoftware

• командное сотрудничество

  Совместная работа в команде — это подход к коммуникации и управлению проектами, который делает упор на командную работу, новаторское мышление и равенство . ..

• самообслуживание сотрудников (ESS)

  Самообслуживание сотрудников (ESS) — это широко используемая технология управления персоналом, которая позволяет сотрудникам выполнять множество связанных с работой …

• платформа обучения (LXP)

  Платформа обучения (LXP) — это управляемая искусственным интеллектом платформа взаимного обучения, предоставляемая с использованием программного обеспечения как услуги (…

Отдел обслуживания клиентов

• сегментация рынка

  Сегментация рынка — это маркетинговая стратегия, в которой используются четко определенные критерии для разделения общей адресной доли рынка бренда …

• воронка продаж

  Воронка продаж — это визуальное представление потенциальных клиентов и того, где они находятся в процессе покупки.

• анализ потребительской корзины

  Анализ потребительской корзины — это метод интеллектуального анализа данных, используемый розничными торговцами для увеличения продаж за счет лучшего понимания покупок клиентов.