Тема 3. Положение прямой относительно плоскостей проекций. Следы прямой
В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения. 1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.3.1).
Рисунок 3.1 Прямая общего положения
2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:
2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.3.2).
Рисунок 3.2 Горизонтальная прямая
2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными илифронталями(рис.3.3).
Рисунок 3.3 Фронтальная прямая
2.3.
Прямые параллельные профильной плоскости
проекций называются профильными (рис.
Рисунок 3.4 Профильная прямая
3. Прямые, перпендикулярные плоскостям проекций, называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:
3.1. Фронтально-проецирующая прямая — АВ (рис. 3.5).
Рисунок 3.5 Фронтально-проецирующая прямая
3.2. Профильно проецирующая прямая — АВ (рис.3.6).
Рисунок 3.6 Профильно-проецирующая прямая
3.3. Горизонтально-проецирующая прямая — АВ (рис.3.7).
Рисунок 3.7 Горизонтально-проецирующая прямая
К началу страницы
Тема 4. Плоскость. Способы задания плоскостей
Плоскость
– одно из основных понятий геометрии.
При систематическом изложении геометрии
понятие плоскость обычно принимается
за одно из исходных понятий, которое
лишь косвенным образом определяется
аксиомами геометрии.
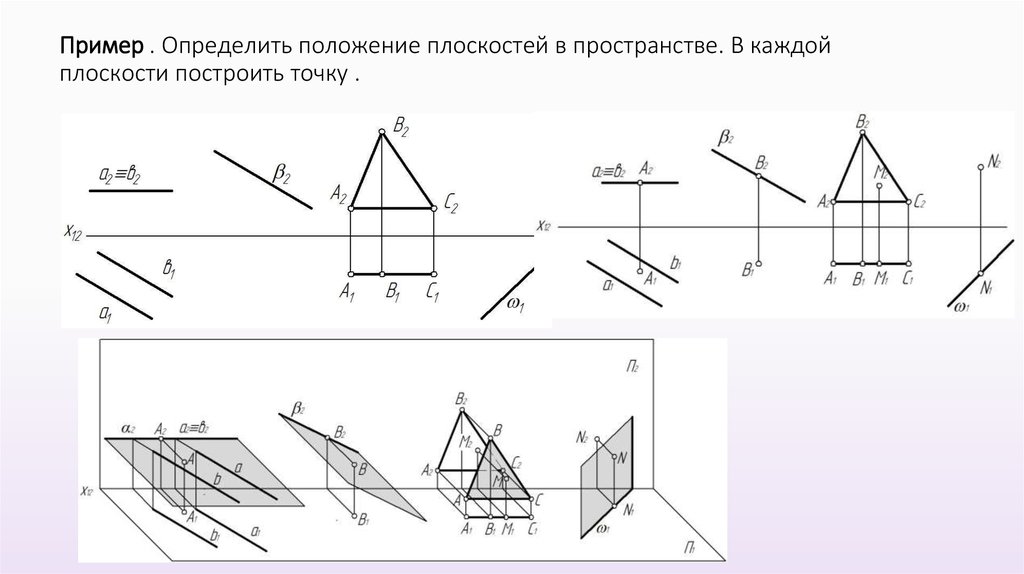
Способы графического задания плоскостей Положение плоскости в пространстве можно определить:
1. Тремя точками, не лежащими на одной прямой линии (рис.4.1).
Рисунок 4.1 Плоскость заданная тремя точками, не лежащими на одной прямой
2. Прямой линией и точкой, не принадлежащей этой прямой (рис.4.2).
Рисунок 4.2 Плоскость заданная прямой линией и точкой, не принадлежащей этой линии
3. Двумя пересекающимися прямыми (рис.4.3).
Рисунок 4.3 Плоскость заданная двумя пересекающимися прямыми линиями
4. Двумя параллельными прямыми (рис.4.4).
Рисунок 4.4 Плоскость заданная двумя параллельными прямыми линиями
Тема 5.
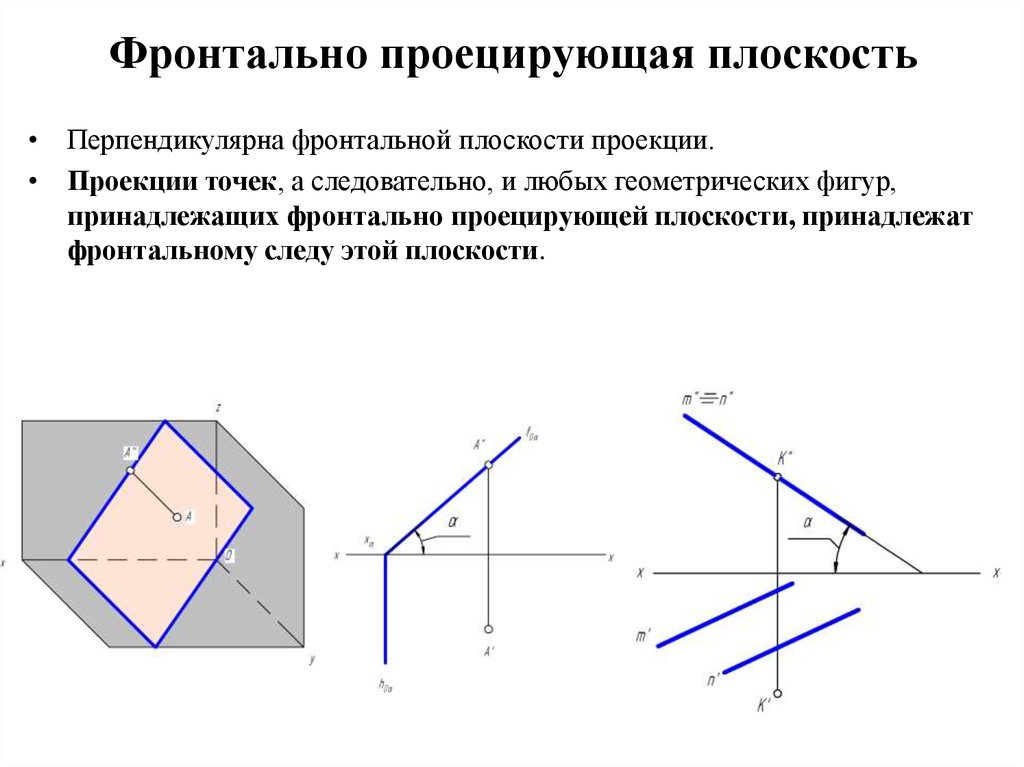 Положение плоскости. Следы плоскости
Положение плоскости. Следы плоскостиК началу страницы
Различное положение плоскости относительно плоскостей проекций
В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: — горизонтальный 1; — фронтальный2; — профильный3). Следы плоскости общего положения пересекаются попарно на осях в точках ax,ay,az. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций. Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях (рис.5.1).
2.
Плоскости перпендикулярные плоскостям
проекций – занимают частное положение
в пространстве и называются проецирующими. П2).
Любая фигура в этой плоскости проецируется
на плоскость П3 без искажения, а на
плоскости П1 и П2 в прямые — следы плоскости1
и2
(рис.5.7).
П2).
Любая фигура в этой плоскости проецируется
на плоскость П3 без искажения, а на
плоскости П1 и П2 в прямые — следы плоскости1
и2
(рис.5.7).
Рисунок 5.7 Профильная плоскость
2. Положение плоскости относительно плоскостей проекций.
Рис.14 | Плоскость занимает произвольное положение относительно плоскостей проекций и, следовательно, пересекает все 3 плоскости проекций. Соответствующие следы плоскостиобозначают: PH=H — горизонтальный след плоскости. PV=V — фронтальный след плоскости. PW=W — профильный след плоскости. |
Точки: Px=x=PHPVPy=y=PHPWPz=z=PVPW, в которых пересекаются два следа, называют точками схода следов.
Плоскость, у которой углы наклона к
плоскостям проекций произвольны (не
равны 0или 90),
называют плоскостью общего положения.
Рис.15 | Чтобы построить профильный след плоскости надо найти точки Px, Pyи Pz, затем построить Py1и соединить её с точкой Pz. |
Кроме рассмотренного общего случая плоскость, по отношению к плоскостям проекций, может занимать следующие частные положения:
Плоскости, перпендикулярные к плоскостям проекции называют проецирующими.
Проецирующие плоскости различают:
Горизонтально-проецирующая плоскость, PH
Рис.16 | Свойства
горизонтально-проецирующей плоскости:
1.
Фронтальный след (PV) перпендикулярен
оси х. PVх.
P(PH)H.
2.
Угол-
является линейным углом двугранного
угла между плоскостями V и P.=||=|PV|. |
Рис.17 | 3. Горизонтальные проекции точек, прямых, плоских фигур, лежащих в горизонтально-проецирующей плоскости, лежат на горизонтальном следе этой плоскости. APA1PH. |
Фронтально-проецирующая плоскость, PV
Рис.18 | Свойства фронтально-проецирующей плоскости: 1. Горизонтальный след (PH) перпендикулярен оси х. PHх. P(PV)V. 2. Угол- угол наклона плоскости P к плоскости проекций H.=||=|PH|. |
Рис.19 | 3. Фронтальные проекции
точек, прямых, плоских фигур, лежащих
в фронтально-проецирующей плоскости,
лежат на фронтальном следе этой
плоскости. |
Профильно-проецирующая плоскость, PW
Рис.20 | Свойства профильно-проецирующей плоскости: 1. P Vz. PHy. P(PW)W. 2. Угол- угол наклона плоскости P к плоскости проекций H.=||=|TH|. Угол- угол наклона плоскости P к плоскости проекций V.=||=|TV|. |
Рис.21 | 3. Профильные проекции точек, прямых, плоских фигур, лежащих в профильно-проецирующей плоскости, лежат на профильном следе этой плоскости. APA3PW. |
Плоскости, перпендикулярные к двум плоскостям проекций называют плоскостями уровня.
а). Плоскость, параллельная горизонтальной
плоскости проекций называется
горизонтальной плоскостью.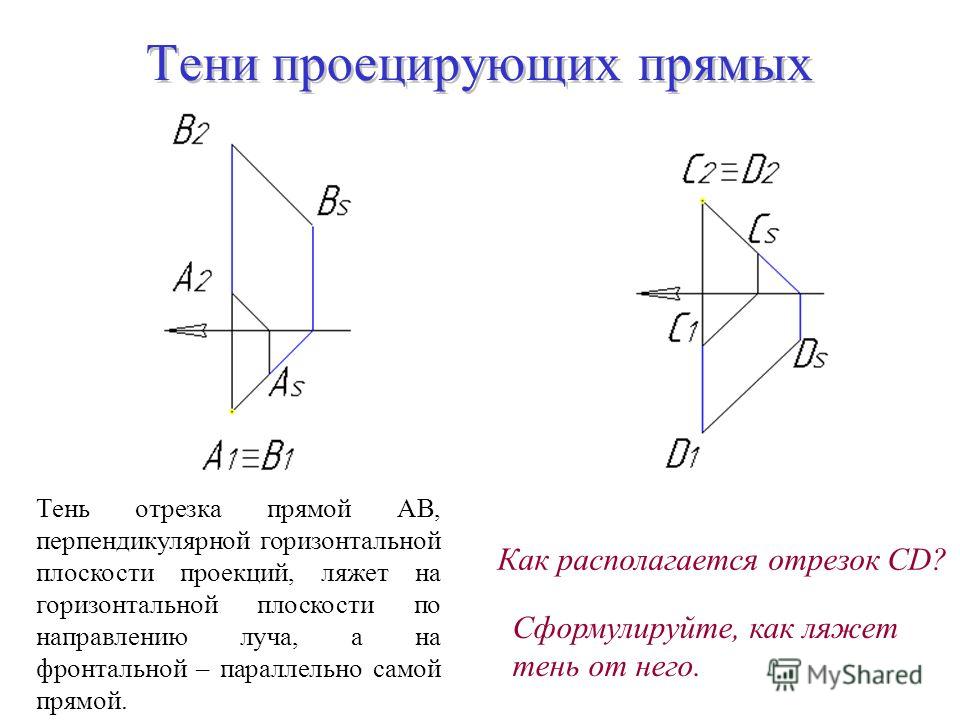 b). Плоскость,
параллельная фронтальной плоскости
проекций называется фронтальной
плоскостью.
c). Плоскость, параллельная
профильной плоскости проекций называется
профильной плоскостью.
b). Плоскость,
параллельная фронтальной плоскости
проекций называется фронтальной
плоскостью.
c). Плоскость, параллельная
профильной плоскости проекций называется
профильной плоскостью.
Проецирующие плоскости, проходящие через биссектрисы углов, образованных осями координат, называют биссекторными плоскостями.
Свойство биссекторной плоскости 2-го и 4-го октантов: Горизонтальная и фронтальная проекции любых геометрических фигур, принадлежащих этой плоскости, совпадают (так как любая точка этой плоскости удалена на одинаковые расстояния от горизонтальной и фронтальной плоскостей проекций).
Учебное пособие 5
CSC204/CPE411/SC20 Учебник 5
Просмотр в 3D
Решения
. прогнозы? Описать подклассы плоских геометрических проекций.
Если
проекция на плоскость, а не на некоторую кривую поверхность и
проекционные лучи (называемые проекторами) прямые, а не изогнутые, проекция
называется плоской геометрической проекцией.
Плоский геометрические проекции можно разделить на два основных класса: перспективные и параллельно.
Если расстояние между центром проекции (COP) и плоскостью проекции равно конечно, проекторы не параллельны друг другу. Такие проекции называется перспективной проекцией. Перспективные проекции далее подразделяется на количество точек схода, поэтому называется 1-точечным, 2-точечным или 3-точечные перспективы.
Если расстояние между КС и плоскостью проекции бесконечно, проекторы параллельны друг другу. Такие проекции называются параллельная проекция. Параллельные проекции делятся на два типа: в зависимости от соотношения между направлением проецирования (DOP) и нормали к плоскости проекции. В ортогональной проекции проекторы перпендикулярно плоскости проекции. В косой проекции их нет.
Нажмите на рисунок, чтобы увидеть демонстрацию VRML. Эта демонстрация иллюстрирует, как перспективные проекции могут быть изменена на параллельную проекцию, удалив наблюдателя и уменьшив угол поля зрения.
Нажмите кнопку PageDown при просмотре сцены, чтобы перемещаться между точками обзора. первая точка обзора поместит наблюдателя перед единичным кубом, а 2 метрах от него.
Точка зрения {
описание «Перспективная проекция»
позиция 0 0 2
полевиев 0,784999
}
Мы видим, что куб проецируется с искажением перспективы. Далее, когда При нажатии PageDown точка обзора перемещается на 1000 м от куба. Куб затем отображается как одна точка на экране.
Точка обзора {
описание «Параллельная ортогональная проекция»
позиция 0 0 1000
полевиев 0,784999
}
Далее, снова нажав PageDown, мы уменьшаем угол обзора с 0,784999 рад до 0,0012 рад и увидеть куб, как если бы он проецировался с помощью параллельной проекции.
Точка обзора {
описание «Параллельное орфографическое проекция»
позиция 0 0 1000
полевиев 0,0012
}
2. Как выполнить орфографическую проекцию некоторых трехмерных объектов на
плоскость проекции, которая содержит ось y и имеет угол 30 с плоскостью z =0? Получить один
матрица преобразования.
Как выполнить орфографическую проекцию некоторых трехмерных объектов на
плоскость проекции, которая содержит ось y и имеет угол 30 с плоскостью z =0? Получить один
матрица преобразования.
Плоскость проекции расположена следующим образом:
матрица ортогональной проекции на плоскость xy , мы должны вращать объекты проецироваться на ось и на -30. Итак, объединенный преобразование
это
существенно, что мы не должны делать никакого обратного вращения. Мы заинтересованы в
получение 2 координат на плоскости. Для этого мы переместили плоскость проекции
и объекты, которые нужно спроецировать так, чтобы плоскость проекции стала одной из
координатные плоскости. После этого спроецируем на координатную плоскость и рассмотрим
соответствующие 2 координаты. В данном примере — это координаты х и у .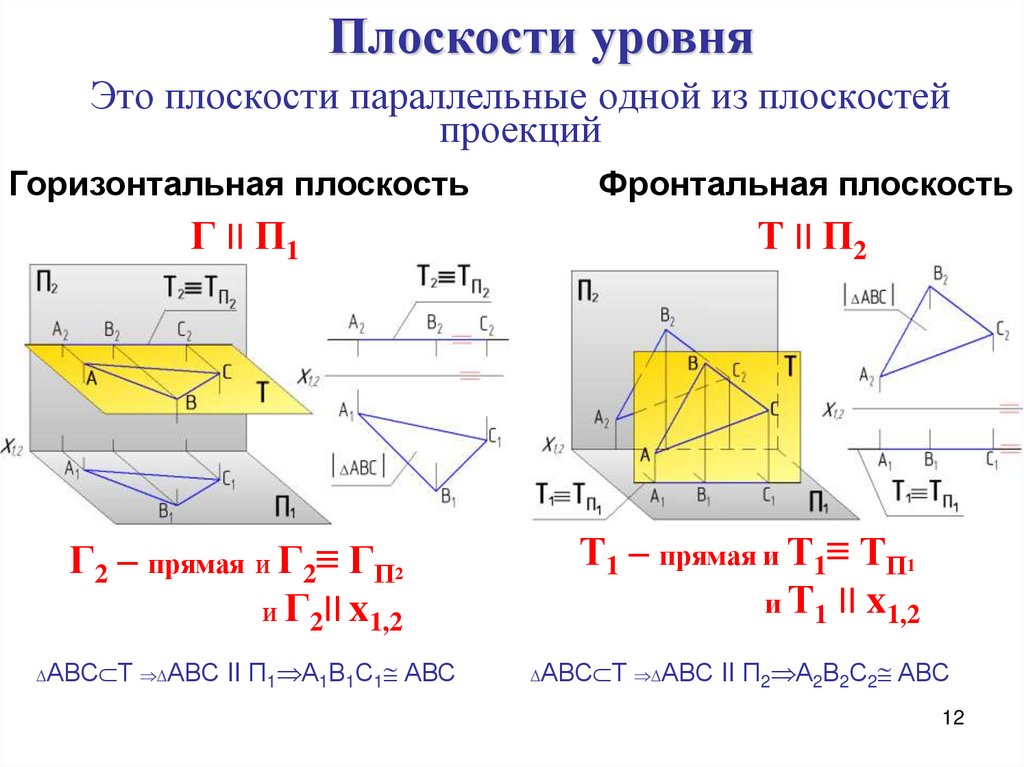
Если вопрос речь идет о перспективной проекции, преобразование должно быть таким, чтобы оно двигалось плоскость проекции становится одной из координатных плоскостей, а центр проекция на соответствующую ось координат, которая ортогональна координатная плоскость.
3. Рассмотрим единичный куб с центром в начале координат. Перевести куб 5 единиц в x и y направлений и выполнить одноточечное перспективная проекция на плоскость z=0 из центра проекции в точке z=10.
The position vectors of the origin-centered unit cube are
The concatenated transformation matrix is
The resulting transformed векторы положения:
4. Единый куб центрирован по телефону (0, 0, -0,5).
и его три стороны параллельны осям X, Y и Z соответственно. Найдите его
проецируемое изображение на плоскость X-Y, когда (i) DOP = (0,0,-1), (ii) DOP = (0,-1,-1) и (iii) DOP = (0,-1,-2) . Что
типы проекции они?
Единый куб центрирован по телефону (0, 0, -0,5).
и его три стороны параллельны осям X, Y и Z соответственно. Найдите его
проецируемое изображение на плоскость X-Y, когда (i) DOP = (0,0,-1), (ii) DOP = (0,-1,-1) и (iii) DOP = (0,-1,-2) . Что
типы проекции они?
(i) Когда DOP=(0,0,-1), проекция является ортогональной проекцией из перед. Проецируемое изображение представляет собой квадрат, ограниченный (-0,5, -0,5,0), (-0,5, 0,5, 0), (0,5, 0,5, 0) и (0,5, -0,5, 0).
(ii)
Когда
DOP =(0, -1, -1), проектор расположен под углом 45° к
проекционная плоскость. Это кавалерийская проекция. Проецируемое изображение такое
показано на рисунке ниже.
(iii) Когда DOP= (0, -1, -2), проектор угол 63,43 с плоскостью проекции. это кабинет проекция. Проецируемое изображение показано на рисунке ниже.
Нажмите на рисунок, чтобы увидеть сцену VRML
иллюстрирующий этот вопрос. Вместо изменения вектора DOP кубы на
слева вращались вокруг оси X
Вместо изменения вектора DOP кубы на
слева вращались вокруг оси X
к 45
и 63,45. Куб справа непрерывно вращается вокруг оси X. Изучите сцену,
перемещая его мышью.
Вы также можете изменить графический режим на «Smooth».
5. Выведите матрицу преобразования вида косой проекцию на плоскость x-y, как показано на рис. Q4.
Сначала найдите вектор направления проектора В . Из приведенного выше рисунка для единичного вектора вдоль направления проектора его x, y, z Компоненты могут быть записаны как
x V = COS Q COS F Y V = COS Q SIN 2 11211211211211211211211211211211211211211211211211211211211211211211211211211211211211211211211211211211211211121121121121121121121121121121121121121121121121121121121121121121. q
q
Следовательно, вектор направления V проектора есть (cosqcosf, cosqsinf, -sinq).
Рассмотрим один произвольная точка P(x,y,z). Это был спроецирован на плоскость XY в точке P(x,y,0). Вектор имеет то же направление, что и . V и =k V . Для точки P мы можем написать следующее:
x’ = x + k cos q cos f y = y + k cos q sin f 0 = z — k sin q
90z02 Отсюда k = 90z02 /sinq и
Напоминая, что q = f = 45, тогда матрица преобразования проекций будет следующей: Линии и плоскости, пожалуй, самые простые из кривых и поверхностей в трехмерное пространство. Они также окажутся важными, поскольку мы стремимся понимать более сложные кривые и поверхности.
Уравнение линии в двух измерениях: $ax+by=c$; это
разумно ожидать, что линия в трех измерениях
задается $ax + by +cz = d$; разумно, но неправильно — оказывается, что
это уравнение плоскости.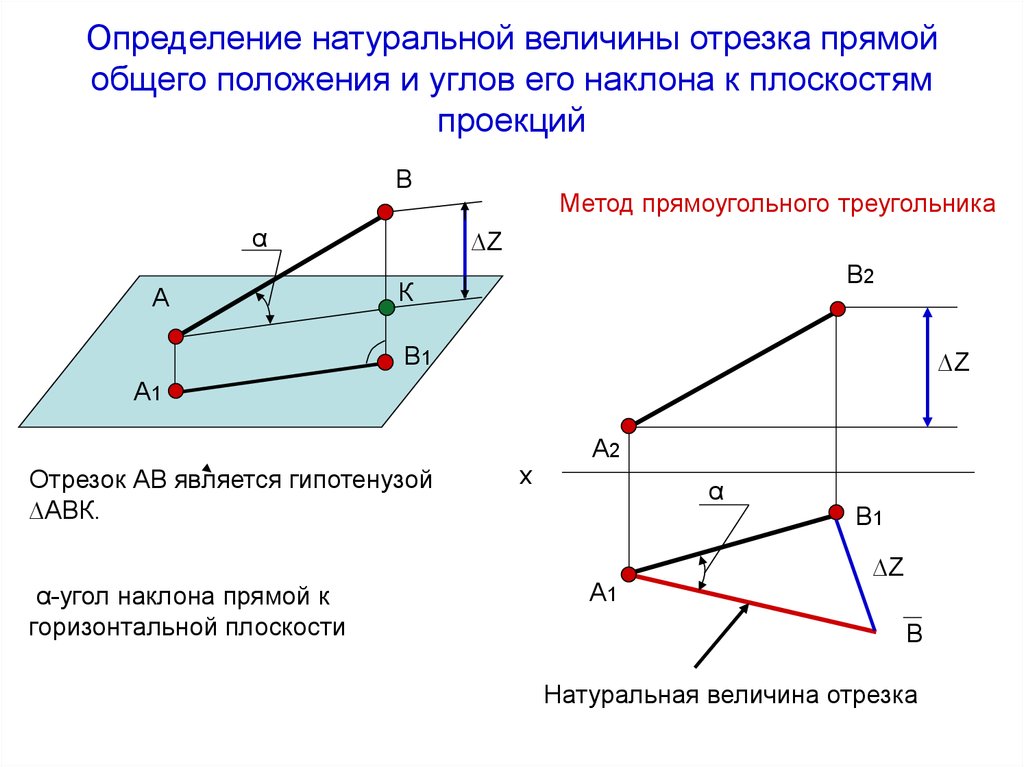
У плоскости нет очевидного «направления», как у линии. можно связать плоскость с направлением очень полезным способом, однако: есть ровно два направления, перпендикулярные самолет. Любой вектор с одним из этих двух направлений называется нормальный в самолет. Таким образом, хотя векторов нормали к данной плоскости много, все они параллельны или антипараллельны друг другу.
Предположим, две точки $\ds (v_1,v_2,v_3)$ и $\ds (w_1,w_2,w_3)$ лежат в плоскости;
тогда вектор $\ds\langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$ параллелен
к самолету; в частности, если этот вектор положить хвостом в
$\ds (v_1,v_2,v_3)$, то его головка находится в точке $\ds (w_1,w_2,w_3)$ и лежит в
самолет. В результате любой вектор, перпендикулярный плоскости,
перпендикулярно $\ds \langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$. На самом деле, это
Легко видеть, что плоскость состоит из именно те точки
$\ds (w_1,w_2,w_3)$, для которых $\ds \langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$ равно
перпендикулярно нормали к плоскости, как показано на
рисунок 12.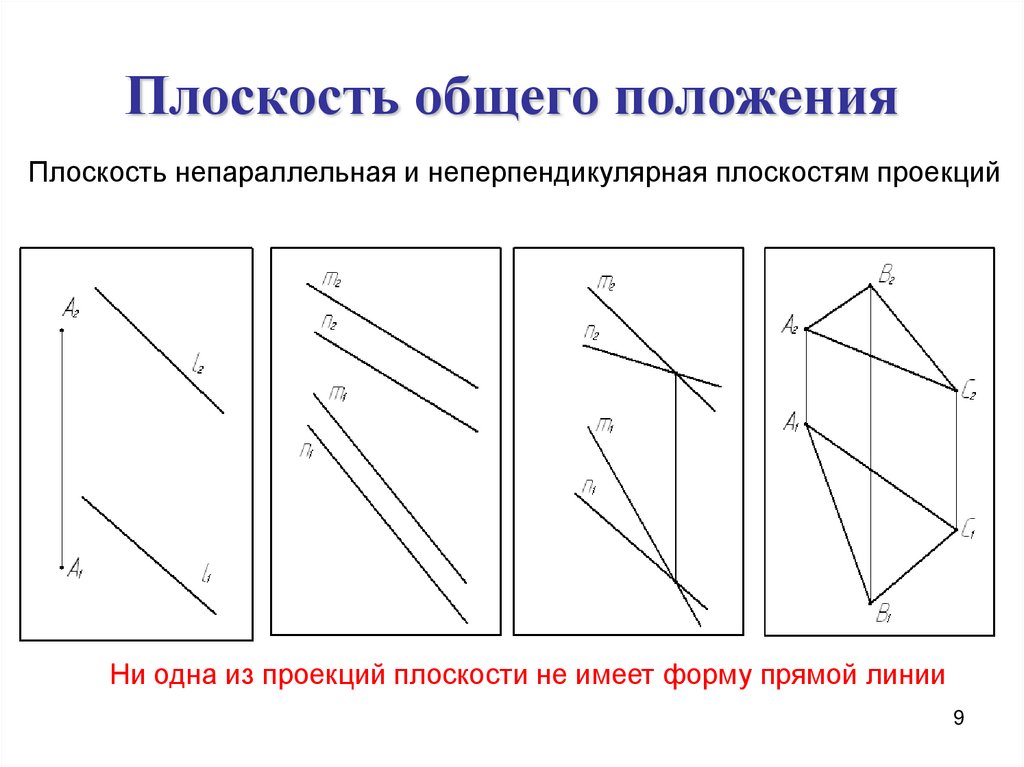 5.1. То есть предположим
мы знаем, что $\langle a,b,c\rangle$ нормальна к плоскости, содержащей
точка $\ds (v_1,v_2,v_3)$. Тогда $(x,y,z)$ лежит в плоскости тогда и только тогда
если $\langle a,b,c\rangle$ перпендикулярно $\ds \langle
x-v_1,y-v_2,z-v_3\rangle$. В свою очередь, мы знаем, что это правда
именно тогда, когда $\ds \langle a,b,c\rangle\cdot\langle
x-v_1,y-v_2,z-v_3\rangle=0$. Таким образом, $(x,y,z)$ лежит в плоскости, если и
только если
$$\выравнивание{
\langle a,b,c\rangle\cdot\langle x-v_1,y-v_2,z-v_3\rangle&=0\cr
a(x-v_1)+b(y-v_2)+c(z-v_3)&=0\cr
топор+by+cz-av_1-bv_2-cv_3&=0\cr
топор+by+cz&=av_1+bv_2+cv_3.\cr
}$$
Работая в обратном направлении, обратите внимание, что если $(x,y,z)$ — точка, удовлетворяющая
$ax+by+cz=d$ тогда
$$\выравнивание{
топор+by+cz&=d\cr
топор+by+cz-d&=0\cr
a(x-d/a)+b(y-0)+c(z-0)&=0\cr
\langle a,b,c\rangle\cdot\langle x-d/a,y,z\rangle&=0.\cr
}$$
А именно, $\langle a,b,c\rangle$ перпендикулярен вектору с
хвост в $(d/a,0,0)$ и голова в $(x,y,z)$.
5.1. То есть предположим
мы знаем, что $\langle a,b,c\rangle$ нормальна к плоскости, содержащей
точка $\ds (v_1,v_2,v_3)$. Тогда $(x,y,z)$ лежит в плоскости тогда и только тогда
если $\langle a,b,c\rangle$ перпендикулярно $\ds \langle
x-v_1,y-v_2,z-v_3\rangle$. В свою очередь, мы знаем, что это правда
именно тогда, когда $\ds \langle a,b,c\rangle\cdot\langle
x-v_1,y-v_2,z-v_3\rangle=0$. Таким образом, $(x,y,z)$ лежит в плоскости, если и
только если
$$\выравнивание{
\langle a,b,c\rangle\cdot\langle x-v_1,y-v_2,z-v_3\rangle&=0\cr
a(x-v_1)+b(y-v_2)+c(z-v_3)&=0\cr
топор+by+cz-av_1-bv_2-cv_3&=0\cr
топор+by+cz&=av_1+bv_2+cv_3.\cr
}$$
Работая в обратном направлении, обратите внимание, что если $(x,y,z)$ — точка, удовлетворяющая
$ax+by+cz=d$ тогда
$$\выравнивание{
топор+by+cz&=d\cr
топор+by+cz-d&=0\cr
a(x-d/a)+b(y-0)+c(z-0)&=0\cr
\langle a,b,c\rangle\cdot\langle x-d/a,y,z\rangle&=0.\cr
}$$
А именно, $\langle a,b,c\rangle$ перпендикулярен вектору с
хвост в $(d/a,0,0)$ и голова в $(x,y,z)$. Это означает, что точки
$(x,y,z)$, удовлетворяющие уравнению $ax+by+cz=d$, образуют плоскость
перпендикулярно $\langle a,b,c\rangle$. (Это не
работать, если $a=0$, но в этом случае мы можем использовать $b$ или $c$ в роли
$а$. То есть либо $a(x-0)+b(y-d/b)+c(z-0)=0$, либо
$a(x-0)+b(y-0)+c(z-d/c)=0$.)
Это означает, что точки
$(x,y,z)$, удовлетворяющие уравнению $ax+by+cz=d$, образуют плоскость
перпендикулярно $\langle a,b,c\rangle$. (Это не
работать, если $a=0$, но в этом случае мы можем использовать $b$ или $c$ в роли
$а$. То есть либо $a(x-0)+b(y-d/b)+c(z-0)=0$, либо
$a(x-0)+b(y-0)+c(z-d/c)=0$.)
Рисунок 12.5.1. Плоскость, определяемая векторами, перпендикулярными нормали.
Таким образом, для вектора $\langle a,b,c\rangle$ мы знаем, что все плоскости перпендикулярные этому вектору, имеют вид $ax+by+cz=d$, и любая поверхность этой формы является плоскостью, перпендикулярной $\langle a,b,c\rangle$.
Пример 12.5.1 Найдите уравнение для плоскости, перпендикулярной $\langle 1,2,3\rangle$ и содержащий точку $(5,0,7)$.
Используя приведенный выше вывод,
плоскость равна $1x+2y+3z=1\cdot5+2\cdot0+3\cdot7=26$. Поочередно, мы
знаем, что плоскость равна $x+2y+3z=d$, и чтобы найти $d$, можно подставить
известную точку на плоскости, чтобы получить $5+2\cdot0+3\cdot7=d$, поэтому $d=26$. Мы могли бы также записать это просто как $(x-5)+2(y)+3(z-7)=0$, что для
много целей прекрасное представление; всегда можно умножить
чтобы получить $x+2y+3z=26$.
$\квадрат$
Мы могли бы также записать это просто как $(x-5)+2(y)+3(z-7)=0$, что для
много целей прекрасное представление; всегда можно умножить
чтобы получить $x+2y+3z=26$.
$\квадрат$
Пример 12.5.2 Найдите вектор нормали к плоскости $2x-3y+z=15$.
Одним из примеров является $\langle 2, -3,1\rangle$. Любой вектор, параллельный или антипараллельно с этим также работает, например $-2\langle 2, -3,1\rangle=\langle -4,6,-2\rangle$ также нормальна к плоскости. $\квадрат$
Нам часто нужно будет найти уравнение для плоскости при заданных информация о самолете. Хотя иногда может быть немного более короткие пути к желаемому результату, это всегда возможно, и обычно целесообразно использовать данную информацию, чтобы найти нормаль к плоскость и точку на плоскости, а затем найти уравнение в виде выше.
Пример 12.5.3. Плоскости $x-z=1$ и $y+2z=3$ пересекаются по прямой. Найди третья плоскость, содержащая эту прямую и перпендикулярная плоскости $x+y-2z=1$.
Во-первых, заметим, что две плоскости перпендикулярны тогда и только тогда, когда их
нормальные векторы перпендикулярны.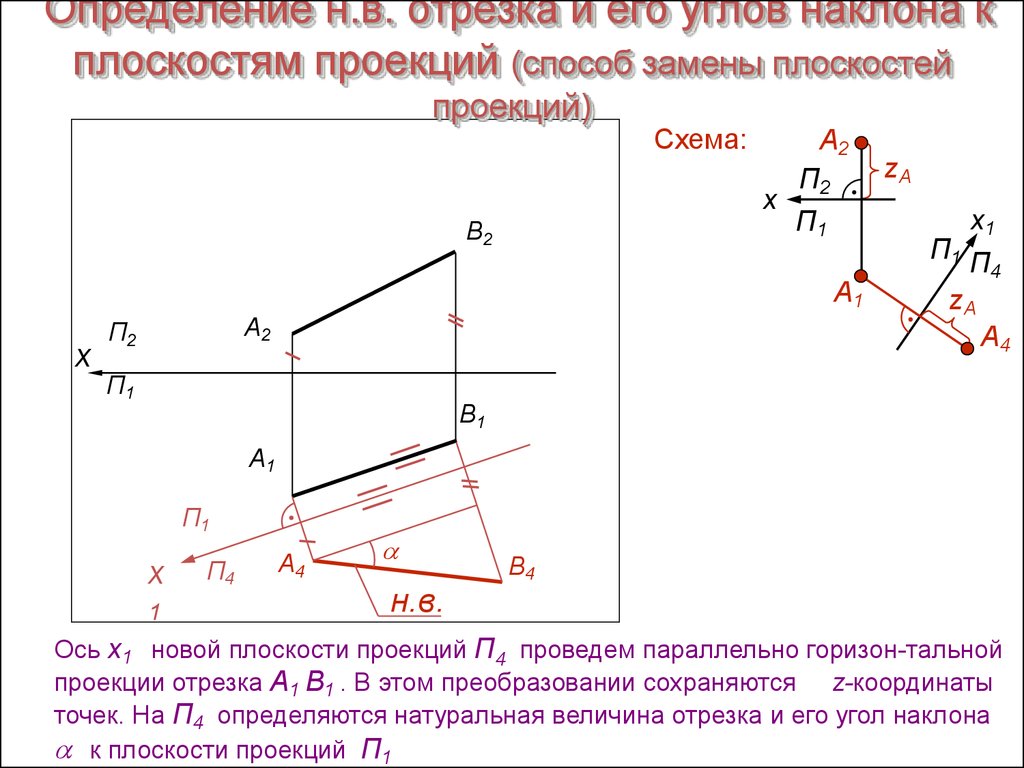 Таким образом, мы ищем вектор $\langle
a,b,c\rangle$, то есть
перпендикулярно $\langle 1,1,-2\rangle$. Кроме того, поскольку
желаемая плоскость должна содержать определенную линию, $\langle
a,b,c\rangle$ должны быть перпендикулярны любому вектору, параллельному этому
линия. Так как $\langle
a,b,c\rangle$ должны быть перпендикулярны двум векторам, мы можем найти это по
вычисление перекрестного произведения двух. Итак, нам нужен вектор, параллельный
к линии пересечения данных плоскостей. Для этого достаточно
знать две точки на прямой. Чтобы найти две точки на этой прямой,
необходимо найти две точки, находящиеся одновременно на двух плоскостях,
$x-z=1$ и $y+2z=3$. Любая точка на обеих плоскостях будет удовлетворять
$x-z=1$ и $y+2z=3$. Легко найти значения для $x$ и $z$
удовлетворяющие первому, такие как $x=1, z=0$ и $x=2, z=1$. Затем
мы можем найти соответствующие значения для $y$, используя второе уравнение,
а именно $y=3$ и $y=1$, поэтому
$(1,3,0)$ и $(2,1,1)$ находятся на прямой
пересечения, потому что оба находятся в обеих плоскостях.
Таким образом, мы ищем вектор $\langle
a,b,c\rangle$, то есть
перпендикулярно $\langle 1,1,-2\rangle$. Кроме того, поскольку
желаемая плоскость должна содержать определенную линию, $\langle
a,b,c\rangle$ должны быть перпендикулярны любому вектору, параллельному этому
линия. Так как $\langle
a,b,c\rangle$ должны быть перпендикулярны двум векторам, мы можем найти это по
вычисление перекрестного произведения двух. Итак, нам нужен вектор, параллельный
к линии пересечения данных плоскостей. Для этого достаточно
знать две точки на прямой. Чтобы найти две точки на этой прямой,
необходимо найти две точки, находящиеся одновременно на двух плоскостях,
$x-z=1$ и $y+2z=3$. Любая точка на обеих плоскостях будет удовлетворять
$x-z=1$ и $y+2z=3$. Легко найти значения для $x$ и $z$
удовлетворяющие первому, такие как $x=1, z=0$ и $x=2, z=1$. Затем
мы можем найти соответствующие значения для $y$, используя второе уравнение,
а именно $y=3$ и $y=1$, поэтому
$(1,3,0)$ и $(2,1,1)$ находятся на прямой
пересечения, потому что оба находятся в обеих плоскостях.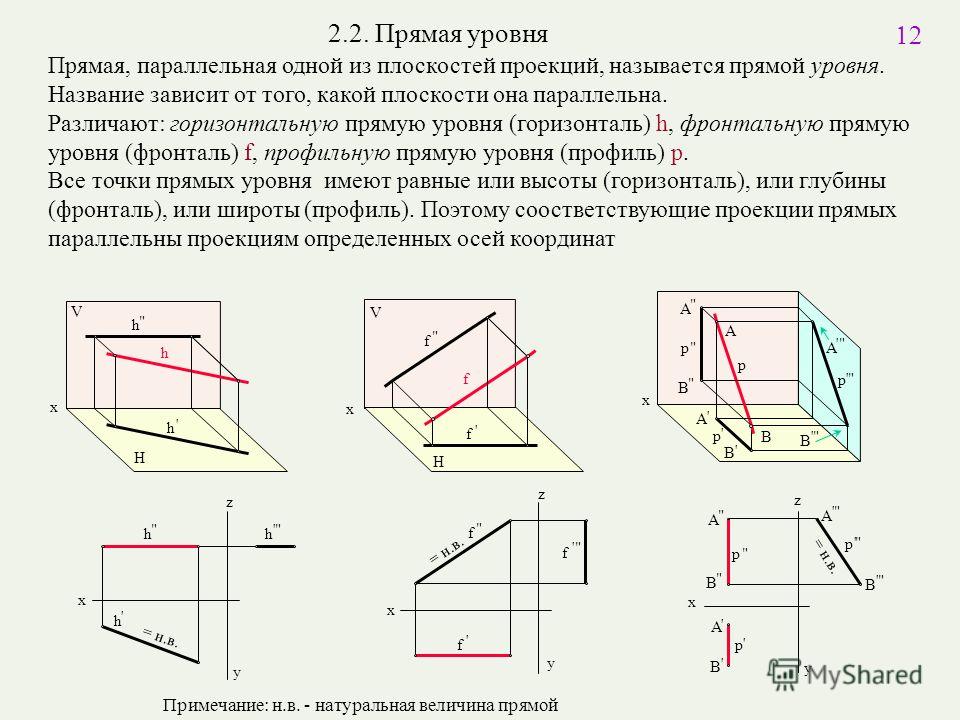 Сейчас
$\langle 2-1,1-3,1-0\rangle=\langle 1,-2,1\rangle$ параллелен
линия. Наконец, мы можем выбрать $\langle a,b,c\rangle=\langle
1,1,-2\rangle\times \langle 1,-2,1\rangle=\langle -3,-3,-3\rangle$.
Хотя этот вектор прекрасно подойдет, любой вектор, параллельный или
антипараллельное к нему также будет работать, поэтому, например, мы могли бы выбрать
$\langle 1,1,1\rangle$, который ему антипараллелен.
Сейчас
$\langle 2-1,1-3,1-0\rangle=\langle 1,-2,1\rangle$ параллелен
линия. Наконец, мы можем выбрать $\langle a,b,c\rangle=\langle
1,1,-2\rangle\times \langle 1,-2,1\rangle=\langle -3,-3,-3\rangle$.
Хотя этот вектор прекрасно подойдет, любой вектор, параллельный или
антипараллельное к нему также будет работать, поэтому, например, мы могли бы выбрать
$\langle 1,1,1\rangle$, который ему антипараллелен.
Теперь мы знаем, что $\langle 1,1,1\rangle$ нормальна к искомой плоскости. и $(2,1,1)$ — точка на плоскости. Поэтому уравнение плоскость равна $x+y+z=4$. В качестве быстрой проверки, поскольку $(1,3,0)$ также находится на линия, она должна быть в самолете; поскольку $1+3+0=4$, мы видим, что это действительно дело.
Обратите внимание, что если бы мы использовали $\langle -3,-3,-3\rangle$ в качестве нормали, мы открыли бы уравнение $-3x-3y-3z=-12$, то мы вполне могли бы заметили, что мы можем разделить обе части на $-3$, чтобы получить эквивалент $x+y+z=4$. $\квадрат$
Итак, теперь мы понимаем уравнения плоскостей; давайте обратимся к
линии.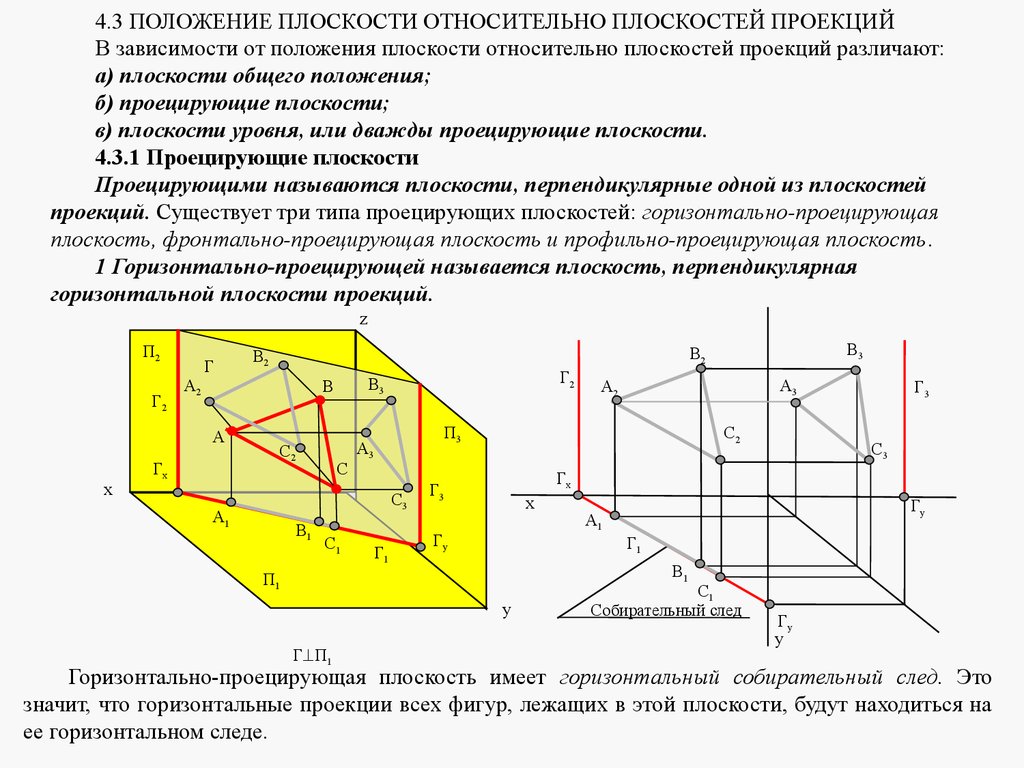 К сожалению, это оказывается весьма неудобным
представить типичную линию одним уравнением; нам нужно подойти
линии по-другому.
К сожалению, это оказывается весьма неудобным
представить типичную линию одним уравнением; нам нужно подойти
линии по-другому.
В отличие от плоскости, линия в трех измерениях имеет очевидную направление, а именно направление любого параллельного ему вектора. Фактически линия может быть определена и однозначно идентифицирована путем предоставления одной точки на прямой и вектор, параллельный прямой (в одном из двух возможных направления). То есть линия состоит именно из тех точек, которые мы можем достичь, начав с точки и пройдя некоторое расстояние в направление вектора. Давайте посмотрим, как мы можем перевести это на более математический язык.
Предположим, что прямая содержит точку $\ds (v_1,v_2,v_3)$ и параллельна
к вектору $\langle a,b,c\rangle$; мы называем $\langle a,b,c\rangle$ a вектор направления для линии.
Если мы поместим вектор $\ds
\langle v_1,v_2,v_3\rangle$ с хвостом в начале координат и головой
в $\ds (v_1,v_2,v_3)$, и если мы поместим вектор $\langle
a,b,c\rangle$ хвостом в $\ds (v_1,v_2,v_3)$, то голова
$\langle a,b,c\rangle$ находится в точке на прямой. Мы можем добраться до любой точки на линии, делая то же самое, за исключением использования
$t\langle a,b,c\rangle$ вместо $\langle a,b,c\rangle$, где $t$
некоторое действительное число. Из-за того, как работает сложение векторов,
точка в начале вектора $t\langle a,b,c\rangle$ — это точка
в начале вектора $\ds\langle v_1,v_2,v_3\rangle+t\langle
a,b,c\rangle$, а именно $\ds (v_1+ta,v_2+tb,v_3+tc)$; видеть
рисунок 12.5.2.
Мы можем добраться до любой точки на линии, делая то же самое, за исключением использования
$t\langle a,b,c\rangle$ вместо $\langle a,b,c\rangle$, где $t$
некоторое действительное число. Из-за того, как работает сложение векторов,
точка в начале вектора $t\langle a,b,c\rangle$ — это точка
в начале вектора $\ds\langle v_1,v_2,v_3\rangle+t\langle
a,b,c\rangle$, а именно $\ds (v_1+ta,v_2+tb,v_3+tc)$; видеть
рисунок 12.5.2.
Рисунок 12.5.2. Векторная форма линии.
Другими словами, когда $t$ проходит через все возможные действительные значения,
вектор $\ds \langle v_1,v_2,v_3\rangle+t\langle a,b,c\rangle$ указывает на
каждая точка на линии, когда ее конец находится в начале координат. Другой
общий способ записать это как набор параметрические уравнения :
$$ x= v_1+ta\qquad y=v_2+tb \qquad z=v_3+tc.$$
Иногда полезно использовать эту форму линии даже в двух случаях.
размеры; векторная форма прямой на плоскости $x$-$y$ есть
$\ds \langle v_1,v_2\rangle+t\langle a,b\rangle$, что совпадает с
$\ds \langle v_1,v_2,0\rangle+t\langle a,b,0\rangle$.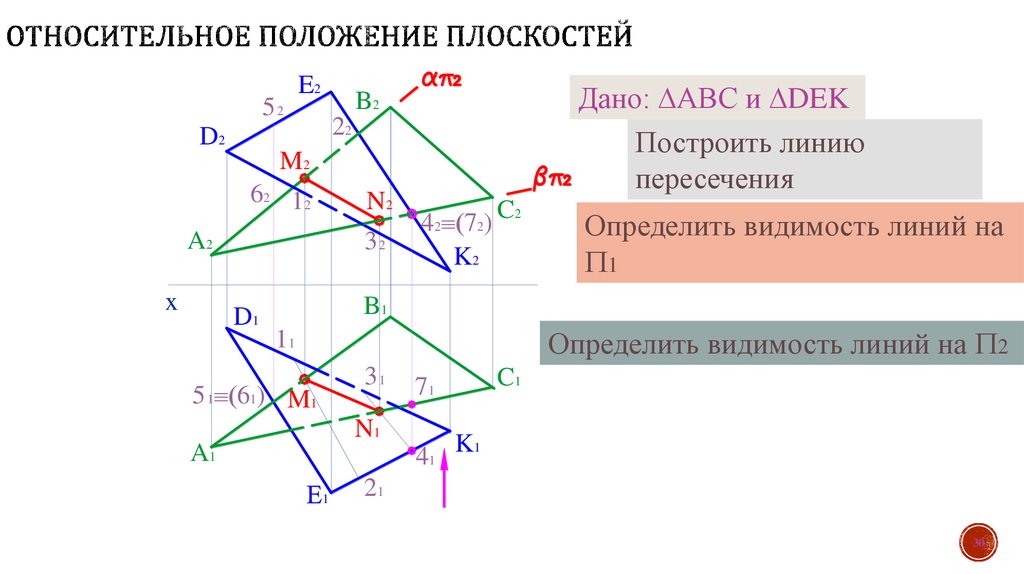
Пример 12.5.4. Найдите векторное выражение для линии, проходящей через $(6,1,-3)$ и $(2,4,5)$. Чтобы получить вектор, параллельный прямой, мы вычитаем $\langle 6,1,-3\rangle-\langle2,4,5\rangle=\langle 4,-3,-8\rangle$. Линия тогда задается как $\langle 2,4,5\rangle+t\langle 4,-3,-8\rangle$; там конечно, много других возможностей, таких как $\langle 6,1,-3\rangle+t\langle 4,-3,-8\rangle$. $\квадрат$
Пример 12.5.5 Определить, совпадают ли прямые $\langle 1,1,1\rangle+t\langle 1,2,-1\rangle$ и $\langle 3,2,1\rangle+t\langle -1,-5,3\rangle$ параллельны, пересекаются или ни один.
В двух измерениях две линии либо пересекаются, либо параллельны; в
В трех измерениях линии, которые не пересекаются, могут быть не параллельны.
В этом случае, поскольку векторы направления линий не
параллельны или антипараллельны, мы знаем, что прямые не параллельны.
Если они пересекаются, то должно быть два значения $a$ и $b$, так что
$\langle 1,1,1\rangle+a\langle 1,2,-1\rangle=
\langle 3,2,1\rangle+b\langle -1,-5,3\rangle$, то есть
$$\выравнивание{
1+а&=3-б\кр
1+2а&=2-5б\кр
1-а&=1+3б\кр
}$$
Это дает три уравнения с двумя неизвестными, поэтому может быть, а может и не быть. решение в общем. В этом случае легко обнаружить, что $a=3$
и $b=-1$ удовлетворяет всем трем уравнениям, поэтому прямые пересекаются в
точка $(4,7,-2)$.
$\квадрат$
решение в общем. В этом случае легко обнаружить, что $a=3$
и $b=-1$ удовлетворяет всем трем уравнениям, поэтому прямые пересекаются в
точка $(4,7,-2)$.
$\квадрат$
Пример 12.5.6. Найти расстояние от точки $(1,2,3)$ до плоскости $2x-y+3z=5$. Расстояние от точки $P$ до плоскости является кратчайшим расстояние от $P$ до любой точки плоскости; это расстояние, измеряемое от $P$ перпендикулярно плоскости; видеть рисунок 12.5.3. Это расстояние является абсолютным значением скалярной проекции $\ds \overrightarrow{\распорка QP}$ на вектор нормали $\bf n$, где $Q$ — любая точка плоскости. Легко найти точку на плоскости, скажем, $(1,0,1)$. Таким образом, расстояние равно $$ {\ overrightarrow {\ распорка QP} \ cdot {\ bf n} \ over | {\ bf n} |} = {\ langle 0,2,2 \ rangle \ cdot \ langle 2, -1,3 \ rangle \ over | \ langle 2, — 1,3 \ rangle |} = {4\over\sqrt{14}}. $$ $\квадрат$
Рисунок 12.5.3. Расстояние от точки до плоскости.
Пример 12.5.7. Найти расстояние от точки $(-1,2,1)$ до прямой
$\langle 1,1,1\rangle + t\langle 2,3,-1\rangle$.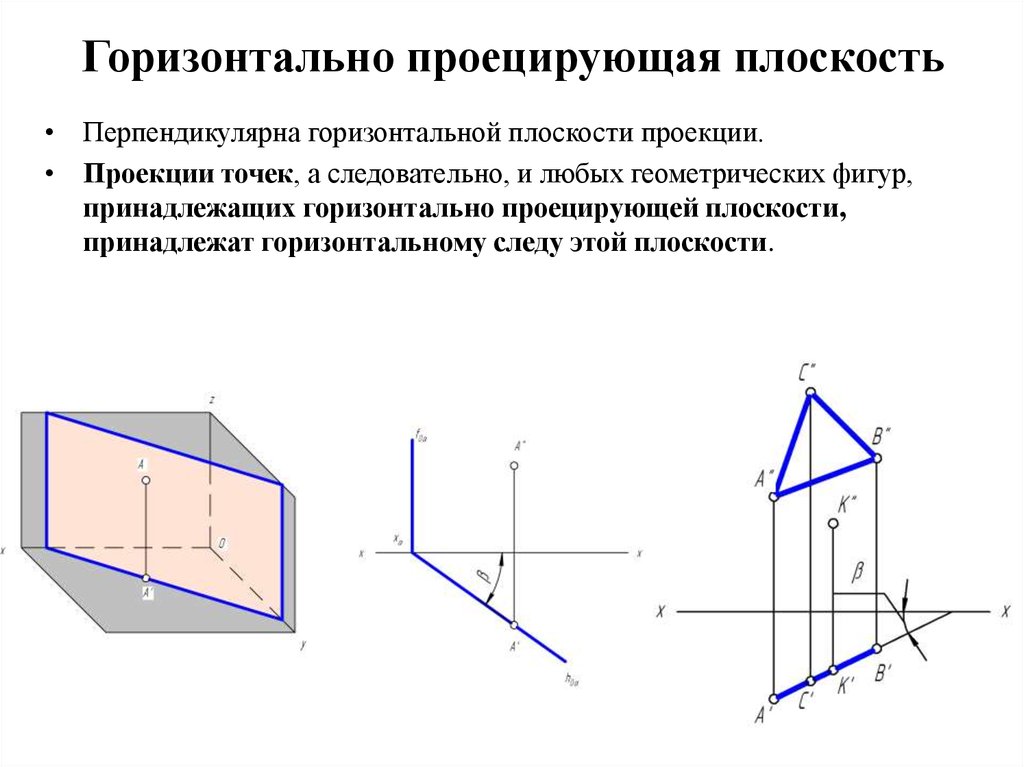 Мы снова хотим расстояния
измеряется перпендикулярно линии, как показано на
рисунок 12.5.4. Желаемое расстояние равно
$$
|\overrightarrow{\ распорка QP}|\sin\theta=
{|\overrightarrow{\strut QP}\times{\bf A}|\over|{\bf A}|},
$$
где $\bf A$ — любой вектор, параллельный прямой. Из уравнения
линии, мы можем использовать $Q=(1,1,1)$ и ${\bf A}=\langle 2,3,-1\rangle$, поэтому
расстояние
$$
{|\langle -2,1,0\rangle\times\langle2,3,-1\rangle|\over\sqrt{14}}=
{|\langle-1,-2,-8\rangle|\over\sqrt{14}}={\sqrt{69}\over\sqrt{14}}.
$$
$\квадрат$
Мы снова хотим расстояния
измеряется перпендикулярно линии, как показано на
рисунок 12.5.4. Желаемое расстояние равно
$$
|\overrightarrow{\ распорка QP}|\sin\theta=
{|\overrightarrow{\strut QP}\times{\bf A}|\over|{\bf A}|},
$$
где $\bf A$ — любой вектор, параллельный прямой. Из уравнения
линии, мы можем использовать $Q=(1,1,1)$ и ${\bf A}=\langle 2,3,-1\rangle$, поэтому
расстояние
$$
{|\langle -2,1,0\rangle\times\langle2,3,-1\rangle|\over\sqrt{14}}=
{|\langle-1,-2,-8\rangle|\over\sqrt{14}}={\sqrt{69}\over\sqrt{14}}.
$$
$\квадрат$
Рисунок 12.5.4. Расстояние от точки до прямой.
Вы можете использовать Sage для вычисления расстояний до линий и плоскостей, так как это просто включает векторную арифметику, которую мы уже видели. Конечно, вы также можете использовать Sage для выполнения некоторых вычислений, связанных с нахождение уравнений плоскостей и прямых.
Пример 12.5.1 Найдите уравнение плоскости, содержащее $(6,2,1)$ и
перпендикулярно $\langle 1,1,1\rangle$. (отвечать)
(отвечать)
Пример 12.5.2 Найдите уравнение плоскости, содержащее $(-1,2,-3)$ и перпендикулярно $\langle 4,5,-1\rangle$. (отвечать)
Пример 12.5.3 Найдите уравнение плоскости, содержащее $(1,2,-3)$, $(0,1,-2)$ и $(1,2,-2)$. (отвечать)
Пример 12.5.4 Найдите уравнение плоскости, содержащее $(1,0,0)$, $(4,2,0)$ и $(3,2,1)$. (отвечать)
Пример 12.5.5 Найдите уравнение плоскости, содержащее $(1,0,0)$ и строка $\langle 1,0,2\rangle + t\langle 3,2,1\rangle$. (отвечать)
Пример 12.5.6 Найдите уравнение плоскости, содержащей прямую пересечение $x+y+z=1$ и $x-y+2z=2$ и перпендикулярно плоскость $2x+3y-z=4$. (отвечать)
Пример 12.5.7 Найдите уравнение плоскости, содержащей прямую пересечение $x+2y-z=3$ и $3x-y+4z=7$ и перпендикулярно плоскость $6x-y+3z=16$. (отвечать)
Пример 12.5.8 Найдите уравнение плоскости, содержащей прямую
пересечение $x+3y-z=6$ и $2x+2y-3z=8$ и перпендикулярно
плоскость $3x+y-z=11$.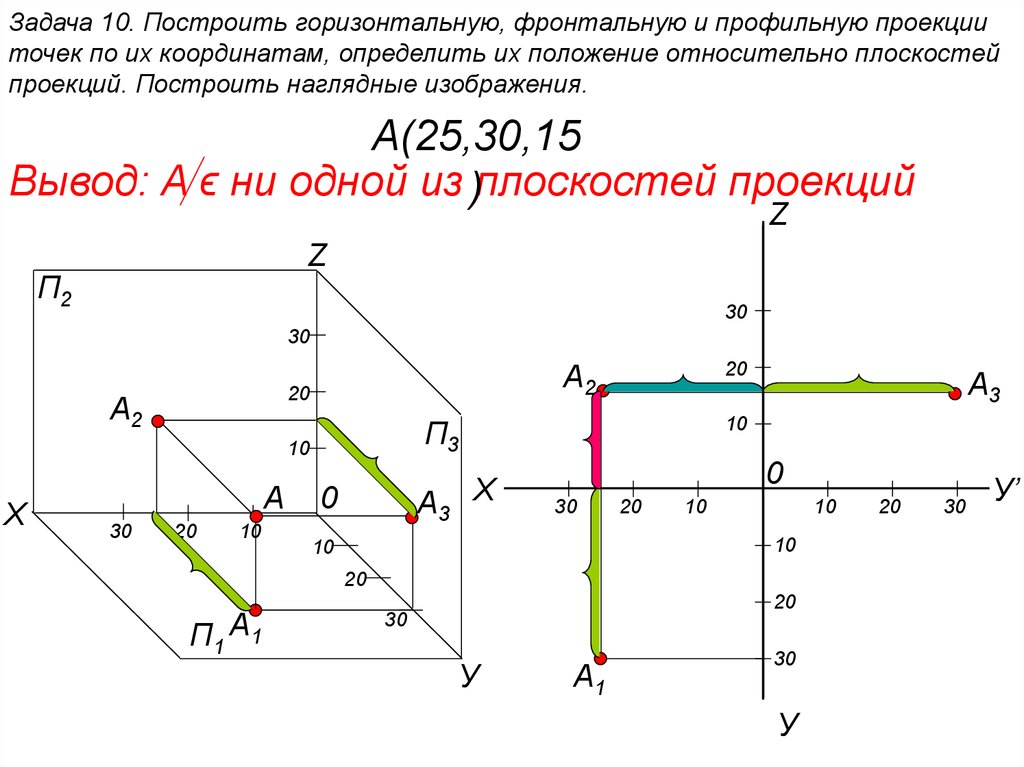 (отвечать)
(отвечать)
Пример 12.5.9 Найдите уравнение прямой через $(1,0,3)$ и $(1,2,4)$. (отвечать)
Пример 12.5.10 Найдите уравнение прямой через $(1,0,3)$ и перпендикулярно плоскости $x+2y-z=1$. (отвечать)
Пример 12.5.11 Найдите уравнение прямой, проходящей через начало координат и перпендикулярно плоскости $x+y-z=2$. (отвечать)
Пример 12.5.12 Найдите $a$ и $c$ так, чтобы $(a,1,c)$ лежало на прямой, проходящей через $(0,2,3)$ и $(2,7,5)$. (отвечать)
Пример 12.5.13 Объясните, как найти решение в пример 12.5.5.
Пример 12.5.14 Определить, являются ли строки $\langle 1,3,-1\rangle+t\langle 1,1,0\rangle$ и $\langle 0,0,0\rangle+t\langle 1,4,5\rangle$ параллельны, пересекаются или ни то, ни другое. (отвечать)
Пример 12.5.15 Определить, являются ли строки $\langle 1,0,2\rangle+t\langle
-1,-1,2\rangle$ и $\langle 4,4,2\rangle+t\langle 2,2,-4\rangle$
параллельны, пересекаются или ни то, ни другое. (отвечать)
(отвечать)
Пример 12.5.16 Определить, являются ли строки $\langle 1,2,-1\rangle+t\langle 1,2,3\rangle$ и $\langle 1,0,1\rangle+t\langle 2/3,2,4/3\rangle$ параллельны, пересекаются или ни то, ни другое. (отвечать)
Пример 12.5.17 Определить, являются ли строки $\langle 1,1,2\rangle+t\langle 1,2,-3\rangle$ и $\langle 2,3,-1\rangle+t\langle 2,4,-6\rangle$ параллельны, пересекаются или ни то, ни другое. (отвечать)
Пример 12.5.18 Найдите единичный вектор нормали к каждой из координатных плоскостей.
Пример 12.5.19 Покажите, что $\langle 2,1,3 \rangle + t \langle 1,1,2 \rangle$ и $\langle 3, 2, 5 \rangle + s \langle 2, 2, 4 \rangle$ одинаковы линия.
Пример 12.5.20 Дайте краткое описание каждого из следующих процессов:
а. Даны две различные точки, найти прямую, которая проходит через них.
б. Даны три точки (не все на одной прямой), найдите плоскость что проходит через них. Зачем нужна оговорка, что не все точки лежат на одной прямой?
с.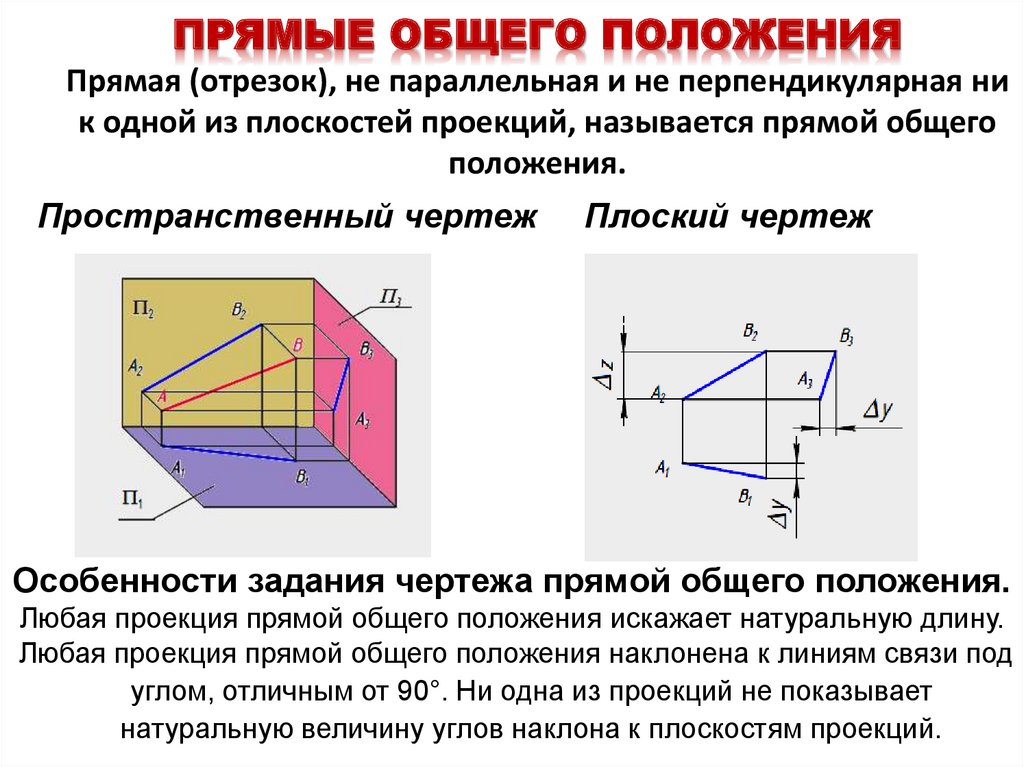 Даны прямая и точка, не лежащие на этой прямой, найти плоскость, на которой
содержит их обоих.
Даны прямая и точка, не лежащие на этой прямой, найти плоскость, на которой
содержит их обоих.
д. Даны плоскость и точка, не лежащие на плоскости, найти прямую, перпендикулярен плоскости, проходящей через данную точку.
Пример 12.5.21 Найдите расстояние от $(2,2,2)$ до $x+y+z=-1$. (отвечать)
Пример 12.5.22 Найдите расстояние от $(2,-1,-1)$ до $2x-3y+z=2$. (отвечать)
Пример 12.5.23 Найдите расстояние от $(2,-1,1)$ до $\langle 2,2,0\rangle+t\langle 1,2,3\rangle$. (отвечать)
Пример 12.5.24 Найдите расстояние от $(1,0,1)$ до $\langle 3,2,1\rangle+t\langle 2,-1,-2\rangle$. (отвечать)
Пример 12.5.25 Найдите расстояние между линиями $\langle 5,3,1\rangle+t\langle 2,4,3\rangle$ и $\langle 6,1,0\rangle+t\langle 3,5,7\rangle$. (отвечать)
Пример 12.5.26 Найдите расстояние между линиями
$\langle 2,1,3\rangle+t\langle -1,2,-3\rangle$ и
$\langle 1,-3,4\rangle+t\langle 4,-4,1\rangle$.

 APA2PV.
APA2PV.