Векторы и матрицы в MathСad
Вы уже наверняка не раз сталкивались с такими понятиями как векторы и матрицы. Вектор – это обыкновенный столбец с числами. Матрица представляет собой сборный блок с объектами. Именно на работе с этими элементами построен принцип функционирования программы Excel. В этом уроке мы расскажем о том, как работать с такими вычислениями в программе Маткад и акцентируем внимание на том, почему процесс работы в данном ПО куда проще и удобнее.
Мы уже рассказывали в своих уроках о том, что все наши векторы начинались с элемента с нулевым значением. Сейчас же мы поставим номером первого элемента цифру один, ведь так нам гораздо проще будет сориентироваться в учебном материале.
Данное значение можно внести прямо в рабочее поле.
Посмотрите на матрицы на рисунке ниже.
Как вы можете заметить, в них входят и числа, и функции. Помимо этого, сюда можно внести и текст. Чтобы вывести элемент матрицы, воспользуйтесь подстрочным индексом.
Матрицы, описанные на скрине повыше, относятся к квадратному типу. Тем не менее, пользователь может самостоятельно устанавливать их размерные рамки.
Примите во внимание, что первое число обозначает общую нумерацию строчки, а второе – номер столбика.
Для векторного столбца второй индекс можно удалить. Для строки же он является обязательным.
Нужные команды, для всевозможного выделения строчек или столбиков вы всегда сможете отыскать во вкладке «Математика».
Большинство операций для векторных и матричных конструкций вполне соответствуют работе со стандартными числами и функциями. Для того, чтобы отыскать обратную матрицу, потребуется действовать по аналогии с операциями деления. Пользователь может записать операторы, задав им наименования матриц и векторов. Например, это может выглядеть так:
Более подробно мы рассмотрим данный опционал немного погодя.
Стоит отметить, что такая функция нуждается в девяти операциях умножения и в таком же количестве деления. Согласитесь, что расписывать все эти процессы достаточно скучно. К тому же, с большими матрицами такой подход нерациональный.
Методика применения векторов отличается значительным разнообразием. Чтобы разработать вектор или матрицу, понадобится открыть вкладку «Вставить матрицу». На экране появится сетка с изображением маленьких квадратиков.
Перемещаем указатель на эту сетку. Настраиваем курсор на нужные габариты матрицы. Кликаем дважды ЛКМ.
На экране появляется новая матрица.
Матрица может быть переименована, после того, как пользователь дважды кликнет по левой скобке.
Чтобы быстро вставить или удалить строчки да столбцы, можно вызвать контекстное меню «Операторы с векторами\матрицами» на одноименной вкладке.
Работа с матрицами
Эффекты от матриц или вектором гораздо проще сообразить, пользуясь специально разработанными символами.
Обратите внимание на скрин ниже.
Оператор транспортировки вызывается посредством выполнения операции Математика –> Операторы –> Векторы и матрицы:
Кликаем по правой стороне матрицы и применяем оператор. Он подходит как для символьных, так и численных матриц.
Операции в векторах часто выполняются по одному элементу. В этой ситуации можно воспользоваться очень удобным оператором, который отвечает за разработку вектора. Чтобы перемножить два вектора, понадобится выполнить простой пример.
Теперь нам нужно выбрать нужные параметры и активировать векторизацию.
Вычисляем заданные параметры и смотрим на результат. Первый элемент приумножился на второй, и так далее.
Еще примеры таких опций.
Операции поэлементного типа могут применяться исключительно к массивам одинакового размера.
Добавление и вычитание
Данные операции относятся к поэлементному типу.
Она также применяется к массивам одинакового размерного типа.
Пользуясь оператором, предназначенным для суммирования, можно отыскать сумму всех векторных частей.
Скалярное произведение работает по представленному ниже принципу.
При таком типе умножения матриц, программа занимается умножением данных элементов по столбцам. Данная операция может применяться исключительно к тем матрицам, которые характеризуются равным количеством строчек и столбцов.
Обратите внимание, что немалая роль отводится поочередности множителей.
Только в редких случаях скалярное произведение может стать коммутативным.
Скаляр двух векторов показывает результат как на фотографии ниже.
Данная опция может использоваться исключительно для двух векторных столбов из трех элементов.
Векторное произведение часто используется для механики, гидродинамики и огромного количества подобных сфер деятельности.
Обратная матрица может быть применима для квадратных матриц:
В результате у нас получится матрица единичного типа
Если произвести матрицу и единичную матрицу, мы получим первоначальный вариант.
Определитель может быть разработан исключительно для матрицы квадратного типа. Он может быть нулевым в любых условиях. Обратная матрица имеет в своей структуре дроби, в состав которых входит определитель.
В ситуациях, когда определитель установлен на ноль, к нему нереально подобрать обратную матрицу. Сама матрица автоматически становится сингулярной. О таких изменениях пользователь узнает из оповещения программы.
В ситуациях со скалярами, определитель соответствует их модулям
Команда «определитель» помогает отыскать длину вектора.
Самоучитель MathCAD
Матрица Гильбер
та является примером плохо обусловленной матрицы. Элементы матрицы Гиль
берта определяются как H(i,j)=1/(i+j-1).
Пример:
>> H = hilb(5)
H=
1.0000 0.5000
0.5000 0.3333
0.3333 0.2500
0.2500 0.2000
0.2000 0.1667
>> cond(hilb(5))
ans = 4.7661e+005
1
1
-1
-1
1
-1
-1
1
0.3333
0.2500
0.2000
0.1667
0.1429
0.2500
0.2000
0.1667
0.1429
0.1250
0.2000
0.1667
0.1429
0.1250
0.1111
4.3.4. Матрицы Ганкеля
Матрицы Ганкеля относятся к симметричным матрицам с постоянными значе
ниями на антидиагоналях. Элементы матриц Ганкеля определяются выражением
Значение числа обусловленности матрицы Гильберта указывает на очень пло
хо обусловленную матрицу.
invhilb(n) – возвращает матрицу, обратную матрице Гильберта порядка n
Точная обратная матрица – это матрица с очень большими целочисленными зна
чениями. Эти целочисленные значения могут быть представлены как числа с пла
вающей запятой без погрешности округления до тех пор, пока порядок матрицы n
не превышает 15.
Пример:210
>>H = invhilb(5).
H=
25
-300
-300
4800
1050
18900
-1400 26880
630
-12600
>> inv(hilb(5))
ans =
1.0e+005 *
0.0002
-0.0030
0.0105
-0.0140
0.0063
Операции с векторами и матрицами
Создание и вычисление специальных матриц
211
1050
–18900
79380
-117600
56700
-1400
26880
-117600
179200
-88200
630
-12600
56700
-88200
44100
А вот результат обращения матрицы Гильберта с плавающей запятой:
бцов) Холецкого для матрицы Паскаля. Полученная матрица, все элементы
которой выше главной диагонали равны нулю, является своей обратной
матрицей, то есть квадратным корнем из единичной матрицы;
• pascal(n,2) – возвращает матрицу, полученную в результате транспони
рования и перестановок матрицы pascal(n,1), при этом результат явля
ется кубическим корнем из единичной матрицы.
Примеры:
>> A=pascal(4)
A=
1
1
1
2
1
3
1
4
>> A=pascal(4,2)
A=
0
0
0
0
0
1
1
1
-0.0030
0.0105
0.0480 -0.1890
-0.1890
0.7938
0.2688 -1.1760
-0.1260
0.5670
-0.0140 0.0063
-1.1760 0.5670
1.7920 -0.8820
-0.8820 0.4410
1
3
6
10
1
4
10
20
4.3.6.
<< Назад 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 Вперед >>
обратная матрица Matlab | Различные примеры обратной матрицы Matlab
В следующей статье представлен обзор обратной матрицы Matlab.
Синтаксис получения обратной матрицы в Matlab:
I = инверсия (M)
Описание:
- I = инверсия (M) входной матрицы M используется для получения обратной матрицы M. Пожалуйста, имейте в виду, что ‘M’ здесь должна быть квадратной матрицей.
Примеры обратной матрицы Matlab
Ниже приведены примеры обратной матрицы Matlab:
Пример #1
В первом примере мы получим обратную матрицу 2 X 2.
Ниже приведены шаги, которые мы выполним для этого примера:
- Определите матрицу, обратную которую мы хотим вычислить.
- Передайте эту матрицу в качестве входных данных обратной функции.
- Проверьте результат, умножив входную матрицу на выходную матрицу. Это должно дать идентификационную матрицу в качестве вывода.
Код:
М = [3 2 ; 2 1];
[Создание квадратной матрицы 2 X 2]
I = инв(М)
[Передача входной матрицы в функцию inv] [Обратите внимание, что, поскольку мы использовали матрицу 2 x 2 в качестве входных данных, наша выходная матрица также будет матрицей 2 x 2. Это, при умножении на входную матрицу, даст на выходе единичную матрицу]
И*М
[Код для проверки того, что «I» является обратным «M». Это должно дать матрицу идентичности в качестве вывода]
Вот как будут выглядеть наши ввод и вывод в командном окне MATLAB:
Ввод:
М = [3 2 ; 2 1];
I = inv(M)
I*M
Выход 1: (обратная матрица)
Выход 2: (это должна быть единичная матрица)
3 выход 1, функция ‘inv’ дала нам обратную входную матрицу.
Выход 2 подтверждает, что «I» является инверсией «M».Пример #2
В этом примере мы получим обратную матрицу 3 X 3.
Ниже приведены шаги, которые мы будем выполнять для этого примера:
- Определите матрицу 3 X 3, обратную которую мы хотим вычислить.
- Передайте эту матрицу в качестве входных данных обратной функции.
- Проверьте результат, умножив входную матрицу на выходную матрицу. Это должно дать идентификационную матрицу в качестве вывода.
Код:
М = [3 2 3; 4 2 1; 3 4 1];
[Создание квадратной матрицы 3 X 3]
I = инв(М)
[Передача входной матрицы 3 X 3 в функцию inv] [Обратите внимание, что, поскольку мы использовали матрицу 3 x 3 в качестве входных данных, наша выходная матрица также будет матрицей 3 x 3. Это, при умножении на входную матрицу, даст на выходе единичную матрицу]
И*М
[Код для проверки того, что «I» является обратным «M».
Это должно дать матрицу идентичности в качестве вывода]
Вот как будут выглядеть наши ввод и вывод в командном окне MATLAB:
Ввод:
M = [3 2 3; 4 2 1; 3 4 1];
I = inv(M)
I*M
Выход 1: (Обратная матрица)
Выход 2: (Это должна быть единичная матрица 9012)0003 Как мы видим на выходе 1, функция «inv» дала нам обратную входную матрицу. Выход 2 подтверждает, что «I» является инверсией «M». В этом примере мы получим обратную матрицу 4 X 4. Ниже приведены шаги, которые мы выполним для этого примера: Код: М = [1 3 3 6; 4 2 8 2; 3 3 4 5; 2 6 3 1]; [Создание квадратной матрицы 4 X 4] I = инв(М) [Передача входной матрицы 4 X 4 в функцию inv]
[Обратите внимание, что поскольку мы использовали матрицу 4 х 4 в качестве входных данных, наша выходная матрица также будет матрицей 4 х 4. Это, при умножении на входную матрицу, даст на выходе единичную матрицу] И*М [Код для проверки того, что «I» является обратным «M». Это должно дать матрицу идентичности в качестве вывода] Вот как будут выглядеть наши ввод и вывод в командном окне MATLAB: Ввод: Выход 1: (обратная матрица) Выход 2: (это должна быть единичная матрица) Как мы видим на выходе 1, функция «inv» дала нам обратную входную матрицу. Обратная любой матрице, «M» определяется как матрица, которая при умножении на матрицу M дает на выходе единичную матрицу. Мы используем функцию «inv» в Matlab, чтобы получить обратную матрицу. Мы можем найти только обратную квадратную матрицу. Это руководство по обращению матрицы Matlab. Здесь мы обсуждаем введение в Matlab Matrix Inverse вместе с примерами соответственно. Вы также можете ознакомиться со следующими статьями, чтобы узнать больше: спросил
9(-12) ). Однако в моем приложении мне нужна большая точность. Что я могу сделать в этой ситуации? . В документации по Это связано с тем, что оператор обратной косой черты или Просто чтобы вы знали, какой алгоритм MATLAB выбирает в зависимости от ваших входных матриц, вот полная блок-схема алгоритма, представленная в их документации Универсальность Пример #3
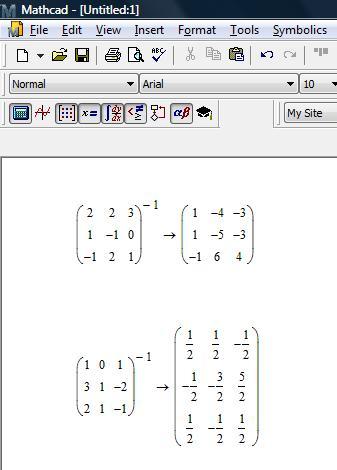
M = [1 3 3 6; 4 2 8 2; 3 3 4 5; 2 6 3 1];
I = inv(M)
I*M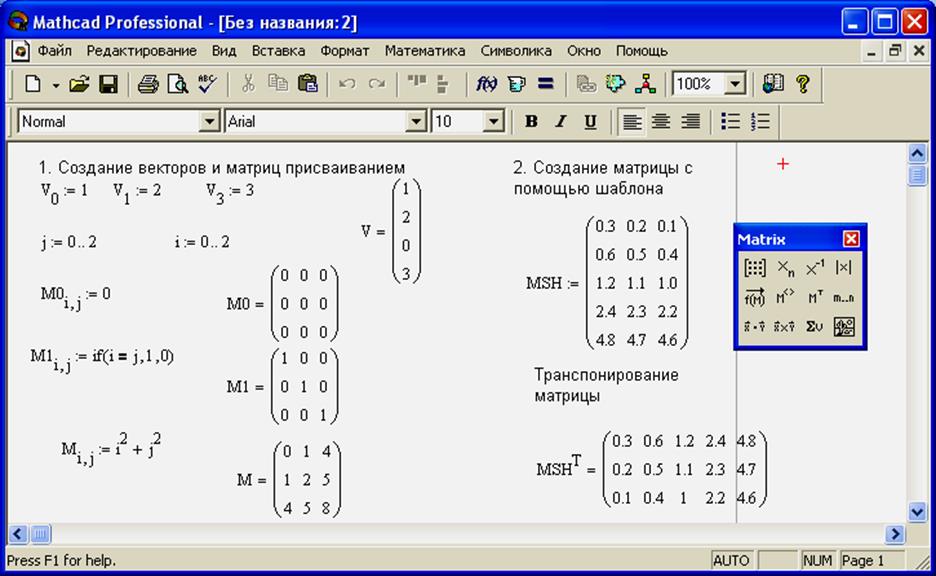 
Выход 2 подтверждает, что «I» является инверсией «M». Заключение
Рекомендуемые статьи
matlab — Как точно вычислить обратную матрицу?
inv() явно указано: х = А\б вычисляется иначе, чем x = inv(A)*b , и рекомендуется для решения систем линейных уравнений. x = A\B решает систему линейных уравнений A*x = B . Матрицы A и B должны иметь одинаковое количество строк. MATLAB® отображает предупреждающее сообщение, если плохо масштабируется или почти одинаков, но все равно выполняет вычисления. mldivide при решении линейных систем проистекает из его способности использовать преимущества симметрии в задаче путем отправки на соответствующий решатель.