Обратная кинематика: Инверсная кинематика в 3D / Хабр

Инверсная кинематика в 3D / Хабр

В этом туториале я расскажу о том, как освоить инверсную кинематику в 3D: методику, позволяющую решить задачу перемещения манипулятора робота к определённой цели.

Об инверсной кинематике в 2D можно прочитать здесь:

• Инверсная кинематика в двухмерном пространстве

Ссылка на скачивание всего пакета Unity находится в конце туториала.

Введение

В моём блоге часто повторяются некоторые темы: одной из них, без всяких сомнений, является инверсная кинематика. Я работал с этой восхитительной темой уже в двух сериях туториалов, в сумме составляющих 8 статей. Тем не менее, ещё многое можно написать об инверсной кинематике в контексте видеоигр.

Почему инверсная кинематика настолько интересна и сложна, что требует такого количества постов? Дело в том, что инверсная кинематика часто встречается не только в видеоиграх, но и в инженерном проектировании, а также в науке в целом.

От проектирования манипуляторов роботов до понимания управления моторикой в человеческом мозге — во всём этом важную роль в том или ином виде играет инверсная кинематика.

Краткое описание

Первая серия, посвящённая этой теме, An Introduction to Procedural Animations [перевод на Хабре], вышла в 2017 году, ещё сильнее популяризировав термин «процедурные анимации» в среде инди-разработчиков. В ней представлено общее решение на основании алгоритма градиентного спуска, которое потенциально можно использовать для довольно «экзотических» моделей, например, щупалец или паучьих ног.

Вторая серия, Inverse Kinematics in 2D, вышла годом позже, в ней рассматривался очень специфический случай: двухшарнирный манипулятор, ограниченный 2D-плоскостью (см. ниже). Суть можно понять из названия: инверсная кинематика в 2D. Каждый из двух шарниров контролируется углом и . При изменении этих двух углов конец манипулятора, называемый

конечным звеном, достигает различных точек.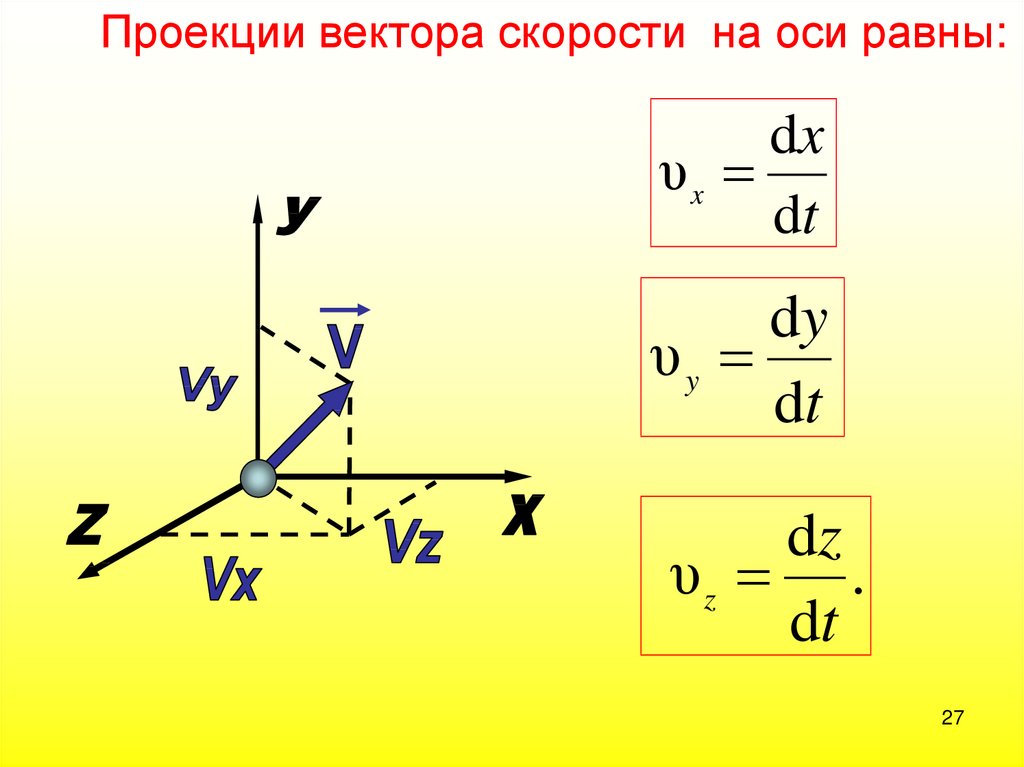

Задача инверсной кинематики (ИК) заключается в нахождении углов и , таких, чтобы конечное звено достигало нужной целевой точки. В анимации показан манипулятор, рисующий окружность на плоскости XY.

Строго говоря, решение, представленное в Inverse Kinematics for Robotic Arms, потенциально может работать с любым количеством шарниров. Так почему же мы сосредоточились на менее мощной методике? Ответ прост: эффективность. Об этом стоило написать потому, что в описанном выше сценарии решение можно найти при помощи простого уравнения, а не достаточно сложного алгоритма. Это возможно благодаря тому, что мы можем представить манипулятор робота как треугольник (см. ниже) с двумя внутренними углами и .

Применив простую тригонометрию, мы выяснили, что значения таких углов будут равны:

(1)

(2)

где , и — стороны этого построенного нами «воображаемого» треугольника.

Однако шарниры манипулятора управляются при помощи и , которые оказываются равными:

(3)

(4)

где:

(5)

Показать вывод уравнения

Полный вывод можно найти в статье Inverse Kinematics in 2D: The Mathematics

.

Переходим в три измерения

Если вы ранее читали серию Inverse Kinematics in 2D, то для вас в предыдущем разделе не было ничего нового. Если не читали, то не волнуйтесь: этого вполне будет достаточно.

Этот упрощённый случай стоит обсудить потому, что его можно использовать в качестве начальной точки для решения задачи ИК в 3D.

Во-первых, нам нужно понять, что сценарий с двухшарнирным манипулятором в 2D — это задача с двумя степенями свободы (2DOF). В противоположность тому, что можно представить, это не значит, что у нас есть два сегмента; на самом деле, у нас есть контроль над двумя переменными (которые, в данном случае, оказываются углами шарниров).

Когда мы расширяем эту задачу на третье измерение, наш манипулятор по-прежнему имеет два сегмента и два шарнира. Однако теперь задача имеет

три степени свободы (3DOF), если предположить, что мы можем ещё и свободно вращать манипулятор вокруг первого шарнира.

При таком сценарии второй шарнир () остался неизменным. Однако, мы предполагаем, что первый () теперь может свободно вращаться в другом измерении. Из-за этого первый шарнир часто называют бедром, а второй — коленом. Колено человека имеет одну степень свободы (вперёд-назад), а бедро — две (вперёд-назад и внутрь-наружу). Угол, на который вращается бедро, обозначается .

Мы можем представить манипулятор робота, у которого оба шарнира имеют две степени свободы, что в сумме даёт четыре. Проблема здесь заключается в том, что может быть много решений, из-за чего наш подход перестаёт быть эффективным. «Ногоподобные» манипуляторы (то есть имеющие шарниры бедра и колена) очень распространены и в играх, и в промышленности.

Поэтому, вероятно, стоит изучить этот подход.

Если вы читали предыдущие статьи, то можете помнить, что если цель достижима в 2D, то всегда существует два «зеркальных» решения (см. ниже).

Та же проблема возникает и в 3D; однако в этом случае решений бесконечно много. Конфигурация может вращаться вокруг оси симметрии, представленной прямой линией, соединяющей начальную точку с целью. Чтобы решить задачу, нужно сосредоточиться только на одном решении! В этом туториале мы рассмотрим решение, которое найти проще всего, оно предполагает, что (0, 1, 0) — это направление «вверх».

Из 2D в 3D

Пока мы знаем только, как решить задачу ИК, когда движение ограничено плоскостью XY. Хитрость при переходе из 2D в 3D заключается в том, чтобы снова использовать 2D-решение. В анимации показан манипулятор, движущийся к точке в 3D-пространстве, вращающейся вокруг оси Y. Довольно очевидно, что единственное, что делает манипулятор — это тоже вращается; его углы и не меняются, меняется только .

Это означает, что если мы знаем, как выполнить ИК на плоскости XY (а мы знаем!), то и знаем, как выполнить её во всём пространстве XYZ при помощи двух простых поворотов. В целом, можно решить эту задачу в три этапа:

1. Поворачивать целевую точку вокруг оси Y, пока она не окажется на плоскости XY
2. Переместить манипулятор робота так, чтобы он смог достичь точки, как если бы она была в 2D
3. «Отменить» поворот, повернув весь манипулятор в противоположном направлении по оси Y.

Это можно сделать эффективнее, просто выполнив ИК в 2D не на плоскости XY, а на вертикальной плоскости, проходящей из опорной точки манипулятора к целевой точке.

Поворот вокруг оси Y

Чтобы выполнить ИК в 3D, нам первым делом нужно вычислить , то есть угол, на который вращается весь манипулятор. Это дополнительная степень свободы, добавленная к шарниру бедра.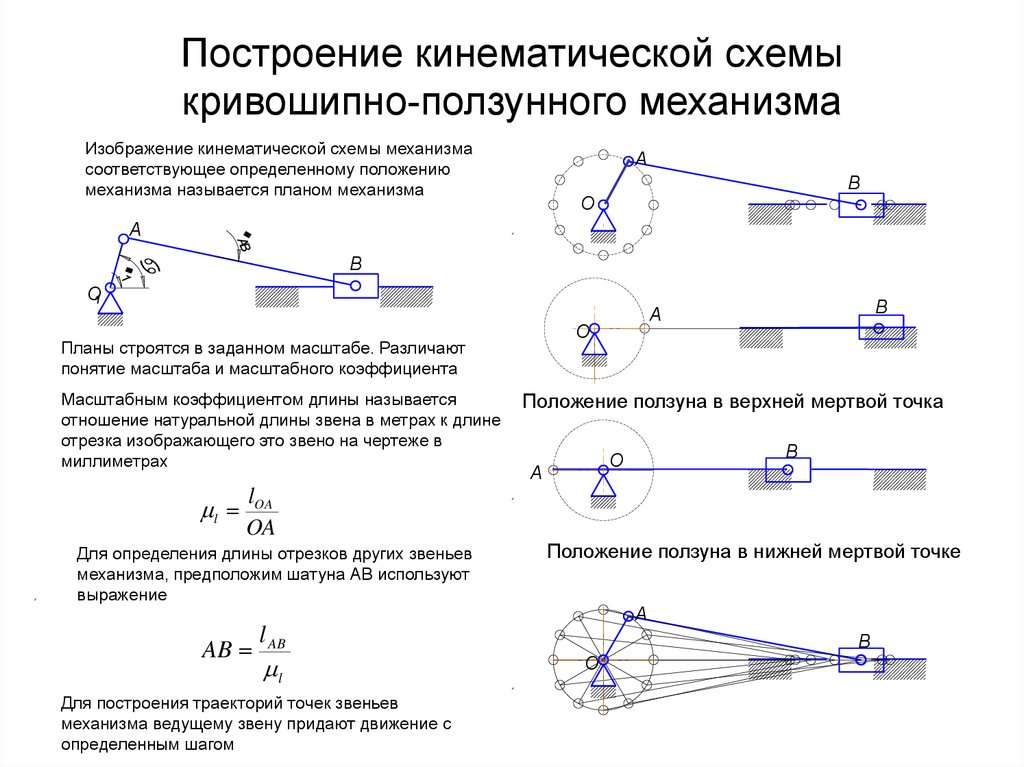

Удобнее всего найти его, предположив, что манипулятор уже достиг позиции (то есть уже находится в целевой позиции) и вычислив получившийся угол . Так как — это угол, на который переместилось бедро по оси Y, мы можем смотреть на манипулятор ровно сверху. При виде сверху на плоскость XZ (см. ниже) манипулятор выглядит как отрезок прямой. Так получилось, потому что за исключением бедра два остальных шарнира ограничены плоскостью.

Если мы рассмотрим отрезок как гипотенузу прямоугольного треугольника, то при помощи тригонометрии сможем вычислить угол :

(6)

Вывод уравнения

Вычисление угла между двумя точками — довольно частая задача для разработчиков игр и решить её можно тригонометрически.

Хитрость в данном случае заключается в том, чтобы добавить наклон линии (см. ниже), который является соотношением её подъёма () и пролёта (). Наклон прямой можно вычислить между двумя любыми точками и он везде даст одинаковый результат.

Наклон прямой имеет прямую связь с углом прямой :

(7)

Если вы изучали тригонометрию, то должны понять, что подъём на самом деле является , а пролёт — . А функция тангенса, по определению — это соотношение синуса и косинуса

.

Чтобы извлечь из (7), можно использовать функцию, обратную тангенсу, то есть арктангенс:

(8)

Всё это замечательно работает в теории, однако существуют проблемы со знаком и . На самом деле, наклон даёт одинаковый результат, когда и одновременно являются или отрицательными, или положительными. Однако с геометрической точки зрения это соответствует двум противоположным углам! Решение заключается в том, чтобы использовать не напрямую, а его «программного» близкого родственника atan2. В большинстве фреймворков существует реализация функции арктангенса, получающая два параметра, обычно называемые dy и dx.

Инверсная кинематика на плоскости WY

Строго говоря, знания более чем достаточно для решения ИК в 3D. На самом деле, мы можем реализовать алгоритм, описанный в предыдущем разделе: повернуть целевую точку на градусов по оси Y, выполнить ИК на плоскости XY, а затем повернув весь манипулятор на градусов.

Быстрее было бы выполнить ИК не на 2D-плоскости, а непосредственно на вертикальной плоскости, проходящей через шарнир бедра и целевую точку. Однако, кое-что мешает нам это сделать. Давайте ещё раз взглянем на схему со всеми используемыми углами:

Чтобы вычислить , то есть угол, контролирующий первый шарнир, нам нужно вычислить . Это угол между первым шарниром и целевой точкой. Если вспомнить уравнение (5), использованное для вычисления , то мы заметим серьёзную проблему: оно предполагает, что все точки находятся на плоскости XY:

В нашем 3D-сценарии манипулятор, к сожалению, будет вращаться на по оси Y. Однако новая схема остаётся почти такой же, если мы повернём вид вмести с манипулятором. Мы назовём эту новую систему координат WY, потому что ось X теперь заменена на W, которая была осью X, не повёрнутой на градусов по оси Y.

Мы не можем просто выполнить , как делали это с , потому что хотя и параллельны оси Y, и не параллельны оси X. Они параллельны оси W. Следовательно, лучшим способом вычисления будет получение расстояния от до . При этом теряется знак , однако, к счастью, это не вызовет проблем в наших вычислениях. Если манипулятор будет двигаться в противоположном направлении, то мы просто сменим знак в коде.

(9)

где — длина отрезка от до . Её можно легко вычислить функцией наподобие Vector3.Distance, или просто применить теорему Пифагора:

(10)

В показанном выше уравнении вклад Y из теоремы Пифагора сокращается, потому что точка имеет ту же компоненту Y, что и , поэтому их равна нулю.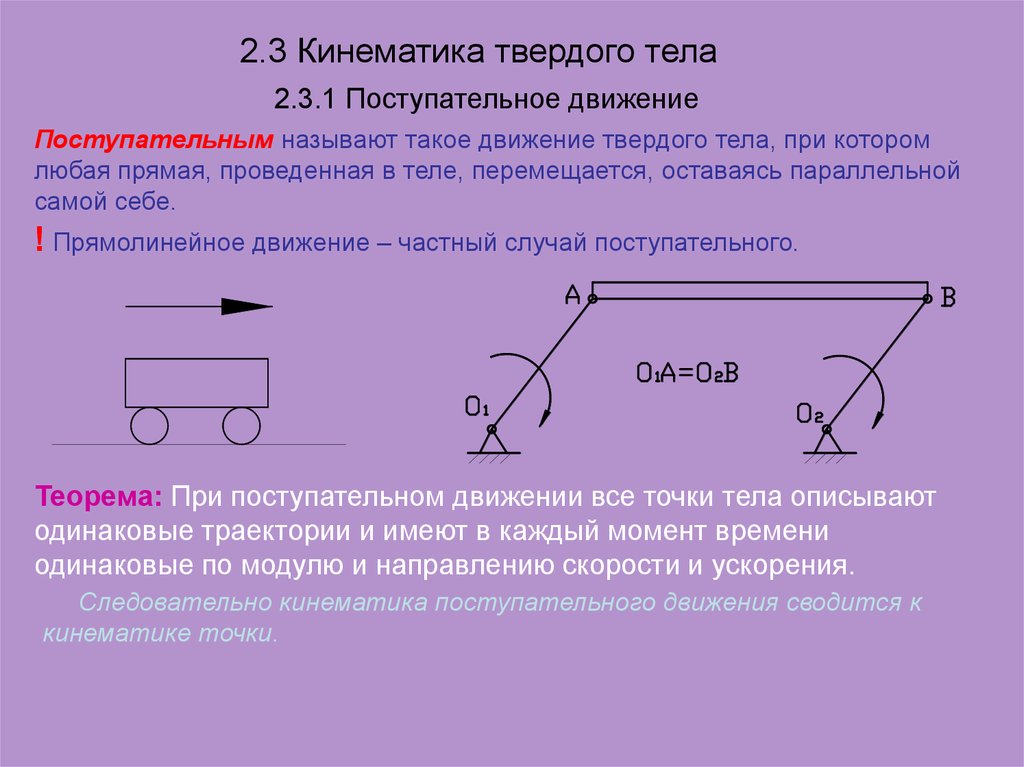

Теперь у нас есть всё для выполнения ИК в 3D для манипулятора робота с одним коленом и одним бедром:

(11)

(12)

(13)

Хотя уравнения выглядят пугающе, их легко реализовать и они позволяют максимально бысро выполнять ИК в 3D.

Что дальше

В следующем туториале этой серии я покажу, как использовать ИК для создания реалистичных многоногих существ. Да, долгожданный туториал по ИК паучьих ног наконец появится!

Скачивание пакета Unity

Скачать все использованные в этом туториале ассеты с полнофункциональным манипулятором для Unity можно, подписавшись на мой Patreon.

прямая и обратная задачи – RoboCraft

В робототехнике, есть две основные задачи кинематики:
прямая и обратная.

Рассмотрим эти задачи на стандартном примере манипулятора.

Прямая задача — это вычисление положения (X, Y, Z) рабочего органа манипулятора по его кинематической схеме и заданной ориентации (A1, A2… An) его звеньев (n — число степеней свободы манипулятора, A — углы поворота).

Обратная задача — это вычисление углов (A1, A2… An) по заданному положению (X, Y, Z) рабочего органа и опять же известной схеме его кинематики.

Т.о., решение прямой задачи говорит — где будет находиться рабочий орган манипулятора, при заданных углах его суставов, а обратная задача, наоборот, говорит: как нужно «вывернуться» манипулятору, чтобы его рабочий орган оказался в заданном положении.

Очевидно, что более распространённой и важной является именно обратная задача кинематики.
Но нужно иметь в виду, что эта задача редко может быть решена однозначно.
Дело в том, что хотя для углов (A1, A2, …, An) всегда существует ЕДИНСТВЕННОЕ положение (X, Y, Z) рабочего органа, но не факт, что для положения (X, Y, Z) отыщется такая же единственная комбинация углов (A1, A2, …, An).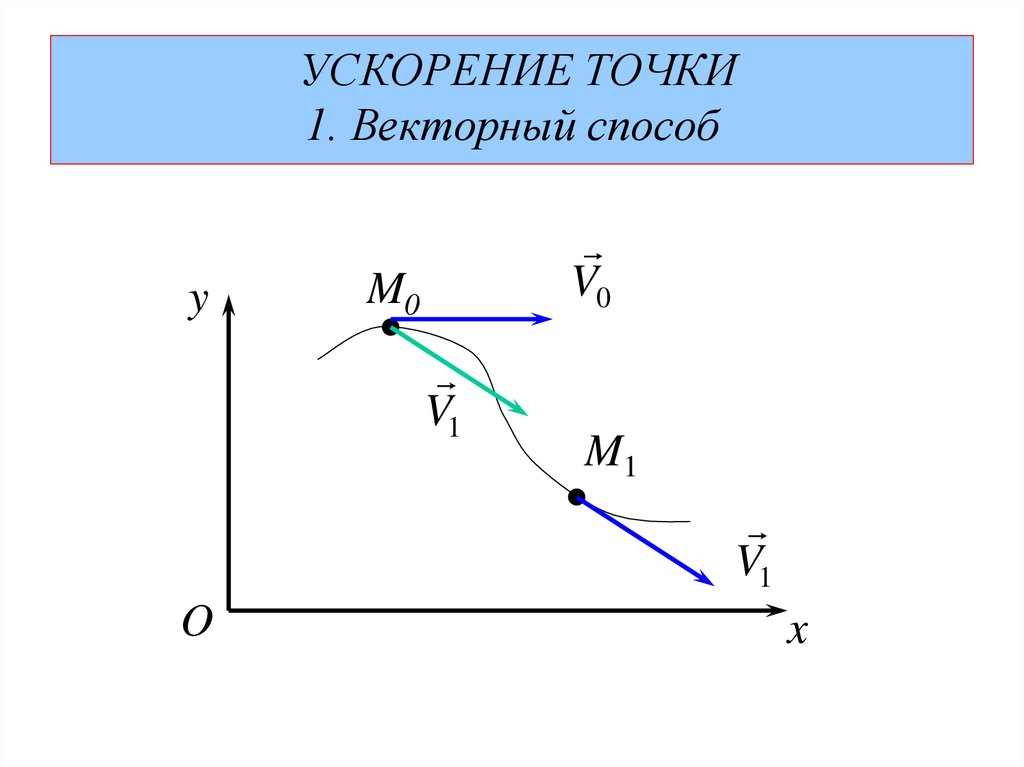
Скорее всего, достичь заданного положения (X, Y, Z) возможно и при другой комбинации углов (A1′, A2′, …, An’).
При решении обратной задачи аналитически, эта неоднозначность проявляется в явном виде (например, через квадратные корни).

Рассмотрим пример прямой задачи кинематики.

у нас есть манипулятор, способный работать только в одной плоскости и имеющий два сустава.
Первый сустав L1 закреплён на основании и повёрнут на угол Q1,
второй сустав L2, крепится к концу первого сустава и повёрнут относительно него на угол Q2.
Рабочий орган манипулятора находится на конце второго сустава.
Прямая задача кинематики состоит в нахождении координат рабочего органа (x, y) по заданным L1, L2, Q1, Q2.
L1 и L2 — это, соответственно, длины плеча и локтя манипулятора; определены конструкцией манипулятора.

Решение:
здесь, мы имеем две системы отсчёта — первая, связанная с точкой крепления плеча L1 — O, а вторая — с началом координат в точке крепления локтя — A. 2 / 2*L1*L2 )

Очевидно, что руку можно расположить и по-другому:

формулы для Q1 и Q2 не изменятся, но изменятся знаки углов:

Q1 = q1 + q2

а Q2 нужно брать с противоположным знаком.

Откуда берётся изменение знака? Из вычисления квадратного корня, которое всегда даёт ответ со знаком плюс-минус.

Ссылки
http://ru.wikipedia.org/wiki/Прямая_кинематика
http://ru.wikipedia.org/wiki/Инверсная_кинематика
http://ru.wikipedia.org/wiki/Принципиальная_кинематическая_схема
http://ru.wikipedia.org/wiki/Теорема_косинусов
http://ru.wikipedia.org/wiki/Тригонометрические_формулы
Robot Forward Kinematics

Книги
К. Фу, Р. Гонсалес, К. Ли «Робототехника»

Что такое инверсная кинематика? — MATLAB & Simulink

Кинематика — это изучение движения без учета причин движения, таких как силы и крутящие моменты. Обратная кинематика — это использование кинематических уравнений для определения движения робота для достижения желаемого положения. Например, для автоматизированного подбора контейнеров роботизированному манипулятору, используемому на производственной линии, требуется точное перемещение из исходного положения в желаемое положение между контейнерами и производственными машинами. Захватывающий конец манипулятора робота обозначается как рабочий орган. Конфигурация робота представляет собой список положений суставов, которые находятся в пределах положения модели робота и не нарушают никаких ограничений, которые есть у робота.

Учитывая желаемое положение рабочих органов робота, инверсная кинематика (IK) может определить подходящую конфигурацию сустава, при которой рабочие органы перемещаются в целевое положение.

 

Настройка положения суставов робота с использованием прямой или инверсной кинематики.

После расчета углов сочленения робота с использованием инверсной кинематики можно создать профиль движения с использованием матрицы Якоби для перемещения рабочего органа из исходного положения в целевое. Матрица Якоби помогает определить взаимосвязь между параметрами суставов робота и скоростями рабочих органов.

В отличие от прямой кинематики (FK), роботы с несколькими вращающимися соединениями обычно имеют несколько решений обратной кинематики, и в зависимости от цели были предложены различные методы. В общем, они подразделяются на два метода: один получают аналитически (т. е. аналитическое решение), а другой использует численный расчет.

Численные решения обратной кинематики

Для аппроксимации конфигурации робота, которая достигает заданных целей и ограничений для робота, можно использовать численные решения. Каждый угол сустава рассчитывается итеративно с использованием алгоритмов оптимизации, таких как методы на основе градиента.

Численные IK-решатели являются более общими, но требуют нескольких шагов для сходимости к решению нелинейности системы, в то время как аналитические IK-решатели лучше всего подходят для простых задач IK. Численный IK более универсален, поскольку кинематические ограничения робота могут быть указаны, а внешние ограничения, такие как ограничение прицеливания для руки камеры, указывающей на целевое местоположение, могут быть установлены для решателей IK. Определение того, какой решатель IK следует применить, в основном зависит от приложений роботов, таких как интерактивные приложения в реальном времени, и от нескольких критериев производительности, таких как плавность конечной позы и масштабируемость для резервных робототехнических систем.

Пример: планирование траектории достижения с несколькими кинематическими ограничениями

Вы можете использовать Robotics System Toolbox™ и Simscape Multibody™ для IK с помощью численного расчета. Связанные рабочие процессы включают:

• Создание модели робота с твердым телом в виде дерева
• Импорт определений роботов из параметров URDF или DH
• Построение многотельной модели на основе информации, определенной в CAD
• Вычисление геометрического якобиана
• Анализ обратной кинематики
• Разработка решателей инверсной кинематики, конфигураций и путевых точек
• Решение для конфигурации кинематики с несколькими ограничениями с использованием решателей обобщенной инверсной кинематики
• Анализ механизма параллельного звена
• Создание эквивалентного кода C/C++ и встраивание его в другое приложение

См. Robotics System Toolbox и Simscape Multibody для получения дополнительной информации.

Аналитические решения обратной кинематики

Каждый угол шарнира рассчитывается на основе положения рабочего органа на основе математической формулы. Путем символического определения параметров соединения и положения рабочего органа IK может найти все возможные решения углов соединения в аналитической форме в зависимости от длин звеньев, его исходного положения и ограничений вращения.

Аналитическая ИК в основном используется для роботов с низкими степенями свободы (DoF) из-за нелинейности уравнений кинематики и отсутствия масштабируемости для избыточных конфигураций роботов.

Пример: получение и применение инверсной кинематики к двухзвенному манипулятору робота

Двухзвенный манипулятор с углами шарнира θ1 и θ2 и параметрами шарнира для расчета решений инверсной кинематики.

Аналитические обратные кинематические решения углов соединения θ1 и θ2 при желаемом положении рабочего органа.

Robotics System Toolbox™ и Symbolic Math Toolbox™ можно использовать для аналитической IK.

С помощью этих продуктов вы можете:

• Генерировать аналитические IK-решатели для подмножеств роботов с 6 степенями свободы, определенных в MATLAB
• Напишите пользовательские решатели, определяя положение рабочего органа робота и параметры соединения символически как функции синуса и косинуса
• Решение уравнений обратной кинематики для углов соединения и создание профилей движения
• Преобразование производных выражений в MATLAB ^® функциональных блоков и создайте модель Simulink ^® или Simscape™ для имитации робота
.
• Создайте эквивалентный код C для интеграции с другими приложениями.

Обзор инверсной кинематики. Что такое инверсная кинематика? Что такое… | Луис Бермудес | Unity3DAnimation

Вы, наверное, слышали об инверсной кинематике. IK — популярный инструмент в Unity и компьютерной графике, но если вы впервые пытаетесь создать или использовать систему инверсной кинематики, вам могут понадобиться дополнительные сведения. Я объясню, что такое ИК, определю словарный запас и рассмотрю варианты использования.

Прежде чем мы углубимся в суть IK, нам нужно определить некоторые словари, связанные с IK. IK — это метод, который применяется к сочлененному телу. Что такое шарнирное тело?

Сочлененное тело

Сочлененное тело может представлять собой большинство анимированных тел, таких как люди и животные со скелетами. Проще говоря, сочлененное тело — это дерево связанных цепей. Связанные цепи состоят из суставов и звеньев, где звено представляет собой жесткий цилиндр. На рис. 1 показано сочлененное тело, представляющее собой гуманоида.

Рисунок 1: Сочлененное тело человека

Даже простая игрушка на фотографии на обложке выше представляет сочлененное тело. Не хватает только локтевых и коленных суставов.

Типы соединений

Что касается соединений, то они бывают двух типов. Соединение первого типа представляет собой вращающееся соединение . Он соединен со звеном, которое вращается вокруг него. На рис. 2 показано вращательное соединение.

Рисунок 2: Вращающееся соединение

Вращающееся соединение очень похоже на центральный штифт часов — с часовой стрелкой в ​​качестве звена.

Золотой штифт часов представляет собой вращающееся соединение.

Призматическое соединение представляет собой соединение, в котором соединенное звено перемещается из соединения, удлиняя/укорачивая звено. На рис. 3 показано призматическое соединение.

Рисунок 3: Призматический шарнир

Призматический шарнир действует так же, как удлинение/убирание выдвижной ручки на вашем багаже. Если присмотреться, выдвижная багажная ручка имеет 4 призматических шарнира. 2 призматических шарнира посередине ручки и еще 2 призматических шарнира по всей длине ручки в верхней части чемодана.

Четыре красные стрелки указывают на четыре призматических шарнира на выдвижной ручке багажа.

Если вас смущают призматические соединения, не волнуйтесь. Они не так часто используются в инверсной кинематике, и, как вы могли заметить, у людей нет призматических суставов — только вращательные суставы.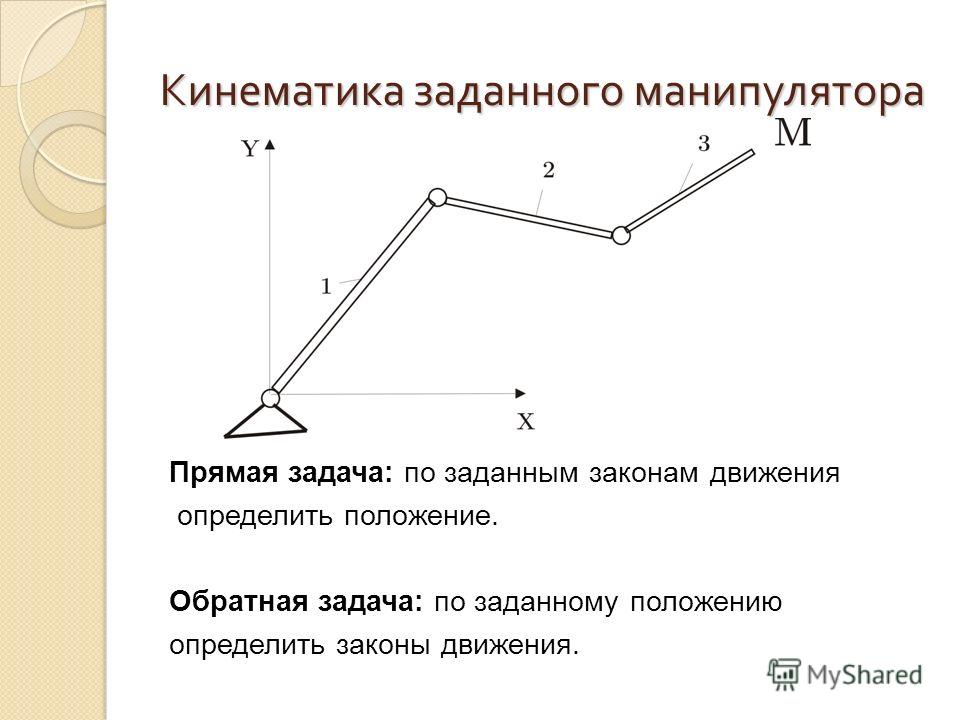

Иерархическая структура

Сочлененное тело имеет корневой шарнир . Корневой сустав является основой конструкции. Корневой сустав гуманоида обычно находится в центре бедра. Шарнирное тело образуется из дерева суставов и звеньев, начиная с корневого сустава. Новый сустав и ссылка подобны новой ветке на дереве. внутреннее звено/соединение — это звено/соединение, которое находится ближе к корневому соединению в древовидной иерархии сочлененного тела, поскольку оно относится к данному соединению/сочленению. Внешнее звено/шарнир — это звено/шарнир, который находится дальше от корневого шарнира в древовидной иерархии сочлененного тела. На рисунке 4 соединение A является корневым соединением, звено 1 — внутренним звеном соединения B, звено 2 — внешним звеном соединения B.

Концевой эффектор

Концевой эффектор — это позиция в крайнем внешнем положении самого внешнего звена. Это свободный конец цепи чередующихся суставов и звеньев. Конечный эффектор не является суставом. Концевой эффектор — это просто положение на конце сочлененного тела. Сочлененное тело может иметь несколько конечных эффекторов, как бинарное дерево может иметь несколько листьев.

Рисунок 4: Концевой эффектор представлен зеленым кругом.

Артикуляции и позы

Артикуляция — это вращение/перемещение сустава, которое перемещает связанное звено. Например, на рисунке 5 сустав А имеет угол сочленения 45°, сустав В имеет угол сочленения 15°, а сустав С имеет угол сочленения -60°. С другой стороны, поза представляет собой набор суставных сочленений, которые приводят к позиционированию сочлененного тела. Другими словами, поза представляет собой векторное значение, а не скалярное значение. Например, на рисунке 4 положение сочлененного тела составляет <45°, 15°, -60°>.

Рисунок 5: Сочлененное тело с A в качестве корневого соединения

Прежде чем мы сможем понять, что такое инверсная кинематика, нам нужно выяснить, что такое прямая кинематика. Функция/алгоритм прямой кинематики принимает позу в качестве входных данных и вычисляет положение концевого эффектора в качестве выходных данных. Прямая кинематика является обратной функцией обратной кинематики. С помощью прямой кинематики вам необходимо определить всю позу сочлененного тела, чтобы обеспечить функцию/алгоритм вводом позы. Это означает, что вам необходимо определить сочленение каждого сустава в сочлененном теле. Это может быть хорошо, если у вас мало суставов, но с большим количеством суставов это может быть утомительно.

Теперь представьте, что вы хотите, чтобы конечный эффектор вашего шарнирного тела достиг определенного целевого положения. Это означает, что вы знаете положение конечного эффектора, на которое хотите нацелиться, но не знаете, какое положение шарнирного тела должно быть, чтобы конечный эффектор достиг этого целевого положения. Вот где сияет инверсная кинематика!

Рисунок 6: Целевое положение представлено красным кругом. Целевое положение определяется как вход, а результирующая поза, необходимая для того, чтобы концевой эффектор достиг целевого положения, является выходом.

Обратная кинематика — это функция/алгоритм, обратная прямой кинематике. Функция/алгоритм обратной кинематики принимает целевое положение в качестве входных данных и вычисляет позу, необходимую для того, чтобы концевой эффектор достиг целевого положения — поза является выходом.

Как видите, вход и выход переключаются между FK и IK. С инверсной кинематикой вам не нужно определять всю позу сочлененного тела — она рассчитывается для вас алгоритмом IK. С IK вам нужно только определить позицию в качестве ввода.

Обратная кинематика выполняет всю сложную вычислительную работу по вычислению позы. На рис. 6 это хорошо показано. В сцене «До» есть сочлененное тело в какой-то известной позе. Он определяет целевое положение конечного эффектора, которого он пытается достичь. Как только алгоритм IK применяется к сочлененному телу, мы достигаем After Scene. After Scene показывает, что была рассчитана новая поза, так что конечный эффектор теперь находится в целевом положении.

На данный момент мы знаем, что IK применяется к сочлененному телу, мы знаем, из чего состоит сочлененное тело, и мы знаем разницу между IK и FK. На данный момент у нас есть хороший обзор IK, но давайте завершим его некоторыми хорошими примерами использования IK. Как мы видели, ИК можно использовать для того, чтобы гуманоидная рука тянулась к объекту/цели. IK также можно использовать для шагания ногой, так что мы говорим ступне, куда ступить, а IK выясняет, как настроить суставы ног. ИК обычно используется не как анимация (достижение объекта), а скорее как инструмент анимации. Таким образом, если вы реализуете цикл ходьбы, вы можете расположить некоторые ключевые кадры с помощью инструмента IK.

Рисунок 7: IK применяется с вращением стопы в качестве цели. Соединения L и R вращаются, чтобы соответствовать наклонной плоскости.

Еще один ключевой момент в отношении IK заключается в том, что ваша цель/задача не ограничивается только позицией — ваша цель может быть определена как ротация. Например, если ваши ноги должны вращаться из-за неровной поверхности, ваша цель вращения IK может быть определена на основе нормалей пола. См.