Уклон в процентах и промилле
Угол уклона — показатель наклона какой либо поверхности (дороги, крыши, пандуса, лестничного марша и пр.) относительно уровня горизонта.Угловые размеры указывают на чертежах в градусах, минутах и секундах с обозначением единицы измерения (ГОСТ 2.307-2011 «Единая система конструкторской документации (ЕСКД). Нанесение размеров и предельных отклонений«).
В соответствии с ГОСТ Р 21.1101-2013 «Система проектной документации для строительства (СПДС). Основные требования к проектной и рабочей документации», на планах направление уклона плоскостей указывают стрелкой, над которой при необходимости проставляют числовое значение уклона в процентах или в виде отношения единицы высоты плоскости к соответствующей горизонтальной проекции. Допускается числовое значение уклона указывать в промилле или в виде десятичной дроби с точностью до третьего знака.
острый угол которого должен быть направлен в сторону уклона (кроме крутизны откосов насыпей и выемок). Обозначение уклона наносят непосредственно над линией контура или на полке линии-выноски.
Также вместо знака угла, на чертежах встречается и буквенное обозначение уклона ( i ).
В процентах обычно обозначают углы уклонов крыш, пандусов, лестничных маршей и т.п.
В промилле обозначают углы уклонов плоскостных сооружений — спортивные игровые площадки, поля, беговые дорожки, а также линейные сооружения — автомобильные и железные дороги.
Процент ( % ) — одна сотая доля.
Промилле ( ‰ ) — одна тысячная доля.
Например: уклон при высоте 0,2 метра и протяженностью по горизонтали 4 метра
будет равен 5 % (читается как — пять сотых) или 50 ‰ (читается как — пятьдесят тысячных), это значение также будет соответствовать приблизительно — 3 о.
Чертеж 1
Часто спрашивают, что означает уклон, на пример 0,05 — это соотношение высоты к длине горизонтального участка (0,2 м / 4 м = 0,05 — см. чертеж 1), которое при необходимости можно перевести в проценты или промилле, смотря что требуется.
Для определение угла уклона в процентах (%) (см. чертеж 1) необходимо: 0,2 м / 4 м х 100 = 5 %.
Для определение угла уклона в промилле (‰) необходимо: 0,2 м / 4 м х 1000 = 50 ‰.
Ту же величину уклона можно обозначить и как соотношение высоты к длине горизонтального участка
Если требуется определить протяженность горизонтального участка, зная величину уклона в процентах и его высоту из чертежей, необходимо — 0,2 м / (5 % / 100) = 4 м.
Чтобы определить высоту уклона, зная величину уклона в процентах и протяженность участка из чертежей, необходимо — 5 % / 100 х 4 м = 0,2 м.
Аналогичным образом вычисляются размеры для угла уклона выраженного в промилле, только вместо деления на 100, выполняется деление на 1000.
Примечание: для того чтобы ввести на компьютере символ промилле (‰), необходимо включить NumLock, нажать клавишу Alt и удерживая ее набрать на цифровом блоке клавиатуры 0137, отпустить клавишу Alt после чего появится символ ‰.
Если требуется определить уклон с точностью до 1 градуса, нужно: 0,2 м / 4 м = 0,05. Полученное число — 0,05 необходимо найти в таблице tg (тангенсов) для углов. Приближенное значение в таблице — 0,0524, будет соответствовать углу 3 о (см.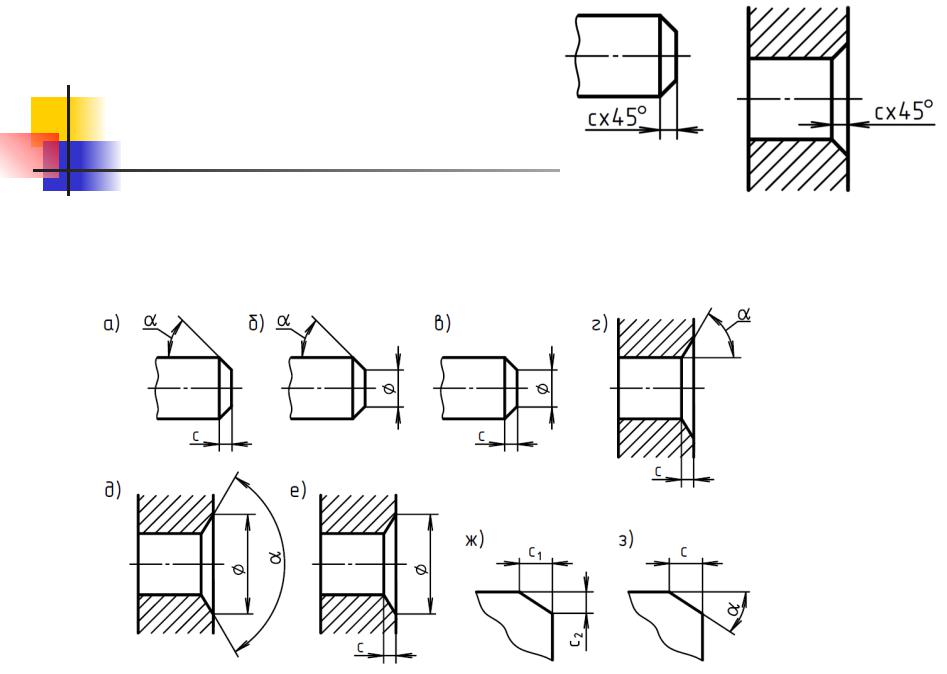 таблицу).
таблицу).
Полная таблица тангенсов для углов от 0о до 360о
Как правильно обозначать размеры на чертежах
Чертеж — это универсальный документ, в котором конструктор дает исчерпывающую информацию о конструкции изделия, которое он разработал. Любой специалист, взявший в руки этот документ, должен получить информацию об изделии полностью и без искажений, даже находясь за тысячи километров. Для этого правила построения технических документов формализованы и зафиксированы в государственных стандартах.
Правила нанесения размеров на чертежах ГОСТ 2.307-68 и ГОСТ 2.307-2011
Указанные на конструкторских документах размеры предназначены для точного указания габаритов изделия, а также его узлов. Нанесение размеров следует организовать так, чтобы, руководствуясь ими, возможно было сделать деталь без проведения дополнительных расчетов. В то же время недопустимо перегружать документ избыточными сведениями, затрудняющими его понимание. Недопустимо также дублирование нанесения размеров на чертежах.
Как предписывается государственным стандартом, численные величины в конструкторских документах указывают в мм, единицы при этом опускают. Величины углов приводят в градусах, минутах, секундах с обязательным указание единиц.
Правила нанесения размеров на чертеж
Размерные линии изображают параллельно оси, на расстоянии не менее 10 мм от контура изделия, выносные изображают перпендикулярно размерным.
Нанесение размеров
Указанное значение обязано точно соответствовать истинной величине объекта вне зависимости от выбранного масштаба.
Схема нанесения размеров
Размерные линии следует размещать снаружи контура детали. На элементах контура нанесение значений запрещено. Большие величины наносят дальше, меньшие — ближе. Это делают для того, чтобы избежать пересечений размерные и выносные линии. На концах размерной линии изображают стрелки, упирающиеся в выносные.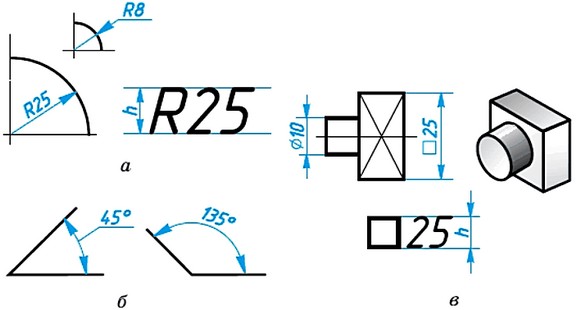 Численные значения размещают над линией возле ее середины. Расстояние между размерными линиями — от 7 миллиметров.
Численные значения размещают над линией возле ее середины. Расстояние между размерными линиями — от 7 миллиметров.
Размерные линии положено размещать без пресечений с другими элементами чертежа. Осевые, центровые и штриховочные линии при пересечении с размерной следует прервать.
Нанесение размеров конкретного элемента конструкции рекомендуется проводить, группируя их рядом с ним.
При изображении дуги на чертеже показывают ее радиус (цифры предваряются литерой R), для окружности — ее диаметр (обозначается знаком >)
Если деталь имеет сферическую форму, а из двумерного изображения это не очевидно, то обозначение сферы на чертеже наносят так «Сфера R50»
При нанесении фаски под углом 45° используют единое обозначение величины и угла, например 5×45 ° . Для фасок с другими углами предусмотрено отдельное указание линейного размера и угла
Сфера 50 на чертеже
Нанесение предельных отклонений размеров
Указание значений предельных отклонений имеет большое значение с точки зрения технологии изготовления. Исходя из этих данных, технологи будут выбирать конкретные способы механической и термической обработки, конкретный вид станочного оборудования, инструмент и оснастку.
Значения отклонений наносят сразу после величин. Если высокая точность изготовления не требуется, то нанесение этих требований в каждом месте чертежа необязательно, достаточно сформулировать их в общем виде в области технических требований. Данная формулировке должна содержать как значения, так и знак отклонений.
Если в общей записи не указываются конкретные значения допусков, допустимо использовать указание квалитета, или класса точности. Обозначается он литерами ±IT/2 , за которыми следует номер квалитета.
Указание предельных отклонений для валов и отверстий круглой формы сопровождается знаком ∅.
Отклонения угловых величин наносят только цифрами.
Если на различных участках одной и той же поверхности требуется выдержать различные отклонения, границу между ними указывают тонкой сплошной чертой, а размеры на чертежах вкупе с отклонением указывают для каждого участка по отдельности.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Правильное нанесение размеров на чертеже имеет огромное значение. Чертеж без размеров дает лишь представление о форме изображенной на ней детали. Он не имеет практического значения, так как по нему не может быть изготовлена данная деталь. Правильно проставленные размеры на чертеже обеспечивают соблюдение наиболее рациональной технологии и точности изготовления.
Нанесение размеров регламентировавно ГОСТ 2.307-68 для всех отраслей промышленности. Различают размеры рабочие (исполнительные), каждый из которых используют при изготовлении изделия и его приемке (контроле), и справочные, указываемые только для большего удобства пользования чертежом. Справочные размеры отмечают знаком «*», а в технических требованиях, располагаемых над основной надписью, записывают: «* Размер для справок». Не допускается повторять размеры одного и того же элемента на разных изображениях. Линейные размеры на чертежах указывают в миллиметрах, без обозначения единицы измерения, угловые – в градусах, минутах и секундах, например: 4°; 10°30`24“. Размерные числа наносят над размерной линией, возможно ближе к середине; Высота размерного числа равна 5 мм и отстоит от размерной линии на расстояние 1 мм; Размерные числа не допускается разделять или пересекать линиями чертежа. В месте нанесения размерного числа осевые, центровые линии и линии штриховки прерывают; Размеры, относящиеся к одному и тому же элементу (пазу, выступу, отверстию) рекомендуется группировать в одном месте. Располагая на том изображении, на котором диаметрическая форма данного элемента показана наиболее наглядно; Размеры двух симметрично расположенных элементов изделия наносят один раз без указания их количества, группируя в одном месте все размеры; При нанесении радиального размера перед размерным числом наносят букву R; При нанесении диаметрального размера перед размерным числом указывают знак диаметра Ǿ; При проведении нескольких радиусов из одного центра размерную линию не располагают на одной прямой.
Нанесение размеров заключается в: – построении размерных линий со стрелками на концах и выносных линий к ним; – написании размерного числа над размерной линий.
Размерные линии проводятся между линиями видимого контура, между выносными линиями, а также между осевыми и центровыми. Размерные линии предпочтительно наносить вне контура изображения. Выносные линии перпендикулярны размерной и выступают за нее не более на 1 – 5 мм. Выносные линии для угловых размеров проводятся радиально, а для линейного размера дуги – параллельно одна другой. При проведении нескольких параллельных или концентричных размерных линий размерные числа над ними располагают в шахматном порядке. Для нанесения длины дуги окружности размерную линию следует проводить концентрично дуге. Знак дуги должен быть расположен над размерным числом. Для обозначения сферы перед размерным числом радиуса или диаметра следует добалять слово Сфера, например Сфера R10. Допускается написание на выноске R10/Сфера.
Нанесение размеров предполагает также выполнение множества других требований:
| Условия нанесения размеров | Условия нанесения размеров | ||
| Величина стрелок размерных линий определяется соответственно толщине линий видимого контура | Размерные линии наносятся тонкими сплошными линиями от одной выносной линии до другой, если недостаточно места для стрелок они наносятся с обратной стороны выносной линии | ||
| При недостатке места для стрелок на размерных линиях, расположенных цепочкой, стрелки можно заменить засечками, наносимыми под углом 45° к размерным линиям, или точками | Расстояние между размерной линией и линей контура не менее 10 мм. Выносные линии перпендикулярны размерной и выступают за нее не более 2 мм. | ||
Размеры пишутся вдоль размерной линии напротив ее середины. Написание линейных размеров при различных наклонах размерной линии показаны на рис. Указывать размеры в 30° зоне допускается только с применением линии выноски. Указывать размеры в 30° зоне допускается только с применением линии выноски. | При нанесении угловых размеров имеется два сектора 40° и 30° (выделеные красным цветом) в которых наносить размерные числа вдоль размерной линии не рекомендуется, в этом случае допускается применение линии выноски | ||
| Нанесение угловых размеров. При указании размера угла: – размерную линию следует проводить радиусом из вершины угла; – размерное число наносить над размерной линией параллельно ей и возможно ближе к ее середине. | Нанесение угловых размеров. Допускается наносить размерные числа в разрыве размерной линии. При недостатке места для простановки размерного числа оно наносится на выноске | ||
| Размеры следует равномерно распределять по изображению и выносить их за его пределы. Размерные линии и выносные не должны пересекаться между собой | При указании размеров симметричной поверхности допускается размерные линии наносить с обрывом с одной стороны | ||
| Размеры дуг окружностей, равных или менее 180°, указывают размерной линией с одной стрелкой и прописной буквой R перед размерным числом | Размеры призматических поверхностей с равными сторонами (квадрат), параллельными оси предмета, наносятся как линейные размеры, но перед размерным числом ставится квадрат | ||
| Проведение выносных линий не под прямым углом к размерной допускается как исключение. При проведении нескольких параллельных размерных линий размерные числа над ними располагают в шахматном порядке. Расстояние между соседними размерными линиями не менее 7 мм | При проведении нескольких концентричных размерных линий размерные числа над ними располагают в шахматном порядке. Расстояние между соседними размерными линиями не менее 7 мм. |
Нанесение размеров для линий и поверхностей имеющих уклон
заключается в: – построении размерных линий со стрелками на концах и выносных линий к ним где пишется: – слово Уклон и его величина; – знак уклона и его величина.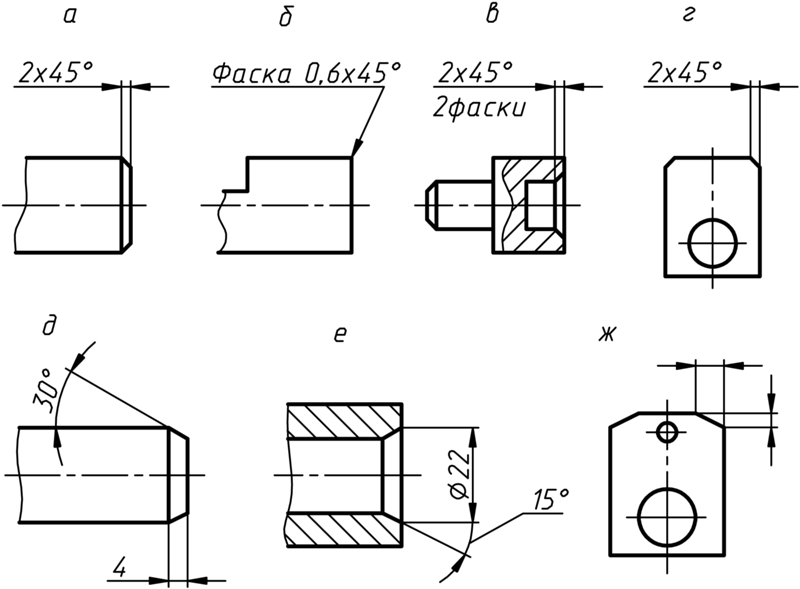
Нанесение размеров для конических поверхностей
заключается на чертеже: – нанесении на нее надписи Конусность с указанием ее величины; – указывающей на нее стрелкой с полкой где пишется: – Конусность с указанием ее величины; – знак конусности и ее величина.
Нанесение размеров фасок
Размеры фасок под углом 45° указываются в виде произведения величины катета в треугольнике,образованном фаской на ее угол. Вариант нанесения размера фаски выбирается в зависимости от наличия свободного места на чертеже для простановки размеров.
Для фасок с углом отличным от 45°, нанесение размеров осуществляется по общим правилам – двумя линейными размерами или одним линейным и одним угловым.
Если на чертеже изделия имеется несколько фасок одинакового размера, то они обозначаются надписью по типу – 2 фаски 2×45°, 3 фаски 2×45° или 2×45°/2 фаски
Стандарт (ГОСТ 2.307-68) устанавливает правила нанесения размеров на чертежах.
Линейные размеры на чертежах проставляются в миллиметрах без обозначения единиц измерения (мм). При других единицах измерения (сантиметрах, метрах) размерные числа записываются с обозначением единиц измерения (см, mi). Угловые размеры указывают в градусах, минутах, секундах с обозначением единиц измерения. Общее количество размеров на чертежах должно быть минимальным, но достаточным для изготовления и контроля изделия.
Существуют строго определенные правила нанесения размеров. При нанесении размера прямолинейного отрезка размерную линию проводят параллельно этому отрезку, а выносные линии — перпендикулярно размерным (рис. 40, б). Выносные линии выходят за размерные на 1-3 мм. Расстояние от размерной линии до контура изображения должно быть не менее 10 мм, а расстояние между двумя близлежащими размерными линиями — не менее 7 мм (рис. 40, б).
На концах размерных линий наносят стрелки. Форма и размеры стрелки показаны на рис. 40, а. Величина стрелок должна быть одинаковой на всем чертеже. Стрелки при недостатке места могут заменяться засечками или точками (рис. 41, б, в). Допускается проставлять размеры так, как показано на рис. 41, г.
40, а. Величина стрелок должна быть одинаковой на всем чертеже. Стрелки при недостатке места могут заменяться засечками или точками (рис. 41, б, в). Допускается проставлять размеры так, как показано на рис. 41, г.
Размерные числа наносят над размерной линией ближе к середине (рис. 42).
При нанесении нескольких параллельных или концентрических размерных линий размерные числа над ними располагают в шахматном порядке (рис. 43).
На чертежах необходимо избегать пересечения размерных и выносных линий. Если для нанесения размерного числа недостаточно места над размерной линией, то размеры проставляются так, как показано на рис. 44.
В местах нанесения размерного числа осевые, центровые линии и линии штриховки прерывают (рис. 45, а, б).
При нанесении размеров дуг перед размерным числом помещают знак радиуса — R. Высота знака радиуса и размерного числа должна быть одинаковой (рис. 46, а). При проведении нескольких радиусов из одного центра размерные линии любых двух радиусов не располагают на одной прямой (рис. 46, б). При большой величине радиуса центр разрешается приближать к дуге. В таких случаях размерную линию показывают с изломом (рис. 46, в).
При нанесении размеров окружностей перед размерным числом ставят знак диаметра — 0 (рис. 47). При недостатке места на чертеже размеры диаметра проставляют так, как показано на рис. 47, б.
Размеры нескольких одинаковых элементов изделия наносят один раз с указанием их количества на полке-выноске, рис. 48.
Размеры квадрата или квадратного отверстия наносятся, как показано на рис. 49.
Толщина плоской детали обозначается буквой S с последующим указанием размерного числа (рис. 50).
Длина изделия обозначается малой буквой латинского алфавита — I (рис. 51).
Нанесение размеров фаски — скошенной кромки стержня, бруска, отверстия — осуществляется либо простановкой двух линейных размеров (рис. 52, б), либо линейным и угловым размерами (рис. 52, в, г).
52, в, г).
Если на чертеже встречается несколько одинаковых фасок, то размер наносят один раз так, как показано на рис. 52, в. Эта надпись означает, что снято две фаски размером 2 мм под углом 45°.
На чертежах необходимо проставлять габаритные размеры.
Габаритными размерами называют размеры, определяющие предельные величины внешних очертаний изделий. К габаритным размерам относятся размеры длины, ширины, высоты изделия.
Габаритные размеры всегда больше других, поэтому их на чертеже располагают дальше от изображения, чем остальные.
На рис. 53 (валик) — габаритными являются размеры 75 мм и 40 мм.
На рис. 53 (полуцилиндр) — к габаритным относятся размеры 80 мм, 50 мм.
На чертежах иногда наносят справочные размеры. Размеры, нанесенные на чертеже, но не подвергающиеся контролю, называют справочными. На чертеже они отмечаются знаком * (рис. 54). На месте расположения технических требований (над основной надписью) делают запись: * — размер для справок.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9517 – | 7534 – или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Как правильно определять углы — Инженер ПТО
Измерить угол – значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.
Обычно за единицу измерения углов принимают градус. Градус – это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).
Измерение углов транспортиром
Для измерения углов используют специальный прибор – транспортир:
У транспортира две шкалы – внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.
Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:
Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов и пишут: ∠BOC = 60°, ∠MON = 120°.
Для более точного измерения углов используют доли градуса: минуты и секунды. Минута – это угол, равный части градуса. Секунда – это угол, равный части минуты. Минуты обозначают знаком ‘, a секунды – знаком ». Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:
Свойства измерения углов
Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.
Рассмотрим угол AOB:
Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.
Развёрнутый угол равен 180°.
Любой угол имеет определённую величину, большую нуля.
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками.
Калькулятор расчета диагонали прямого угла
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!
Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!
Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла.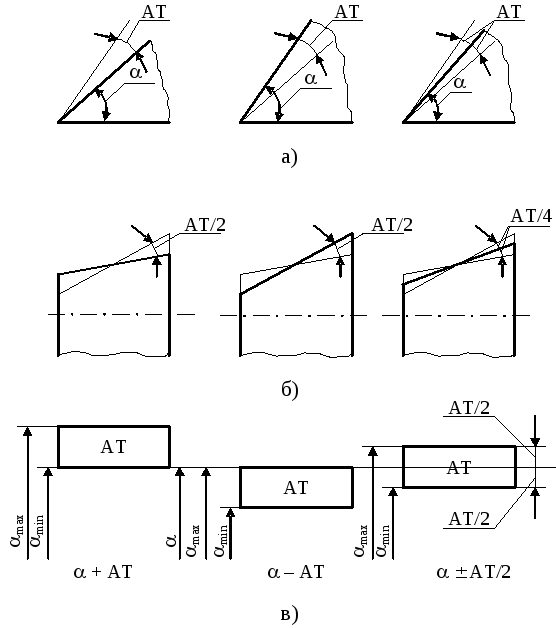 Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.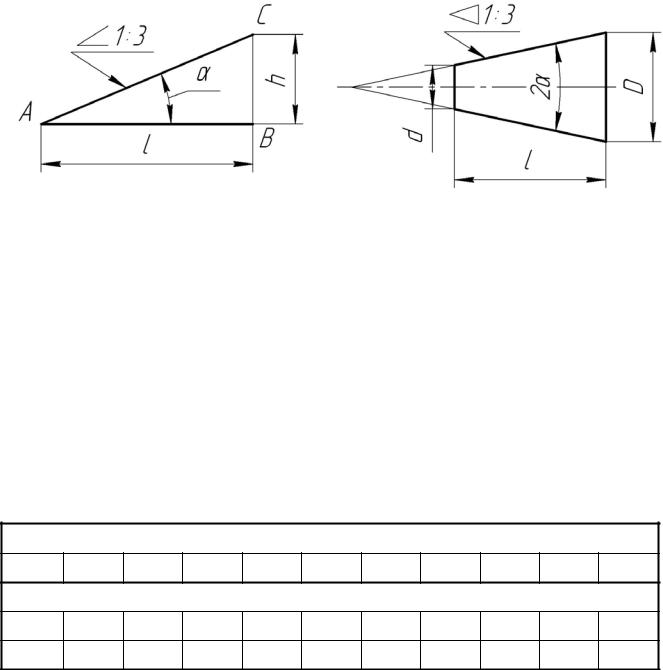
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Минутой называют одну шестидесятую часть градуса.
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « ‘ », а секунды « » ». Имеет место обозначение:
1 ° = 60 ‘ = 3600 » , 1 ‘ = ( 1 60 ) ° , 1 ‘ = 60 » , 1 » = ( 1 60 ) ‘ = ( 1 3600 ) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 ‘ 59 » .
Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17 ° 3 ‘ 59 » . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».
В геометрии используется мера угла из интервала ( 0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале ( 0 , 90 ) , а тупой – ( 90 , 180 ) . Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С , С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения.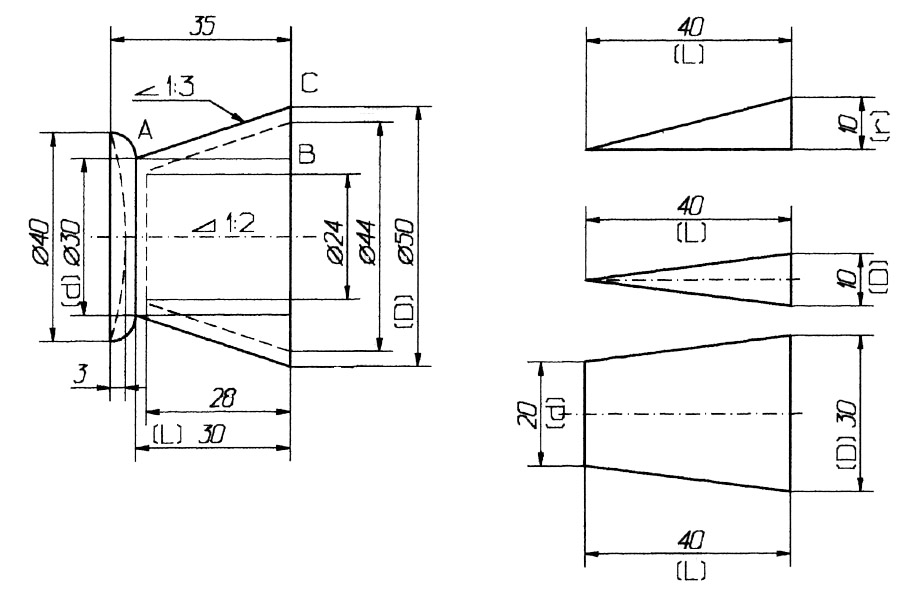 Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В . По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А .
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям.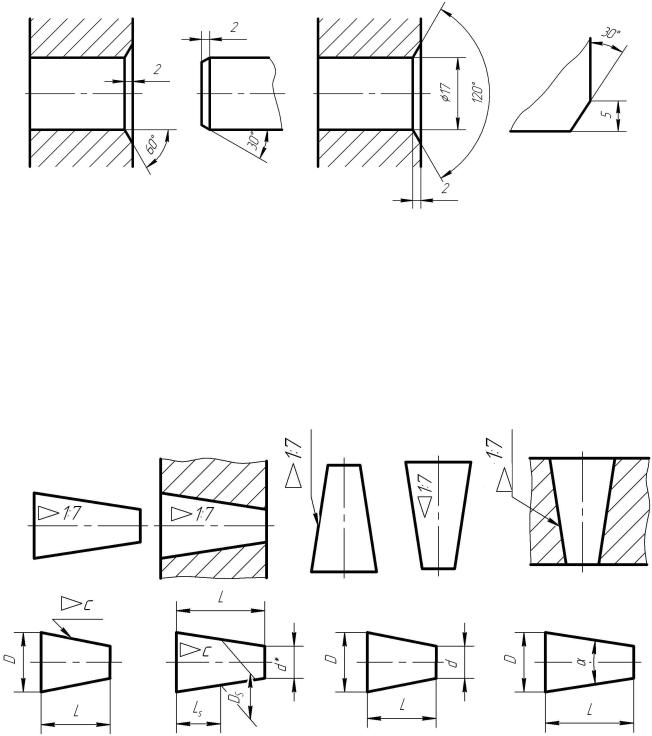 При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Правила обозначения шероховатости поверхностей на чертежах :: ТОЧМЕХ
Правила обозначения шероховатости поверхностей устанавливает ГОСТ 2.309-73.
Параметры и другие показатели шероховатости устанавливает ГОСТ 2789-73.
Правила нанесения обозначений шероховатости поверхностей на чертежах
Обозначения шероховатости поверхностей на изображении изделия располагают на линиях контура, выносных линиях (по возможности ближе к размерной линии) или на полках линий-выносок.
Допускается при недостатке места располагать обозначения шероховатости на размерных линиях или на их продолжении, а так же разрывать выносную линию.
На линии невидимого контура допускается наносить обозначение шероховатости только в случаях, когда от этой линии нанесен размер.
Обозначение шероховатости поверхности, в которых знак имеет полку располагают с учетом его поворота относительно основной надписи чертежа.
Обозначение шероховатости поверхности, в которых знак не имеет полки располагают учетом его поворота относительно основной надписи чертежа, но по иным правилам.
При изображении изделия с разрывом обозначение шероховатости наносят только на одной части изображения, по возможности ближе к месту указания размеров.
При указании одинаковой шероховатости для всех поверхностей изделия обозначение шероховатости помещают в правом верхнем углу чертежа и на изображении не наносят. Размеры и толщина линий знака вынесенного в угол чертежа, должны быть примерно в 1,5 раза больше чем на изображении.
Обозначение шероховатости, одинаковой для части поверхностей, может быть помещено в правом верхнем углу чертежа только вместе со знаком, взятым в скобки, размеры которого равны размерам знаков на чертеже.
Обозначение шероховатости поверхностей повторяющихся элементов изделия (отверстий, пазов, зубьев и т.п.), количество которых указано на чертеже, а также обозначение шероховатости одной и той же поверхности наносят один раз, независимо от числа изображений.
Обозначение шероховатости симметрично расположенных элементов симметричных изделий наносят один раз.
Если шероховатость одной и той же поверхности различна на отдельных участках, то эти участки разграничивают сплошной тонкой линией с нанесением соответствующих размеров и обозначений шероховатости. Через заштрихованную зону линию границы между участками не проводят.
Обозначение шероховатости рабочих поверхностей зубьев зубчатых колес, шлицев и т.п., если на чертеже не приведен их профиль, условно наносят на линии делительной поверхности, а для глобоидных червяков и сопряженных с ними колес — на линии расчетной окружности.
Обозначение шероховатости поверхности профиля резьбы наносят по общим правилам при изображении профиля, или условно на выносной линии для указания размера резьбы, на размерной линии или на ее продолжении.
Если шероховатость поверхностей, образующих контур, должна быть одинаковой, обозначение шероховатости наносят один раз с дополнительным значком (кругом).
В обозначении одинаковой шероховатости поверхностей плавно переходящих одна в другую, дополнительный знак не приводят.
Обозначение одинаковой шероховатости поверхности сложной конфигурации допускается приводить в технических требованиях чертежа со ссылкой на буквенное обозначение поверхности, нанесенное на полке линии-выноски проведенной от утолщенной штрихпунктирной линии, которая обозначает соответствующую поверхность.
Другие статьи по сходной тематике
Как определить величину угла в градусах в документе photoshop
Каждый наверняка знает, что в приложениях ПК для вызова каждой функции есть свой определенный путь. И вовсе не нужно нервно перебирать все пункты меню в поисках нужного инструмента.
И вовсе не нужно нервно перебирать все пункты меню в поисках нужного инструмента.
Нужно лишь соблюдать заложенную в программе последовательность действий или нажать нужную комбинацию клавиш. Но зачастую пользователи забывают путь к открытию той или иной функции в программе.
А возможно, даже и не знают его вовсе.
В программе Photoshop принцип действий заключен в визуализации. Для того чтобы вызвать ту или иную функцию, нужно перейти в раздел меню, отвечающий за эту область. Однако порой случается ситуация, что поиск не приносит результатов и пользователь начинает нервничать. Если помощи ждать неоткуда, нижеизложенный материал вам непременно поможет.
В этой статье подробно рассказано о том, как вызвать инструмент «Линейка» в Фотошопе, а также как им правильно пользоваться.
Как включить линейку
Инструмент «Линейки» в англоязычной версии Фотошопа будет звучать как Rulers. Найти этот пункт можно в соответствующем разделе основного меню — «Просмотр».
Либо же можно вызвать линейки сочетанием клавиш CTRL + R. Убрать линейку можно той же комбинацией кнопок.
Помимо умения вызывать или убирать этот инструмент, пользователю необходимо знать еще кое-что. В линейке Фотошопа имеется возможность смены шкалы измерения.
При включении линейки через меню “Просмотр”, по умолчанию откроется стандартная линейка, со шкалой измерения в сантиметрах. Однако есть и другие виды линеек: пункты, дюймы, пиксели и другие. Для смены единиц измерения кликните по линейке правой кнопкой мыши. И далее в появившемся списке выберите нужный вам вариант.
Линейка измерительная, с транспортиром
В основном блоке инструментов программы можно найти всем знакомый инструмент «Пипетка», наверняка каждый без труда его найдет. А в выпадающем меню, при наведении на “Пипетку”, прямо под «Пипетками», располагается нужная нам кнопка для вызова линейки.
В фотошопе линейка применяется для точного вычисления местоположения нужной точки, откуда и производится измерение.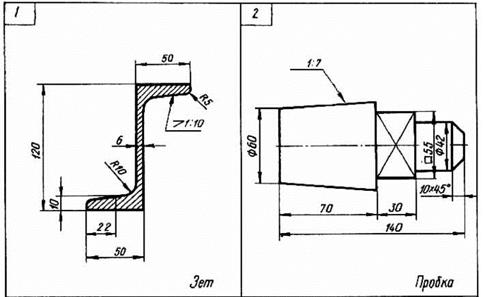 После чего измеряется расстояние от этой точки до чего-либо. Может потребоваться измерить длину отрезка, ширину или высоту элемента, углы.
После чего измеряется расстояние от этой точки до чего-либо. Может потребоваться измерить длину отрезка, ширину или высоту элемента, углы.
Подведите курсор мыши к точке начала измерения, и потяните по направлению к конечной точке.
Эта манипуляция также вызовет инструмент «Линейки», а данные по измерению можно посмотреть на верхней панели программы.
Щелчком мыши остановите формирование линейки и перейдите в режим измерения.
Крестики на концах полученной линии позволяют скорректировать направление линейки.
Наверху, в параметрах инструмента буквы X и Y отвечают за координаты начальной точки измерения. Символы Ш и В — тут все понятно (ширина и высота). У (не путайте с игреком) — градус угла. L1 – обозначает отрезок между заданными точками.
Для того чтобы вызвать функцию транспортира требуется проделать следующие действия. Зажмите на клавиатуре кнопку ALT и поместите курсор мыши к начальной точке линейки (где крестик). Транспортир позволяет провести угол относительно положения линейки. Второй луч на панели сверху имеет обозначение L2, а угол между L1 и L2 обозначается буквой Y.
Данные в верхнем меню выглядят так:
Также в верхнем меню вы можете найти подсказку “По шкале измерений”. Нужно поставить галочку и это позволит вычислить данные инструмента “Линейка” с помощью шкалы измерений.
Как по линейке выровнять слой
Порой требуется выровнять картинку, для этой задачи применяется линейка. Вызовите инструмент «Линейка» любым удобным способом. После чего в настройках укажите горизонтальный тип выравнивания. Затем потребуется найти и нажать пункт «Выровнять слой».
Выравнивание будет выполнено путем обрезки изображения по размерам указанной рамки.
Либо же можно при этом зажать клавишу ALT. Тогда изображение и все его элементы не изменят своего изначального положения.
Если вы желаете потренироваться и поэкспериментировать с линейкой, то стоит учесть одну вещь. С линейкой невозможно работать на пустом холсте. Необходимо открыть какую-либо картинку, или создать новый документ.
С линейкой невозможно работать на пустом холсте. Необходимо открыть какую-либо картинку, или создать новый документ.
С каждой последующей версией Фотошопа в программу добавляются новые функции. Однако же алгоритм вызова линейки не меняется.
Источник: https://MyPhotoshop.ru/lineyka-guide/
Геометрическая фигура угол: определение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной – ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Определение 6
Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение:
1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» .
Определение 11
Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600.
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны.
Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными.
В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Источник: https://Zaochnik.com/spravochnik/matematika/vektory/geometricheskaja-figura-ugol/
Как в фотошопе повернуть текст на определенный угол? Различные способы
Снова доброго всем времени ! Сегодня продолжим изучать фотошоп, и темой будет редактирование текста. Да-да, именно текста.
Не удивляйтесь, в Photoshop можно не только заниматься рисунками и фотографиями, но и применять к ним текст. Многие наверняка видели в интернете смешные картинки-демотиваторы.
В них как правило всегда есть какой-либо текст, с помощью которого можно очень ёмко и остроумно выражать мысли или эмоции.
Фотошоп — это не текстовый редактор. И конечно, редактировать так, как это делается в специализированном редакторе типа «Word», не получится (да это и ни к чему), но совершить нужные манипуляции с текстом, вроде поворотов, отражений, закручиваний и прочих вполне можно. Photoshop – в первую очередь редактор графический, а потому и изменения текста будут в нем исключительно графические.
Поворачиваем текст под углом 90 градусов
Начнем с простого примера, а именно с поворота текста под определенным углом. В частности, под углом в 90 градусов. Прежде чем начать это делать, необходимо создать новый слой.
Можно, конечно писать сразу на слое-картинке, но лучше все-таки, делать это на новом слое. В приведенных картинках-примерах я использую только слой с текстом. Нижний слой с названием «Фон» — это та самая картинка.
Итак, создаем слой и пишем на нем то что необходимо.
Фон у нового слоя не сплошной, а в квадратиках. Все нормально, это так отображается прозрачность слоя. Если вы включите фоновый слой, то эти квадратики исчезнут. Что бы написать текст, выбираем на панели инструментов иконку с буквой Т – это и есть «Текст», кликаем по слою и пишем.
Чтобы выбрать цвет текста, жмем перед тем как написать на той же панели инструментов на большой квадрат в самом низу – выбор основного цвета и в открывшемся окне выбираем нужный. Изменить размер шрифта можно на главной панели, где рядом с изображением буквы «Т» показана строка с выпадающем меню, в которой выбирается размер шрифта в пунктах.
Написали текст, нажимаем на стрелку, которая первая на панели инструментов. Тем самым мы закрыли редактор написания текста. Если эту стрелку подвести к тексту и зажать левую кнопку мыши, то текст можно перемещать в любом направлении.
Однако, нам его надо повернуть. Заходим в верхнее меню «Редактирование» и выбираем там «Свободное трансформирование». Вокруг текста появится рамка с квадратиками по углам и по середине.
Если подвести стрелку мыши к одному из углов текста, то увидим, что она приняла форму изогнутой стрелки. Зажав левую кнопку мыши можно вращать текст как угодно.
При этом, на главной панели имеются значки, отображающие поворот и перемещение текста. Поворот показан символом угла, рядом отображаются цифры, показывающие на сколько градусов повернулся текст.
Чтобы точно повернуть текст на заданное количество градусов, (в нашем случае 90), достаточно в этом окне ввести необходимую цифру. В результате текст повернется на столько градусов, на сколько задали. Мы подобные приемы уже изучали в одной из статей «Как повернуть картинку в фотошоп«. Как видите и с текстом мы делаем такие же однотипные операции.
Все просто. Одно но, текст повернулся так, что читается он не совсем хорошо. О том как сделать текст развернутым по вертикали и читабельным, будет рассказано дальше.
Как в Photoshop повернуть текст по кругу
Несколько более сложная операция – написание текста по кругу. Сделать это можно двумя способами. Первый, более простой, при помощи деформации. И второй, при помощи контуров. Начнем с простого. Написали текст. Теперь в главном меню находим букву «Т» над дугой. При этом должен быть активирован инструмент «Текст».
Буква «Т» над дугой это и есть кнопка, вызывающая окно деформации текста.
Кстати, может получится такая «фишка», вы нажали на кнопку «Деформации текста», а у вас вместо ожидаемого окна вылезла надпись, что «Невозможно выполнить запрос текстовый слой использует шрифт без данных обвода». Это значит у вас стоит по умолчанию системный шрифт, а он не поддерживает деформирование. В окне выбора шрифта вам надо заменить системный на любой другой.
Итак, открылось окно деформации. Здесь нажимаем на вкладку «стиль» и увидим множество самых различных вариантов деформации текста.
Поскольку нам нужен текст по кругу, выбираем дугой. Ниже видим несколько ползунков, по которым можно изменять конфигурацию текста. Чтобы понять их суть, надо будет немного потренироваться с ними и посмотреть, какие изменения происходят.
Однако деформация не дает написания текста точно по окружности. Здесь придется применить написание текста по контуру. Для этого воспользуемся инструментом «Эллипс». И, самое главное, на главной панели, когда выбрали инструмент эллипс, необходимо заменить его значение «Фигура» на «Контур».
Теперь, удерживая клавишу Shift, рисуем ровный круг-контур. В отличии от круга-фигуры он будет внутри пустой.
Теперь выбираем инструмент текст и подводим его к нарисованному контуру. Когда иконка текста изменится как показано ниже, можно приступать к написанию.
Это изменение текстового курсора означает, что из обычного, он стал привязанным к контуру. При написании текста, вы увидите, что текст идет точно по кругу.
Вот и вся процедура написания. В принципе, ничего сложного.
Как сделать поворот текста вертикально?
Теперь посмотрим, как написать текст вертикально, но не так, как в примере рассмотренном ранее, более читабельно. Здесь, вообще, все очень просто. На панели инструментов нажимаем на уголок инструмента текст и в раскрывшемся меню выбираем «Вертикальный текст». После этого кликаем по рабочему полю и начинаем писать. Текст сразу отображается как надо.
Зеркальный поворот текста в Photoshop
Вся операция по повороту текста зеркально проводится аналогично с поворотом изображений. Пишем текст, далее через верхнее меню заходим в «Редактирование»- «Свободное трансформирование» и там выбираем «Отразить или по вертикали» (или по горизонтали). В результате проделанной операции получится текст зеркально отраженный по вертикали и горизонтали соответственно:
Вот, собственно и все базовые приемы работы с текстом. Теперь Вы знаете, как можно легко можно решать различные творческие задачи. Удачи вам в освоении программы фотошоп.
Источник: https://fast-wolker.ru/kak-v-fotoshope-povernut-tekst.html
Функция ГРАДУСЫ для выполнения геометрических расчетов в Excel
Функция ГРАДУСЫ в Excel используется для преобразования радианной меры угла в соответствующей величину, выраженную в градусах, и возвращает полученное значение.
Пример 1. Для определения количества оборотов вала электродвигателя используется датчик, который определяет и возвращает значение угла в радианах. Спустя минуту работы двигателя было получено значение 2350π. Определить количество оборотов за 1 минуту.
Исходные данные:
- Для расчета используем формулу:
- =ГРАДУСЫ(2350*ПИ())/360
- Описание составляющих:
- 2350*ПИ() – функция, преобразует радианную меру угла 2350*ПИ() и возвращающая значение, выраженное в градусах.
- 360 – полное количество градусов в окружности.
В результате получим:
То есть, двигатель сделал 1175 оборотов за 1 минуту.
Пример 2. Автомобиль движется по круговой трассе. Определить, на какой угол он отклонится относительно начальной точки пути через 17 минут, если за 10 минут он проехал расстояние, равное радиусу окружности трассы.
Исходные данные:
Для определения угловой скорости разделим количество радиан на время пути. Известно, что за 10 минут был пройден путь, равный радиусу окружности. Из этого следует, что автомобиль отклонился на 1 радиан от начальной точки пути. Искомая угловая скорость:
- 1 – количество радиан;
- 10 – время пути в минутах.
Результат:
То есть, 1 рад/мин. Для нахождения искомого угла используем формулу:
Описание:
- B3 – скорость в рад/мин;
- 17 – время пути в минутах.
Результат вычислений:
То есть, автомобиль отклонится примерно на 97°.
Как перевести радианы в градусы в Excel
Пример 3. Определить угол (в градусах), который проходит минутная стрелка механических часов, если часовая успела отклониться от момента отсчета на 0,05236 радиана?
Исходные данные:
Описание величин:
- B3 – количество делений для минутной стрелки.
- B3/B2 – количество делений, которые проходит часовая стрелка за полный оборот минутной. То есть, выражение B3/(B3/B2) определяет, во сколько раз скорость минутной стрелки превышает скорость часовой стрелки.
- B4 – отклонение часовой стрелки в радианах.
Полученный результат:
Минутная стрелка отклонится на 36°.
Особенности использования функции ГРАДУСЫ в Excel
Функция ГРАДУСЫ имеет следующую синтаксическую запись:
=ГРАДУСЫ(угол)
Единственным аргументом данной функции является угол (обязательный для заполнения). Он характеризует величину угла, выраженную в радианах.
Примечания 1:
- Excel выполняет автоматическое преобразование данных к требуемому типу в тех случаях, где это возможно. Например, запись типа =ГРАДУСЫ(ИСТИНА) соответствует записи =ГРАДУСЫ(1) и вернет значение 57,29577951, то есть количество градусов в 1 радиане.
- Рассматриваемая функция может принимать в качестве аргумента числа из диапазона отрицательных значений. Например, если в аргументе функции указано значение (-1,5), тогда результат равен -85,94366927.
- Функция вернет код ошибки #ЗНАЧ!, если в качестве аргумента была передана текстовая строка, которая не может быть преобразована в числовой тип данных.
Примечания 2:
- В геометрии углом считается фигура, образованная двумя лучами, которые проведены из одной точки (точки их пересечения), при этом данные лучи называются сторонами угла, а точка – его вершиной.
- Градусы и радианы являются двумя количественными характеристиками размера угла.
- 1 градус соответствует 1/180 развернутого угла, то есть угла, стороны которого лежат на одной прямой.
- Если точка пересечения сторон угла (вершина) является центром окружности, а его стороны – радиусы данной окружности, то радиан – центральный угол, радиусы и длина образованной данным углом дуги являются равными величинами (AO=BO=AmB):
- Между градусной и радианной мерами угла установлена следующая взаимосвязь: град=2π*рад/360°, где рад – количество радиан, а град – рассчитываемое количество градусов.
Источник: https://exceltable.com/funkcii-excel/primer-funkcii-gradusy
Уклон и Конусность
Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.
Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.
Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки.
Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали.
Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона.
Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.
Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
Обозначение конусности на чертежах.
Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.
Источник: https://chertimvam.ru/uklon-konusnost/
Инструмент линейка в фотошоп: основные функции
Приветствую покорителей фотошопа!
Сегодня речь пойдет о таком инструменте в фотошоп как линейка. Инструмент линейка позволяет не только измерить расстояние между точками, но также повернуть изображение, расположив его строго горизонтально.
Где находится линейка?
Инструмент находиться там же, где и «Пипетка» Для быстрого доступа можно использовать комбинацию Shift + I, нажимайте эти клавиши, программа перебором будет включать все инструменты блока «Пипетка», пока не дойдет до «Линейки».
На экране появится черная стрелочка с маленькой линейкой. Левой кнопкой мыши укажите первую точку, не отпуская мышку, ведите курсор ко второй точке замеряемого отрезка. Фотошоп нарисует отрезок.
- Чтобы сделать абсолютно ровную линию, зажмите клавишу Shift, теперь можно отложить отрезок ровно по горизонтали, по вертикали, а также под углом в 45 градусов в любом из направлений.
- После того, как вторая точка отрезка указана, программа покажет все параметры на дополнительной панели, которая находиться над рабочей областью.
Функционал линейки
Здесь информация представлена в виде блоков. Первый показывает координаты первой точки отрезка относительно осей X и Y.
Второй блок показывает проекцию нарисованной линии на ось X и Y. Это не длина отрезка.
Например, если на изображении нарисован прямоугольник, и инструментом «Линейка» указать диагональ этого прямоугольника, то второй блок покажет расстояние сторон прямоугольника. Это и есть прямая проекция отрезка на оси X и Y.
Следующий блок отображает угол наклона отрезка. И только дальше можно увидеть непосредственную длину линии, она указывается в параметре «L1».
Параметр «L2» указывает угол между двумя линиями, нарисованными с помощью инструмента «Линейка». После того, как указан один отрезок, зажмите клавишу Alt, подведите курсор к любому концу отрезка, курсор поменяет свой вид, теперь нарисуйте еще один отрезок, обязательно начиная его с любого из концов первой линии.
Нарисованную линию отрезка вы всегда можете перемещать или изменять. Наведите курсор на тело линии, зажмите левую кнопку мышки и двигайте отрезок в любое место.
Если отрезок надо уменьшить или удлинить, нажмите левую кнопку мышки, размещая курсор на одном из концов отрезка, станет доступна возможность изменить отрезок и указать его новую конечную точку.
Дальше отображается функция «По шкале измерений» (Use Measurement Scale).
Установите флажок, если хотите, чтобы параметры инструмента «Линейка» выводились в тех же единицах, что и разбивочная линейка вокруг всего изображения. Чтобы изменить отображение разбивочной линейки, подведите к ней курсор, нажмите правую кнопку мышки и из списка выберете удобную шкалу линейки.
Чтобы повернуть изображение так, чтобы любая линия на рисунке была строго горизонтальной, используйте следующий блок, который называется «Выровнять слой» (Straighten Layer).
Нарисуйте отрезок с помощью инструмента «Линейка» вдоль любого элемента и нажмите функцию этого блока. Изображение повернется так, что нарисованный отрезок будет расположен строго горизонтально, под каким бы углом он не был раньше.
Последний блок позволяет удалить нарисованный отрезок. Предыдущая линия удаляется автоматически, если вы начинаете рисовать новый отрезок. Если нарисованный отрезок не удалить, при печати он не отображается – это вспомогательный, а не графический элемент.
На этом все. Благодарю за внимание!
Источник: https://CompforLife.ru/fotoshop/instrument-linejka-v-fotoshop.html
Измерение углов
- Измерение углов транспортиром
- Свойства измерения углов
Измерить угол – значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.
Обычно за единицу измерения углов принимают градус. Градус – это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).
Измерение углов транспортиром
Для измерения углов используют специальный прибор – транспортир:
У транспортира две шкалы – внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.
Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:
Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов и пишут: ∠BOC = 60°, ∠MON = 120°.
Для более точного измерения углов используют доли градуса: минуты и секунды. Минута – это угол, равный части градуса. Секунда – это угол, равный части минуты. Минуты обозначают знаком ‘, a секунды – знаком ». Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:
- 50°34’19»
- Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.
- Рассмотрим угол AOB:
Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.
Развёрнутый угол равен 180°.
Любой угол имеет определённую величину, большую нуля.
Источник: https://naobumium.info/planimetriya/ugol5.php
Транспортир онлайн, инструмент для измерения углов
Это прозрачный онлайн-транспортир, также помогает измерять углы на изображении, вы можете легко измерить угол любого объекта вокруг вас, сфотографировать и загрузить его, затем перетащить среднюю точку транспортира к вершине угла.
Как пользоваться этим онлайн-транспортиром?
- Вы можете измерить угол любого реального объекта прямо на вашем экране
- Если вы хотите переместить транспортир, перетащите его середину.
- Нажмите на край снаружи транспортира, чтобы добавить к нему метку
- Размещение двух кнопок покажет градусы этого угла
- Двойной щелчок на кнопке удалит ее
Каждый раз, когда я хочу измерить угол, я всегда не могу найти транспортир. К счастью, вот онлайн-транспортир, который удобен и практичен. Теперь мы можем использовать ноутбуки, компьютеры, планшеты или смартфоны для измерения угла наклона чего угодно, вокруг нас в любое время и в любом месте.
Если вы хотите измерить что-то маленькое, просто поместите его на экран и измерьте прямо; Если вы хотите измерить что-то большее, Вы можете сделать снимок и загрузить его, а затем переместить центральную точку транспортира, чтобы измерить его угол.
Используйте камеру или изображение для измерения угла
Вы можете сфотографировать любой объект, который вы хотели бы измерить, например, автомобиль, дорога, дом, лестница или гора, транспортир прозрачный, после того как вы загрузили изображение, оно будет отображаться в фоновом режиме. затем вы можете убрать транспортир или добавить кнопки, чтобы определить градусы углов, загрузить файл только принять файл изображения в форматах JPG, JPEG, GIF, PNG
На панели управления если цвет фона близок к транспортиру, и это не легко отличить, Вы можете изменить цвет транспортира, чтобы видеть это ясно. Также вы можете переместить его, уменьшить или увеличить размер транспортира, в соответствии с вашими потребностями.
Углы и градусы
- Углы измеряются в градусах. Символом градусов является маленький кружок °
- Полный круг составляет 360 ° (360 градусов)
- Полукруг или прямой угол 180 °
- Четверть круга или прямой угол составляет 90 °
Что вы думаете об этом транспортире?
Источник: https://ginifab.com/feeds/angle_measurement/online_protractor.ru.php
Определение натуральной величины угла
Чтобы определить натуральную величину угла, нужно перевести его в положение, в котором его стороны будут параллельны плоскости проекции. Наиболее рациональный путь решения данной задачи – использовать способ вращения вокруг линии уровня. Более трудоемкими вариантами являются метод замены плоскостей проекций и параллельное перемещение.
Задача
Приведенный ниже пример иллюстрирует нахождение угла между пересекающимися прямыми m и n способом вращения вокруг фронтали.
Последовательность построений:
- В произвольном месте чертежа проводим фронталь f. Она пересекает прямые m и n в точках 1 и 2. Определяем их недостающие проекции.
- Через точку K» проводим перпендикуляр к f». На пересечении этого перпендикуляра с фронталью находится проекция центра вращения O». По линии связи определяем положение т. O’.
- Находим величину радиуса R поворота точки K. Для этого перпендикулярно O»K» откладываем отрезок K»K0 = yk – yo. Таким образом, R равен O»K0 – гипотенузе прямоугольного треугольника O»K»K0.
- Проводим дугу радиусом R до её пересечения с перпендикуляром O»K» в точке K»1. Соединяем K»1 c точками 1» и 2». Натуральная величина угла между прямыми m и n равна углу ϕ при вершине K»1.
Более подробную информацию о методе вращения вокруг линии уровня, который мы здесь использовали, вы можете найти на следующей странице.
Определение угла между скрещивающимися прямыми
Углом между скрещивающимися прямыми называют плоский угол, стороны которого параллельны данным прямым. На изображении, приведенном ниже, прямые e и d скрещивающиеся и друг с другом не пересекаются. Чтобы найти угол между ними, выполним ряд графических построений:
Описание решения
- На любом свободном месте чертежа отмечаем точку S. Располагаем её произвольно (проекции S» и S’ показаны на рисунке).
- Через точку S проводим прямые a и b так, чтобы они были параллельны e и d. В нашем случае a||e, b||d соответственно.
- Строим горизонталь h, которая будет играть роль оси вращения. Перпендикулярно h’ из точки S’ проводим прямую. Она пересекает h’ в т. O’ – горизонтальной проекции центра вращения.
- Определяем радиус поворота R как гипотенузу треугольника O’S’S0. При этом катет S’S0 равен разности удаления точек S» и O» от горизонтальной плоскости.
- Находим т. S’1 на пересечении дуги радиуса R с прямой S’O’. Соединяем S’1 c точками 1′ и 2′, которые своего положения не меняют. Угол ϕ при вершине S’1 искомый. Задача решена.
Похожие задачи:
Источник: https://ngeometry.ru/kak-opredelit-naturalnuyu-velichinu-ugla.html
Как читаются углы. Развернутый, тупой, вертикальный и неразвернутый: виды углов геометрии
Что такое угол?
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160).
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.
Например, вместо «угол АОВ» пишут короче: «угол О».
Вместо слова «угол» пишут знак .
Например, AОВ, O.
На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла.
Как и все геометрические фигуры, углы сравниваются с помощью наложения.
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
Например, на рисунке 162 ABC = MNK.
Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Пишут: COP
Прямой и развернутый угол
Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164).
Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165).
Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166).
Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми.
Прямым углом называют половину развернутого угла.
Чертежный треугольник
Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо:
а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА;
б) провести вдоль второй стороны треугольника луч ОВ.
В результате получим прямой угол АОВ.
Вопросы к теме
1.Что такое угол?
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О.
Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных.
Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла.
А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым.
Свойства развернутого угла
Развернутый угол обладает такими свойствами:
Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую;
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.
Измерение углов
Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам.
То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид: « ° ».
Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным.
А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. Это и есть развернутый угол.
Практическое задание
1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения.
1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ?
1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD.
1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170).
1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях.
1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения.
1620. Укажите прямые углы в классной комнате.
а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1.
1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600?
1630. Найдите пропущенное число:
а) 2 5 3 б) 2 3 5
13 6 12 1
2 3? 42?
1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года?
1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
1635. Найдите с помощью микрокалькулятора:
а) 4,5% от 168; в) 28,3% от 569,8;
б) 147,6% от 2500; г) 0,09% от 456 800.
1636. Решите задачу:
1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось?
1637. Выполните действия:
1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85;
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)).
1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла.
1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК?
1640. Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь.
1642. Найдите значение выражения:
а) 14,791: а + 160,961: b, если а = 100, b = 10;
б) 361,62с + 1848: d, если с = 100, d =100.
1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день?
1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке?
1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики?
1646. Найдите, сколько составляют:
а) 1% от тонны; в) 5% от 7 т;
б) 1% от литра; г) 6% от 80 км.
1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т?
1648. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
С понятием угол учащиеся знакомятся еще в начальной школе. Но как геометрическую фигуру, имеющую определенные свойства, начинают изучать его с 7-го класса в геометрии. Кажется, довольно простая фигура , что о ней можно сказать. Но, приобретая новые знания, школьники всё больше понимают, что можно узнать о ней довольно интересные факты.
Вконтакте
Когда изучаются
Школьный курс геометрии разделён на два раздела: планиметрию и стереометрию. В каждом из них немалое внимание уделяется углам :
- В планиметрии дается их основное понятие, происходит знакомство с их видами по величине. Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
- В стереометрии изучаются пространственные углы – двугранные и трехгранные.
Внимание! В данной статье рассматриваются все виды и свойства углов именно в планиметрии.
Определение и измерение
Приступая к изучению, первоначально определяют, что такое угол в планиметрии.
Если на плоскости взять определённую точку и провести от нее два произвольных луча, то получим геометрическую фигуру – угол, состоящую из следующих элементов:
- вершина – та точка, из которой и проводились лучи, обозначается заглавной буквой латинского алфавита;
- стороны – полупрямые, проведенные из вершины.
Все элементы, образующие рассматриваемую нами фигуру, разбивают плоскость на две части :
- внутренняя — в планиметрии не превышает 180 градусов;
- внешняя.
Принцип измерения углов в планиметрии объясняют на интуитивной основе. Для начала знакомят учащихся с понятием развернутый угол.
Важно! Угол называется развернутым, если полупрямые, выходящие из его вершины, образуют прямую линию. Неразвернутый угол это все остальные случаи.
Если его разделить на 180 равных частей, то принято считать меру одной части равной 10. В таком случае говорят, что измерение производится в градусах, а градусная мера такой фигуры составляет 180 градусов.
Основные виды
Виды углов подразделяются по таким критериям, как градусная мера, характер их образования и представленные ниже категории.
По величине
Учитывая величину, углы разделяют на:
- развернутый;
- прямой;
- тупой;
- острый.
Какой угол называется развернутым, было представлено выше. Определимся с понятием прямого.
Его можно получить при делении развернутого на две равные части. В этом случае легко ответить на вопрос: прямой угол, сколько градусов составляет?
180 градусов развернутого делим на 2 и получаем, что прямой угол равен 90 градусам . Это замечательная фигура, так как многие факты в геометрии связаны именно с ней.
Имеет она и свои особенности в обозначении. Чтобы на рисунке показать прямой угол, его обозначают не дугой, а квадратиком.
Углы, которые получаются при делении произвольным лучом прямого, называют острыми. По логике вещей следует, что острый угол меньше прямого, но его мера отлична от 0 градусов. То есть, он имеет величину от 0 до 90 градусов.
Тупой угол больше прямого, но меньше развернутого. Его градусная мера варьируется в интервале от 90 до 180 градусов.
Данный элемент можно разбить на разные виды рассматриваемых фигур, исключая развёрнутый.
Вне зависимости от того, как разбивается неразвернутый угол, всегда пользуются базовой аксиомой планиметрии — «основное свойство измерения».
При разделении угла одним лучом или несколькими, градусная мера данной фигуры равна сумме мер углов, на которые она разбита.
На уровне 7-го класса виды углов по их величине на этом заканчиваются. Но для повышения эрудиции можно добавить, что существуют и другие разновидности, которые обладают градусной мерой больше 180 градусов.Их называют выпуклыми.
Фигуры при пересечении прямых
Следующие типы углов, с которыми знакомятся учащиеся – элементы, образованные при пересечении двух прямых. Фигуры, которые размещаются друг напротив друга, называют вертикальными. Их отличительное свойство – они равны.
Элементы, которые прилегают к одной и той же прямой, называют смежными. Теорема, отображающая их свойство, говорит о том, что смежные углы в сумме дают 180 градусов .
Элементы в треугольнике
Если рассматривать фигуру как элемент в треугольнике, то углы подразделяют на внутренний и внешний. Треугольник ограничен тремя отрезками и состоит из трёх вершин. Углы, расположенные внутри треугольника при каждой вершине, называют внутренними .
Если взять любой внутренний элемент при любой вершине и продлить любую сторону, то угол, который образовался и является смежным с внутренним, называется внешним. Эта пара элементов имеет следующее свойство: их сумма равна 180 градусам.
Пересечение двух прямых секущей
Пересечение прямых
При пересечении двух прямых секущей также образуются углы , которые принято распределять по парам. Каждая пара элементов имеет свое название. Выглядит это следующим образом:
- внутренние накрест лежащие:∟4 и ∟6, ∟3 и ∟5;
- внутренние односторонние: ∟4 и ∟5, ∟3 и ∟6;
- соответствующие: ∟1 и ∟5, ∟2 и ∟6, ∟4 и ∟8, ∟3 и ∟7.
В том случае, когда секущая пересекает две
В этой статье будет рассматриваться одна из основных геометрических фигур — угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.
- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.
- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.
- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла — это прямой угол.
Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4. Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.
- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х. Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам .
В морской терминологии углы обозначаются румбами .
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation . 2010 .
Смотреть что такое «Развернутый угол» в других словарях:
Угол, равный двум прямым. *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
угол — ▲ разность направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона. образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… …
Угол — Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми. УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
Геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия
Угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь
Раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия
поперек — ▲ под углом максимум, косой угол поперечный. поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
градус — а, м. 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка
Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном… … Википедия
В этой статье мы всесторонне разберем одну из основных геометрических фигур – угол. Начнем со вспомогательных понятий и определений, которые нас приведут к определению угла. После этого приведем принятые способы обозначения углов. Далее подробно разберемся с процессом измерения углов. В заключении покажем как можно отметить углы на чертеже. Все теорию мы снабдили необходимыми чертежами и графическими иллюстрациями для лучшего запоминания материала.
Навигация по странице.
Определение угла.
Угол является одной из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур как точка, прямая и плоскость. Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и .
Итак, будем отталкиваться от понятий точки, прямой на плоскости и плоскости.
Дадим сначала определение луча.
Пусть нам дана некоторая прямая на плоскости. Обозначим ее буквой a . Пусть O – некоторая точка прямой a . Точка O разделяет прямую a на две части. Каждая из этих частей вместе с точкой О называется лучом , а точка О называется началом луча . Еще можно услышать, что луч называют полупрямой .
Для краткости и удобства ввели следующие обозначения для лучей: луч обозначают либо малой латинской буквой (например, луч p или луч k ), либо двумя большими латинскими буквами, первая из которых соответствует началу луча, а вторая обозначает некоторую точку этого луча (например, луч ОА или луч СD ). Покажем изображение и обозначение лучей на чертеже.
Теперь мы можем дать первое определение угла.
Определение.
Угол – это плоская геометрическая фигура (то есть целиком лежащая в некоторой плоскости), которую составляют два несовпадающих луча с общим началом. Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла .
Возможен случай, когда стороны угла составляют прямую линию. Такой угол имеет свое название.
Определение.
Если обе стороны угла лежат на одной прямой, то такой угол называется развернутым .
Предлагаем Вашему вниманию графическую иллюстрацию развернутого угла.
Для обозначения угла используют значок угла «». Если стороны угла обозначены малыми латинскими буквами (например, одна сторона угла k , а другая h ), то для обозначения этого угла после значка угла записывают подряд буквы, соответствующие сторонам, причем порядок записи значения не имеет (то есть, или ). Если стороны угла обозначены двумя большими латинскими буквами (к примеру, одна сторона угла OA , а вторая сторона угла OB ), то угол обозначают следующим образом: после значка угла записывают три буквы, участвующие в обозначении сторон угла, причем буква, отвечающая вершине угла, располагается посередине (в нашем случае угол будет обозначен как или ). Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1 , 2 и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла , а другую – внешней областью угла . Следующее изображение разъясняет, какая часть плоскости отвечает внутренней области угла, а какая — внешней.
Любую из двух частей, на которые развернутый угол разделяет плоскость, можно считать внутренней областью развернутого угла.
Определение внутренней области угла приводит нас ко второму определению угла.
Определение.
Угол – это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла.
Следует отметить, что второе определение угла строже первого, так как содержит больше условий. Однако не следует отметать первое определение угла, также не следует рассматривать первое и второе определения угла по отдельности. Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Дадим еще определения смежных и вертикальных углов.
Определение.
Смежные углы – это два угла, у которых одна сторона общая, а две другие образуют развернутый угол.
Из определения следует, что смежные углы дополняют друг друга до развернутого угла.
Определение.
Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого.
На рисунке изображены вертикальные углы.
Очевидно, что две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов.
Сравнение углов.
В этом пункте статьи мы разберемся с определениями равных и неравных углов, а также в случае неравных углов разъясним, какой угол считается большим, а какой меньшим.
Напомним, что две геометрические фигуры называются равными, если их можно совместить наложением.
Пусть нам даны два угла. Приведем рассуждения, которые помогут нам получить ответ на вопрос: «Равны эти два угла или нет»?
Очевидно, что мы всегда можем совместить вершины двух углов, а также одну сторону первого угла с любой из сторон второго угла. Совместим сторону первого угла с той стороной второго угла, чтобы оставшиеся стороны углов оказались по одну сторону от прямой, на которой лежат совмещенные стороны углов. Тогда, если две другие стороны углов совместятся, то углы называются равными .
Если же две другие стороны углов не совместятся, то углы называются неравными , причем меньшим считается тот угол, который составляет часть другого (большим является тот угол, который полностью содержит другой угол).
Очевидно, что два развернутых угла равны. Также очевидно, что развернутый угол больше любого неразвернутого угла.
Измерение углов.
Измерение углов основывается на сравнении измеряемого угла с углом, взятым в качестве единицы измерения. Процесс измерения углов выглядит так: начиная от одной из сторон измеряемого угла, его внутреннюю область последовательно заполняют единичными углами, плотно укладывая их один к другому. При этом запоминают количество уложенных углов, которое и дает меру измеряемого угла.
Фактически, в качестве единицы измерения углов может быть принят любой угол. Однако существует множество общепринятых единиц измерения углов, относящихся к различным областям науки и техники, они получили специальные названия.
Одной из единиц измерения углов является градус .
Определение.
Один градус – это угол, равный одной сто восьмидесятой части развернутого угла.
Градус обозначают символом «», следовательно, один градус обозначается как .
Таким образом, в развернутом угле мы можем уложить 180 углов в один градус. Это будет выглядеть как половинка круглого пирога, разрезанная на 180 равных кусочков. Очень важно: «кусочки пирога» плотно укладываются один к другому (то есть, стороны углов совмещаются), причем сторона первого угла совмещается с одной стороной развернутого угла, а сторона последнего единичного угла совпадет с другой стороной развернутого угла.
При измерении углов выясняют, сколько раз градус (или другая единица измерения углов) укладывается в измеряемом угле до полного покрытия внутренней области измеряемого угла. Как мы уже убедились, в развернутом угле градус укладывается ровно 180 раз. Ниже приведены примеры углов, в которых угол в один градус укладывается ровно 30 раз (такой угол составляет шестую часть развернутого угла) и ровно 90 раз (половина развернутого угла).
Для измерения углов, меньших одного градуса (или другой единицы измерения углов) и в случаях, когда угол не удается измерить целым числом градусов (взятых единиц измерения), приходится использовать части градуса (части взятых единиц измерения). Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определение.
Минута – это одна шестидесятая часть градуса.
Определение.
Секунда – это одна шестидесятая часть минуты.
Иными словами, в минуте содержится шестьдесят секунд, а в градусе – шестьдесят минут (3600 секунд). Для обозначения минут используют символ «», а для обозначения секунд – символ «» (не путайте со знаками производной и второй производной). Тогда при введенных определениях и обозначениях имеем , а угол, в котором укладываются 17 градусов 3 минуты и 59 секунд, можно обозначить как .
Определение.
Градусной мерой угла называется положительное число, которое показывает сколько раз градус и его части укладываются в данном угле.
Например, градусная мера развернутого угла равна ста восьмидесяти, а градусная мера угла равна .
Для измерения углов существуют специальные измерительные приборы, наиболее известным из них является транспортир.
Если известно и обозначение угла (к примеру, ) и его градусная мера (пусть 110 ), то используют краткую запись вида и говорят: «Угол АОВ равен ста десяти градусам».
Из определений угла и градусной меры угла следует, что в геометрии мера угла в градусах выражается действительным числом из интервала (0, 180] (в тригонометрии рассматривают углы с произвольной градусной мерой, их называют ). Угол в девяносто градусов имеет специальное название, его называют прямым углом . Угол меньший 90 градусов называется острым углом . Угол больший девяноста градусов называется тупым углом . Итак, мера острого угла в градусах выражается числом из интервала (0, 90) , мера тупого угла – числом из интервала (90, 180) , прямой угол равен девяноста градусам. Приведем иллюстрации острого угла, тупого угла и прямого угла.
Из принципа измерения углов следует, что градусные меры равных углов одинаковы, градусная мера большего угла больше градусной меры меньшего, а градусная мера угла, который составляют несколько углов, равна сумме градусных мер составляющих углов. На рисунке ниже показан угол АОВ , который составляют углы АОС , СОD и DОВ , при этом .
Таким образом, сумма смежных углов равна ста восьмидесяти градусам , так как они составляют развернутый угол.
Из этого утверждения следует, что . Действительно, если углы АОВ и СОD – вертикальные, то углы АОВ и ВОС — смежные и углы СОD и ВОС также смежные, поэтому, справедливы равенства и , откуда следует равенство .
Наряду с градусом удобна единица измерения углов, называемая радианом . Радианная мера широко используется в тригонометрии. Дадим определение радиана.
Определение.
Угол в один радиан – это центральный угол , которому соответствует длина дуги, равная длине радиуса соответствующей окружности.
Дадим графическую иллюстрацию угла в один радиан. На чертеже длина радиуса OA (как и радиуса OB ) равна длине дуги AB , поэтому, по определению угол AOB равен одному радиану.
Для обозначения радианов используют сокращение «рад». Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Стоит отдельно отметить, что величина угла, выраженная в радианах, не зависит от длины радиуса окружности. Это связано с тем, что фигуры, ограниченные данным углом и дугой окружности с центром в вершине данного угла, подобны между собой.
Измерение углов в радианах можно выполнять так же, как и измерение углов в градусах: выяснить, сколько раз угол в один радиан (и его части) укладываются в данном угле. А можно вычислить длину дуги соответствующего центрального угла, после чего разделить ее на длину радиуса.
Для нужд практики полезно знать, как соотносятся между собой градусная и радианная меры, так как довольно часть приходится осуществлять . В указанной статье установлена связь между градусной и радианной мерой угла, и приведены примеры перевода градусов в радианы и обратно.
Обозначение углов на чертеже.
На чертежах для удобства и наглядности углы можно отмечать дугами, которые принято проводить во внутренней области угла от одной стороны угла до другой. Равные углы отмечают одинаковым количеством дуг, неравные углы – различным количеством дуг. Прямые углы на чертеже обозначают символом вида «», который изображают во внутренней области прямого угла от одной стороны угла до другой.
Если на чертеже приходится отмечать много различных углов (обычно больше трех), то при обозначении углов кроме обычных дуг допустимо использование дуг какого-либо специального вида. К примеру, можно изобразить зубчатые дуги, или нечто подобное.
Следует отметить, что не стоит увлекаться с обозначением углов на чертежах и не загромождать рисунки. Рекомендуем обозначать только те углы, которые необходимы в процессе решения или доказательства.
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
Нормальные конусности и углы
Источник: ГОСТ 8593-81
Конусность К есть отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними.
Уклон «i» есть отношение разности размеров двух поперечных сечений к расстоянию между ними.
Таблица 1. Углы конусности
|
Конусность К |
Угол конуса 2а |
Угол уклона а |
Исходное значение (К или 2а) |
|
1:200 |
0°7’11» |
0°8’36» |
1:200 |
|
1:100 |
0°34’23» |
0°17’11» |
1:100 |
|
1:50 |
1°8’46» |
0°34’23» |
1:50 |
|
1:30 |
1°54’35» |
0°57’17» |
1:30 |
|
1:20 |
2°51’51» |
1°25’56» |
1:20 |
|
1:15 |
3°49’6″ |
1°54’33» |
1:15 |
|
1:12 |
4°46’19» |
2°23’9″ |
1:12 |
|
1:10 |
5°43’29» |
2°51’45» |
1:10 |
|
1:8 |
7°9’10» |
3°34’35» |
1:8 |
|
1:7 |
8°10’16» |
4°5’8″ |
1:7 |
|
1:5 |
11°25’16» |
5°42’38» |
1:5 |
|
1:3 |
18°55’29» |
9°27’44» |
1:3 |
|
1:1,866 |
30° |
15° |
30° |
|
1:1,207 |
45° |
22°30′ |
45° |
|
1:0,866 |
60° |
30° |
60° |
|
1:0,652 |
75° |
37°30′ |
75° |
|
1:0,500 |
90° |
45° |
90° |
|
1:0,289 |
120° |
60° |
120° |
К оглавлению
Angle Projection — обзор
3.1 Уравнения движения
Рассмотрена система с двумя степенями свободы жесткого ротора, поддерживаемого отталкивающим магнитным подшипником. Угол наклона вокруг верхней точки опоры обозначен как θ , а углы проекции θ на плоскости x — z и y — z обозначены как θ x и θ. и соответственно. Уравнения движения представлены следующим образом с использованием характеристики возвращающей силы, показанной на рис.2 и уравнения (3) [12].
(4) Iθ¨x + Ipψ¨θy + Ipψ¨θ˙y + cθ˙x + lkx + β0x2 + y2x = l1meψ˙2cosψ + l1meψ¨sinψIθ¨y − Ipψ¨θx − Ipψ˙θ˙x + cθ ˙y + lky + β0x2 + y2y = l1meψ˙2sinψ − l1meψ¨cosψ
где, ψ — угол поворота вала, I — диаметральный момент инерции ротора в верхней точке опоры, I p — полярный момент инерции, c — коэффициент демпфирования, k и β (0) — линейный и кубический нелинейный коэффициенты пружины возвращающей силы, как показано на рис.2, ∆ z — осевое смещение, l — расстояние между верхней точкой опоры и центром магнита, l 1 — расстояние между верхней точкой опоры и центром диска, м — масса диска. Предполагается, что статический дисбаланс e существует только в диске. Значения параметров соответствуют экспериментальной установке в разделе 6. В данной статье исследуются стационарные колебания, при которых угловая скорость ψ˙ постоянна, и нестационарные колебания, при которых угловое ускорение ψ¨ постоянное.Угловое ускорение обозначено λ. ψ выражается следующим образом:
(5) ψ = 12λt2 + ω0t + ψ0, ψ˙ = ω = λt + ω0
Предполагается, что θ мало, поэтому θ x и θ y преобразуются в смещение вала внутреннего магнетика x и y с помощью соотношений x = lθ x и y = lθ y . Значение k при осевом смещении ∆ z = 0 обозначается как k st .Собственная частота pst = kst / I в невращающемся состоянии и в невращающемся состоянии, а также радиальный зазор между внутренним и внешним магнитами δ установлены как стандартные значения. Безразмерные переменные определены следующим образом:
(6) c ′ = c1Ikst, k ′ = kkst, β0 ‘= β0δ2kstl2, Δz ′ = Δzlm, ip = IpI, t ′ = tkstI, ω ′ = ωIkst, λ ′ = λIkst, x ′ = xδ, y ′ = yδ, e ′ = l1lmeIδ
Только для ∆ z длина внутреннего магнита l A устанавливается как стандартное значение. Уравнения движения в безразмерной форме, определяющие нестационарные колебания этой системы, с этими безразмерными переменными получаются следующим образом.Обозначение ´, обозначающее безразмерное значение, в дальнейшем опускается.
(7) x¨ + ipψ¨y + ipψ˙y˙ + cx˙ + kx + β0x2 + y2x = eψ˙2cosψ + eψ¨sinψy¨ + ipψ¨x − ipψ˙x˙ + cy˙ + ky + β0x2 + y2y = eψ˙2sinψ − eψ¨cosψ
Стационарная вибрация выражается в уравнениях (7) для ψ˙ = 0 и ψ˙ = ω.
Характеристическое уравнение для незатухающей системы получается следующим образом из уравнений (7), если положить e = c = β (0) = 0, ψ˙ = 0 и ψ˙ = ω [ 12]. Незатухающие собственные частоты прямого и обратного вихревых движений p f , p b получены путем решения этого характеристического уравнения.
(8) GpΔz≡k + ipωp − p2 = 0
Ортогональная проекция под первым и третьим углом
Часто трехмерный объект необходимо точно и ясно изобразить на плоской поверхности. Графические представления трехмерного объекта на плоскости адекватны только в том случае, если объект простой, однако для более сложных объектов необходимо использовать другой метод представления — тот, который покажет истинные формы их поверхностей.
Наблюдая за тенями объектов, отбрасываемыми источниками света, можно увидеть, что объект можно «спроецировать» на двумерную поверхность (т.е.е. плоскость проекции), проецируя точки объекта на поверхность и соединяя их по порядку.
1.1 Ортографическая проекция — Определение
Ортографическая проекция — это способ представления трехмерного объекта в двух измерениях. Он использует несколько видов объекта с точек обзора, повернутых относительно центра объекта с шагом 90 градусов. Эквивалентно, виды можно считать полученными путем поворота объекта вокруг его центра с шагом 90 градусов.
Виды располагаются относительно друг друга по одной из двух схем: проекция под первым углом или проекция под третьим углом. В каждом из этих случаев виды можно рассматривать как «спроецированные» на плоскости, которые образуют прозрачную «коробку» вокруг объекта.
1.2 Первичная или главная плоскости проекции
При рисовании нескольких видов объекта объект просматривается через плоскость проекции из точки, находящейся на бесконечности, тем самым получая точный контур видимой стороны объекта.Однако проекция одной грани не дает полного описания объекта; должны использоваться другие плоскости проецирования. Для определения истинной высоты, ширины и глубины объекта требуются виды спереди, сверху и сбоку, которые называются основными плоскостями проекции. Три основных (или основных) плоскости проекции известны как вертикальная, горизонтальная и профильная плоскости. Углы, образованные между горизонтальной и вертикальной плоскостями, называются первым, вторым, третьим и четвертым углами, как показано на схеме ниже.В практических целях используется только первый и третий угол.
Основные плоскости проекции.
1.3 Первая угловая проекция
В проекции под первым углом каждый вид объекта проецируется в направлении (смысле) взгляда объекта на внутренние стенки коробки.
Затем создается двухмерное представление объекта путем «разворачивания» коробки для просмотра всех внутренних стен.
Графический рисунок, см. Рис.1 обозначает форму компонента с единым видом.
Орфографический чертеж указывает форму компонента с помощью нескольких видов, каждое из которых смотрит на разные грани компонента. Обычно, однако, показаны три вида, чтобы прояснить внутренние и внешние детали:
- A Вид спереди
- A Вид сверху
- A Вид сбоку
-
Вид спереди или вид спереди (рис.2) представляет то, что можно увидеть, если смотреть на переднюю часть компонента в направлении стрелки F.
Фиг.2
-
На виде сверху (рис. 3) показано, что можно увидеть, если смотреть на верхнюю часть компонента в направлении стрелки P под углом 90 ° к стрелке F.
Фиг.3
- Вид сбоку или вид сбоку (рис. 4 и 5) представляет то, что можно увидеть, если смотреть на сторону компонента в направлении стрелки R или стрелки L. Эти стрелки расположены под углом 90 ° к обеим стрелкам F. и стрела стр.
Вид в направлении стрелки R. | Вид в направлении стрелки L. |
Отдельные виды компонента объединяются, чтобы сформировать полный орфографический чертеж, как показано ниже.
Вид спереди и вид сбоку вычерчиваются на одной линии, так что вид сбоку можно «проецировать» из вида спереди и наоборот.
Вид сверху отображается на одной линии с видом спереди и под ним. Другими словами, план проецируется спереди.
На что следует обратить внимание при создании чертежа с использованием ортогональной проекции под первым углом:
- Соответствующие высоты на виде спереди и сбоку одинаковы. Например, высота отверстия от основания H одинакова как на виде спереди, так и сбоку. Толщина основания T одинакова как спереди, так и сбоку.
- Ширина на виде сбоку соответствует глубине на плане.Например, общая ширина D на виде сбоку равна общей глубине D на плане. Ширина d одинакова как на виде сверху, так и на виде сбоку. Проецирование ширины от вида сбоку на план упрощается за счет использования линии поворота под углом 45 °, как показано выше.
- Вид сверху обычно проецируется под видом спереди. Это может быть и выше, но это называлось бы «перевернутым» планом.
- Вид сбоку справа показан на виде спереди слева.
- Отель L.Х. вид сбоку показан на правой стороне вида спереди.
Примечание: Чертежи следует читать (или интерпретировать), глядя с правой стороны или нижнего правого угла рисунка.
1.4 Построение ортогонального чертежа
-
Лицо, которое будет использоваться в качестве вида спереди компонента, было выбрано, в данном случае смотрящее в направлении стрелки F (рис.1) выше. Выбор вида спереди абсолютно произвольный. -
Контур вида спереди отображается слабо в положении, показанном выше, оставляя место на листе чертежа для вида в плане, а также обоих видов с торца, которые будут добавлены. - Контуры вида сверху и видов сбоку слабо проецируются на виде спереди и расположены, как показано выше.
-
Все остальные внешние детали были добавлены, а центральные линии вставлены, как показано выше. - Все скрытые детали, т.е.е. для отверстия и выемки добавляются, и контур становится более заметным, чтобы завершить рисунок, как показано выше.
1,5 Третий угол проекции
В проекции под третьим углом каждый вид объекта проецируется противоположно направлению (ощущению) взгляда объекта на внутренние стенки коробки.
Затем создается двухмерное представление объекта путем «разворачивания» коробки для просмотра всех внутренних стен.
Дополнительная информация
Термин «третий угол» используется потому, что по сравнению с проекцией «под первым углом» направления проецирования поворачиваются на два прямых угла относительно объекта. Проекция под вторым и четвертым углом также определяется, но не дает полезных изображений.
Проекция под третьим углом часто считается более интуитивной, чем проекция под первым углом.
В то время как проекция под третьим углом распространена в США и Канаде, проекция под прямым углом более популярна в Европе и Азии.
1.6 Ортографические проекционные символы для первого и третьего углов
Стандартные символы
Рекомендуемые пропорции символов: символы для первого и третьего угла основаны на усеченной части конуса, как показано.
Усадка конуса в первой четверти: проекция первого угла; Вид слева появляется справа.
1.7 Стандартные сокращения и символы на чертежах
Некоторые часто используемые символы и сокращения.
Ключевые моменты обучения
- Чертеж строительной техники
- Методы определения размеров согласно BS 8888: 2004
- Набросок от руки
- Четкость и аккуратность в рисунке
- Логический подход к рисованию и соблюдение стандартов рисования
- Использование скрытых деталей
- Использование осевых линий
2.1 Инженерные чертежи — графический язык
Инженерный чертеж — это графический или международный язык, и это одна из основных форм общения в мастерской или на месте.Устное или письменное общение было единственным средством общения при решении технических вопросов, могло возникнуть недопонимание, особенно в отношении формы и размера, что могло иметь серьезные последствия для компании. Неправильно изготовленные и установленные рабочие места могут привести к потере времени и материалов, потере прибыли, плохим отношениям с клиентами, нарушению контракта и судебным разбирательствам. Тем не менее, общепринятые методы, используемые в графической коммуникации через инженерные чертежи, помогают устранить многие из упомянутых выше трудностей за счет правильного представления и компоновки работы со всеми деталями и информацией, отображаемыми на чертежах.Ошибки все же могут быть сделаны, однако они значительно уменьшаются за счет хорошей практики инженерного рисования.
Для обеспечения единообразия интерпретации Британский институт стандартов выпустил буклет под названием BS 8888: 2004.
2.2 Функции инженерного чертежа
Персонал отдела чертежей использует инженерный чертеж для передачи мысленного изображения объекта в мастерскую или на объект. Чтобы не запутать получателя, следует соблюдать следующие правила.
- Чертеж должен быть точным.
- Линии должны быть четкими и отчетливыми.
- Названия компонентов и используемые термины должны соответствовать правильной инженерной терминологии.
- Чертеж должен содержать достаточно информации, позволяющей мастеру преобразовать предоставленную информацию в готовый компонент или работу без дальнейшего контакта с чертежным бюро.
- Поскольку чертежник является человеком и подвержен человеческим ошибкам, все рабочие чертежи должны подвергаться независимой проверке.Одна небольшая ошибка в чертежном офисе может стать причиной напрасной траты времени и материалов.
2.3 Строки и буквы
Типы линий
Типы линий для инженерных чертежей, рекомендованные Британским институтом стандартов в BS 8888: 2004. Рекомендуются две толщины линий: толщина 0,7 мм в ширину и тонкая 0,3 мм в ширину. Для карандашных рисунков рекомендацию можно интерпретировать как означающую, что толстые линии должны быть примерно вдвое шире тонких.
Видимые контуры объекта нарисованы сплошными толстыми линиями. Они должны быть самыми заметными линиями на рисунке.
Скрытые очертания объекта представлены линиями, состоящими из коротких тонких штрихов. Штрихи и промежутки между ними должны быть одинаковой длины и приблизительно соответствовать показанным пропорциям. В углах и точках касания дуг должны встречаться черточки.
Непрерывная тонкая линия используется для размерных линий, линий проекции, выноски для заметок, штриховки или выравнивания сечения, контуров смежных деталей и вращающихся сечений и фиктивных контуров.
Пределы частичных видов и сечений показаны непрерывными неправильными линиями, когда линия не является осью. Эти линии тонкие и нарисованы от руки.
Центральные линии и крайние положения подвижных частей показаны тонкими цепными линиями. Они состоят из длинных черточек, чередующихся с короткими черточками, а не точек, пропорциональных примерно, как показано. Длину тире и расстояние между ними можно увеличивать для очень длинных линий.
Плоскости разреза для секций представлены цепными линиями, толстыми на концах и при изменении направлений, тонкими в других местах.
Толстые линии цепи обозначают поверхности, которые должны отвечать особым требованиям. Длина частей этих линий и расстояние между ними должны быть такими же, как у тонких цепочек.
Все линии цепочки должны начинаться и заканчиваться длинным тире. Линии центра должны выходить за пределы объекта, к которому они относятся, только на короткое расстояние, если это не требуется для определения размеров. Они не должны проходить через промежутки между видами и не должны заканчиваться на другой линии чертежа.Также они должны пересекаться друг с другом в сплошных частях линий.
Цепные линии, имеющие образованные в них углы, следует рисовать длинными черточками, сходящимися под углами. Дуги должны соединяться в точках касания.
Стрелки на концах размерных линий должны касаться линий проекции, а стрелки на концах выноски должны касаться другой линии на чертеже. Они должны быть острыми, черными, заполненными, длиной около 3 мм.
Надпись и нумерация
Важнейшими особенностями надписей на технических чертежах являются четкость, единообразие и возможность быстрого изготовления.Разборчивость и скорость достигаются за счет использования блочного одноходового стиля, который может быть как вертикальным, так и наклонным. Студентам рекомендуется использовать вертикальный стиль, так как его легче производить. Однографический шрифт имеет все штрихи одинаковой толщины, и каждый штрих выполняется одним движением карандаша. Заглавные буквы предпочтительнее строчных, они менее перегружены и с меньшей вероятностью будут неправильно прочитаны при уменьшении размера на отпечатках. Однако следует использовать строчные буквы, когда они являются частью стандартного символа, кода или сокращения.
Показаны подходящий алфавит и цифры, и с этой моделью следует часто консультироваться на ранних стадиях, пока не будут запоминаться формы знаков. Обратите внимание, что символы имеют простейшие формы. Расцветки и орнамент неуместны на инженерном чертеже.
Все надписи карандашом должны быть выполнены от руки и нарисованы между парой слабых направляющих линий. Для размеров и примечаний следует использовать высоту символов около 3 мм, и символы должны быть примерно такой же высоты.Заголовки обычно делаются более крупными буквами. Символы должны касаться направляющих и быть одинаковой по ширине. Чтобы помочь последовательно расставлять слова через интервалы, представьте, что между ними стоит «я». Расстояние между строками букв не должно быть меньше половины высоты символа.
2.4 Определение размеров
Добавление размеров и размеров к чертежу называется «простановкой размеров». Размеры говорят нам о точном расстоянии между двумя точками поверхностей, поэтому важно, чтобы они были разборчивыми.Будьте особенно внимательны при написании размеров и основывайте их на цифрах, показанных ниже.
- Используйте рекомендации по размерам.
- Как правило, высота большинства размеров составляет 3 мм.
- Буквенные трафареты содержат цифры соответствующего размера.
В десятичной системе счисления
- Десятичный маркер должен быть жирным, четким и размещаться на нижней направляющей цифр.
-
Если значение меньше 1, поместите ноль перед десятичным маркером, как показано ниже.
Элементы обмерования
При определении размеров каждого объекта будут задействованы элементы, показанные на схеме ниже. Считайте этот объект куском листового металла. И проекционные, и размерные линии представляют собой тонкие непрерывные линии.
Окончание размерных линий
В зависимости от ситуации размерные линии могут заканчиваться одним из следующих способов:
- Сплошные наконечники стрел, охватывающие угол не более 45 °.Обычно они рисуются, как указано, и имеют длину около 3 мм.
- Открытые стрелки, охватывающие угол 90 °.
- Короткие косые штрихи с центрами на конце размерной линии.
- Точки или кружки в конце размерной линии.
Для общего использования предпочтительны сплошные стрелки. Как правило, на любом рисунке следует использовать только один тип «концовки».
Окончание размерной линии
Размеры окружностей и дуг
Методы определения размеров
Параллельный расчет параметров состоит из нескольких размеров, происходящих из признака нулевых точек.Этот тип определения размеров используется там, где требуется высокий стандарт точности.
Нанесение размеров с наложением — это упрощенное определение параллельных размеров, которое может использоваться там, где пространство ограничено. Общее происхождение указано, как показано на рисунке выше. Размеры помещаются рядом со стрелкой и не касаются размерной линии.
Цепи размеров используются там, где сложение измерений не влияет на точность компонента.
Комбинированный размер использует как цепочку, так и параллель
определение размеров.
Нанесение размеров по координатам : наложенные беговые размеры могут использоваться в двух направлениях под прямым углом, как показано на рисунке выше. Общим началом может быть любой подходящий элемент базы.
Размерные углы : обратите внимание, что все размеры находятся вне дуг и являются горизонтальными.
Нанесение размеров фасок : важно понимать, что размеры не должны добавляться к чертежу случайным образом.
2.5 весов
Все рисунки должны быть выполнены в полном размере, если это возможно, но если размер объекта таков, что это невозможно, его необходимо нарисовать пропорционально, то есть в едином масштабе. Используемый масштаб должен быть указан на чертеже как пропорция или репрезентативная дробь, например масштаб 1: 2, что означает половинный размер. Обычно в заметках предостерегают от масштабирования рисунка, поскольку отпечатки могут растягиваться или сжиматься.
Рекомендуются масштабные множители и делители 2,5 и 10, а репрезентативная доля наиболее часто используемых шкал:
1: 1 Полный размер
1: 2 Половина полного размера
1: 5 Одна пятая от полного размера
1: 10 Одна десятая полного размера
2: 1 Двойной полный размер
5: 1 В пять раз больше размера
10: 1 В десять раз больше размера
Ортогональная проекция использует несколько видов объекта с точек обзора, повернутых относительно центра объекта с шагом 90 градусов.В проекции под первым углом каждый вид объекта проецируется в направлении (ощущении) зрения объекта. В проекции под третьим углом каждый вид объекта проецируется противоположно направлению (ощущению) зрения объекта.
Инженерный чертеж — это графический язык или международный язык, и это одна из основных форм общения в мастерской или на месте. Устное или письменное общение было единственным средством общения при решении технических вопросов, могло возникнуть недопонимание, особенно в отношении формы и размера, что могло иметь серьезные последствия для компании.Инженерный чертеж используется для передачи мысленного изображения объекта из чертежного кабинета в мастерскую или на объект.
Чертеж должен содержать достаточно информации, позволяющей мастеру преобразовать данную информацию в готовый компонент или работу без дальнейшего контакта с чертежным бюро.
Типы линий для инженерных чертежей, рекомендованные Британским институтом стандартов в BS 8888: 2004. Рекомендуются две толщины линий: толщина 0,7 мм и ширина 0.Ширина 3 мм.
Все рисунки должны быть выполнены в полном размере, если это возможно, но если размер объекта таков, что это невозможно, вы должны быть нарисованы пропорционально, то есть в едином масштабе. Используемый масштаб должен быть указан на чертеже как пропорция или репрезентативная дробь, например масштаб 1: 2, что означает половинный размер. Обычно в заметках предостерегают от масштабирования рисунка, поскольку отпечатки могут растягиваться или сжиматься.
Источник: http: // local.ecollege.ie/Content/APPRENTICE/liu/ind_insulation/mod2/m2_u2.doc
Если вы являетесь автором приведенного выше текста и не соглашаетесь делиться своими знаниями для обучения, исследований, стипендий (для добросовестного использования, как указано в авторские права США низкие) отправьте нам электронное письмо, и мы быстро удалим ваш текст. Добросовестное использование — это ограничение и исключение из исключительного права, предоставленного законом об авторском праве автору творческой работы. В законах США об авторском праве добросовестное использование — это доктрина, которая разрешает ограниченное использование материалов, защищенных авторским правом, без получения разрешения от правообладателей.Примеры добросовестного использования включают комментарии, поисковые системы, критику, репортажи, исследования, обучение, архивирование библиотек и стипендии. Он предусматривает легальное, нелицензионное цитирование или включение материалов, защищенных авторским правом, в работы других авторов в соответствии с четырехфакторным балансирующим тестом. (источник: http://en.wikipedia.org/wiki/Fair_use)
Информация о медицине и здоровье, содержащаяся на сайте, носит общий характер и цель , которая является чисто информативной и по этой причине не может в любом случае заменить совет врача или квалифицированного лица, имеющего законную профессию.
Тексты являются собственностью их авторов, и мы благодарим их за предоставленную нам возможность бесплатно делиться своими текстами с учащимися, преподавателями и пользователями Интернета, которые будут использоваться только в иллюстративных образовательных и научных целях.
Определение размеров — чтение базовых чертежей
- Цифры
- Размеры
- Внутренние линии
- Наконечники стрел
- Габаритные размеры
- Изометрические размеры
- Ортогональные размеры
Если рисунок должен быть законченным, чтобы объект, представленный на рисунке, мог быть выполнен так, как задумано дизайнером, он должен рассказывать две полные истории.Он сообщает об этом с помощью видов , которые описывают форму объекта, и размеров и примечаний , которые дают размеры и другую информацию, необходимую для создания объекта.
Следовательно, ваш следующий шаг — изучить основы определения размеров. Таким образом, вы поймете не только, как интерпретировать чертеж, чтобы получить необходимую информацию, но и как определить размеры своих эскизов, чтобы их можно было использовать для передачи информации о размерах другим.
ЦифрыЭто может показаться немного простым, но несколько упражнений с фигурами чисел предшествуют измерению. Причина такой проверки просто в том, что неправильно или небрежно нанесенные числа на чертеже или эскизе могут быть легко неверно истолкованы кем-то на работе. Это может стоить дорого.
Таким образом, изучение форм чисел оправдано.
Представленные здесь числовые формы признаны наиболее удобочитаемыми и используются в промышленности по всей стране.Стандартизированные в США вертикальные числа 1/8 дюйма правильно сформированы следующим образом:
Размерные линииРазмерная линия представляет собой тонкую темную сплошную линию со стрелками на каждом конце. Он указывает направление и протяженность измерения. На эскизах и чертежах машин, в которых для размеров используются дроби и десятичные дроби, размерная линия обычно прерывается около середины, чтобы обеспечить свободное пространство для размерных цифр. На архитектурных и конструктивных эскизах и чертежах цифры обычно располагаются над сплошной размерной линией.
В любом случае размерная линия, ближайшая к объекту, должна располагаться примерно на
1/2 дюйма. Остальные размеры за пределами первого измерения (если есть) должны находиться на расстоянии примерно 3/8 дюйма друг от друга. Вам не обязательно помнить об этом, но вы должны помнить, что не следует перегружать размерные линии и держать их на одинаковом расстоянии друг от друга.
Самым важным является то, что чертеж должен быть «чистым», а размеры должны быть размещены в пространстве, где их нельзя спутать с поверхностью, для которой они не предназначены.
Вот как следует рисовать размерные линии:
Примечание. Размеры менее шести футов (72 дюймов) указаны в дюймах. Размеры более шести футов обычно указываются в футах и дюймах. Убедитесь, что ясно, как называются размеры. При вызове размеров, превышающих 12 дюймов, убедитесь, что ВСЕ размеры указаны в дюймах или футах на всем чертеже. Либо 4’-5 ”, либо 53”, они оба означают одно и то же, но если есть сочетание размеров, можно легко взглянуть на 4’-8 ”и увидеть 48”.
Внутренние линииВыносные линии на чертеже — это тонкие темные сплошные линии, идущие наружу от точки на чертеже, к которой относится размер. Обычно размерная линия пересекает выносную линию под прямым углом. Должен быть зазор размером около 1/16 дюйма, где линия расширения должна совпадать с контуром объекта, а линия расширения должна выходить за край крайнего наконечника стрелки примерно на 1/8 дюйма. Также не должно быть зазоров на пересечении выносных линий.Обратите внимание, что в этом примере большие размеры правильно размещены снаружи или за меньшими размерами, и что размеры предпочтительно не наносятся на сам объект. Однако иногда необходимо измерить объект.
Важно не забывать размещать размеры на видах на чертеже с двумя или тремя видами, где они будут наиболее легко понимаемыми. Избегайте нанесения размеров на скрытую линию и избегайте дублирования размеров.Используй здравый смысл; сохраняйте размеры как можно более четкими и простыми. Помните, что человек, читающий ваш рисунок, должен четко понимать, вне всяких сомнений, как действовать дальше. В противном случае будет потрачено дорогое время и материал.
Существует два основных метода нанесения размеров на эскиз. Их можно разместить так, чтобы они читались снизу эскиза (однонаправленные размеры) или снизу и справа (выровненные размеры). Однонаправленная система обычно лучше всего, потому что она легче читается рабочими.
Когда размеры не помещаются в пространстве обычным способом, используются другие методы для точного определения размеров, когда существуют такие переполненные условия.
Наконечники стрел
Стрелки размещаются на каждом конце размерных линий, на линиях выноски и т. Д. Правильно сделанные стрелки имеют длину от 1/8 до 3/16 дюймов и примерно в три раза длиннее своей ширины. Обычно они имеют небольшую зазубрину, очень похожую на рыболовный крючок.
Чтобы ваш рисунок выглядел чистым, используйте один и тот же стиль во всем рисунке или эскизе.
Размерные цифрыЦифры, используемые для измерения объекта, обычно имеют высоту около 1/8 дюйма.
Если размер включает дробь, высота дроби составляет примерно 1/4 дюйма, поэтому дробные числа немного меньше, чтобы оставить место над и под дробной чертой.
Опять же, особенно важно, чтобы числа и дроби, которые вы можете нанести на эскиз или рисунок, были удобочитаемыми.Неряшливые числа могут стать причиной дорогостоящих ошибок.
БанкнотыПримечания используются на чертежах для предоставления дополнительной информации. Они должны быть краткими и тщательно сформулированными, чтобы избежать неверного толкования, и располагаться на эскизе в малолюдном месте. Линии выноски, идущие к заметке, должны быть короткими. Примечания обычно добавляются после того, как на эскизе были нанесены размеры, чтобы не мешать размерам.
Тест
Указания: Измерьте размеры примеров, как указано.
Обмерьте этот прямоугольник 3 ¼ x 6 15/32 в одном направлении сверху и справа.
В примечании покажите просверленное отверстие 5/16.
Измерьте размер этого объекта. Более короткие линии составляют 3 дюйма в длину.
Измерьте размер этого объекта. Используйте линейку или шкалу, чтобы определить длину линий.
Наклонные размерыНаклонные размеры — это в основном необходимость избегать нанесения размеров на самом объекте (когда это возможно) и использовать принципы определения размеров, основанные на здравом смысле.Также обычно лучше, чтобы размеры считывались снизу (однонаправленно), как показано здесь.
Хотя лучше не устанавливать размеры на самом виде, обычно принято указывать размеры диаметра и радиуса на видах, если позволяет пространство.
Иногда пространство и время ограничены, и вам, возможно, придется нарушить типичные правила рисования и определения размеров. Главное, чтобы чертеж был чистым, лаконичным, старались не повторять размеры, а указывать все необходимые.
Указания: Завершите, как указано.
Измерьте размер трехдюймового куба.
Более короткая часть этого стержня составляет 5/8 дюйма в диаметре и 2 1/8 дюйма в длину. Более длинная часть имеет диаметр 7/8 дюйма и длину 3 ½ дюйма. Нанесите размеры на чертеж.
Изометрические размерыПри нанесении размеров на изометрический эскиз важно, чтобы размеры не касались самого объекта, и размещать размер на той же плоскости, что и поверхность объекта, размер которого измеряется.Вы, вероятно, обнаружите, что для правильного измерения в изометрии потребуется некоторая практика.
Размещайте примечания на изометрическом чертеже, не обращая внимания на то, чтобы они располагались на одной плоскости с размерами. Это легче сделать и легче читать.
Изометрические банкноты не обязательно должны находиться в одной плоскости.
Обратите внимание, что в приведенном выше примере часть каждой линии выноски, ведущей к нотам, нарисована примерно под углом 15, 30, 45, 60 или 75 градусов.Это сделано во избежание путаницы с другими строками. Никогда не рисуйте линии выноски полностью горизонтально или вертикально .
Тест
Указания: заполните, как указано.
Обмерьте этот чертеж. Размеры: 3 дюйма в длину, 2 1/8 дюйма в ширину, 1 5/8 дюйма в высоту и угол 45 ° в глубину ½ дюйма. Угол начинается как середина трехдюймового размера.
Обмерьте этот чертеж. Основание — квадрат ½ «x 1 ½». Цилиндр имеет диаметр 1 дюйм.x 1-1 / 8 ”, длина
. Просверленное сквозное отверстие 5/8 ”.
Тест
Указания: Вам будет предоставлен объект для эскиза и измерения.
Ортогональные размерыКогда вы посмотрите на объект в форме ласточкина хвоста на несколько страниц назад, легко увидеть, что изометрический эскиз может быстро стать загроможденным размерами. Из-за этого более сложные эскизы и чертежи имеют размерную орфографию.Этот метод обеспечивает лучший способ четкого и детального измерения.
Вот семь общих правил, которым нужно следовать при расчете размеров.
- Покажите достаточно размеров, чтобы можно было определить предполагаемые размеры без того, чтобы рабочий вычислял или предполагал какие-либо расстояния.
- Четко укажите каждое измерение, чтобы оно понималось только одним способом.
- Отображение размеров между точками, линиями или поверхностями, которые имеют необходимое отношение друг к другу или которые определяют расположение других компонентов или сопрягаемых деталей.
- Выберите или расположите размеры, чтобы избежать накопления размеров, которое может привести к неудовлетворительному стыковке деталей. (Другими словами, обеспечьте увеличение допусков, как в примере ниже.
- Показать каждое измерение только один раз. (Не дублируйте размеры).
- По возможности, обмерьте каждый объект на виде там, где он наиболее четко виден и где проявляется его истинная форма.
- По возможности указывайте размеры, чтобы использовать легкодоступные материалы, детали и инструменты.
Обратите внимание, что размеры правильно размещены между видами, а не по внешним краям чертежа.
Тест
Направления: на отдельном листе бумаги сделать размерный орфографический эскиз этого объекта.
Указания: на отдельном листе бумаги сделать размерный орфографический эскиз объекта.
Тест
Указания: Вам будет предоставлен объект для эскиза и измерения.
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.ЯЗЫК}} {{$ select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Геометрия
Геометрия — это все о формах и их свойствах.
Если вам нравится играть с объектами или рисовать, то геометрия для вас!
Геометрию можно разделить на:
Плоская геометрия — это плоские формы, такие как линии, круги и треугольники … формы, которые можно нарисовать на листе бумаги
Solid Geometry — это трехмерные объекты, такие как кубы, призмы, цилиндры и сферы.
| Подсказка: попробуйте нарисовать некоторые формы и углы по мере обучения… помогает. |
Точка, линия, плоскость и твердое тело
Точка не имеет размеров, только позиция
Линия одномерная
Самолет двумерный (2D)
Твердое тело трехмерное (3D)
Почему?
Почему мы делаем геометрию? Чтобы открывать закономерности, находить площади, объемы, длины и углы, а также лучше понимать мир вокруг нас.
Плоская геометрия
Плоская геометрия — это все о формах на плоской поверхности (например, на бесконечном листе бумаги).
Полигоны
Многоугольник — это двумерная фигура, состоящая из прямых линий. Треугольники и прямоугольники — это многоугольники.
Вот еще несколько:
Круг
Теоремы о круге (расширенная тема)
Символы
В геометрии используется много специальных символов.Вот вам краткая справка:
Геометрические символы
Конгруэнтные и похожие
Уголки
Типы углов
Преобразования и симметрия
Преобразований:
Симметрия:
Координаты
Более сложные темы по геометрии плоскости
Пифагор
Конические секции
Теоремы о круге
Центр треугольника
Тригонометрия
Тригонометрия — отдельная тема, поэтому вам, возможно, захочется посетить:
Твердая геометрия
Solid Geometry — это геометрия трехмерного пространства, в котором мы живем…
… начнем с самых простых форм:
Общие 3D-фигуры
Многогранники и неполиэдры
Есть два основных типа твердых тел: «Многогранники» и «Неполиэдры»:
Многогранники (у них должны быть плоские грани) :
Non-Polyhedra (когда любая поверхность
не плоский) :
ОСНОВЫ ЧЕРТЕЖА
ОСНОВЫ ЧЕРТЕЖА РИСОВАНИЕ ПРИМЕЧАНИЯ К КЛАССАМСоздание инженерных чертежей это отдельная предметная область; в Черчение Технология.Это также освященный веками вид искусства. Рисунки находятся использовала все области инженерии (механическое, гражданское, архитектурное, Электрические, Аэрокосмическая промышленность и т. Д.) Типы чертежей, которые мы будем создавать в этом класс механический, но все концепции могут быть перенесены на Другие Инженерные области.Основное назначение техники рисунки это сообщить другим инженерам, машинистам и т. д. Чертежи общаться лучше всего лишь потому, что фотография стоит тысяча слова .Предоставление всей информации, необходимой для создания продукт и быть точным в этой информации является главной целью. Инженеры очень разборчивы в своих рисунках и должны уделять внимание деталям.
Ниже приведены основные концепции Инженерное дело Рисунки. Попытка взять объемы редакционного текста материал и свести к минимуму то, что вам нужно для этого класса.
В их числе:
Ортографические Просмотры Половина Просмотры и частичное Просмотры Типы линий Размеры и примечания Половина Просмотры и частичное Просмотры Вспомогательный Просмотры Раздел Просмотры Полный Раздел Половина Раздел Смещение (Набросал) Раздел Оборотный Раздел Сломанный Вне (Местный) Раздел Подробный Просмотры Обычный Разрывы Масштабирование
ОРТОГРАФИЧЕСКИЕ ИЗОБРАЖЕНИЯ
Ортогональных изображений двумерный виды объектов, где точка обзора объекта находится под прямым углом к (или глядя прямо на) поверхности.Они используются в технический и инженерные чертежи для точности. Если чья-то точка зрения не под прямым углом считается «ракурсом».
Вы также можете подумать об этих взгляды как объект внутри коробки, поверхности которого «выступают» на стороны коробки. Затем вы можете развернуть коробку, чтобы проецировать виды на плоская поверхность.
Потому что взгляды Только двухмерный, требуется более одного вида, чтобы полностью описать в объект. Обычно достаточно двух или трех представлений (Спереди, Сверху и Боковая сторона), но часто требуется больше.Вернуться к началуТрадиционно представления содержат Габаритные размеры следующим образом:
ПРОСМОТР РАЗМЕРЫ Передний Ширина и высота Верх Ширина и глубина Сторона Ширина и высота
ТИПЫ ЛИНИЙ
ЛИНИИ ОБЪЕКТОВЛинии объекта изображают видимые края объекта. В края, которые вы увидите, глядя на объект невооруженным глазом. Они показаны темными сплошными линиями.СКРЫТЫЕ ЛИНИИСкрытые линии обозначают невидимые края внутри объект. Края, которые вы не увидите, глядя на объект голым глаза. Они показаны пунктирными линиями.
ЦЕНТРАЛЬНЫЕ ЛИНИИВернуться к началуЦентральные линии обозначают центр цилиндрической формы объект будь то цилиндр или дыра. Они показаны длинной линией последовал короткой строкой, за которой следует длинная строка.
РАЗМЕРЫ, ИХ КОМПОНЕНТЫ И ПРИМЕЧАНИЯ
Размеры говорят, как далеко он находится от одной точки объекта до другой точки. Самый простой тип называется линейным размером , потому что он дает прямая линия расстояние от одной точки до другой. Также есть Radial , Диаметр и Угловой Размеры.Размеры состоят из четырех основных компонентов:
Обратите внимание, что выносные линии могут пересекаться более Объект Линии (видимые края объекта), ведущие к месту назначения, но все еще оставляю пробел.
- Размерный текст
- Размерная линия и стрелки
- Внутренние линии
- Зазор
Примечания добавлен текст для описания вещей на Рисунок. Самый простой тип — это просто текст, как в названии рисунка. В другой тип примечания содержит выноску, которая представляет собой стрелку, указывающую на тема заметки.
Рамка вокруг чертежа называется основной надписью или Формат .
ОСНОВНЫЕ СОВЕТЫ ПО РАЗМЕРАМ:
РАЗМЕЩЕНИЕ СТРЕЛКИ И ТЕКСТАРазмещение ваших размерных линий (стрелки) и измерение текст зависит от количества места между расширениями линии.
Вернуться к началу
ВИДЫ ПОЛОВИНЫ И ЧАСТИЧНЫЕ ВИДЫ
Половинные и частичные виды используются для простой экономии места когда половина или часть представления не требуется или является избыточной.
ДОПОЛНИТЕЛЬНЫЕ ВИДЫ
Вспомогательные виды используются для точного изображения объектов на Наклонные поверхности . Если на наклонном поверхность, нет необходимости создавать вспомогательный вид.Вернуться к началу
ВИД РАЗРЕЗА
Виды разрезов используются, чтобы избавиться от запутанных скрытых линии:
Это способ в нашем воображении разрезать объект а также создать ортогональный вид внутри объекта. Это как если бы объект были разрезаны пополам.
Место разреза объекта называется плоскостью разреза и направление обзора обозначено стрелками.Примечание РАЗДЕЛ A-A используется, если представление находится на странице, отличной от основных представлений.
Предположительно вырезанный материал «заштрихован» с узоры. Узоры часто изображают фактический материал объекта.
Вернуться к началу
ПОЛНЫЕ РАЗДЕЛЫВиды в полном сечении проходят по всему объекту.Полных видов разрезов можно разместить на той же странице или на другой. страница.
Плоскость разреза и стрелки всегда отображаются .
Вернуться к началу
ПОЛОВИНКАВиды половинного сечения используются в основном на симметрично расположенных сформированный предметы (где обе половинки одинаковые). Они отличный ярлык так как вы можете изобразить внутри и снаружи объекта все в одном Посмотреть.видов половинного разреза можно разместить на той же странице или на другой. страница.
Если вид отображается на другой странице, плоскость сечения и Стрелки всегда отображаются.
Вернуться к началу
СМЕЩЕНИЕ (Эскиз) РАЗРЕЗЫвидов сечений со смещением (называется эскизов разрезов в Pro / E) похожи на виды в полном сечении, за исключением того, что плоскость разреза следить определенные особенности внутри объекта.Виды сечения со смещением могут быть размещены на той же странице или на другая страница.
Плоскость разреза и стрелки всегда отображаются .
Вернуться к началу
ОБНОВЛЕННЫЕ ПРОСМОТРЫПовернутые виды — это быстрый способ отображения разреза что показывает внутреннюю форму объекта без создания полностью отдельный вид в разрезе. Режущая плоскость проходит через объект в желаемом месте и поворачивается на месте, чтобы показать в вид в разрезе.Виды вращающихся сечений размещаются на одной странице.Вернуться к началуПовернутые виды могут находиться внутри обычного вида:
Или сняли.
ВЫЛОМАННЫЕ (МЕСТНЫЕ) СЕКЦИИсломанных секций (называется местными секциями в Pro / E) — еще один ярлык для секционирования. Это способ сделать раздел смотреть только определенной и обычно небольшой площади.Вернуться к началуРазбитых видов разрезов помещаются на одну страницу.
Плоскость разреза и стрелки не отображаются.
ПОДРОБНЫЕ ПРОСМОТРЫСозданы детальные просмотры к показывать небольшие детализированные области вида в специальном увеличенном масштабе. Масштаб обычно в два раза больше, чем у обычного вида. Можно разместитьдетальных представлений на та же страница или другая страница.
Вернуться к началу
ОБЫЧНЫЕ ПЕРЕРЫВЫОбычные паузы — это способ изображения очень длинных объект без отображения всей длины.Часто используется для объектов нравиться стержни, трубки / трубопроводы или деревянные предметыВернуться к началу
МАСШТАБМасштабирование используется для изображения объектов на бумаге, которые либо больше или меньше бумаги.Вернуться к началуВ механических чертежах мы обычно используем десятичное или метрическое масштабирование.
- Если объект на больше, чем бумага, на взгляды на объект масштабируются вниз
- Если объект на меньше, чем бумага на , то взгляды на объект масштабируются вверх
- Если объект умещается на бумаге, то изображаются виды при Полный масштаб (1: 1)
Число слева от двоеточия указывает единицы на Страница.
Число справа от двоеточия указывает единицы на объекте. или СТРАНИЦА: ОБЪЕКТВы хотите думать об этом так, когда видите Десятичный дюйм масштаб 1: 2ОДИН БЛОК НА СТРАНИЦЕ = ДВА БЛОКА НА ОБЪЕКТЕ , или 1/2 Масштаб .
Стальные уголки с равными ножками
Свойства стальных уголков с равными ножками в имперских единицах указаны ниже.
| Размер (дюймы x дюймы) | Размеры | Статические параметры | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Глубина — h — (дюймы) | 06 (5) дюйм) | Площадь сечения (дюйм 2 ) | Масса (фунт на / фут) | Момент инерции — I x — (дюйм) 4 ) | |||||
| 12 x 12 | 12 | 1 3/8 | 30.9 | 105 | 410,0 | ||||
| 12 | 1 1/4 | 28,3 | 96,4 | 377,5 | |||||
| 12 | 1 1/8 | 12 | 1 | 22,9 | 77,8 | 310,4 | |||
| 10 x 10 | 10 | 1 3/8 | 25,6 | 8726 | 232,1 | 8726 | 232,1 | 23.5 | 79,9 | 215,1 |
| 10 | 1 1/8 | 21,2 | 72,3 | 196,2 | |||||
| 10 | 1 | 8 19,0 | 9019 9019 9019 9019 9019 9019 9019 90197/8 | 16,7 | 56,9 | 157,6 | |||
| 10 | 3/4 | 14,4 | 49,1 | 137,2 | |||||
| 826 8 1 | 16.7 | 56,9 | 98,0 | ||||||
| 8 | 1 | 15,0 | 51,0 | 89,0 | |||||
| 8 | 7/8 | 13,2 45199 | 13,2 45192 | 9026 3/411,4 | 38,9 | 69,7 | |||
| 8 | 5/8 | 9,6 | 32,7 | 59,4 | |||||
| 8 | 9/16 | 729,6 | 54,1 | ||||||
| 8 | 1/2 | 7,8 | 26,4 | 48,6 | |||||
| 6 x 6 | 6 | 1 | 6 | 1 | 9026|||||
| 6 | 7/8 | 9,7 | 33,1 | 31,9 | |||||
| 6 | 3/4 | 8,4 | 28,7 | 28,2 | 1 | 24,2 | 24,2 | ||
| 6 | 9/16 | 6,4 | 21,9 | 22,1 | |||||
| 6 | 1/2 | 5,8 | 9026 5,8 1947/16 | 5,1 | 17,2 | 17,7 | |||
| 6 | 3/8 | 4,4 | 14,9 | 15,4 | |||||
| 6 | 26 5712,4 | 13,0 | |||||||
| 5 x 5 | 5 | 7/8 | 8,0 | 27,2 | 17,8 | ||||
| 5 | 9/4 | ||||||||
| 5 | 5/8 | 5,9 | 20,0 | 13,6 | |||||
| 5 | 1/2 | 4,8 | 16,2 | 11,3 | 14,3 | 10,0 | |||
| 5 | 3/8 | 3,6 | 12,3 | 8,74 | |||||
| 5 | 5/16 | 3,016 7,4 | 3,016 9,4 | 3,016 7,4 | х 44 | 3/4 | 5,4 | 18,5 | 7,67 |
| 4 | 5/8 | 4,6 | 15,7 | 6,66 | 4/2 3.8 | 12,8 | 5,56 | ||
| 4 | 7/16 | 3,3 | 11,3 | 4,97 | |||||
| 4 | 3/8 | 2,9 826 9 | 2,9 | 2,9 | 5/16 | 2,4 | 8,2 | 3,71 | |
| 4 | 1/4 | 1,9 | 6,6 | 3,04 | |||||
| 3 1/2 x 3 1/2 | / 21/2 | 3.3 | 11,1 | 3,64 | |||||
| 3 1/2 | 7/16 | 2,9 | 9,8 | 3,26 | |||||
| 3 1/2 | 3/8 | 8,5 | 2,87|||||||
| 3 1/2 | 5/16 | 2,1 | 7,2 | 2,45 | |||||
| 3 1/2 | 1/4 | 1,7 | 5,8 | 13 2,01 | 902 x 33 | 1/2 | 2.75 | 9,4 | 2,22 |
| 3 | 7/16 | 2,43 | 8,3 | 1,99 | |||||
| 3 | 3/8 | 2,11 7,2 | 2,11 7,2 | 2,11 7,2 | 5/16 | 1,78 | 6,1 | 1,51 | |
| 3 | 1/4 | 1,44 | 4,9 | 1,24 | |||||
| 316 | 3/409 | 3,7 | 0,96 | ||||||
| 2 1/2 x 2 1/2 | 2 1/2 | 1/2 | 2,25 | 7,7 | 1,23 | ||||
| 2 1/2 | 3/8 | 1,73 | 5,9 | 0,98 | |||||
| 2 1/2 | 5/16 | 1,46 | 5,0 | 0,85 | |||||
| 2 1/2 | 1/4 | 4,1 | 0,70 | ||||||
| 2 1/2 | 3/16 | 0. | |||||||