Программирование на языке R, if else, циклы for и while
автор: Samoedd Ноябрь 29, 2017 17 Комментарии
Создание скриптов и функций в R зачастую требует навыки программирования, а именно: использования логических операторов (например, >= «больше или равно») и управляющих структур (if else, for и while). Благодаря им мы можем задавать условия, при которых будет выполняться то или иное действие, а также определять порядок выполнения действий и их повторяемость.
Другими словами, управляющие структуры автоматизируют процессы анализа данных, прописав возможные сценарии и условия их выполнения. Программирование на языке R позволяет не только уменьшить код скрипта/функции, но и существенно сэкономить время, доверив всю рутинную работу компьютеру.
Логические операторы в R
Операторы в R можно разделить на две категории: арифметические и логические. Арифметическими операторами являются знакомые нам со школы знаки сложения, вычитания, умножения и деления, а также знак возведения в степень и модульные операции (+, -, *, /, ^, %% и %/%, соответственно).
В языке R существует 9 логических операторов, без знания которых программирование не представляется возможным.
| Оператор | Описание |
|---|---|
| > | Больше |
| >= | Больше или равно |
| < | Меньше |
| <= | Меньше или равно |
| == | Равно |
| != | Не равно |
| & | Логическое И |
| | | Логическое ИЛИ |
| ! | Логическое НЕ |
Обратите внимание, что «=» и «==» — это два разных оператора: в то время как первый присваивает значение переменной, второй сравнивает их на предмет равенства и выдает результат в виде TRUE или FALSE. 3
b = 11*11*11
a & b == 1331
[1] TRUE
3
b = 11*11*11
a & b == 1331
[1] TRUE
В целом принцип простой: на левой стороне от логического оператора находится «значение/переменная 1», на правой — «значение/переменная 2», в то время, как сам оператор является критерием, по которому R «судит» о правильности утверждения. Если утверждение верно, то в командной строке будет выведено TRUE, если утверждение ложно — FALSE. Следует добавить, что логические операторы работают со всеми типами данных: от векторов до таблиц, что делает их незаменимым инструментом в стат. анализе.
a <- c(1,2,3,5,8,10) a >= 5 [1] FALSE FALSE FALSE TRUE TRUE TRUE b <- a[a >= 5] b [1] 5 8 10
Теперь мы знаем, что такое логические операторы и готовы к изучению второй части этой статьи — работе с управляющими структурами в R.
Программирование и управляющие структуры
Существует около десятка управляющих структур на которых базируется программирование в R. Среди них можно выделить три наиболее используемые: оператор условий if else и два типа циклов — for и while.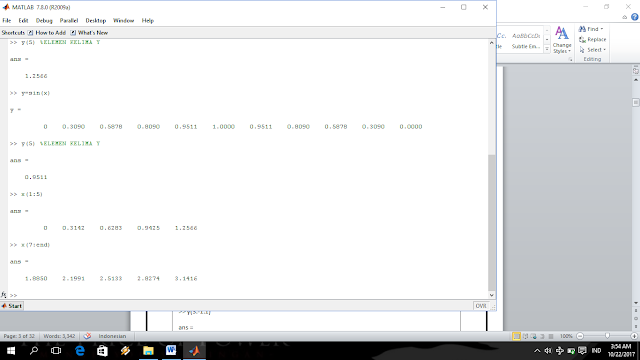
Оператор условий if else используется, когда есть два и более варианта развития сценария: если условие выполняется — «делай это», если не выполняется — «делай то». Суть же циклов в том, что они повторяют одно и то же действие несколько раз: в цикле while действие повторяется пока не выполнится условие цикла, а в цикле for — определенное пользователем количество раз.
На рисунке изображены три вида управляющих структур, где стрелки отображают поток данных. Если условие выполняется (TRUE), то поток данных движется вниз от условия, если нет (FALSE), то вправо и вниз. Как можно заметить в структурах типа while и for при выполнении условия, поток данных циркулирует по кругу: именно по этой причине их и называют циклами. Давайте разберем каждую из этих структур на практике!
Оператор условий if else в R
В языке программирования R оператор условий if else состоит из трех элементов:
- индикатор структуры: if, else или else if (в случае, когда условий больше одного)
- условие структуры, заключенного в круглые скобки (где находится условие для выполнения действия).

- тело структуры, заключенного в фигурные скобки (где находится код самого действия)
Пример 1: покупай больше, плати меньше —
if без elseДавайте создадим простейший вариант структуры if else, когда есть только одно условие при соблюдении которого, требуется выполнить дополнительное действие в сценарии. Допустим, в магазине акция: при покупке на сумму от 100$, предоставляется 12.5% скидка. Сколько мы в итоге потратим если наша покупка (x) была на сумму 120$?
x = 120
if(x >= 100){
x = x - x*12.5/100
print(x)
}
[1] 105Итак, в скобках находится условие, что общая стоимость покупок будет меняться только в случае, если x >= 100. Внутри фигурных скобок отображен код, иллюстрирующий механизм изменения финальной стоимости. Как Вы видите, индикатор else был не указан в конструкции. Мы его опустили, так как в случае, если x < 100, то никаких действий производиться не будет.
Следует также отметить, что для того, чтобы изменить показатель x, и проверить финальную цену, нам придется запускать весь код конструкции заново. Это непрактично, именно поэтому конструкцию if else чаще всего используют внутри функции. Давайте создадим и запустим функцию с оператором условий if else внутри.
shop <- function(x){
if(x >= 100){
x = x - x*12.5/100
print(x)
}
}
shop(120)
[1] 105
shop(50)
[1] 50Пример 2: прогрессивная система скидок — индикатор
else ifДобавим второе условие: если сумма покупок больше или равна 1000$, то магазин предоставит 25% скидку. Для этого условия мы будем использовать индикатор else if. В этом случае, нужно также изменить параметры первого условия, где x должно быть больше или равно 100, но меньше 1000. Если же ни первое, ни второе условие не соблюдается, то выведем на экран сообщение «No discounts» после финальной цены при помощи индикатора else.
shop <- function(x){
if(x >= 100 && x < 1000){
x = x - x*12.5/100
print(x)
}
else if(x >= 1000){
x = x - x*20/100
print(x)
}
else{
print(c(x, "No discounts"))
}
}
shop(20)
[1] 20 "No discounts"
shop(200)
[1] 175
shop(2000)
[1] 1600
Также внутрь оператора условий if else можно вставить другой оператор if else, либо циклы while или for. Подобное свойство вложения управляющих структур позволяет реализовывать сложные многоуровневые сценарии (алгоритмы) на практике, создавая функции с несколькими аргументами, и множеством условий и циклов внутри.
Циклы while и for в R
Ранее мы упоминали, что при неоднократном повторении кода в скрипте следует использовать R функции, чтобы уменьшить размер кода и сделать его более читабельным. Однако, в большинстве ситуаций это будет сделать невозможно без использования циклов внутри функции. Если есть условие, при исполнении которого потребуется повторить действие, используйте цикл while (перевод с англ.: «до тех пор, пока»). Если условия нет, но надо выполнить действие определенное количество раз, воспользуйтесь циклом for.
Если есть условие, при исполнении которого потребуется повторить действие, используйте цикл while (перевод с англ.: «до тех пор, пока»). Если условия нет, но надо выполнить действие определенное количество раз, воспользуйтесь циклом for.
Пример 3: уникальная методика бега — цикл for
Допустим у нас есть друг который решил заняться бегом. До этого он не бегал и находится в ужасной физической форме: максимум сколько он смог пробежать за первую тренировку — 100 метров. Друг пообещал, что через 100 дней он за тренировку будет пробегать больше 10 км, так как он разработал собственную методику: он будет заниматься ежедневно и прибавлять по 5% к дистанции от предыдущей нагрузки.
Проверим при помощи цикла for сработает ли его методика в теории. Для этого создадим функцию run.10km и переменную y, обозначающую дистанцию тренировки (в км). Внутри круглых скобок цикла for напишем что круг будет повторяться 100 раз, а внутри квадратных код вычислений дистанции для каждого дня. Дистанция последнего дня будет выделена на экран при использовании функции.
Дистанция последнего дня будет выделена на экран при использовании функции.
run.10km <- function(y){
for(i in 1:100){
y<-y+y*0.05
}
print(y)
}
run.10km(0.1)
[1] 13.15013
Оказалось, Ваш друг действительно прав: благодаря этой методике он сможет пробежать через 100 дней более 13 км за тренировку! Теоретически…
Пример 4: может тренироваться реже, но интенсивнее — цикл while
Однако, тренироваться ежедневно без выходных для начинающего — это неминуемый путь к физическому и психическому истощению. Чтобы у друга дни нагрузок чередовались с днями отдыха, давайте предложим ему альтернативную методику: тренироваться через день, но прибавляя к дистанции по 10% от предыдущей нагрузки (вместо 5%).
Рассчитаем, используя цикл while, через сколько дней друг начнет пробегать более 10 км за тренировку и выведем результат в виде таблицы каждая строчка которой отображает день тренировки и предполагаемую дистанцию.
alter.10km <- function(y){
i <- 1
Day <- i
Distance <- y
while(y <= 10){
i <- i + 2
y<-y+y*0.1
Day <- append(Day,i)
Distance <- append(Distance,y)
}
DF <- data.frame(Day, Distance)
return(DF)
}
results <- alter.10km(0.1)
tail(results, 3)
Day Distance
48 95 8.819749
49 97 9.701723
50 99 10.671896Таким образом, наш друг с 99-го дня станет пробегать более 10 км за тренировку занимаясь реже, но интенсивнее! Выглядит, как более реалистичный вариант, но что скажет друг?
Заключение
Сегодня мы использовали простые и наглядные примеры, чтобы понять принцип и суть программирования на языке R. Знания логических операторов и структур управления позволят Вам реализовывать любые идеи в статистическом анализе, не ограничиваясь существующими решениями в R пакетах и интернете. Программирование на R не только экономит Ваше время, но и делает статистический анализ увлекательным и творческим занятием. Дерзайте!
Дерзайте!
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Что такое реляционные операторы в MATLAB?
Заин Али Бабар
Устали от LeetCode? 😩
Изучите 24 шаблона, чтобы решить любой вопрос на собеседовании по кодированию, не заблудившись в лабиринте практических задач в стиле LeetCode. Практикуйте свои навыки в практической среде кодирования, не требующей настройки. 💪
Обзор
Операторы — это специальные ключевые слова или символы, выполняющие определенные функции. MATLAB поддерживает использование операторов как для скалярных, так и для нескалярных данных. реляционные операторы , поддерживаемые в MATLAB, перечислены и объяснены ниже:
MATLAB поддерживает использование операторов как для скалярных, так и для нескалярных данных. реляционные операторы , поддерживаемые в MATLAB, перечислены и объяснены ниже:
Реляционные операторы
Равно (
== ) Оператор == используется для определения равенства двух чисел или массивов.
В случае чисел ответ будет 1 , если значения равны, и 0 , если значения не равны.
В случае массива возвращается массив ответов. Соответствующие записи 1 , если элементы равны, и 0 , если элементы не равны.
//Сравнение скаляра со скаляром Х = 5 Y = 5 X == Y // мы получим ответ 1, так как утверждение X == Y верно //Сравнение массива с массивом Х = [5 6 7 9] Y = [5 7 6 9] Х == У // получим ответ [1 0 0 1]. Мы получаем 1 по индексам 0 и 3, так как они равны. Остальные индексы равны 0, так как они не равны //Сравнение массива со скаляром Х = [5 6 7] Y = 5 Х == У // получим ответ [1 0 0].Мы получаем 1 по индексу 0, так как он равен. Мы получаем 0 по индексам 1 и 2, так как они не равны
Не равно (
~= ) Оператор ~= используется для определения неравенства двух чисел или массивов.
В случае чисел ответ будет 1 , если значения не равны, и 0 , если они равны.
В случае массива возвращается массив ответов. Соответствующие записи: 1 , если элементы не равны, и 0 , если элементы равны.
//Сравнение скаляра со скаляром Х = 5 Y = 5 Х ~= Y // мы получим ответ 0 //Сравнение массива с массивом Х = [5 6 7 9] Y = [5 7 6 9] Х ~= Y // получим ответ [0 1 1 0] //Сравнение массива со скаляром Х = [5 6 7] Y = 5 Х ~= Y // получим ответ [0 1 1]
Больше чем (
> ) Оператор > используется для определения большего из двух чисел или массивов.
В случае чисел ответ 1 , если значение слева от > больше, чем значение справа. В противном случае ответ будет
В противном случае ответ будет 0 .
В случае массива возвращается массив ответов. Соответствующие записи равны 1 , если правые элементы массива больше, чем левые элементы массива. В противном случае элементы массива ответов имеют вид 0 .
//Сравнение скаляра со скаляром Х = 6 Y = 5 Х > У // получим ответ = 1 //Сравнение массива с массивом Х = [5 6 7 9] Y = [5 7 6 10] Х > У // получим ответ [0 0 1 0] //Сравнение массива со скаляром Х = [5 6 7] Y = 5 Х > У // получим ответ [0 1 1]
Больше или равно (
>= ) Оператор >= используется для определения большего из двух чисел или массивов или их равенства.
В случае чисел ответ будет 1 , если значение слева от >= больше или равно значению справа. В противном случае ответ 0 .
В случае массива возвращается массив ответов. Соответствующие записи равны 1 , если правые элементы массива больше или равны соответствующим левым элементам массива. В противном случае элементы массива ответов равны
В противном случае элементы массива ответов равны 0 .
//Сравнение скаляра со скаляром Х = 6 Y = 5 X >= Y // мы получим ans = 1, так как X больше Y. //Сравнение массива с массивом Х = [5 6 7 9] Y = [5 7 6 10] Х >= Y // получим ответ [1 0 1 0] //Сравнение массива со скаляром Х = [5 6 7] Y = 5 Х >= Y // получим ответ [1 1 1].
Меньше чем (
< ) Оператор < используется для определения меньшего из двух чисел или массивов.
В случае чисел ответ будет 1 , если значение слева от < меньше значения справа. В противном случае ответ будет 0 .
В случае массива возвращается массив ответов. Соответствующие записи равны 1 , если правые элементы массива меньше соответствующих левых элементов массива. В противном случае элементы массива ответов равны 0 .
//Сравнение скаляра со скаляром Х = 6 Y = 5 Х < Y // мы получим ответ 0 //Сравнение массива с массивом Х = [5 6 7 9] Y = [5 7 6 10] Х < Y // получим ответ [0 1 0 1] //Сравнение массива со скаляром Х = [5 2 3] Y = 5 Х < Y // получим ответ [0 1 1]
Меньше или равно (
<= ) Оператор <= используется для определения меньшего из двух чисел или массивов или определения их равенства.
В случае чисел ответ будет 1 , если значение слева от <= меньше или равно значению справа. В противном случае ответ будет 0 .
В случае массива возвращается массив ответов. Соответствующие записи равны 1 , если правые элементы массива меньше или равны соответствующему левому элементу массива. В противном случае элементы массива ответов равны 0 .
//Сравнение скаляра со скаляром Х = 6 Y = 5 Х <= Y // мы получим ответ 0 //Сравнение массива с массивом Х = [5 6 7 9] Y = [5 7 6 10] Х <= Y // получим ответ [1 1 0 1] //Сравнение массива со скаляром Х = [5 6 7] Y = 5 Х <= Y // получим ответ [1 0 0].
Связанные теги
MATLAB
CommunityCreator
Relationaloperator
Вклад
Zain Ali Babar
Лицензия: Creative Commons-Attribution-Sharealike 4.0 (CC-BY-SA 4.0)
Опепировки | Обработка данных с помощью MATLAB
В этой заметке рассматриваются некоторые наиболее широко используемые операторы в MATLAB.
Операторы MATLAB
Полный список операторов MATLAB можно найти здесь. Для каждого оператора есть также функция MATLAB, которая делает то же самое за вас. Ниже приводится сводка наиболее важных операторов и соответствующих им функций в MATLAB.
| Символ | Роль | Альтернатива | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
+ | Addition | plus() | |||||||||||||||||||||||||
+ | Unary plus | uplus() | |||||||||||||||||||||||||
- | Subtraction | minus () | |||||||||||||||||||||||||
- | Unary minus | uminus() | |||||||||||||||||||||||||
. | Element-wise multiplication | times() | |||||||||||||||||||||||||
* | Matrix multiplication | mtimes() | |||||||||||||||||||||||||
./ | Поэлементное правое деление | rdivide() | |||||||||||||||||||||||||
/ | Matrix right division | mrdivide() | |||||||||||||||||||||||||
.\ | Element-wise left division | ldivide() | |||||||||||||||||||||||||
\ | Левое деление матрицы (обратная косая черта) | mldivide() | |||||||||||||||||||||||||
| 9 | Мощность матрицы | mpower() | |||||||||||||||||||||||||
.' | Transpose | Transpose () | |||||||||||||||||||||||||
' | Комплексный конъюгат | CTRANPOVE () 22022020 | CTRANPOVE () 22022020 | CTRANPOVE () 22022020 | () 220 220220 | . |
| Символ | Роль | Альтернатива |
|---|---|---|
и | Логическое И | и() |
| | Logical OR | or() |
&& | Logical AND (with short-circuiting) | -- |
|| | Логическое ИЛИ (с коротким замыканием) | -- |
~ | Логическое НЕ | not() |
Логический оператор короткого замыкания в MATLAB
Обратите внимание, что существует два типа логических операторов, один из которых называется коротким замыканием. Более подробную информацию о них и их значениях можно найти здесь.
Более подробную информацию о них и их значениях можно найти здесь.
Специальные символы в MATLAB
Существует также набор символов, играющих особую роль в MATLAB, некоторые из которых мы уже обсуждали. Вы можете узнать о них здесь.
Типовое литье
В информатике преобразование типов, приведение типов или приведение типов — это разные способы изменения выражения из одного типа данных в другой. Примером может служить преобразование целочисленного значения/переменной в значение/переменную с плавающей запятой или его текстовое представление в виде строки и наоборот.
Неявное приведение типов и перегрузка операторов
MATLAB — это язык со слабой или слабой типизацией, что имеет ряд практических последствий. Первое и, вероятно, наиболее заметное различие между MATLAB и строго типизированным языком заключается в том, что вам не нужно явно объявлять типы используемых вами переменных. Например, объявления x=5; x='foo', следующие друг за другом, вполне допустимы; первое объявление заставляет x рассматриваться как число, второе изменяет его обработку на строку.
Основным преимуществом использования языка со слабой типизацией является возможность быстрого прототипирования . Количество строк кода, необходимых для объявления и использования динамически размещаемого массива в C (и правильной очистки после его использования), намного больше, чем количество строк, необходимых для того же процесса в MATLAB. Слабая типизация также хороша для повторного использования кода. Вы можете написать скалярный алгоритм в MATLAB и с относительно небольшими усилиями модифицировать его для работы с массивами так же, как со скалярами. Тот факт, что MATLAB является скриптовым, а не компилируемым языком, также способствует быстрому прототипированию.
Однако слабая типизация не лишена подводных камней. Например, слабая типизация в сочетании с неожиданным вводом пользователем может иногда приводить к ошибочным результатам,
>> x=5; >> у=4; >> х/у
ответ =
1.2500
, тогда как тот же самый код на компилируемых языках со строгой типизацией, таких как C и Fortran, дал бы целочисленное значение 1 .
Слабая типизация в сочетании с внутренней перегрузкой операторов MATLAB также может привести к неожиданным результатам при выполнении операций между смешанными типами. Подумайте, что произойдет, если вы добавите 1+'1' , то есть скаляр 1 и символ '1'. Удивительный результат — 50. MATLAB автоматически преобразует символ '1' в его значение представления ASCII, равное 49 (вы можете получить код ASCII для любого символа, используя функцию abs() ). После этого неявного преобразования MATLAB добавляет скалярное значение 1 , чтобы вернуть 50 .
Примечание: Хотя этот пример несколько надуман, он может легко возникнуть, особенно при передаче аргумента функции, тип которого не определен. Чтобы написать полностью безопасный слаботипизированный код, пользовательский ввод всегда должен проверяться перед выполнением над ним операций.
Ситуация может быть более сложной, если вы имеете дело со строками, а не с отдельными символами. Например,
Например,
>> х=10; >> у='10'; >> х+у
ответ =
59 58
Выше произошло то, что '10' считается вектором символов, поэтому, когда вы добавляете его к 10 , Matlab автоматически преобразует эту строку в вектор соответствующих значений ASCII и добавляет значение 10 каждому.
>> «Привет» + «Мир»
ответ =
159 212 222 216 211
Явное приведение типов
В отличие от неявного приведения типов, которое выполняется MATLAB под капотом, как описано выше, что также может быть опасным, вы также можете явно запросить MATLAB преобразовать тип переменной в какой-либо другой тип, используя встроенную функцию MATLAB. -in функции, такие как cast , или одна из многих других функций, которые MATLAB имеет для этой цели.
Операции с массивами и матрицами
Мы уже узнали, что массивы и матрицы в MATLAB — это не одно и то же. В результате операторы, которые могут на них воздействовать, также не идентичны.
Операции с матрицами следуют правилам линейной алгебры и несовместимы с многомерными массивами. Требуемый размер и форма входных матриц зависят от типа операции. Для нескалярных входных данных матричные операторы обычно вычисляют ответы, отличные от их аналогов операторов массива.
Операции с массивами выполняют поэлементные операции над соответствующими элементами векторов, матриц и многомерных массивов. Если операнды имеют одинаковый размер, то каждый элемент в первом операнде сопоставляется с элементом в том же месте во втором операнде. Если операнды имеют совместимые размеры, то каждый вход неявно расширяется по мере необходимости, чтобы соответствовать размеру другого.
Вы можете узнать больше о них в руководстве по MATLAB.
Приоритет оператора в MATLAB
Вы можете создавать выражения, использующие любую комбинацию арифметических, реляционных и логических операторов. Уровни приоритета определяют порядок, в котором MATLAB® оценивает выражение. В пределах каждого уровня приоритета операторы имеют одинаковый приоритет и оцениваются слева направо. Правила приоритета для операторов MATLAB показаны в этом списке, упорядоченном от самого высокого уровня приоритета до самого низкого уровня приоритета:
В пределах каждого уровня приоритета операторы имеют одинаковый приоритет и оцениваются слева направо. Правила приоритета для операторов MATLAB показаны в этом списке, упорядоченном от самого высокого уровня приоритета до самого низкого уровня приоритета:
- Скобки
(). - Транспонировать 9~ работают со секунды справа налево. Рекомендуется использовать круглые скобки для явного указания предполагаемого приоритета операторов, содержащих эти комбинации операторов.)
- Унарный плюс
+, унарный минус-, логическое отрицание~. - Умножение
.*, правое деление./, левое деление.\, умножение матриц*, матрица правое деление/, матрица левое деление\. - Сложение
+, вычитание-. - Оператор двоеточия
:. - Меньше
<, меньше или равно<=, больше>, больше или равно>=, равно==, не равно~=.
 СПАСИБО АНДРЕЙ !!!
СПАСИБО АНДРЕЙ !!!  Для вызова из файла ему нужно просмотреть все пути поиска и выбрать нужную функцию, на ээто вроде как время уходит.
Для вызова из файла ему нужно просмотреть все пути поиска и выбрать нужную функцию, на ээто вроде как время уходит.

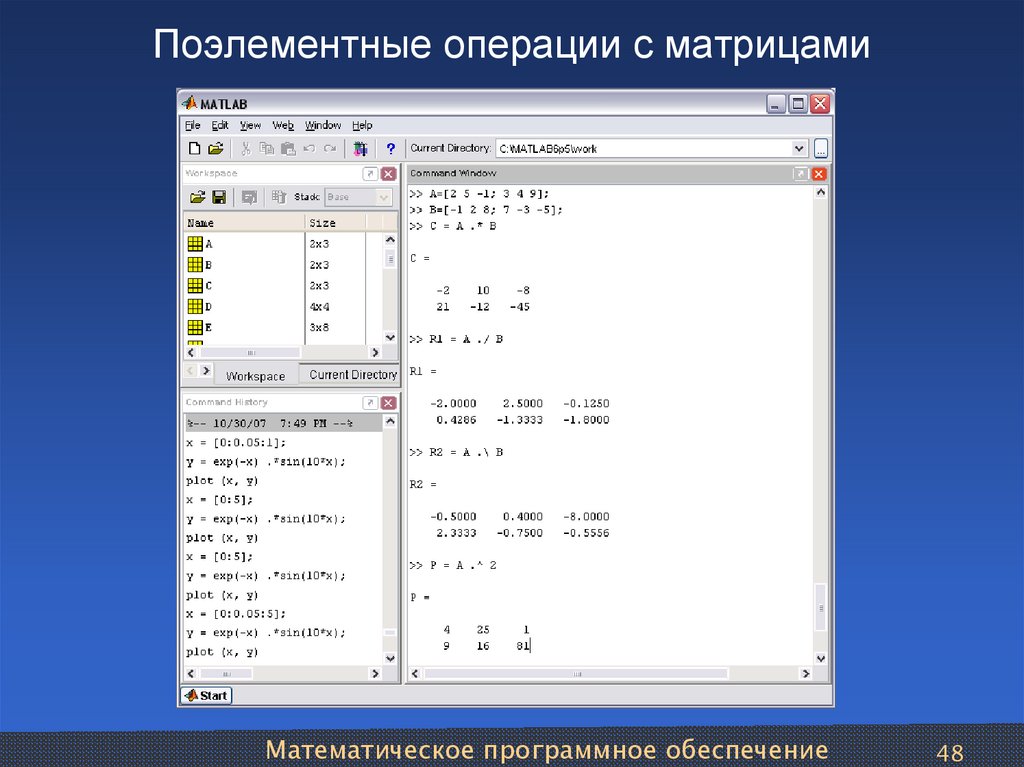
 .. он тебе раскажет сколько раз ты каждую из строчек исполняешь
.. он тебе раскажет сколько раз ты каждую из строчек исполняешь научил но он походу вперед меня откоментил
научил но он походу вперед меня откоментил Он мне говорит сколько времени он в каждой функции сидел, как мне сделать так что он быстрее все это делать будет?
Он мне говорит сколько времени он в каждой функции сидел, как мне сделать так что он быстрее все это делать будет?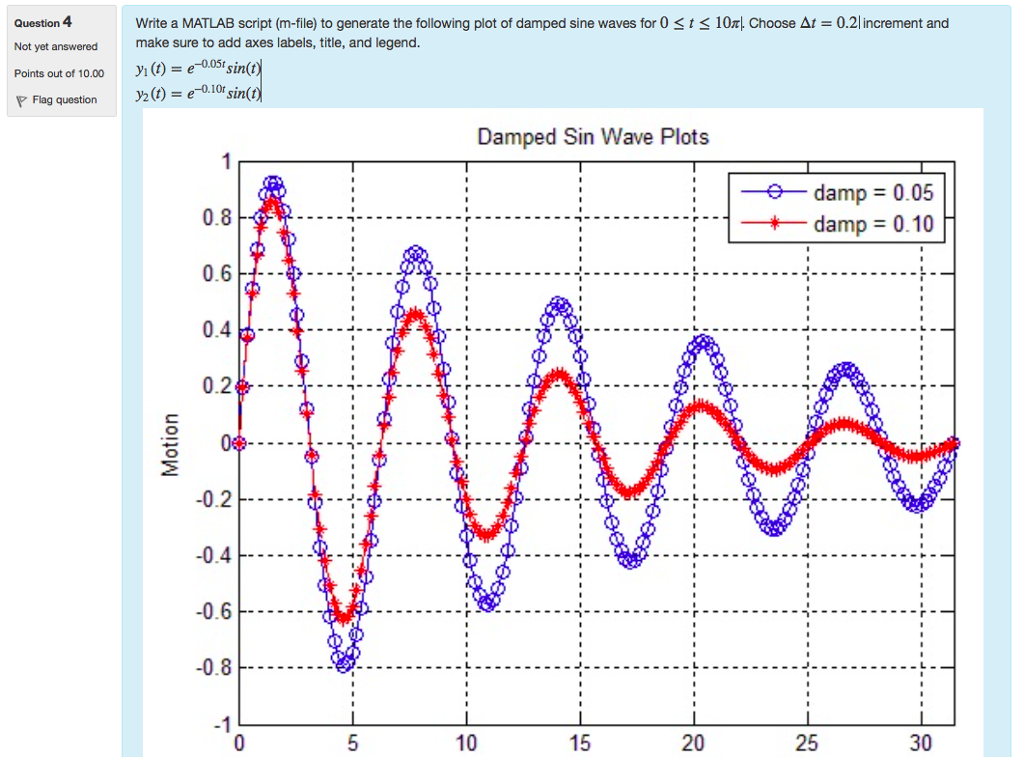 The pcode command performs the parsing step and stores the result on the disk as a P-file to be loaded later.
The pcode command performs the parsing step and stores the result on the disk as a P-file to be loaded later.
 Только покупать надо на их стенде только. Мне обяз нужны кисти (расположу в порядке обязательности 🙂 182, 266, 209. Палетка теней Heatherette Trio 1, рефиллы теней Satin Taupe, Patina, подводку для глаз Ffluidline черную… Я пока остановлюсь, я итак не уверенна, что человек потратиться. Могу вам перевод денюжки сделать, как скажите, так и сделаю.
Только покупать надо на их стенде только. Мне обяз нужны кисти (расположу в порядке обязательности 🙂 182, 266, 209. Палетка теней Heatherette Trio 1, рефиллы теней Satin Taupe, Patina, подводку для глаз Ffluidline черную… Я пока остановлюсь, я итак не уверенна, что человек потратиться. Могу вам перевод денюжки сделать, как скажите, так и сделаю.
 *
*  Таблица рациональных операторов в MATLAB.
Таблица рациональных операторов в MATLAB.