|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж… Интересное: Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль. Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 3Следующая ⇒ В ML существует большое количество элементарных математических функций для выполнения действий с числами: тригонометрические, степенные, логарифмические, экспоненциальные и функции округления. Существуют встроенные тригонометрические и гиперболические функции: sin(x), cos(x), tan(x), cot( Некоторые часто используемые математические функции: · exp(x)–экспонента числа x; · log(x)– натуральный логарифм; · log10(x)– десятичный логарифм; · sqrt(x)– квадратный корень; · abs(x)– абсолютное значение x; · mod(x, y)– остаток от целочисленного деления с учетом знака; · rem(x, y)– остаток от целочисленного деления без учета знака; · real(z)– вещественная часть комплексного числа; · imag(z)– мнимая часть комплексного числа;· round(x)– округление до ближайшего целого. Более полный список основных математических функций MatLab:
С использованием вышеупомянутых функций, записать и сосчитать значение арифметического выражения: Вычислить: res= Составление арифметического выражения лучше всего начинать с расстановки основных скобок выражения. res = 1.0207e+006 Для эффективной работы с большими наборами данных или при необходимости многократных вычислений рассмотренных средств недостаточно. В Файлы-программы (их называют скриптами или сценариями) являются самым простым типом m-файлов. Script-файл состоит из последовательности команд, не содержит заголовка, а также входных и выходных параметров. Все объекты, используемые внутри script-файла, считаются глобальными. Если в рабочем пространстве есть данные, то внутри script-файла их можно использовать, а по окончании его выполнения использовать данные, созданные с его помощью. Перед запуском программы на выполнение необходимо установить каталог, содержащий скрипт-файл, в качестве текущего. Запуск файла на выполнение можно осуществить двумя способами: из окна редактора и из командного окна. Для выполнения файла-программы достаточно в командной строке указать имя этого скрипта. Для запуска программы на выполнение из окна редактора надо выбрать пункт меню Debug, Run или нажать функциональную клавишу F5, или выбрать соответствующую пиктограмму на панели инструментов. Выполнить программу, уже сохраненную на диске, можно из командного окна ML, просто набрав имя файла без расширения.
⇐ Предыдущая123Следующая ⇒ Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций. Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… |
Каждая функция обладает именем и списком аргументов, которые задаются в круглых скобках и, если их несколько, перечисляются через запятую.
2-sin(x-pi/3))/(log(abs(y))+exp (sqrt (x+1))/(2*x))*1E6
Такие файлы используются для автоматизации выполнения большого набора инструкций. Их текст набирают в окне встроенного редактора ML.
Алгебраические и арифметические функции MatLab
Арифметические операторы и функции
Операторы отношения и их функции
Логические операторы
Специальные символы
Системные переменные и константы
Функции поразрядной обработки
Функции обработки множеств
Функции времени и даты
Элементарные функции
Алгебраические и арифметические функции
Тригонометрические и обратные им функции
Гиперболические и обратные им функции
Функции округления и знака
Функции комплексного аргумента
Что нового мы узнали?
В системе MATLAB определены следующие алгебраические и арифметические функции:
abs(X)
— возвращает абсолютную величину для каждого числового элемента вектора
X.
Если X содержит комплексные числа, abs(X) вычисляет модуль каждого числа.
Примеры:
abs(-5) = 5
abs(3+4i) =5
» abs([1 -2 1 3i 2+3i ])
ans =
1.0000 2.0000 1.0000 3.0000 3.6056
ехр(Х) — возвращает экспоненту для каждого элемента X. Для комплексного числа z = х + i*y функция exp(z) вычисляет комплексную экспоненту: exp(z)=exp(x)*(cos(y)+i*sin(y)).
Примеры:
» ехр([1 23])
ans =
2.7183 7.3891 20.0855
» exp(2+3i)
ans =
-7.
3151
+ 1.0427i
factor(n) — возвращает вектор-строку, содержащую простые множители числа п. Для массивов эта функция неприменима. Пример:
f = factor(221)
f =
13 17
G=gcd(A, В) — возвращает массив, содержащий наибольшие общие делители соответствующих элементов массивов целых чисел А и В. Функция gcd (0.0) возвращает значение 0, в остальных случаях возвращаемый массив G содержит положительные целые числа;
[G, С.
D] = gcd(A, В) — возвращает массив наибольших общих делителей G и массивов
С и D, которые удовлетворяют уравнению A(i) .*С(1) + B(i) .*D(i) = G(i).
Они полезны для выполнения элементарных эрмитовых преобразований.
Примеры:
» А=[2 6 9]:
» В=[2 3 3]:
» gcd(A.B)
ans =
2 3 3
» [G.C.D]=gcd(A.B)
G =
2 3 3
C =
0 0 0
D=
1 1 1
lcm(A.B) — возвращает наименьшие общие кратные для соответствующих парных
элементов массивов А и В. Массивы А и В должны содержать положительные целые
числа и иметь одинаковую размерность (любой из них может быть скаляром).
Пример:
» А=[1 354];
» В=[2 462];
» lcm(А.В)
ans =
2 12 30 4
log (X) — возвращает натуральный логарифм элементов массива X. Для комплексного или отрицательного z, где z = х + y*i, вычисляется комплексный логарифм в виде log(z) = log(abs(z)) + i*atan2(y,x). Функция логарифма вычисляется для каждого элемента массива. Область определения функции включает комплексные и отрицательные числа, что способно привести к непредвиденным результатам при некорректном использовании. Пример:
» Х=[1.2 3.34 5 2.3];
» log(X)
ans=
-0.
1823
1.2060 1.6094 0.8329
log2(X) — возвращает логарифм по основанию 2 элементов массива X;
[F,E] = log2(X) — возвращает массив действительных значений F и массив целых чисел Е. Элементы массива F обычно лежат в диапазоне 0.5 J abs(F) < 1. Для действительных X возвращаемые массивы F удовлетворяют уравнению вида X = F. *2. Е. Для нулевых значений X возвращаются F = 0 и Е = 0.
Пример:
» Х=[2 4.678 5;0.987 1 3];
» [F.E] = log2(Х)
F =
0.5000 0.5847 0.6250
0.9870 0.5000 0.7500
Е =
2 3 3
0 1 2
log10(X)
— возвращает логарифм по основанию 10 для каждого элемента X.
Область функции
включает комплексные числа, что способно привести к непредвиденным результатам
при некорректном использовании.
Пример:
» Х=[1.4 2.23 5.8 3];
» log10(X)
ans =
0.1461 0.3483 0.7634 0.4771
mod(x.y) — возвращает х mod у;
mod(X, Y) — возвращает остаток от деления X на Y (т. е., X — Y.*floor(X./Y)) для ненулевого Y, и X в противном случае. Если операнды X и Y имеют одинаковый знак, функция mod(X, Y) возвращает тот же результат, что mod(Х, Y). Однако (для положительных X и Y) mod(-x.y) = rem(-x,y)+y.
Примеры:
»
М = mod(5.
2)
М =
1
» mod(10.4)
ans =
2
pow2(Y) — возвращает массив X, где каждый элемент есть Z Y ;
pow2(F.E) — вычисляет Х=Р*2 £ для соответствующих элементов F и Е. Аргументы F и Е — массивы действительных и целых чисел соответственно.
Пример:
» d=pow2(pi/4,2)
d =
3.1416
р = nextpow2(A)
— возвращает такой показатель степени р, что
2
Р
i
abs(A).
Эта функция эффективно применяется для выполнения быстрого преобразования
Фурье. Если А не является скалярной величиной, то nextpowZ возвращает значение nextpow2(length(A)).
Пример:
» х=[2 678934567784324];
» length(x)
ans =
16
» р = nextpow2(x)
Р =
4
» х=4:
» р = nextpow2(x)
Р =
2
» Х=45;
» р = nextpow2(x)
Р =
6
Функция primes(n)
возвращает вектор-строку простых чисел, меньших или равных n.
Пример:
» р = primes(25)
Р =
2 3 5 7 11 13 17 19 23
[N,D] = rat(X) — возвращает массивы N и D, такие что N./D аппроксимирует X с точностью 1 .е-6*norm(Х(:),!). Даже при том, что все числа с плавающей запятой — рациональные числа, иногда желательно аппроксимировать их дробями, у которых числитель и знаменатель являются по возможности малыми целыми числами. Функция rat пытается это сделать;
[N.D] = rat(X.tol) — возвращает массивы N и D, такие что N./D аппроксимирует X с точностью tol.
rat (X) без выходных параметров просто выдает на экран массив цепных дробей;
rats(X.
strlen)
— возвращает ряд, полученный путем упрощенной рациональной аппроксимации
элементов X. Аргумент strlen — длина возвращаемой строки. Функция возвращает
знак «*», если полученное значение не может быть напечатано
в строке, длина которой задана значением strlen. По умолчанию strlen=13.
Тот же алгоритм аппроксимации используется в командном окне MATLAB при задании
рационального формата вывода командой format rat.
Пример:
» [g.j]=rat(pi.le-10)
g=
312689
j =
99532
sqrt(A)
— возвращает квадратный корень каждого элемента массива X. Для отрицательных
и комплексных элементов X функция sqrt(X) вычисляет комплексный результат.
Пример:
» А=[25 21.23 55.8 3]:
» sqrt(A)
ans =
5.0 4.6076 7.4699 1.7321
На рис. 8.1 представлены графики ряда распространенных алгебраических функций. Эти графики получены в результате исполнения следующего файла-сценария:
syms x
subplot(2,2.1).ezplot(x*2.[-5 5]).xlabel( » ).grid on
subplot(2,2.2).ezplot(exp(x),[-2 2]),xlabel(«).grid on
subplot(2.2.3).ezplot(log(x).[0 5]),grid on
subplot(2.2.4),ezplot(sqrt(x).[0 10]).grid on
Рис.
8.1.
Графики ряда алгебраических функций
Графики дают наглядное представление о поведении представленных на них функций. Обратите внимание на применение графической команды ezplot из пакета Symbolic Math ToolBox (она отличается от обычной команды ezplot MATLAB отсутствием заключения символьных переменных в’), команды syms, также входящей в пакет Symbolic Math .Toolbox и задающей символьную переменную х, и несколько необычное применение команды xlabel (»). Эта команда с аргументом в виде пустой строки снимает вывод обозначения горизонтальной оси на двух верхних графиках. Если этого не сделать, то символ «х» окажется наложенным на наименование функций нижних графиков, которое команда ezpl ot выводит над графиками автоматически.
Нравится
Твитнуть
| Главная Другое |
страница 1 Яремко Н. Новый алгоритм вычисления логарифма матрицы Н.Н. Яремко Пензенский государственный педагогический университет Дается интегральное определение логарифма, позволяющее вычислять логарифмы от матриц символьно. Для матриц малой размерности данное определение реализовано в системе компьютерной математики Matlab. Yaremko N.N. New algorithm for computing the matrix logarithm and its implementation in MatLab. The integral definition of the logarithm, which allows calculating the logarithms of matrices symbolically, is given. For matrices of small dimension this definition is implemented in the computer mathematics Matlab. Для вычислений функции от матрицы используют оператор funm(X, @function), который возвращает любую функцию от квадратной матрицы X, если правильно ввести имя, составленное из латинских букв. Команды funm(X ,@exp), funm(X,@sqrt), funm(X.@log) Hexpm(X),sqrtm(x),logm(X) вычисляют одинаковые функции, но используют разные алгоритмы. Однако, предпочтительнее использовать ехрт(Х), sqrtm(x), logm(X), например, ехрт(Х) – возвращает е х от матрицы X. Пример 1. Дана матрица , найти еS. Решение производим в MATLAB. Зададим матрицу S=[l.0.3:1.3.1:4.0.0]. Функция expm(S) возвращает значение экспоненты от матрицы: a = expm(S). Таким образом, . Функция logm(X) – возвращает логарифм матрицы. Результат получается комплексным, если X имеет отрицательные собственные значения. Пример 2. Решение производим в MATLAB, применяя функцию logm(a). Получаем: . Для вычислений MATLAB использует различные численные алгоритмы. Пакет ToolBox Symbolic Math стандартным образом применить не возможно. В предлагаемой статье приводится интегральное определение логарифма, позволяющее вычислять логарифмы от матриц символьно. Будем считать, что все собственные числа матрицы X размера nxn различны и положительны. Определим натуральный логарифм матрицы E+X по формуле (1) где E – единичная матрица. Формула (1) получается переносом числового равенства на матричный случай. Пусть – собственные числа матрицы X, тогда имеем равенство (2) где – присоединенная матрица к матрице , . Из формул (1) и (2) следует выражение для логарифма матрицы (3) Отметим, что на практике формулу (3) использовать не всегда удобно. Бывает выгоднее применить формулу (1). Пример 3. Пусть дана матрица , найти . Вычисления в последней формуле определителя и четырех интегралов выполнены в ToolBox Symbolic Math. Смотрите также: Решение производим в matlab. Зададим матрицу S=[l 3 1 0]. Функция expm(S) возвращает значение экспоненты от матрицы: a = expm(S). Таким образом 21.38kb. 1 стр. Функция сегодня — возвращает текущую дату. Функция сегодня 28.45kb. 1 стр. Арифметические функции Модуль System Function Abs(X) 165.85kb. 1 стр. Приведение матрицы к диагональному виду. Каноническое разложение матрицы 38.46kb. 1 стр. Жалоба на нарушение избирательных прав в соответствии с п. 1 ст. 22 Фз «О прокуратуре рф» 59.88kb. 1 стр. Lu-разложение матрицы 25.9kb. 1 стр. Общие принципы работы с матрицами в системе matlab лабораторная работа №3 149.49kb. 1 стр. Решение этой задачи известно, когда f(x) многочлен:, тогда. Определение f(A) в общем случае 184.93kb. 1 стр. Программа дисциплины «Анализ финансовых данных в среде matlab» 27.03kb. 1 стр. Posh concept историческая справка Значение posh – прилагательное – 74.81kb. 1 стр. Доктринальные тексты Махаяны 212.92kb. 1 стр. Таким образом, родники представляют собой важный компонент природы 46.76kb. 1 стр. |
Н. Новый алгоритм вычисления логарифма матрицы и его реализация в Matlab. // Проблемы информатики в образовании, управлении, экономике и технике: Сб. статей XII Междунар. научно-техн. конф. – Пенза: ПДЗ, 2012. – С. 56 58.
Дана матрица , найти ln(a).
Для решения выберем . Согласно (1) получаем
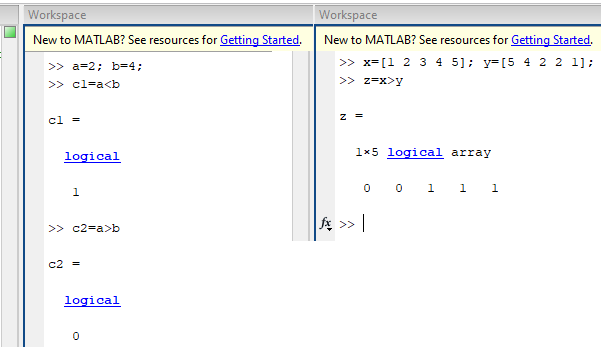
Здесь основание равно 2, а показатель степени, который мы получили, равен 3.Работа с натуральным логарифмом в Matlab с примерами
Натуральные логарифмы составляют важную тему в математике и Matlab. Основание логарифмического уравнения может быть изменено в зависимости от случая. Если логарифмическое уравнение записывается без основания, то считается, что оно имеет основание равное 10 и называется десятичным логарифмом. В то время как если основание логарифмического уравнения представлено с помощью e (также известного как число Эйлера), то оно известно как натуральный логарифм. Значение e равно 2,71828 и также обозначается логарифмом. Таким образом, мы должны быть осторожны при использовании основания в любом логарифмическом уравнении. 9y) =y+ai2π, где a — целое число, а мнимая часть результата находится в диапазоне от – π до π.
Если тип входного аргумента — с плавающей запятой, то выход также с плавающей запятой. Если результат содержит мнимую часть, то он находится в диапазоне от – π до π. Входной аргумент логарифмического уравнения может быть представлен в виде вектора, скаляра, матрицы или многомерного массива. Он может обрабатывать одиночные и двойные типы данных с поддержкой комплексных чисел. Вывод также может быть в виде вектора, матрицы, скаляра или многомерного массива. Если есть положительные значения для y в диапазоне от 0 до бесконечности, то выход, т. е. X, находится в диапазоне от –Inf до Inf. Если входной аргумент находится в комплексной и отрицательной форме, то выход также является комплексным. Тип данных, используемый во входном аргументе, всегда должен совпадать с выходным аргументом. Арифметические операции, такие как log(ab) = log(a)+log(b), недействительны для комплексных чисел в Matlab.
Пример #1
Чтобы найти натуральный логарифм числа 1.
log (1)
Вывод:
Пример #2
7 Найти натуральный логарифм.
log (-1)
Вывод:
Мы также можем найти натуральный логарифм массивов. Здесь входной аргумент имеет тип массива, тогда выход также имеет тип массива. Размер входных и выходных аргументов должен быть одинаковым, а входной массив должен содержать только положительные элементы. В Matlab мы используем функцию real log(), чтобы найти натуральный логарифм каждого элемента, присутствующего в массиве. Пожалуйста, найдите приведенный ниже пример, показывающий, как натуральный логарифм используется в массивах:
X= reallog(y)
Здесь y — входной аргумент, представляющий собой массив, а X дает натуральный логарифм каждого элемента, присутствующего в y.
Пример #3
Чтобы найти натуральный логарифм приведенного ниже массива, заданного A:
A = [2 5 3 6; 7 13 11 8; 9 16 10 12; 15 7 14 1]
reallog(A)
Вывод:
Пример #4
Найдите натуральный логарифм следующего выражения:
log (7.
8 + 5.6*i)
Вывод:
Существуют различные функции, обрабатывающие натуральные логарифмы, такие как diff, limit, float и т. д. Log и log следует использовать с осторожностью, поскольку обе дают разные результаты. Log означает, что он рассматривает основание как 10, а log считает основание как e для получения результатов.
В натуральном логарифме есть четыре различных свойства или правила, такие как:
- Свойство умножения или произведения: Это правило гласит, что если натуральный логарифм произведения m и n равен сумме натурального логарифма m и натуральный логарифм n. 9n) =n*log(m)
Применение натурального бревна
Давайте обсудим применение натурального бревна.
- Натуральный логарифм используется в области математики, которая имеет дело с математическими задачами.
- Натуральный логарифм также используется в области физики для задач, связанных с интегрированием и дифференциальными уравнениями.
- Натуральный логарифм используется для решения задач, связанных с распадом.
- Логарифмы также играют важную роль в области анализа данных и науки о данных. Например, в линейной регрессии есть допущение, согласно которому независимые и зависимые переменные должны иметь линейную зависимость, но каким-то образом, если переменные не являются линейными, мы можем использовать многие методы преобразования, такие как логарифмическое преобразование, чтобы удовлетворить допущение, а затем применить уравнение регрессии между независимыми и зависимыми переменными, удовлетворяющее условию линейности.
- Логарифмические коэффициенты также используются в логистической регрессии для определения взаимосвязи между зависимыми и независимыми переменными, а также для прогнозирования выходных данных.
Заключение
Натуральные логарифмы в основном используются для решения любых экспоненциальных или убывающих задач. В основном они используются в области математики и физики.
Иногда он используется в финансовой сфере для решения проблем, связанных со сложными процентами. Логарифмы также используются в науке о данных для преобразования любой переменной, если она не соответствует каким-либо требованиям. Таким образом, важно изучить свойства логарифма, чтобы правильно его использовать.
Рекомендуемые статьи
Это руководство по Natural Log в Matlab. Здесь мы обсуждаем введение и приложения, а также работу Natural Log в Matlab с примерами. Вы также можете просмотреть следующие статьи, чтобы узнать больше:
- Как создать тепловую карту в MATLAB?
- Преимущества визуализации данных и ее приложений
- Типы логических операторов с примерами
- Как мы можем транспонировать матрицу в Matlab?
Как вы делаете естественный журнал в Matlab?
Как вы пишете натуральный журнал e в Matlab?
Принятый ответ
log() или Log[] , по-видимому, представляет собой естественный журнал почти на всех языках.
Как Matlab вычисляет логарифм?
Y = log10( X ) возвращает десятичный логарифм каждого элемента в массиве X . Функция принимает как вещественные, так и комплексные входные данные. Для реальных значений X в интервале (0, Inf) log10 возвращает реальные значения в интервале (-Inf, Inf). Для комплексных и отрицательных действительных значений X функция log10 возвращает комплексные значения.
Является ли log10 таким же, как ln?
Нет, log10 (x) не то же самое, что ln(x) , хотя оба они являются специальными логарифмами, которые чаще встречаются при изучении математики, чем любые другие логарифмы.
Логарифм с основанием 10, log10 (x), называется десятичным логарифмом, и он записывается, опуская основание как log(x). … То есть ln(x) = loge(x).
Как вы пишете естественный журнал?
Натуральный логарифм – это логарифм с основанием e. Мы пишем l o g e ( x ) \displaystyle {\mathrm{log}}_{e}\left(x\right) loge(x) просто как l n ( x ) \displaystyle \mathrm{ln}\left(x\ справа) ln(x) .
Связанные
Является ли число по основанию 10?
Поскольку логарифмы в физике обычно берутся за основание, ln используется гораздо реже. Математически это можно представить как база журнала 10 .
Связанные
Что такое Lnx?
ln(x) — это время, необходимое для роста до x, а e x — величина роста, произошедшая после времени x. … Естественный журнал просто позволяет людям, читающим задачу, узнать, что вы берете логарифм числа по основанию e. Итак, ln(x) = log e (x) . Например, ln(5) = log e (5) = 1,609..17 января 2020 г.
Похожие
Как написать log2 в Matlab?
Y = log2( X ) возвращает логарифм по основанию 2 числа X, так что 2 Y = X. Если X является массивом, то log2 действует поэлементно на X . [ F , E ] = log2( X ) возвращает массивы мантиссы и показателей, F и E , такие что X = F ⋅ 2 E . Значения, возвращаемые в F, находятся в диапазоне 0,5 <= abs(F) < 1 .
Родственный
Основание журнала Matlab e?
, в то время как Wolfram Mathematics определяет его как «Натуральный логарифм — это логарифм, имеющий основание e.
..». На самом деле MATLAB не имеет «универсальной» функции логарифмирования, которая работает с любым произвольным основанием.
Связанные
Чему равно log2?
Значение журнала 2 по основанию 10 равно 0,301 .
Логарифмическая функция или логарифмическая функция используется в большинстве математических задач, связанных с экспоненциальными функциями.
Связанные
Каково значение журнала 2 по основанию 2?
. Следовательно, log2(2) = 1 . Вопрос 3) Каково значение журнала 2 по основанию 10?
Связанные
Почему мы используем ln?
Мы предпочитаем натуральные логарифмы (то есть логарифмы по основанию е), потому что, как описано выше, коэффициенты в натурально-логарифмической шкале непосредственно интерпретируются как приблизительные пропорциональные разности : с коэффициентом 0,06 разница 1 в x соответствует примерно 6%-ной разнице в y и так далее.
Связанные
Что означает ln в логарифмах?
ln — натуральный логарифм . Это журнал по основанию e. e — иррациональное и трансцендентное число, первые несколько цифр которого: 2,718281828459… В высшей математике обычно используется натуральный логарифм.
общий Информация СМИ Нажмите галерея иллюстрация
Поделиться этой записью:
Как получить естественный вход в Matlab
от Admin
Содержание
Как использовать Natural Log в Matlab?
Y = log( X ) возвращает натуральный логарифм ln(x) каждого элемента в массиве X .
Если вы хотите, чтобы отрицательные и комплексные числа возвращали сообщения об ошибках, а не возвращали сложные результаты, используйте вместо них reallog.
Как взять натуральное бревно?
Натуральный журнал просто позволяет людям, читающим задачу, понять, что вы берете логарифм по основанию e числа. Итак, ln(x) = log e (x) . Например, ln(5) = log e (5) = 1,609.
Как войти в систему Matlab?
Y = log10( X ) возвращает десятичный логарифм каждого элемента в массиве X . Функция принимает как вещественные, так и комплексные входные данные. Для реальных значений X в интервале (0 Inf) log10 возвращает реальные значения в интервале (-Inf Inf). Для комплексных и отрицательных действительных значений X функция log10 возвращает комплексные значения.
Как написать натуральный логарифм e в Matlab?
Просто запись в лог(14-й) . В Matlab log(x) означает ln(x).
Как ввести ln в Mymathlab?
Дважды нажмите ln, чтобы использовать функцию журнала для вычисления десятичного логарифма числа.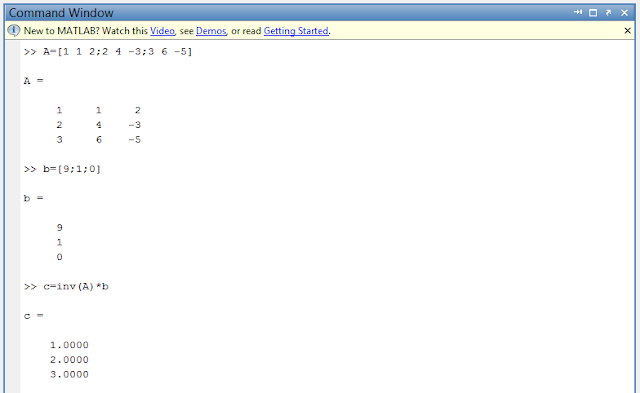
Если аргумент включает несколько терминов, запишите их в круглых скобках. Нажмите клавишу ln три раза, чтобы ввести логарифм по основанию 2.
Как записать журнал в натуральный журнал?
1 Ответ эксперта
- Чтобы преобразовать базовый журнал A в базовый журнал B, используйте формулу:
- log A x = (log B x)/(log B A)
- Итак, чтобы преобразовать логарифм 13 4 в натуральный логарифм (основание e).
- log 13 4 = (log e 4)/(log e 13) = ln4/ln13.
Логин естественный или ln?
Натуральный логарифм числа — это его логарифм по основанию математической константы e, которая является иррациональным и трансцендентным числом, приблизительно равным 2,718281828459. Натуральный логарифм x обычно записывается как ln x log e x или иногда, если основание e неявно, просто log x.
Журнал такой же, как ln?
Разница между log и ln заключается в том, что log определяется как основание 10, а ln обозначается как основание e .
… Натуральный логарифм можно назвать степенью, в которую нужно возвести основание «е», чтобы получить число, называемое его логарифмическим числом. Здесь e — экспоненциальная функция.
Как написать log10?
Log(x) означает логарифм по основанию 10 и также может быть записан как log 10 (x).
Как вы используете log10?
Что такое Lnx?
Функция натурального логарифма ln(x) является обратной функцией показательной функции e x . Для x>0 f (f – 1 (x)) = e ln ( x ) = x. Или же. f – 1 (f (x)) = ln(e x ) = х.
Как записать корень 2 в MATLAB?
B = sqrt( X ) возвращает квадратный корень каждого элемента массива X .
Для элементов X, которые являются отрицательными или сложными, sqrt(X) дает сложные результаты.
Каковы правила журнала?
Правила применяются для любого логарифма logbx , за исключением того, что вы должны заменить любое вхождение e новым основанием b. Натуральный логарифм определялся уравнениями (1) и (2).
…
Основные правила логарифмирования.
| Правило или особый случай | Формула |
|---|---|
| Частное | пер (х/у) = пер (х) — пер (у) |
| Журнал мощности | лн(ху)=илн(х) |
| Лог е | ln(e)=1 |
| Бревно одного | ln(1)=0 |
Как написать натуральный журнал в латексе?
ln – Используется для рисования символа натурального логарифма.
Как вы вводите журналы?
Откройте документ и поместите курсор в то место, где вы хотите вставить логарифм. Введите «log », а затем значок нижнего индекса, указанный в категории «Шрифт» на вкладке «Главная» .
Введите основание логарифма в нижнем индексе, например «2». Нажмите значок нижнего индекса еще раз, чтобы вернуться к обычному шрифту.
Как ввести E в Matlab?
Экспоненциальная функция и число e
как exp(x), поэтому число e в MATLAB равно exp(1) .
Пример натурального логарифма?
Натуральный логарифм числа N — это степень или показатель степени, в которую нужно возвести «е», чтобы получить число, равное N. Константа «е» — это константа Непье, которая приблизительно равна 2,718281828. ln N = x , что совпадает с N = e x . Натуральный логарифм в основном используется в чистой математике, например, в исчислении.
Как решить Lnx?
Чему равно натуральное бревно?
Натуральный логарифм числа x равен логарифм по основанию e где e — математическая константа, приблизительно равная 2,718 .
Обычно он записывается с использованием сокращенной записи lnx вместо logex, как можно было бы ожидать.
Почему натуральное бревно называют натуральным?
Натуральные логарифмы имеют более простые производные, чем другие системы логарифмов. Другая причина, по которой логарифмы по основанию е по праву могут называться натуральными логарифмами, состоит в том, что эта система имеет самую простую производную из всех систем логарифмов.
Почему мы берем естественный журнал данных?
В статистике естественный логарифм может использоваться для преобразования данных по следующим причинам: Чтобы сделать умеренно асимметричные данные более нормально распределенными или для достижения постоянной дисперсии . Чтобы позволить моделировать данные, попадающие в кривую, с помощью прямой линии (простая линейная регрессия)
Что такое значение log1?
Значение log 1 по основанию 10 равно и равно 0 .
Его можно оценить с помощью функции логарифмирования, которая является одной из важных математических функций.
Всегда ли журнал имеет основание 10?
Журнал с основанием 10 или «общий» популярен по историческим причинам и обычно записывается как «log(x)» . … Если в журнале не записано основание, вы должны обычно (на уроках алгебры) предполагать, что основание равно 10. Другим важным журналом является «натуральный» или журнал с основанием-e, обозначаемый как «ln(x)» и обычно произносится как « элл-энн-оф-х».
Что такое журнал А?
журнал A + журнал B = журнал AB . Этот закон говорит нам, как сложить два логарифма. Сложение журнала A и журнала B приводит к логарифму произведения A и B, который равен журналу AB. Например, мы можем написать. log10 5 + log10 4 = log10(5 × 4) = log10 20,
Журнал и лог10 одно и то же?
Обычно log(x) означает логарифм по основанию 10, его также можно записать как log10(x) .