Калькулятор систем счисления с решением
Исходное число
Система счисления исходного числа 23456789101112131415161718192021222324252627282930313233343536
Система счисления для перевода 23456789101112131415161718192021222324252627282930313233343536
Количество знаков после запятой (для чисел с дробной частью)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100
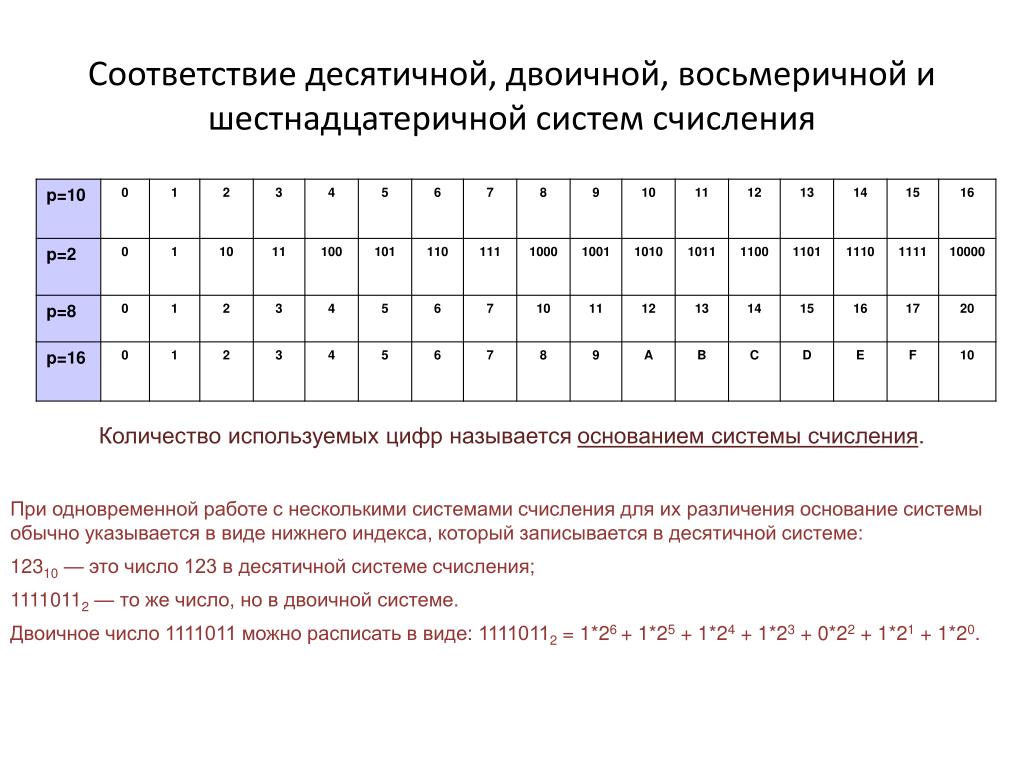
Что такое система счисления
Система счисления – это набор правил записи чисел, при помощи цифр и букв.
Системы счисления можно разделить на позиционные и непозиционные. Примером непозиционной системы счисления является римская система счисления, в которой вместо цифр используют буквы латинского алфавита.
В позиционной системе счисления, напротив позиция числа имеет большое значение и определяет количественное значение числа. Примерами позиционной системы счисления выступает нам всем знакомая десятичная система счисления, а также двоичная, троичная и др.
Данный калькулятор перевода чисел из одной системы счисления в другую предназначен именно для позиционных систем счисления и дает наглядное понимание как перевести число из одной системы счисления в другую.
У каждой системы счисления есть основание, которое определяется количеством используемых цифр. Основание системы счисления определяет мощность алфавита – набору цифр, используемых в системе счисления. Самое маленькое основание в двоичной позиционной системе счисления, там для записи числа используют только две цифры – 0 и 1.
Рассмотрим две самые популярные системы счисления – двоичную и десятичную. Десятичная система счисления является самой распространенной, в ней используется десять арабских цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Основание равно 10.
В десятичной системе счисления значение цифры в записи числа зависит от позиции цифры, например, число 444 можно записать как:
44410 = 4 ⋅ 102 + 4 ⋅ 101 + 4 ⋅ 100 = 400 + 40 + 4.
Такая запись числа называется развернутой. Можно заметить, что, двигаясь справа на лево значение каждой цифры увеличивается в 10 раз.
В двоичной системе счисления развернутая запись числа строиться аналогичным образом, рассмотрим число 1101111002:
1101111002 = 1 ⋅ 2
Записав число 1101111002 в развернутом виде мы тем самым перевели его в десятичную систему счисления.
Рассмотрим пример, переведем число 100112 из двоичной системы в десятичную систему счисления
Переведем число 100112 в десятичную систему счисления, для этого сначала запишем позицию каждой цифры в числе с права налево, начиная с нуля
| Позиция в числе | 4 | 3 | 2 | 1 | 0 |
| Число | 1 | 0 | 0 | 1 | 1 |
Каждая позиция цифры будет степенью числа 2, так как система счисления 2-ичная. Необходимо последовательно умножить каждое число 10011 2 на 2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
100112 = 1 ⋅ 24 + 0 ⋅ 23 + 0 ⋅ 22 + 1 ⋅ 21 + 1 ⋅ 20 = 1910
Теперь давайте посмотрим, как перевести число из десятичной системы счисления в двоичную.
Переведем число 1210 из десятичной в двоичную систему счисления
Переведем число 1210 в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
| 12 | : | 2 | = | 6 | остаток: 0 |
| : | 2 | = | 3 | остаток: 0 | |
| 3 | : | 2 | = | 1 | остаток: 1 |
| 1 | : | 2 | = | 0 | остаток: 1 |
1210 = 11002
Как переводить десятичные дроби в двоичную систему счисления
Переведем число 12.310 из десятичной в двоичную систему счисления
При переводе десятичной дроби в двоичную систему счисления, необходимо сначала перевести целую часть в двоичную систему, а затем дробную часть. Причем для целой части мы будем последовательно делить на 2, а для дробной умножать на 2.
Причем для целой части мы будем последовательно делить на 2, а для дробной умножать на 2.
Переведем целую часть 12 числа 12.310 в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
| 12 | : | 2 | = | 6 | остаток: 0 |
| 6 | : | 2 | = | 3 | остаток: 0 |
| 3 | : | 2 | = | 1 | остаток: 1 |
| 1 | : | 2 | = | 0 | остаток: 1 |
1210 = 11002
Переведем дробную часть 0.3 числа 12.310 в 2-ичную систему счисления, при помощи последовательного умножения на 2, до тех пор, пока в дробной части произведения не получиться ноль или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.
Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.
| 0.3 | · | 2 | = | 0.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
0. 8 8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0. |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
1210 = 11002 0.310 = 0.0100110011001100110011001100112
Обратите внимание, что в результате умножения на 2 получается бесконечная двоичная дробь, поэтому в данном случае можно и дальше продолжать умножение, но в дробной части произведения ноль так и не получится. В таких случаях необходимо определить сколько чисел после запятой необходимо оставить. Из данного примера можно сделать вывод, что не всегда конечная десятичная дробь будет конечной в двоичной системе счисления и наоборот.
Теперь необходимо соединить получившиеся целую и дробную части.
12.310 = 1100.010011001100110011001100110011 2
Как перевести двоичную дробь в десятичную систему счисления
Переведем число 11. 1012 из двоичной системы в десятичную систему счисления
1012 из двоичной системы в десятичную систему счисления
Алгоритм перевода такой же, как и для целых чисел, только из двоичной дроби необходимо будет убрать точку, и как и в предыдущих примерах записать позицию цифр.
Переведем число 11.1012 в десятичную систему счисления, для этого сначала запишем позицию каждой цифры в числе
| Позиция в числе | 1 | 0 | -1 | -2 | -3 |
| Число | 1 | 1 | 1 | 0 | 1 |
Каждая позиция цифры будет степенью числа 2, так как система счисления 2-ичная. Необходимо последовательно умножить каждое число 11.1012 на 2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
11.1012 = 1 ⋅ 21 + 1 ⋅ 20 + 1 ⋅ 2-1 + 0 ⋅ 2-2 + 1 ⋅ 2-3 = 3. 62510
62510
Примеры решения задач повышенной сложности для расширенной подготовки учащихся профильного информационно-технологического класса
Профильное предметное обучение учащихся предполагает углубленный уровень решения задач. В данной работе предлагается набор задач, которые могут быть использованы в классе с профильным изучением информатики с целью дополнительной, расширенной подготовки. Задачи представляют три основные направления, ставшие уже классическими: арифметическое, логическое и алгоритмическое. Начнем, как обычно, с арифметики.
1. Арифметические операции над числами в недесятичных системах счисления
Учащийся должен хорошо понимать, что такое число, уметь работать с числами в позиционных системах счисления с недесятичным основанием. Просто переводить числа из одной системы счисления в другую уже не достаточно для сдачи ЕГЭ по информатике. Интерес представляют задачи специального вида. Некоторые разновидности таких задач представлены в этом наборе.
ЗАДАЧА 1. Даны два действительных числа в системах счисления с различными основаниями. Сравнить между собой значения данных чисел (если числа не равны, то определить, какое из них больше).
M = 0,10(110)(2)
Основная трудность решения заключается в том, что первое число представляет собой бесконечную периодическую двоичную дробь. Прежде чем сравнивать числа между собой, требуется записать это число в форме обыкновенной дроби. Для устранения бесконечной периодической части можно использовать очевидные арифметические преобразования.
Обозначим исходное число как М. Тогда:
100 M = 10,(110)
100000 M = 10110,(110)
Вычитая меньшее число из большего, получим:
10110,(110) – 10,(110) = 10100
100000 M – 100 M = 11100 M
Таким образом:
11100 M = 10100
Отсюда можно найти значение М в форме обыкновенной дроби и перевести его в десятичную систему счисления.
Теперь достаточно перевести второе число в десятичную систему счисления и сравнить числа между собой. Для сравнения обыкновенных дробей достаточно определить значение разности между ними.
M — N < 0
Разность между первым и вторым числами меньше нуля, следовательно первое число меньше второго.
Ответ: M < N
ЗАДАЧА 2. Вычислить значение числового выражения. Результат записать в четверичной системе счисления. Число под знаком корня является пятой степенью целого положительного числа.
Решение этой задачи, как и всех задач вычислительного типа, сводится к арифметическим операциям над недесятичными числами, целыми и дробными. В случае большого размера выражения вычисления удобнее выполнять по частям.
Для левой части выражения вычисления можно выполнить в десятичной системе счисления.
Мы получили десятичное число 88. В шестнадцатиричной системе счисления это число имеет запись 58=5×16+8. Вычитая шестнадцатиричную дробь из полученного числа, получим:
В шестнадцатиричной системе счисления это число имеет запись 58=5×16+8. Вычитая шестнадцатиричную дробь из полученного числа, получим:
Теперь необходимо найти значение корня пятой степени из шестнадцатиричного числа.
Известно, что значение корня является целым положительным числом и это упрощает необходимые рассуждения. Сначала попробуем определить границы для искомого значения, чтобы максимально сократить область поиска.
( 10(16) )5 = 100000(16) < M
( 10(16)) )5 = 10000000000(16) > M
Мы видим, что пятая степень наименьшего двухразрядного шестнадцатиричного числа меньше М. С другой стороны, пятая степень наименьшего трехразрядного шестнадцатиричного числа больше М. Таким образом, искомое значение может быть только двухразрядным числом.
N = XY(16) = 16X + Y
Попробуем определить значение первой цифры (X). Возведем в пятую степень шестнадцатиричное число 20 и сравним полученное значение с М. Для чисел, заканчивающихся нулем сделать это не сложно.
Возведем в пятую степень шестнадцатиричное число 20 и сравним полученное значение с М. Для чисел, заканчивающихся нулем сделать это не сложно.
20 × 20=400
400 × 20=8000
8000 × 20=100000
100000 × 20=2000000 > M
Полученное значение больше М. Это значит, что значение первой цифры N уже определено: она равна 1. Таким образом, искомое число начинается с единицы и имеет следующий вид:
N = 1Y(16) = 16 + Y
Теперь надо найти значение цифры Y. Очевидно, что при умножении четных цифровых разрядов могут получаться только четные значения. В последнем разряде числа М расположена нечетная цифра D. Следовательно, значение младшей цифры в числе N может быть только нечетным. Значение 1 можно исключить сразу, т.к. единица при умножении дает в последнем разряде только саму себя.
Y = 2n + 1; Y ǂ 1; Y ϵ { 3, 5, 7, 9, B, D, F }
Посмотрим, как ведут себя нечетные цифры при возведении числа в степень. Нас интересуют только последние цифровые разряды, поэтому выполнять умножение в полном объеме не обязательно. Для цифры 3 покажем результаты полностью, для остальных укажем только цифры в последних разрядах произведений.
Нас интересуют только последние цифровые разряды, поэтому выполнять умножение в полном объеме не обязательно. Для цифры 3 покажем результаты полностью, для остальных укажем только цифры в последних разрядах произведений.
Вторая степень: 3 × 3 = 9
Третья степень: 9 × 3 = *B
Четвертая степень: 1B × 3 = *1
Пятая степень: 51 × 3 = *3
Начиная с шестой степени цифры в последних разрядах образуют периодическую последовательность вида: ( 9, B, 1, 3, … ). Похожие результаты получаются для всех нечетных цифр от 3 до F.
5: 9, D, 1, 5, …
7: 1, 7, …
9: 1, 9, …
B: 9, 3, 1, B, …
D: 9, 5, 1, D, …
F: 1, F, …
Таким образом, только две цифры дают значение D в последних разрядах своих степеней, при этом только для цифры D это значение образуется именно для пятой степени. Это значит, что последняя цифра числа найдена: Y = D.
Итак, число N найдено.
Теперь мы можем выполнить последнюю операцию вычитания и перевод результата в четверичную систему счисления.
1D(16) – 0,2(16) = 1C,E(16)
1C,E(16) = 11100,111(2)
11100,111(2) = 130,32(4)
Ответ: 130,32(4)
ЗАДАЧА 3. Дана запись операции умножения двух целых чисел в системе счисления с основанием четыре. При этом все цифровые разряды чисел, кроме нулевых, не известны и обозначены буквами латинского алфавита X,Y,Z. Определить значения данных чисел (цифровые разряды).
Для четверичного основания найти решение задачи не очень сложно. Цифра 0 исключается. Следовательно, для неизвестных значений цифровых разрядов остаются только три допустимых значения: 1, 2, 3. Таким образом, общее количество возможных вариантов равно 6 = 3! (факториал 3). При этом нет необходимости рассматривать все варианты умножения в полном объеме. Две младшие цифры в первом частичном произведении являются равными. Если это не так, то вариант можно отбрасывать.
При этом нет необходимости рассматривать все варианты умножения в полном объеме. Две младшие цифры в первом частичном произведении являются равными. Если это не так, то вариант можно отбрасывать.
| 1 | 2 | 3 | 4 | 5 | 6 |
1232 | 1323 | 2131 | 2313 | 3121 | 3212 |
Из представленной таблицы видно, что необходимый результат дает только один вариант: X=1, Y=2, Z=3. Для полной уверенности подставим эти значения в текст примера и убедимся в правильности решения.
Для полной уверенности подставим эти значения в текст примера и убедимся в правильности решения.
Ответ: X=1; Y=2; Z=3; Первое число 1232; Второе число 23.
ЗАДАЧА 4. Определить основания систем счисления X и Y, для которых выполняются все следующие условия:
1) 234(X) < 165(Y)
2) 543(X)) + 22(X) = 565(X)
3) 345(Y) × 44(Y) = 16522(Y)
В подобных задачах самое главное, это как можно больше ограничить область допустимых значений для неизвестных величин. В данном случае к данным условиям можно сразу добавить еще три:
X > 6; Y > 6; Y > X;
Основания не могут быть меньше 7, потому что в записи чисел наибольшей цифрой является шесть. Третье неравенство является прямым следствием первого условия: трехзначное число, начинающееся с 1, может быть больше другого трехзначного числа, начинающегося с двойки, только в том случае, когда оно задано в системе счисления с большим основанием.
Третье неравенство является прямым следствием первого условия: трехзначное число, начинающееся с 1, может быть больше другого трехзначного числа, начинающегося с двойки, только в том случае, когда оно задано в системе счисления с большим основанием.
Дальше можно рассуждать следующим образом. Уравнение для X не дает нам однозначного решения: оно образует тождество для множества значений X:
543(7) + 22(7) = 565(7)
543(8) + 22(8) = 565(8)
543(9) + 22(9) = 565(9)
543(10) + 22(10) = 565(10)
…
Следовательно, надо перейти к анализу условий, заданных для Y.
Произведение 5 на 4 равно 20. Если при умножении в системе с основанием Y получено число 20, которое в этой системе счисления имеет запись вида N2, то полученный результат можно записать следующим образом:
NY + 2 = 20
NY= 18
Число 18 делится без остатка только на 1, 3, 6, 9, 18. Если учесть при этом, что Y>6, то возможными решениями остаются только 9 и 18. Но решение Y=18 не подходит, потому что в этом случае следующее умножение 4 на 4 с учетом единицы переноса дает значение 17 и следующий по порядку разряд произведения не может быть равен двум. Напротив, умножение по основанию 9 дает требуемый результат:
Если учесть при этом, что Y>6, то возможными решениями остаются только 9 и 18. Но решение Y=18 не подходит, потому что в этом случае следующее умножение 4 на 4 с учетом единицы переноса дает значение 17 и следующий по порядку разряд произведения не может быть равен двум. Напротив, умножение по основанию 9 дает требуемый результат:
Следовательно, решение для Y найдено: Y = 9.
Теперь надо найти решение для X. Для X остаются возможными два значения: X=7; X=8; Чтобы выбрать единственное, остается рассмотреть данное нам неравенство.
Запишем числа в виде алгебраических функций от X и Y.
2X2 + 3X + 4 < Y2 + 6Y + 5
После подстановки значения Y=9 и несложных преобразований получим:
2X2 + 3X + 4 < 92 + 6 × 9 + 5
2X2 + 3X < 81 + 54 + 5 — 4
2X2 + 3X < 136
X(2X+3) < 136
Допустимых значений для X всего два, поэтому решение неравенства можно найти с помощью простой подстановки:
7(14+3) = 119 < 136
8(16+3) = 152 > 136
Значение X=8 нарушает неравенство. Следовательно, единственным допустимым значением для X является X=7. Задача решена.
Следовательно, единственным допустимым значением для X является X=7. Задача решена.
Ответ: X=7; Y=9.
ЗАДАЧА 5. При сложении трех неизвестных чисел в двенадцатиричной системе счисления выполняется следующее равенство:
XYZ + ZY + Z = ZXY
Число X возвели в степень N=YZ и результат записали в шестнадцатиричной системе счисления. Определить значение последней цифры в записи полученного шестнадцатиричного числа.
Первое, что требуется для решения задачи, это найти неизвестные значения цифровых разрядов. Начнем с исследования суммы последних разрядов.
При сложении трех цифр образуется число, которое заканчивается на цифру Y. Если первый разряд этого числа равен 1, то можно составить уравнение и получить возможное значение для Z.
Z + Y + Z = 1Y
2Z + Y = 12 + Y
2Z = 12
Z = 6;
Никаких других решений для Z нет. Если предположить, что старший разряд суммы равен 2, то мы получим следующее:
Z + Y + Z = 2Y
2Z + Y = 24 + Y
2Z = 24
Отсюда Z=12, что невозможно в c/c с основанием 12;
Таким же образом, путем анализа ситуации при сложении средних разрядов, получим решение для Y и X. Не забудем, что здесь необходимо учесть единицу переноса из младшего разряда суммы. На основе анализа сложения в средних разрядах получим:
Y + 6 + 1 = 1X
Y + 7 = 12 + X
Y = X + 5
При этом в старшем разряде суммы разряд Z=6 может образоваться только при сложении цифры X и единицы переноса.
X + 1 = 6
X = 5
Соответственно для цифры Y имеем следующее:
Y = 5 + 5 = A
Проверим значения разрядов путем подстановки.
Теперь можно приступить ко второй части задания. Показатель степени, в которую возвели число X равен:
N = YZ = A6 = 106 = 1000000(10)
Чтобы ответить на вопрос, какая цифра будет в последнем разряде шестнадцатиричной степени, надо понять, как ведет себя число 5 при возведении в степень в шестнадцатиричной системе счисления. При этом нас интересуют только те значения цифр, которые образуются в последних разрядах.
Первая степень: 5
Вторая степень: 5 × 5= 19
Третья степень: 5 × 5 × 5 = *D
Четвертая степень: 5 × 5 × 5 × 5 = *1
Дальше образуется период с длиной 4:
( 5; 9; D; 1 )
Одинаковые цифры образуются в последнем разряде степени для всех показателей степени, которые имеют одинаковые остатки при делении на длину периода, т. е. на четыре. Например, на цифру 1 заканчиваются все степени с показателями, которые кратны четырем: 4, 8, 12, 16, и т.д. Один миллион делится на четыре без остатка. Следовательно, последняя цифра в миллионной степени шестнадцатиричного числа равна 1.
е. на четыре. Например, на цифру 1 заканчиваются все степени с показателями, которые кратны четырем: 4, 8, 12, 16, и т.д. Один миллион делится на четыре без остатка. Следовательно, последняя цифра в миллионной степени шестнадцатиричного числа равна 1.
Ответ: Последняя цифра в записи полученного шестнадцатиричного числа равна 1.
ЗАДАЧА 6. Дана периодическая дробь в троичной системе счисления (M). Записать число в системе счисления с основанием шестнадцать. Определить значение цифры, которая находится в полученном шестнадцатиричном числе в позиции с троичным номером N=201211221(3) после запятой.
M = 201201,(201)(3)
Переведем данное число в шестнадцатиричную систему счисления. Сначала выполним перевод из троичной системы в десятичную, потом – из десятичной в шестнадцатиричную. Для целой части числа используем обычные алгоритмы преобразования, для дробной части воспользуемся методом, который мы уже применяли для устранения периодической части дроби (см. решение задачи №1).
решение задачи №1).
Переводим целую часть числа в десятичную систему счисления.
201201(3) = 2 × 35 + 0 + 1 × 33 + 2 × 32 + 0 + 1 = 2 × 243 + 27 + 18 + 1 = 486 + 27 + 18 + 1 = 532(10)
Переводим дробную часть числа в десятичную систему счисления.
X = 0,(201)(3)
1000X = 201,(201)(3)
201,(201) (3) — 0,(201)(3) = 201
1000X — X = 222X
Теперь выполним перевод целой и дробной частей числа в шестнадцатиричную систему счисления.
532 : 16 = 33; остаток = 4;
33 : 16 = 2; остаток = 1;
2 : 16 = 0; остаток = 2;
532(10) = 214(16)
19 : 16 = 1; остаток = 3;
1 : 16 = 0; остаток = 1;
19(10) = 13(16)
26 : 16 = 1; остаток = A;
1 : 16 = 0; остаток = 1;
26(10) = 1A(16)
Мы получили число в форме обыкновенной шестнадцатиричной дроби. Для того, чтобы получить запись числа с шестнадцатиричной запятой, надо разделить числитель обыкновенной дроби на ее знаменатель.
Для того, чтобы получить запись числа с шестнадцатиричной запятой, надо разделить числитель обыкновенной дроби на ее знаменатель.
Мы получили бесконечную периодическую дробь в шестнадцатиричной системе счисления.
M = 214,B(B13)(16)
Первая цифра после запятой не входит в состав периода. Поэтому удобнее нумеровать цифры, начиная со второй цифры после запятой. Другими словами, нам надо найти значение цифры с номером S=N-1 от начала периодической части числа.
S = N-1 = 201211221(3) — 1 = 201211220(3)
Значения цифр в периодической части числа повторяются через каждые три разряда. Это значит, что остаток от деления номера цифры на три позволяет нам определить значение цифры с любым номером. Если число в троичной системе счисления заканчивается на цифру 0, то это значит, что данное число делится на 3 без остатка.
Но если номер цифры делится на три без остатка, то эта цифра занимает третье место в составе периода. Третья цифра в периоде дроби это цифра три.
Ответ: Цифра с троичным номером 201211221 после запятой в шестнадцатиричной записи троичного числа 201201,(201) равна 3.
2. Решение логических задач с использованием аппарата алгебры логики
Системы счисления. Основные приёмы — презентация онлайн
Похожие презентации:
Пиксельная картинка
Информационная безопасность. Методы защиты информации
Электронная цифровая подпись (ЭЦП)
Этапы доказательной медицины в работе с Pico. Первый этап
История развития компьютерной техники
От печатной книги до интернет-книги
Краткая инструкция по CIS – 10 шагов
Информационные технологии в медицине
Информационные войны
Моя будущая профессия. Программист
1. Определения
Системы счисления, 8 класс1
Определения
Позиционная система: значение цифры определяется
ее позицией в записи числа.

развёрнутая форма
тысячи сотни десятки единицы
записи числа
3
2
1
разряды
0
6 3 7 5 = 6·103 + 3·102 + 7·101 + 5·100
6000 300 70
5
основание
Алфавит системы счисления — это используемый в
ней набор цифр.
Основание системы счисления — это количество цифр
в алфавите (мощность алфавита).
Разряд — это позиция цифры в записи числа. Разряды в
записи целых чисел нумеруются с нуля справа налево.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
2. Перевод в десятичную систему
Системы счисления, 8 класс2
Перевод в десятичную систему
43210
разряды
100112 = 1·24 + 0·23 + 0·22 + 1·21 + 1·20
= 16 + 2 + 1 = 19
Перевод из любой системы счисления в десятичную:
1. Подписать над числом номера разрядов
(последний разряд имеет номер 0)
2. Каждую цифру умножить на основание
текущей системы счисления в степени её разряда
3. Вычислить сумму
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.
 spb.ru
spb.ru3. Перевод в десятичную систему
Системы счисления, 8 класс3
Перевод в десятичную систему
2 1 0
разряды
1 + 12·16
0
B
C
1BC16= 1·162 + 11·16
= 256 + 176 + 12 = 444
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
4. Поиск основания системы
Системы счисления, 8 класс4
Поиск основания системы
Задача. В некоторой системе счисления число 58
записывается как 46x. Определите основание
x этой системы счисления.
Переведём 46x в десятичную систему:
1 0
46x = 4 x1 + 6 x0 = 4x + 6
4x + 6 = 58
4x = 52
К.Ю. Поляков, Е.А. Ерёмин, 2018
x = 13
http://kpolyakov.spb.ru
5. Поиск основания системы
Системы счисления, 8 класс5
Поиск основания системы
Решение:
Переведем каждый элемент равенства в десятичную систему:
1 0
1 0
1 0
Подставим полученные значения в равенство и приведем подобные слагаемые:
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.
 spb.ru
spb.ru6. Поиск основания системы
Системы счисления, 8 класс6
Поиск основания системы
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
7. Метод таблицы
Системы счисления, 8 класс7
Метод таблицы
77
210
10 2
29
1024 512
28
27
26
25
24
23
22
21
20
256
128
64
32
16
8
4
2
1
1
0
0
1
1
0
1
77 =
64 + 13
8+5
4+
1
77 = 10011012
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
8. Метод деления уголком
Системы счисления, 8 класс8
Метод деления уголком
Для перевода числа из десятичной
системы в систему с любым другим
основанием нужно:
1. Разделить число в десятичной системе
на основание системы счисления, в которую
число переводится
2. Полученный результат деления также
разделить на основание системы, в которую
выполняется перевод
19
18
1
2
9
8
1
2
4
4
0
2
2
2
2
1
0
19 = 100112
3.
 Продолжать деление до получения частного, меньшего основания
Продолжать деление до получения частного, меньшего основаниясистемы
последний результат
результат деления
деления ии все
все
4. Записать последовательно последний
полученные остатки,
остатки, начиная с конца.
полученные
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
9. Метод деления уголком
Системы счисления, 8 класс9
Метод деления уголком
10 8
100 8
96 12 8
8 1
4
4 0
8
0
100 = 1448
1
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
10. Метод деления уголком
Системы счисления, 8 класс10
Метод деления уголком
10 16
444 16
432 27
16
12 16 1 16
С
11 0 0
B
1
К.Ю. Поляков, Е.А. Ерёмин, 2018
444 = 1BC16
http://kpolyakov.spb.ru
11. Сложение в двоичной системе
Системы счисления, 8 класс11
Сложение в двоичной системе
10
111
789
+567
?
Когда перенос?
1356
2
1 1111
1 0 1 1 02
+ 1 1 1 0 1 12
1 0 1 0 0 0 12
К.
 Ю. Поляков, Е.А. Ерёмин, 2018
Ю. Поляков, Е.А. Ерёмин, 2018!
Перенос, когда > 1!
1 + 1 = 2 = 102
1 + 1 + 1 = 3 = 112
http://kpolyakov.spb.ru
12. Вычитание в двоичной системе
Системы счисления, 8 класс12
Вычитание в двоичной системе
10
+10
+10
0 9 1
1021
– 567
2
?
Когда берем заём?
Чему он равен?
0454
+2
0 1 1
0
+2
1 0 0 0 1 0 12
–
1 1 0 1 12
0 1 0 1 0 1 02
К.Ю. Поляков, Е.А. Ерёмин, 2018
!
Заём равен 2!
http://kpolyakov.spb.ru
13. Сложение в восьмеричной системе
Системы счисления, 8 класс13
Сложение в восьмеричной системе
сложение
1 в перенос
1 1 1
1 5 68
+ 6 6 28
1 0 4 08
К.Ю. Поляков, Е.А. Ерёмин, 2018
1 в перенос
6+2=8=8+0
5 + 6 + 1 = 12 = 8 + 4
1+6+1=8=8+0
1 в перенос
http://kpolyakov.spb.ru
14. Вычитание в восьмеричной системе
Системы счисления, 8 класс14
Вычитание в восьмеричной системе
вычитание
4 5 68
– 2 7 78
1 5 78
К.
 Ю. Поляков, Е.А. Ерёмин, 2018
Ю. Поляков, Е.А. Ерёмин, 2018заём
(6 + 8) – 7 = 7
заём
(5 – 1 + 8) – 7 = 5
(4 – 1) – 2 = 1
http://kpolyakov.spb.ru
15. Шестнадцатеричная система
Системы счисления, 8 класс15
Шестнадцатеричная система
Основание: 16
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
10 11 12 13 14 15
Что неправильно?
?
34AF516
9FF6116
К.Ю. Поляков, Е.А. Ерёмин, 2018
5BG616
ADh3316
http://kpolyakov.spb.ru
16. Сложение в шестнадцатеричной системе
Системы счисления, 8 класс16
Сложение в шестнадцатеричной системе
сложение
1
A 5 B16
+ C 7 E16
1 6 D 916
1
10 5 11
+ 12 7 14
1 6 13 9
1 в перенос
11+14=25=16+9
1 в перенос
5+7+1=13=D16
10+12=22=16+6
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
17. Вычитание в шестнадцатеричной системе
Системы счисления, 8 класс17
Вычитание в шестнадцатеричной системе
вычитание
С 5 B16
– A 7 E16
1 D D16
заём
12 5 11
– 10 7 14
1 13 13
заём
(11+16)–14=13=D16
(5 – 1)+16 – 7=13=D16
(12 – 1) – 10 = 1
К.
 Ю. Поляков, Е.А. Ерёмин, 2018
Ю. Поляков, Е.А. Ерёмин, 2018http://kpolyakov.spb.ru
18. Связь с двоичной системой
Системы счисления, 8 класс18
Связь с двоичной системой
8 = 23
!
Каждая восьмеричная цифра может быть
записана как три двоичных (триада)!
{
{
{
{
16258 = 001 110 010 1012
1
6
2
5
0
1
2
3
4
5
6
7
000
001
010
011
100
101
110
111
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
19. Перевод из двоичной в восьмеричную
Системы счисления, 8 класс19
Перевод из двоичной в восьмеричную
10010111011112
Шаг 1. Разбить на триады, начиная справа:
001 001 011 101 1112
Шаг 2. Каждую триаду записать одной
восьмеричной цифрой:
001 001 011 101 1112
1
Ответ:
1
3
5
7
10010111011112 = 113578
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
English Русский Правила
Сложение двоичных чисел онлайн
Назначение сервиса. Онлайн-калькулятор предназначен для сложения двоичных чисел в прямом, обратном и дополнительном кодах.
Онлайн-калькулятор предназначен для сложения двоичных чисел в прямом, обратном и дополнительном кодах.
- Решение онлайн
- Видеоинструкция
- Также решают
Число №1
Число №2
Числа представлены в 102 системе счисления.Операция с числами СложениеВычитание Для дробных чисел использовать 2345678 знака после запятой.
Действие производить в: Прямом кодеОбратном кодеДополнительном кодеПодробнее.
Вместе с этим калькулятором также используют следующие:
Перевод чисел в двоичную, шестнадцатеричную, десятичную, восьмеричную системы счисления
Умножение двоичных чисел
Формат представления чисел с плавающей запятой
Пример №1. Представить число 133,54 в форме числа с плавающей точкой.
Решение. Представим число 133.54 в нормализованном экспоненциальном виде:
1.3354*102 = 1.3354*exp102
Число 1.3354*exp102 состоит из двух частей: мантиссы M=1.3354 и экспоненты exp10=2
Если мантисса находится в диапазоне 1 ≤ M Представление числа в денормализованном экспоненциальном виде.
Если мантисса находится в диапазоне 0,1 ≤ M Представим число в денормализованном экспоненциальном виде: 0.13354*exp103
Пример №2. Представить двоичное число 101.102 в нормализованном виде, записать в 32-битом стандарте IEEE754.
Таблица истинности
Вычисление пределов
Арифметика в двоичной системе счисления
Арифметические действия в двоичной системе выполняются так же, как и в десятичной. Но, если в десятичной системе счисления перенос и заём осуществляется по десять единиц, то в двоичной — по две единицы. В таблице представлены правила сложения и вычитания в двоичной системе счисления.
В таблице представлены правила сложения и вычитания в двоичной системе счисления.
- При сложении в двоичной системе системе счисления двух единиц в данном разряде будет 0 и появится перенос единицы в старший разряд.
- При вычитании из нуля единицы производится заём единицы из старшего разряда, где есть 1. Единица, занятая в этом разряде, даёт две единицы в разряде, где вычисляется действие, а также по единице, во всех промежуточных разрядах.
| Сложение
0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 10 |
Вычитание
0 – 0 = 0 1 – 0 = 1 1 – 1 = 0 10 – 1 = 1 |
Сложение чисел с учетом их знаков на машине представляет собой последовательность следующих действий:
- преобразование исходных чисел в указанный код;
- поразрядное сложение кодов;
- анализ полученного результата.

При выполнении операции в дополнительном (модифицированном дополнительном) коде если в результате сложения в знаковом разряде возникает единица переноса, она отбрасывается.
Операция вычитания в ЭВМ выполняется через сложение по правилу: Х-У=Х+(-У). Дальнейшие действия выполняются также как и для операции сложения.
Пример №1.
Дано: х=0,110001; y= -0,001001, сложить в обратном модифицированном коде.
Дано: х=0,101001; y= -0,001101, сложить в дополнительном модифицированном коде.
Пример №2. Решить примеры на вычитание двоичных чисел, используя метод дополнения до 1 и циклического переноса.
а) 11 — 10.
Решение.
Представим числа 112 и -102 в обратном коде.
Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Двоичное число 0000011 имеет обратный код 0,0000011
Двоичное число 0000010 имеет обратный код 1,1111101
Сложим числа 00000011 и 11111101
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 |
В 1-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 2-й разряд.

| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 |
В 2-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 3-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 |
В 3-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 4-й разряд.
Поэтому записываем 0, а 1 переносим на 4-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 |
В 4-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 5-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
В 5-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 6-й разряд.
Поэтому записываем 0, а 1 переносим на 6-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 |
В 6-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 7-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В 7-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 8-й разряд.
Поэтому записываем 0, а 1 переносим на 8-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Возник перенос из знакового разряда.
 Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).
Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Результат сложения: 00000001. Переведем в десятичное представление. Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
00000001 = 27*0 + 26*0 + 25*0 + 24*0 + 23*0 + 22*0 + 21*0 + 20*1 = 0 + 0 + 0 + 0 + 0 + 0 + 0 + 1 = 1
Результат сложения (в десятичном представлении): 1
б) 111-010
Представим числа 1112 и -0102 в обратном коде.
Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Двоичное число 0000111 имеет обратный код 0,0000111
Двоичное число 0000010 имеет обратный код 1,1111101
Сложим числа 00000111 и 11111101
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | |||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 |
В 1-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 2-й разряд.
Поэтому записываем 0, а 1 переносим на 2-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 |
В 2-ом разряде возникло переполнение (1 + 1 + 1 = 11). Поэтому записываем 1, а 1 переносим на 3-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | |||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 |
В 3-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 4-й разряд.
Поэтому записываем 0, а 1 переносим на 4-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | ||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 |
В 4-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 5-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 |
В 5-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 6-й разряд.
Поэтому записываем 0, а 1 переносим на 6-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 |
В 6-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 7-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
В 7-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 8-й разряд.
Поэтому записываем 0, а 1 переносим на 8-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
Возник перенос из знакового разряда.
 Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).
Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
Результат сложения: 00000101
Получили число 00000101. Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
00000101 = 27*0 + 26*0 + 25*0 + 24*0 + 23*0 + 22*1 + 21*0 + 20*1 = 0 + 0 + 0 + 0 + 0 + 4 + 0 + 1 = 5
Результат сложения (в десятичном представлении): 5
Сложение двоичных вещественных чисел с плавающей запятой
В компьютере любое число может быть представлено в формате с плавающей точкой. Формат с плавающей точкой показан на рисунке:
Например, число 10101 в формате с плавающей точкой можно записать так:
В компьютерах используется нормализованная форма записи числа, в которой положение запятой всегда задается перед значащей цифрой мантиссы, т.е. выполняется условие:
Формат с плавающей точкой показан на рисунке:
Например, число 10101 в формате с плавающей точкой можно записать так:
В компьютерах используется нормализованная форма записи числа, в которой положение запятой всегда задается перед значащей цифрой мантиссы, т.е. выполняется условие:
b-1≤|M|<b0=1
Нормализованное число — это число, у которого после запятой идет значащая цифра (т.е. 1 в двоичной системе счисления). Пример нормализации:
0,00101*2100=0,101*210
111,1001*210=0,111001*2101
0,01101*2-11=0,1101*2-100
11,1011*2-101=0,11011*2-11
При сложении чисел с плавающей точкой выравнивание порядков выполняют в сторону большего порядка:
Алгоритм сложения чисел с плавающей точкой:
- Выравнивание порядков;
- Сложение мантисс в дополнительном модифицированном коде;
- Нормализация результата.

Пример №4.
A=0,1011*210, B=0,0001*211
1. Выравнивание порядков;
A=0,01011*211, B=0,0001*211
2. Сложение мантисс в дополнительном модифицированном коде;
MAдоп.мод.=00,01011
MBдоп.мод.=00,0001
00,01011
+ 00,00010
=
00,01101
A+B=0,01101*211
3. Нормализация результата.
A+B=0,1101*210
Пример №3. Записать десятичное число в двоично-десятичной системе счисления и сложить два числа в двоичной системе счисления.
Оптимальная система счисления: sevabashirov — LiveJournal
Давно хотел определить с точки зрения банальной эрудиции и формальной математики, какая из позиционных систем счисления является наиболее удобной, в некотором смысле — эргономичной. Потому что — как многим известно — привычная современной цивилизации десятичная система выбрана не из соображений оптимальности, а прямо вытекает из анатомии человека. Было бы не 10 пальцев на руках — укоренилось бы другое основание. Когда люди считали окружающие предметы буквально по пальцам, десятичная система была разумным выбором, да и то: почему именно пальцы-«штуки»? Кому-то было удобнее по фалангам 4 пальцев одной руки, указывая на них большим — так получила некоторую популярность 12-ричная система. Но дальше — просто сила привычки, QWERTY-эффект в чистом виде: используем не потому, что удобнее всего, а потому, что так сложилось исторически, в силу традиции.
Было бы не 10 пальцев на руках — укоренилось бы другое основание. Когда люди считали окружающие предметы буквально по пальцам, десятичная система была разумным выбором, да и то: почему именно пальцы-«штуки»? Кому-то было удобнее по фалангам 4 пальцев одной руки, указывая на них большим — так получила некоторую популярность 12-ричная система. Но дальше — просто сила привычки, QWERTY-эффект в чистом виде: используем не потому, что удобнее всего, а потому, что так сложилось исторически, в силу традиции.___
Как математически определить удобство использования той или иной системы счисления? Во-первых можно рассмотреть, как в них записываются числа. Чем больше основание n, тем меньше разрядов требует одно и то же число, но при этом растет «алфавит» — количество цифр, что влечет за собой и размеры таблиц сложения и умножения, и все такое прочее. Результирующим будет произведение-комбинация этих факторов: lg(n) * (1/n). Логарифм (все равно какой, взял десятичный) основания системы отражает компактность записи чисел, обратное число — компактность алфавита. 5 — вчетверо меньше… А можно просто 60 разных цифр и один разряд, как вавилоняне — вот и будут лишь числа от 0 до 59.
5 — вчетверо меньше… А можно просто 60 разных цифр и один разряд, как вавилоняне — вот и будут лишь числа от 0 до 59.
Так вот, эти выкладки — давно уже не секрет, кто их только не делал. В непрерывном случае максимум приходится на число e=2,718…, так что основание 3 выглядит лучше всех, 2 и 4 — одинаково чуть похуже: http://phg.su/basis2/X51.HTM — наглядно.
___
Но этого явно мало. При таком подходе учтено удобство записи чисел, но есть же еще и вычисления, операции над ними. Частично это уже учтено (см. выше фразу про таблицы сложения-умножения). И здесь приходится к месту аргумент, который — если кто в курсе — был основным доводом у сторонников двенадцатеричной системы: 12 делится нацело на 1, 2, 3, 4, 6 и собственно 12 против 1, 2, 5 и 10 у десятки. Это еще Перельман описывал в «Занимательной арифметике». И действительно, чем больше круглых чисел в произведениях и чем меньше периодических дробей в частных — очевидно, тем удобнее и быстрее подсчеты. Таким образом, домножаем нашу комбинацию двух факторов на третий — количество делителей числа d(n).
Таким образом, домножаем нашу комбинацию двух факторов на третий — количество делителей числа d(n).
Итоговая формула: коэффициент эргомичности системы счисления q(n) = lg(n) / n * d(n) * 2,5 — домножил для приведения коэффициента десятичной системы к единице. Мы вправе это делать, поскольку основание логарифма все равно взято произвольно, у абсолютных значений q(n) нет смыслового наполнения. Ниже — таблица 25 лидеров:
| n | lg(n) | d(n) | q(n) |
| 12 | 1,079 | 6 | 1,349 |
| 6 | 0,778 | 4 | 1,297 |
| 24 | 1,380 | 8 | 1,150 |
| 4 | 0,602 | 3 | 1,129 |
| 8 | 0,903 | 4 | 1,129 |
| 18 | 1,255 | 6 | 1,046 |
| 10 | 1,000 | 4 | 1,000 |
| 30 | 1,477 | 8 | 0,985 |
| 20 | 1,301 | 6 | 0,976 |
| 36 | 1,556 | 9 | 0,973 |
| 16 | 1,204 | 5 | 0,941 |
| 60 | 1,778 | 12 | 0,889 |
| 48 | 1,681 | 10 | 0,876 |
| 14 | 1,146 | 4 | 0,819 |
| 40 | 1,602 | 8 | 0,801 |
| 3 | 0,477 | 2 | 0,795 |
| 9 | 0,954 | 3 | 0,795 |
| 15 | 1,176 | 4 | 0,784 |
| 28 | 1,447 | 6 | 0,775 |
| 72 | 1,857 | 12 | 0,774 |
| 42 | 1,623 | 8 | 0,773 |
| 2 | 0,301 | 2 | 0,753 |
| 32 | 1,505 | 6 | 0,706 |
| 5 | 0,699 | 2 | 0,699 |
| 120 | 2,079 | 16 | 0,693 |
Итак, «дозеналисты» были правы, у основания 12 действительно отличная репутация! А привычная нам десятка занимает седьмую позицию — достойную, но существенно уступающую.
 Если отойти в бытовую сферу, то главный недочет десятки — то, что она не делится на 3, а между тем на 3 делить приходится крайне часто. Ну и чтобы четвертые доли содержали лишь один знак после запятой вместо двух — тоже хороший бонус. Вкупе с сокращением длины больших чисел на 8% это оправдывает заучивание чуть большей таблицы умножения.
Если отойти в бытовую сферу, то главный недочет десятки — то, что она не делится на 3, а между тем на 3 делить приходится крайне часто. Ну и чтобы четвертые доли содержали лишь один знак после запятой вместо двух — тоже хороший бонус. Вкупе с сокращением длины больших чисел на 8% это оправдывает заучивание чуть большей таблицы умножения.А с учетом огромной роли двоичной системы и бинарной логики в нашу компьютерную эпоху (тернарную пытались одно время привить, но не зашло) следует обратить внимание на основания 4, 8, 16. Переводить из них в двоичную — вообще плевое дело. Кстати, у 4 и 8, а также 3 и 9 коэффициенты равны, это не издержки округления.
Само собой, прикидка крайне грубая и многих вещей не учитывает. Но тут, как говорится, выделяйте гранты на дальнейшие исследования.
Тема поста интересна в первую очередь френдам aaamibor, doncunita, lrlay777, sly2m, spamsink, vmenshov и другим.
ПРОДОЛЖЕНИЕ ПОСТА С УТОЧНЕНИЕМ ФОРМУЛЫ: https://sevabashirov. livejournal.com/270269.html
livejournal.com/270269.html
Основные понятия информатики Лекция 3 План 1. Информационная
Основные понятия информатики Лекция 3
План 1. Информационная модель 2. Алгоритм 3. Системы счисления 4. Классификация компьютеров 5. Основные области применения вычислительной техники
П.1 Информационная модель Моделью называется материальный или идеальный образ некоторой совокупности реальных объектов или явлений, полученный отбрасыванием всех несущественных и концентрацией внимания только на некоторых важнейших с точки зрения решаемой задачи атрибутах рассматриваемых предметов или явлений.
При решении задач в различных областях деятельности приходится строить различные модели. В информатике рассматриваются в основном информационные и математические модели.
Примеры: Информационная модель личности. Личный листок по учету кадров. В этом документе отражаются такие атрибуты сотрудников, как фамилия, имя и отчество, дата рождения, пол, образование, домашний адрес и т. д. А такие атрибуты, как цвет глаз, рост, вес, в личном листке никак не отражаются. Можно считать, что этот документ представляет собой информационную модель личности сотрудника учреждения.
д. А такие атрибуты, как цвет глаз, рост, вес, в личном листке никак не отражаются. Можно считать, что этот документ представляет собой информационную модель личности сотрудника учреждения.
Информационная модель печатного издания. В библиотеке на каждое печатное издание заводится библиографическая карточка. В ней отражаются инвентарный и каталожные номера, название, фамилия автора или авторов, год и место издания, том, номер и т. д.
Понятие математической модели очень близко к понятию информационной модели, и многие специалисты рассматривают математическую модель как специфический, частный случай информационной модели. Характерной чертой математической модели является необходимость привлечения математических соотношений, уравнений, ограничений для адекватного описания рассматриваемых явлений или связей между объектами.
Пример: Необходимо определить виновника аварии. В некоторых случаях может помочь измерение длины тормозного пути, по которому, с учетом состояния дорожного покрытия, погодных условий и некоторых других факторов, можно с помощью специальных математических соотношений определить скорости машин, участвовавших в происшествии. Строится математическая модель ситуации, включающая в себя такие атрибуты, как длина тормозного пути, вес и габариты машин, состояние дорожного покрытия, специальные коэффициенты, учитывающие погодные условия, и математические соотношения, связывающие между собой все рассматриваемые величины. Выполнив необходимые математические расчеты, можно решить поставленную задачу и с большой долей уверенности определить виновника аварии.
Строится математическая модель ситуации, включающая в себя такие атрибуты, как длина тормозного пути, вес и габариты машин, состояние дорожного покрытия, специальные коэффициенты, учитывающие погодные условия, и математические соотношения, связывающие между собой все рассматриваемые величины. Выполнив необходимые математические расчеты, можно решить поставленную задачу и с большой долей уверенности определить виновника аварии.
Отвлечение от несущественных деталей, о котором шла речь выше, принято называть абстрагированием. Таким образом, абстрагирование является одним из важнейших инструментов при построении модели какой-либо предметной области. Естественно, что при абстрагировании осуществляется определенное огрубление реальной действительности.
П. 2 Алгоритм Последовательность действий, которую необходимо выполнить над исходными данными, чтобы достичь поставленной цели, принято называть алгоритмом. Алгоритм – это конечная последовательность указаний на языке понятном исполнителю, задающая процесс решения задач определенного типа и ведущая к получению результата, однозначно определяемого допустимыми исходными данными.
Слово «алгоритм» происходит от имени ученого IX века Муххамеда бен Аль-Хорезми («аль-хорезми» -> «алгоритм»), который описал правила выполнения арифметических действий в десятичной системе счисления. Словом «алгоритм» потом и стали обозначать эти правила вычислений. Однако с течением времени понятие алгоритма видоизменялось и в XX веке под ним стали понимать какую-либо последовательность действий, приводящую к решению поставленной задачи.
Свойства алгоритма Дискретность (в данном случае, разделенность на части) и упорядоченность. Алгоритм должен состоять из отдельных действий, которые выполняются последовательно друг за другом. Детерминированность (однозначная определенность). Многократное применение одного алгоритма к одному и тому же набору исходных данных всегда дает один и тот же результат. Формальность. Алгоритм не должен допускать неоднозначности толкования действий для исполнителя. Результативность и конечность. Работа алгоритма должна завершаться за определенное число шагов, при этом задача должна быть решена. Массовость. Определенный алгоритм должен быть применим ко всем однотипным задачам.
Массовость. Определенный алгоритм должен быть применим ко всем однотипным задачам.
Исполнитель и разработчик алгоритма Разработчик алгоритма в конечном итоге должен описать алгоритм в допустимых командах определенного исполнителя (той машины, которой будет поручено выполнение алгоритма). Совокупность команд, которые данный исполнитель может выполнять, называется системой команд исполнителя. Объекты (данные), над которыми исполнитель может выполнять действия, формируют среду исполнителя.
Язык блок-схем Алгоритм можно описать разными способами: словами, на языке программирования, а также с помощью блок-схем. На языке блок-схем каждый шаг алгоритма описывается с помощью соответствующей фигуры, а последовательность выполнения шагов определяется линиями-связями. Блок схемы читаются сверху вниз и слева направо.
Прямоугольник – выполнение действия (например, c = a + b) Ромб – проверка условия (например, a > b). Если условие выполняется, то алгоритм идет по линии «да», если не выполняется – то по линии «нет». Скругленный прямоугольник – начало и конец алгоритма Скошенный прямоугольник – ввод-вывод данных (например, получение значения переменной, вывод результата на экран монитора).
Скругленный прямоугольник – начало и конец алгоритма Скошенный прямоугольник – ввод-вывод данных (например, получение значения переменной, вывод результата на экран монитора).
Алгоритмические структуры (типы алгоритмов) Следование. Предполагает последовательное выполнение команд сверху вниз. Если алгоритм состоит только из структур следования, то он является линейным. Ветвление. Выполнение программы идет по одной из двух, нескольких или множества ветвей. Выбор ветви зависит от условия на входе ветвления и поступивших сюда данных. Цикл. Предполагает возможность многократного повторения определенных действий. Количество повторений зависит от условия цикла. Функция (подпрограмма). Команды, отделенные от основной программы, выполняются лишь в случае их вызова из основной программы (из любого ее места). Одна и та же функция может вызываться из основной программы сколь угодно раз.
Описание различных алгоритмических структур на языке блок-схем Ветвление if Это самый простой тип ветвления. Если результат вычисления выражения-условия возвращает true (правда), то выполнение алгоритма идет по ветке «Да», в которую включены дополнительные выражения-действия. Если условие возвращает false (ложь), то выполнение алгоритма идет по ветке «нет», т.е продолжает выполняться основная ветка программы.
Если результат вычисления выражения-условия возвращает true (правда), то выполнение алгоритма идет по ветке «Да», в которую включены дополнительные выражения-действия. Если условие возвращает false (ложь), то выполнение алгоритма идет по ветке «нет», т.е продолжает выполняться основная ветка программы.
Ветвление if-else Если выражение-условие возвращает true (правда), то выполнение алгоритма идет по ветке «Да», если условие не выполняется (false), то выполнение идет по ветке «Нет». При любом результате выражения-условия нельзя вернуться в основную ветку программы, минуя дополнительные действия.
Ветвление if-elif-else Количество условий может быть различно. Если выполняется первое, то после выполнения действий, программа переходит к основной ветке, не проверяя дальнейшие условия. Если первое условие возвращает ложь, то проверяется второе условие. Если второе условие возвращает правду, то выполняются действия, включенные в вторую ветку конструкции. Последнее условие проверяется лишь в том случае, если ни одно до него не дало в результате true. Данную алгоритмическую конструкцию (if – elif – else) не следует путать с алгоритмической конструкцией «Выбор».
Данную алгоритмическую конструкцию (if – elif – else) не следует путать с алгоритмической конструкцией «Выбор».
Цикл while Пока условие выполняется (результат логического выражения дает true), будут выполняться действия тела цикла. После очередного выполнения вложенных действий условие снова проверяется. Для того чтобы выполнение алгоритма не зациклилось, в теле цикла (помимо прочих действий) должно быть выражение, в результате выполнения которого будет изменяться переменная, используемая в условии. Тело цикла может ни разу не выполнится, если условие с самого начала давало false.
Цикл do В этом цикле первый раз условие проверяется лишь после выполнения действий тела цикла. Если условие возвращает true, то выражения-действия повторяются снова. Каким бы ни было условие, тело данного цикла хотя бы раз, но выполнится.
Цикл for Данный цикл также называют циклом «Для» (for). В его заголовке указывается три параметра: начальное значение переменной (от), конечно значение (до) и ее изменение с помощью арифметической операции на каждом «обороте» цикла (шаг).
Алгоритм Евклида (нахождение наибольшего общего делителя) Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел. Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.
Описание алгоритма нахождения НОД делением Большее число делим на меньшее. Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла). Если есть остаток, то большее число заменяем на остаток от деления. Переходим к пункту 1.
Найти НОД для 30 и 18. 30/18 = 1 (остаток 12) 18/12 = 1 (остаток 6) 12/6 = 2 (остаток 0). Конец: НОД – это делитель. НОД (30, 18) = 6
Системы счисления. Позиционная и непозиционная системы счисления Система счисления – это способ записи чисел. Обычно, числа записываются с помощью специальных знаков – цифр . Арабская СС : используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и это позиционная система счисления. Римская СС– I, V, X, L, C, D, M и это непозиционная система счисления.
Арабская СС : используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и это позиционная система счисления. Римская СС– I, V, X, L, C, D, M и это непозиционная система счисления.
В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет. Например: 11 – здесь первая единица обозначает десять, а вторая – 1. II – здесь обе единицы обозначают единицу.
345, 259, 521 – здесь цифра 5 в первом случае обозначает 5, во втором – 50, а в третьем – 500. XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.
Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т.к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел).
В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная. Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.
Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная. Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.
Основание системы счисления – это количество знаков, которое используется для записи цифр. Разряд — это позиция цифры в числе. Разрядность числа — количество цифр, из которых состоит число(например, 264 — трехразрядное число, 00010101 — восьмиразрядное число). Разряды нумеруются справа на лево (например, в числе 598 восьмерка занимает первый разряд, а пятерка — третий).
Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления.
Двоичная система счисления В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)
Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)
Восьмеричная система счисления Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7. Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.
Шестнадцатеричная система счисления Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
П.4 Классификация компьютеров Рассмотрим две наиболее распространенные в настоящее время схемы — классификация по поколениям, соответствующая историческому процессу развития вычислительной техники, и классификация по применениям.
Классификация по поколениям К настоящему времени принято выделять пять поколений вычислительной техники.
Первое поколение К первому поколению относят машины, построенные на электронных лампах накаливания. В эту группу входят машины, созданные в период, начинающийся с электронной вычислительной машины «EDSAC» и заканчивающийся примерно в конце пятидесятых годов. Если судить с современной точки зрения, то можно сказать, что эти машины стоили очень дорого, занимали огромные площади, были не совсем надежны в работе, имели маленькую скорость обработки информации и могли хранить очень мало данных. Создавались они в единичных экземплярах и использовались в основном для военных и научных целей. Типичная скорость обработки данных для машин первого поколения составляла 5-30 тысяч операций в секунду.
Второе поколение Ко второму поколению относят машины, построенные на транзисторных элементах в период с конца пятидесятых и до середины шестидесятых годов. У этих машин значительно уменьшились стоимость и габариты, выросли надежность, скорость работы и объем хранимой информации. С появлением специальных алгоритмических языков существенно упростилось применение машин для решения практических задач в различных областях. Машины стали использовать для стандартных инженерных расчетов, в экономической деятельности для оптимизации работы отдельных предприятий и даже отраслей, и во многих других областях. Типичные представители машин второго поколения — IBM-7090 (США), ATLAS (Великобритания), БЭСМ-4, М-220, Минск-32, БЭСМ-6 (СССР). Скорость обработки данных у машин второго поколения возросла до 1 миллиона операций в секунду.
Третье поколение Машины третьего поколения выполнены на так называемых интегральных схемах, которые сокращенно обозначают ИС. Интегральная схема представляет собой электрическую цепь определенного функционального назначения, которая с помощью специальной технологии размещается на очень маленькой кремниевой (или какой-либо другой подходящей по свойствам) пластинке — «основе».
Площадь такой схемы — порядка одного квадратного сантиметра, но по своим функциональным возможностям интегральная схема эквивалентна сотням и тысячам транзисторных элементов. Из-за очень маленьких размеров и толщины интегральную схему иногда называют микросхемой, а также чипом (chip — тонкий кусочек). Переход от транзисторов к интегральным схемам вызвал соответствующие изменения в стоимости, размерах, надежности, скорости и емкости машин.
Начиная с третьего поколения, вычислительные машины становятся повсеместно доступными и широко используются для решения самых различных задач. Характерным для этого времени является коллективное использование машин, так как они все еще достаточно дороги, занимают большие залы и требуют сложного и дорогостоящего обслуживания. Правда, доступ к возможностям машины уже организуется и с индивидуально используемых устройств — терминалов (terminal -конечный пункт), которые находятся на некотором удалении от основного оборудования машины, иногда даже на рабочих местах пользователей.
В состав терминала, как правило, входят клавиатура, используемая для набора данных и выполнения простейших операций по управлению работой компьютера, и дисплей, служащий для отображения текущей ситуации и полученных результатов вычислений. Носителями первичной информации все еще являются перфокарты и перфоленты, хотя уже значительный объем информации сосредоточивается на магнитных носителях — дисках и лентах. Скорость обработки информации у машин третьего поколения достигла нескольких миллионов операций в секунду.
Четвертое поколение ЭВМ В первой половине семидесятых годов происходит переход от обычных интегральных схем к схемам с большей плотностью монтажа — большим интегральным схемам (БИС). Если обычные интегральные схемы эквивалентны тысячам транзисторных элементов, то большие интегральные схемы заменяют уже десятки тысяч.
Отличительная черта четвертого поколения — наличие в одной машине нескольких (обычно 2-6, иногда до нескольких сотен и даже тысяч) центральных, главных устройств обработки информации — процессоров (от слова process — обработка), которые могут дублировать друг друга или независимым образом выполнять вычисления. Такая структура позволяет резко повысить надежность машин и скорость вычислений. Другая важная особенность — появление мощных средств, обеспечивающих работу компьютерных сетей. Это позволило впоследствии создавать и развивать на их основе глобальные, всемирные компьютерные сети.
Такая структура позволяет резко повысить надежность машин и скорость вычислений. Другая важная особенность — появление мощных средств, обеспечивающих работу компьютерных сетей. Это позволило впоследствии создавать и развивать на их основе глобальные, всемирные компьютерные сети.
Пятое поколение ЭВМ О проекте создания машин этого поколения, рассчитанном на десять лет, объявили в начале восьмидесятых годов японские разработчики. За ними в эту стратегическую гонку втянулись ученые США, СССР и ряда стран Западной Европы. Было заявлено, что к началу 90-х годов будет создано принципиально иное по стилю обработки информации и взаимодействия с пользователем поколение машин. Если ранее человек тщательно и подробно формулировал машине последовательность действий по обработке информации, то теперь машина по поставленной перед ней цели должна самостоятельно составить план действий и выполнить их.
Такой способ решения задач принято называть логическим программированием. Кроме того, планировалось ввести общение с машиной на уровне естественного языка. Однако решить полностью весь комплекс задач проекта не удалось и до сих пор. Хотя имеются впечатляющие достижения по каждому из направлений проекта, возникли определенные финансовые и технические трудности. Кроме того, усилия значительной части разработчиков были переключены на микропроцессорную технику и развитие сетевых технологий.
Однако решить полностью весь комплекс задач проекта не удалось и до сих пор. Хотя имеются впечатляющие достижения по каждому из направлений проекта, возникли определенные финансовые и технические трудности. Кроме того, усилия значительной части разработчиков были переключены на микропроцессорную технику и развитие сетевых технологий.
Классификация по применениям ЭВМ Персональный компьютер — это настольная электронно-вычислительная машина индивидуального использования. В 1999 году был введен в действие международный стандарт «спецификации РС99», который определяет классификацию, а также требования к аппаратным и программным средствам персональных компьютеров. Термин «спецификация» означает формализованное описание свойств, характеристик и функций некоторого объекта. Таким образом, «спецификации РС99» представляют собой описание характеристик персональных компьютеров (PC — сокращение английского словосочетания personal computer), сформулированное в 1999 году. Сразу же отметим, что классификация персональных компьютеров, предложенная в стандарте РС99, сохранилась и в стандартах, принятых в последующие годы.
Согласно указанным стандартам вводится пять категорий персональных компьютеров (в скобках указаны соответствующие официальные термины): пользовательский, потребительский, массовый компьютер (Consumer PC), предназначенный для работы, в основном, в домашних условиях; офисный, деловой компьютер (Office PC) предназначен для выполнения канцелярской работы в составе компьютерных сетей предприятия, организации и т. д.; мобильный, переносной, портативный компьютер (Mobile PC) предназначен для специалистов, которые используют компьютерные технологии в поездках, во время деловых встреч и т. д., когда использование стационарных машин затруднено или вообще невозможно; рабочая станция (Workstation PC) используется в качестве сервера в компьютерных сетях, а также как рабочий инструмент разработчиками программных средств, конструкторами, то есть там, где предъявляются повышенные требования к ресурсам компьютера; игровые или развлекательные компьютеры (Entertainment PC) используются для игр, а также для высококачественной работы со звуком и видеозаписями.
Мини-ЭВМ — состоит из машин, используемых для работы в условиях реального производства, для управления поточной линией, цехом, для обеспечения работы научной лаборатории или относительно небольшого учреждения. Как правило, мини-ЭВМ выполнена в виде нескольких напольных стоек, содержащих все ее устройства. В настоящее время мини-ЭВМ практически полностью вытеснены из употребления более мощными и дешевыми персональными компьютерами.
Группа универсальных ЭВМ характеризуется возможностью решать подавляющее большинство задач обработки информации и практически неограниченными возможностями ее хранения. Универсальные машины (соответствующий англоязычный термин mainframe — главный каркас, центральное строение) применяются как центральное звено в системах управления производственным циклом, для обеспечения работы крупных НИИ, организаций и учреждений. В последнее время часто используются как ведущий элемент глобальных и локальных сетей, который предоставляет свои вычислительные ресурсы подключенным к сети персональным компьютерам. Как и группа мини-ЭВМ, эта группа машин постепенно вытесняется мощными персональными компьютерами.
Как и группа мини-ЭВМ, эта группа машин постепенно вытесняется мощными персональными компьютерами.
СуперЭВМ используются для решения задач так называемых предельных классов, для которых требуется колоссальное сосредоточение вычислительных мощностей. Это задачи метеопрогноза в планетарных масштабах, задачи расчета и проектирования современных самолетов и космических кораблей, задачи из области ядерной физики и космогонических исследований, задачи управления системами противоракетной и космической обороны, задачи обеспечения работы глобальных сетей общемирового значения и т. Д. Во всем мире насчитывается не так много машин класса суперЭВМ в силу их чрезвычайно высокой сложности и стоимости.
П.5. Основные области применения вычислительной техники Сферы применения вычислительной техники: Военное дело, например системы противоракетной обороны, космические системы. Моделирование физических явлений и исследование моделей с помощью ЭВМ. Например, задачи термоядерного синтеза, космогонические модели. Моделирование чаще всего применяется в тех случаях, когда проведение прямого физического эксперимента либо слишком дорого, либо в принципе невозможно. Обработка конкретных экспериментальных данных при проведении математических, физических, химических, биологических, социологических, исторических, археологических и т. д. исследований. Решение задач метеопрогноза.
Моделирование чаще всего применяется в тех случаях, когда проведение прямого физического эксперимента либо слишком дорого, либо в принципе невозможно. Обработка конкретных экспериментальных данных при проведении математических, физических, химических, биологических, социологических, исторических, археологических и т. д. исследований. Решение задач метеопрогноза.
Автоматизированные рабочие места (АРМ) специалиста, например АРМ бухгалтера, руководителя, врача и т. д. Системы автоматического проектирования, обеспечивающие поддержку работы инженера-конструктора, существенно повышающие производительность его труда и сокращающие сроки разработок. Широко применяются при проектировании таких изделий, как космические челноки «Буран», «Шаттл», современные сверхзвуковые самолеты и т. д. Управление работой отдельных станков (станки с числовым программным управлением), роботы (роботы на ликвидации Чернобыльской аварии, роботы, ухаживающие за больными, роботы-художники), робототехнические линии, цеха и заводы-автоматы. Автоматизированные системы планирования и управления производством, начиная с отдельных предприятий и кончая управлением целыми отраслями (железнодорожный транспорт, авиация и т. д.).
Автоматизированные системы планирования и управления производством, начиная с отдельных предприятий и кончая управлением целыми отраслями (железнодорожный транспорт, авиация и т. д.).
Получение изображений внутренних частей непрозрачных тел, в том числе в медицине — компьютерная томография и на производстве — контроль качества, не разрушающий изделия. Системы массового обслуживания и информационно-справочные системы. Например, системы резервирования и продажи авиа- и железнодорожных билетов. Обслуживание крупных спортивных мероприятий — мировых и европейских чемпионатов, Олимпийских игр. Базы данных правовой информации (быстрый доступ к нормативным актам, указам и постановлениям правительства, статьям Уголовного и других кодексов), криминалистические базы данных, хранящие сведения о преступниках и т. д. Банковские и биржевые компьютерные системы. Библиографические компьютерные системы. Подготовка различных документов, отчетов и других печатных материалов, рекламное дело. Компьютерная верстка и подготовка к изданию газет, журналов, книг. Аранжировка музыкальных произведений, цветомузыка. Скульптура и архитектура.
Аранжировка музыкальных произведений, цветомузыка. Скульптура и архитектура.
Компьютерный дизайн разрабатываемых устройств, помещений. Компьютерный подбор прически, модели одежды. Компьютерная мультипликация и анимация («оживление» изображений — воспроизведение последовательности изображений, создающее впечатление движения). Машинный перевод с различных естественных языков. Например, еще в 1985 году демонстрировалась система машинного перевода, работавшая с 4 языками и словарным запасом в 260 000 слов (человек в среднем активно использует 3000-5000 слов). Лингвистика, расшифровка неизвестных языков. Криптография — шифровка и расшифровка документов, доступ к которым должен быть ограничен. Компьютерная геодезия и картография. Обучающие, тестирующие и контролирующие программы. Цифровая аудио- и видеозапись. Бытовые применения, игровые программы. Новые средства связи, базирующиеся на локальных и глобальных сетях.
Гипертекст При работе с различного рода словарями и справочниками достаточно часто приходится сталкиваться с ситуацией, когда в определении или переводе какого-либо слова, термина встречается ссылка «смотри . ..», отсылающая читателя за получением дополнительной информации в какое-то другое место. Например, в словаре иностранных слов дано следующее определение термина «информация»: «Информация [
..», отсылающая читателя за получением дополнительной информации в какое-то другое место. Например, в словаре иностранных слов дано следующее определение термина «информация»: «Информация [
Гипертекст представляет собой текст со ссылками, читаемый с помощью специальной программы, которая автоматически находит в компьютере связанную с выбранной ссылкой дополнительную информацию и выводит ее на экран дисплея. Ссылки в гипертексте принято называть полями. Полями могут быть встречающиеся в тексте символы, понятия, словосочетания, изображения. Как правило, поля отличаются от остального текста более ярким или интенсивным цветом. Выбор любого поля в гипертексте приводит к выполнению какого-либо действия, например, автоматическому поиску определения выделенного в поле термина. Это определение может в свою очередь содержать произвольное количество новых гипертекстовых ссылок — полей. С полем может быть связано выполнение какой-либо дополнительной программы, проигрывание фрагмента аудио- или видеозаписи. После выполнения связанных с полем действий можно вернуться в исходное место или перейти дальше по новой ссылке, встретившейся в вызванном фрагменте гипертекста. Гипертексты широко используются в различного рода справочных системах, обучающих программах, электронных учебниках.
После выполнения связанных с полем действий можно вернуться в исходное место или перейти дальше по новой ссылке, встретившейся в вызванном фрагменте гипертекста. Гипертексты широко используются в различного рода справочных системах, обучающих программах, электронных учебниках.
Мультимедиа Мультимедиа представляет собой совокупность аппаратных и программных средств, обеспечивающих создание звуковых и визуальных эффектов, а также влияние человека на ход выполнения программы, предусматривающей их создание.
Сети Сетью ЭВМ называется объединение двух и более вычислительных машин с помощью специальных электрических или оптоволоконных кабелей, обычных телефонных линий, радиосвязи, спутниковой или иных средств связи. По этим линиям связи можно осуществлять обмен информацией между любыми включенными в сеть компьютерами.
Электронная почта Электронное письмо — текстовое сообщение, которое по каналам связи передается от компьютера отправителя к компьютеру адресата, где письмо и будет ожидать, пока его не прочитают.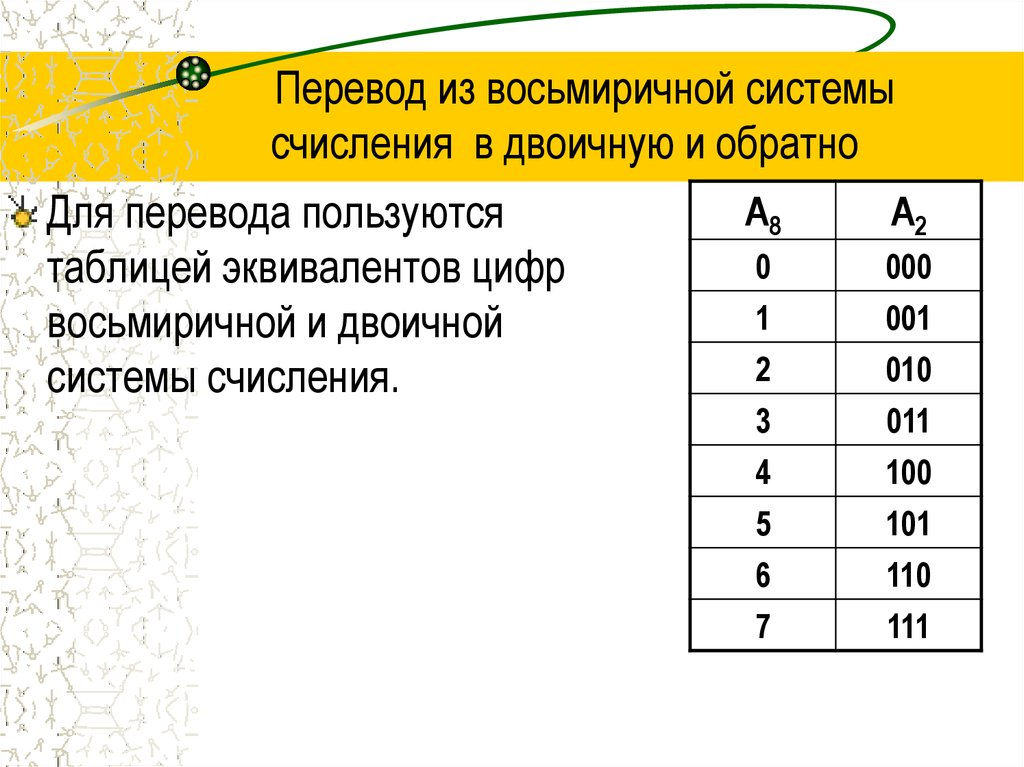
Средства общения (социальные сети, микроблоги) Facebook Вконтакте Мой мир Одноклассники Твиттер New Space Google+ Instagram
Numbers in Different Bases
Numbers in Different Bases- About
- Statistics
- Number Theory
- Java
- Data Structures
- Cornerstones
- Calculus
Changing to base 10 from another база
Когда мы пишем обычное число (с основанием 10), например 5763, мы имеем в виду значение:
$5000 + 700 + 60 + 3$$или, выражаясь в более откровенной форме: 90$$
Обратите внимание, «цифры» нашего числа соответствуют коэффициентам при степенях десяти, которые складываются вместе, чтобы получить значение нашего числа.
Аналогичным образом мы можем указать числа в других «основаниях» (помимо 10), используя разные цифры, соответствующие коэффициентам при степенях (данного основания), которые нужно сложить, чтобы получить значение нашего числа.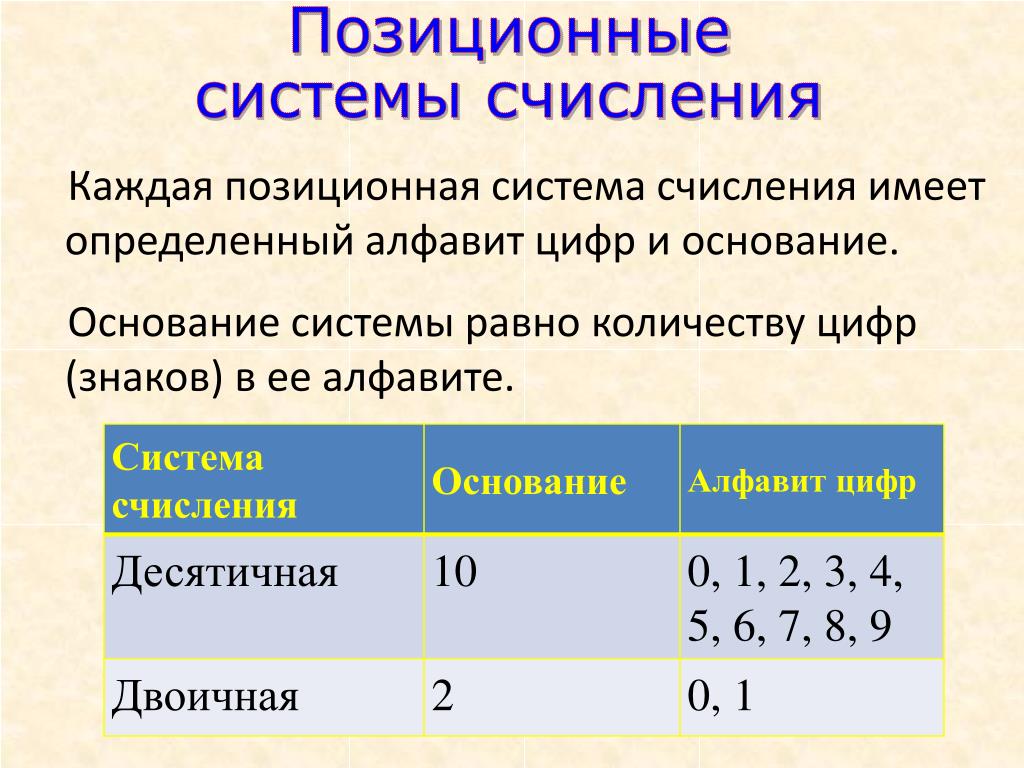
Например, число «основание 8» (или « восьмеричное число «) (как указано в нижнем индексе) 90$$
Чтобы каждое число имело представление по основанию b, но ни одно число не имеет более одного такого представления, мы должны использовать только цифры от 0 до (b-1) в любом данном числе по основанию b.
Это согласуется с числами с основанием 10, где мы используем цифры 0-9.
Для меньших баз мы используем подмножество этих цифр. Например, в базе 5 мы используем только цифры 0-4; в базе 2 (которую также называют двоичной ) мы используем только цифры 0 и 1.
Для больших оснований нам нужно иметь однозначные числа для значений после 9.0 = 23288$$
( Примечание. Как показано выше, нижний индекс, указывающий на используемую базу, часто опускается в случае шестнадцатеричных и/или двоичных чисел. В этих случаях контекст их использования обычно делает основу ясной. )
Переход с базы 10 на другую базу
Один (прямой, но неэффективный) способ преобразования базы 10 в другую:
- Определите наибольшую степень основания, которое входит в число ненулевое число раз.

- Определите, сколько раз эту степень можно вычесть из числа, чтобы результат не был отрицательным (т. е. разделить число на степень). Запишите эту цифру.
- Переопределите число, чтобы оно было наименьшим положительным остатком от деления на рассматриваемую степень
- Переопределите мощность как мощность, деленную на основание.
- Вернитесь к шагу 2, если сила теперь не меньше единицы — в этом случае все готово.
Например, чтобы преобразовать 1073 в основание 5, мы вспоминаем, что:
5 0 = 1 5 1 = 5 5 2 = 25 5 3 = 125 5 4 = 625 5 5 = 3125
Затем мы замечаем, что 5 4 = 625 — это наивысшая степень числа 5 меньше 1073.
1073 = 1 * 625 + 448 448 = 3 * 125 + 73 73 = 2 * 25 + 23 23 = 4 * 5 + 3 3 = 3 * 1 + 0
Красные цифры 13243 показывают представление числа 1073 по основанию 5.
Этот процесс, однако, неэффективен, поскольку необходимо знать и использовать различные способности желаемого основания.
Есть более простой способ!
Рассмотрим остатки при делении следующих чисел на 5:
1073 = 214 * 5 + 3 214 = 42 * 5 + 4 42 = 8 * 5 + 2 8 = 1 * 5 + 3 1 = 0 * 5 + 1
Примечание: представление по основанию 5 происходит от считывания остатков (выделено красным) снизу вверх! На каждом шаге выше мы просто делим на 5 и смотрим как на частное, так и на остаток — никаких знаний о высших степенях числа 5 не требуется!
Удивительно, но эта техника работает на любой базе. ( Можете ли вы объяснить почему? )
Так, например, если мы хотим найти двоичное (с основанием 2) представление числа 1000, мы просто вычисляем следующее:
1000 = 500 * 2 + 0 500 = 250 * 2 + 0 250 = 125 * 2 + 0 125 = 62 * 2 + 1 62 = 31 * 2 + 0 31 = 15 * 2 + 1 15 = 7 * 2 + 1 7 = 3 * 2 + 1 3 = 1 * 2 + 1 1 = 0 * 2 + 1
Таким образом, 1000 в двоичном формате равно 1111101000 .
Подсчет в другой базе
Счет по другим основаниям не слишком отличается от счета по основанию 10. Чтобы увидеть сходство, давайте посчитаем до 41 по основанию 10 и 3 (как показано в таблице ниже).
Обратите особое внимание на то, что «2» в системе счисления 3 играет ту же роль, что и «9» в базе 10. Она представляет собой последнюю цифру, которую вы можете использовать перед увеличением цифры слева.
| База 10 | База 3 | База 10 | База 3 | |
|---|---|---|---|---|
| 0 | 0 | 21 | 210 | |
| 1 | 1 | 22 | 211 | |
| 2 | 2 | 23 | 212 | |
| 3 | 10 | 24 | 220 | |
| 4 | 11 | 25 | 221 | |
| 5 | 12 | 26 | 222 | |
| 6 | 20 | 27 | 1000 | |
| 7 | 21 | 28 | 1001 | |
| 8 | 22 | 29 | 1002 | |
| 9 | 100 | 30 | 1010 | |
| 10 | 101 | 31 | 1011 | |
| 11 | 102 | 32 | 1012 | |
| 12 | 110 | 33 | 1020 | |
| 13 | 111 | 34 | 1021 | |
| 14 | 112 | 35 | 1022 | |
| 15 | 120 | 36 | 1100 | |
| 16 | 121 | 37 | 1101 | |
| 17 | 122 | 38 | 1102 | |
| 18 | 200 | 39 | 1110 | |
| 19 | 201 | 40 | 1111 | |
| 20 | 202 | 41 | 1112 |
Добавление в другую базу
Вы можете добавить другое основание (без преобразования в основание 10), если вы помните, что вы «переносите», когда у вас есть сумма, которая больше или равна вашей базе (вместо больше или равна 10), и что то, что вы «несете», — это количество раз, которое вы можете вытащить из своей суммы.
Лучше всего это иллюстрируется примером. Предположим, вы хотите добавить шестнадцатеричные числа 4EF5A и 6ACF7:
1111 <---- Это "несущие" цифры 4EF5A +6ACF7 ------ B9C51
Давайте рассмотрим пример. Заметь
А + 7 = 11 (шестнадцатеричные вычисления) 10 + 7 = 17 = 1 * 16 + 1 (десятичные вычисления)
Итак, мы записываем 1 в столбце «единицы» и переносим 1. Затем
1 + 5 + F = 15 (шестнадцатеричные вычисления) 1 + 5 + 15 = 21 = 1 * 16 + 5 (десятичные вычисления)
Итак, мы записываем 5 в колонке «десятки/шестнадцать» и переносим 1. Затем
1 + F + C = 1C (шестнадцатеричные вычисления) 1 + 15 + 12 = 28 = 1 * 16 + 12 (десятичные вычисления)
Итак, мы записываем C в следующем столбце и переносим 1. Затем
1 + E + A = 19 (шестнадцатеричные вычисления) 1 + 14 + 10 = 25 = 1 * 16 + 9 (десятичные вычисления)
Итак, мы записываем 9 в следующем столбце и переносим 1. Затем
Затем
1 + 4 + 6 = B (шестнадцатеричные вычисления) 1 + 4 + 6 = 11 (десятичные вычисления)
Итак, мы пишем букву B в следующем столбце, и все готово.
Ярлык для переключения между основанием 2 и основанием 16
Рассмотрим следующее преобразование из двоичного в шестнадцатеричное:
100100010101111 (двоичный) = 0100 1000 1010 1111
4 8 10 15
= 4 8 А F
Следовательно, 10010001010111 (двоичный) = 48AF (шестнадцатеричный)
Удивительно, но всегда можно разбить двоичное число на группы из 4 цифр (начиная справа и добавив начальные нули, если цифры заканчиваются), а затем интерпретировать эти группы из 4 цифр как шестнадцатеричные значения и получить шестнадцатеричное представление для исходное двоичное число. ( Можете ли вы понять, почему? )
Обратный процесс так же прост.
Предположим, мы хотим преобразовать FC7 (hex) в двоичную форму. Обратите внимание, что
Обратите внимание, что
F (шестнадцатеричный) = 15 = 1111 (двоичный) C (шестнадцатеричный) = 12 = 1100 (двоичный) 7 (шестнадцатеричный) = 7 = 0111 (двоичный) Следовательно, FC7 (шестнадцатеричный) = 111111000111 (двоичный)
числовая база | Brilliant Math & Science Wiki
Гаутам Шарма, Нихил Амминабхави, Алоизиус Нг, а также
способствовал
Содержимое
- Целочисленные базы чисел
- Числовая база — преобразование в другие базы
- Преобразование в десятичную систему
- От десятичной системы к другим основаниям
- От одной базы к другой
- Числовая база — решение проблем
Поскольку чаще всего используется десятичная система счисления, мы разделим переводы на три части:
- из любой системы счисления в десятичную систему счисления
- от десятичной до любой системы счисления
- с любой базы на любую другую базу.

А пока мы изучим преобразование целых чисел и преобразование десятичных чисел с плавающей запятой. 9{-1})=1,5. \ _ \ квадрат (1 × 80) + (4 × 8−1) = 1,5. □
Для целых чисел:
Для перевода из десятичной системы в другую выполните следующие действия:
- Разделите десятичное число, которое необходимо преобразовать, на новую систему счисления и запишите остаток.
- Разделите частное, полученное при предыдущем делении, на новое основание и запишите остаток.
- Повторяйте шаг 2, пока частное не станет равным 0.
- Теперь, после того как частное станет равным 0, запишите полученные остатки справа налево в том порядке, в котором они были получены; если вы получили 1 в качестве остатка от первого деления, 3 от второго деления и 6 от третьего деления, то запишите это как 631.
Преобразование 271027_{10}2710 в основание 8.
Используя описанные выше шаги, мы имеем следующее:
- делим 27 на 8, получаем остаток 3 и частное 3,
- деля 3 на 8, получаем остаток 3 и частное 0.
Следовательно, его эквивалентное восьмеричное представление равно 33833_8338. □_\квадрат□
Для плавающих десятичных чисел:
Предположим, что у нас есть натуральное число cncn−1⋯c3c2c1c0.c−1c−2⋯c−m‾\overline{c_nc_{n-1}\cdots c_3c_2c_1c_0.c_{- 1}c_{-2}\cdots c_{-m}}cncn−1⋯c3c2c1c0.c−1c−2⋯c−m в десятичной системе счисления с nnn цифры до запятой и цифры ммм после. Затем целая часть и дробная часть могут быть преобразованы отдельно, а затем добавлены.
Целую часть можно преобразовать, как в приведенном выше примере, поэтому теперь нам нужно преобразовать дробную часть. То есть 0.c−1c−2⋯c−m0.c_{-1}c_{-2}\cdots c_{-m}0.c−1c−2⋯c−m в десятичной системе счисления должен быть преобразован в базовый bbb. Это можно сделать, выполнив следующие действия:
- Умножьте десятичную дробную часть на bbb.
- Запишите целую часть полученного числа.
- Теперь снова возьмите дробную часть предыдущего результирующего числа в качестве новой дробной части.
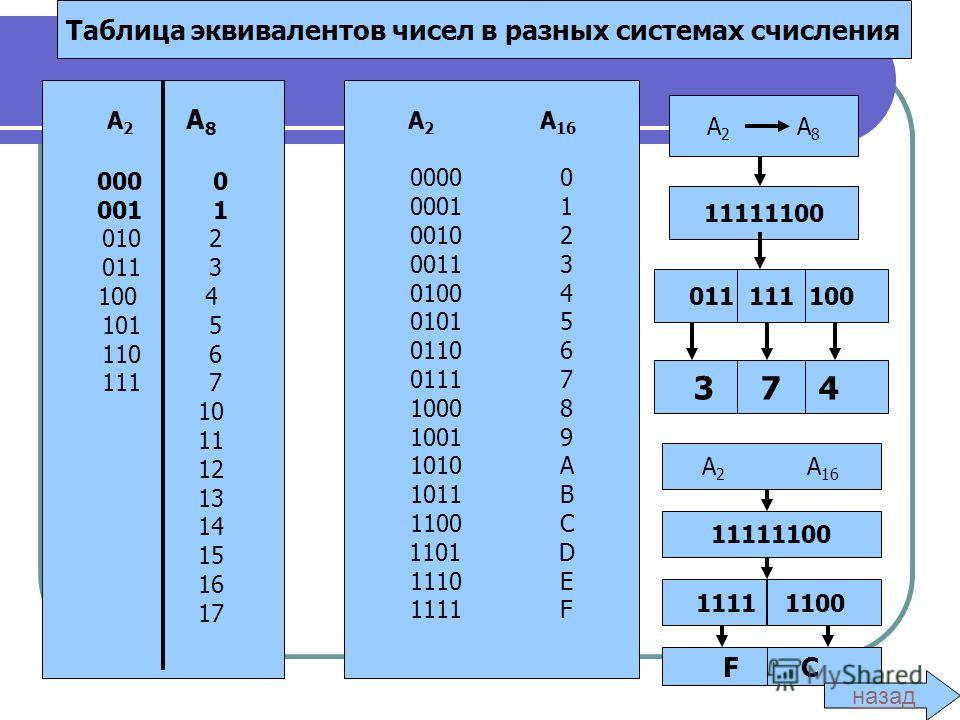 Если он равен нулю, то мы закончили. Если нет, то повторим вышеописанные шаги.
Если он равен нулю, то мы закончили. Если нет, то повторим вышеописанные шаги. - Все отмеченные целые части записываются слева направо в порядке их получения, с предшествующей десятичной точкой.
Наглядно можно понять на примере:
Преобразование 987,11111111111…987,11111111111\ldots 987,11111111111… в восьмеричную систему счисления.
Во-первых, целая часть 987987987 будет равна 173317331733 в восьмеричном основании по приведенной выше теории.
Теперь возьмем дробную часть 0,111111111111…0,111111111111\ldots0,111111111111….
- Умножая на 8, получаем 0,888888888888888888…0,888888888888888888\ldots0,888888888888888888….
- Теперь целая часть равна нулю, а новая дробная часть равна 0,888888888888…0,8888888888888\ldots0,888888888888….
- Снова умножая эту новую дробную часть на 8, мы получаем 7,1111111111111…7,1111111111111\ldots7,1111111111111….
- Теперь целая часть равна 7, а новая дробная часть равна 0,111111111…0,111111111\ldots0,111111111….
- Здесь мы видим, что у нас снова 0,111111111…0,111111111\ldots0,111111111…, поэтому цифры будут повторяться.
Следовательно, восьмеричное представление 0,11111111111…0,11111111111\ldots0,11111111111… равно 0,070707070707…0,070707070707\ldots0,070707070707….
Таким образом, новый номер будет 1733.07070707…1733.07070707\ldots1733.07070707… в восьмеричной системе счисления. □_\квадрат□
Это можно легко сделать, сначала преобразовав исходное число в десятичную систему счисления, а затем в требуемую базу.
Преобразование 10210_2102 в основание 8.
Мы можем легко преобразовать его в десятичное число, то есть 2.
Затем мы можем преобразовать это число в восьмеричное, что также равно 2.
Следовательно, 102=2810_2=2_8102=28. □_\квадрат□Примечание: Этот пример дает нам еще одно представление о том, что если начальное значение меньше основания, в которое оно должно быть преобразовано, то число остается прежним.
Например, 78=710=716=71007_8=7_{10}=7_{16}=7_{100} 78=710=716=7100 и т. д.
Если 128=x212_8=x_2128=x2, найдите сумму цифр xxx.
Обратите внимание, что aba_bab – это число aaa в базе bbb. 92, \ldots50,51,52,…, где каждую степень числа 5 можно использовать не более трех раз?
Пусть fff — многочлен с целыми неотрицательными коэффициентами. Если f(1)=7f(1)=7f(1)=7 и f(7)=7597f(7)=7597f(7)=7597, чему равно f(10)?f(10)?f(10 )?
Да №
(11221133112211)12\large (11221133112211)_{12}(11221133112211)12
Делится ли указанное выше число на (143)10?(143)_{10}?(143)10? (Калькуляторы не нужны!)
Уточнение: Нижний индекс 12 означает, что мы работаем в базе 12.
Попробуйте задать больше вопросов по базам.
0 1 2 3 4 5 6 7
(102030405060504030201)7\large (102030405060504030201)_7(102030405060504030201)7 на (8)10(8)_{10}(8)10?
Уточнение:
- Пожалуйста, без калькуляторов!
- Нижний индекс 7 указывает на то, что мы работаем в базе 7.

Попробуйте больше вопросов по базам.
По основанию 10 можно определить делимость на 3 или 9просто сложив все цифры в номере; если результаты делятся на 3 или 9, то числа делятся на 3 или 9 соответственно.
Какое наименьшее основание nnn такое, что мы можем проделать тот же трюк со всеми числами от 2 до 6?
Другими словами, какое наименьшее целое число n>1n > 1n>1 такое, что для любого числа xxx, записанного в системе счисления nnn, можно определить делимость на все целые числа mmm (2≤m≤6),(2 \leq m \leq 6),(2≤m≤6), сложив все цифры xxx и, если результат делится на mmm, сделать вывод, что xxx делится на m?m?m?
Попробуйте больше вопросов по базам.
Цитировать как: База номеров. Brilliant.org . Извлекаются из https://brilliant.org/wiki/number-base/
Числовые базы | Математика | Компьютеры
Существует более простое объяснение системы счисления, а также интерактивные страницы. на двоичные, двоичные дроби, нормализованные двоичные числа с плавающей запятой и
шестнадцатеричный в разделе Interactive .
Существует также число оснований Счеты , которые вы можете использовать для экспериментов с различными системами счисления, и вы можете
смотрите видео по числовым базам на YouTube-канале AdvancedICT . Для большинства курсов GCSE по информатике требуется преобразование между системами счисления.
на двоичные, двоичные дроби, нормализованные двоичные числа с плавающей запятой и
шестнадцатеричный в разделе Interactive .
Существует также число оснований Счеты , которые вы можете использовать для экспериментов с различными системами счисления, и вы можете
смотрите видео по числовым базам на YouTube-канале AdvancedICT . Для большинства курсов GCSE по информатике требуется преобразование между системами счисления.
Что такое числовая база?
Немецкий математик Леопольд Кронекер однажды сказал, что «Бог дал нам целые числа, а все остальное — дело рук человека». Я думаю, он имел в виду, что числа существуют, но мы можем представлять их по-разному и делать с ними разные вещи. Не вдаваясь в философию, полезно помнить, что часто то, о чем мы думаем как о числах, на самом деле является символами, представляющими число — так же, как то, как вы пишете свое имя, не является вами, и вы все еще тот же человек, если вы печатаете свое имя, напишите его другим цветом или используйте другой алфавит.
Основы счисления — это разные способы записи и использования одного и того же числа. Для нашей арифметики мы используем систему, называемую основанием 10, или десятеричным числом, но существует почти столько же числовых оснований, сколько и самих чисел. Многие люди думают, что мы используем основание 10, потому что у нас есть 10 пальцев, на которых мы можем считать. Компьютеры и другие электронные устройства могут надежно использовать только электрический ток или отсутствие тока для счета (например, наличие двух пальцев), и поэтому они, как правило, используют основание 2 (двоичное) внутри.
Важно помнить, что числовые основания — это просто разные способы записи чисел — так же, как римские цифры или таблицы подсчета, — но в остальном числа ведут себя как обычно. Это не означает, что их арифметика принципиально отличается — на самом деле то, как ведут себя системы счисления, полностью согласовано.
Как они работают?
Вы будете знакомы с идеей основания 10 и заголовками столбцов, о которых вы говорили в начальной школе — единицы, десятки, сотни, тысячи и т. д. — другие системы счисления работают точно так же. У них есть столбцы с заголовками, которые используются для представления чисел, а разные цифры располагаются в разных позициях, начиная справа.
д. — другие системы счисления работают точно так же. У них есть столбцы с заголовками, которые используются для представления чисел, а разные цифры располагаются в разных позициях, начиная справа.
Заголовки столбцов для общих оснований и общее основание x показаны в таблице ниже:
| Заголовки столбцов | Базовый номер | |||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | 2 (двоичный) |
| и т.д. | 262144 | 32768 | 4096 | 512 | 64 | 8 | 1 | 8 (восьмеричный) |
| и т. Д. | 100000 | 10000 | 1000 | 100 | 10 | 1 | 10 (Denary) | |
| и т. Д. | 65536 | 4096 | 256 | 16 | 1 | 16 (Hexadecimal) | ||
и т.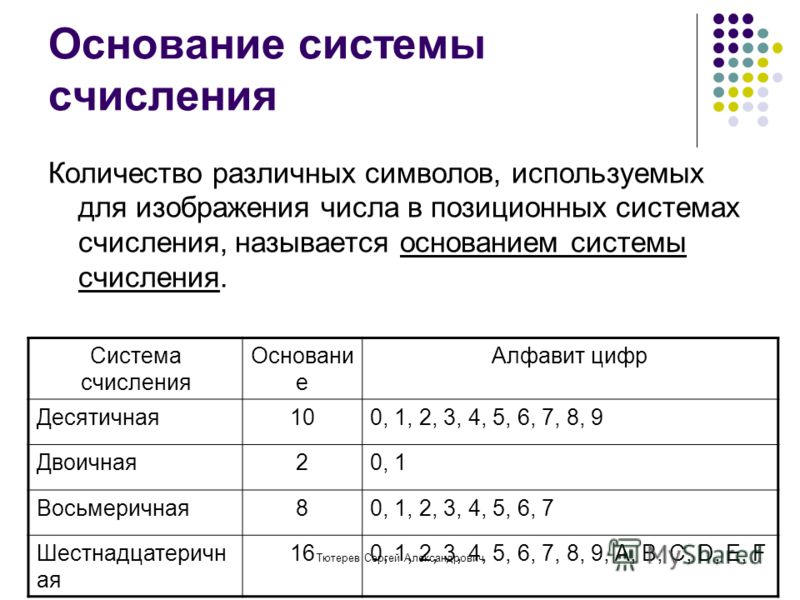 д. д. | Х 6 | Х 5 | Х 4 | Х 3 | Х 2 | Х 1 | Х | х |
Основание обычно записывается в виде нижнего индекса после числа, поэтому вы можете сказать, что 111 2 — это 7 в двоичном формате, а не сто одиннадцать.
Вы можете работать с любой системой счисления (кроме 1, что на самом деле не имеет смысла), и некоторые языки программирования, такие как Лисп, позволяют вам это делать. Однако в вычислительной технике вы, как правило, сталкиваетесь только со следующими четырьмя основаниями, и вы уже знаете основание 10. Эти общие основы также имеют собственные имена, указанные в скобках:
- основание 2 (двоичный)
- основание 8 (восьмеричное)
- основание 10 (денарий)
- основание 16 (шестнадцатеричное)
Самая большая цифра, которая может быть в любом столбце, на единицу меньше числа основания. Таким образом, для двоичного (по основанию 2) это 1, затем 7 для восьмеричного (по основанию 8), 9 для десятичного (по основанию 10) и т. д.
Таким образом, для двоичного (по основанию 2) это 1, затем 7 для восьмеричного (по основанию 8), 9 для десятичного (по основанию 10) и т. д.
Однако после основания 10 у нас закончились цифры для представления чисел, поэтому мы должны использовать буквы, где A = 10, B = 11, C = 12 и т. д. Таким образом, последовательность чисел, записанных в шестнадцатеричном формате, равна 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, за которыми следуют 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F и т. д.
Когда мы записываем число с основанием 10, мы знаем его значение, потому что мы умножаем отдельные цифры на соответствующие им заголовки столбцов. Например, когда мы видим 123, даже если мы не думаем об этом, мы вычисляем 1 х 100 + 2 х 10 + 3 х 1, чтобы получить сто двадцать три. Точно так же работают и другие системы счисления.
Вы можете использовать эту информацию для преобразования чисел в других системах счисления в систему с основанием 10, например:
| 32 | 16 | 8 | 4 | 2 | 1 | |
| 1 | 0 | 1 | 1 2 | = 8 + 2 + 1 = 11 10 |
| 32768 | 512 | 64 | 8 | 1 | |
| 1 | 2 | 3 | 4 8 | = 1 x 512 + 2 x 64 + 3 x 8 + 4 x 1 10 = 512 + 128 + 24 + 4 10 668 10 | 5
Двоичный (основание 2)
В наши дни вы, вероятно, редко будете сталкиваться с двоичным кодом, но полезно понимать, как компьютеры работают внутри, чтобы вы могли понять такие концепции, как параллельная передача. Тот факт, что компьютеры используют двоичный код, объясняет, почему все кратно 2 — почему компьютеры имеют 8 МБ, 16 МБ, 32 МБ, 64 МБ и т. д. памяти, а не 10 МБ, 20 МБ, 30 МБ и т. д., а также почему существует 1024 байтов в килобайте (1024 = 2 10 ), а не 1000 байт.
Тот факт, что компьютеры используют двоичный код, объясняет, почему все кратно 2 — почему компьютеры имеют 8 МБ, 16 МБ, 32 МБ, 64 МБ и т. д. памяти, а не 10 МБ, 20 МБ, 30 МБ и т. д., а также почему существует 1024 байтов в килобайте (1024 = 2 10 ), а не 1000 байт.
Основное использование, вероятно, в сочетании с методами побитовой логики, показанными на предыдущей странице, для объединения и разделения значений, хранящихся в одном байте (или слове).
Есть и другие термины, связанные с двоичными файлами, которые вам необходимо знать. Во-первых, бит — это двоичная цифра , то есть единичное вхождение 0 или 1. Это наименьшая единица хранения, которую вы можете иметь внутри компьютера. Группы из 8 бит называются байт . Байт может использоваться для представления числа, цвета или символа (например, с использованием ASCII). Вы также можете услышать термин nibble , что составляет 4 бита. Наконец, слово — это наибольшее количество битов, которое процессор может обработать за один раз — например, когда мы говорим, что новые компьютеры имеют 64-битные процессоры, мы имеем в виду, что длина слова составляет 64 бита или 8 байт. .
.
Максимальное значение, которое вы можете сохранить, используя определенное количество битов, может быть определено довольно легко. Использование n бит, максимальное значение, которое вы можете сохранить, равно 2 n - 1 , а количество различных значений, которые вы можете сохранить, равно 2 n (от 1 до 2 n
Восьмеричный (основание 8)
Я никогда не встречал ничего, что использовало бы восьмеричное число! Я думаю, что он, вероятно, включен в требования к экзамену по чисто академическим причинам, а также потому, что его легко преобразовать в двоичный код (см. ниже).
ниже).
Шестнадцатеричный (основание 16)
Шестнадцатеричное число по-прежнему используется достаточно часто, особенно для таких вещей, как цвета в HTML или языках программирования. Это также весьма полезно, потому что представление больших чисел относительно компактно, но легко преобразуется в двоичное, чтобы вы могли видеть битовые комбинации.
Сдвиг битов
Вы, несомненно, заметили, что с числами по основанию 10 вы можете перемещать цифры влево или вправо на одно место, умножая или разделяя число на 10. Тот же трюк работает с разными основаниями счисления - вы просто умножаете и делите по основанию число (например, умножьте на 2 в двоичном формате, чтобы сдвинуть биты влево на одну позицию).
Это может быть полезно для таких вещей, как создание шестнадцатеричных значений цвета (например, для веб-страниц). В 24-битной системе (такой как HTML) цвета представлены 24-битными числами от 000000 до FFFFFF (каждая шестнадцатеричная цифра соответствует 4 битам — см. ниже). 24 бита состоят из 8 битов, соответствующих количеству красного, зеленого и синего цветов.
ниже). 24 бита состоят из 8 битов, соответствующих количеству красного, зеленого и синего цветов.
Итак, каждый компонент представлен 8 битами, то есть числом от 0 до 255. Если вы знаете, сколько красного, зеленого и синего вам нужно, как их объединить, чтобы получить полный цвет? Для HTML правильный порядок битов — RRGGBB (r = красный, g = зеленый, b = синий), поэтому нам нужно «сдвинуть» значения зеленого и красного компонентов, а затем сложить все три компонента вместе. .
Мы можем оставить синее значение как есть, но нам нужно переместить зеленое значение на две позиции. Чтобы переместиться на одно место в шестнадцатеричном формате, мы умножаем на 16, поэтому, чтобы переместиться на два места, просто сделайте это дважды - 16 x 16 = 256 - таким образом, умножьте зеленое значение на 256. Для красного значения нам нужно переместиться на четыре места. - 16 х 16 х 16 х 16 = 65 536 - значит, умножаем значение красного компонента на 65 536.
Очевидно, что если бы вы просто пытались самостоятельно определить цвет, вам не нужно было бы выполнять эти шаги, но если бы вам нужно было создать программу, подобную моему микшеру цветов, то вы бы сделали это следующим образом.
Преобразование между базами
Вы можете преобразовать восьмеричную в двоичную и наоборот, сгруппировав эти двоичные цифры (или биты) в тройки, а затем преобразовав их в их двоичные эквиваленты. Например:
Что такое 101100 2 в восьмеричной системе?
| 101 2 = 5 10 100 2 = 4 10 | Просто объедините две цифры: 101100 2 = 54 8 |
То же самое можно сделать и для шестнадцатеричного, только биты должны быть сгруппированы по четыре, например
Что такое 10110110 2 в шестнадцатеричном формате?
| 1011 2 = 11 10 = В 16 0110 2 = 6 10 | Просто объедините два результата: 10110110 2 = B6 16 |
Наконец-то шутка с числовой базой! Почему программисты путают Рождество с Хэллоуином? Потому что 31 ОКТЯБРЯ = 25 ДЕКАБРЯ!
База 3 | Математика Новой Зеландии
Цели достижения
NA5-2: Используйте простые числа, общие множители и кратные, а также степени (включая квадратные корни).
Разработка АО и другие учебные ресурсы
Деятельность учащихся
Мы говорим, что число 1202 является числом по основанию 3, когда запишем его как 1 x 3 3 + 2 x 3 2 + 0 x 3 + 2 x 3 0 .
Это равно 27 + 18 + 2 = 47 в нашем обычном основании, основание 10.
Каково значение числа 21021 по основанию 3?
Чему равна сумма двух чисел с основанием 3 в основании 3?
Запишите число 582 по основанию 10 по основанию 3.
Конкретные результаты обучения
Запись чисел по основанию 3
Выполнение арифметических действий по основанию 3
Объяснение «связей» между основанием 3 и десятичными числами
Разработайте и используйте стратегии решения задач для математического исследования ситуаций (будьте систематичны).
Описание математики
Эта задача позволяет учащимся лучше понять нашу десятичную систему, рассматривая сопоставимую систему — систему с основанием 3.
Учащиеся должны увидеть, что числа могут быть представлены более чем одним способом. Иногда одна система имеет преимущество перед другой.
Например, основание 2 очень полезно в телекоммуникациях. Электричество можно заставить пульсировать или не пульсировать через цепи. Используя импульс для представления 1 и неимпульсный для представления 0, числа могут передаваться по линии. Как только это будет сделано, письма также могут быть переданы. Это потому, что мы можем кодировать буквы цифрами. Таким образом, система с основанием 2 позволяет нам отправлять сообщения по телефонным линиям или в виде радиоволн.
Существуют и другие способы использования баз. Например, мы представляем векторы в трех измерениях с помощью единичных векторов i , j и k . В семи измерениях мы можем использовать семь единичных векторов и так далее для более высоких измерений.
Необходимые исходные материалы
Копи-мастер задачи (маори)
Копи-мастер задачи (английский)
Деятельность
Проблема
Мы говорим, что число 1202 является числом по основанию 3, когда мы записываем его как 1 x 3 3 + 2 x 3 2 + 0 x 3 + 2 x 3 0 .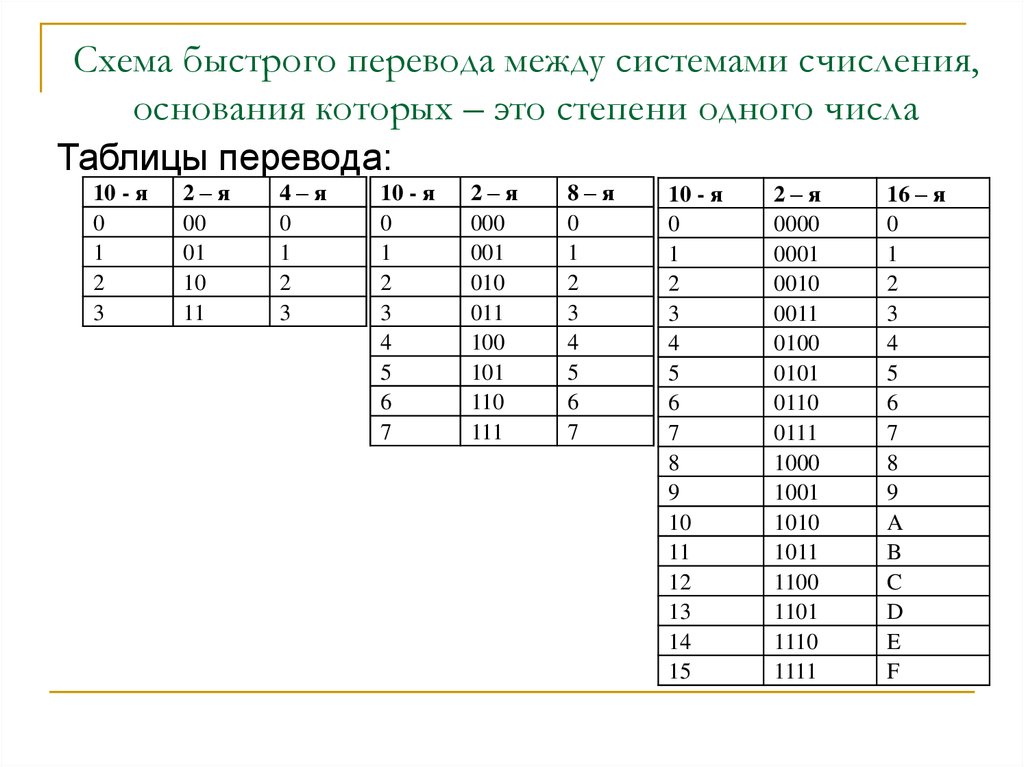 Это равно 27 + 18 + 2 = 47 в нашем обычном основании, основании 10.
Это равно 27 + 18 + 2 = 47 в нашем обычном основании, основании 10.
Какое значение числа 21021 по основанию 3?
Запишите число 582 по основанию 10 по основанию 3.
Обучающая последовательность
- Представьте задачу, сначала поговорив о десятичных числах.
Что такое 10 2 ? Как насчет 10 7 ?
Что на самом деле означают цифры 1, 2 и 0 в числе 120?
Можете ли вы разложить число 2376 в степени 10? - Тогда поговорим о числах с основанием 3.
Что такое 34? Как насчет 38?
Что на самом деле означают цифры 1, 2, 0 в числе 120 по основанию 3?
Можете ли вы разложить число 21102 по основанию 3 по степени 3?
Чему равно число 220011 с основанием 3 в системе счисления с основанием 10? - Поставьте задачу и предложите учащимся поработать над ней в своих группах.
- По мере работы групп вам может понадобиться давать им более простые задачи, чтобы помочь им решить части b) и c).

- Попросите несколько групп поделиться и объяснить классу свои решения.
- Дайте учащимся время написать и объяснить свои решения.
Расширение задачи
Найдите способ превратить любое число с основанием 10 в число с основанием 3.
Решение
- 21021 = 2 x 3 4 + 1 x 3 3 + 0 x 3 2 + 2 x 3 + 1 = 162 + 27 + 6 + 1 = 9016.
- Обратите внимание, что 1 + 2 = 10 по основанию 3 и 2 + 2 = 11. Итак,
| 2 2 0 2 1 |
| +2 1 2 1 0 |
| 12 1 0 0 1 |
- Ключевые числа в системе счисления 3: 1, 3, 9, 27, 81, 243, 729, … Другими словами, степени числа 3.
Наибольшая степень числа 3, меньшего, чем 582, равна 243, а 2 x 243 = 486 меньше 582. Таким образом, форма числа с основанием 3 будет начинаться с 2… = 2 x 3 5 + …
582 – 486 = 96.
81 — это наибольшая степень числа 3 меньше 96.
Итак, 582 начинается с 21… = 2 x 3 5 + 1 x 3 4 + …
Поскольку 96 – 81 = 15, что равно 9 + 6,
тогда 582 = 2101… = 2 x 3 5 + 1 x 3 4 + 0 x 3 3 + 90 x 3 2 + 2 х 3 + 0 х 3 0 .
Решение расширения
Покажем частный пример общего метода
3 | 582 |
|
3 | 194 | |
3 | 64 | 2 |
3 | 21 | 1 |
3 | 7 | |
3 | 2 | 1 |
| 2 |
Тройки слева делят соответствующие числа в центре. Частное записывается строкой ниже, а остаток идет справа.
Частное записывается строкой ниже, а остаток идет справа.
Начните с 299.
3 | 299 |
|
| 3 | 299 |
|
| 3 | 299 |
|
| 99 | 2 |
| 3 | 99 | 2 |
| 3 | 99 | 2 |
|
|
|
|
| 33 |
| 3 | 33 | ||
|
|
|
|
|
|
|
|
| 11 |
3 | 299 |
|
| 3 | 299 |
|
3 | 99 | 2 |
| 3 | 99 | 2 |
3 | 33 |
| 3 | 33 | ||
3 | 11 |
| 3 | 11 | ||
3 | 3 | 2 |
| 3 | 3 | 2 |
|
|
|
| 3 | 1 | |
|
|
|
| 3 | 1 |
В первой таблице делим 299 на 3 получаем 99 (в таблице) и остаток от 2 (справа). Это 2 - последняя цифра справа от основания 3 формы 29.9. Затем 3 в 99 идет 33 раза (в таблице) и в остатке 0 (вправо). Этот остаток от 0 становится второй цифрой справа в окончательной форме числа с основанием 3. Мы продолжаем спускаться.
Это 2 - последняя цифра справа от основания 3 формы 29.9. Затем 3 в 99 идет 33 раза (в таблице) и в остатке 0 (вправо). Этот остаток от 0 становится второй цифрой справа в окончательной форме числа с основанием 3. Мы продолжаем спускаться.
Этот алгоритм изменяет числа по основанию 10 на числа по основанию 3. Просто проверьте, 582 по основанию 3 равно 210120 (мы это уже видели). Но 299 по основанию 3 — это 102002.
Почему этот алгоритм работает?
Если основание 3 хорошо изучено, попробуйте работать с основанием 4 или любым другим основанием, которое вы можете придумать.
Приложения
Добавить в план
Пятый уровень
Как написать калькулятор систем счисления на Python | Мартин Андерссон Оберж
Двоичный, десятичный или шестнадцатеричный, иди ко мне, братан!
Фото Андреа Пиаккуадио из Pexels В этой статье мы создадим калькулятор, который можно использовать для преобразования любого числа из любого основания в любое другое основание. В системах счисления «База» говорит нам, сколько чисел у вас есть. Двоичный имеет 2, восьмеричный имеет 8, десятичный имеет 10 и т. д.
В системах счисления «База» говорит нам, сколько чисел у вас есть. Двоичный имеет 2, восьмеричный имеет 8, десятичный имеет 10 и т. д.
Программа, которую мы собираемся написать, может обрабатывать любое число и с основанием , которое мы ей подкинем. Когда мы выясним математику, стоящую за этим, его очень легко настроить.
Что мы будем создавать:
Этот калькулятор основан на математике (Разве они не все?). Возможно, нам придется освежить нашу память в теории преобразования между системами счисления (или узнать что-то новое).
Если вы изучали математику в школе или изучали компьютеры на любом уровне, скорее всего, вы преобразовали одну систему счисления в другую. . Возможно, вы помните двоичную таблицу или говорите о « в десятичной системе » , « в восьмеричной системе » и « в шестнадцатеричной системе» .
Десятичная система счисления (с основанием 10) — это та, которую мы используем ежедневно при счете. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Когда у нас заканчиваются числа, мы добавляем еще одну позицию слева → 10, 11, 12, 13, 14, 15, 16, 17 , 18, 19, 20, 21… и т.д. Когда у нас снова закончатся числа, мы добавим новую позицию → 100, 101, 102…118, 119, 120.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Когда у нас заканчиваются числа, мы добавляем еще одну позицию слева → 10, 11, 12, 13, 14, 15, 16, 17 , 18, 19, 20, 21… и т.д. Когда у нас снова закончатся числа, мы добавим новую позицию → 100, 101, 102…118, 119, 120.
Да, да… Я помню начальную школу….
Мы об этом не задумываемся, потому что учимся этому в 2–3 года. Попросите ребенка считать в восьмеричной системе счисления с основанием 8, и он, скорее всего, несколько секунд будет смотреть на вас, прежде чем вернуться к своей домашней работе на своем iPad. Теория проста и идентична десятичной системе, просто мы к ней не привыкли.
Счет в восьмеричной системе будет выглядеть так:
0,1,2,3,4,5,6,7 → 10,11,12,13,14,15,16,17 → 20,21…
Первое преобразование, на которое мы должны обратить внимание, это переход из любой системы счисления (Base-N) в десятичную систему (Base-10). Очень легко преобразовать десятичную систему в любую другую систему. Поэтому полезно знать, как перейти к десятичной системе.
Поэтому полезно знать, как перейти к десятичной системе.
Если мы продолжаем использовать в десятичной системе и в восьмеричной системе в качестве примеров, мы можем преобразовать число в восьмеричной системе в его эквивалент в десятичной системе . Давайте выберем случайное число.
256(Base-8) → ???(Base-10)
(обещаю, 256 было на самом деле случайным)
- У нас есть три позиции 2 (сотни), 5 (десятки) и 6 (единицы). Эти позиции могут занимать от 0 до 7 (8 цифр), как вы помните из вступления.
- Нам нужно перевести каждое из чисел во всех позициях в десятичную систему. Десятичная система может содержать 0–9должность)). Если мы начнем с наименьшего числа справа, мы умножим 6 на 8⁰, 5 на 8¹ и 2 на 8².
Вот иллюстрация, которая значительно облегчит понимание:
переходит от восьмерки 256 к десятичной системе счисления 174Когда у нас есть число в десятичной системе (основание-10), очень легко перейти к любая система.
 Вернемся от 174 (основание-10) к 256 (основание-8)
Вернемся от 174 (основание-10) к 256 (основание-8)Найдем число в другом основании, разделив его на основание и сохранив остаток. Остатки построят для нас число в другом основании. Когда у нас есть остатки, мы читаем число от наименее значимого числа до наиболее значимого числа, то есть снизу вверх. Теперь у вас есть новый номер, представленный в вашей новой базе!
174/2 дает нам 21,75. Обратите внимание, что 21 — красный, а 0,75 — зеленый. Отправляем 21 на следующую строку и имеем дело с 0,75. Если мы умножим 0,75 на основание, у нас останется остаток (это число, которое мы ищем). Этот номер отправлен в крайний правый угол синим цветом.
Когда мы достигнем 0, мы официально закончим и можем паковать чемоданы с красивым номером в нашу новую базу.
переходит от основания 10 174 к основанию 8 256Это не только означает, что мы можем перейти от основания 10 к основанию 8 и наоборот. Мы можем перейти от Base-X к Base-Y. Любая база, которую мы хотим.
Ощущения примерно такие:
Фото Marcin Dampc с PexelsЕсли вы до сих пор не понимаете, как это работает, предлагаю ознакомиться с «Репетитором по органической химии».
 Его видео — лучшее, что я знаю по этому предмету:
Его видео — лучшее, что я знаю по этому предмету:Репетитор по органической химии
Этот канал фокусируется на предоставлении обучающих видео по органической химии, общей химии, физике, алгебре…
www.youtube.com
Пришло время погрузиться в код!
Примечание. Я программирую большую часть программ вручную. Это означает, что я не использую слишком много библиотек, потому что хочу узнать как можно больше. В этом коде я do используйте стандартные функции Python, такие как
bin(), потому что я хочу показать вам, что это возможно, но вместо того, чтобы использоватьhex(), я думаю, что было веселее вручную кодировать те же функции. В производственной среде вы, вероятно, захотите сделать ее короткой и использовать библиотеки, которые решают ваши проблемы, вместо того, чтобы писать все с нуляЭта программа представляет собой всего один файл
main.pyсо всем кодом в одном документе. Если вы хотите, вы можете расширить это, как вам нравится. Числовой класс? Конечно, почему бы и нет. графический интерфейс? Также кое-что, на что мы должны обратить внимание.
Если вы хотите, вы можете расширить это, как вам нравится. Числовой класс? Конечно, почему бы и нет. графический интерфейс? Также кое-что, на что мы должны обратить внимание.Я рекомендую работать с онлайн-калькулятором базового конвертера во время кодирования, чтобы перепроверить, что ваш код выводит правильные значения.
Вот суть:
полный код сути.Логика кода заключается в том, что мы передаем функции три аргумента.
-
input_base— это база, которую мы хотим преобразовать. -
выходная_база— это база, на которую мы хотим преобразовать.
Раньше я не использовал многострочную строку для вывода меню, но создание такого меню имело бы смысл.
Функция возвращает всю строку меню, поэтому мы можем использовать ее где угодно. Нам также не нужно беспокоиться о новой строке.
возврат (
'''
------------------------------------------ ------------------
Добро пожаловать в конвертер числовой базы
Система запросит у вас:
- Число для преобразования
- Какое основание вы хотите преобразовать ИЗ
- Какое основание вы хотите преобразовать В ** ПОМНИТЕ: Все числа должны быть целыми числами! (кроме HEX) **
--------- --------------------------------------------------
''')
Вместо проверки пользовательского ввода в функции преобразователя я хотел создать валидаторы как функции. Делая это, мы создаем код, который можно использовать повторно.
Делая это, мы создаем код, который можно использовать повторно.
def validate_bin(check_number):
Эта функция просто проверяет, является ли число допустимым двоичным числом.
Мы не хотим проверять длинную строку с несколькими вхождениями одного и того же числа. Если мы преобразуем его в набор, мы удалим дубликаты. Наборы не могут содержать несколько экземпляров элемента. Мы используем понимание списка, чтобы преобразовать ввод в целое и проверить его на [0,1]
[int(item) для элемента в наборе(list(check_number))]
Я решил передать строки из взаимодействия с пользователем и создавать целые числа ввода, когда это необходимо. int(item) удостоверяется, что все числа являются целыми числами (мы также можем сверить строку со строкой ( ‘0’ , ‘1’ ), если захотим).
Вот как это будет выглядеть за кадром:
'10010011' → ['1','0','0','1','0','0','1', '1'] → [0,1]
, если 0 находится в [0,1], проверка проходит нормально, если 1 находится в [0,1], проверка также проходит нормально. Если бы у вас было число вроде 23, обе цифры не сработали бы, и функция вернула бы
Если бы у вас было число вроде 23, обе цифры не сработали бы, и функция вернула бы False
def validate_input(check_number):
Здесь ничего особенного… Код проверяет, содержит ли ввод определенные допустимые символы. Работаем с числами 0–9 , и поскольку мы поддерживаем HEX, мы также включаем a-f в качестве допустимого ввода.
def validator(input_number,input_base,output_base):
Эта функция использует другие валидаторы и проверяет все входные данные, чтобы мы знали, есть ли смысл продолжать преобразование.
- Сначала он проверяет, ввели ли мы число или шестнадцатеричное значение.
- Затем проверяем базы. Если input_base равно 2, мы конвертируем двоичное число. Следовательно, input_number должен состоять только из цифр, и если это так, то он должен быть равен 0 или 1.
- Если вводятся как цифры, так и буквы, это шестнадцатеричное число. Если input_base НЕ равен 16, мы не можем его преобразовать.
 HEX - это Base-16, и любая другая база будет вычисляться неправильно. Мы могли бы рассмотреть возможность создания предварительно заполненной базы ввода во время взаимодействия, когда кто-то вводит шестнадцатеричное число.
HEX - это Base-16, и любая другая база будет вычисляться неправильно. Мы могли бы рассмотреть возможность создания предварительно заполненной базы ввода во время взаимодействия, когда кто-то вводит шестнадцатеричное число. - Наконец, мы проверяем, пытается ли пользователь преобразовать в или из Base-1. Это невозможно, поэтому вместо сбоя программы мы хотим вернуть ошибку.
Теперь пришло время для основной части кода. Здесь мы будем использовать наши математические способности. Эта функция выполняет сопоставление, которое мы рассмотрели ранее, и у нее есть несколько мер безопасности, чтобы убедиться, что мы выводим правильно
def convert_number_system(input_number, …):
convert_number_system суть rester_list содержит числа, которые мы хотим вернуть. Если вы помните математику, вы должны мгновенно распознать остаток ключевого слова.
sum_base_10 . Мы хотим использовать Base-10 в качестве промежуточного шага. Мы устанавливаем начальное значение равным 0, а затем добавляем к этой переменной любые значения, которые вычисляем.
выходной двоичный код:
если output_base == 2:
return (bin(input_number)[2:])
Если пользователю нужен двоичный вывод, мы можем использовать встроенную функцию bin(). Нам не нужно, потому что математика одинакова, независимо от того, что мы проходим, но попробовать интересно.
bin() возвращает 0b и двоичный файл. 0b говорит нам, что это двоичное число. Мы хотим вернуть фактическое число. Вот для чего [2:]. Если вы запустите это в своем терминале, вы увидите разницу:
>>> check_number = 23
>>> print(bin(check_number))
0b10111
>>> print(bin(check_number)[2:])
10111
Он будет печатать с индекса 2 и далее.
Обратите внимание, что я оставил версию hex() в коде, но закомментировал. Вы можете использовать его, если хотите.
Основание НЕ равно 10:
Если основание не равно 10, мы проходим наш промежуточный шаг. Во-первых, мы переворачиваем список (вам не нужно этого делать, но потом вам нужно перевернуть индекс в цикле позже. Мне проще перевернуть список). Переворачивать списки в Python можно с помощью этого фантастического встроенного -в коде [::-1]
Во-первых, мы переворачиваем список (вам не нужно этого делать, но потом вам нужно перевернуть индекс в цикле позже. Мне проще перевернуть список). Переворачивать списки в Python можно с помощью этого фантастического встроенного -в коде [::-1]
reversed_input_number = input_number[::-1]
hex_helper_dict помогает нам обрабатывать числа выше 9, если пользователь отправил шестнадцатеричный ввод. Если вы помните нашу формулу, мы умножаем числа в каждой позиции на базовый индекс, зависящий от позиции.
Вот снова 256 от восьмеричное до десятичное:
2*(8²) + 5*(8¹) + 6*(8⁰) = 174
Если число шестнадцатеричное, например 23e, оно на самом деле читается 2 , 3, 14
2*(16²) + 3*(16¹) + 14*(16⁰) = 574
Этот цикл помогает нам со всем этим:
для индекса, число в enumerate(reversed_input_number):
для ключа, значение в hex_helper_dict.items():
if str(number).lower() == key:
number = value sum_base_10 += (int(number)*(int(input_base)**index))
Если вы посмотрите на приведенный выше код, вы увидите, что мы используем как enumerate, так и . items(), чтобы убедиться, что мы можем получить доступ ко всему, что нам нужно для выполнения нашей операции.
items(), чтобы убедиться, что мы можем получить доступ ко всему, что нам нужно для выполнения нашей операции.
Используя enumerate, мы можем получить доступ как к значению, так и к индексу переменной. Когда мы перебираем переменную, мы проверяем, является ли число (например, e ) равно любому из ключей в словаре. В случае 23e это так, и вместо этого мы хотим установить число 14, чтобы мы могли использовать его для фактического расчета.
sum_base_10 += (int(number)*(int(input_base)**index))
Теперь, когда мы уверены, что числа не являются буквами, мы можем перебирать числа (давайте останемся с 256) и выполнять операции . Для каждого числа, которое мы прокручиваем, мы выполняем умножение, о котором говорили ранее.
(целое(число)*(целое(input_base)**индекс))
6*(8**0)
Полученные значения добавляются к sum_base_10.
База IS 10:
Отлично, продолжайте. Мы просто присваиваем входное число sum_base_10:
elif input_base == 10:
sum_base_10 = int(input_number)
Выполняем математические вычисления
Теперь, когда у нас есть значение Base-10, мы можем выполнить деление, чтобы найти остатки и найти наш новый номер.
в то время как sum_base_10 > 0:
разделить = sum_base_10// int(output_base)
rester_list.append(str(sum_base_10 % int(output_base))
sum_base_10 = разделить
Нам нужно делить, пока мы не достигнем 0. Цикл while гарантирует, что мы это делаем.
Используя деление пола // мы делим число и остаются с целой частью частного. Это означает, что мы переносим только целое число (21), а не то, что стоит после точки (75) на основе нашего примера во вступлении (174/8 = 21,75 )
присвоив это число разделяемому, мы также можем отправить это значение в sum_base_10 для следующей итерации в конце.0029
Используя модуль,%, мы получим остаток. Это добавляется к оставшемуся_списку, чтобы мы могли вывести его позже.
Это цикл while, который продолжается до тех пор, пока мы не нажмем 0
Если база вывода равна 16
Если база_вывода равна 16, это означает, что пользователю нужен шестнадцатеричный вывод. Нам нужно преобразовать любое число больше 9 в букву.
Нам нужно преобразовать любое число больше 9 в букву.
Так же, как и раньше, мы создаем словарь для облегчения преобразования. Если мы находим совпадение, мы преобразуем число в букву и добавляем его в список.
И наконец:
return ''.join(remainder_list[::-1])
Это переворачивает и превращает наш список в строку, которую мы можем вернуть. Если вы хотите вернуть целое число, вы можете использовать int(). Убедитесь, что вы учитываете шестнадцатеричные числа, если пользователь запрашивает вывод Base-16.
def execute_converter():
Фу! Большая часть нашего кода готова.
Последняя часть головоломки — взаимодействие с пользователем. Это прямой цикл while, когда пользователь вводит числа, мы проверяем их и запускаем конвертер, если он подтверждает. У пользователя есть возможность сделать это столько раз, сколько он хочет.
Мне нравится создавать взаимодействия с пользователем с помощью циклов while на основе состояния переменной; как продолжить у нас есть здесь. Таким образом, мы можем продолжать работать столько, сколько захочет пользователь.
Таким образом, мы можем продолжать работать столько, сколько захочет пользователь.
Имеет два уровня. Первый цикл while инициирует основной цикл на основе continue.lower() == 'y'.
Второй объявляет valid_input=False , потому что мы хотим проверить весь ввод, прежде чем передать его в convert_number_system() . Пока вход равен False нам нужны новые данные. После того, как пользователь дает нам свой ввод, он запускает валидатор. Если он проходит, мы можем инициировать convert_number_system()
В конце мы спрашиваем пользователя, хочет ли он пройти еще раз. Если пользователь вводит «y», мы снова запускаем код. Если он/она напечатает что-то еще, мы выходим из программы.
Альтернативный способ сделать это — попросить пользователя либо ввести число, которое он хочет преобразовать, либо выйти. в переменной number_input .
Эта программа охватывает несколько аспектов программирования. Во-первых, нам нужно найти проблему. Проблема в том, что на ручное преобразование всех чисел уходит много времени.
Во-первых, нам нужно найти проблему. Проблема в том, что на ручное преобразование всех чисел уходит много времени.
Затем мы находим/изучаем математику, чтобы решить задачу и найти общее. Как оказалось, мы можем преобразовать что угодно во что угодно с помощью одной и той же формулы. Нам нужно обрабатывать только двоичный и шестнадцатеричный ввод, и нам нужно убедиться, что мы не пытаемся вычислить Base-1. Это означает, что мы можем использовать функции для обработки нашего кода.
Все завернуто в меню, взаимодействие с пользователем, а лежащий в основе код выполнения скрывается в фоновом режиме.
Надеюсь, вы узнали что-то новое, прочитав это. Если вы обнаружите какие-либо проблемы с кодом или у вас есть другие идеи, сообщите мне об этом. Не стесняйтесь брать код и продолжать разрабатывать его для своих собственных проектов.
-M
Как найти основание уравнения
Основание означает количество цифр, которые используются при представлении числовых чисел в позиционной системе счисления. Максимальное количество используемых уникальных чисел называется основанием. Основание может включать «0». Например, десятичная система содержит 10 уникальных цифр от 0 до 9.. Таким образом, основанием десятичной системы является 10, или основание 10.
Максимальное количество используемых уникальных чисел называется основанием. Основание может включать «0». Например, десятичная система содержит 10 уникальных цифр от 0 до 9.. Таким образом, основанием десятичной системы является 10, или основание 10.
Как найти основание уравнения — это не совсем то же самое, что найти основание числа в позиционной системе счисления. Поиск системы счисления в уравнении больше похож на просмотр уравнения и определение системы счисления, в которой выполняются вычисления.
Система счисления и система счисления
Обычно, чтобы найти основание числа, достаточно взглянуть на его индекс. Написанное число является его основанием или основанием. Например, (a) b означает, что число «a» записывается через «b». Этот номер содержит "b" уникальных цифр в своей системе.
Популярные системы счисления
Ниже приведены распространенные системы счисления, которые могут быть полезны при вычислении системы счисления в ваших уравнениях.
- Десятичная система счисления (10) : Если вы читаете это, значит, вы использовали десятичную систему счисления в своей жизни. Это самая популярная система счисления во всем мире! Он используется в повседневной математике, механических счетчиках и арифметике. Он варьируется от 0 до 9 и состоит из 10 цифр.
- Двоичная система счисления (2) : Как вы, должно быть, уже догадались, это последовательность нулей и единиц, которые используются в большинстве компьютеров и телефонов. Он содержит всего две цифры: 0 и 1.
- Восьмеричная система счисления (8) : Восьмеричная система иногда используется для компьютерных систем из-за сокращения, которое она обеспечивает для двоичной системы. Это восемь чисел в диапазоне от 0 до 7, которые представляют собой 3 бита (23).
- Шестидесятеричная система счисления : Эта система счисления имеет интересную историю, которая восходит к вавилонянам.
 Он до сих пор используется в понятиях минут, секунд и градусов.
Он до сих пор используется в понятиях минут, секунд и градусов. - Двенадцатеричная система счисления (12) : Эта система в основном используется в десятках и брутто. С ними легче работать и манипулировать, потому что 2, 3, 4 и 6 могут легко входить в них.
- Шестнадцатеричная система счисления (16) : Шестнадцатеричная система счисления также используется в качестве сокращения для двоичной системы счисления. Каждая из его цифр работает с последовательностью из четырех двоичных цифр. Поскольку оно больше десятичной дроби, остальные представлены буквами от «а» до «f».
Указатели системы счисления
Не существует общего или правильного способа найти систему счисления системы счисления. Вы можете использовать различные методы исключения, не решая уравнения, чтобы выяснить, какой может быть система счисления.
Например, уравнение, содержащее число 9означает, что все все основания ниже основания 10 (десятичная система счисления) исключаются.
Если вы видите 11 или 10 в уравнении, это может быть частью десятичной или двоичной системы счисления или любой системы счисления в этом отношении. Но когда вы видите такое уравнение, как 11 + 10 = 21, вы автоматически понимаете, что из-за наличия 2 (21) двоичное число исключается.
Примеры
Пример 1
x2 – 3x - 10 = 0 . Корни равны 5 и -2
Если вы знакомы с квадратными уравнениями, возможно, вы знаете, что стандартное выражение равно 9.0735 ах2 + Ьх + с . Мы будем использовать это ниже.
Solution
Let's assume that m is the first root and n is the second root so:
m + n = - b/a
m + n = b
м x n = c/a
Теперь, подставив наше фактическое квадратное уравнение:
м + n = - (-3)/1
м + n = 3
907 9028 900 N = -25 x (-2) = 10/1
1010 = 10R
1 x 10 + 0 = 1 x r + 0
5550 = 10
5555. 9.
9.
55.935 R + 0
55.935. Поскольку результат равен 10, это означает, что основание десятичное. Найдите основание уравнения 137 + 144 = 303 . Решение В таком уравнении можно посмотреть на цифры и сразу исключить двоичное число. Теперь удалите первые две цифры каждого числа. 7 + 4 = 3 В десятичном виде это должно равняться 11, поэтому десятичное число также исключается. Но если вы вычтете 3 из 11, вы получите 7. Это самая старшая цифра, доступная в восьмеричной системе счисления. Это сужает его. Чтобы подтвердить, это будет означать, что значение 137 равно 95, 144 – 100, а 303 – 195 в десятичном виде, поэтому все подходит. Найдите основание уравнения 106 + 74 = 202 Решение Для таких простых уравнений можно использовать другой подход. Примечание: вы не можете использовать этот метод на сложных фигурах. Второй пример
Пример третий