Начертить многоугольник с шестью вершинами фото: Как нарисовать 6 угольник

Инструменты «Многоугольник» и «Линия», построение звёзд и стрелок

Автор Дмитрий Евсеенков На чтение 6 мин Просмотров 1.6к. Обновлено 28.10.2021

Ранее я рассказал о следующих векторных фигурах Photoshop:

?  Прямоугольник (Rectangle Tool)
?  Прямоугольник со скруглёнными углами (Rounded Rectangle
Tool)
?  Эллипс (Ellipse Tool)

Как совмещать и вычитать векторные фигуры в Photoshop, Вы можете узнать из этой статьи.

В этом уроке я расскажу двух о следующих инструментах этой группы — Многоугольник (Polygon Tool) и Линия (Line Tool).

Содержание

Инструмент Многоугольник (Polygon Tool)

Следующим после «Эллипса», в стеке векторных инструментов располагается «Многоугольник», с помощью которого можно получить весьма интересные фигуры:

Выбор инструмента «Многоугольник» Polygon Tool.

 

В то время как фигура, создаваемая при помощи инструмента «Прямоугольник», ограничена четырьмя углами, инструмент «Многоугольник» позволяет нам создавать фигуры многоугольной формы с числом углов от трёх и до ста. Кроме того, с помощью этого инструмента мы можем создавать фигуры в форме звезд. Чтобы нарисовать фигуру с помощью Polygon Tool, сначала введите нужное вам количество сторон в опцию «????Стороны» (Sides) на панели параметров. Как я упоминал выше, Вы можете ввести любое число от 3 ??до 100. Я оставлю значение по умолчанию 5:

Введите нужное вам число сторон в опцию «Стороны» (Sides) на панели параметров.

 

После того, как вы ввели число сторон, нажмите и перетащите курсор в документе. Photoshop всегда создаёт многоугольник от центра, так что нет необходимости удерживать клавишу Alt. Зажатая клавиша ??Shift после начала перетаскивания выравнивает фигуры с чётным количеством сторон:

Пятиугольник, построенный с помощью инструмента «Многоугольник» (Polygon Tool).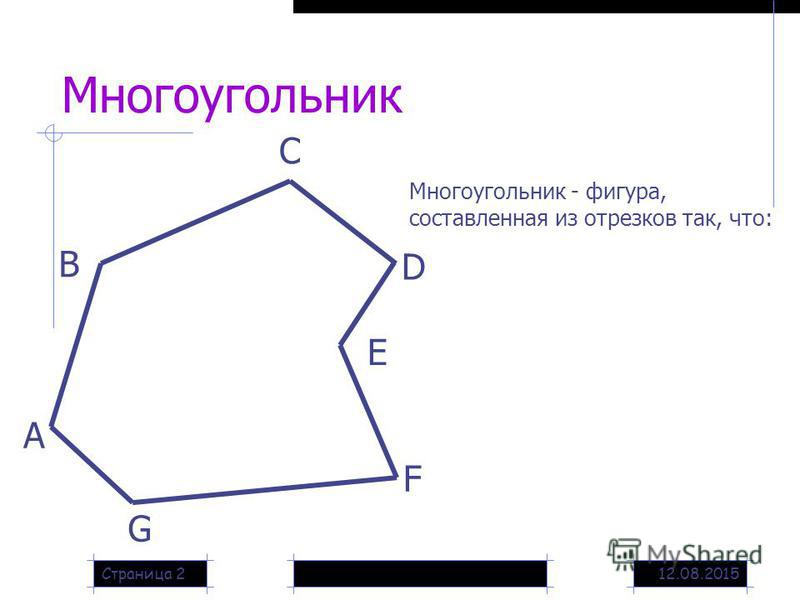

 

Установка числа сторон 3 в панели параметров дает нам простой способ создания треугольника:

Равносторонний треугольник, построенный с помощью инструмента «Многоугольник» (Polygon Tool).

 

А вот пример фигуры многоугольника с количеством сторон 12

Двенадцатиугольник, отображение контура отключено

 

Как и в случае с радиусом скруглений для инструмента «Прямоугольник со скруглёнными углами», Photoshop не позволяет изменить число сторон после создания фигуры, так что если перед началом построения фигуры вы неправильно указали количество сторон, остаётся только нажать Ctrl+Z для отмены шага по построению фигуры, а затем ввести другое значение в опцию «Стороны» (Sides) и начать рисовать многоугольник заново:

Рисование звезды с помощью «Многоугольника» (Polygon Tool)

Чтобы нарисовать звезду при помощи этого инструмента, нажмите на значок шестеренки в панели параметров, а затем выберите опцию «Звезда» (Star):

Нажатие на значок шестеренки и выбор опции «Звезда» (Star).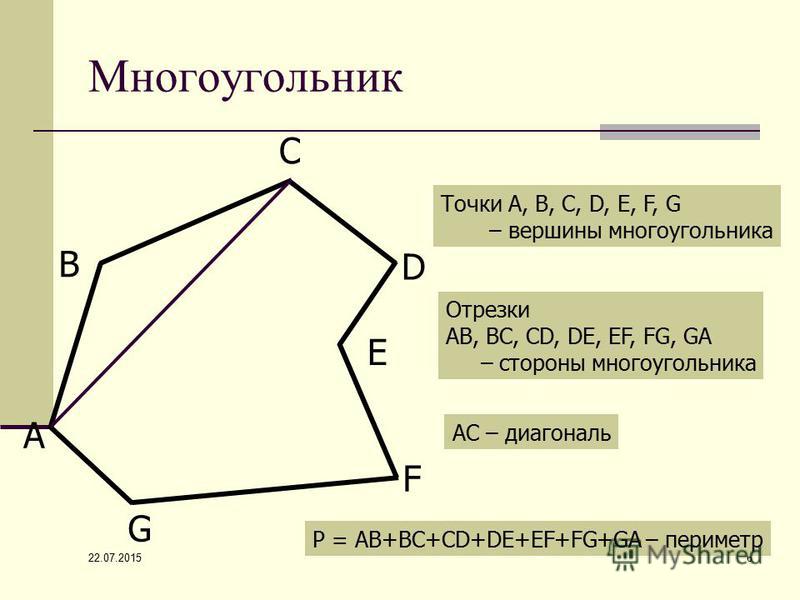

 

Затем просто нажмите внутри документа и создайте фигуру звезды методом перетаскивания курсора. При активной опции «Звезда» (Star), опция «Стороны» (Sides) в панели параметров задаёт количество лучей звезды. Так, при его значении 5 у нас получится пятиконечная звезда:

Пятиконечная звезда, начерченная с помощью инструмента «Многоугольник», параметры фигуры заданы по умолчанию.(Polygon Tool).

 

Изменение значения сторон на 8 дает нам восьмиконечную звезду:

Управление количеством лучей звезды.

 

Мы можем изменять у звездообразной фигуры не только количество лучей, но и положение внутренних вершин между центром звезды и внешними вершинами. По умолчанию, внутренние вершины находятся посередине, за это отвечает параметр «Глубина лучей» (Indent Sides By), по умолчанию он равен 50%:

Изменение параметра «Глубина лучей» (Indent Sides By) с 50 процентов, заданных по умолчанию, до 90%.

 

Посмотрите, что получилось:

Та же восьмиконечная звезда, но со значением параметра «Глубина лучей» (Indent Sides By) 90%.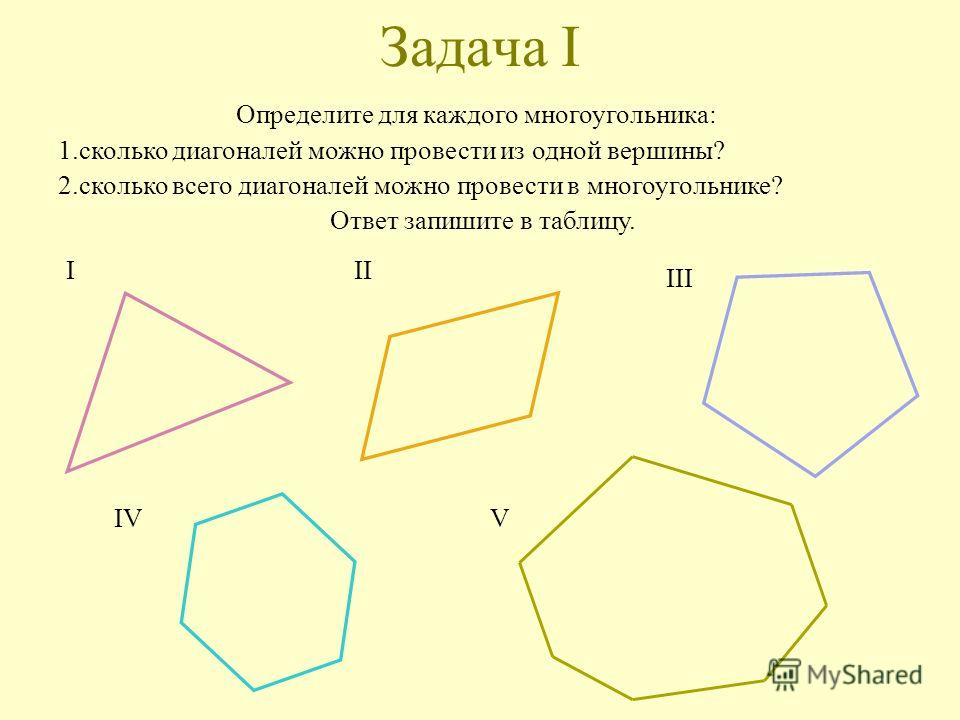 Контур скрыт.

 

По умолчанию, звезды имеют острые углы на вершинах, но мы можем сделать их закруглёнными, выбрав опцию «Сгладить внешние углы» (Smooth Corners):

Включение скругления углов при помощи опции «Сгладить внешние углы» (Smooth Corners).

 

Во как будет выглядеть стандартная пятиконечная звезда со сглаженными вершинами лучей при включенной опции «Сгладить внешние углы» (Smooth Corners):

Опция сглаживания углов придает звезде веселый, дружелюбный вид.

 

Мы можем сгладить не только вершины лучей, но и вершины впадин с помощью опции «Сгладить внутренние углы» (Smooth Indents):

Включение опции «Сгладить внутренние углы» (Smooth Indents).

 

При включении обеих этих опций мы получаем форму, похожую на морскую звезду:

Звезда с сглаженными углами и впадинами получена при одновременном включении опций «Сгладить внешние углы» (Smooth Corners) и «Сгладить внутренние углы» (Smooth Indents).

 

Инструмент Линия (Line Tool)

Последним из основных геометрических инструментов формы Photoshop является инструмент «Линия» (Line Tool). Я выберу его на панели инструментов:

Выбор инструмента «Линия» (Line Tool).

 

Инструмент «Линия» позволяет создавать простые прямые линии, но кроме этого мы можем использовать его для рисования фигур в виде стрелки. Чтобы нарисовать прямую линию, во-первых, установите толщину линии, которую следует задать в пикселях в поле ввода «Толщина» (Weight) в панели параметров. Значение по умолчанию задано в 1 пиксель. Я увеличу его до 16-ти пикселей:

Опция «Толщина» (Weight) задаёт толщину (ширину) линии.

 

Также, как и при работе другими инструментами векторных форм, для создания линии, нажмите левой клавишей мыши внутри документа и перетащите вашу линию. Чтобы проще было построить горизонтальную, вертикальную или линию под углом 45 градусов, зажмите клавишу ??Shift в процессе перетаскивания курсора, и отпустите клавишу Shift после отпускания клавиши мыши:

Держите клавишу Shift при перетаскивании курсора для создания горизонтальных или вертикальных линий.

 

Рисование указательных стрелок (стрелок направления)

Чтобы из линии получить стрелку, нажмите на значок шестеренки на панели параметров, чтобы открыть окно опции «Стрелки» (Arrowhead) с вариантами изменения наконечника (острия) стрелки. Выберите, чтобы наконечник отобразился в начале линии, в конце линии или же с обоих сторон сразу:

Нажмите на значок шестеренки для доступа к опции «Стрелки» (Arrowhead).

 

Вот линия, начерченная, как и ранее, но на этот раз со стрелкой на конце:

Инструмент «Линия» позволяет легко рисовать указательные стрелки, размеры наконечника стрелки заданы Photoshop по умолчанию.

 

Если размеры по умолчанию наконечника стрелки вам не подходят, вы можете настроить их, изменив параметры «Ширина» (Width) и «Длина» (Length).
«Ширина» и «Длина» наконечника задаются в процентах от толщины линии, значит, на данный момент ширина моего наконечника стрелки 80 пикселей, а длина -160.
Вы также можете заострить хвостовик наконечника путем увеличения параметра «Кривизна» (Concavity). Я повышу его значение с 0% по умолчанию до 50%:

Опция «Кривизна» (Concavity) для изменения формы наконечника стрелы методом заострения его краев.

 

Вот так стрелка выглядит теперь. Перед тем, как начать рисовать фигуру, убедитесь, что вы правильно задали параметры инструмента «Линия», так как они не могут быть скорректированы после (если вам необходимо внести изменения, вам нужно отменить форму и рисовать новую).

Шестиугольник, виды, свойства и формулы

Шестиугольник, виды, свойства и формулы.

 

 

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.

 

Шестиугольник, выпуклый и невыпуклый шестиугольник

Правильный шестиугольник (понятие и определение)

Свойства правильного шестиугольника

Формулы правильного шестиугольника

Правильный шестиугольник в природе, технике и культуре

Звездчатый шестиугольник

Восьмиугольник

 

Шестиугольник, выпуклый и невыпуклый шестиугольник:

Шестиугольник – это многоугольник с шестью углами.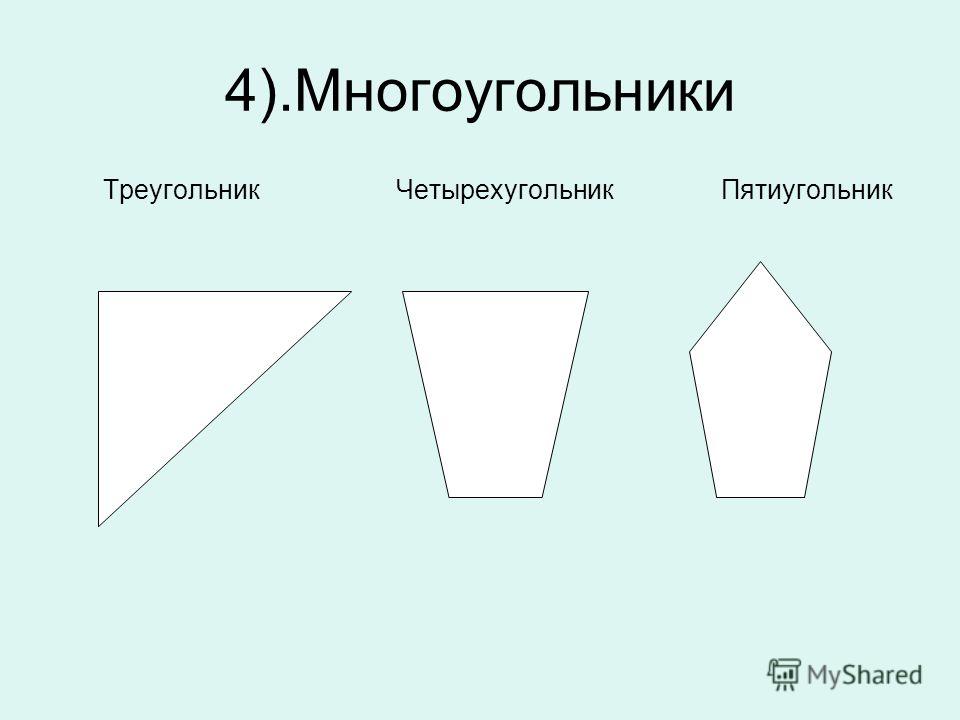

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.

Шестиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый шестиугольник

  Рис. 2. Невыпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

.

 

Правильный шестиугольник (понятие и определение):

Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.

Рис. 3. Правильный шестиугольник

Правильный шестиугольник имеет 6  сторон, 6 углов и 6 вершин.

Углы правильного шестиугольника образуют шесть равносторонних треугольников.

Правильный шестиугольник можно построить с помощью циркуля и линейки.

 

Свойства правильного шестиугольника:

1. Все стороны правильного шестиугольника равны между собой.

a₁ = a₂ = a₃ = a₄= a₅= a₆. 

2. Все углы равны между собой и составляют 120°.

α₁ = α₂ = α₃ = α₄ = α₅ = α₆ = 120°.

Рис. 4. Правильный шестиугольник

3. Сумма внутренних углов любого правильного шестиугольника равна 720°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.

Рис. 5. Правильный шестиугольник

5. Количество диагоналей правильного шестиугольника равно 9.

Рис. 6. Правильный шестиугольник

6. Центр вписанной окружности O₁ совпадает с центром описанной окружности O₂, что и образуют центр многоугольника O.

Рис. 7. Правильный шестиугольник

7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).

8. Радиус описанной окружности правильного шестиугольника и его сторона равны.

Рис. 8. Правильный шестиугольник

R = a

 

Правильный шестиугольник в природе, технике и культуре:

Пчелиные соты имеют форму правильного шестиугольника.

Графит, графен имеют гексагональную кристаллическую решетку.

Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.

Рис. 9. Гигантский гексагон на Сатурне

Сечение гайки и многих карандашей имеет вид правильного шестиугольника.

Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.

Панцирь черепахи состоит из шестиугольников.

Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.

Рис. 10. Материковая часть Франции

 

Формулы правильного шестиугольника:

Пусть a – сторона шестиугольника, r – радиус окружности, вписанной в шестиугольник, R – радиус описанной окружности шестиугольника, P – периметр шестиугольника, S – площадь шестиугольника.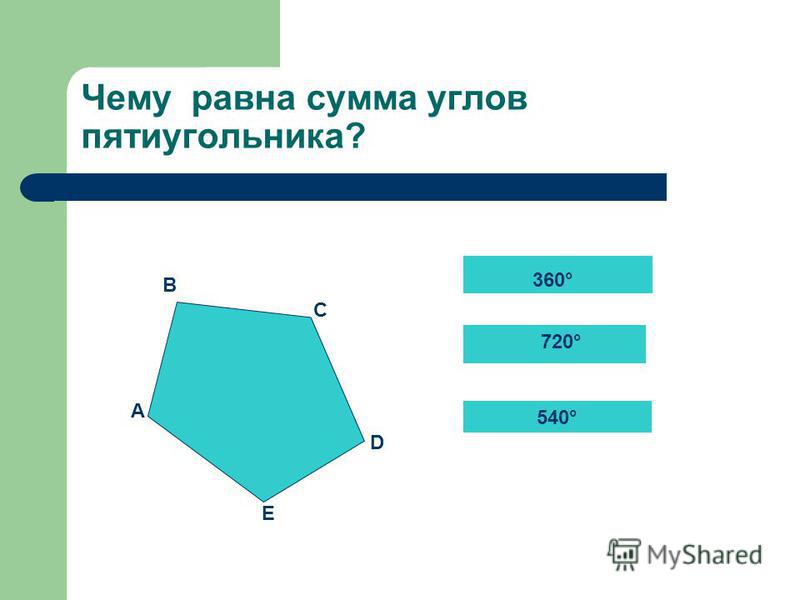

Формулы периметра правильного шестиугольника:

Формулы площади правильного шестиугольника:

Формула радиуса окружности, вписанной в правильный шестиугольник:

 

Формула радиуса окружности, описанной вокруг правильного шестиугольника:

R = a

 

Звездчатый шестиугольник:

Звездчатый шестиугольник (гексаграмма) – это многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника.

Гексаграмма (др.-греч. ἕξ – «шесть» и γραμμή – «черта, линия») – это звезда с шестью углами, которая образуется из двух наложенных друг на друга равносторонних треугольников.

 

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Шестиугольник

 

Примечание: © Фото https://www. pexels.com, https://pixabay.com

 

 

 

Коэффициент востребованности 5 647

Правильные многогранники. Часть 1. Трёхмерие / Хабр

Введение. Постановка вопроса.

В школьной программе, к сожалению, сферическую геометрию и геометрию Лобачевского не изучают. Тем временем, их изучение совместно с Евклидовой геометрией, позволяет глубже понять происходящее с объектами. Например, понять связь правильных многогранников с разбиениями сферы, разбиениями плоскости Евклида и разбиениями плоскости Лобачевского.
Знания геометрии пространств постоянной кривизны помогает подниматься над трёхмерием и выявлять многогранники в пространствах размерности 4 и выше. Вопросы нахождения многогранников, нахождения разбиений пространств постоянной кривизны, вывода формулы двугранного угла правильного многогранника в n-мерном пространстве — так тесно переплетены, что выносить всё это в название статьи оказалось проблематично.

Пусть в центре внимания будут, всем понятные, правильные многогранники, хотя они не только результат всех выводов, но и, одновременно, инструмент для постижения пространств высших размерностей и равномерно искривлённых пространств.

Для тех кто не знает (забыл) сообщаю (напоминаю), что в привычном нам трёхмерном Евклидовом пространстве всего пять правильных многогранников:

1. Тетраэдр:	2. Куб:	3. Октаэдр:	4. Додекаэдр:	5. Икосаэдр:

В трёхмерном пространстве правильным многогранником называется выпуклый многогранник, у которого все вершины равны между собой, все рёбра равны между собой, все грани равны между собой и грани являются правильными многоугольниками.

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны.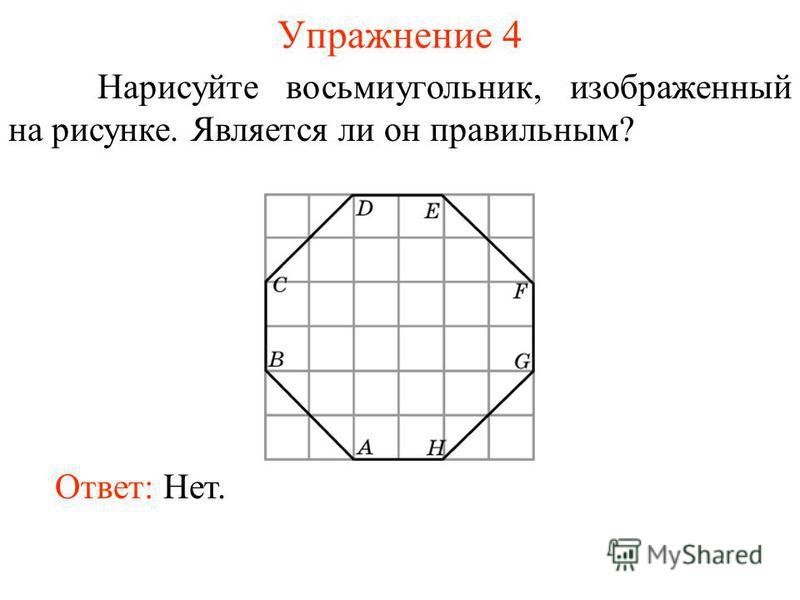

Вершины равны между собой означает, что количество рёбер и количество граней подходящих к каждой вершине одинаковое и подходят они под одинаковыми углами, в каждой вершине.

Оказывается, правильные многогранники удобно обозначать их символом Шлефли {p1, p2}, характеризующим их комбинаторное строение. Который означает, что p1 угольники, сошлись по p2 штук в вершине. Т.е. по определению p1, p2 — целые числа, большие либо равные 3. Для тех кто не знаком с понятием Символ Шлефли написал отдельную статью с картинками Символ Шлефли. Часть 2.6

В такой записи наши многогранники получат обозначения:
1. Тетраэдр {3, 3},
2. Куб {4, 3},
3. Октаэдр {3, 4},
4. Додекаэдр {5, 3},
5. Икосаэдр {3, 5}
Например, {4, 3} — куб имеет 4 угольные грани, в каждой вершине сходится по 3 таких грани.
У октаэдра {3, 4} наоборот, грани 3 угольные, сходятся по 4 штуки в вершине.
Таким образом символ Шлефли полностью определяет комбинаторное строение многогранника.

Почему правильных многогранников всего 5? Может быть их больше?

Чтобы сполна дать ответ на этот вопрос, нужно сначала получить интуитивное представление о геометрии на сфере и на плоскости Лобачевского. Тем у кого такого представления ещё нет постараюсь дать необходимые объяснения.

Сфера

1. Что такое точка на сфере? Думаю, что всем интуитивно понятно. Мысленно не сложно представить точку на сфере.

2. Что такое отрезок на сфере? Берём две точки и соединяем их кратчайшим расстоянием на сфере, получится дуга, если смотреть на сферу со стороны.

3. Если продолжить этот отрезок в обе стороны, то он замкнётся и получится окружность. При этом плоскость окружности содержит центр сферы, это следует из того, что две исходные точки мы соединили кратчайшим, а не произвольным, расстоянием. Это со стороны она выглядит, как окружность, а в терминах сферической геометрии это прямая, так как была получена из отрезка, продолжением до бесконечности в обе стороны.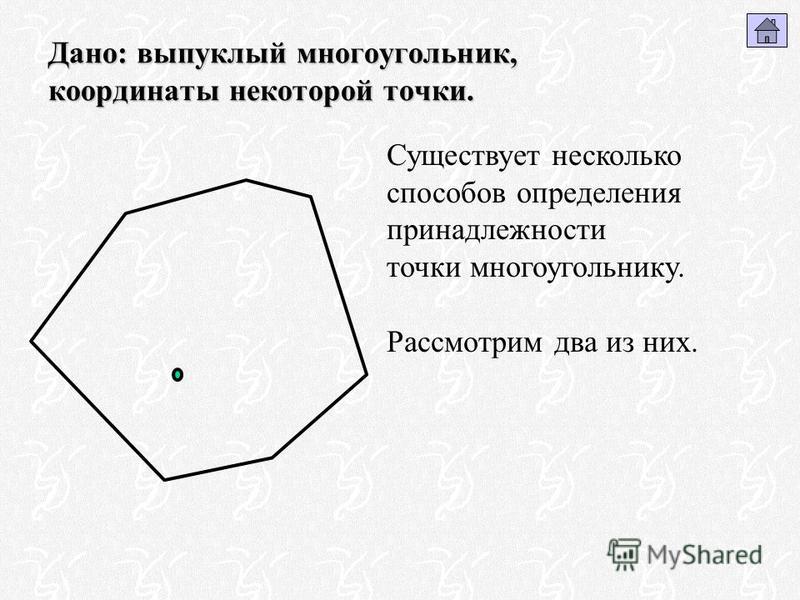

4. И, наконец, что такое треугольник на сфере? Берём три точки на сфере и соединяем их отрезками.

По аналогии с треугольником можно нарисовать произвольный многоугольник на сфере. Для нас принципиально важно свойство сферического треугольника, заключающееся в том, что сумма углов у такого треугольника больше 180 градусов, к которым мы привыкли в Евклидовом треугольнике. Более того, сумма углов у двух различных сферических треугольников различна. Чем больше треугольник, тем БОЛЬШЕ у него сумма углов.

Соответственно, появляется 4-й признак равенства треугольников на сфере — по трём углам: два сферических треугольника равны между собой, если у них соответствующие углы равны.

Для простоты саму сферу проще не рисовать, тогда треугольник будет выглядеть немного раздутым:

Сферу ещё называют пространством постоянной положительной кривизны. Кривизна пространства как раз и приводит к тому, что кратчайшим расстоянием является дуга, а не привычный нам прямолинейный отрезок.

Отрезок как бы искривляется.

Лобачевский

Теперь, когда мы познакомились с геометрией на сфере, понять геометрию на гиперболической плоскости, открытую великим русским учёным Николаем Ивановичем Лобачевским, будет тоже не сложно, так как тут всё происходит аналогично сфере, только «наизнанку», «наоборот». Если дуги на сфере мы проводили окружностями, с центром внутри сферы, то теперь дуги надо проводить окружностями с центром за пределами сферы.

Приступим. Плоскость Лобачевского будем представлять в интерпретации Пуанкаре II (Жюль Анри́ Пуанкаре́, великий французский учёный), эту интерпретацию геометрии Лобачевского ещё называют диском Пуанкаре.

1. Точка в плоскости Лобачевского. Точка — она и в Африке точка.

2. Отрезок на плоскости Лобачевского. Соединяем две точки линией по кратчайшему расстоянию в смысле плоскости Лобачевского.

Кратчайшее расстояние строится следующим образом:

Надо провести окружность ортогональную диску Пуанкаре, через заданные две точки (Z и V на рисунке). Центр этой окружности будет находиться всегда за пределами диска. Дуга соединяющая исходные две точки будет кратчайшим расстоянием в смысле плоскости Лобачевского.

3. Убрав вспомогательные дуги, получим прямую E1 — h2 в плоскости Лобачевского.

Точки E1, h2 «лежат» на бесконечности плоскости Лобачевского, вообще край диска Пуанкаре — это всё бесконечно удалённые точки плоскости Лобачевского.

4. И наконец, что такое треугольник в плоскости Лобачевского? Берём три точки и соединяем их отрезками.

По аналогии с треугольником, можно нарисовать произвольный многоугольник на плоскости Лобачевского. Для нас принципиально важно свойство гиперболического треугольника, заключающееся в том, что сумма углов у такого треугольника всегда меньше 180 градусов, к которым мы привыкли в Евклидовом треугольнике. Более того, сумма углов у двух различных гиперболических треугольников различна. Чем больше треугольник по площади, тем МЕНЬШЕ у него сумма углов.

Соответственно, тут тоже имеет место 4-й признак равенства гиперболических треугольников — по трём углам: два гиперболических треугольника равны между собой, если у них соответствующие углы равны.

Для простоты сам диск Пуанкаре иногда можно не рисовать, тогда треугольник будет выглядеть немного «усохшим», «сдутым»:

Плоскость Лобачевского (и вообще пространство Лобачевского любой размерности) ещё называют пространством постоянной ОТРИЦАТЕЛЬНОЙ кривизны. Кривизна пространства как раз и приводит к тому, что кратчайшим расстоянием является дуга, а не привычный нам прямолинейный отрезок. Отрезок как бы искривляется.

Правильные разбиения двумерной Сферы и правильные трёхмерные многогранники

Всё сказанное про сферу и плоскость Лобачевского относится к двумерию, т.е. поверхность сферы — двумерна. Какое это имеет отношению к трёхмерию, указанному в заголовке статьи? Оказывается, каждому трёхмерному правильному Евклидову многограннику взаимно однозначно соответствует своё разбиение двумерной сферы. Лучше всего это видно на рисунке:

Чтобы из правильного многогранника получить разбиение сферы, нужно описать вокруг многогранника сферу. Вершины многогранника окажутся на поверхности сферы, соединив эти точки отрезками на сфере (дугами), получим разбиение двумерной сферы на правильные сферические многоугольники. Для примера сделана видео демонстрация как икосаэдр соответствует разбиению сферы на сферические треугольники и обратно, как разбиение сферы на сферические треугольники, сходящиеся по пять штук в вершине, соответствует икосаэдру.

Чтобы по разбиению сферы построить многогранник, соответствующие дугам вершины разбиения нужно соединить обычными, прямолинейными, Евклидовыми отрезками.

Соответственно символ Шлефли икосаэдра {3, 5} — трёхугольники, сходящиеся по пять штук в вершине, задаёт не только структуру этого многогранника, но и структуру разбиения двумерной сферы. Аналогично и с другими многогранниками, их символы Шлефли задают и структуру соответствующих разбиений. Более того, разбиения плоскости Евклида и плоскости Лобачевского на правильные многоугольники, тоже можно задавать символом Шлефли. Например, {4, 4} — четырёхугольники, сходящиеся по четыре — это всем привычная нам тетрадь в клеточку, т. е. это разбиение плоскости Евклида на квадраты. А есть ли другие разбиения плоскости Евклида? Увидим дальше.

Построение разбиений двумерной сферы, плоскости Евклида и плоскости Лобачевского

Для построения разбиений двумерных пространств постоянной кривизны (таково общее название этих трёх пространств) нам потребуется элементарная школьная геометрия и знание того, что сумма углов сферического треугольника больше 180 градусов (больше Пи), что сумма углов гиперболического треугольника меньше 180 градусов (меньше Пи) и что такое символ Шлефли. Обо всём об этом уже сказано выше.

Итак, возьмём произвольный символ Шлефли {p1, p2}, он задаёт разбиение одного из трёх пространств постоянной кривизны (для плоскости это верно, для пространств высших размерностей дело обстоит сложнее, но ничто нам не мешает исследовать все комбинации символа).

Рассмотрим правильный p1 угольник, проведём отрезки, соединяющие его центр и вершины. Получим p1 штук равнобедренных треугольника (на рисунке показан только один такой треугольник). Сумму углов каждого из этих треугольников обозначим за t и выразим t через пи и коэффициент лямда.

Тогда если лямда = 1, то треугольник Евклидов, т.е. находится в Евклидовой плоскости, если лямда в интервале (1, 3), то это значит, что сумма углов больше пи и значит этот треугольник сферический (не трудно представить, что при увеличении сферического треугольника в пределе получается окружность с тремя точками на ней, в каждой точке угол треугольника получается равным пи, а в сумме 3*пи. Это объясняет верхнюю границу интервала = 3). Если же лямда в интервале (0, 1), то треугольник гиперболический, так как сумма углов у него меньше пи (т.е. меньше 180 градусов). Коротко это можно записать так:

Не трудно посчитать, что:

С другой стороны, для сходимости в вершине p2 штук (т.е. целого числа) таких же многоугольников нужно, чтобы

Приравнивая выражения для 2*бетта, найденные из условия сходимости и из многоугольника:

Получили уравнение которое показывает какое из трёх пространств разбивает фигура заданная своим символом Шлефли {p1, p2}. Для решения этого уравнения надо вспомнить, так же, что p1, p2 — целые числа, большие либо равные 3. Это, так сказать, следует из их физического смысла, так как это p1 угольники (не меньше 3 углов), сходящиеся по p2 штук в вершине (тоже не меньше 3, иначе это не вершина получится).

Решение этого уравнения заключается в переборе всех возможных значений для p1, p2 больших либо равных 3 и вычислении значения лямда. Если оно получится равным 1, то {p1, p2} разбивает плоскость Евклида, если больше 1 но меньше 3, то это разбиение Сферы, если от 0 до 1, то это разбиение плоскости Лобачевского. Все эти вычисления удобно свести в таблицу.

Откуда видно, что:
1. Сфере соответствует всего 5 решений, когда лямда больше 1 и меньше 3, они выделены зелёным цветом в таблице. Это: {3, 3} — тетраэдр, {3, 4} — октаэдр, {3, 5} — икосаэдр, {4, 3} — куб, {5, 3} — додекаэдр. Их картинки были представлены в начале статьи.
2. Разбиениям Евклидовой плоскости соответствует всего три решения, когда лямда = 1, они выделены синим цветом в таблице. Вот как выглядят эти разбиения.

3. И наконец, все остальные комбинации {p1, p2} соответствуют разбиениям плоскости Лобачевского, соответственно таких разбиений бесконечное (счётное) количество. Осталось только проиллюстрировать некоторые из них, для примера.

{3, 7}

{4, 5}

{4, 6}

{4, 7}

{5, 4}

{5, 5}

{5, 6}

{5, 7}

{6, 4}

Итоги

Таким образом, правильных многогранников всего 5, они соответствуют пяти разбиениям двумерной сферы, разбиений плоскости Евклида всего 3, и разбиений плоскости Лобачевского счётное количество.
Какое приложение этих знаний?

Есть люди, которые напрямую интересуются разбиениями сферы: dxdy.ru/topic62800.html,
Есть статьи на Хабре (вот), где также рассматриваются интерпретации геометрии Лобачевского. Данная статья, возможно поможет кому-то лучше понять и познакомиться с геометрией Лобачевского.

Знание многогранников так же помогает ответить на вопрос: сколько у футбольного мяча правильных шестиугольников и сколько пятиугольников. Зная, что футбольный мяч — это усечённый икосаэдр, сразу можно дать ответ на этот вопрос: пятиугольников столько, сколько вершин у икосаэдра, шестиугольников столько, сколько граней у икосаэдра, значит, пятиугольников 12, шестиугольников 20.

Да, хотелось бы ещё рассказать про комбинаторную формулу вычисления количества вершин, рёбер и граней у этих пяти правильных многогранников, но это уже в следующий раз. И без того как-то сложновато получилось, хотя я рассчитывал на школьный уровень знаний читателей.

Так же в следующей статье при наличии интереса читателей планирую показать, как обобщается данный подход на пространства высших размерностей.

Лично для меня знание разбиений позволяет понять структуру этих пространств, особенно это актуально в размерностях выше 3.

Если вам мало трёхмерного пространства, вам понятна эта публикация и хочется забраться повыше, по размерности, то «переходите на следующий уровень» 🙂
Ссылки:
Правильные многогранники. Часть 1. Трёхмерие
Правильные многогранники. Часть 2. Четырёхмерие
Правильные многогранники. Часть 2.5 (вспомогательная)
Символ Шлефли. Часть 2.6

Hexagon — Shape, Sides of Hexagon

Шестиугольник определяется как замкнутая 2D-форма, состоящая из шести прямых линий. Это двумерная фигура с шестью сторонами, шестью вершинами и шестью внутренними углами. Название делится на «гекс», что означает шесть, и «гония», что означает углы. Давайте узнаем о форме шестиугольника подробно в этой статье.

1.	Что такое шестиугольник?
2.	Правильный шестигранник
3.	Стороны шестиугольника
4.	Углы шестиугольника
5.	Диагонали шестиугольника
6.	Типы шестигранников
7.	Свойства шестиугольника
8.	Часто задаваемые вопросы о шестигранной форме

Что такое шестиугольник?

Шестиугольник — двумерная геометрическая фигура, состоящая из шести сторон, имеющих одинаковые или разные размеры длины. Некоторыми реальными примерами шестиугольника формы являются шестиугольная напольная плитка, поперечное сечение карандаша, часы, соты и т. д. Он может быть либо правильным (с 6 равными длинами сторон и равными углами), либо неправильным (с 6 неравными сторонами). длины сторон и углы).

Обычный шестигранник

Правильный шестиугольник определяется как замкнутая двумерная фигура, состоящая из шести равных сторон и шести равных углов. Каждый угол правильного шестиугольника равен 120 градусам. А сумма всех внутренних углов равна 120×6=720 градусов. Когда дело доходит до внешних углов, мы знаем, что сумма внешних углов любого многоугольника всегда равна 360°. В шестиугольнике 6 внешних углов. Итак, каждый из внешних углов правильного шестиугольника равен 360 ÷ 6 = 60 градусов.

Правильный шестиугольник отличается от неправильного тем, что в неправильном шестиугольнике нет определенного измерения углов, а длины сторон различны. Некоторые из свойств, которые являются общими для неправильных и правильных шестиугольников, приведены ниже:

• В обоих случаях 6 сторон, 6 внутренних углов и 6 вершин.
• Сумма всех 6 внутренних углов всегда равна 720 градусов.
• Сумма всех шести внешних углов всегда равна 360 градусам.

Стороны шестиугольника

У шестиугольника шесть сторон, как показано на рисунке выше. Все прямые края и образуют замкнутую форму. В правильном шестиугольнике у нас шесть равных сторон, а в неправильном шестиугольнике по крайней мере две стороны шестиугольника различны по размеру. Если мы возьмем сумму всех шести сторон, мы получим периметр шестиугольника.

В правильном шестиугольнике, если известно значение периметра, то длину каждой стороны можно рассчитать как «Периметр ÷ 6». Например, если периметр правильного шестиугольника равен 72 единицам, то длина каждой из сторон шестиугольника равна 72 ÷ 6 = 12 единиц.

Углы шестиугольника

В шестиугольнике шесть внутренних и шесть внешних углов. Сумма всех шести углов шестиугольника равна 720 градусов, а сумма его внешних углов равна 360 градусам. Посмотрите на некоторые свойства, связанные с углами шестиугольника, перечисленные ниже:

• Измерение каждого внутреннего угла в правильном шестиугольнике составляет 720° ÷ 6 = 120°.
• Размер каждого внешнего угла правильного шестиугольника равен 360° ÷ 6 = 60°.
• По крайней мере, два угла в неправильном шестиугольнике имеют разную величину.

Диагонали шестиугольника

Диагональ — это отрезок прямой, соединяющий любые две несмежные вершины многоугольника. Количество диагоналей многоугольника равно n(n-3)/2, где n — количество сторон многоугольника. Количество диагоналей в шестиугольнике определяется как 6 (6 — 3) / 2 = 6 (3)/2, что равно 9. Из 9 диагоналей 3 проходят через центр шестиугольника.

Диагонали шестиугольника бывают двух типов: длинные диагонали (3 диагонали проходят через центр) и короткие диагонали. Длину каждой длинной диагонали в правильном шестиугольнике можно измерить по формуле «2s». А длину каждой короткой диагонали можно измерить по формуле «√3s», где s — длина каждой стороны шестиугольника.

Типы шестигранников

Шестиугольники можно классифицировать по длинам сторон и внутренним углам. Учитывая стороны и углы шестиугольника, типы шестиугольника:

• Правильный шестиугольник: У него равные стороны и углы. Все внутренние углы правильного шестиугольника равны 120° каждый. Внешние углы равны 60° каждый. Сумма внутренних углов правильного шестиугольника равна 6 умножить на 120°, что равно 720°. Сумма внешних углов равна 6 умножить на 60°, что равно 360°.
• Неправильный шестиугольник: Имеет стороны и углы разных размеров. Все внутренние углы не равны 120°. Но сумма всех внутренних углов одинакова, то есть 720 градусов.
• Выпуклый шестиугольник: В этом шестиугольнике все внутренние углы меньше 180°. Выпуклые шестиугольники могут быть правильными или неправильными, что означает, что они могут иметь равные или неравные длины сторон и углы. Все вершины выпуклого шестиугольника направлены наружу.
• Вогнутый шестиугольник: Это такой шестиугольник, в котором хотя бы один из внутренних углов больше 180°. Есть хотя бы одна вершина, указывающая внутрь.

Свойства шестиугольника

Шестиугольник — это плоская двумерная фигура с шестью сторонами. Он может иметь или не иметь равные стороны и углы. Основываясь на этих фактах, важные свойства шестиугольника следующие:

• У него шесть сторон, шесть ребер и шесть вершин.
• Все длины сторон равны или неравны по измерению.
• В правильном шестиугольнике все внутренние углы равны 120° каждый.
• Сумма внутренних углов всегда равна 720°.
• В правильном шестиугольнике все внешние углы равны 60° каждый.
• Сумма внешних углов равна 360°.
• Количество диагоналей (отрезка, соединяющего две несмежные вершины многоугольника), которые можно нарисовать, равно 9.
• Правильный шестиугольник также является выпуклым шестиугольником, так как все его внутренние углы меньше 180°.
• Его можно разделить на шесть равносторонних треугольников.
• Он симметричен, так как длины всех его сторон равны.
• Противоположные стороны правильного шестиугольника всегда параллельны друг другу.
• Площадь правильного шестиугольника равна 3√3a ² /2 квадратных единиц, где a — длина стороны.
• Периметр шестиугольника можно найти, сложив длины всех шести сторон.

☛ Похожие темы

Ознакомьтесь с некоторыми интересными статьями, посвященными форме шестиугольника в математике.

• Пятиугольник — 5-сторонний многоугольник
• Гептагон — 7-сторонний многоугольник
• Octagon — 8-сторонний многоугольник
• Decagon — 10-сторонний многоугольник

 

Примеры шестиугольников

1. Пример 1: Какова площадь правильного шестиугольника со стороной 3 единицы?

   Решение:

   Площадь правильного шестиугольника = 3√3a ² /2 квадратных единиц.

   Дано, сторона «а» = 3 единицы.

   Следовательно, площадь = 3(√3)3 ² /2

   = (3 × √3 × 9) /2

   = (27× √3) / 2

   = 23,38 квадратных единиц

   Следовательно, требуемая площадь составляет 23,38 квадратных единиц.

2. Пример 2: Найдите длину каждой стороны правильного шестиугольника, если его площадь равна 150√3 квадратных единиц.

   Решение:

   Применение формулы площади правильного шестиугольника0174 2 /2

   300√3 = 3√3a ²

   Canceling √3 on both sides,

   300/3 = a ²

   100 = a ²

   a = √100

   Следовательно, длина каждой стороны равна 10 единицам.

3. Пример 3: Какова длина каждой стороны правильного шестиугольника, если его периметр равен 108 единицам?

   Решение:

   Дан периметр = 108 единиц.

   Поскольку это правильный шестиугольник, все его стороны имеют одинаковую длину. Чтобы найти длину каждой стороны, нам просто нужно разделить периметр на 6.

   ⇒ Периметр ÷ 6

   ⇒ 108 ÷ 6

   = 18 единиц

   Следовательно, длина каждой из сторон шестиугольника равна 18 единицам. .

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по Hexagon

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о Hexagon

Что такое шестиугольник?

Шестиугольник — это двумерная плоская форма, имеющая шесть углов, шесть ребер и шесть вершин.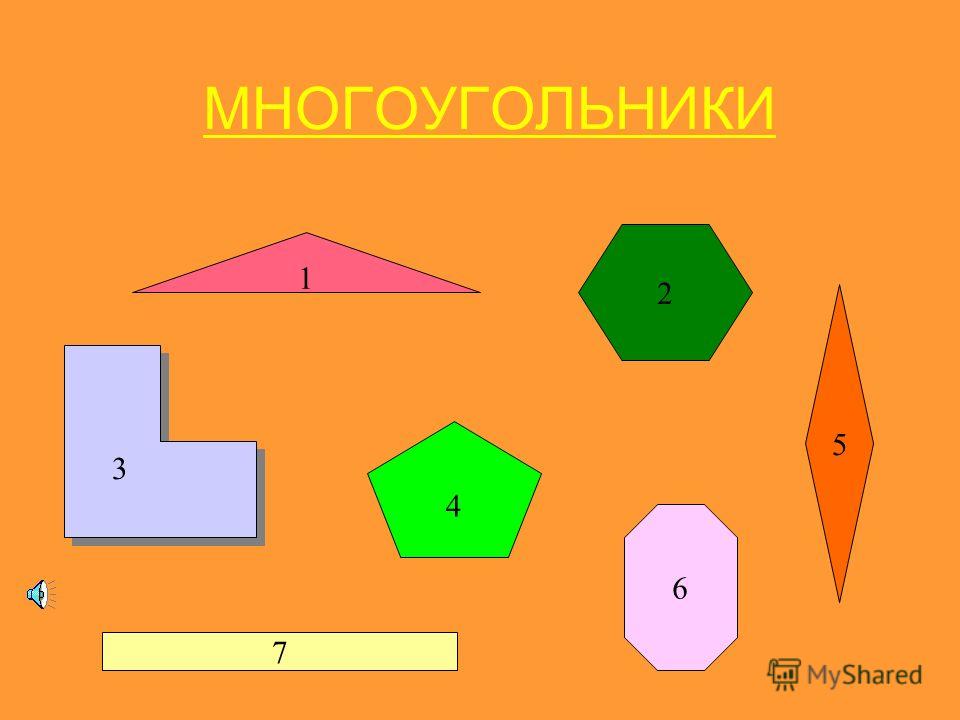 Он может иметь равные или неравные стороны и внутренние углы. Это 6-сторонний многоугольник, подразделяющийся на два основных типа — правильный и неправильный шестиугольник.

Что такое углы шестиугольника?

Шестиугольник имеет шесть углов, а сумма всех шести внутренних углов составляет 720 градусов. В правильном шестиугольнике каждый внутренний угол равен 120 градусам.

Что такое правильный шестиугольник?

Правильный шестиугольник определяется как особый тип шестиугольника, у которого все стороны равны. Все шесть углов правильного шестиугольника также равны.

Сколько сторон у шестиугольника?

У шестиугольника шесть сторон. Все шесть сторон соединены вместе и образуют замкнутую форму, известную как шестиугольник. В правильном шестиугольнике все шесть сторон имеют одинаковую длину, а в неправильном шестиугольнике нет определенного соотношения между сторонами, так как они различны по размеру.

Что такое периметр шестиугольника?

Периметр шестиугольника равен сумме его границ.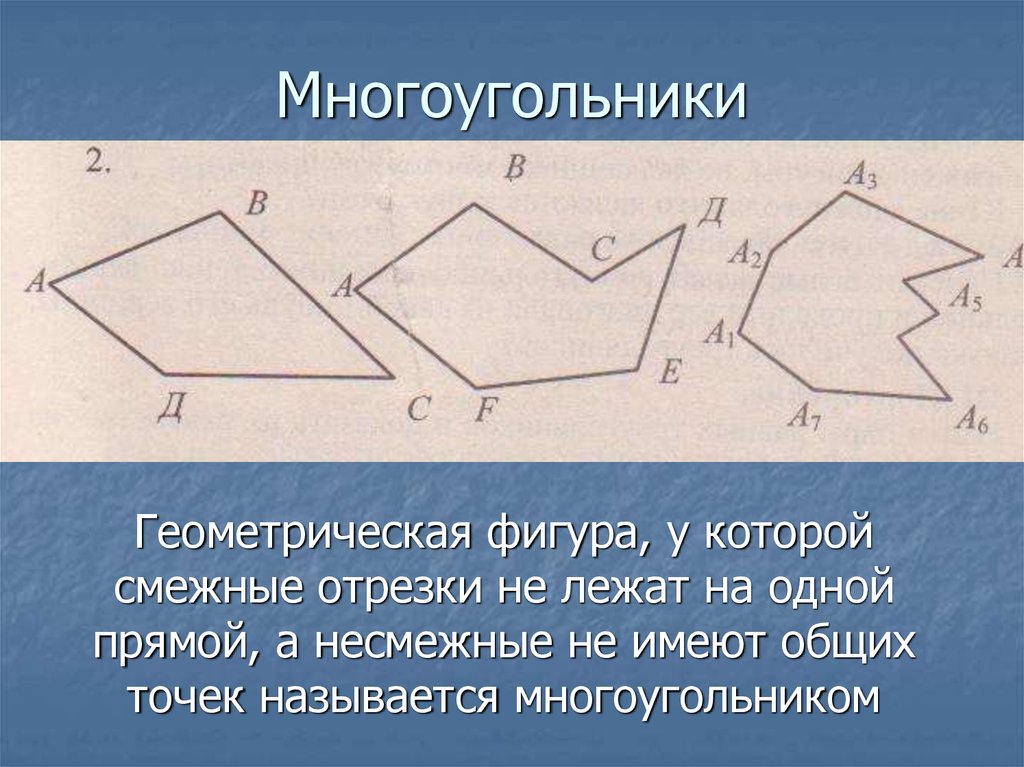 Это сумма всех шести сторон. В случае правильного шестиугольника формула для расчета его периметра равна 6 × длина стороны.

Что такое неправильный шестиугольник?

У неправильного шестиугольника по крайней мере одна сторона и угол не равны по сравнению с другими сторонами и углами. Определенного измерения каждого из углов нет, но сумма всех 6 внутренних углов всегда равна 720 градусам, а сумма всех 6 внешних углов равна 360 градусам.

Каковы три атрибута шестиугольника?

Три атрибута шестиугольника:

• Шестиугольник
• Имеет 6 углов
• Имеет 6 вершин

Всегда ли у шестиугольника равные стороны?

Шестиугольник может не обязательно иметь все стороны равными. Он также может иметь стороны переменной длины. Шестиугольник с равными сторонами называется правильным шестиугольником, а тот, у которого стороны разные, называется неправильным шестиугольником.

Как классифицируются шестиугольники?

Шестиугольник классифицируется на основе длин сторон и углов. Исходя из этого, шестиугольники делятся на правильные (с равными сторонами и углами) и неправильные (с равными сторонами и углами) шестиугольники. Его также можно разделить на выпуклые и вогнутые шестиугольники. Выпуклые шестиугольники — это те, у которых все внутренние углы меньше 180°, а вогнутые шестиугольники — те, у которых хотя бы один из внутренних углов больше 180°.

Какова сумма внутренних углов шестиугольника?

В шестиугольнике сумма всех 6 внутренних углов всегда равна 720º. Сумма внутренних углов многоугольника рассчитывается по формуле (n-2) × 180°, где n — количество сторон многоугольника. Так как шестиугольник имеет 6 сторон, приняв n за 6, мы получим. (6-2) × 180°, что дает 720°.

Сколько диагоналей можно провести в правильном шестиугольнике?

Формула для расчета количества диагоналей многоугольника: n(n-3)/2, где ‘n’ — количество сторон многоугольника. Шестиугольник имеет 6 сторон. следовательно, количество диагоналей равно 6(6-3)/2, что равно 9.

Сколько линий симметрии в правильном шестиугольнике?

Для всех правильных многоугольников количество линий симметрии равно количеству сторон. Таким образом, для правильного шестиугольника имеется шесть осей симметрии.

Как найти площадь шестиугольника?

Мы можем определить площадь шестиугольника с помощью i , определяя длину стороны шестиугольника. Чтобы найти площадь правильного шестиугольника, мы используем формулу A = (3√3 S ² )/2 квадратных единиц, где S — длина одной стороны.

По какой формуле вычисляется периметр шестиугольника?

Формула для расчета периметра правильного шестиугольника составляет 6а единиц, где «а» — длина стороны шестиугольника. В случае неправильного шестиугольника мы добавляем длины сторон. Математически это можно выразить как

Периметр шестиугольника = (a + b+ c+ d + e + f) единиц.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по шестиугольнику [PDF]

Дискретная математика: открытое введение, 3-е издание

Расследовать!

Когда связный граф можно нарисовать без пересечения ребер, он называется планарным . Когда планарный граф рисуется таким образом, он делит плоскость на области, называемые гранями .

1. Нарисуйте, если возможно, два разных планарных графа с одинаковым количеством вершин, ребер и граней.

2. Нарисуйте, если возможно, два разных планарных графа с одинаковым количеством вершин и ребер, но разным количеством граней.

Когда можно нарисовать граф так, чтобы ни одно ребро не пересекалось? Если это является возможным , мы говорим, что граф является плоским (поскольку вы можете нарисовать его на плоскости ).

Обратите внимание, что определение планарного включает фразу «можно». Это означает, что даже если граф не выглядит плоским, он все равно может им быть. Возможно, вы сможете перерисовать его так, чтобы края не пересекались. Например, это планарный граф:

Это потому, что мы можем перерисовать его вот так:

Графики одинаковые, поэтому если один плоский, то и другой должен быть таким же. Однако исходный рисунок графа не был плоскостным представлением графа.

Когда планарный граф рисуется без пересечения ребер, ребра и вершины графа делят плоскость на области. Мы будем называть каждый регион лицом . Граф выше имеет 3 грани (да, мы делаем включаем «внешнюю» область как грань). Количество граней не меняется независимо от того, как вы рисуете граф (пока вы делаете это без пересечения ребер), поэтому имеет смысл приписать количество граней как свойство плоского графа.

ПРЕДУПРЕЖДЕНИЕ: подсчет граней возможен только в том случае, если график нарисован плоско. Например, рассмотрим эти два представления одного и того же графа:

Если вы попытаетесь подсчитать лица, используя график слева, вы можете сказать, что лиц 5 (включая внешние). Но рисование графика с плоским представлением показывает, что на самом деле граней всего 4.

Существует связь между количеством вершин (\(v\)), количеством ребер (\(e\)) и количеством граней (\(f\)) в любом связном планарном графе. Это соотношение называется формулой Эйлера.

Формула Эйлера для плоских графиков.

Для любого связного планарного графа с \(v\) вершинами, \(e\) ребрами и \(f\) гранями имеем

\begin{уравнение*} ve + f = 2\text{.} \end{equation*}

Почему формула Эйлера верна? Один из способов убедиться в ее достоверности — шаг за шагом нарисовать планарный график. Начните с графика \(P_2\text{:}\)

Любой связный граф (кроме одной изолированной вершины) должен содержать этот подграф. Теперь создайте свой граф, добавив ребра и вершины. Каждый шаг будет состоять либо из добавления новой вершины, соединенной новым ребром с частью вашего графа (таким образом создается новый «шип»), либо из соединения двух вершин, уже находящихся в графе, с новым ребром (завершение цепи).

Что делают эти «движения»? При добавлении шипа количество ребер увеличивается на 1, количество вершин увеличивается на одну, а количество граней остается прежним. Но это означает, что \(v — e + f\) не меняется. Завершение цепи добавляет одно ребро, добавляет одну грань и сохраняет количество вершин прежним. Итак, снова \(v — e + f\) не меняется.

Поскольку мы можем построить любой граф, используя комбинацию этих двух ходов, и при этом никогда не изменится величина \(v — e + f\text{,}\), эта величина будет одинаковой для всех графов. Но обратите внимание, что наш начальный граф \(P_2\) имеет \(v = 2\text{,}\) \(e = 1\) и \(f = 1\text{,}\), поэтому \(v — e + f = 2\text{.}\) Этот аргумент по существу является доказательством по индукции. Хорошим упражнением было бы переписать его как формальное индукционное доказательство.

Подраздел Непланарные графы

Расследовать!

Для полных графов \(K_n\text{,}\) мы хотели бы иметь возможность сказать что-то о количестве вершин, ребер и (если граф планарный) граней. Давайте сначала рассмотрим \(K_3\text{:}\)

1. Сколько вершин имеет \(K_3\)? Сколько ребер?

2. Если \(K_3\) плоское, сколько граней у него должно быть?

Повторить части (1) и (2) для \(K_4\text{,}\) \(K_5\text{,}\) и \(K_{23}\text{. }\)

Как насчет полных двудольных графов? Сколько вершин, ребер и граней (если бы оно было плоским) имеет \(K_{7,4}\)? Для каких значений \(m\) и \(n\) являются \(K_n\) и \(K_{m,n}\) плоскими?

Не все графы плоские. Если ребер слишком много, а вершин слишком мало, то некоторые ребра должны пересекаться. Наименьший граф, в котором это происходит, равен \(K_5\text{.}\)

.

Если вы попытаетесь перерисовать это без пересечения краев, у вас быстро возникнут проблемы. Кажется, что одного края слишком много. На самом деле, мы можем доказать, что независимо от того, как вы это нарисуете, \(K_5\) всегда будет иметь пересечение ребер.

Теорема 4.3.1.

\(K_5\) не является плоским.

Доказательство.

Доказательство от противного. Итак, предположим, что \(K_5\) является планарным. Тогда граф должен удовлетворять формуле Эйлера для плоских графов. \(K_5\) имеет 5 вершин и 10 ребер, поэтому мы получаем

\begin{уравнение*} 5 — 10 + f = 2\текст{,} \end{уравнение*}

, в котором говорится, что если граф нарисован без пересечения ребер, то будет \(f = 7\) граней.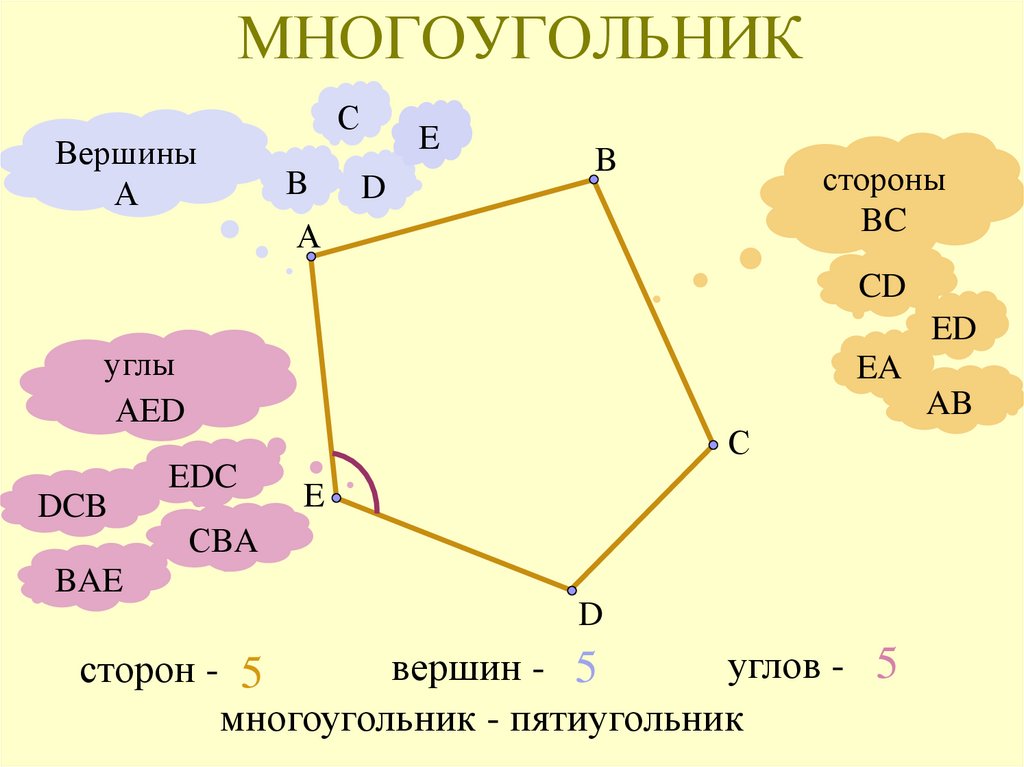

Теперь посчитайте, сколько ребер окружает каждую грань. Каждая грань должна быть окружена не менее чем тремя ребрами. Пусть \(B\) будет общим числом ограничивает вокруг всех граней графа. Таким образом, мы имеем это \(3f \le B\text{.}\) Но также и \(B = 2e\text{,}\), так как каждое ребро используется в качестве границы ровно дважды. Объединив это, мы получим

.

\begin{уравнение*} 3f \le 2e\текст{.} \end{уравнение*}

Но это невозможно, так как мы уже определили, что \(f = 7\) и \(e = 10\text{,}\) и \(21 \not\le 20\text{.}\) Это противоречие, так что на самом деле \(K_5\) не является плоским.

Другой простейший непланарный граф: \(K_{3,3}\)

Доказательство того, что \(K_{3,3}\) не является плоским, отвечает на загадку домов и коммуникаций: невозможно соединить каждый из трех домов с каждым из трех коммуникаций без пересечения линий.

Теорема 4.3.2.

\(K_{3,3}\) не является плоским.

Доказательство.

Снова поступаем от противного. Предположим, что \(K_{3,3}\) были плоскими. Тогда по формуле Эйлера граней будет 5, так как \(v = 6\text{,}\) \(e = 9\text{,}\) и \(6 — 9 + f = 2\text{.} \)

Сколько границ окружает эти 5 граней? Пусть \(B\) будет этим числом. Поскольку каждое ребро используется в качестве границы дважды, мы имеем \(B = 2e\text{.}\) Также \(B \ge 4f\), так как каждая грань окружена 4 или более границами. Мы знаем, что это так, потому что \(K_{3,3}\) двудольный, поэтому не содержит 3-реберных циклов. Таким образом,

\begin{уравнение*} 4f \le 2e\текст{.} \end{уравнение*}

Но это означало бы, что \(20 \le 18\text{,}\), что явно неверно. Таким образом, \(K_{3,3}\) не является плоским.

Обратите внимание на сходства и различия этих доказательств. Оба являются доказательствами от противного, и оба начинаются с использования формулы Эйлера для получения (предполагаемого) количества граней в графе. Затем мы находим отношение между количеством граней и количеством ребер в зависимости от того, сколько ребер окружает каждую грань. Это единственная разница. В доказательстве для \(K_5\text{,}\) мы получили \(3f \le 2e\), а для \(K_{3,3}\) мы идем \(4f \le 2e\text{.}\ ) Коэффициент при \(f\) является ключевым. Это наименьшее количество ребер, которые могут окружать любую грань. Если грань окружает некоторое количество ребер, то эти ребра образуют цикл. Таким образом, это число является размером наименьшего цикла в графе.

В общем, если мы допустим \(g\) размер наименьшего цикла в графе (\(g\) обозначает обхвата , что является техническим термином для этого), то для любого планарного графа мы имеем \ (gf \le 2e\text{.}\) Когда это противоречит формуле Эйлера, мы точно знаем, что граф не может быть плоским.

Подраздел Многогранники

Расследовать!

Куб является примером выпуклого многогранника. Он содержит 6 одинаковых квадратов граней, 8 вершин и 12 ребер. Куб это правильный многогранник (также известный как Платоново тело ), потому что каждая грань является идентичным правильным многоугольником, и каждая вершина соединяет равное количество граней.

Существует ровно четыре других правильных многогранника: тетраэдр, октаэдр, додекаэдр и икосаэдр с 4, 8, 12 и 20 гранями соответственно. Сколько вершин и ребер у каждого из них?

Еще одна область математики, где вы, возможно, слышали термины «вершина», «ребро» и «грань», — это геометрия. А 9Многогранник 0389 представляет собой геометрическое тело, состоящее из плоских многоугольных граней, соединенных ребрами и вершинами. Нас особенно интересуют выпуклых многогранников, что означает, что любой отрезок, соединяющий две точки внутри многогранника, должен полностью содержаться внутри многогранника. ⁷

Обратите внимание, что поскольку \(8 — 12 + 6 = 2\text{,}\) вершины, ребра и грани куба удовлетворяют формуле Эйлера для плоских графов. Это не совпадение. Мы можем представить куб в виде плоского графа, спроецировав вершины и ребра на плоскость. Одна из таких проекций выглядит так:

На самом деле, любой выпуклый многогранник можно спроецировать на плоскость без пересечения ребер.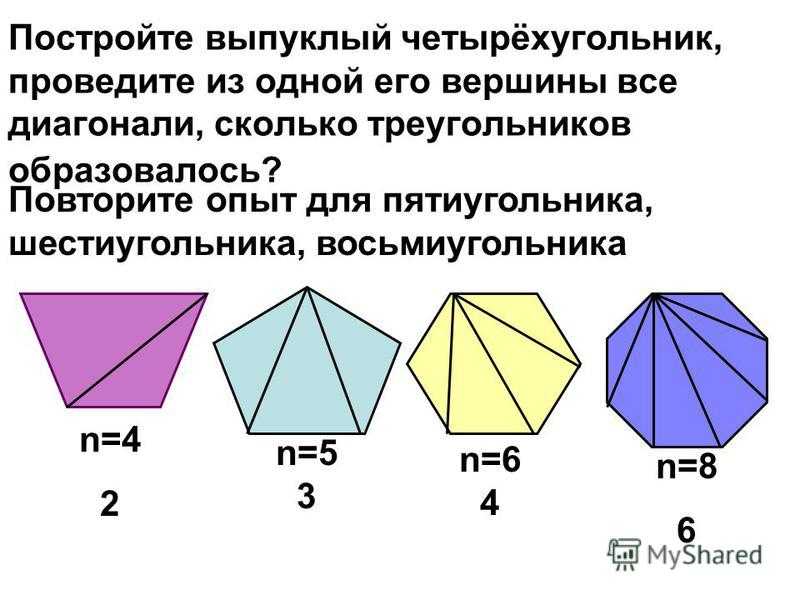 Подумайте о размещении многогранника внутри сферы со светом в центре сферы. Ребра и вершины многогранника отбрасывают тень внутрь сферы. Затем вы можете вырезать отверстие в сфере посередине одной из спроецированных граней и «растянуть» сферу, чтобы она легла на плоскость. Проколотая грань становится «внешней» гранью плоского графа.

Дело в том, что мы можем применить наши знания о графах (в частности, о планарных графах) к выпуклым многогранникам. Поскольку каждый выпуклый многогранник может быть представлен в виде плоского графа, мы видим, что формула Эйлера для плоских графов верна и для всех выпуклых многогранников. Мы также можем применить те же рассуждения, которые мы используем для графов в других контекстах, к выпуклым многогранникам. Например, мы знаем, что не существует выпуклого многогранника с 11 вершинами, все из которых имеют степень 3, так как это дало бы 33/2 ребра.

Пример 4.3.3.

Существует ли выпуклый многогранник, состоящий из трех треугольников и шести пятиугольников? Как насчет трех треугольников, шести пятиугольников и пяти семиугольников (многоугольников с 7 сторонами)?

Раствор. \circ\)), поэтому сумма степеней вершин не менее 75. Поскольку сумма степеней должна быть ровно в два раза больше числа ребер, это говорит о том, что ребер строго больше 37. Опять же, такого многогранника нет.

Чтобы завершить это применение плоских графов, рассмотрим правильные многогранники. Мы утверждали, что их всего пять. Откуда мы знаем, что это правда? Мы можем доказать это, используя теорию графов.

Теорема 4.3.4.

Существует ровно пять правильных многогранников.

Доказательство.

Напомним, что все грани правильного многогранника являются одинаковыми правильными многоугольниками и что каждая вершина имеет одинаковую степень. Рассмотрим четыре случая в зависимости от типа правильного многоугольника.

Случай 1: Каждая грань представляет собой треугольник. Пусть \(f\) будет количеством граней. Тогда есть \(3f/2\) ребер. Используя формулу Эйлера, мы имеем \(v — 3f/2 + f = 2\), поэтому \(v = 2 + f/2\text{.}\) Теперь каждая вершина имеет одинаковую степень, скажем, \(k\text{ . }\) Таким образом, число ребер также равно \(kv/2\text{.}\). Если сложить это вместе, получится

.

\begin{уравнение*} e = \frac{3f}{2} = \frac{k(2+f/2)}{2}\text{,} \end{уравнение*}

что говорит

\begin{уравнение*} k = \frac{6f}{4+f}\text{.} \end{уравнение*}

И \(k\), и \(f\) должны быть целыми положительными числами. Обратите внимание, что \(\frac{6f}{4+f}\) является возрастающей функцией для положительных \(f\text{,}\), ограниченных сверху горизонтальной асимптотой в \(k=6\text{.}\ ) Таким образом, единственными возможными значениями для \(k\) являются 3, 4 и 5. Каждое из них возможно. Чтобы получить \(k = 3\text{,}\), нам нужно \(f = 4\) (это тетраэдр). В качестве \(k = 4\) возьмем \(f = 8\) (октаэдр). В качестве \(k = 5\) возьмем \(f = 20\) (икосаэдр). Таким образом, имеется ровно три правильных многогранника с треугольниками вместо граней.

Случай 2: Каждая грань представляет собой квадрат. Теперь у нас есть \(e = 4f/2 = 2f\text{.}\) Используя формулу Эйлера, мы получаем \(v = 2 + f\text{,}\) и считаем ребра, используя степень \(k\) каждая вершина дает нам

\begin{уравнение*} е = 2f = \frac{k(2+f)}{2}\text{. } \end{уравнение*}

Решение для \(k\) дает

\begin{уравнение*} k = \frac{4f}{2+f} = \frac{8f}{4+2f}\text{.} \end{уравнение*}

Это снова возрастающая функция, но на этот раз горизонтальная асимптота находится в точке \(k = 4\text{,}\), поэтому единственное возможное значение, которое может принимать \(k\), равно 3. Получается 6 граней, и у нас есть куб. Существует только один правильный многогранник с квадратными гранями.

Случай 3: Каждая грань представляет собой пятиугольник. Мы выполняем те же вычисления, что и выше, на этот раз получая \(e = 5f/2\), поэтому \(v = 2 + 3f/2\text{.}\) Тогда

\begin{уравнение*} e = \frac{5f}{2} = \frac{k(2+3f/2)}{2}\text{,} \end{уравнение*}

так

\begin{уравнение*} k = \frac{10f}{4+3f}\text{.} \end{уравнение*}

Теперь горизонтальная асимптота находится в точке \(\frac{10}{3}\text{.}\) Это меньше 4, поэтому мы можем только надеяться получить \(k = 3\text{.}\) Мы можно сделать это, используя 12 пятиугольников, получив додекаэдр. Это единственный правильный многогранник с пятиугольниками в качестве граней.

Случай 4: Каждая грань является \(n\)-угольником с \(n \ge 6\text{.}\). Следуя той же процедуре, что и выше, мы выводим, что

\begin{уравнение*} k = \frac{2nf}{4+(n-2)f}\text{,} \end{уравнение*}

, которое будет возрастать до горизонтальной асимптоты \(\frac{2n}{n-2}\text{.}\) Когда \(n = 6\text{,}\) эта асимптота находится в точке \(k = 3\text{.}\) Любое большее значение \(n\) даст еще меньшую асимптоту. Следовательно, правильных многогранников с гранями больше пятиугольника не существует. ⁸

Упражнения Упражнения

1.

Может ли планарный граф иметь 6 вершин, 10 ребер и 5 граней? Объяснять.

Раствор.

Нет. Планарный (связный) граф должен удовлетворять формуле Эйлера: \(v — e + f = 2\text{.}\) Здесь \(v — e + f = 6 — 10 + 5 = 1\text{ .}\)

2.

Граф \(G\) имеет 6 вершин со степенями \(2, 2, 3, 4, 4, 5\text{. }\) Сколько ребер имеет \(G\)? Может ли \(G\) быть плоским? Если да, то сколько лиц у него будет. Если нет, объясните.

Раствор.

\(G\) имеет 10 ребер, так как \(10 = \frac{2+2+3+4+4+5}{2}\text{.}\) может быть плоским, и тогда иметь 6 граней, используя формулу Эйлера: \(6-10+f = 2\) означает \(f = 6\text{.}\) Однако, чтобы убедиться, что он действительно плоский, нам нужно нарисовать график с те степени вершин без пересечения ребер. Это можно сделать методом проб и ошибок (и возможно).

3.

Можно ли нарисовать связный граф с 7 вершинами и 10 ребрами так, чтобы ни одно ребро не пересекалось и не образовывало 4 грани? Объяснять.

Подсказка.

Что скажет вам формула Эйлера?

4.

Может ли граф с 10 вершинами и ребрами быть связным плоским графом? Объяснять.

5.

Существует ли связный планарный граф с нечетным числом граней, в котором каждая вершина имеет степень 6? Докажите свой ответ.

Подсказка.

Вы можете использовать лемму о рукопожатии, чтобы найти количество ребер в терминах \(v\text{,}\) количества вершин.

6.

Я думаю о многограннике с 12 гранями. Семь треугольников и четыре четырехугольника. Многогранник имеет 11 вершин, включая вершины вокруг загадочной грани. Сколько сторон у последней грани?

Раствор.

Допустим, последний многогранник имеет \(n\) ребер, а также \(n\) вершин. Тогда общее количество ребер многогранника равно \((7 \cdot 3 + 4 \cdot 4 + n)/2 = (37 + n)/2\text{.}\) В частности, мы знаем последнюю грань должно иметь нечетное число ребер. Мы также имеем, что \(v = 11 \text{.}\) По формуле Эйлера мы имеем \(11 — (37+n)/2 + 12 = 2\text{,}\) и решая для \(n \) мы получаем \(n = 5\text{,}\), поэтому последняя грань представляет собой пятиугольник.

7.

Рассмотрим некоторые классические многогранники.

1. Октаэдр — правильный многогранник, состоящий из 8 равносторонних треугольников (похож на две пирамиды со склеенными основаниями). Нарисуйте плоское графическое представление октаэдра. Сколько вершин, ребер и граней у октаэдра (и вашего графа)?

2. Традиционный дизайн футбольного мяча на самом деле представляет собой (сферическую проекцию) усеченный икосаэдр. Он состоит из 12 правильных пятиугольников и 20 правильных шестиугольников. Никакие два пятиугольника не являются смежными (поэтому ребра каждого пятиугольника являются общими только для шестиугольников). Сколько вершин, ребер и граней имеет усеченный икосаэдр? Объясните, как вы пришли к своим ответам. Бонус: нарисуйте представление усеченного икосаэдра на плоской диаграмме.

3. Ваш «друг» утверждает, что построил выпуклый многогранник из 2 треугольников, 2 квадратов, 6 пятиугольников и 5 восьмиугольников. Докажите, что ваш друг лжет. Подсказка: каждая вершина выпуклого многогранника должна граничить не менее чем с тремя гранями.

8.

Докажите формулу Эйлера, используя индукцию по количеству ребер в графе.

Раствор.

Доказательство.

Пусть \(P(n)\) будет утверждением «каждый связный планарный граф, содержащий \(n\) ребер, удовлетворяет \(v — n + f = 2\text{.}\)». Мы покажем \(P (n)\) верно для всех \(n \ge 0\text{.}\)

Базовый случай: существует только один граф с нулевыми ребрами, а именно одна изолированная вершина. В этом случае \(v = 1\text{,}\) \(f = 1\) и \(e = 0\text{,}\), поэтому формула Эйлера верна.

Индуктивный случай: предположим, что \(P(k)\) верно для некоторого произвольного \(k \ge 0\text{.}\). Теперь рассмотрим произвольный граф, содержащий \(k+1\) ребер (и \(v \) вершины и \(f\) грани). Независимо от того, как выглядит этот граф, мы можем удалить одно ребро, чтобы получить граф с \(k\) ребер, к которому мы можем применить индуктивную гипотезу.

Возможны два случая: либо в графе есть цикл, либо нет. Если граф содержит цикл, выберите ребро, являющееся частью этого цикла, и удалите его. Это не отключит граф и уменьшит количество граней на 1 (поскольку ребро граничило с двумя разными гранями). Таким образом, по индуктивному предположению мы будем иметь \(v — k + f-1 = 2\text{.}\) Добавление ребра обратно даст \(v — (k+1) + f = 2\) по мере необходимости.

Если граф не содержит циклов, то он является деревом, а значит, имеет вершину степени 1. Тогда мы можем выбрать ребро, которое нужно удалить, инцидентное такой вершине степени 1. В этом случае также удалите эту вершину. Меньший граф теперь будет удовлетворять \(v-1 — k + f = 2\) по предположению индукции (удаление ребра и вершины не уменьшило количество граней). Добавление ребра и вершины назад дает \(v — (k+1) + f = 2\text{,}\) по мере необходимости.

Следовательно, по принципу математической индукции формула Эйлера верна для всех плоских графов.

9.

Докажите формулу Эйлера индукцией по количеству вершин в графе.

10.

Формула Эйлера (\(v — e + f = 2\)) верна для всех связных плоских графов. Что делать, если граф несвязен? Предположим, что планарный граф состоит из двух компонентов. Каково теперь значение \(v — e + f\)? Что, если он имеет \(k\) компонент?

11.

Докажите, что граф Петерсена (ниже) не является плоским.

Подсказка.

Какова продолжительность самого короткого цикла? (Эта величина обычно называется обхватом графика.)

12.

Докажите, что любой планарный граф с \(v\) вершинами и \(e\) ребрами удовлетворяет \(e \le 3v — 6\text{.}\)

Раствор.

Доказательство.

Мы знаем, что в любом плоском графе число граней \(f\) удовлетворяет условию \(3f \le 2e\), так как каждая грань ограничена по крайней мере тремя ребрами, но каждое ребро граничит с двумя гранями. Объедините это с формулой Эйлера:

\begin{уравнение*} v — е + f = 2 \end{уравнение*}

\begin{уравнение*} v — e + \frac{2e}{3} \ge 2 \end{уравнение*}

\begin{уравнение*} 3в — е\ге 6 \end{уравнение*}

\begin{уравнение*} 3v — 6 \ge e\text{. } \end{уравнение*}

13.

Докажите, что любой планарный граф должен иметь вершину степени 5 или меньше.

14.

Тщательно докажите, что приведенный ниже граф не является плоским.

Подсказка.

Обхват графа 4.

15.

Объясните, почему мы не можем использовать тот же вид доказательства, что и в упражнении 4.3.14, чтобы доказать, что приведенный ниже граф не является планарным. Затем объясните, откуда вы знаете, что граф в любом случае не является плоским.

Подсказка.

Что случилось с подпругой? Осторожно: у нас также разное количество ребер. Лучше проверь формулу Эйлера.

Альтернативное определение выпуклости состоит в том, что внутренний угол, образованный любыми двумя гранями, должен быть меньше \(180\deg\text{.}\)

Обратите внимание, что вы можете замостить плоскость шестиугольниками. Это бесконечный планарный граф; каждая вершина имеет степень 3. Эти бесконечно много шестиугольников соответствуют пределу как \(f \to \infty\), чтобы сделать \(k = 3\text{.}\)

Урок Видео: Именование многоугольников | Nagwa

Стенограмма видео

Именование полигонов

В этом видео мы научимся подсчитайте стороны и вершины многоугольников, чтобы определить, являются ли они треугольник, четырехугольник, пятиугольник, шестиугольник или восьмиугольник.

Многоугольники — это формы с прямыми стороны. Какая из этих двух групп фигур иметь прямые стороны? Эта форма имеет прямые стороны. Эта форма также имеет прямые стороны. Все формы этой группы иметь прямые стороны. Мы можем назвать эту группу многоугольники. Формы второй группы имеют изогнутые стороны или некоторые изогнутые стороны. Эти фигуры не являются многоугольниками.

Существуют различные типы полигон. Чтобы помочь нам идентифицировать полигоны, мы можно посчитать количество сторон и количество углов. Каждый из этих многоугольников имеет три стороны. Они также имеют три угла. Углы или вершины находятся там, где встречаются две стороны. Фигура с тремя сторонами и тремя углов называется треугольником. Все эти многоугольники имеют четыре стороны и четыре угла.

Мы называем четырехгранные фигуры четырехугольники. Мы называем фигуры с пятью сторонами и пять углов или вершин пятиугольников. Мы называем многоугольники с шестью сторонами и шесть углов шестиугольников. И мы называем многоугольники с восемью стороны и восемь углов восьмиугольников. У осьминога восемь ног. Это хороший способ запомнить восьмиугольник имеет восемь сторон. Давайте попробуем ответить на несколько вопросов, которые помогут нам попрактиковаться в определении различных многоугольников по количеству сторон и углов.

Сколько вершин в треугольнике?

В этом вопросе нас спрашивают, как много вершин у треугольника.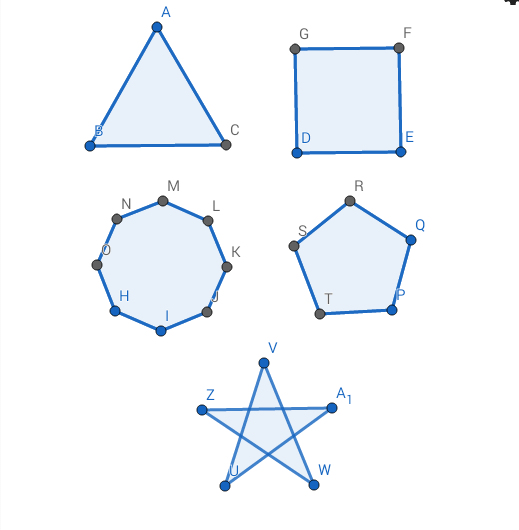 Вершина — это другое слово для угол, и это точка, где встречаются две линии. Давайте нарисуем треугольник, чтобы помочь нам ответить на вопрос. Сколько сторон у треугольника имеют? Раз два три. Подсчитаем количество углов или вершины. Есть раз, два, три. Есть три вершины в треугольник.

Как называется шестигранник многоугольник?

Мы должны назвать многоугольник с шесть сторон. Многоугольники – это фигуры, состоящие из прямые стороны, поэтому шестиугольник имеет шесть прямых сторон. Давайте нарисуем шестигранную фигуру. Раз, два, три, четыре, пять, шесть. Шестигранный многоугольник называется шестиугольник.

Как называется эта фигура? Это восьмиугольник, пятиугольник, четырехугольник, треугольник или шестиугольник?

Восьмиугольник — это фигура с восемью стороны. Пятиугольник – это фигура с пятью стороны. Четырехугольник – это четырехугольник форма. Треугольники имеют три стороны и шестиугольников шесть. Сколько сторон у этой фигуры имеют? Раз, два, три, четыре, пять. Какая фигура имеет пять сторон? Это пятиугольник. Многоугольник с пятью сторонами называется пятиугольник. Название этой формы пятиугольник.

Сколько еще палочек у Мэтью нужно изменить этот шестиугольник на восьмиугольник?

Мы знаем, что Мэтью сделал шестиугольник с помощью своих палочек. И вопрос спрашивает нас, как еще много палочек ему понадобится, чтобы сделать восьмиугольник. Этот вопрос заставляет нас задуматься о том, сколько сторон у шестиугольника и сколько сторон у восьмиугольника. Шестиугольники, в том числе Матфея шестиугольник, имеют шесть сторон. Восьмиугольник имеет восемь сторон. В чем разница между восьмеркой а шесть? Ответ — два. Из восьми вычесть шесть будет два. Мэтью понадобятся еще две палки превратить его шестиугольник в восьмиугольник.

Правда или ложь? Количество сторон многоугольника равно равно количеству вершин.

Этот вопрос заставляет нас задуматься про полигоны. Нас спрашивают, количество количество сторон многоугольника равно количеству вершин, которые он имеет. Давайте нарисуем несколько полигонов, чтобы помочь нам подумайте над вопросом. Треугольник – это многоугольник с тремя стороны и три угла. Значит, этот многоугольник имеет равный количество сторон и вершин.

Четырехугольники имеют четыре стороны и четыре угла. Количество сторон и вершин равны. Пятиугольники — это многоугольники с пятью стороны и пять углов. Количество сторон и вершин равно равный. Шестиугольник – это многоугольник с шестью стороны и шесть углов.