Музыкальный строй в котором октава делится на двенадцать равных полутонов: Темперированный строй: понятие, история возникновения и основы теории музыки

Содержание

Темперированный строй: понятие, история возникновения и основы теории музыки

19.01.2019 Петр Мамонтов Музыка

Одно из самых знаменитых творений Иоганна Себастьяна Баха называется «Хорошо темперированный клавир», или сокращенно «ХТК». Как следует понимать этот заголовок? Он указывает на то, что все произведения в цикле написаны для клавира, имеющего темперированный строй, то есть тот, который характерен для большинства современных музыкальных инструментов. В чем его особенности, и как он появился? Об этом и многом другом вы узнаете из статьи.

Общие сведения

Темперированный строй предполагает, что каждая октава (расстояние между одноименными нотами разной высоты) разделена на определенное количество равных интервалов. В большинстве случаев использования такого строяз звуки расположены по полутонам. Если представить клавиатуру фортепиано, то именно такому интервалу равно расстояние между каждой соседней клавишей. То же самое можно сказать про любой другой клавишный, духовой или иной инструмент.

Например, на гитаре между соседними нотами, находящимися на одной струне, помещается интервал малая секунда, который равен половине тона.

Значение темперированного строя

Название данной системы произошло от латинского корня, обозначающего измерение. Следовательно, это достижение можно приписать не только теории музыки, но и математике. И действительно, попытки разработки такого строя издревле предпринимались людьми, которые являлись профессионалами в этих двух областях знания, а также прекрасно знали другие науки, например, физику. И это неудивительно, поскольку в данном случае человек имеет дело с колебаниями воздуха, которые и производят звуки.

Математические вычисления помогали исследователям таким образом систематизировать звуки, входящие в состав октавы, чтобы облегчить музыкантам некоторые исполнительские задачи. Например, введение темперированного строя музыки позволило значительно упростить транспортирование произведений. Теперь игра одной и той же композиции в разных тональностях не требует повторного разучивания. Если человек знает основы теории музыки и гармонии, то он сможет сыграть произведение в любой тональности. Многолетний опыт позволяет делать это достаточно быстро.

Характеристики

Темперированный строй оказался полезным в первую очередь при исполнении вокальной музыки. С его введением певцы получили возможность исполнять произведения в наиболее удобной для них тональности. А значит, вокалисты избавились от необходимости перенапрягать свои голосовые связки, беря слишком низкие или высокие ноты, нехарактерные для их диапазона. Конечно же, такое вольное обращение с музыкальным материалом приветствуется далеко не во всех жанрах. В первую очередь это касается классической музыки. Например, исполнение оперных арий в других, не оригинальных тональностях, считается неприемлемым.

Также недопустимо транспортирование симфоний, классических инструментальных концертов, сонат, сюит и произведений многих других жанров. В отличие от эстрадной музыки, тональность здесь имеет гораздо большее значение. История знает примеры наличия у некоторых композиторов «цветного» музыкального слуха. То есть для этих деятелей искусств каждая тональность ассоциировалась с определенным оттенком. Таким восприятием музыки отличались Скрябин и Римский-Корсаков.

Другие же классические композиторы, хотя и не имели такого «цветного» восприятия звука, но все же различали тональности по другим характеристикам (теплоте, насыщенности и так далее). Транспортирование их произведений в произвольные тональности является недопустимым, так как искажает замысел автора.

Незаменимый помощник

Однако и такие композиторы не отрицали значения равномерно-темперированного строя для развития музыкального искусства. Свободный переход из одной тональности в другую имеет не только явную «практическую» пользу, поскольку позволяет обеспечить исполнителям удобство при игре и пении. При правильном подборе тональности голос вокалиста звучит гораздо ярче и естественнее, чем когда он всеми силами старается исполнить нехарактерные для его диапазона (низкие или высокие) ноты.

Темперированный строй (а значит, и свободная смена тональностей) обеспечивает возможность писать произведения с большим количеством тональных отклонении и модуляций. А это, в свою очередь, является ярким изобразительным приемом, который широко применялся в классической музыке. С наступлением эпохи эстрадного искусства применение модуляций приобрело еще большее значение. Так, в джазовых импровизациях часто используются гармонические последовательности, переходящие из одной тональности в другую. Поэтому темперированный строй можно назвать одним из двигателей прогресса в музыке.

История

Теоретические исследования в области музыки начались в глубокой древности. Одним из первых ученых, кто стал уделять внимание строю, был древнегреческий математик Пифагор. Однако еще до появления на свет этого выдающегося человека существовало множество музыкальных инструментов с уже оформившимся строем. Люди, которые играли на них, часто не имели ни малейшего представления ни о физических свойствах звука, ни об основах теории музыки. Своему искусству они учились, постигая многие его премудрости интуитивно.

То есть в то далекое время люди методом проб и ошибок усваивали акустические законы, которые лежат в основе музыкальной теории и гармонии. А эти науки, как известно, не уступают в своей сложности высшей математике. Один мыслитель впоследствии сказал, что музыканты и композиторы бессознательно занимаются решением сложнейших физических и математических задач. Первым же серьезным исследователем этих вопросов был уже упомянутый Пифагор.

Пифагоров строй

Древнегреческий ученый проводил опыты со звучанием простейшего музыкального инструмента, который состоял из деревянного корпуса и натянутого на него источника звучания — одной единственной струны.

Он изобрел собственный строй, который получил название Пифагорова. Звуки в нем были расположены по чистым квинтам. Использование такой системы позволило у некоторых инструментов уменьшить количество струн. До этого все инструменты были устроены наподобие арфы, то есть каждая их струна могла издавать только одну ноту. Зажимание пальцами не применялось. Однако с введением Пифагорова строя музыканты по-прежнему не могли изменять тональность ни всего произведения, ни какой-либо его части. Такая система настройки применялась вплоть до средневековья. Тогда органы для исполнения церковной музыки были настроены по древнегреческому образцу. У этой системы, кроме перечисленных недостатков, имелись еще два минуса. Во-первых, звукоряд в них не был замкнут. Это значит, что начав играть гамму от до, нельзя было прийти в ту же ноту, но более высокой октавы.

И во-вторых, инструменты, настроенные таким образом, имели всегда несколько так называемых «волчьих» звуков, то есть клавиш или ладов, чье звучание выбивало ось из тональности, в которой был настроен весь инструмент.

Музыка до эпохи Барокко

Музыканты, композиторы, а также мастера, занимавшиеся изготовлением инструментов, в средние века были заняты постоянным поиском идеального строя. Артисты бродячих театров славились своей виртуозной игрой на лютнях.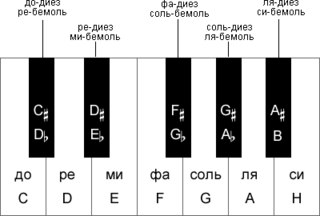 Под аккомпанемент данного инструмента исполнялись шуточные куплеты на злободневные темы. В поисках подходящей тональности, соответствующей диапазону голоса, артистам приходилось перестраивать свой инструмент, а это было связано не только с ослаблением или усилением натяжения струн, как сегодня.

Такая процедура требовала перестановки ладов. Они не были прочно прикрепленными к грифу, как в современных гитарах. Тогда их заменяли жгуты, сделанные из кожи животных, и свободно перемещавшиеся по грифу. Так, при перестройке инструмента приходилось передвигать и эти лады. Не случайно в те времена шутили, что лютнисты тратят треть своей жизни на настройку инструмента.

Кроме того, в пифагорейской системе не существовало понятия энгармонически равных звуков. То есть нота «фа диез» звучала тогда не так, как «соль бемоль».

Разные варианты

Система настройки, приближенная к современной, появилась во времена Иоганна Себастьяна Баха.

Она называлась «хорошо темперированный строй».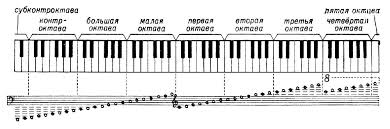 В чем заключалась ее суть? Как уже было сказано, до этого не было энгармонически равных звуков. То есть если бы тогда существовало современное фортепиано, то между клавишами «до» и «ре» должны были бы находиться две черных: «до диез» и «ре бемоль», вместо сегодняшней одной, выполняющей обе эти функции.

Во времена Иоганна Себастьяна Баха получила широкую популярность музыка в тональностях с большим количеством диезов и бемолей. Композиторы стали использовать хитрый ход — для удобства исполнения они нередко делали энгармонические замены. Например, вместо «соль бемоль» они стали писать в партитурах «фа диез». Но эти ноты не были в то время равными друг другу. То есть их звучание, пусть не сильно, но отличалось. Поэтому прослушивание такой музыки вызывало у людей чувство легкого дискомфорта.

Неточно, но удобно

Но вскоре был найден выход из данного положения. Две ноты, находящиеся между соседними ступенями звукоряда, заменили одной, которая находилась между ними. Этот звук был лишь приблизительно равен двум этим нотам, а точнее, он являлся их усредненным значением.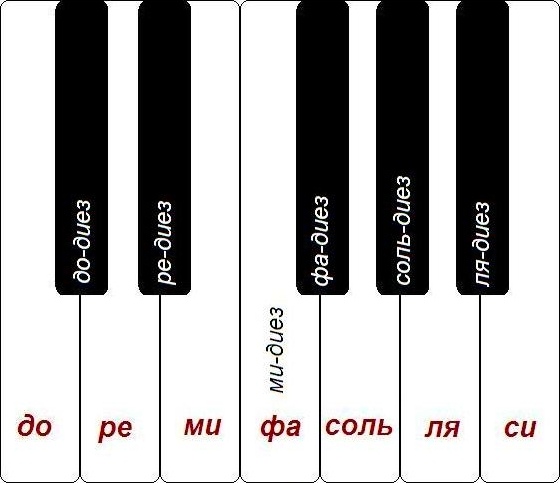 Но, тем не менее, такое нововведение открыло перед композиторами и исполнителями возможности.

Натуральный строй и темперированный

Натуральным называется такой строй, который содержит в себе только основные ступени звукоряда. Соотношения между ними следующие: два тона — полутон — три тона — полутон. По такой схеме настраиваются простейшие народные инструменты: свирели, дудочки и так далее.

На каждом из них можно играть только в двух тональностях — мажоре и миноре.

Появление нового строя

В 18 веке несколько теоретиков музыки предложили ввести в употребление новый строй. В нем октава делилась на 12 нот, отстающих друг от друга ровно на полтона. Такая система получила название равно темперированного строя. У нее было много сторонников, но нашлось и достаточное количество суровых критиков. Роль создателя темперированного строя приписывается сразу нескольким людям. Наиболее часто в этой связи звучат имена Генриха Граматеуса, Винченцо Галилея и Марена Марсенна.

Противоречие

На вопрос «Какой строй называется равномерно темперированным?» достаточно полным может считаться следующий ответ: «Это строй, где октава содержит двенадцать нот, расположенных по полутонам». Некоторые критики такого подхода к настройке инструментов говорили, что он не является идеально точным, и натуральный строй звучит гораздо чище. Именно в таком строе поют и играют музыканты-любители из народа. В воспоминаниях писателя, композитора и теоретика музыки Владимира Одоевского можно найти рассказ, как он однажды пригласил к себе в гости одного такого певца. Когда Одоевский начал аккомпанировать гостю, то услышал, что темперированный строй фортепиано не совпадает с нотами, которые пел этот человек.

После того случая композитор настроил свой рояль иным образом. Его звучание приблизилось к натуральному.

Заключение

Случилось это в девятнадцатом веке. Но до сих пор не умолкают споры между сторонниками и противниками равномерно темперированного строя в музыке.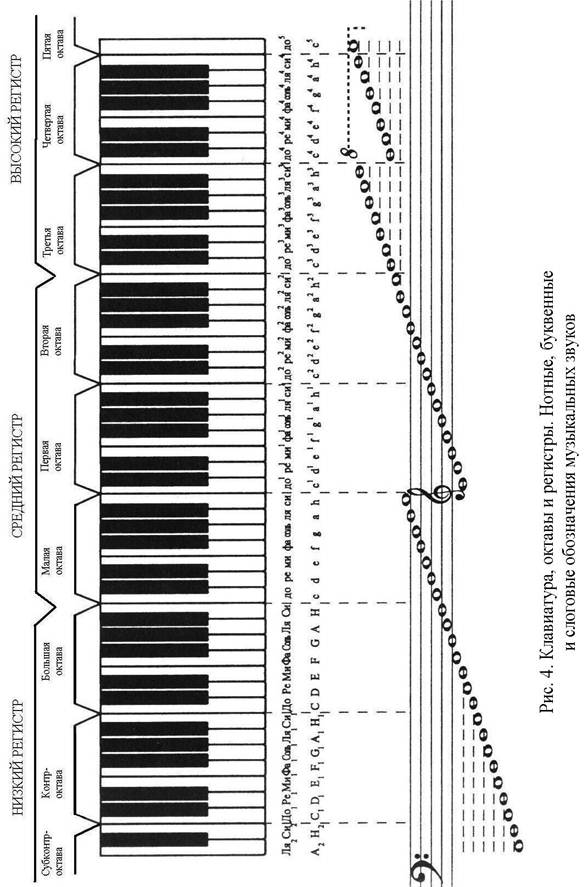 Первые из них защищают возможность свободного перехода в разные тональности, а вторые выступают за чистоту настройки инструмента. Существуют также и другие, более экзотические варианты настройки. В качестве примера можно назвать микротоновую гитару. Но подавляющее количество инструментов в мире имеет все-таки равномерно темперированный строй.

Автор: Лаев Алексей

Источник: fb.ru

Музыкальный строй.Темперированный строй.Полутон и целый тон. – Nesta

Соотношение абсолютной высоты звуков в музыкальной системе называется музыкальным строем. Современный музыкальный строй исходит из 440 колебаний в секунду звука «ЛЯ» первой октавы.

В общепринятой музыкальной системе каждая октава делится на двенадцать равных частей — полутонов. Такой строй называют темперированным строем. Он отличается от натурального строя, тем что все полутоны октавы в нем равны.

Благодаря тому, что октава разделена на 12 равных полутонов, полутон является самым узким расстояние между звуками музыкальной системы.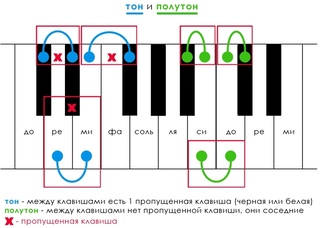 Расстояние, образованное двумя полутонами, называется целым тоном.

Между основными ступенями звукоряда имеются два полутона пять целых тонов.

ДО -1тон- РЕ -1тон- МИ -1/2тона- ФА -1тон- СОЛЬ -1тон- ЛЯ -1тон- СИ — 1/2тона — ДО.

Целые тоны, образующиеся между основными ступенями, разделены на полутоны. Звуки которые делят их на полутоны, извлекаются на клавишах

черного цвета. Таким образом, октава состоит из двенадцати звуков , расположенных на равном расстоянии друг от друга.

Каждая основная ступень звукоряда может быть повышена или понижена. Звуки, соответсвующиее повышенным и пониженным ступеням, считаются производными ступенями. Поэтому название производных ступенней происходят от основных.

Повышение основных ступеней на полтона обознаечтся словом диез,понижение на полутон — бемоль, повышение на два полутона дубль-диез, понижение, соответственно дубль-бемоль.

Описанное понижение, или повышение основных ступеней называется альтерацией!!

ЭНГАРМОНИЗМ ЗВУКОВ

Благодаря тому, что все полутоны октавы равны, один и тот же звук может быть производным от повышения основной ступени, находящейся полутоном ниже его, так же от понижения основной ступени, находящейся полутоном выше его, например фа-диез, или соль-бемоль.

Равенство ступеней по высоте. но различных по названию и обозначению, называют энгармонизмом звуков.

ДИАТОНИЧЕСКИЕ И ХРОМАТИЧЕСКИЕ ЦЕЛЫЕ И ПОЛУТОНЫ.

ПОЛУТОНА.

Диатоническим называют полутон, образующийся между двумя соседними ступенями звукоряда. Как было сказано, основные ступени звукоряда образуют два полутона — МИ-ФА и СИ-ДО.

Кроме указанных полутонов, диатонические полутоны могут образовываться между основной ступенью и соседней производной ступенью повышенной или пониженной, или между двумя производными ступенями.

Хроматическим называется полутон, образующийся между основной ступенью и ее повышенннием или пониженнием, так же между повышенной ступенью и ее двойным повышением, пониженной ступенью и ее двойным понижением.

ЦЕЛЫЕ ТОНЫ.

Диатоническими называют целые тоны, образующиеся между двумя соседними ступенями.Основные ступени образуют пять целых тонов: ДО — РЕ, РЕ -МИ, ФА — СОЛЬ, СОЛЬ -ЛЯ, ЛЯ — СИ.

Так же, диатонические тоны могут быть образованны между основной и производной ступенями, а так же между двумя производными ступенями.

Хроматическими называют целые тоны, образующиеся между основной ступенью и ее двойным повышением, или понижением, между двумя производными ступенями от одной основной ступени, между сутпенями, расположеными через одну ступень.

Пифагорейское математическое обоснование музыкальной гаммы / Хабр

Глава из книги Александра Волошинова «Математика и искусство» (Москва: Просвещение, 1992)

Почтенный Пифагор отвергал оценку музыки, основанную на свидетельстве чувств. Он утверждал, что достоинства ее должны восприниматься умом, и потому судил о музыке не по слуху, а на основании математической гармонии и находил достаточным ограничить изучение музыки пределами одной октавы.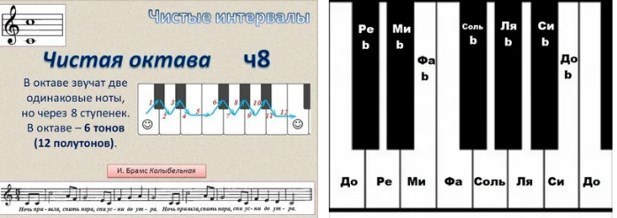

Плутарх

Строго говоря, речь здесь пойдет о пифагоровом строе. Что же такое гамма и строй в музыке?

Гаммой, или звукорядом, называется последовательность звуков (ступеней) некоторой музыкальной системы (лада), расположенных, начиная от основного звука (основного тона), в восходящем или нисходящем порядке. Название «гамма» происходит от греческой буквы Гγ (гамма), которой в средние века обозначали крайний нижний тон звукоряда, а затем и весь звукоряд.

Важнейшей характеристикой музыкального звука является его высота, представляющая отражение в сознании частоты колебания звучащего тела, например струны. Чем больше частота колебаний струны, тем «выше» представляется нам звук.

Каждый отдельно взятый звук не образует музыкальной системы и, если он не слишком громкий, не вызывает у нас особой реакции. Однако уже сочетание двух звуков в иных случаях получается приятным и благозвучным, а в других, наоборот «режет» ухо.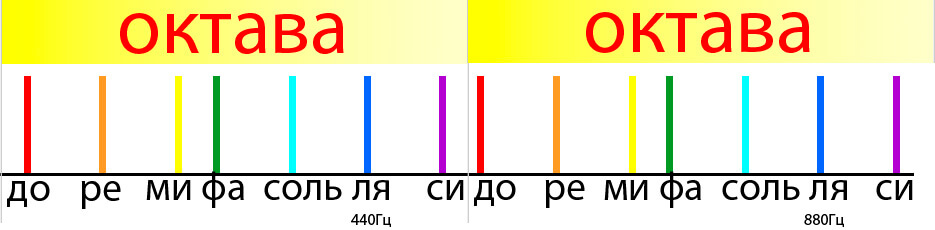 Согласованное сочетание двух звуков называется консонансом, несогласованное — диссонансом. Ясно, что консонанс или диссонанс двух тонов определяются высотным расстоянием между этими тонами или интервалом.

Интервалом между двумя тонами назовем порядковый номер ступени верхнего тона относительно нижнего в данном звукоряде, а

интервальным коэффициентом I₂₁ двух тонов — отношение частоты колебаний верхнего тона к частоте нижнего^*:

(6.1)

^* (В теории музыки понятия интервала и интервального коэффициента строго не разграничены. Следуя традиции, мы часто для краткости будем называть интервальный коэффициент интервалом. )

Рассмотрим теперь некоторую совокупность звуков, нажав, например, на фортепиано последовательно несколько клавиш. Скорее всего, у нас получится бессвязный набор звуков, как говорится, ни складу ни ладу. В других случаях звуки вроде бы подходят, ладятся между собой, но их совокупность покажется оборванной, незаконченной.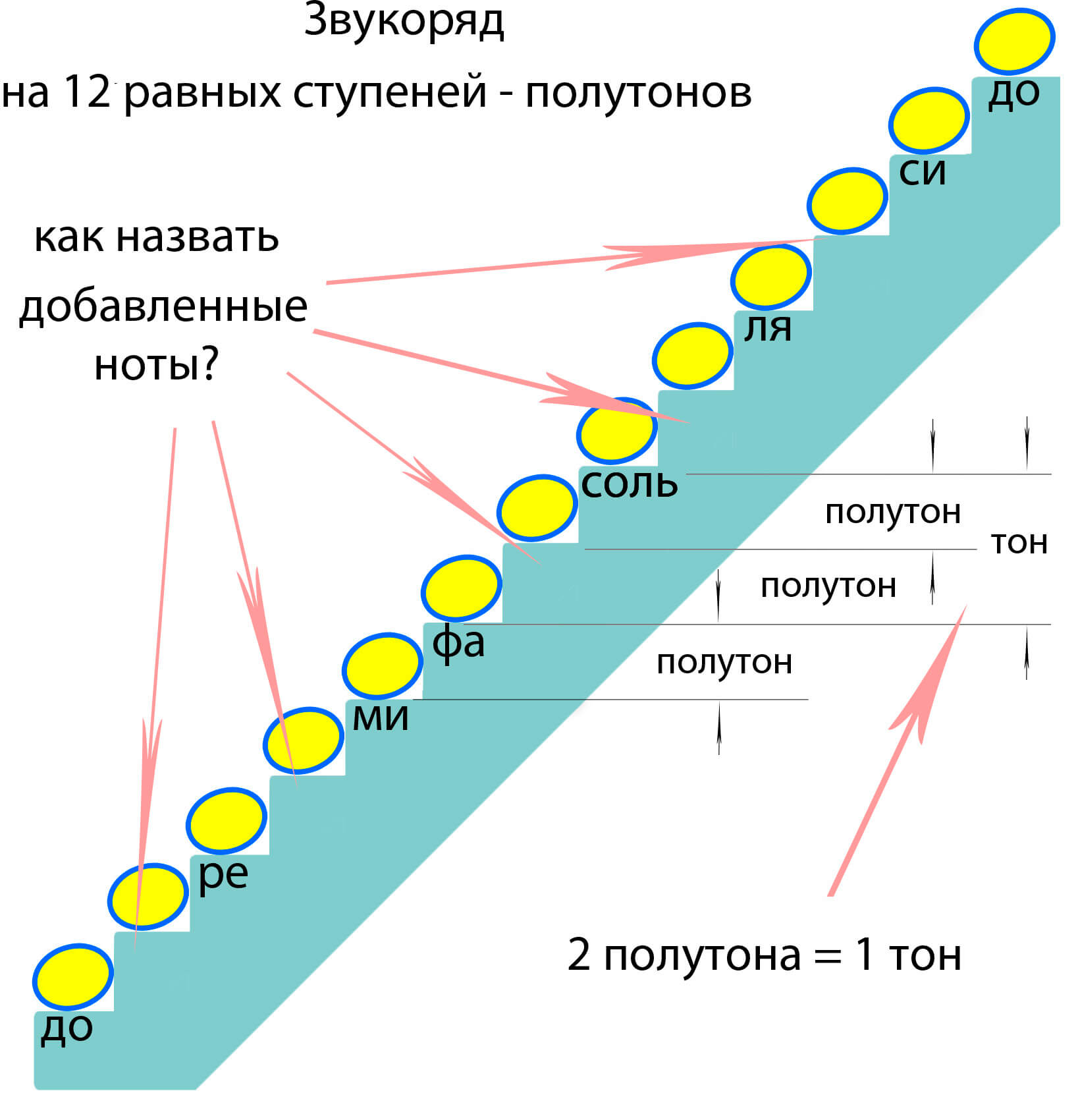 Эту последовательность так и хочется продолжить до определенной ноты, которая в данной системе звуков кажется наиболее устойчивой, основной и называется тоникой. Итак, звуки в музыкальной системе связаны между собой определенными зависимостями, одни из них являются

неустойчивыми и тяготеют к другим — устойчивым.

Но не только тоника и совокупность устойчивых и неустойчивых звуков определяют характер музыкальной системы. Легко убедиться, нажав подряд восемь белых клавиш от ноты до (гамма до мажор натуральный) и от ноты ля (ля минор натуральный), что эти гаммы звучат по-разному: первая — мажор — звучит бодро и светло, а вторая — минор — грустно и пасмурно^*. Следовательно, существует и другая характеристика системы звуков — наклонение: мажорное или минорное. Таким образом, мы приходим к одному из самых сложных понятий в теории музыки — понятию лада.

^* (Характер звучания лада, конечно, не определяется столь грубо и однозначно. Вопрос этот очень деликатный, и о нем мы еще поговорим в конце главы. )

Ладом называется приятная для слуха взаимосвязь музыкальных звуков, определяемая зависимостью неустойчивых звуков от устойчивых, и прежде всего от основного устойчивого звука — тоники, и имеющая определенный характер звучания — наклонение. История музыкальной культуры знает множество ладов, свойственных разным народам и разным временам. Древние греки знали с десяток ладов, а лады некоторых восточных стран и Индии чрезвычайно сложны, своеобразны и непривычны для европейского слуха. Наиболее распространенные современные лады состоят из семи основных ступеней, каждая из которых может повышаться или понижаться, что дает еще пять дополнительных звуков. Таким образом, диатоническая (7-ступенная) гамма лада превращается в хроматическую (12-звуковую). Первой ступенью лада является тоника. Законы строения лада — это целая наука, краеугольный камень музыкознания, а изучению этих законов многие ученые и композиторы посвятили всю свою жизнь.

Нас же будут в первую очередь интересовать математические закономерности, описывающие строение лада, т. е. музыкальный строй. Музыкальным строем называется математическое выражение определенной системы звуковысотных отношений. Помимо чисто теоретического интереса строй находит применение при настройке музыкальных инструментов с фиксированной высотой звуков, таких, как фортепиано или орган.

В заключение заметим, что наши эксперименты с нажатием клавиш на фортепиано могут закончиться самым редким и самым приятным феноменом, когда взятая система звуков будет не только принадлежать к какому-либо ладу, но и будет носить осмысленный характер. Такой художественно осмысленный последовательный ряд звуков разной высоты называется мелодией. Это как раз то, что мы так любим напевать в зависимости от нашего настроения — бодрого, грустного, веселого…

После такого кратчайшего экскурса в теоретическое музыкознание мы можем вернуться на берега солнечной Эллады во времена мудрого Пифагора.

Попытаемся восстановить рассуждения Пифагора и его учеников при построении пифагорова строя, ибо именно этот строй определил на тысячелетия, если не навечно, все развитие музыкальной культуры, не только европейской, но и восточной. Сам Пифагор не оставил никаких письменных работ, да и наследие пифагорейцев представляется безнадежной грудой развалин, т. е. собранием случайно уцелевших фрагментов и более поздних цитат. Бесспорно, развалины эти прекрасны и поныне поражают воображение, как развалины знаменитого Парфенона, однако многое в этих обломках бесследно утеряно и о целом часто можно только догадываться. И все-таки…

Монохорд — однострунный — был одним из первых музыкальных инструментов древних греков. Это был длинный ящик, необходимый для усиления звука, над которым натягивалась струна. Снизу струна поджималась передвижной подставкой для деления струны на две отдельно звучащие части. На деревянном ящике под струной имелась шкала делений, позволявшая точно установить, какая часть струны звучит.

Конечно, как музыкальный инструмент монохорд покажется нам слишком примитивным, однако он был прекрасным физическим прибором и учебным пособием, на котором античные созерцатели постигали премудрости музыкальной грамоты.

Древние уверяли, что уже Пифагор знал законы колебания струны монохорда и построения музыкальных созвучий (консонансов), однако запись об этих законах мы находим у пифагорейца Архита из Тарента (428-365 гг. до н. э.), жившего На полтора столетия позже Пифагора. Архит был, безусловно, самым выдающимся представителем пифагорейской школы, другом философа Платона и учителем математика Евдокса (ок. 408 — ок. 355 гг. до н. э.), государственным деятелем и полководцем. Многосторонность Архита поразительна: он решил знаменитую де-лосскую задачу об удвоении куба, заслуженно считался крупнейшим пифагорейским теоретиком музыки, первым упорядочил механику на основе математики и свел движения механизмов к геометрическим чертежам, работал над деревянной моделью летающего голубя.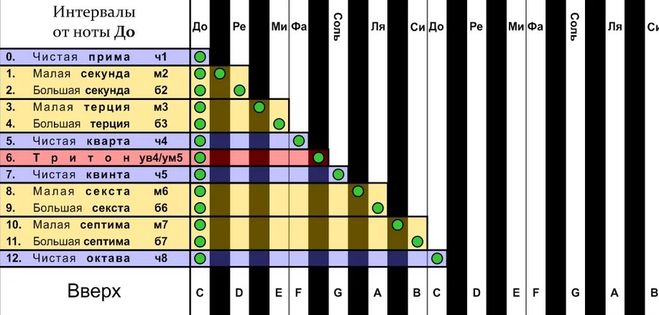 По мнению Ван дер Вардена, Архит является автором VIII книги «Начал» Евклида, в которой изложена арифметическая теория пропорций. Как государственный деятель Архит пользовался исключительным уважением: он семь лет подряд избирался стратегом^*, хотя по закону стратеги выбирались лишь на один год. Путем искусных дипломатических маневров Архит вызволил из плена Платона и тем самым спас жизнь великому философу. «Славный Архит, земель, и морей, и песков исчислитель…» — писал Гораций.

* (Стратег — в древнегреческих городах-государствах военачальник, облеченный ши-кими военными и политическими полномочиями. )

«Законы Пифагора — Архита», на которых основывалась вся пифагорейская теория музыки, можно сформулировать так:

1- Высота тона (частота колебаний f) звучащей струны обратно пропорциональна ее длине l:

(6.2)

здесь а — коэффициент пропорциональности, зависящий от физических свойств струны (толщины, материала и т. п.).

2. Две звучащие струны дают консонанс лишь тогда, когда их длины относятся как целые числа, составляющие треугольное число 10 = 1 + 2 + 3 + 4, т. е. как 1:2, 2:3, 3:4.

Эти интервалы — «совершенные консонансы», и их интервальные коэффициенты позже получили латинские названия^*:

^* (Названиями интервалов в музыке служат латинские числительные, которые указывают порядковый номер ступени звукоряда, составляющей интервал с исходной ступенью: октава — восьмая, квинта — пятая, кварта — четвертая и т. д.)

октава

квинт

кварта

Треугольное число 10

Было замечено также, что наиболее полное слияние тонов дает октава (2/1), затем идут квинта (3/2) и кварта (4/3), т. е. чем меньше число п в отношении вида тем созвучнее интервал.

«Второй закон Пифагора — Архита» и сейчас кажется удивительным. Что же говорить о пифагорейцах, которых он просто привел в восторг! Здесь они нашли подтверждение всей своей философии: целые числа, более того, числа тетрактиса правят всем, даже музыкой! Пифагорейцы не заставили себя долго ждать и распространили закон музыкальных отношений всюду, где это возможно, в том числе и на строение вселенной.

Итак, если в качестве цены деления шкалы монохорда взять отрезок l, равный 1/12 длины струны монохорда l₁, то вместе со всей струной монохорда длины l₁ = 12l будут созвучны ее части длины l₂ = 6l — звук на октаву выше (l₂/l₁ = l/2), l₃ = 9l — звук на квинту выше (l₃/l₁ = 2/3) и l₄ = 8l — звук на кварту выше (l₄/l₁ = 3/4). Это созвучие и определяющие его числа 6, 8, 9, 12 назывались тетрада (четверка). Пифагорейцы считали, что тетрада — это «та гамма, по которой поют сирены». При настройке античной лиры, ставшей символом музыки, четыре ее струны обязательно настраивались по правилу тетрады, а настройка остальных струн зависела от лада, в котором предстояло на ней играть.

Но для античного мыслителя было мало установить численные значения изучаемых величин. Пифагорейский глаз и ум привыкли не только измерять, но и соизмерять, т. е. раскрывать внутренние связи между изучаемыми предметами, другими словами, устанавливать пропорциональные отношения.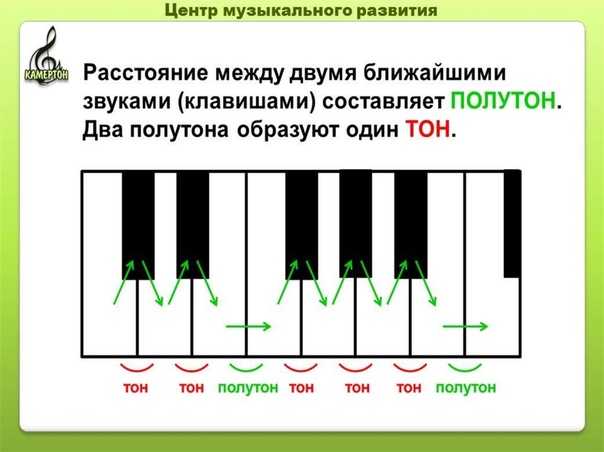 Архит был истинным пифагорейцем, и он установил пропорциональные отношения между основным совершенным консонансом — октавой, квинтой и квартой. Решение это было получено Архитом в связи с желанием разделить октаву на благозвучные интервалы. Вероятно, Архит исходил из того интуитивно очевидного предположения, что вместе с тонами f₁ и f₂ = 2f₁, дающими основной консонанс — октаву, должно дать консонанс и их среднее арифметическое f₃ = (f₁ + f₂)/2. Но тогда длина струны l₃ выразится через длины струн l₁ и l₂ согласно (6.2) следующим образом:

т. е. l₃ есть среднее гармоническое l₁ и l₂ (см. 5.1). Легко обнаружить и обратное: среднее гармоническое для частот f₁ и f₂ переходит в среднее арифметическое для длин l₁ и l₂:

Вспоминая, что мы вместе с Архитом приходим к важному выводу:

(6. 3)

(6.4)

т. е. квинта есть среднее гармоническое длин струн основного тона l₁ и октавы l₂, а кварта — среднее арифметическое l₁ и l₂.

Но произведение среднего арифметического на среднее гармоническое равно произведению исходных чисел:

(6.5)

откуда, разделив обе части на l₁², получаем второй важный вывод:

(6.6)

или

т. е. октава есть произведение квинты на кварту.

Разделив же (6.5) на l₁l₃, Архит получает и третью из основных пропорций -геометрическую:

(6.7)

которую называли «музыкальной»: октава так относится к квинте, как кварта к основному тону.

Деление струны монохорда (l₁) на части, образующие с ней совершенные консонансы: октаву (l₂), квинту (l₃) и кварту (l₄) и соотношения между ними. Интервалы, которые целая струна монохорда образует со своими частями, показаны красными стрелками

Легко получить еще два соотношения:

(6. 8)

т. е. октава делится на два неравных консонансных интервала — квинту и кварту. Интервал, дополняющий данный интервал до октавы, называется его обращением. Таким образом, квинта есть обращение кварты и наоборот.

Наконец, найдем интервальный коэффициент между струнами квинты l₃ и кварты l₄, который вместе со своим интервалом называется тоном (не нужно путать тон-интервал и тон-звук данной высоты):

(6.9)

т. е. тон-интервал равен отношению квинты к кварте.

Заметим, что в отличие от обычного расстояния на прямой r₂₁ = х₂ — x₁ определяемого как разность координат конца и начала, интервальный коэффициент — высотное расстояние — определен как отношение составляющих его тонов Тогда три тона f₁ <f₂ <f₃, расположенных на равных расстояниях r и образующих арифметическую прогрессию x₁, х₂ = x₁ + r, x₃ = x₁ + 2r.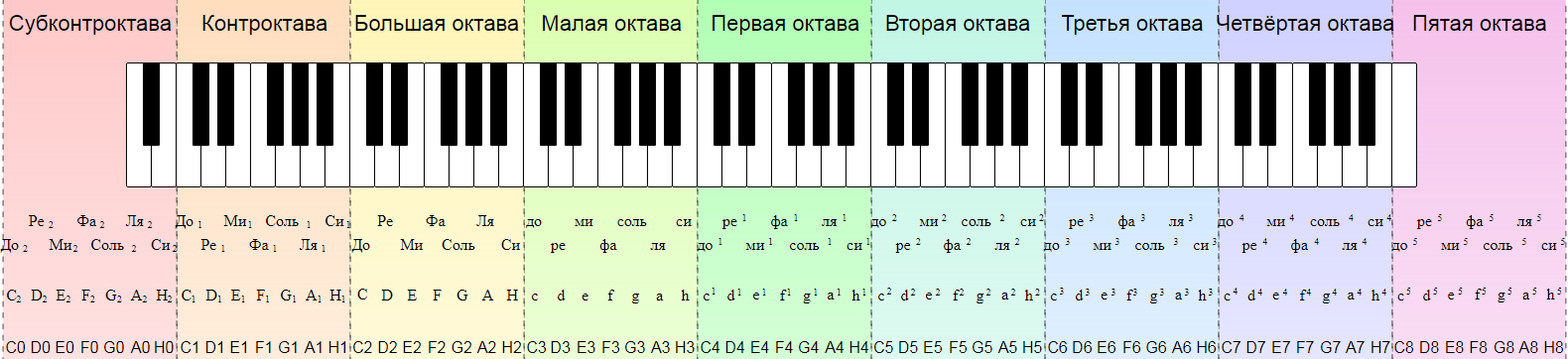 Поэтому интервальные коэффициенты складываются и вычитаются «геометрически», а сами интервалы — «арифметически», как обычные расстояния, а именно:

сумма двух интервалов равна произведению их интервальных коэффициентов:

(6.10)

разность двух интервалов равна частному их интервальных коэффициентов:

(6.11)

разделить интервал на n равных частей означает извлечь корень степени n из его интервального коэффициента:

(6.12)

и т. д.

Чтобы перейти от интервальных коэффициентов к интервалам-расстояниям, достаточно ввести логарифмический интервал L = log_a I и логарифмическую частоту F = log_a f. Тогда, логарифмируя определение (6.1) и равенства (6.10) — (6.12) получаем привычное определение и правила действия с расстояниями:

(6.13)

Решение проблемы деления октавы подсказало Архиту сразу два доказательства иррациональности . В самом деле, если попытаться разделить октаву на два равных интервала I, то, полагая в (6.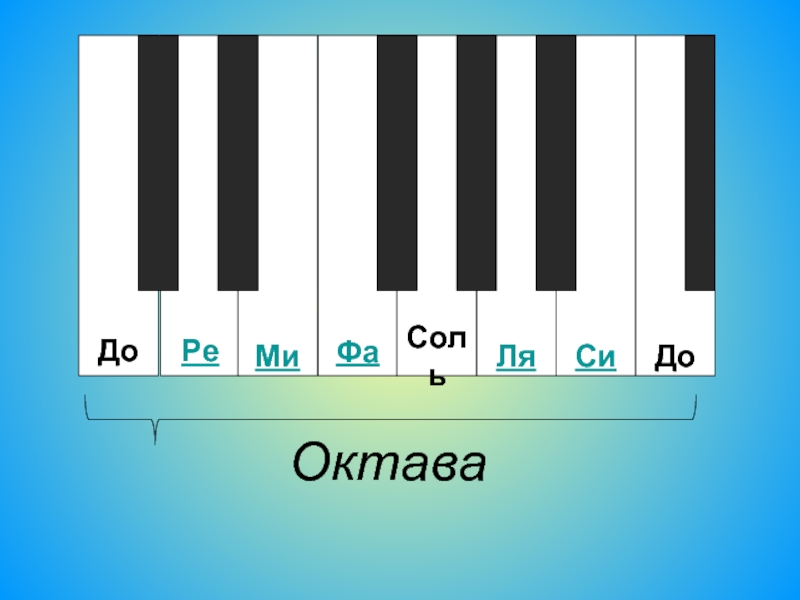 8) I₂₃ = I₃₁ = I, имеем

Но при таком соотношении длин струн прослушивается явный диссонанс. Поскольку же консонанс определяется отношением целых чисел вида (n+1):2, то напрашивается мысль, что число не может быть выражено отношением двух целых чисел, т. е. является иррациональным.

Второе доказательство иррациональности менее музыкально, но более математично. Чтобы найти квадратный корень числа, не являющегося полным квадратом, Архит разлагает его на два неравных сомножителя (2 = 1*2), затем образует из этих сомножителей среднее арифметическое ³/₂ и среднее гармоническое ⁴/₃ и составляет из этих чисел музыкальную пропорцию (6.7):

Произведение средних членов этой пропорции равно данному числу 2, а их разность меньше, чем разность нулевого приближения 2 — 1 = 1. Следовательно, можно рассматривать как приближенные значения .

(³/₂ с избытком, ⁴/₃ с недостатком ].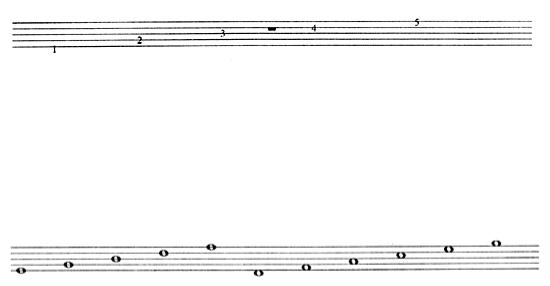

Проделав ту же процедуру над первыми приближениями, получим вторые приближения:

причем

а затем — и третьи приближения:

причем

1,414216-1,414211=0,000005.

Поскольку данную процедуру можно повторять неограниченно, то ясно, что число иррациональное. Попутно мы убеждаемся в справедливости пифагорейской мысли о том, что чем больше целые числа в отношении, тем точнее они выражают иррациональное число (см. с. 96). Наконец, вспоминая, что значение равно 1,414213…, мы видим, что «музыкальный» метод Архита очень быстро сходится к точному значению и уже третье приближение дает пять верных знаков после запятой!

Но вернемся к нашим интервалам. Итак, октава делится на два неравных консонанса квинту и кварту, а квинта — на консонанс кварту и диссонанс тон. Тон-интервал и был принят за интервал между соседними по высоте звуками (ступенями) при построении пифагоровой гаммы. Здесь и находится ключ к построению лада. По мнению советского музыковеда Л. А. Мазеля, интервал квинты, разделенный на кварту и тон, является основным музыкальным элементом. Выбрав тон в качестве основной ладообразующей ступеньки, античным теоретикам осталось только отложить от основного звука , затем — еще один тон , а оставшийся интервал между вторым тоном и тоном кварты назвать полутоном Название это вполне оправдано, так как деление тона-интервала пополам по формуле (6.12) дает т. е. полутон практически равен половине тона^*. Так была получена основа всей древнегреческой музыки — тетрахорд — четырехструнный звукоряд в пределах кварты.

^* (Интервал тона (полутона) в теории музыки принят в качестве единицы арифметического измерения интервалов, а сами интервалы тона и полутона в отличие от их интервальных коэффициентов называют большой и малой секундами.)

Ясно, что имеется только три возможности для положения полутона в пределах тетрахорда, что и определяло характер и название тетрахорда:

дорийский: полутон — тон — тон;

фригийский: тон — полутон — тон;

лидийский: тон — тон — полутон.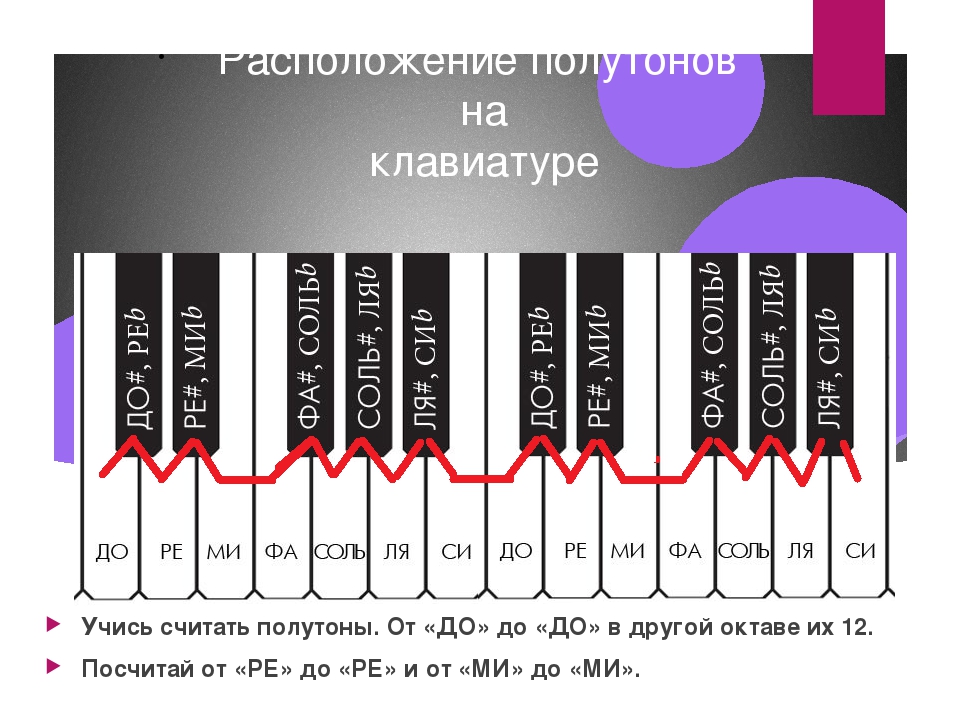

Названия тетрахордов указывают на соответствующие области Греции и Малой Азии, каждая из которых пела в своем ладу.

Конечно, четырех струн в пределах кварты было мало для ведения мелодии, поэтому тетрахорды соединялись. Мы уже выяснили, что октава состоит из двух кварт и тона; следовательно, в пределах октавы можно расположить два тетрахорда, разделенных интервалом в тон. Объединяя с помощью разделительного тона два одноименных тетрахорда, получили октаву, которую греки называли «гармония». Именно в античной теории музыки слово «гармония» обрело свое современное значение — согласие разногласного. Таких основных видов гармонии по числу тетрахордов получалось три:

Здесь 1 обозначает тон, 1/2 — полутон, разделительный тон обведен кружком. Эти античные гармонии сопоставимы с современными гаммами. В самом деле, каждый, знакомый с азами музыкальной грамоты, узнает в лидийской гармонии обычный натуральный мажор (2 тона — полутон, 3 тона — полутон, или на белых клавишах фортепиано до—ре—ми—фа—соль—ля—cи—дo), а в дорийской и фригийской — почти натуральный минор^*.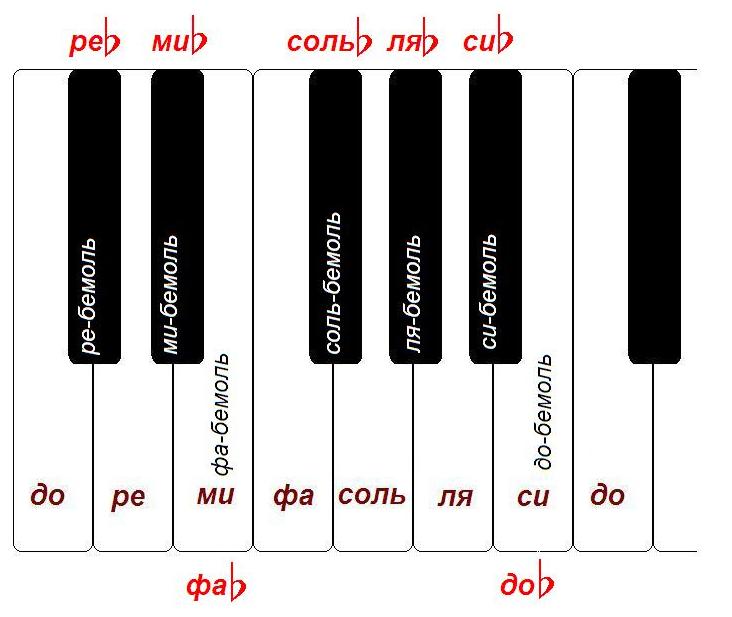

^* («Почти» потому, что в сравнении с натуральным минором (1 — 1/2 — 1 — 1 — 1/2 — 1 — 1) у дорийской гаммы понижена вторая ступень, а у фригийской — повышена шестая.)

Пифагоров строй лидийской гаммы и его математические характеристики

Зная размеры интервалов, образующих, например, лидийскую гармонию и правила действия с ними, легко получить математическое выражение этой гаммы, т. е. построить ее пифагоров строй. Приняв частоту нижнего тона за единицу f₁ = 1, oнаходим первый тетрахорд: f₁ = 1, f₂ = ⁹/₈, f₃ = ⁹/₈*⁹/₈=⁸¹/₆₄, f₄=⁴/₃. Второй тетрахорд получается сдвигом первого на квинту: f₅ = ³/₂f_l = ³/₂, f₆ = ³/₂f₂ = ²⁷/₁₆, f₇ = ³/₂f₃ = ₂₄₃/₁₂₈, f₈ = ³/₂f₄ = 2. Окончательно для интервальных коэффициентов имеем

(6.14)

Это и есть канон Пифагора. По преданию, канон Пифагора впервые нашел практическое применение при настройке лиры легендарного Орфея.

Существовал и другой способ расположения тетрахордов в октаве. Античные теоретики «склеивали» тетрахорды так, что верхний звук одного тетрахорда являлся нижним звуком второго. Тогда дополняющий до октавы тон помещали внизу или наверху такой системы. Если этот тон помещался внизу, то к названию тетрахорда прибавляли приставку гипо-(под-), а если наверху — приставку гипер- (над-). Так получалось еще 6 гармоний, среди которых две пары (гипо-фригийская — гиперлидийская и гиподорийская — гиперфригийская) оказывались совершенно одинаковыми. Отбросив две лишние гаммы, оставалось семь основных ладов. Эти лады имели огромное значение не только в античной музыке, но и через тысячу лет продолжали жить в средневековых ладах, а через две тысячи лет живут в современных натуральных ладах.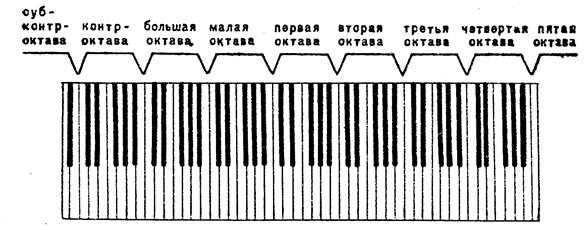 Правда, средневековые монахи перепутали названия своих ладов в сравнении с античными, что часто порождает различные недоразумения. В таблице 1 собраны все основные античные лады, указан порядок следования в них интервалов, считая, что нижний звук расположен слева, а верхний — справа, приведены их древнегреческие и средневековые названия и указано их наклонение. Разделительный тон обведен кружком.

Таблица 1. Порядок следования интервалов тон (1) и полутон (1/2) в античных ладах (снизу вверх), древнегреческие и средневековые названия ладов и их наклонения

Если вспомнить, что сейчас господствуют только два лада — мажор и минор, то остается только удивляться, насколько утонченным было античное музыкальное сознание. Каждый лад греки наполняли определенным этико-эстетическим содержанием, его «этосом», устанавливая ясную связь между музыкальными образами и состояниями души. Музыке приписывали магические и даже врачебные Функции, но особенное значение придавалось музыке как средству воспитания.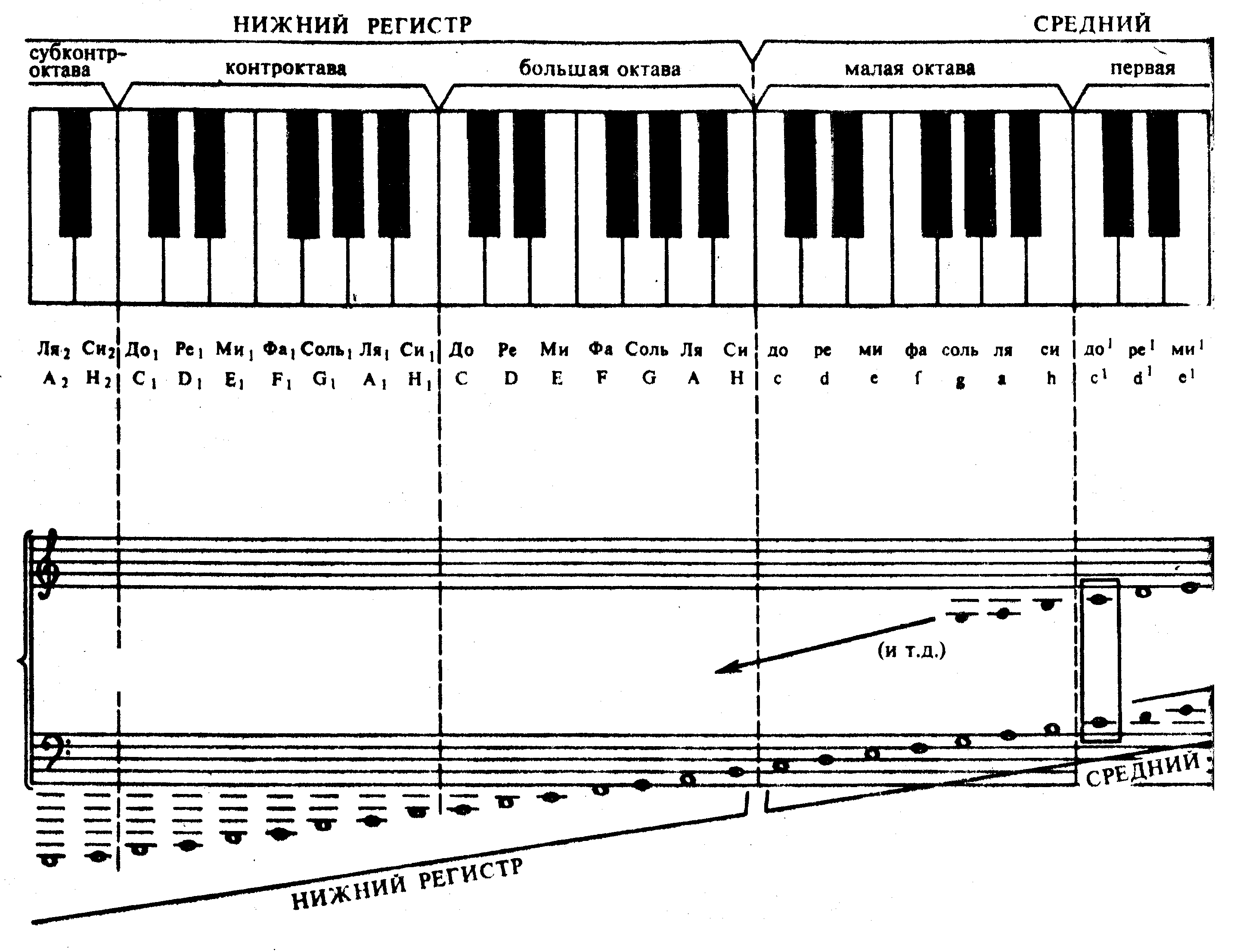

Пляшущая менада. Рельеф

Так, развивая в работе «Государство» теорию идеального государства, Платон исключительное значение придает воспитательной роли музыки. Примечательно, что здесь Платон перекликается с другим выдающимся мыслителем, жившим на другом конце Земли за двести лет до Платона,- древнекитайским философом Конфуцием (ок. 551-479 гг. до н. э.), сказавшим: «Если хотите знать, как страна управляется и какова ее нравственность — прислушайтесь к ее музыке». Платон для мирной жизни оставляет один строгий дорийский лад, считая его подлинно греческим, мужественным, деятельным. Для чрезвычайного события, каковым, например, является война, Платон оставляет фригийский лад как наиболее страстный. Лидийский же лад он называет печальным, погребальным, соответствующим женской, а не мужской психике и потому неуместным в идеальном государстве. Остальные лады как слишком утонченные Платон также отбрасывает, неукоснительно проводя в воспитании принцип строгости и простоты. Безусловно, это не означает, что Платон плохо разбирался в музыке. Напротив, в музыке он находил чистый и возвышенный, «платонический» идеал прекрасного, идеал, лишенный вычурности, размягченности, грубых и разнузданных страстей.

Аристотель в «Политике» судит о ладах, пожалуй, еще строже Платона, признавая только дорийский лад как лад, способный тренировать психику. Тем не менее Аристотель делает подробную «этическую» классификацию ладов, различая лады, которые вызывают психическое равновесие (дорийский), напротив, нарушают его (гипофригийский — «застольный» лад), возбуждают волю и стремление к действию (гиподорийский — лад греческой трагедии), вызывают восторженное и экстатическое состояние (фригийский, гиполидийский).

Прекрасное описание «этоса» греческих ладов мы находим в книге древнеримского писателя Апулея (ок. 124 — ?) «Флориды»: «Жил когда-то флейтист по имени Антигенид. Сладостен был каждый звук в игре этого музыканта, все лады были знакомы ему, и он мог воссоздать для тебя, по твоему выбору, и простоту эолийского лада, и богатство ионийского, и грусть лидийского, и приподнятость фригийского, и воинственность дорийского».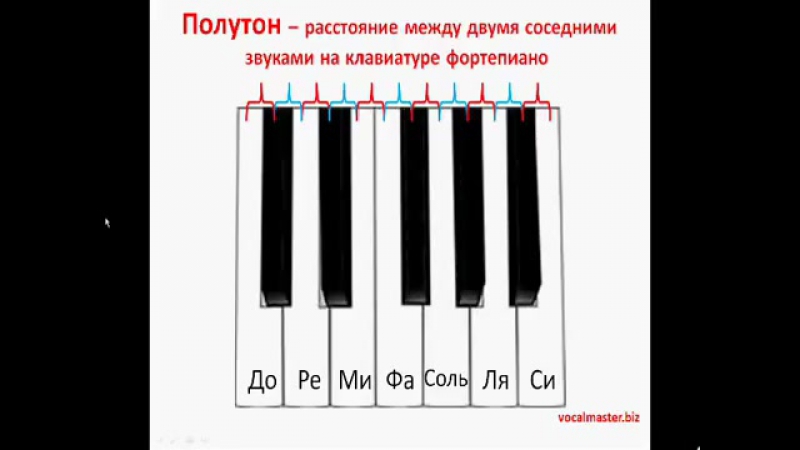

Впрочем, стоп! Нет ли здесь противоречия? Дорийский лад называется воинственным, а ведь это, по существу, наш минор! Поскольку именно дорийский лад считался истинно греческим, то получается, что основной характер греческой музыки печальный, минорный. Для греков же дорийский лад является выражением бодрости, жизнерадостности и даже воинственности. Вот как объясняет это кажущееся противоречие выдающийся современный знаток античности, последний философ русского «серебряного века» профессор А. Ф. Лосев (1893-1988)^*: «Греческое искусство — неизменное жизнеут-верждение. Благородная сдержанность и даже печаль не оставляют грека и тогда, когда он веселится, когда он бодро строит жизнь, когда он воюет и погибает. „Веселые“ же лады так или иначе тяготеют к этому прекрасному, благородному, бодрому, важному и в то же время величественно-печальному ладу — дорийскому. Дорийский лад — это скульптурный стиль греческой музыки… Так задумчива, печальна и благородна вся греческая скульптура».

^* (Судьба Алексея Федоровича Лосева счастлива и трагична. Счастлива, потому что до последнего дня своей 95-летней жизни Лосев сохранил поразительную работоспособность и успел завершить главный труд — восьмитомную «Историю античной эстетики». Трагична, потому что другие восемь томов его сочинений, написанных на полвека ранее (1927 — 1930), были преданы анафеме, а сам автор, будучи незаконно репрессирован, продолжил свои философские изыскания на строительстве Беломорско-Балтийского канала, откуда он писал: «Я закован в цепи, когда в душе бурлят непочатые и неистощимые силы». Одна из этих работ Лосева — «Музыка как предмет логики» — могла бы служить путеводной звездой к этой книге. И все-таки судьба А. Ф. Лосева счастлива, ибо рукописи не горят. Сегодня огромное философское наследие А. Ф. Лосева обретает свое второе рождение. )

Ну а лидийский лад? Ведь это в точности наш мажор, тогда как Апулей называет его грустным, а Платон — погребальным! Что ж, в оценке лидийского лада с Платоном не соглашался уже Аристотель, находя в лидийском ладу наивную детскость и прелесть и относя его к ладам, вызывающим психическое равновесие. С течением времени лидийский лад утратил плачевный характер, и античные теоретики стали чаще говорить о «сладкой лидийской мелодии» или о «разнообразной лидийской мелодии».

Таким образом, мы видим, что вопрос об «этосе» ладов не решается однозначно и во многом определяется традицией применения того или иного лада. И в наше время слушатель, воспитанный, например, на тонкой и своеобразной индийской музыке, вообще не отличит мажора от минора, не говоря уж об их «этосе». Конечно, мажорный лад отличается более светлыми и радостными тонами и тому есть объективные причины, о которых мы расскажем в главе 10. Но реализация этих возможностей зависит от массы других факторов (темп, ритм, мелодический рисунок и т. д.), и поэтому есть много веселых, энергичных произведений в миноре и грустных, задумчивых — в мажоре. Вспомним хотя бы «Патетическую сонату» до минор Бетховена, этот огненно-страстный монолог Героя, зовущего на яростную схватку и даже на смерть. Многие художники подобрали многие эпитеты к этой сонате (хотя, пожалуй, лучший из них — патетическая — принадлежит самому Бетховену), но только грустной — минорной — ее назвать никак нельзя. Напротив, Ноктюрн № 2 соч. 9 ми бемоль мажор Шопена пронизан настроением нежной мечтательности. Это подернутые дымкой грусти воспоминания автора, но отнюдь не веселая — мажорная — пьеса. В заключение попытаемся сказать несколько слов об «этосе интервалов», ибо именно анализу музыкальных интервалов и посвящена настоящая глава. Попытаемся, потому что данный вопрос еще более спорный и неразработанный, чем «этос ладов». И все-таки…

До сих пор мы ничего не говорили о «самом совершенном консонансе» — приме (унисоне) (l₂/l₁ = 1, т. е. две струны издают звук одинаковой высоты), ибо с точки зрения математики этот интервал не представляет интереса. Однако в оркестре этот простейший интервал играет огромную роль, придавая данному звуку объемность и яркость.

Следующий совершенный консонанс — октава. При одновременном звучании октава также дает впечатление объемности звука, а при последовательном — ощущение простора и широты. Прекрасной тому иллюстрацией является «Песня о Родине» композитора И. О. Дунаевского (1900-1955). В ее запеве («От Москвы до самых до окраин…») дважды звучит восходящая октава (l₁/l₂ = 2), рисуя необъятные просторы нашей Родины. Здесь же после двух октав идет восходящая квинта. Квинта (l₁/l₂ = 3/2) также звучит широко, но более рельефно и динамично, чем октава.

Мелодии многих революционных песен и гимнов начинаются интервалом восходящей кварты (l₁/l₂ = 4/3), например «Интернационал», «Гимн Советского Союза», «Марсельеза». Здесь интервал кварты звучит решительно и активно, как призыв к действию.

Особый «этос» у интервала секунды: при одновременном звучании он диссонирует и неприятен, но при последовательном предыдущий звук как бы переливается в последующий, образуя естественное течение мелодии от одного звука к другому. В мелодии интервалы между двумя опорными звуками часто заполняются последовательными секундовыми интервалами. Например, песня «Во поле береза стояла» начинается интервалом квинты, заполненным последовательными секундами, что создает впечатление спокойного и величавого течения мелодии, как величавы и спокойны картины русской природы.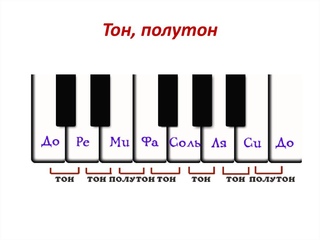

А наиболее неприятным и неблагозвучным является интервал тритон или полуоктава (l₁/l₂ = ). Своей неблагозвучностью этот интервал «подсказал» Архиту «музыкальное доказательство» иррациональности .

Благодарность «Библиотеке по математике» за оцифровку книги.

Полутон. Основы теории музыки

В равномерно-темперированном строе каждая октава делится на 12 равных частей — полутонов. Для этого к семи основным ступеням добавили пять производных ступеней, которые образуются путем повышения или понижения основных ступеней. Повышение основной ступени на полтона обозначается словом диез, а понижение на полтона — словом бемоль. Производные ступени не имеют собственных названий. Их названия образуются из названий основных ступеней и обозначения повышения или понижения, например, до-диез, ре-бемоль. Производным ступеням на клавиатуре фортепиано соответствуют чёрные клавиши (рис.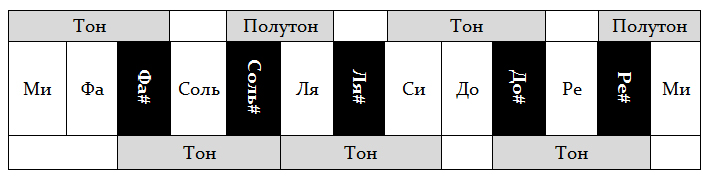

Вершины галочек (гор) – чёрные клавиши, а точки их оснований – белые. Для простоты можно сказать, что это 2 + 3. Есть ещё такой замечательный советский фильм «три плюс два». А у нас наоборот «два плюс три»

Из рисунка видно, что, например, до-диез и ре-бемоль – это одна и та же клавиша. Зачем одну и туже клавишу называть двумя разными названиями? Об этом будет рассказано позже при изучения понятия лада.

Двенадцать полутонов, которые делят октаву, показаны на рис. 2.

Рис. 2. Равномерно-темперированный строй с 12-ю полутонами

Основные ступени и интервалы между ними показаны на рис. 3.

Рис. 3. Основные ступени

На рис. 2 видно, что между ступенями ми и фа, си и до образуется полутон. Если посмотреть на рис. 3, то догадаться о том, что между этими ступенями находится полутон невозможно, потому что ноты располагаются на одинаковом расстоянии друг от друга. Посмотрите теперь на гитару, баян, флейту. Вы можете показать на них основные ступени с такой же лёгкостью, как на клавиатуре фортепиано. Нет! Из этого следует то, что большая часть построений в равномерно-темперированном строе наиболее наглядно демонстрируются с использованием клавиатуры фортепиано. Отсюда следует вывод о том, что, если вы хотите уверенно использовать теорию музыки на практике, то необходимо уверенно знать и помнить построения на клавиатуре фортепиано.

В пространстве расстояние между объектами измеряется в сантиметрах, метрах и других величинах. В музыке расстояния между ступенями измеряется в полутонах. Полутон имеет значение 1/2 (0.5). Два полутона образуют тон, 1/2 + 1/2 = 1 или 2 * 1/2 = 1. Посмотрите на рис. 2. Расстояние между ступенями до и ре равно одному тону, между ми и соль – полтора тона, а между соль и до – два с половиной тона. Красным цветом на этом рисунке показана ломаная линия, каждый отрезок которой можно условно принять за полутон. Для определения расстояния между ступенями нужно посчитать количество отрезков ломаной линии между интересующими клавишами. Между клавишами до и ре два отрезка, значит между ними два полутона или один тон. Между клавиши ми и соль три отрезка или 3 * 1/2 = 1,5 тона и т.д. Данная ломаная линия поможет начинающим музыкантам не запутаться в расчётах. Чёрные клавиши короче, и явно не видно то, что у большинства белых клавиш соседними являются чёрные клавиши, а не белые, как может показаться, если смотреть на широкие части белых клавиш.

Зачем нужно уметь вычислять расстояния между ступенями? Существует несколько подходов к изучению музыки:

воспринимать всё на слух
всё учить и запоминать
понять систему и запомнить схемы различных построений

Первый подход во многом напоминает метод «тыка». Благодаря слуху можно найти гармоничные сочетания звуков и использовать их при игре на музыкальном инструменте. Без знания теории музыки можно даже стать виртуозным исполнителем. Однако отсутствие или пробелы в знании теории часто сильно ограничивает возможности человека в практике..

Второй подход часто используется учащимися, когда они пытаются не понять, а запомнить материал. Результат такого подхода один – теория музыки быстро становится непонятным и ненавистным предметом, так как запомнить всё невозможно.

Третий подход является наиболее эффективным, так как при его использовании требуется запомнить относительно небольшой объем информации, на основе которой можно производить большое количество различных построений. Мы же не старамся запомнить то, как производить математические операции над всеми возможными числами. Это просто невозможно сделать. Достаточно выучить таблицу умножения и запомнить правила действия и выполнений математических операций. Аналогичный подход используется и для выполнений построений в музыке.

Александр Страшко
admin@starport.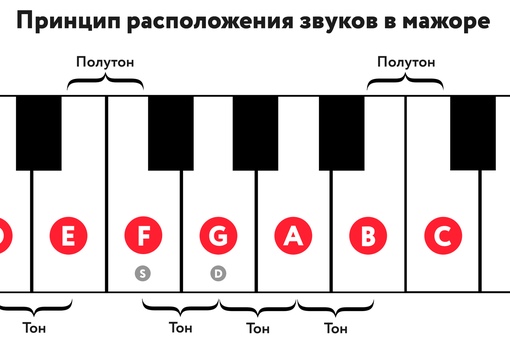 ru
15.06.20

Рубрики

Школа

Дом

В помощь начинающим

Обучающие материалы

Звук

Свет

Общие вопросы

Диатонические и хроматические тоны и полутоны — Мегаобучалка

ГБОУ СПО РО РОСТОВСКИЙ КОЛЛЕДЖ КУЛЬТУРЫ

РАБОЧАЯ ТЕТРАДЬ ПО ПРЕДМЕТУ

«ЭЛЕМЕНТАРНАЯ ТЕОРИЯ МУЗЫКИ»

студента ___ курса _____________________ отделения

_______________

преподаватель: Топчий О. Н.

2015г.

ЗВУК

В окружающей нас природе существует огромное количество самых разнообразных звуков, которые можно разделить на две группы:

1. Музыкальные звуки (с определенной высотой)

2. Шумы (с неопределенной высотой звука – треск, стук, шорох, гром…)

Музыкальные звуки, в отличие от шумовых, обладают рядом отличительных свойств и составляют основу музыки. Шумовые звуки применяются в отдельных музыкальных произведениях для достижения различных эффектов (ударная группа симфонического оркестра).

Свойства музыкального звука:

1. Высота – зависит от частоты колебаний упругого тела или столба воздуха

2. Длительность – зависит от продолжительности колебаний

3. Громкость – зависит от силы колебаний (их амплитуды)

4. Тембр – зависит от качества материала, из которого сделан инструмент (сорт дерева, состав металлического сплава и т.д.), конструкции инструмента, способа звукоизвлечения, среды, в которой распространяется звук и др.

Тембром называется характер звучания или окраска звука. Тембр имеет громадное выразительное значение. Лирические темы обычно поручаются струнным инструментам, воинственные – медным духовым, пасторальные (рисующие картины безмятежной природы) – деревянным духовым инструментам.

В тембровой окраске звука огромную роль играют призвуки (обертоны), которые появляются от вибрации струны. Каждый инструмент или человеческий голос обладает характерным для него тембром. Звук одинаковой высоты, воспроизведенный разными музыкальными инструментами, отличается у каждого инструмента своей окраской. Различие тембров зависит от количество слышимых обертонов и распределения громкости между ними.

МУЗЫКАЛЬНАЯ СИСТЕМА

Музыкальная система — комплекс различных по высоте звуков, образующих звуковой фонд музыки. Расположение звуков музыкальной системы по высоте называется звукорядом, а каждый звук звукоряда – его ступенью.

Основные ступени звукоряда соответствуют белым клавишам фортепиано и имеют самостоятельные названия: до, ре, ми, фа, соль, ля, си.

до

ре

ми

фа

соль

ля

си

до

Эти звуки периодически повторяются, схватывая весь музыкальный звукоряд, который соответствует клавиатуре фортепиано. В ней 88 звуков-клавиш от 16 до 4176 колебаний в секунду (Гц), которые способно различать человеческое ухо. Многие звуки человек не слышит, например, инфразвук (сверхнизкий) во время землетрясения или ультразвук (сверхвысокий), которым пользуются дельфины, летучие мыши, кошки.

Октавы

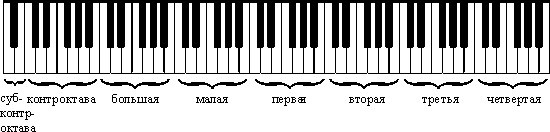
Расстояние между звуками одинаковых ступеней называется октавой. Так же называется и часть звукоряда, включающая все семь основных ступеней.

Началом октавы принято считать звук «до». Весь звукоряд состоит из семи полных и двух неполных (по краям клавиатуры) октав.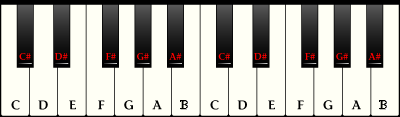 Названия октав (от низких звуков к высоким, или слева направо по клавиатуре): субконтроктава, контроктава, большая октава, малая, первая, вторая, третья, четвертая и пятая октавы.

Камертон

Соотношение абсолютной высоты звуков музыкальной системы называется музыкальным строем. Современный музыкальный строй исходит из 440 колебаний в секунду (Гц) – звука ля первой октавы. Он является международным эталоном, по которому производится настройка всех музыкальных инструментов и определяется высота остальных звуков музыкальной системы. Для воспроизведения этого звука пользуются камертоном – никогда не расстраивающимся инструментом, издающим при ударе только один, первоначально заданный тон с абсолютно точно выверенным числом колебаний в секунду. Он представляет собой цельнолитую металлическую двузубую вилку с рукояткой, на которой внизу выбит звук настройки или свисток.

Тон и полутон

В общепринятой музыкальной системе октава делится на 12 равных частей – полутонов. Такой музыкальный строй называется темперированным строем. Его главным характерным признаком является то, что все полутоны октавы в нем равны. Следовательно, полутон – наименьшее расстояние между звуками музыкальной системы (соответственно и клавишами фортепиано). Например, полутон между звуками: ми – фа, си – до, фа – фа #, ля – ля b.

Расстояние из двух полутонов называется целым тоном. Например, целый тон между звуками: фа – соль, до – ре, ми – фа #, си b – до, ре bb — ре. Между основными ступенями звукоряда пять тонов и два с половиной полутона.

Целые тоны между основными ступенями разделены на полутоны черными клавишами фортепиано – они называются производными ступенями звукоряда, поскольку они образуются от повышения или понижения основных ступеней звукоряда. Например, черная клавиша между звуками соль и ля будет называться соль-диез или ля-бемоль, черная клавиша между звуками ре и ми – ре-диез или ми-бемоль.

Знаки альтерации

Повышение и понижение основных ступеней называется альтерацией. Знаки, указывающие на повышение или понижение данного звука ставятся перед нотой, называются знаками альтерации. Их всего пять:

1. Диез — # — повышает звук на полтона;

2. Бемоль — b — понижает звук на полтона;

3. Дубль диез — х — повышает звук на целый тон;

4. Дубль бемоль — bb — понижает звук на целый тон;

5. Бекар — — отменяет все предыдущие знаки альтерации, т.е. восстанавливает звучание основной ступени (белой клавиши).

Например, си # — это находящаяся на полтона выше клавиши си — клавиша до; фа bb – это черная клавиша на целый тон ниже клавиши фа – ми b и т.д.

Знаки альтерации пишутся слева перед нотой на той же высоте, что и сама нота:

Энгармонизм звуков

Тождество (равенство) звуков по высоте при их различном обозначении и названии называется энгармонизмом звуков. Таким образом, энгармонически равные звуки, это звуки, которые одинаково звучат, но записываются на нотном стане и называются по-разному. Одна и та же ступень звукоряда (клавиша, звук) может быть производной от соседних основных ступеней звукоряда и иметь несколько названий, например: фа # = соль b = ми x; ля # = си b = до bb. Почти все звуки имеют по два энгармонически равных звука, исключением являются звуки соль # = ля b.

Диатонические и хроматические тоны и полутоны

Диатонический полутон — образуется между соседними звуками с различными названиями:

до – ре b; ре – ми b; ми — фа.

Диатонический тон — образуется между соседними звуками с различными названиями:

до – ре; ре — ми; до # – ре #; соль bb – ля b.

Хроматический полутон – образуется между различными звуками с одинаковыми названиями и разными знаками: до – до #; ре – ре b; фа – фа #.

Хроматический тон – образуется между различными звуками с одинаковыми названиями и разными знаками, здесь используются двойные повышения или понижения звуков: ми b – ми #; соль – соль x; ре – ре bb.

Также хроматические тона образуются между звуками, расположенными через одну ступень:

до # – ми b; соль x – си; ля # – до.

Образец построения на нотном стане в скрипичном ключе

диатонических и хроматических тонов и полутонов от ноты соль ↑ и ↓

д.1т.↑ д.1т.↓ д.1/2т.↑ д.1/2т.↓ х.1т.↑ х.1т.↓ х.1/2т.↑ х.1/2т.↓

Математика музыкального строя — основы.: rainy_sunny — LiveJournal

Сегодня я расскажу о том, что такое чистые музыкальные интервалы, почему невозможна абсолютная их чистота и на какие компромиссы музыкантам приходилось идти из-за этого. [Cпойлер]И до сих пор приходится! Кто верит во вселенскую гармонию, лучше не читайте, тлен гарантирован )

Для понимания потребуется базовое знакомство с нотами и интервалами. В поcте много цифр, но вам считать ничего не придётся, достаточно понимать, что происходит.

Любую музыкальную ноту можно выразить цифрой — частотой колебания в герцах. А интервал между двумя нотами — соотношением двух частот. Например, нота на октаву выше данной всегда имеет частоту в 2 раза больше. Поэтому октава — это соотношение 2:1 или множитель 2.

Когда я буду говорить «интервал между двумя нотами равен 5:4», я буду иметь в виду, что частота более высокой ноты в 5:4 (или 1,25) раз выше, чем частота нижней ноты.

Имеет значение именно соотношение («во сколько раз выше»), а не разница частот («на сколько герц больше»). Например, между 100 и 200 Гц такой же интервал, как между 300 и 600 Гц, — октава (2:1).

Чтобы сложить два интервала, мы перемножаем их соотношения. «На октаву выше» значит «в 2 раза выше по частоте», поэтому на две октавы выше — в 4 раза выше, на три октавы — в 8 раз выше, и так далее.

—

Интервалы, которые выражаются простым соотношением (то есть дробью, у которой и числитель и знаменатель — небольшие целые числа), называются чистыми интервалами.

Основные чистые интервалы:

2:1 — октава
3:2 — квинта
4:3 — кварта
5:4 — большая терция
6:5 — малая терция.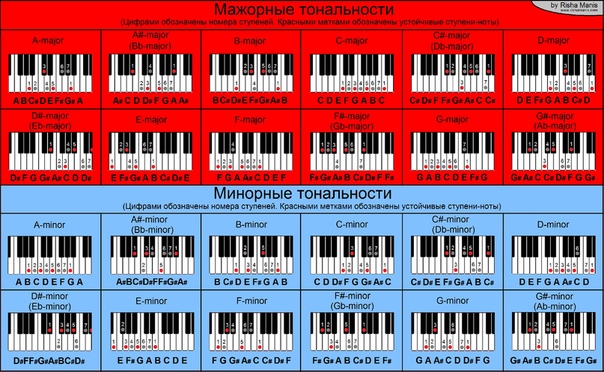

Если интервал между нотами чистый, то эти ноты очень хорошо «сливаются» вместе. Музыканты издавна стремились к таким созвучиям.

Этому есть физическое объяснение. Любая нота состоит из гармоник — колебаний, кратных друг другу по частоте. Если соотношение между нотами простое, то часть гармоник у этих двух нот будут совпадать и полностью сливаться друг с другом.
Например, возьмём ноту с частотой 300 Гц и ноту на октаву выше (300*2=600 Гц) и выделим у них общие гармоники:
300, 600, 900, 1200, 1500, 1800, 2100, 2400,…
600, 1200, 1800, 2400,…
Теперь возьмём ноту с частотой 300 Гц и ноту на чистую квинту выше:
300, 600, 900, 1200, 1500, 1800, 2100, 2400, 2700,…
450, 900, 1350, 1800, 2250, 2700,…
На спектрограмме эти совпадающие гармоники хорошо видно (для сравнения я взял негармоничную пару — 300 и 520 Гц):
Кроме того, гармоники любой отдельной ноты содержат в себе чистые интервалы. Например, третья гармоника любой ноты в ³/₂ раза выше по частоте, чем вторая гармоника этой же ноты. Так что чистые интервалы происходят из базовых физических свойств звука.

Самый простой из чистых интервалов — это октава: ²/₁. Она обладает важным свойством — если взять две ноты с разницей в октаву, то ВСЕ гармоники верхней ноты будут совпадать с чётными гармониками нижней (пример — в предыдущей сноске). Такие ноты максимально «сливаются» вместе и воспринимаются как одна. Поэтому они и назваются одинаково (До и следующая До). Сравните одну и ту же мелодию сыгранную большими терциями, квинтами и октавами, и всё станет понятно:

В посте я буду говорить про разные квинты, терции, и т.д. Но величина октавы будет всегда одна — ²/₁.

—

Когда одновременно звучат колебания близкой частоты (например, 200 и 202 Гц), между ними возникают так называемые биения — звук «плавает» или «дрожит» оттого что колебания медленно сдвигаются по фазе относительно друг друга.

Поэтому если интервал между двумя нотами не совсем чистый, но близок к чистому, то биения возникнут между некоторыми гармониками этих нот. Для примера — квинта, которая немного больше чистой:

200, 400, 600, 800, 1000, 1200,…
302, 604, 906, 1208,…

Чем сильнее интервал отклоняется от чистого, тем чаще биения и тем «нестабильнее» он звучит.

—

Ещё интервалы измеряют в центах. Цент — это очень маленький интервал: 1,0005777895… (корень 1200-й степени из 2х). Это одна сотая современного полутона. Он понадобится, чтобы оценить мелкие различия между интервалами.

Вот пример, который поможет ощутить масштабы цента:

—

Последнее примечание: из интервалов я буду говорить только о секундах, терциях и квинтах, потому что интервалы, которые являются обращениями друг друга, ведут себя совершенно аналогично. Например, если в каком-то строю терция C-E получается немного больше, чем чистая терция, то секста E-C — ровно настолько же меньше. И так далее: с квартами дела обстоят так же, как с квинтами, а с септимами — так же, как с секундами.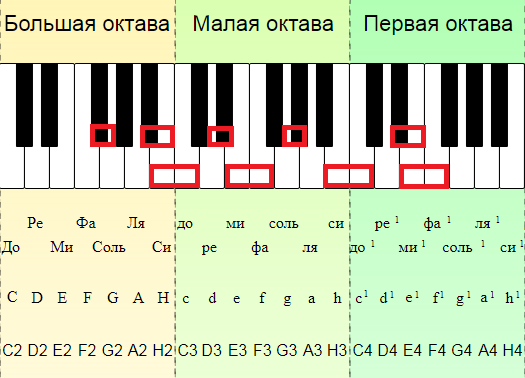

Невозможность совершенства

Если посмотреть на таблицу частот разных нот, видно, что чистых интервалов там практически нет. Между нотами A3 и A4 одна октава разницы (220 Гц * 2=440 Гц). А, скажем, нота E4, которая на квинту выше A3, имеет частоту не 330 Гц (220 Гц * ³/₂), а немного меньше.

Всё дело в том, что с чистыми интервалами есть проблема: они в очень многих случаях НЕ СХОДЯТСЯ друг с другом.

Например, возьмём ноту До (C), прибавим к ней две октавы и одну большую терцию. То есть два раза удвоим частоту, а потом умножим на ⁵/₄.

Получилась нота Ми (E) через две октавы.

Теперь отложим от той же самой До четыре квинты вверх. То есть, четыре раза умножим частоту на ³/₂. Получилась та же самая нота Ми.

Или не та же самая?

В первом случае частота Ми ровно в 5 раз выше, чем До: 2*2*⁵/₄=5.
А во втором — в ⁸¹/₁₆ раз выше (³/₂*³/₂*³/₂*³/₂=⁸¹/₁₆).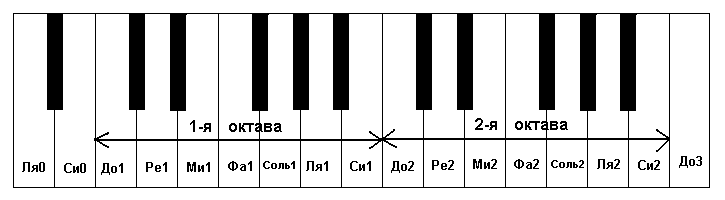 То есть в 5,0625 раз выше.

Получается, что две октавы плюс чистая большая терция не равны четырём чистым квинтам, из-за чего невозможно определить правильную частоту Ми относительно До. И таких расхождений много¹.

—

Ещё пример: простая мелодия, которая начинается с До и движется так: квинта вверх, кварта вниз, квинта вверх, кварта вниз, большая терция вниз — вернулись в ту же До.

НО! Если все эти интервалы чистые, то До в конце мелодии получается выше, чем До, которая была в начале! А именно — в ⁸¹/₈₀ раз выше: ³/₂*³/₄*³/₂*³/₄*⁴/₅=⁸¹/₈₀, и не равно 1. Повторим эту мелодию ещё раз, начав с новой До — и До станет выше почти на полтона. Вот, послушайте (в конце я для наглядности повторяю изначальную До):

Чтобы этого сдвига не происходило, придётся, например, пожертвовать чистотой большой терции и немного её увеличить.

А вот здесь, с 4:15, очень наглядно показывают этот сдвиг на примере аккордов.

—

Из всего этого ясно, что для построения нотной системы неизбежно придётся идти на какие-то компромиссы. Например, чтобы в предпоследнем примере получались не разные Ми, а одинаковые, придётся либо сделать квинту немного меньше, чем ³/₂, либо сделать большую терцию немного больше, чем ⁵/₄, либо сделать понемножку и то и другое. Именно это и происходило, когда музыканты пытались найти компромисс. В одни исторические периоды предпочтение отдавали чистой квинте, в другие — чистой терции.

Вот теперь можно рассказать про несколько исторических строёв.

Пифагоров строй

Начнём с того, что строй этот создал не Пифагор. Насколько я понимаю, строй оформился в период поздней античности, а название получил потому что был основан на идеях пифагорейцев, которым очень нравилась идея гармонии чисел.

Пифагоров строй — это звукоряд, построенный на двух самых простых соотношениях — октаве и чистой квинте.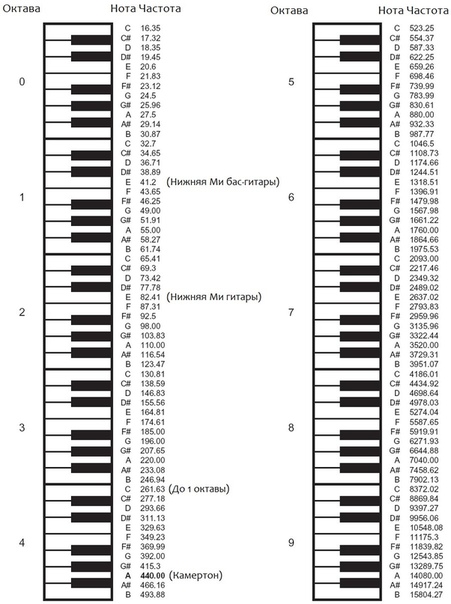 Берём основную ноту, откладываем от неё вверх и вниз цепочку квинт и таким образом находим частоты для всех остальных нот.

Начнём, например, с До. Прибавим к ней чистую квинту и получим Соль, частота которой в ³/₂ раза выше До. Прибавим к этой Соль чистую квинту — получим Ре, частота которой в ³/₂ выше, чем у Соль, и в ⁹/₄ раз выше, чем у исходной До (³/₂*³/₂). Дальше — Ля, с частотой в ²⁷/₈ выше исходной До, и так далее.

В обратную сторону от До тоже можно откладывать квинты. Получится Фа, с множителем ²/₃, Си-бемоль с множителем ⁴/₉, и так далее.

На верхней клавиатуре изображены несколько первых шагов процесса:

На нижней клавиатуре полученные ноты собраны в одну октаву с До. Например, Ре (⁹/₄), которая получилась из двух квинт, мы понизили на октаву (=поделили на 2), и получилась Ре, которая на тон выше исходной До: ⁹/₈.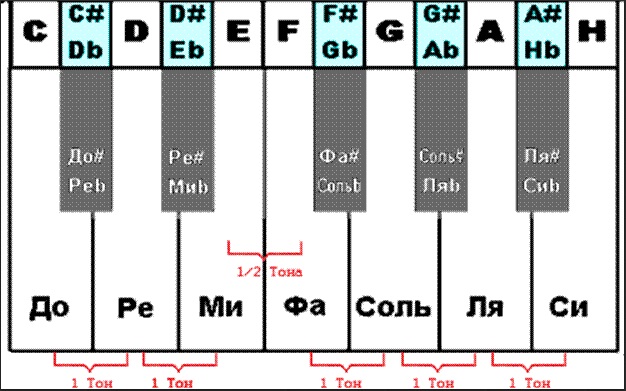 Ля тоже понизим на октаву — получится ²⁷/₁₆. Ми понизим на две октавы, Фа повысим на октаву, и так далее.

Если начать с Ре и отложить от неё по три квинты в обе стороны, получится 7 нот (F-C-G-D-A-E-B), составляющих До-мажор. Переместим их в одну октаву и получим такие соотношения:

Нота	C		D		E		F		G		A		B		C
Соотношение с первой С	¹/₁		⁹/₈		⁸¹/₆₄		⁴/₃		³/₂		²⁷/₁₆		²⁴³/₁₂₈		²/₁
Соотношение между соседними нотами		⁹/₈		⁹/₈		²⁵⁶/₂₄₃		⁹/₈		⁹/₈		⁹/₈		²⁵⁶/₂₄₃

Если продолжить процесс дальше и отложить от Ре по шесть квинт в обе стороны, то получится такой ряд нот:

Нота	Соотношение с D
Ab	¹⁰²⁴/₇₂₉
Eb	²⁵⁶/₂₄₃
Bb	¹²⁸/₈₁
F	³²/₂₇
C	¹⁶/₉
G	⁴/₃
D	1
A	³/₂
E	⁹/₈
B	²⁷/₁₆
F#	⁸¹/₆₄
C#	²⁴³/₁₂₈
G#	⁷²⁹/₅₁₂

Получилось 13 нот, причём ноты Ab и G# получились разными: соотношение ¹⁰²⁴/₇₂₉ близко, но не равно ⁷²⁹/₅₁₂ (1,40466. ..<1,423828…).

Так проявляется ещё одна проблема чистых интервалов: 7 чистых октав не равны 12 чистым квинтам. 7 октав — это ¹²⁸/₁. А 12 чистых квинт — это ⁵³¹⁴⁴¹/₄₀₉₆, то есть 129,746…

Наша пифагорова G# ровно на 12 квинт выше, чем Ab, поэтому когда мы их приводим в одну октаву, получается не одна нота а две близких.

Разница между ними называется Пифагоровой коммой. Это небольшой интервал, примерно 23,46 цента, то есть чуть меньше четверти нынешнего полутона.

Нам нужно 12 нот, поэтому отбросим Ab и оставим G#.

Можно, конечно, ввести в наш строй обе ноты — Ab и G#, но это во-первых, непрактично на многих инструментах², а во вторых, не решит проблему полностью. Например, мы не сможем сыграть чистую квинту от G#, потому что ноты D# у нас нет, а если играть вместо неё Eb, квинта будет не чистая, а опять же уменьшенная на пифагорову комму.
А если продолжать добавлять ноты, то придётся строить инструмент с такой, например, клавиатурой:
Если играть в До-мажоре или каких-то близких тональностях, достаточно будет среднего ряда клавиш. А вот чистую квинту от G# придётся играть так: G# на средней клавиатуре и D# на верхней. И вообще: в тональностях, в которых много «чёрных клавиш» часть нот придётся брать на одной клавиатуре, часть на другой.

И теперь одна квинта из двенадцати не чистая, а на пифагорову комму меньше чистой.

Эту квинту назвали «волчьей» квинтой. «Биения», которые возникают в «волчьей» квинте, напомнили кому-то волчий вой, отсюда название.

Одна плохая квинта из двенадцати — ещё не беда (в конце концов, мы можем избегать игры в тональностях, в которых эта квинта встречается — а это половина всех тональностей). Беда в том, что ВСЕ интервалы в пифагоровом строе получены из квинт, а значит — любой интервал, в котором участвует волчья квинта, уменьшается или увеличивается на пифагорову комму. Например, большая секунда получается из двух квинт, поэтому из 12-ти больших секунд 10 штук получаются чистыми, а две (C#-D# и G#-A#) — уменьшены на пифагорову комму. Септимы D#-C# и A#-G#, соответственно, увеличены на пифагорову комму.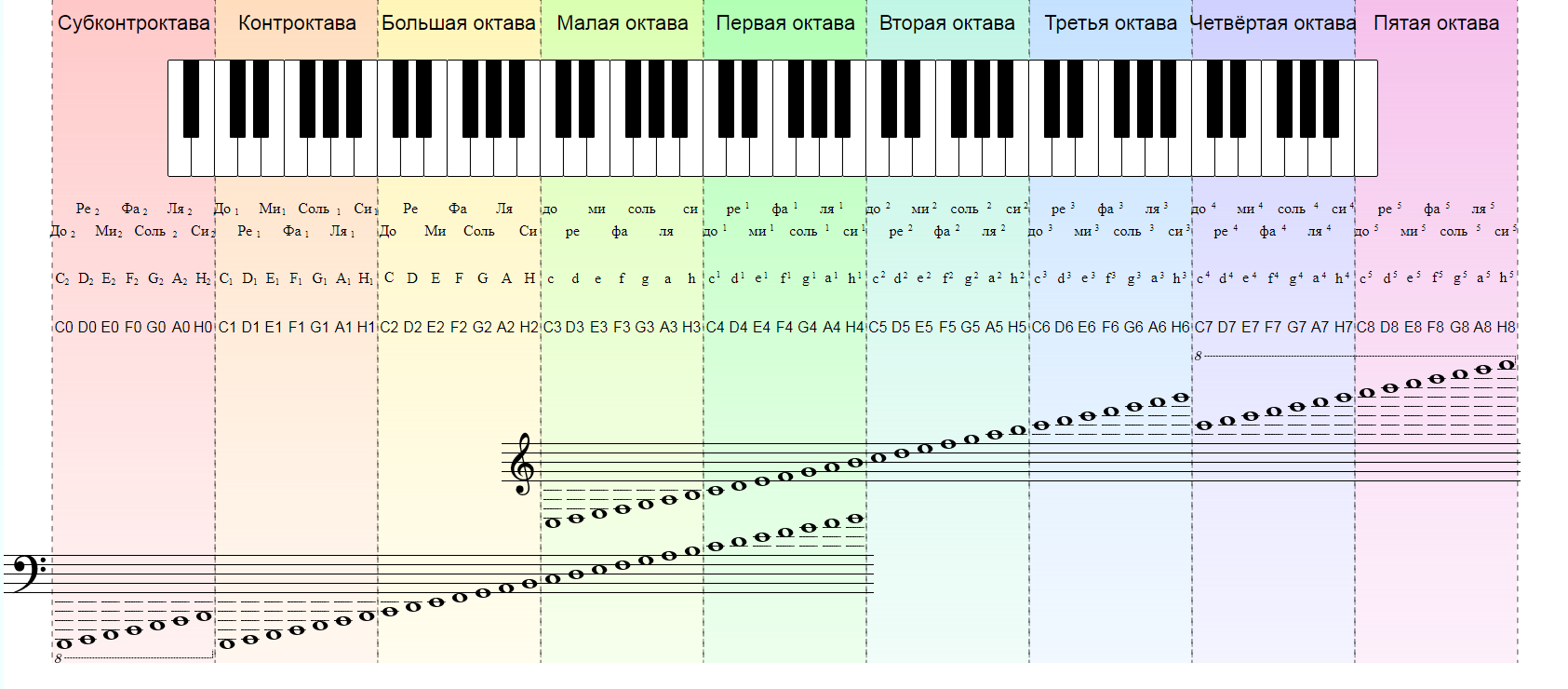 С другими интервалами такая же беда, только там изменённых интервалов получится ещё больше. Например, большая терция строится из четырёх квинт, поэтому из 12-ти больших терций 8 будут «обычного» размера, а 4 штуки — на пифагорову комму меньше.

—

Ещё одна проблема с пифагоровым строем — терции в нём серьёзно отличаются от чистых. Пифагорова большая терция — это «четыре чистых квинты минус две октавы». То есть, ³/₂*³/₂*³/₂*³/₂:4. Получается ⁸¹/₆₄, а это заметно больше, чем чистая большая терция ⁵/₄ (1,265625 > 1,25).

То же самое с малой терцией. Пифагорова малая терция — это «две октавы минус три чистые квинты», или ²/₃*²/₃*²/₃*4. Получается³²/₂₇, и это заметно меньше, чем чистая малая терция ⁶/₅ (1,185185… < 1,2).

	Малая терция	Большая терция
Чистая	6:5 315. 64 центов	5:4 386.31 центов
Пифагорова	32:27 294.13 цента	81:64 408 центов
Разница	на 21.51 цент меньше	на 21.51 цент больше

Интервал, на который они отличаются, называется синтонической коммой. Её размер — 81:80 или 21.51… цент (примерно одна пятая нынешнего полутона). С этой коммой мы уже встречались в начале текста — именно настолько повышалась До в мелодии, состоящей из чистых интервалов — и встретимся ещё.

Пифагоровы терции звучат для нас вполне норм, потому что они близки к нашим нынешним терциям (которые тоже совсем нечистые, но мы привыкли). Но средневековым музыкантам это было не норм, поэтому терция в то время не использовалась как основа гармонии.

Пифагоров строй использовали примерно до 15 века. Потом его стали модифицировать, чтобы как-то поправить ситуацию с терциями.

Среднетоновый строй на 1/4 коммы

В 16 веке появился новый строй — среднетоновый на 1/4 коммы. Он устроен так же как пифагоров, только размер всех квинт уменьшен ровно настолько, чтобы большая терция стала чистой.

Вот как это работает. Пифагорова большая терция создаётся с помощью четырёх квинт: строим цепочку квинт С-G-D-A-E, понижаем полученную E на две октавы, и получаем терцию C-E, которая, как я показывал выше, не чистая, а на синтоническую комму больше чистой. Если уменьшить каждую квинту на 1/4 синтонической коммы, то терция, полученная из четырёх квинт, уменьшится на одну синтоническую комму, а значит, станет равна чистой терции. При этом квинта перестала быть чистой, но и не сильно пострадала — уменьшилась всего на 5 центов.

Все остальные интервалы тоже получены из квинты, поэтому их размеры тоже изменились. Одним это пошло на пользу, другим — нет. Например, малая терция стала почти чистой (всего на 6 центов меньше чистой), большая секунда стала на 11 центов меньше чистой, и так далее. Но в целом интервалы получились приемлемые.

К сожалению, проблемы с «волчьей квинтой» и прочими волчьими интервалами здесь ещё хуже, чем в пифагоровом строе.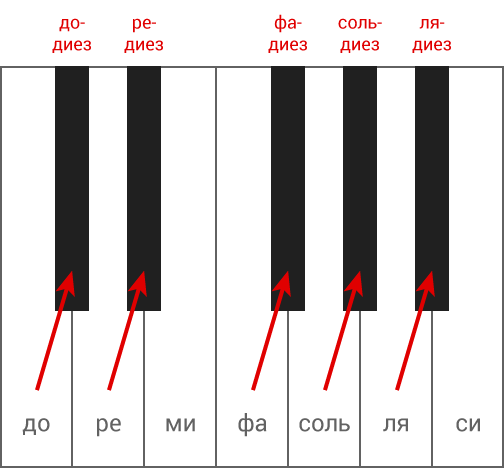 В пифагоровом строе «волчья квинта» на пифагорову комму меньше чистой, а в среднетоновом — на полторы пифагоровы коммы больше. Поэтому одна квинта из двенадцати у нас получается безобразно, на 35 центов, увеличенной. Две большие секунды из двенадцати получаются безобразно увеличенными (на 30 центов больше чистой). 9 из 12-ти малых терций почти чистые, зато остальные три — на 47(!!) центов уменьшены. 8 из 12-ти больших терций совершенно чистые, зато остальные на 41(!) цент увеличены.

В итоге, при игре в тональностях, недалеко отходящих от основной ноты, мы получаем совершенно чистые большие терции и приемлемо чистые остальные интервалы. А вот в каком-нибудь Фа-диез мажоре будет много фальшивящих интервалов.

Одна и та же последовательность аккордов в разных тональностях. Начинаем с базового До мажора и сдвигаемся каждый раз на тон выше. Где-то в середине — там, где аккорды максимально далеки от базовой тональности — можно услышать некую фальшь.

Среднетоновый строй на 1/4 коммы был основным строем в европейской музыке до начала 18-го века, а на многих органах — до середины 19-го века.

Натуральный строй

Другая идея, которая возникла в конце 16 века — построить такой звукоряд, чтобы интервалы были максимально чистыми хотя бы в пределах одной тональности.

Возьмём ноту F и прибавим к ней чистую большую терцию, получив ноту A. К этой A прибавим чистую малую терцию и получим C. Продолжим чередовать большие и малые терции пока не получится 7 нот:

Нота	F		A		C		E		G		B		D
Соотношение		5:4		6:5		5:4		6:5		5:4		6:5

Чистая большая терция и чистая малая терция дают в сумме чистую квинту (⁵/₄*⁶/₅=³/₂; хоть где-то эти чистые интервалы сходятся!), поэтому квинты F-C, A-E, C-G, E-B и G-D здесь получились чистые.

Соберём эти ноты в одну октаву и получим звукоряд До-мажор — CDEFGABC, в котором почти все интервалы чистые. Чистыми получились все большие терции (CE, FA и GB) и три из четырёх малых терций (E-G, A-C и B-D). Однако, полного совершенства не получилось даже здесь: квинта D-A и малая терция D-F на пифагорову комму меньше, чем чистые.

Кроме того, получились две разных больших секунды. Одна — C-D, F-G и A-B — такая же как в пифагоровом строе (9:8 или 204 цента). Вторая — D-E и G-A — на пифагорову комму меньше (10:9 или 182 цента). Малые секунды E-F и B-C одинаковые — 15:16 (112 центов).

Итак, у нас есть 7 «белых» нот, интервалы между которыми чисты настолько, насколько это возможно. Добавим к ним 5 оставшихся «чёрных» нот (например, вычтем квинту из F и получим Bb, и так далее).

Получился строй, в котором интервалы в «исходной» тональности (До-мажор) и близких к ней тональностях — в основном чистые. Но если фальши убавилось в одном месте, её должно прибавиться где-то ещё, поэтому интервалы в далёких от До-Мажора тональностях будут сильно фальшивить.

Сейчас в чистом строю играют только музыканты, аутентично исполняющие древнюю музыку. А с другой стороны, инструменты, у которых высота нот не фиксированная (вокал, безладовые струнные, часть духовых), на практике часто склоняются к чистым интервалам. Например, певцы, поющие терцию, могут подстраиваться друг под друга так, чтобы исчезли «биения».

Все терции и квинты в натуральном До мажоре.

«Хорошо темперированные» строи

В конце 17-начале 18 века появились строи, разработанные так, чтобы можно было играть во всех или почти всех тональностях с минимальной «лажей» в интервалах. Идея была в том, чтобы понижать не все квинты, как в среднетоновом строе, а выборочно понижать часть из них.

Этих строёв было множество. Например, в одной из темпераций Веркмейстера пять квинт (C-G, D-A, E-B, F#-C#, and Bb-F) уменьшены на 1/3 коммы, две квинты (G#-D# и Eb-Bb) увеличены на 1/3 коммы, а остальные квинты — чистые.

В «хорошо темперированных» строях одни интервалы получаются чистыми, другие — почти чистыми, и лишь некоторые отклоняются сильно. В итоге стало возможно играть во всех тональностях без сильной фальши. Тональности получились разными — в одних было больше отклонений от чистых интервалов, чем в других, и распределение этих отклонений получалось разное. Если в нынешнем, равномерно темперированном строе перенести музыку в другую тональность, то она прозвучит точно так же (в том смысле, что соотношения между всеми нотами останутся такими же). А в «хорошо темперированном» строе от этого изменится «оттенок» музыки, потому что интервалы будут немного другими.

Здесь нельзя не упомянуть «Хорошо темперированный клавир» — сборник произведений Баха, вышедший в 1722 году. Он состоит из произведений во всех 24-х тональностях (12 мажорных и 12 минорных). Название, скорее всего, отсылает к «хорошо темперированным» строям, тем более что и состав сборника как бы говорит: наконец-то появился строй, в котором можно играть во всех тональностях!

Бах был недоволен общепринятым тогда среднетоновым строем и настраивал свои инструменты как-то по своему. Неизвестно, какую именно темперацию он использовал. Некоторые музыковеды даже полагают, что строй Баха каким-то образом зашифрован в тринадцати петлях, нарисованных им на заглавии сборника:

Равномерно темперированный строй

Идея разбить октаву на 12 равных частей высказывалась с древних времён. Это решает проблему с несходящимся квинтовым кругом, делает все интервалы одинаковыми, а все тональности равноправными. Однако на практике её применять не спешили. Во первых, терции в этом строе почти такие же нечистые, как и в пифагоровом. Во-вторых, для расчётов соотношений между нотами нужна продвинутая математика — ведь всё основано на корне 12-й степени из двух. В-третьих, в эпоху «хорошо темперированных строёв» композиторам очень нравилось то, что у разных тональностей разный «оттенок» и характер.

В течение 19 века многие композиторы (например, Бетховен) начали широко применять в музыке модуляции в далёкие тональности, и идея о равноправности тональностей становилась всё более привлекательной.

Итак, берём октаву (²/₁) и разбиваем её на 12 равных интервалов — полутонов, из которых будем составлять все остальные интервалы (большая терция — это 4 полутона, чистая квинта — 7 полутонов, и так далее). Каждый полутон равняется корню 12-й степени из двух (2^¹/₁₂) — примерно 1.059463. Теперь между двумя соседними нотами ВСЕГДА интервал в 100 центов. Все терции одинаковы по размеру, все квинты одинаковые, и так далее.

В этом строю нет ни одного чистого интервала кроме октавы — все остальные определяются не то чтобы непростыми дробями (как в пифагоровом строе), а вообще иррациональными отношениями. Очень близки к чистым оказались квинта (выше чистой всего на 2 цента), и большая секунда (ниже чистой всего на 4 цента). А вот терциям не повезло. Малая терция получилась на 16 центов меньше чистой, а большая — на 14 центов больше. Это серьёзная разница, приводящая к заметным биениям:

Тем не менее к 20 веку практически все музыканты перешли на этот строй (а лютни и гитары на нём всегда и были). Равноправие тональностей и полное отсутствие «волчьих» интервалов оказалось важнее, чем нечистые терции.

В следующей части поста — ещё аудиопримеры и таблицы с интервалами.

—

¹ — Например:
Три чистые большие терции не равны октаве, а меньше: ⁵/₄*⁵/₄*⁵/₄=1,953125.
Четыре чистые малые терции не равны октаве, а больше: ⁶/₅*⁶/₅*⁶/₅*⁶/₅=2,0736
Шесть чистых тонов не равны октаве, а больше: ⁹/₈*⁹/₈*⁹/₈*⁹/₈*⁹/₈*⁹/₈=2,027286529541015625.

² — тем не менее были попытки решить проблему хотя бы частично и существовали инструменты, на которых одна, две или три из чёрных клавиш в каждой октаве раздвоены — например, Ля-бемоль и Соль-диез.

Например, вот этот клавесин, с 14 клавишами на октаву:

Или этот, с 19-ю клавишами на октаву:

Почему 12 нот на октаву?

Почему к октаве 12 нот?

Любой в меру любопытный человек в какой-то момент спросят себя, почему в западной музыке октава, разделенная на 12 полутонов. С математической точки зрения мы можем легко объяснить, почему 12 хорошо работает.

Греки понимали, что звуки, имеющие частоту рациональная пропорция воспринимаются как гармония.Например, удвоение частоты дает октаву. Утроение частоты дает идеальную пятую часть на одну октаву. выше. Они не знать это с точки зрения частот, но с точки зрения длины вибрирующие струны. Пифагор, экспериментировавший с монохордом, заметил, что деление вибрирующей струны на рациональные пропорции издает согласные звуки. Это переводится в частоты, когда вы знайте, что основная частота струны обратно пропорциональна к его длине, и что его другие частоты просто целые числа, кратные фундаментального.(на самом деле понятие созвучия сложнее чем рациональность — см., например, эта увлекательная статья ).

Во-первых, мы должны изучить, какие соотношения «предназначены» для существуют в западном масштабе. Известность главного триада в западной музыке отражает Греческие открытия, упомянутые выше. Начиная с примечания C как основной, мы получаем мажорное трезвучие от 3-го и 5-й обертон с понижением на одну и две октавы соответственно, получая соотношения 3/2 (G: C) и 5/4 (E: C) соответственно.Две другие характерные черты западной музыки: каденция V I и трезвучия I, IV, V. Оба отражают важность отношения 3/2, с дальнейшим учетом IV учитывать величина, обратная 3/2, а именно 2/3 или 4/3. В музыкальном плане обратное соотношение соответствует понижению, а не росту. В то время как 3/2 соответствует повышению на одну пятую, 2/3 соответствует на пятую, и 4/3 соответствует понижению на пятую и более высокую октаву.Вместе 3/2 и 4/3 делят октаву, так что 3/2, а затем 4/3 дает октаву.

Триады IV и V дают нам четыре новых ноты, B и D G, B, D и F и A из F, A, C. Их отношения относительно C равны 15/8 для B, 9/8 для D, 4/3 для F и 5/3 для A. ноты, образованные из трезвучий I, IV и V мажор, производят до мажор шкала: C D E F G A B C. каждый из этих интервалов дает все интервалы, которые до подъема сочинял западную музыку хроматизма.

             1/1 унисон C
             2/1 октава C

             3/2 идеальной пятой G
             4/3 четвертой Ж
 
             5/4 мажорная треть E
             8/5 минор 6 Ab

             6/5 минор 3-й Eb
             5/3 мажор 6 A

             9/8 мажор 2 D
             16/9 минор 7-й Bb

             15/8 мажор 7 Б
             16/15 минор 2-й C #

Хотя этот список интервалов включает несколько самых простых интервалов и их обратные: унисон, идеальный 5-й, мажорный 3-й основной 6-й = 3-й выше 4-го (или также 4-й выше 3-го), майор 2-й = 5-й над 5-м, и основной 7-й = 3-й выше 5-го (или также 5-й выше 3-го), некоторые очевидные отсутствуют (например, 7/4, 25/16 = третья выше третьей или 9/5 = пятая часть выше несовершеннолетнего 3-го).

Тритон (например, от C до F #) также исключено из этого списка, интервал что не повлияло на эволюцию западного масштаба, поскольку он не использовался в западной музыке до двенадцати нот хроматизма прочно утвердился. Фактически, тритон относится к двум различным возможным интервалам:

             7/5 тритона
             10/7 также называют тритоном.

Идея двенадцати состоит в том, чтобы собрать коллекцию заметок. используя только одно соотношение.Преимущество в этом в том, что он обеспечивает единообразие, которое делает возможно переключение между клавишами. Без компромиссов большинство клавиш было бы непригодным, так как большинство основных интервалов не будет записан в разных ключах (см. таблицу на конец этого очерка).

К сожалению, ни одно соотношение не будет делать трюк точно. Однако соотношение 3/2 бывает работают достаточно хорошо, используя 12 шаги. Если в качестве основы для шкалы используется 3/2, ни одно из указанных выше соотношений помимо унисона, квинта и мажорная 2-я точно захватываются.12 = 1,0136 (после деления на 128) мы вернулись близко к тому месту, откуда начали. (эти 12 частот соответствуют кругу пятых. Начиная с C, получаем G D A E B F # C # Ab Eb Bb F и обратно в C).

Хроматическая гамма отражает этот факт. В 18 и 19 веков хроматическая гамма была настроена с использованием идеи из 3/2. В самом элегантном из них Настройка Томаса Янга, несколько пятых были установлены точно на 3/2, а остальные слегка закалялись (чтобы октавы были точными).(7/12) = 1,49651 …, чуть меньше 3/2, и 12 повторений этого соотношения вернут нас туда, где мы началось (после падения на 7 октав).

Между двумя методами включения 3/2 первый дает различные клавиши персонажа, и я его очень предпочитаю. См. Сочинение, которое я написал на этом.

Из различных интервалов только те, которые действительно хорошо улавливаются закаленными версиями схемы 3/2 являются: унисон, 5-й, мажорный 2-й и их обратные (октава, 4-я, минорная 7-я).

Два вопроса: почему 3/2? Выбор 3/2 говорит что рядом с октавой его следует рассматривать как самый главный интервал. Можно также использовать мажор 3-го (т.е. соотношение 5/4) для построения шкалы. Это обсуждается к конец этого эссе.

Почему 12 шагов работают хорошо? Интересно, что это может быть объясняется в терминах простой теории чисел, а именно непрерывные дроби.

Мы хотим понять, когда степень 3/2 будет близок к степени 2:

           а б
     (3/2) = 2, где a и b - натуральные числа

Конечно, это уравнение нельзя решить точно с помощью натуральные числа a и b, поскольку это означало бы, что однажды мы очищаем знаменатели, что степень 3 была степенью 2 (это невозможно, так как степени трех нечетны, а степени из 2 — четные.Такое выражение также противоречат тому факту, что каждое целое число * уникально * выразимые, на заказ, как произведение простых чисел). Но, взяв корень с обеих сторон:

                     б / а
     (3/2) = 2

мы вынуждены взглянуть на уравнение

                     Икс
     (3/2) = 2, где x - действительное число

и попросите рациональные числа b / a, близкие к x. Взяв бревно с обеих сторон и решив относительно x мы находим, что x = log (3/2) / log (2) =.584962500721 … Чтобы найти хорошие рациональные приближения к этому числу мы должны обратиться к так называемая цепная дробь x. Любое реальное число можно записать в виде непрерывной дроби, которая сумасшедшая фракция, которая, если только исходное число оказывается рациональным, продолжается вечно. В нашем случае первые несколько членов непрерывной дроби выглядят так

    журнал (3/2) / журнал (2) =



                             1
        --------------------------------------------
                               1
        1 + ----------------------------------------
                                 1
            1 + ------------------------------------
                                   1
                2 + --------------------------------
                                     1
                    2 + ----------------------------
                                       1
                        3 + ------------------------
                                         1
                            1 + --------------------
                                           1
                                5 + ----------------
                                             1
                                    2 + ------------
                                                1
                                        23 + -------
                                             2+...

(расширение имеет 1 в числителях и продолжается бесконечно).

Взяв несколько первых членов, мы получим следующую последовательность рациональных приближений к log (3/2) / log (2) = .584962500721 …:

                          1
                     ----------- = 1/2
                            1
                     1 + -------
                            1


                          1
                   --------------- = 3/5
                            1
                   1 + -----------
                              1
                       1 + -------
                              2

                         1
                ------------------- = 7/12
                           1
                1 + ---------------
                             1
                    1 + -----------
                               1
                        2 + -------
                               2

                          1 24
               знак равно
                            1 41
               1 + -------------------
                              1
                   1 + ---------------
                                1
                       2 + -----------
                                  1
                           2 + -------
                                  3


           и т.д

Это приближение 7/12 =.5833333333 … что предполагает октава из 12 шагов, при этом квинта равна 7 полутонам.

Почему мы смотрели на непрерывные дроби: оказывается что они дают наилучшие рациональные приближения к числам, т.е. любое более близкое приближение должно иметь больший знаменатель.

Если аналогично образует непрерывную дробь для журнал (5/4) / журнал (2) =. 32192809 …, можно найти следующий список приближающихся дробей: 1/3, 9/28, 19/59, 47/146 и др.Это говорит о том, например, что примечание 28 шкала будет хорошо работать, используя мажорную 3-ю в качестве основы для его конструкция.

С другой стороны, не всегда нужно работать с лучшими. Например, 11/19 = 0,5789 … достаточно близко к log (3/2) / log (2) = 0,5849 … и 6/19 = 0,3157 … достаточно близко to log (5/4) / log (2) =. 3219 …. Это говорит о том, что шкала из 19 нот при этом основная 3-я часть составляет 6 полутонов, а идеальная 5-я — 11 «полутона» могут подойти.Фактически, 19 стоит в знаменателе. рациональных приближений цепных дробей для log (5/3) / log (2), и журнал (6/5) / журнал (2). Это говорит о том, что 19 также подойдет для захват обратной пары соотношений 5/3 и 6/5.

Если мы используем равномерный темперированный 19-нотный строй, мы получим следующий список соотношений

          к / 19
 k 2 близкое соотношение
--- --------------------- -------------------------- ---------
 0 1 унисон *
 1 1.03715504444611 28/27
 2 1.07562201824742 14/13 близко к 16/15 второстепенная 2-я *
 3 1.11565715436668 10/9 близко к мажорной 2-й (9/8) *
 4 1.1571102372827198253 7/6 также близко к 8/7
 5 1.2001027195781030358 второстепенный 3-й (6/5) (посмотрите, насколько он подходит) *
 6 1.2446925894640233315 мажор 3-й (5/4) *
 7 1,21979474049134 9/7
 8 1,33812244721773 мажор 3-й (4/3) *
 9 1,3886511426146561750 тритон (7/5) *
 10 1,44024653753875
 тритон (10/7) *
 11 1.4937589616544857174 5-я (3/2) *
 12 1,5492596422666557249 14/9
 13 1.6068224531337648149 младший 6-й (8/5) *
 14 1.66652401279708 мажор 6-й (5/3) (посмотрите, насколько он подходит) *
 15 1.7284437865632111533 12/7 также близко к 7/4
 16 1.79266417116385 9/5 близко к второстепенному 7-му (16/9) *
 17 1.8592707100168125609 13/7 близко к 7-му мажору (15/8) *
 18 1.92835199588492 27/14
 19 2 октавы *

 * обозначают ноты, у которых есть соответствующее пятно (более или менее)
 в октаве из 12 нот.

Я не уверен, широко ли кто-нибудь использовал эту шкалу, хотя это кажется интересной альтернативой 12 шагу хроматическая гамма. Возможно, хорошая, хорошо закаленная версия могла бы быть изобретенным. В определенном веб-сайт Посмотрите на Джозефа Персона и Нила Хэверстика, которые используйте различные 19-тональные настройки.

я нашел ссылка, рассказывающая об истории 19 настроек тона.

В следующей таблице в центах (процентах полутона) показано, как плохо настроенное фортепиано в тональности C подойдет для захвата различных интервалов в различных ключах.В последнем столбце это сравнивается с ровный темперамент. Например, в таблице сказано, что в тональности A, большая треть будет меньше на 41% полутона. Обратите внимание на последний столбец, что, в то время как равный темперамент захватывает интервалы 3/2, 9/8, 4/3 и 16/9 неплохо, все остальные интервалы отклонены более чем на 11% полутона.

	К	г	Д	А	E	Б	Ф №	C #	Ab	Eb	Bb	Ф	E.Т.
1	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00
16/15	0.00	0,00	0,00	0,00	0,00	0,00	7,71	-19,55	-41,06	-41,06	-19,55	-27,26	-11,73
9/8	0.00	-21,51	-21,51	0,00	-7,71	19,55	27,26	0,00	-21,51	-21,51	0,00	0,00	-3,91
6/5	0.00	-21,51	-21,51	0,00	0,00	0,00	-13,79	-41,06	-41,06	-48,77	0,00	0,00	-15,64
5/4	0.00	0,00	-7,71	41,06	41,06	41,06	27,26	0,00	0,00	0,00	21,51	0,00	13,69
4/3	0,00	0.00	0,00	21,51	0,00	0,00	7,71	-27,26	0,00	0,00	21,51	0,00	1,96
7/5	0,00	27,26	27.26	48,77	27,26	27,26	34,98	7,71	7,71	-13,79	7,71	7,71	17,49
3/2	0,00	0,00	-21,51	0.00	0,00	-7,71	27,26	0,00	0,00	-21,51	0,00	0,00	-1,95
8/5	0,00	0,00	-21,51	0,00	0.00	0,00	7,71	-41,06	-41,06	-41,06	-27,26	0,00	-13,69
5/3	0,00	0,00	0,00	13,79	41.06	41,06	48,77	0,00	0,00	0,00	21,51	21,51	15,64
16/9	0,00	0,00	0,00	21,51	21,51	0.00	7,71	-19,55	-27,26	0,00	21,51	21,51	3,91
15/8	0,00	-7,71	19,55	41,06	41,06	19.55	27,26	0,00	0,00	0,00	0,00	0,00	11,73

Авторские права Майкл Рубинштейн 2000.

Дом

Создание музыкальной шкалы

г. Создание музыкальных гамм

из математическая и акустическая точки зрения, Часть II,

Томас Váczy Hightower

Моя первый поиск заключался в изучении музыкальной практики в древние времена, а не только в Европе, но во всем мире.Было еще несколько музыкальные гаммы помимо диатонической, где полутоны расположены в других местах, кроме ме-фа и си-до. В григорианском модальные, например, разное расположение полутонов создает определенные режимы.

пентатоника Музыка

В пентатонической народной музыке полутонов не существует. Практическим опытом люди нашли из того, что пятиконечная шкала позволяла играть в любой ключ без существенной дисгармонии.Теоретики сказали бы, что шкала состояла из восходящей и нисходящей пятых, только в двух шаги в каждом направлении. На пентатонике могут играть только используя черные клавиши на пианино.

После изучения древних основная культурная музыка, в основном китайская и индийская, я понял, как универсальное понятие октавы было в каждом мюзикле культура.
Согласно Гельмгольцу, арабской и персидской шкалам, и японская и тихоокеанская гаммы также находятся в пределах октавы.Однако разделение октав отличается от культуры к культура.
Арабская музыка делит октаву на шестнадцать неравных интервалы. Персы разделили октаву на 24 ступени, поэтому они должны были использовать четверть тона. Из раскопок египетских флейт семерка нотная шкала C, D, E, F #, G, A, B, была обнаружена, что идентична синтолидийской шкале Древней Греции. Японский в музыке использовалась в основном пентатоника.

китайский музыка

Музыка была краеугольный камень китайской цивилизации, древнейшая культура в истории.Считалось, что в его тонах воплощены элементы небесный порядок. Слышимый звук, включая музыку, был всего лишь одним форма проявления гораздо более фундаментальной формы Сверхфизический звук. Основной изначальный звук был синонимом с тем, что индуисты называют ОМ. Китайцы считали, что это Первичный звук, гун или «Хуанг Чунг» (прямой перевод «Желтый колокольчик»), хотя и не слышно, присутствовал везде как божественная вибрация.
Кроме того, он также был разделен на 12 меньшие звуки или тоны.Эти двенадцать космических тонов были эманациями и аспект Изначального Звука, но по вибрации были ближе к материальный, физический мир. Каждый из 12 тонов был связан с одним из 12 зодиакальных районы небес.

Звуковой сигнал был задумано как проявление 12 тонов физического уровня. Звук на Земле был своего рода подтоном небесной вибрации. Это считалось, что он содержит небольшую часть божественного тона небесных тел. мощность.
«Как вверху, так и внизу», как египетский Гермес. Тот сказал. В молитве «Отче наш» произносится подобное желание.

Для древних китайцев, выравнивание с божественным основным тоном была самой важной задачей Императора. Выравнивание земли с Небеса и человек со Всевышним были буквально целью жизни. Весь порядок и дела государства зависели от правильная настройка основного тона, «желтого колокола», или кунг.

Как древний текст предупреждает: «Если гун нарушен, значит, есть дезорганизация; князь высокомерен.
Если бы кунг был расстроен, потому что небесное царство изменилось, беспорядок и стало очевидным негармоничное поведение в обществе. Каждый инструмент (включая средства измерений) настроен и утилизирован в соответствие священному тону.

Инструмент, который может дать человеку основной тон музыкальной гаммы в идеальном гармония со вселенной была ключом к земному раю, и необходим для безопасности и развития общества.
стал Китайский Святой Грааль.
Один легенда рассказывает об удивительном путешествии Лин Луня, министра второй легендарный китайский император Хуан Ти. Лин Лун был послан как древний рыцарь короля Артура для поиска особого и уникального набора бамбуковых трубок. Эти трубы были настолько совершенны, что могли воспроизводить точные стандартные высоты звука, к которым все остальные инструменты по всей земле можно было настроить.

Тот священный тон, который относится к современной западной высоте звука F, считался фундаментальный космический тон.Китайцы знали о медленном изменении космическое влияние, и, следовательно, Кунг должен изменить соответственно. Император должен был настроить Кунг так, чтобы он был в выравнивание с космическим тоном.

Тюнинг Священный гун

Кусто в своей книге Космическая октава — интересное наблюдение по этому поводу. Он связывает Кунг с частотой Платонический год. Продолжительность Платонического Года ( Великий год Пифагора) составляет около 25 920 лет и представляет время, необходимое оси Земли для завершения полного вращение.

День весеннего равноденствия точка, в которой экватор (Земли) пересекает эклиптику (или зодиак), то есть положение солнца в начале весны — 21 марта.
Весеннее равноденствие длится в среднем 2160 лет. путешествовать по одному знаку зодиака. Этот период времени известный как возраст. Невозможно точно указать, когда один возраст конец и новое начало, потому что знаки накладываются на определенные степень.
Путешествие в день весеннего равноденствия через каждую из 12 знаков Зодиака равняются одному великому году приблизительно 25 920 лет.(Сейчас мы находимся на пороге Водолея, так как возраст Рыбы заканчиваются).
Это количество лет близко к максимальному количество генерирующих пятых, когда мы попадаем в цикл из 25 524 нот.

Cousto вычисляет ноту платонического года как F в западном равном Высота темперамента, которая находится в 48-й октаве с частотой 344,12 Гц, или в 47 октаве 172,06 Гц. Обратите внимание, что соответствующий a ‘имеет частоту 433.564 Гц. (Современный вестерн концертная высота 440 Гц.)
Расчет: 31 556 925,97 (тропический год в секундах) * 25 920 (платонический год). Поскольку длина (колеблющейся струны или период времени) составляет обратная пропорциональность частоте, длине платонической год в секундах должен быть знаменателем. Частота очень низкая, поэтому мы повысим частоту до диапазона слышимости, умножив с необходимым количеством октав, например 48 октав, поэтому мы приходим к 344,12 Гц.(47 октав будет половина, 172,06 Гц.)
Если мы хотим достигнув спектра света, мы умножаем его на 89 октав, что приводит к нас на частоту 1/31 556 925.97 * 1/25 920 * 2 89 = 7,56 * 10 14 Гц. соответствует длине волны 0,396 мкм, которую мы воспринимать как фиолетовый вблизи ультрафиолета. Это цвет Платонический год. Дополнительный цвет к фиолетовому — желтый. Их основной тон был назван желтым колоколом.

Это чудо для меня как древние китайцы могли знать о своих священных основах тон, Кунг, соответствует Платоническому году, и выберите великий ритм Земли.

Создание шкалы

Это может быть сюрприз что диатоническая гамма была основой древнекитайского и индийская музыка, хотя музыкальные теории и практики различаются от западного.

Для старых китайцев, их музыкальный масштаб развивался кругом идеальных квинтов до 60 градусов или ключей, 60 Лю, хотя обычно они использовали только первые 5 пятых в их пентатонической музыке, потому что они знали, что они представляют собой предел созвучия в модальной музыке.К тому же, древние китайцы видели символическое изображение в пентатонике. масштаб, основанный на их вере в музыку как представление отношения между небом и землей (пятью элементами).

Китайцы были здоровы знали много веков назад о существовании нашего современного Равного Темперамента. Они отвергли такую умеренную шкалу не только из-за ее крайне ложной примечаний, но главным образом потому, что настройка не была согласована с космический тон.
Согласно к книге Дэвида Тайма «Тайная сила музыки» 3 символическое число неба и 2 числа земли; звучит в соотношение 3: 2 гармонизирует небо и землю. Как способ применить это важную концепцию, китайцы взяли основную записку: «Хуан Чунг, и из него получилась вторая нота в соотношении 3: 2.

A более подробно объяснение, сделанное Аленом Даниэлу в его «Музыка и Сила звука »:
« Музыка, представляющая отношения между небом и землей должны вполне естественно иметь это подтверждение центра или тоника (гонга), окруженного четырьмя ноты, ассимилированные с четырьмя направлениями пространства, четыре ощутимые элементы, четыре времени года и так далее.«

«Пентатоника масштаб, таким образом, представляет структуру, которая позволяет ему быть адекватным представление статического влияния неба на землю. Но статическое изображение движущегося мира не могло быть инструментом действия в этом мире. Необходимо развиваться из неподвижен к движению, от углового к круговому, от квадрат к кругу. Чтобы выразить движение Вселенной, звуки должны будут подчиняться циклическим законам, которые сами по себе поле, представлены циклом пятых.”

г. спираль пятых

как мы уже видели, пятая — это третий звук из серии гармоники, первая из которых является основной, а вторая — октавной. Согласно формуле Дао-дэ цзин: «Один произвел два, два дали три, три дали все числа », мы можем понять, почему третий звук, пятый, обязательно должен производят все остальные звуки путем его циклического повторения.
← Наблюдать женские и мужские ноты соответственно розового и голубого.

Первый произведенный будут четыре основных звука, которые образуют сравнительно простые соотношения с тоником.
Для для удобства мы будем использовать западные ноты: см. китайский И западная музыка.
I, C
II, G = 3/2
III, D = 9/8 = (3/2) ² * ½ (нижний октава)
IV, A + (точная запятая) = 27/16 = (3/2) ³ * ½ (нижняя октава)
V, E + (точная запятая) = 81/64 = (3/2) ⁴ * ¼ (нижняя 2 октавы).
Эти пять примарт звуки представляют собой элементарную структуру воспринимаемого мира, пентатоника. Эти звуки используются в музыке, так как вы можете играть пять черных клавиш пианино. Однако следующие две пятых имеют добавляются как два вспомогательных звука:
VI, B +, (точная запятая) = 243/128 = (3/2) ⁵ * ¼ (нижние 2 октавы)
VII, L + F? (увеличьте резкость основного полутона) = 729/512 = (3/2) ⁶ * 1/8 (нижние 3 октавы).

г. семизначная китайская гамма

С	D	E +	(Ж) ¤L + F # 1/1	г	А +	В +	C ‘
1/1	9/8	81/64	4/3 (729/512)	3/2	27/16	243/128	01.02.13

¤ Отметим здесь, что наиболее ярким разница между системой квинт и гармонической отношения к тонику находится в идеальной четверти, которая является существенный интервал в шкале пропорций, но в шкале пятое — это увеличенная четвертая в качестве шестой пятой, (3/2) _{^6. _.}

Два дополнительных звука — 243/128 и 739/512 — не должны использоваться в качестве основы, хотя они необходимы для транспозиции, потому что они принадлежат масштаб невидимых миров, и поэтому мы не можем ни оценить их точность, ни построить системы на них, не выходя из строя.
Вместо того, чтобы начинать с C, мы могли бы начать на одну пятую ниже, то есть с F, и мы получил бы эту важную заметку, ничего не меняя в наша шкала, за исключением того, что мы начинаем с мужского рода интервал вместо женского интервала, изменен характер всей системы.

Пять последовательных пятые, будь то в восходящей или нисходящей серии, представляют предел созвучия в модальной музыке тоже. За этим пределом нет интервал может казаться гармоничным, и его нельзя точно распознать. Правило, основанное на том же принципе, было известно и в средневековье. Европа, где тритон был запрещен как дьявольский, то есть как связаны со сверхъестественными силами и, следовательно, неконтролируемый.
Народная музыка в ее пентатонической форме имела поняли это тоже, используя только две пятых и вниз.
После эти семь нот, следующие пять нот генерируются серией квинты:
VIII, bDb с пониженным полутоном, IX, bAb понижает второстепенный полутон, X, bEb понижает второстепенный полутон, XI, bBb на минорный полутон ниже, XII, F + диез.

Теперь у нас двенадцать звуки, которые хроматически делят октаву на двенадцать половин тонов.
Двенадцатая пятая (примечание 13) в 7-октавный диапазон возвращает нас к основному, но с небольшим разница.
На одну запятую выше основного, запятая Пифагора (312/219 = 531 441/524 288, (5,88 савартов или 23,5 цента). Следовательно, в наших обозначениях C + одна запятая резкий.
Таким образом, последующие серии из двенадцати пятых будут размещены один над другим с интервалом в одну запятую до 52-го пятая (примечание 53), заполняющая октаву.

Китайцы продолжили цикл квинт до 25 524 нот, с базовым интервалом 0.0021174 savarts. Этот цикл очень близок к циклу прецессия равноденствий, или Великий Пифагорейский год, который составляет 25 920 солнечных лет. Почему китайцы продолжали так много октав в цикле квинтэ имеют какое-то отношение к их эталонному тону, Кунг.

На практике по причинам как символические, так и музыкальные, после 52-го пятого (53-го примечание) китайцы следуют за серией только для следующих семи градусов, которые располагаются выше начальных семи нот, и останавливают серию на 60-й ноте.Причина в том, что 12 (количество каждого цикла) * 5 (количество элементов) = 60.

г. шкала 60 Lü

Китайская шкала, являющаяся неизменный, фактически представляет собой единственный режим. Каждое изменение в выражение, следовательно, будет зависеть от модуляции, изменение тоник.
Во-первых, выбор пола: пятые, чьи числа в серии бывают даже женственными. Пятые с нечетным номером мужское начало.
Выбор тоника зависит от сложных правил и ритуалы, основная цель которых — соответствовать небесным а также земной приток или обстоятельства.Соответственно, Китайцы должны выбрать правильный ключ для часа дня и месяц, даже во время спектакля.
Это обширная схема, но чтобы получить представление, мы можем сказать, что это соответствует политическим вопросам, времена года, час дня, стихии, цвет, географическое направление, планеты и луна.
Эта шкала квинт, идеально подходящая для транспонирования из-за своей исключительной точности также позволяет изучать астрологические соответствия и земного притока в их тоне Зодиак.

Мы замечаем, что Китайская гамма очень похожа на пифагорейскую настройку, которая была также производится путем создания идеальной квинты (3: 2). Когда китайцы вывели свою шкалу до 3000 г. до н.э., когда европейский человек каменного века еще бил деревянные бревна. В распространенное на Западе мнение о нашем музыкальном превосходстве должно настоящим быть модератором.

г. Индийская музыкальная система

У древних индейцев менее формализованный подход к своей музыке, чем у китайцев.В общем-то говоря, они подчеркивали личное внутреннее созерцание больше, чем внешне организованные ритуалы. Можно сказать, что искали внутреннего выравнивание с высшим божественным посредством звуков АУМ или ОМ, которые были (являются) земным звуком главного творца, Брахмана.

Для индусов, как Китайцы, произносимые или произносимые слова были носителями некоторых из творческая энергия, составленная Первым Творцом. Выраженный правильно, считалось, что специальные слова могут изменять мысли и чувства людей и буквально изменяются и формируются физическая материя.

Рага — основная форма в классической индийской музыке. Существует целая система Раг, которая различаются соответственно между Северной и Южной Индией. Первоначально там было всего 7 Раг. Возможно, это остатки древнего ссылка на семь космических тонов: семь основных нот, или савары, связанные с семью главными планетами, и двумя вторичными примечания, соответствующие узлам Луны. Это приносит общую количество нот в шкале до девяти основных нот, что составляет относится к девяти группам согласных санскритского алфавита.

Гранты системы Рага музыканты свобода слова в рамках ограничения определенного неприкосновенного режима. Поскольку музыка была такой важной силой в изменении явлений на Земле, они считали это было бы неразумно, опасно и, возможно, даже самоубийственно в бегут, чтобы музыканты могли исполнять все, что они хотели.

Индийское решение было затем применить систему правил, которые, эффективно определяя какая вид музыки исполнялась и даже ее духовная атмосфера и период дня, не указывает примечания самих себя.Это было убедительно успешное решение Проблема в том, что музыка древних цивилизаций всегда возникала против.

У китайцев была более жесткая система. Они создали вариации с помощью инструменты, и особенно в выражении одной ноты. В измерения цвета тона или тембра были высоко развиты в Восток. Пришлось уху научиться различать тонкие нюансы. Такой же нота, произведенная на другой струне, имеет другой тембр.В одна и та же струна, которую тянут разными пальцами, имеет разные тембр и т. д. Кроме того, что очень важно, Решающее значение имела вся духовная сущность самого музыканта. Это относится и к индийской музыке.

Как в западном диатоническая шкала, индийская шкала основана на 7 основных нотах: SA, RE, GA, MA, PA, DHA и NI. Если вернуться к древнейшим текстам о музыки, гаммы разделились на две тетрахорды, похожие на древних греков, а позже положили вместе с целым тоном (9/8) между, Ма — Па, так что полный октава была завершена.
Индийские банкноты в целом относятся к Западные соотношения, хотя настройка очень гармонична и создает мир различий. Мы должны подчеркнуть, что использование гармонии как мы знаем, что это было, но больше не практикуется.

Вот критический момент. Индийская музыка модальна. Есть сильное отношение к тонизирующему. Когда играется третья, всегда относится к третьей степени; тогда как в западной гармоничной традиции третий имеет относительное положение, потому что он может быть корнем, пятая или треть аккорда.
Восточные слушатели часто делают такие замечания, как: «Симфонии Бетховена интересны, но почему? были введены все эти аккорды, портящие очарование мелодии? »
Модальная музыка Индии «горизонтальна». поскольку западный — это «вертикаль». В вертикальная, гармоничная система, в которой группа родственных звуков данные одновременно, могут быть более прямыми, хотя и менее ясными. Точное различение различных элементов, составляющих аккорд обычно невозможен.

Модальный, горизонтальный система, с другой стороны, позволяет точное восприятие и немедленное классификация каждой банкноты и, следовательно, позволяет точное, мощное и подробное описание того, что музыка выражает.
Можно сказать, что концентрация внимания в восточный музыкальный язык должен быть намного длиннее, поскольку со временем разные и отчетливые звуки складываются в сознании слушателя создать аккорды или всю музыкальную идею.Только тогда внимательно запоминая все элементы, составляющие музыкальный образ, можно ли, наконец, понять весь смысл.
Индийская музыкальная система работает с комбинацией фиксированных и изменяемая высота тона, поэтому ключ можно распознать вместе с переменной ноты. 2-я, 3-я, 4-я, 6-я и 7-я ноты переменные, но 1-я (Sa или Do) и идеальное 5-е (Pa или Sol) неизменны и имеют фиксированный шаг. Соответственно, дрон — это часто Do-Sol (Sa-Pa), который становится окончательным открытым аккордом, содержащим все остальные ноты в нем как серия тонких гармоник.
Этот дрон (постоянная нота или тоник), независимо от того, играли ли вы на таком инструменте, как тампура или просто слышимый внутри себя как звук Ом, является постоянным ссылка, без которой не играл бы ни один индийский музыкант.

Нельзя смущает широкое использование микроинтервалов, скольжения или изгиба ноты, известные в индийской музыке. Музыканты могут свободно пользоваться эти микротоны как частные точки, часто свободно перемещающиеся между двумя отмечает как некое бесконечно используемое пространство, в конечном итоге возвращающееся домой тоник Раги.У музыканта есть свобода играть тонов, как того требует его вдохновение, пока он соблюдает священные правила типов и его настроения.

г. 22 Шрутис (градусы)

Музыкальные интервалы могут быть определяется двумя способами, либо числами (длина строки, частота) или их психологическим соответствия, такие как чувства и образы, которые они обязательно вызывают в наших умах. Нет звука без смысла, поэтому индейцы считайте эмоции, которые разные интервалы вызывают столь же точные, как звуковые отношения.Чувство шрути зависит исключительно от их положения по отношению к тонизирующему, а указывает ключ к рагам.

22 различных ключа или градусы охватывают то, что индейцы считают наиболее распространенными чувствами и отражения человеческого разума. Они знали о разделении октаву на 53 равные части, пифагорейскую запятую и ее гармонический эквивалент, запятая умирает (синтоническая запятая, разница между мажорным и минорным тоном).
Однако они выбрал 22-е деление октавы по причинам, основанным на пределе способности человека различать ключи, а также психологические и метафизические причины. Символический соответствия чисел 22 и 7 (7 строк и основные ноты), может также сыграть свою роль, поскольку связь между кругом и диаметр выражается как приблизительное значение Пи, 22/7.

г. модальное или гармоническое деление октавы

Индийская музыка — это по существу модальный, что означает, что интервалы, на которых музыкальное сооружение построено рассчитано по отношению к постоянному тоник.Это не означает, что отношения между нотами, кроме тоника не считается, но каждая нота будет установлена сначала в соответствии с его отношением к фиксированному тонику, а не, как в случай цикла квинт, любыми перестановками основной ноты.

Модальная структура может поэтому сравнивать с пропорциональным делением струны (прямой), а не на периодическую движение спирали пятых.
Все записи, полученные в гармоническая система отличается от циклической системы, которая основан на разных данных.Хотя записи теоретически различны и их последовательность следует совершенно другим правилам, в практика они приводят к аналогичному разделению октавы на пятьдесят три интервала.

шкала пропорций состоит из последовательности синтонных запятые, 81/80, которые делят октаву на 53 интервала. Среди них 22 ноты были выбраны из-за их специфических эмоциональных особенностей. выражения:

Примечание степень	Интервал	Стоимость в центах	Имя интервала	Выразительные качества
1	1/1	0	унисон	чудесный, героический, яростный
2	256/243	90.22504	пифагорейский limma	комикс
3	16/15	111,7313	несовершеннолетний диатонический полутон	любовь
4	10/9	182.4038	несовершеннолетний весь тон	комикс, любовь
5	9/8	203,9100	майор весь тон	сострадание
6	32/27	294.1351	пифагорейский второстепенная треть	комикс, любовь
7	6/5	315.6414	несовершеннолетний третий	любовь
8	5/4	386.3139	майор третий	чудесный, героический, яростный
9	81/64	407,8201	пифагорейский большая треть	комикс
10	4/3	498.0452	идеально четвертый	чудесный, героический, яростный
11	27/20	519,5515	острый четвертый	комикс
12	45/32	590.2239	тритон	любовь
13	729/512	611.7302	пифагорейский тритон	комикс, любовь
14	3/2	701.9553	идеально пятый	любовь
15	128/81	792,1803	пифагорейский второстепенный шестой	комикс, любовь
16	8/5	813.6866	несовершеннолетний шестой	комикс
17	5/3	884,3591	майор шестой	сострадание
18	27/16	905.8654	пифагорейский мажорная шестая	сострадание
19	16/9	996.0905	пифагорейский второстепенный седьмой	комикс
20	9/5	1017.596	всего второстепенный седьмой	комикс, любовь
21	15/8	1088.269	классический мажорная седьмая	чудесный, героический, яростный
22	243/128	1109.775	пифагорейский мажорная седьмая	комикс, любовь

The Древние египтяне

Древние египтяне имел сходные верования с китайцами и индуистами. В их Книге Мертвые и другие источники утверждают, что Бог или его меньший слуга боги создали все, сочетая визуализацию с высказыванием.Сначала бог визуализировал то, что должно было образоваться; тогда он произнесет его имя: и будет.

Еще с правления Александра II, текст, датируемый примерно 310 г. до н.э., все еще имеет Бог Творения, Ра, заявляет: «Многочисленны формы из то, что исходило из моих уст ». Бога Ра также называли Аминь-Ра с приставкой «Аминь». Египетское священство хорошо понимал слово Аминь, или АМН, и его приравнивали к Индуистский OM.

Египетская музыка, как и Греческий язык, скорее всего, имеет свои корни в индийской музыке или, по крайней мере, в эта универсальная система модальной музыки, традиция которой полностью хранятся только у индейцев.
Пирамида легко может быть символическое изображение Земли с ее четырьмя воспринимаемыми элементами, и все его характеристики, которые регулируются числом четыре — четыре времени года, четыре направления пространства и т.д .; особенно проекция одиночного на множественное.

ЗАПАД МУЗЫКА
Пифагор

Греческий философ Пифагор (570 — 490 до н.э.) провел 22 года в Египте, в основном с первосвященник в Мемфисе, где он был посвящен в их тайну познание Богов. Когда персы завоевали Египет, его держали в пленение в Вавилоне на шестнадцать лет, прежде чем он смог вернуться в Греция и начать свое учение.
Я начал изучать теорию пифагорейцев и их эзотерических школ.Очень мало известно их. Пифагор потребовал замолчать об эзотерической работе. Этот историческая школа была основана в греческой колонии Кротон, на юге Италия, около 2500 лет назад.

Я понял после прочтения десятки книг о том, какую выдающуюся роль играет эта школа сыграл в становлении западной цивилизации. Он создал совершенно новая концепция. Любой человек — мужчина или женщина — кто искренне желал знаний мог поступить в школу поэтапно, с рядом инициирований.Традиция монополия священства на познание Бога была нарушена.

Исследование Пифагора движущаяся струна и его открытие гармонической прогрессии простых целые числа была первой настоящей научной работой и созданием современная наука. Но его видение выходило далеко за рамки современной науки в его глубокое понимание интеграции триады: A — наука, Б — работа над бытием, В — любовь и изучение Бог. Что-то современная наука могла учиться!

Никомах Герасы

Никомах Пифагорейцы (II в. До н. Э.C.) был первым, кто написал о Легендарная встреча Пифагора с «гармоничным кузнеца и веса 4 разных молотков равные 12, 9, 8 и 6, что определило разброс высот Пифагор услышал.
Этот рассказ показывает, как числовой были обнаружены пропорции нот. Его методическое измерение молоточки и как звук был произведен и связан (сбор данных), затем экспериментируя со струнами, их натяжением и длины (повторение результатов и, с помощью математики, формулирование их в закон), был первым примером научного метода.

Не будем останавливаться на вопрос о силе удара или натяжении струн, который позже был обнаружен как квадратный корень из силы, но просто придерживаться пропорции веса и высоты звука, которые он слышал, что привело его к открытию.
Эксперименты Пифагора привели к комбинация двух тетрахордов (две четверти), разделены целым тоном 9/8, составляющим октаву. Он изменил традиционную единицу греческой музыки, тетрахорд, на октаву октахордом.

Во времена Пифагор: традиция была прочно основана на семи струнах лира, семахорд. Греки считали число 7 священным. и подарен богом Гермесом, который передал искусство игры на лире Орфею. Семиструнная лира также была связана с семиструнной лирой. планеты среди прочего почитали древние.
Лира часто, но не всегда, состоял из семи струн, состоящих из двух тетрахорды, каждый из которых охватывает самый элементарный аккорд, в-четвертых, оба соединились на ноте mese.

Согласно по легенде, сын Аполлона Линос изобрел четырехструнную лиру с тремя интервалами, полутоном, целым тоном и целым тоном содержащий четвертый; четвертый, «первый и самый элементарный созвучие », как его называет Никомат, и из которого со временем развились музыкальные гаммы древнегреческой музыки.
Трепандер Антиссы на Лесбосе, родившейся около 710 г. до н.э., считается мифологической статус его музыкального гения. Его самый продолжительный вклад был возможно, его преобразование четырехструнной лиры в инструмент, который по традиции стал институционализированным гептахорд.
Трепандер до того, как Пифагор расширил семахорд от его малых седьмых пределов до полной октавы, но без необходимости добавить запрещенную восьмую строку.
Он удалил струну Bb, банальностью конъюнктивного тетрахорда, и добавил октавную струну E1, что дает масштаб E F G A C D E1.
Это расположение оставило пробел в незначительная треть между A и C, и, похоже, усилила дорийский характер композиции Трепандера.

Гармония

Только Пифагор спасся порицание за добавление восьмой струны к старинной и почитаемой лире из-за его положения великого мастера и религиозного пророка.Его целью было научить человека объединяющему принципу и неизменным законам гармония, обращаясь к его высшим силам — рациональному интеллекту а не его ненадежным и тленным чувствам. Пифагор изменили гептахорд исключительно для того, чтобы задействовать человеческий интеллект в надлежащем «Совместимость» — гармония — математических пропорций.

Плутарх (44-120 до н. Э.) утверждает, что для Пифагора и его учеников слово гармония означало «Октава» в смысле настройки, которая проявляет в его пределах и правильное соединение согласных интервалы, четвертый и пятый, и разница между ними, весь тон.
Более того, Пифагор доказал, что все может быть Сказанное об одной октаве можно сказать обо всех октавах. Для каждой октавы нет независимо от того, какой диапазон высоты он охватывает, повторяется без вариации во всем диапазоне высоты звука в музыке. Для этого разум, Пифагор считал достаточным ограничить изучение музыка в октаву.

Это означает, что в пределах рамки любой октавы, независимо от ее высоты диапазона, есть математически предопределенное место для четвертого, пятый, и для всего тона.Это математический вопрос показать что все отношения, участвующие в структуре октавы, постигается единственной конструкцией: 12-9-8-6.
Для у пифагорейцев эта конструкция стала основным парадигма — единства от множественности.

г. среднее арифметическое и гармоническое

Мы видим, что 12: 6 выражает октаву, 2: 1; 9 — арифметика среднее, равное половине суммы экстремумов, (12 + 6) / 2 = 9.
Далее, 8 — гармоника среднее 12: 6, превосходя и уступая крайним такая же фракция.
Выражая эту операцию алгебраически, гармоническое среднее равно 2ac / a + c, или в этой серии 2 * 12 * 6/12 + 6 = 8.

Среди своеобразных Свойства гармонической пропорции заключается в том, что соотношение наибольший член до середины больше, чем средний до середины наименьший член: 12: 8> 8: 6. Именно это свойство сделало гармоническая пропорция противоречит арифметической пропорции.

По музыкальному Согласно теории, эти две пропорции являются основными для деления октавы. поскольку пятое, 3/2, является арифметическим среднее значение октавы, а четвертая, 4/3, является гармонической среднее октавы.
Принцип деления струны на арифметическая пропорция производится по формуле: a: b делится на 2a: (a + b) и (a + b): 2b.

Древние греки предположительно сделали такое разделение в своих исследованиях певческой струны монохорда.

г. полутон

Мы уже видели что в диатоническом роду каждый тетрахорд делился на два полных тонов и один полутон. Полный тон получается из пятой минус четвертое, 3/2 — 4/3 = 9/8. Полутон будет 4/3 — (9/8 + 9/8), или 4/3 — 81/64 = 256/243.
Этот полутон называется лейммой, а несколько меньше полутона, вычисленного путем деления (для разделение музыкальных соотношений означает квадратный корень) весь тон в половина: (9/8) ^½ = 3/2 * 2 ^½.

Квадратный корень из 2 был для пифагорейцев факт шокирующий, потому что их концепция рациональные числа были разрушены. (Для меня это олицетворение красоты настоящая наука, потому что она вскрыла недостатки пифагорейского парадигма чисел). Их собственная математика доказана Учение пифагорейцев о прямоугольном треугольнике (сумма квадраты двух меньших сторон прямоугольного треугольника равны равный квадрату гипотенузы), что в музыке, как и в геометрии, есть дроби, m / n, которые несоизмеримы — например, квадратный корень из 2, который нельзя выразить с помощью целые числа или дроби, тело рациональных чисел, но с иррациональные числа еще не разработаны.
Это открытие считалось секрет среди пифагорейцев и привел к разделению алгебры и геометрия на протяжении веков, до Декарта в 17 веке снова объединил их.

Для музыки это означало, что не было ни центра октавы, ни деления всего тона вдвое, ни идеальный союз противоположностей, никакой «рациональности» космос.
Полутон мог быть «Дверь» в другие измерения!

Моя задача — дать некоторые ключи к метафизическим функциям полутонов, которые кажутся вовлекать возможность перейти в другой мир или войти в другой измерение.Ключ к достижению другого духовного мира существует в поиск точного правильного тона, который резонирует с этим особая «дверь» в другие измерения и миры. В человек содержит больше измерений, чем просто три пространственных Габаритные размеры.

Филолай

Надо иметь в виду что сам Пифагор не оставил письменных записей о своей работе; это было и противоречит эзотерическим принципам. И те немногие студенты кто пережил погром Пифагора.Это один в следующем поколение пифагорейцев, Филолай (ок. 480–? до н. э.), нарушившее заповедь о записи магистерского обучения. Тем не мение, Записи Филолая утеряны, так что это фрагменты Никомаха. его сочинения в «Руководстве по гармоникам», на самом деле единственное источник потомков.

Согласно Никомаху / Филолай, весь тон, 9/8, был разделен иначе, чем Метод Пифагора, представляя весь тон числом 27, куб из 3, число, высоко оцененное пифагорейцами.Филолай разделился весь тон в двух частях, называя меньшую часть из 13 единиц «Diesis», а большая часть из 14 единиц — «апотом». Филолай, по сути, предвосхитил вычисления Платона в Тимей!

Тимей Платон

Платон (427-347 до н. Э.) придал в своей работе Тимей новый смысл пифагорейской гармонии Вселенная — чисто математическим методом — заключая это в математически фиксированных пределах четырех октав и мажорной шестой.Он определялся числами, образующими два геометрических прогрессии, из которых последний член является двадцать седьмым кратным первого члена:
27 = 1 + 2 + 3 + 4 + 8 + 9
Два геометрических прогрессии, в которых соотношение между членами составляет 2: 1 и 3: 1 равны, соответственно:
1-2-4-8 и 1-3-9-27.
Объединение Эти две прогрессии Платон произвел семичленную серию: 1-2-3-4-8-9-27. Цифры в этой серии содержат октаву, октава и квинта, двойная октава, тройная октава, квинта, четвертый и весь тон.Весь компас от одного до двадцать седьмое кратное, таким образом, включает четыре октавы и мажор шестой. В числовом выражении он содержит четыре октавы, 16: 1 * 3: 2. (пятая часть) * 9: 8 (полный тон) равняется 27: 1.
Платон продолжил сначала найти в каждой из октав гармоническое среднее, четвертое, затем среднее арифметическое, пятое. Вставив гармонику и арифметические средства соответственно между каждым из членов в две геометрические прогрессии, математически сформулированные Платоном все, что Пифагор сформулировал путем сбора акустических данных.

Платон, однако, независимо от пифагорейцев, вычислите полутон в четвертый, состоящий из двух полных тонов плюс еще кое-что, меньше половины целого тона, а именно 256: 243, Леймма.
По словам Флоры Левин в ее комментарии к Никромаху «Учебник гармоник», Платон пошел дальше, чем Пифагора, выполнив все степени по диатонической шкале:

1	9/8	81/64	4/3	3/2	27/16	243/128	2
E	F #	G #	A	B	С #	D #	E ‘

Расчеты Платона привели к неизбежному факту отсутствия центра октавы, никакого уменьшения вдвое цельный тон с рациональными числами, без рациональности космоса.
Никомах внес свой вклад в сокрытие тайны искажение Платона и откладывание некоторых разрушительных открытия иррациональных чисел в будущее время.

г. полутонов в разных режимах

Пифагор практиковал музыку задолго до того, как он превратил гептахорд в октахорд что привело его к открытию математических законов, определяющих основные структура октавы. Он полностью понимал терапевтическую ценность музыки в исцелении тела и души.Больше всего он знал набор условий для мелодии. Он твердо осознавал, что каждый тетрахорд, на котором основана мелодия, олицетворяет «естественный» или физическая музыкальная прогрессия всего тона в целом тон-полутон.
Он поддерживал фундаментальную структуру оба тетрахорда в его гамме, и по музыкальным причинам он понимал что такое распределение интервалов должно соблюдаться для всех мелодические цели с их конфигурациями и инверсиями.
Это была основой древнегреческой музыки, которая в дальнейшем превратился в Великая совершенная система.

г. путаница систем

Греческая музыка имеет врожденное смешение музыкальных систем: смесь циклической системы идеальные квинты (настройка Пифагора) и модальная система (тетрахорды). Мы можем получить лишь очень смутное представление о том, что древний Греческая музыка действительно имела значение, потому что европейские теоретики во времени сделали ошибки и недопонимания.

На самом деле арабы а турки случайно получили в наследство непосредственно Грецию.Во многих случаях работы греческих философов и математиков попал в Европу через арабов. Самые серьезные исследования греческой музыки были написаны арабскими учеными, такими как аль-Фараби в Х век и Авиценна чуть позже, а жители Запада — В частности, Боэций — уже совершил самые ужасные ошибки.
Это арабы, поддерживающие музыкальную практику. в соответствии с древней теорией, чтобы получить представление о древних Греческая музыка, нам следует обратиться к арабской музыке.

г. Пифагорейская настройка

Мюзикл гамма, созданная Пифагором, была диатонической музыкальной шкалой. с кратностью как:

9: 8

81:64

4: 3

3: 2

27:16

243: 128

Эта шкала идентична китайской циклической шкале пятых долей, если взять F как тонизирующее.
Имеет 5 основных тонов (9/8) и 2 полутона, leimma (256/243), в интервале ми-фа и си-до.
третья, 81/64, синтоническая запятая резче гармонической трети, 5/4.
Вот семизначный китайский масштаб:

С	D	E +	(F) ¤L + F # 1/1	G	A +	В +	C ‘
1/1	9/8	81/64	4/3 (729/512)	3/2	27/16	243/128	1/2

¤ Отметим здесь, что самое разительное отличие системы пятых и гармонических отношений с тоникой находится в идеальная четверть, что является существенным интервалом в шкале пропорции.
Шкала пятых долей имеет увеличенную четвертую в качестве шестой пятый, (3/2).

Пифагорова шкала был основан на трех основных интервалах: октаве, идеальной пятой и идеальный 4-й. «Все подчиняется тайной музыке, «Тетрактис» — это числовой символ » (Lebaisquais).
Путем создания 12 идеальных пятых на промежутке 7 октав, было произведено 12 тонов. Чтобы разместить тона внутри на одну октаву использовалась нисходящая совершенная 4-я (субдоминанта), и изготовлена 12-нотная хроматическая гамма.

Он открыл то, что позже было названо пифагорейской запятой, несоответствие от 12 пятых до 7 октав дает (3: 2) ¹²> (2: 1) ^7. При вычислении получается: 129,74634: 128 = 1,014. Или в центах: 23,5. Делать не ошибка Запятая Пифагора для синтонической запятой, равная 22 центам, что происходит из разницы между основным тоном и второстепенным тоном в Just Diatonic Scale, или несоответствие между пифагорейскими третья и третья в гармоническом ряду 5: 4.

Еще 2500 лет назад пифагорейцы выяснили, что невозможно вывести шкалу, в которой интервалы могут точно соответствовать октава. Древние греки объясняли это несовершенство — запятая — как пример состояния смертных людей в несовершенный мир.
Эта фундаментальная проблема с 3-мя простыми числами. соотношения: 2: 1, 3: 2, 4: 3 — которые могут быть сформулированы математически термины как взаимосвязанные простые числа, не имеющие общего делитель кроме единицы — был скомпрометирован в ряде различные темпераменты диатонической гаммы до наших дней.

В древнегреческой музыке несколько других режимов использовались на основе тетрахордов с размахом идеальный четвертый. Позже два тетрахорда были соединены полный тон между ними, поэтому была установлена октава. Номер в практическом исполнении музыки использовались разные режимы. В различное размещение двух полутонов сделало разные режимы.
An счет древнегреческого вклада в музыкальный строй не будет полное без упоминания более позднего греческого ученого Птолемея (II в.ОБЪЯВЛЕНИЕ.). Он предложил альтернативную музыкальную систему настройки, которая включал интервал большой трети на основе интервала между 4-я и 5-я гармоники, 5/4. Эта система настройки игнорировалась. на протяжении всего средневековья и всплывал только с развитие полифонической гармонии.

по н.с. церковная музыка

От древнегреческих образует христиан Григорианская церковь получила свою музыку, хотя их имена были полной смесью оригинальных греческих имен для своих режимов.В этом контексте важно размещение двух полутонов в октаве. Они по-разному располагались в для создания различных режимов, которые производят особую тональность или настроение. Взаимодействие между тонами и полутонами сделало каждый характерный режим.
Григорианская церковная музыка позднего Средние века развивались изумительной красоты и духовности. Мы обязаны монахи — и Хильдегард фон Бинген — благодарность за их участие — пение поклоняться утонченности души и Божественности.
Побочный эффект была целительная сила в сильной пропорции высших гармоник, о котором бодрящий эффект Альфред Томатис описал на моей странице. Мощность гармоник.

Пока музыкальный Практика была в основном однотонной, гамм могло быть много. Когда зародилось желание гармоничного полифонического пения, устранение чешуек началось, потому что только те шкалы, которые были в согласование с гармониками может быть использовано.

полифонический музыка

Развитие в музыкальная практика от монофонической до полифонической, а после Возрождение (конец 15 века) к гармонии, сделало необходимым чтобы особенно гармонизировал третий.Пифагорейская треть (81:64) — это синтоническая запятая больше, чем гармоническая третья (5: 4). Необходимость гармонизации третьего в частичные песни стали обязательными, поскольку полифоническая музыка стала преобладающий.

Так как мажорная триада стала основой гармонии в Западная музыка, пифагорейская шкала в значительной степени отброшена в в пользу Just Diatonic Scale, или Zarlino (1540-94).
Частоты нот в корневой позиции мажорное трезвучие дано четвертой, пятой и шестой гармониками в гармонический ряд, т.е.е. частоты должны быть в соотношении 4: 5: 6. (1-5: 4-3: 2).

г. Большая триада как генератор

Если мы посмотрим на эту триаду как C, E и G, тоническое трезвучие, и связать его с его доминантой G, B, D и субдоминанта тоники F, A, C, каждая из которых имеет один тон, общий с триадой тоника, мы получаем полная серия тонов для большой шкалы C:

9: 8

5: 4

4: 3

3: 2

5: 3

15: 8

Эта шкала состоит из три разных интервала: мажорный тон 9/8, минорный тон 10/9 и мажорный тон полутон 16/15. Поэтому при смене тоника мы будем приобретать острые предметы и предметы различной природы, чтобы сохранить рамки шкалы, и сами ноты оригинальной шкалы будут в в некоторых случаях приходится увеличивать или уменьшать на одну запятую (разница между мажорным и минорным тоном).
Те кто знаком с Теорией Небесного Родни Коллина Влияние заметит, что Просто интонация — это шкала, которую он относится к его великой работе по октавам, умножив на 24.

Масштаб Зарлино (Just Intonation) — это в основном смесь нот, созданных квинтами, что позволяет делать правильные транспозиции и заметки, гармонические интервалы; поэтому на практике используются две разные системы вместе, что приводит к неудобным транспозициям.

г. Средний тон

В музыкальной практике, особенно при игре с ключевыми инструментами или простой модуляцией клавиш, Just Intonation вызывает множество трудностей, в основном из-за факт мажорных и минорных тонов.Два разных интервала по этой причине тон в этой шкале был изменен во время 17-го века в среднее или среднее из мажорного и минорного тона. поскольку эти два тона вместе составляют большую треть, средний тон равен до половины основной трети, или 193 цента.

Этот темперамент не неожиданно называется средним тоном темперамента, или средним тоном 1: 4 (квинты все равны, но были смягчены на 5,5 цента, четверть синтонической запятой) и был наиболее часто используемым темпераментом в Музыка барокко.

Возникли проблемы с энгармоническими нотами. Два диатонических полутона не складываются чтобы придать (полный) тон. Среднее полутона составляет 117,5 цента. Так что если желает играть более чем в шести мажорных и трех минорных тональностях, там это беда. Это потому, что гармонически эквивалентные ноты не будут имеют одинаковую частоту. Кроме того, в этом темпераменте есть настоящая фальшивые банкноты, называемые «волчьи банкноты», из-за 3,5 цента короткая пятая, поэтому круг не успеет замкнуться на 12 х 3.5 центов = 42 цента.

равно Темперамент

Идеальный компромисс появляется в Равной Температуре, которая представляет собой круговой темперамент. Пифагорейская запятая (примерно 24 цента) означает круг слишком большой. Если 12 идеальных пятых –702 цента — равномерно распределены, но сжимаются на 2 цента каждый, круг пятых будут замкнуты в круг.
В в конце 17-го и 18-го веков ряд круговых темпераментов были использованы с использованием этого устройства.Часто говорят, что Дж. 48 прелюдий и фуг Баха были написаны для демонстрации эффективность равного темперамента. Однако недавнее исследование (Barnes 1979) показал, что он, вероятно, написал их для циркуляра темперамент, подобный тому, который придумал Веркмайстер (известный как Werckmeister III), где распределение пятых было неравным; несколько были на 6 центов меньше, некоторые были идеальными.

Равный темперамент как мы знаем, что это совершенно одинаково распределенные, немного уменьшенные квинты (700 центов), которые одним ударом снимает вопрос о разных частотах энгармонического примечания и ограничения модуляции.
Октава делится поровну на 12 полутонов по 100 центов. Соотношение частот для каждого из полутонов — корень двенадцатой октавы: (2/1) 1/12 = 1.059463094 … / 1.

У этого темперамента есть два гаммы, мажор и минор. Разница в третьем, шестом и седьмой, которые на полтона ниже в минорной гамме. Запись что в минорной гамме присутствуют те же интервалы, что и в крупный масштаб, хотя порядок другой.
ср не будет иметь дело с гармоническим минором или мелодическим минором шкала.

Давайте сравним в центах указанных выше шкал с помощью Just Diatonic Scale (Just Intonation) в качестве базы:

	Масштаб	С	D	E	F	G	А	Б	C ‘
Просто Диатонический		0	0	0	0	0	0	0	0
Пифагорейский		0	0	+22	0	0	+22	+22	0
Среднее Тон		0	-11	0	+5.5	-5,5	+5,5	-5,5	0
Равный Темперамент		0	-4	+14	+2	-2	+16	+12	0

дюйм западная культура Равный Темперамент утвердилась, и ее тональность настолько настроена в наших ушах, что звучит идеально, хотя третий и шестой должны создать проблемы, потому что они хорошенькие намного резче, чем более чистая и выразительная Just Intonation.

г. искусственный равный темперамент

Великий немец ученый XIX века Герман фон Гельмгольц, который также был способный музыкант, решительно выступил за Just Intonation шкала. Он утверждал в своей книге «Об ощущениях тона», что … смелые модуляционные скачки грозят полностью разрушить чувство тональность. » Далее он заявляет: «Музыка, основанная на темперированная гамма должна рассматриваться как несовершенная музыка… Если мы предположить или даже найти его красивым, это означает, что наше ухо систематически портится с детства ».

Профессор Гельмгольц привел много примеров прекрасного использования Just Intonation в пении с использованием английской системы «Tonic Sol Fa-ists», которая преодолел трудности модуляции, используя другой музыкальный система обозначений. Струнные и духовые инструменты также могут выполнять это; так могут современные клавиатуры.
дискуссии о равном темпераменте против справедливой интонации продолжается до настоящего времени.Дэниел Уайт разместил на своей веб-странице Tuning & Music Scales Theory провела глубокий анализ этого важно, заключая, что ET звучит «слаще», чем JT.

По сравнению с другими шкалы мы перешли, Равный темперамент не имеет определенного отношения между звуками, так как он потерял связь с простые соотношения. Чем сложнее соотношения, тем больше диссонантны аккорды. Мы привыкли к мутным звукам, но люди на Востоке, обученные модальной памяти и четкой гармонической отношения не могут понять значение западной музыки.
Равный темперамент, несмотря на его очевидную слабость, сделал его великие композиторы могут создавать красивую музыку с необычайное количество новых аккордов и модуляций.
В двадцатый век тенденция отхода от простых соотношений между нотами и звуком даже вдали от Equal Temperament проявился в атональной музыке.

Современное Додекафоническая музыка

В наше время число атональных масштабов был разработан для обслуживания нового додекафонного музыка (Шенберг, Берг, Веберн), где классическое понятие гармония и ритм растворяются.В основном древняя диатоническая гамма с пятью полными тонами и двумя полутонами заменена с чистой хроматической шкалой, которая является основным фактором изменения от мелодической тональной музыки до атональной додекафонической музыки.
Хотя я очень люблю нефигуративное искусство, современная атональная музыка все еще мне сложно спонтанно получать удовольствие. Образованные люди уверяют меня в новая красота в современной музыке, которую я слышу головой, но не сердцем.
Однако я заметил безразличие к классической музыке, и я привлекала ранняя европейская музыка и народная (мировая) музыка.

Мой Главное возражение против атональной додекафонической музыки заключается в ее отрешенность от физического мира. Шкала принадлежит невидимая область, потому что она создана отношениями далеко от небольшие числа, относящиеся к воспринимаемому миру и основным эмоции.
В древних музыкальных системах мы видели, как музыкальная гамма должна быть тесно связана с воспринимаемым миром представлены в основном в виде небольших пронумерованных соотношений (малое количество генерирующих квинты в циклической системе или простые гармонические отношения в модальной система).

Циклический и модальные номера

В этом мире пяти элементы, в которых мы живем, простое число больше пяти не может войти в систему звуков, представляющих мелодические или гармонические отношения.Китайская система циклических пятых даже отказывается выходить за рамки этого номер пять; все его интервалы выражаются степенями два или три. Число для циклических систем — три.
Некоторые современные теоретики используют термин «3 предельная шкала »и« 5 предельная шкала ».

Внедрение фактор пяти приводит нас к гармонической модальной шкале, из которой характерными интервалами являются основная шестая гармоника, 5/3, гармоническая мажорная треть, 5/4, мажорная треть, 6/5, мажорная полутон, 16/15 (24/3 * 5), минорный полутон, 25/24, (52/3 * 23) синтонный запятая, 81/80, (34/24 * 5) и так далее.
По сравнению с равными Темперамент, темперированный полутон примерно 1,059,463,094 / 1000000000 против основного полутона гармоники 16/15.

Число пять «Очеловечивает» музыку. Это делает музыку инструментом выражения осязаемой реальности. Введение высшего простого числа числа, такие как семь, выведут нас за пределы этой реальности в регионы, которые выходят за рамки нашего обычного восприятия и понимание.
Семерка тоже считается числом небесным. как адские регионы.На самом деле у нас нет возможности узнать, к какому сторона это может привести нас!

на мой взгляд глубоко прикоснуться к людям можно только если вы играете гармонично или тонально музыку, потому что эти тона принадлежат реальному миру и человеку, который ходит по Земле. Масштаб должен быть более или менее в соответствии с нижние гармоники в серии. В то, как мы слышим и анализируем звук, на самом деле очень похоже на стоячая волна в струне. Базилярная мембрана внутреннего уха ведет себя как «струна», а «программное обеспечение» в мозгу предназначен для поиска гармонических рядов.Это самый приятный — и самый простой. Все сводится к тому, что единственная мера для всех явлений — это человек.

ссылку тон

Перед началом концерта, эталонный тон, концертная высота, играет так, чтобы инструменты могли настроить их середину а ‘. В наше время высота звука была установлена на 440 Гц. по вторая Международная конференция по стандартному питчу в Лондоне в 1938 году. это более высокий тон по сравнению с более старым концертным шагом 435 Гц., который был введен французским правительством в 1859 году в сотрудничестве с такие музыканты, как Гектор Берлиоз, Мейербер и Россини.
концертная подача в прежние времена менялась в зависимости от страны и время. В книге Гельмгольца «Об ощущении тона» запись концертная площадка в Европе занимает много страниц. Характеристика для Западная музыка такова, что концертная подача произвольная. Это не имеет отношения к силам над человеком. Нет ссылки на земной или небесный приток, но только по искусственному стандарту.

Для старых китайцев настройка их основного тона, Кунг, была делом крайнего важность для их цивилизации; он должен был соответствовать Космический тон, чтобы небесное влияние могло быть направлено в общество музыкой.

Мы уже упоминали Расчеты Кусто (в его книге «Космическая октава»). Он связывает Гун к частоте Платонического года. Нота Платона Год обнаруживается как F в тоне Western Equal Temperament, что в 48 октавы с частотой 344.12 Гц.

Индейский метод носил характер медитации, поскольку музыкант не только должен настроить свой инструмент на тон в прелюдии, он также настраивает сам, и дает возможность сделать то же самое. Это длинное вступление необходимо, поскольку музыкантам нужно настраивать в «садджу», вечный, непрекращающийся тон. Согласно индийской традиции это означает изначальную вибрацию, которая называется нада и выражает универсальный ОМ.

Звук ОМ, согласно Кусто, соответствует примерно до-диез в малой октавы современной системы настройки (136 Гц), а до 32-й октавный тон земного года. Это означает, что при понижении тона 136 Гц на 32 октавы, результирующая частота будет такой же медленной, как времени, необходимого Земле, чтобы облететь Солнце.

Интересно обратите внимание, что индейцы пришли к этому тону, который мы можем вычислить математически, «просто» через интуицию и медитация.
(The Расчет: день состоит из 86 400 секунд. У тропического года есть 365 242 дня = 31 556 925 9747 секунд. Обратное значение умноженное на 232 = 136,10221 Гц.)
Концерт высота тона в западной музыке, которая составляет 440 Гц для средней ля, должна быть 435,92 Гц на основании ноты, соответствующей среднему солнечному дню, по словам Кусто.

“ Это ничего не значат, если у него нет таких качелей »
Те знакомые с джазовым (свинговым) музыкантом Дюком Эллингтоном, «Послушайте», как Элла Фицджеральд поет эту песню.Причина, по которой я буду в конце этой ноты, чтобы прояснить, что музыка — это больше, чем гаммы и правильный тюнинг. Музыка состоит из четырех основных элементов:
Мелодия, Ритм, гармония и интерпретация или намерение.

Имея это в виду, я продолжу с Звук Безмолвия, где я расширю закон октав на миры, отличные от масштабов и настройки, путем разработки метафизические свойства звука и музыки.

Отправьте мне комментарий: [email protected]

Индекс страница
Ссылки и литература.

Возможные ошибки, допущенные изучающими русский язык при произношении английских гласных

Фонетика. Его связь с другими отраслями языкознания.

Все разделы Ph. Связаны с грамматикой, лексикологией и стилистикой. Ф. формулирует правила произношения отдельных звуков и звуковых сочетаний.Через систему правил Ph. Связан с грамматикой и помогает правильно произносить формы единственного и множественного числа существительных, формы прошедшего времени и причастия прошедшего времени английских глаголов. Другой феномен Ph. Звукопередачи — это проявление разрыва Ph. С грамматикой. Иногда одна интонация может служить для выделения логического сказуемого предложения. Ф. связана со стилистикой через повторение слов, словосочетаний, звуков. Повторение — основа ритма, любительства.

Классификация английских гласных.

Первым, кто попытался описать и классифицировать гласный звук независимо от родного языка, был Даниэль Джон. Он описал систему из 8 гласных звуков сердца. Русские доктора классифицируют английские гласные по следующим принципам:

1) положение губ

2) зелье языка

3) степень напряженности и характер окончания гласной

4) длина

5) стабильность сочленения

По положению гласных губ делятся на округлые и неокругленные.[o:], [o], [u:], [u].

По положению гласных языка делятся на горизонтальные и вертикальные движения языка. Они делятся на: полностью назад [o, o:, u:], [oi, o]; назад выдвинутый [, u, a:], [ou, u]. Когда передняя часть языка поднята выше к твердому нёбу, называется передним. Они делятся на: полностью передние [i, e,], [ei, ai] передние убранные [i], [au].

По вертикальным движениям языка гласные делятся на:

высокий [i:, i, u, u:]

середина, половина, открытая [e,

низкий, открытый [

высокая-узкая вариация [i:, u:]

— широкая вариация [i, u]

средний — узкий вариант [

— широкий диапазон [

low — узкая вариация [

— широкий диапазон [

По степени напряженности долгие гласные определяются как напряженные, а краткие — как слабые.

По длине гласные делятся на долгие и короткие. Долгие гласные в английском языке — [

Краткие гласные — это [

По устойчивости артикуляции гласные делятся на монофтонги (простые гласные), дифтонги, дифтонгоиды.

Английские монофтонги [

В английском языке есть 2 дифтонгоида [i :, u:].

Дифтонг основан на способности гласной составлять слог.Элемент 1 ^-й дифтонга — это ядро, 2-й элемент ^-й — это скольжение. Дифтонг может падать — когда ядро сильнее, чем скольжение, подниматься, когда скольжение сильнее ядра.

[ei, ou, oi, au, ai] называются закрывающими

[] центрирование.

Возможные ошибки, допущенные изучающими русский язык при произношении гласных английского языка.

В системе русских гласных есть следующие особенности, которых нет в системе русских гласных:

1) долгие и короткие гласные [i: -i], o: -o], [u: -u], [a: -a], []

2) слегка закругленные, но не выпирающие гласные [u :, o:]

3) гласные, артикулируемые при ровном положении губ в [i:, i, e, ei]

4) очень длинные гласные, например []

5) втянутые вперед и выдвинуты назад [i, u, a:]

6) смешанный []

7) дифтонгоидное произношение [i: u] и стабильная артикуляция в произношении [o:]

8) диптонги [

В связи с этими особенностями российские студенты допускают следующие ошибки:

1) Не соблюдают количественный характер гласной (длина)

2) Не наблюдают качественной разницы в артикуляции таких гласных, как

(я: -i), (u: -u), (o: -o)

3) они заменяют английские гласные на аналогичные русские гласные.