Разное

Метод варда: Кластерный анализ

Кластерный анализ



Кластерный анализ


Кластерный анализ

  • Основная цель
  • Проверка статистической значимости
  • Области применения
  • Объединение (древовидная кластеризация)
    • Иерархическое дерево
    • Меры расстояния
    • Правила объединения или связи
  • Двувходовое объединение
    • Вводный обзор
    • Двувходовое объединение
  • Метод K средних
    • Пример
    • Вычисления
    • Интерпретация результатов

Основная цель

Термин кластерный анализ (впервые ввел Tryon, 1939) в действительности включает в себя набор различных алгоритмов классификации.

Общий вопрос, задаваемый исследователями во многих областях, состоит в том, как организовать наблюдаемые данные в наглядные структуры, т.е. развернуть таксономии. Например, биологи ставят цель разбить животных на различные виды, чтобы содержательно описать различия между ними. В соответствии с современной системой, принятой в биологии, человек принадлежит к приматам, млекопитающим, амниотам, позвоночным и животным. Заметьте, что в этой классификации, чем выше уровень агрегации, тем меньше сходства между членами в соответствующем классе. Человек имеет больше сходства с другими приматами (т.е. с обезьянами), чем с «отдаленными» членами семейства млекопитающих (например, собаками) и т.д. В последующих разделах будут рассмотрены общие методы кластерного анализа, см. Объединение (древовидная кластеризация), Двувходовое объединение и Метод K средних.

Проверка статистической значимости

Заметим, что предыдущие рассуждения ссылаются на алгоритмы кластеризации, но ничего не упоминают о проверке статистической значимости. Фактически, кластерный анализ является не столько обычным статистическим методом, сколько «набором» различных алгоритмов «распределения объектов по кластерам». Существует точка зрения, что в отличие от многих других статистических процедур, методы кластерного анализа используются в большинстве случаев тогда, когда вы не имеете каких-либо априорных гипотез относительно классов, но все еще находитесь в описательной стадии исследования. Следует понимать, что кластерный анализ определяет «наиболее возможно значимое решение». Поэтому проверка статистической значимости в действительности здесь неприменима, даже в случаях, когда известны p-уровни (как, например, в методе K средних).

Области применения

Техника кластеризации применяется в самых разнообразных областях. Хартиган (Hartigan, 1975) дал прекрасный обзор многих опубликованных исследований, содержащих результаты, полученные методами кластерного анализа. Например, в области медицины кластеризация заболеваний, лечения заболеваний или симптомов заболеваний приводит к широко используемым таксономиям. В области психиатрии правильная диагностика кластеров симптомов, таких как паранойя, шизофрения и т.д., является решающей для успешной терапии. В археологии с помощью кластерного анализа исследователи пытаются установить таксономии каменных орудий, похоронных объектов и т.д. Известны широкие применения кластерного анализа в маркетинговых исследованиях. В общем, всякий раз, когда необходимо классифицировать «горы» информации к пригодным для дальнейшей обработки группам, кластерный анализ оказывается весьма полезным и эффективным.

В начало

Объединение (древовидная кластеризация)

  • Иерархическое дерево
  • Меры расстояния
  • Правила объединения или связи

Общая логика

Приведенный в разделе Основная цель пример поясняет цель алгоритма объединения (древовидной кластеризации). Назначение этого алгоритма состоит в объединении объектов (например, животных) в достаточно большие кластеры, используя некоторую меру сходства или расстояние между объектами. Типичным результатом такой кластеризации является иерархическое дерево.

Иерархическое дерево

Рассмотрим горизонтальную древовидную диаграмму. Диаграмма начинается с каждого объекта в классе (в левой части диаграммы). Теперь представим себе, что постепенно (очень малыми шагами) вы «ослабляете» ваш критерий о том, какие объекты являются уникальными, а какие нет. Другими словами, вы понижаете порог, относящийся к решению об объединении двух или более объектов в один кластер.

В результате, вы связываете вместе всё большее и большее число объектов и агрегируете (объединяете) все больше и больше кластеров, состоящих из все сильнее различающихся элементов. Окончательно, на последнем шаге все объекты объединяются вместе. На этих диаграммах горизонтальные оси представляют расстояние объединения (в

вертикальных древовидных диаграммах вертикальные оси представляют расстояние объединения). Так, для каждого узла в графе (там, где формируется новый кластер) вы можете видеть величину расстояния, для которого соответствующие элементы связываются в новый единственный кластер. Когда данные имеют ясную «структуру» в терминах кластеров объектов, сходных между собой, тогда эта структура, скорее всего, должна быть отражена в иерархическом дереве различными ветвями. В результате успешного анализа методом объединения появляется возможность обнаружить кластеры (ветви) и интерпретировать их.

Меры расстояния

Объединение или метод древовидной кластеризации используется при формировании кластеров несходства или расстояния между объектами.

Эти расстояния могут определяться в одномерном или многомерном пространстве. Например, если вы должны кластеризовать типы еды в кафе, то можете принять во внимание количество содержащихся в ней калорий, цену, субъективную оценку вкуса и т.д. Наиболее прямой путь вычисления расстояний между объектами в многомерном пространстве состоит в вычислении евклидовых расстояний. Если вы имеете двух- или трёхмерное пространство, то эта мера является реальным геометрическим расстоянием между объектами в пространстве (как будто расстояния между объектами измерены рулеткой). Однако алгоритм объединения не «заботится» о том, являются ли «предоставленные» для этого расстояния настоящими или некоторыми другими производными мерами расстояния, что более значимо для исследователя; и задачей исследователей является подобрать правильный метод для специфических применений.

Евклидово расстояние. Это, по-видимому, наиболее общий тип расстояния. Оно попросту является геометрическим расстоянием в многомерном пространстве и вычисляется следующим образом:

расстояние(x,y) = {i (xi — yi)2 }1/2

Заметим, что евклидово расстояние (и его квадрат) вычисляется по исходным, а не по стандартизованным данным. Это обычный способ его вычисления, который имеет определенные преимущества (например, расстояние между двумя объектами не изменяется при введении в анализ нового объекта, который может оказаться выбросом). Тем не менее, на расстояния могут сильно влиять различия между осями, по координатам которых вычисляются эти расстояния. К примеру, если одна из осей измерена в сантиметрах, а вы потом переведете ее в миллиметры (умножая значения на 10), то окончательное евклидово расстояние (или квадрат евклидова расстояния), вычисляемое по координатам, сильно изменится, и, как следствие, результаты кластерного анализа могут сильно отличаться от предыдущих.

Квадрат евклидова расстояния. Иногда может возникнуть желание возвести в квадрат стандартное евклидово расстояние, чтобы придать большие веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом (см. также замечания в предыдущем пункте):

расстояние(x,y) = i (xi — yi)2

Расстояние городских кварталов (манхэттенское расстояние). Это расстояние является просто средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако отметим, что для этой меры влияние отдельных больших разностей (выбросов) уменьшается (так как они не возводятся в квадрат). Манхэттенское расстояние вычисляется по формуле:

расстояние(x,y) = i |xi — yi|

Расстояние Чебышева. Это расстояние может оказаться полезным, когда желают определить два объекта как «различные», если они различаются по какой-либо одной координате (каким-либо одним измерением). Расстояние Чебышева вычисляется по формуле:

расстояние(x,y) = Максимум|xi — yi|

Степенное расстояние. Иногда желают прогрессивно увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Это может быть достигнуто с использованием

степенного расстояния. Степенное расстояние вычисляется по формуле:

расстояние(x,y) = (i |xi — yi|p)1/r

где r и p — параметры, определяемые пользователем. Несколько примеров вычислений могут показать, как «работает» эта мера. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра — r и p, равны двум, то это расстояние совпадает с расстоянием Евклида.

Процент несогласия. Эта мера используется в тех случаях, когда данные являются категориальными. Это расстояние вычисляется по формуле:

расстояние(x,y) = (Количество xi yi)/ i

Правила объединения или связи

На первом шаге, когда каждый объект представляет собой отдельный кластер, расстояния между этими объектами определяются выбранной мерой. Однако когда связываются вместе несколько объектов, возникает вопрос, как следует определить расстояния между кластерами? Другими словами, необходимо правило объединения или связи для двух кластеров. Здесь имеются различные возможности: например, вы можете связать два кластера вместе, когда любые два объекта в двух кластерах ближе друг к другу, чем соответствующее расстояние связи. Другими словами, вы используете «правило ближайшего соседа» для определения расстояния между кластерами; этот метод называется методом одиночной связи. Это правило строит «волокнистые» кластеры, т.е. кластеры, «сцепленные вместе» только отдельными элементами, случайно оказавшимися ближе остальных друг к другу. Как альтернативу вы можете использовать соседей в кластерах, которые находятся дальше всех остальных пар объектов друг от друга. Этот метод называется метод полной связи. Существует также множество других методов объединения кластеров, подобных тем, что были рассмотрены.

Одиночная связь (метод ближайшего соседа). Как было описано выше, в этом методе расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами (ближайшими соседями) в различных кластерах. Это правило должно, в известном смысле, нанизывать объекты вместе для формирования кластеров, и результирующие кластеры имеют тенденцию быть представленными длинными «цепочками».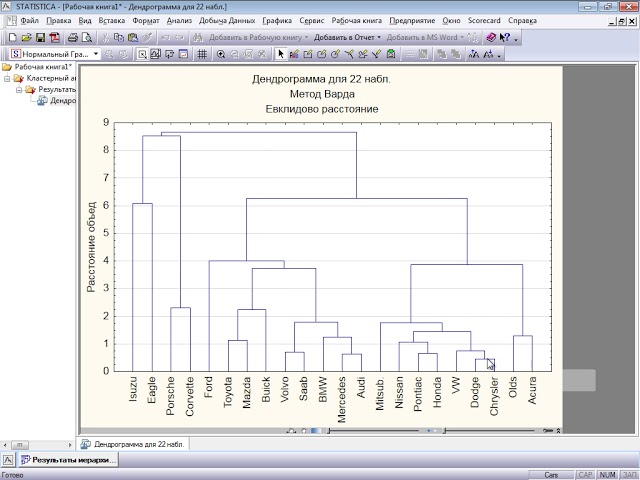

Полная связь (метод наиболее удаленных соседей). В этом методе расстояния между кластерами определяются наибольшим расстоянием между любыми двумя объектами в различных кластерах (т.е. «наиболее удаленными соседями»). Этот метод обычно работает очень хорошо, когда объекты происходят на самом деле из реально различных «рощ». Если же кластеры имеют в некотором роде удлиненную форму или их естественный тип является «цепочечным», то этот метод непригоден.

Невзвешенное попарное среднее. В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты в действительности формируют различные «рощи», однако он работает одинаково хорошо и в случаях протяженных («цепочного» типа) кластеров. Отметим, что в своей книге Снит и Сокэл (Sneath, Sokal, 1973) вводят аббревиатуру UPGMA для ссылки на этот метод, как на метод невзвешенного попарного арифметического среднего — unweighted pair-group method using arithmetic averages.

Взвешенное попарное среднее. Метод идентичен методу невзвешенного попарного среднего, за исключением того, что при вычислениях размер соответствующих кластеров (т.е. число объектов, содержащихся в них) используется в качестве весового коэффициента. Поэтому предлагаемый метод должен быть использован (скорее даже, чем предыдущий), когда предполагаются неравные размеры кластеров. В книге Снита и Сокэла (Sneath, Sokal, 1973) вводится аббревиатура WPGMA для ссылки на этот метод, как на метод взвешенного попарного арифметического среднего — weighted pair-group method using arithmetic averages.

Невзвешенный центроидный метод. В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести. Снит и Сокэл (Sneath and Sokal (1973)) используют аббревиатуру UPGMC для ссылки на этот метод, как на метод невзвешенного попарного центроидного усреднения — unweighted pair-group method using the centroid average.

Взвешенный центроидный метод (медиана). тот метод идентичен предыдущему, за исключением того, что при вычислениях используются веса для учёта разницы между размерами кластеров (т.е. числами объектов в них). Поэтому, если имеются (или подозреваются) значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего. Снит и Сокэл (Sneath, Sokal 1973) использовали аббревиатуру WPGMC для ссылок на него, как на метод невзвешенного попарного центроидного усреднения — weighted pair-group method using the centroid average.

Метод Варда. Этот метод отличается от всех других методов, поскольку он использует методы дисперсионного анализа для оценки расстояний между кластерами. Метод минимизирует сумму квадратов (SS) для любых двух (гипотетических) кластеров, которые могут быть сформированы на каждом шаге. Подробности можно найти в работе Варда (Ward, 1963). В целом метод представляется очень эффективным, однако он стремится создавать кластеры малого размера.

Для обзора других методов кластеризации, см. Двухвходовое объединение и Метод K средних.

В начало

Двувходовое объединение

  • Вводный обзор
  • Двувходовое объединение

Вводный обзор

Ранее этот метод обсуждался в терминах «объектов», которые должны быть кластеризованы (см. Объединение (древовидная кластеризация)). Во всех других видах анализа интересующий исследователя вопрос обычно выражается в терминах наблюдений или переменных. Оказывается, что кластеризация, как по наблюдениям, так и по переменным может привести к достаточно интересным результатам. Например, представьте, что медицинский исследователь собирает данные о различных характеристиках (переменные) состояний пациентов (наблюдений), страдающих сердечными заболеваниями. Исследователь может захотеть кластеризовать наблюдения (пациентов) для определения кластеров пациентов со сходными симптомами. В то же самое время исследователь может захотеть кластеризовать переменные для определения кластеров переменных, которые связаны со сходным физическим состоянием.

Двувходовое объединение

После этого обсуждения, относящегося к тому, кластеризовать наблюдения или переменные, можно задать вопрос, а почему бы не проводить кластеризацию в обоих направлениях? Модуль Кластерный анализ содержит эффективную двувходовую процедуру объединения, позволяющую сделать именно это. Однако двувходовое объединение используется (относительно редко) в обстоятельствах, когда ожидается, что и наблюдения и переменные одновременно вносят вклад в обнаружение осмысленных кластеров.

Так, возвращаясь к предыдущему примеру, можно предположить, что медицинскому исследователю требуется выделить кластеры пациентов, сходных по отношению к определенным кластерам характеристик физического состояния. Трудность с интерпретацией полученных результатов возникает вследствие того, что сходства между различными кластерами могут происходить из (или быть причиной) некоторого различия подмножеств переменных. Поэтому получающиеся кластеры являются по своей природе неоднородными. Возможно это кажется вначале немного туманным; в самом деле, в сравнении с другими описанными методами кластерного анализа (см. Объединение (древовидная кластеризация) и Метод K средних), двувходовое объединение является, вероятно, наименее часто используемым методом. Однако некоторые исследователи полагают, что он предлагает мощное средство разведочного анализа данных (за более подробной информацией вы можете обратиться к описанию этого метода у Хартигана (Hartigan, 1975)).

В начало

Метод K средних

  • Пример
  • Вычисления
  • Интерпретация результатов

Общая логика

Этот метод кластеризации существенно отличается от таких агломеративных методов, как Объединение (древовидная кластеризация) и Двувходовое объединение. Предположим, вы уже имеете гипотезы относительно числа кластеров (по наблюдениям или по переменным). Вы можете указать системе образовать ровно три кластера так, чтобы они были настолько различны, насколько это возможно. Это именно тот тип задач, которые решает алгоритм метода K средних. В общем случае метод K средних строит ровно K различных кластеров, расположенных на возможно больших расстояниях друг от друга.

Пример

В примере с физическим состоянием (см. Двувходовое объединение), медицинский исследователь может иметь «подозрение» из своего клинического опыта, что его пациенты в основном попадают в три различные категории. Далее он может захотеть узнать, может ли его интуиция быть подтверждена численно, то есть, в самом ли деле кластерный анализ K средних даст три кластера пациентов, как ожидалось? Если это так, то средние различных мер физических параметров для каждого кластера будут давать количественный способ представления гипотез исследователя (например, пациенты в кластере 1 имеют высокий параметр 1, меньший параметр 2 и т. д.).

Вычисления

С вычислительной точки зрения вы можете рассматривать этот метод, как дисперсионный анализ (см. Дисперсионный анализ) «наоборот». Программа начинает с K случайно выбранных кластеров, а затем изменяет принадлежность объектов к ним, чтобы: (1) - минимизировать изменчивость внутри кластеров, и (2) — максимизировать изменчивость между кластерами. Данный способ аналогичен методу «дисперсионный анализ (ANOVA) наоборот» в том смысле, что критерий значимости в дисперсионном анализе сравнивает межгрупповую изменчивость с внутригрупповой при проверке гипотезы о том, что средние в группах отличаются друг от друга. В кластеризации методом K средних программа перемещает объекты (т.е. наблюдения) из одних групп (кластеров) в другие для того, чтобы получить наиболее значимый результат при проведении дисперсионного анализа (ANOVA).

Интерпретация результатов

Обычно, когда результаты кластерного анализа методом K средних получены, можно рассчитать средние для каждого кластера по каждому измерению, чтобы оценить, насколько кластеры различаются друг от друга. В идеале вы должны получить сильно различающиеся средние для большинства, если не для всех измерений, используемых в анализе. Значения F-статистики, полученные для каждого измерения, являются другим индикатором того, насколько хорошо соответствующее измерение дискриминирует кластеры.

Все права на материалы электронного учебника принадлежат компании StatSoft

Методы кластеризации

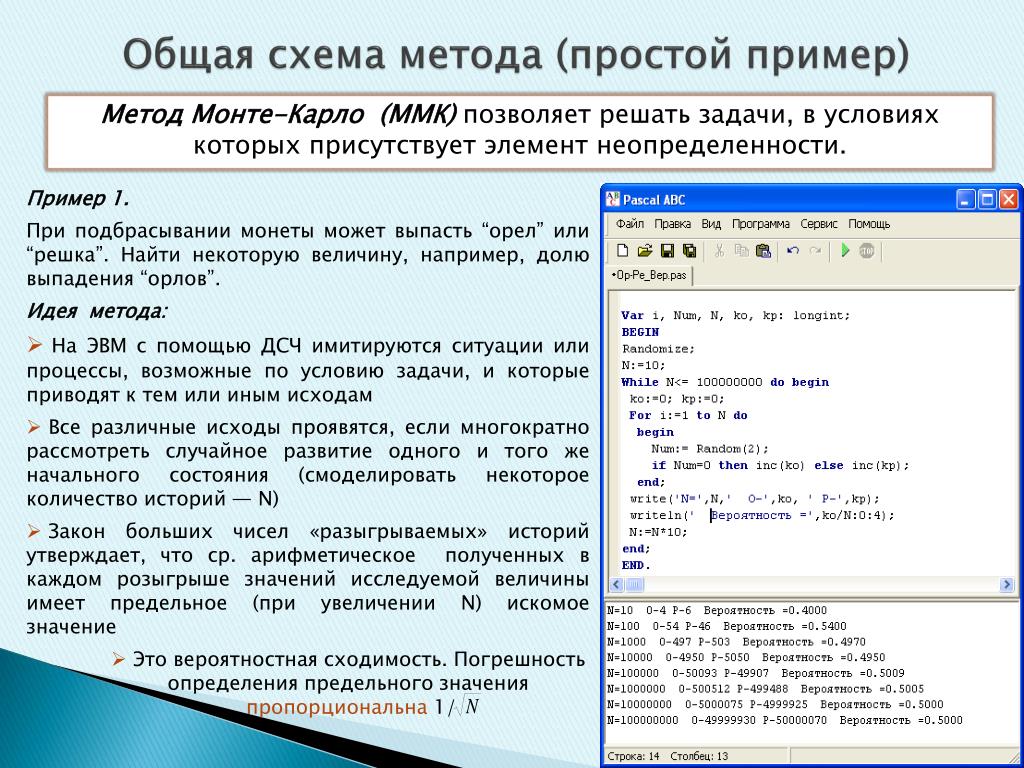
Основные метода кластеризации представлены на схеме 1.

Методы кластеризации

иерархические

неиерархические

агломеративные

методы связи

Дисперсионные методы

метод одиночной связи

метод полной связи

метод средней связи

Иерархическая кластеризация – характеризуется построением иерархии (древовидной структуры). Среди методов иерархической кластеризации выделяют агломеративные и дивизивные методы.

Агломеративная кластеризация – иерархический метод, при котором каждый объект первоначально находится в отдельном кластере. Кластеры формируют, группируя объекты каждый раз во все более и более крупные кластеры.

Разделяющая или дивизивная кластеризация – иерархический метод, при котором все объекты первоначально находятся в одном большом кластере, и кластеры формируют делением этого большого кластера на более мелкие

Обычно в маркетинговых исследованиях используют агломеративные методы, среди которых можно выделить:

Методы связи – агломеративные методы иерархической кластеризации, которые объединяют объекты в кластер, исходя из вычисленного расстояния между ними. В свою очередь методы связи подразделяются на:

  • метод одиночной связи – в основе этого метода лежит минимальное расстояние между объектами или правило «ближайшего соседа»

  • метод полной связи – аналогичен методу одиночной связи, за исключением того, что в его основе лежит максимальное расстояние между объектами или правило «дальнего соседа», то есть расстояние между двумя кластерами здесь – это расстояние между двумя самыми удаленными точками.

  • метод средней связи – действия аналогичны двум предыдущим методам, но в этом методе расстояние между двумя кластерами определяют как среднее значение всех расстояний, измеренных между объектами двух кластеров, при этом в каждую пару входят объекты из разных кластеров.

Дисперсионный метод – агломеративный метод иерархической кластеризации, в котором кластеры формируют так, чтобы минимизировать внутрикластерную дисперсию. Чаще всего используют метод Варда, когда кластеры формирую таким образом, чтобы минимизировать квадраты Евклидовых расстояний до кластерных средних. Для каждого кластера вычисляются средние для всех переменных, затем для каждого объекта вычисляют квадраты Евклидовых расстояний до кластерных средних, и эти квадраты расстояний суммируют для всех объектов, и на каждой стадии (при объединении) объединяют два кластера с наименьшим приростом полной внутрикластерной дисперсии.

Центроидный метод – расстояние между двумя кластерами представляет собой расстояние между их центроидами. Центроид – это средняя для всех переменных.

Из всех иерархических методов метод средней связи и метод Варда показывают наилучшие результаты по сравнению с другими методами.

К другим методам кластеризации относятся неиерархические методы или методы к-средних – это методы, при которых сначала определяется центр кластера, а затем группируют все объекты в переделах заданных от центра пороговых значений.

В последовательном пороговом методе выбирают центр кластера, и все объекты, находящиеся в пределах заданного от центра порогового значения, группируют вместе. Затем выбирают уже новый кластерный центр, и процесс повторяют для несгруппированных точек. Смысл в том, что если объект уже попал в какой-то кластер, то в дальнейшем уже не рассматривается как объект кластеризации.

Аналогично работает параллельный пороговый метод, но за исключением того, что одновременно выбирается несколько кластерных центров, и объекты в пределах порогового уровня группируют с ближайшим центром.

Метод оптимизирующего распределения – отличается от двух предыдущих пороговых методов тем, что объекты можно впоследствии перераспределить, чтобы оптимизировать суммарный критерий. Например, среднее внутрикластерное расстояние для данного числа кластеров.

Вывод: два главных недостатка неиерархических методов состоит в том, что число кластеров определяется заранее, и выбор кластерных центров происходит независимо, более того, результаты кластеризации могут зависеть от выбранных центров, а также от порядка наблюдений. Неиерархическая кластеризация быстрее иерархических методов, и ее выгодно использовать при большом числе объектов наблюдения. Но оптимально использовать оба метода кластеризации во взаимосвязи. Например, такие иерархические методы, как метод средней связи и метод Варда используют для получения оптимального числа кластеров и кластерных центроидов. Их потом используют в качестве исходных данных в методе оптимизирующего распределения.

Инструкция по методу Уорда | Американская ассоциация церковной музыки

  • Живой и систематический подход, Гисберт Брандт
  • Исследование метода преподавания музыки Уорда, Мэри Берри и О. Уилсон
  • Видео по Методу Уорда: Брандт в классе
  • Интервью с Гисбертом Брандтом
  • Интервью с Вилко Брауэрсом
  • Реформа церковной музыки, Джастин Уорд
  • Классические издания книг по методу Уорда
  • Список контактов Метода Уорда

ЧТО ТАКОЕ МЕТОД УОРДА?
Эми Зубербюлер

Метод Уорда в обучении музыке — это прогрессивный метод обучения детей начальной школы посредством обучения вокалу теории музыки, композиции и дирижированию. Метод был разработан для обучения американских католических школьников основам музыки, чтобы они могли петь обширный репертуар духовной музыки, являющейся частью традиции Римско-католической церкви. Метод Уорда уникален тем, что основан на григорианском пении.

ПРОИСХОЖДЕНИЕ

Жюстин Уорд, основательница метода, носящего ее имя, родилась 7 августа 1879 года. музыку, начатую Папой Пием X. Она разработала свой метод в ответ на просьбу о. Томас Э. Шилдс, председатель первого отдела образования Католического университета Америки. При написании своего метода Уорд объединила философию и педагогику Шилдса и музыкальные методы, используемые о. Джон Б. Янг, С.Дж. Родом из Эльзаса, Янг был отправлен в Америку в 1870-х годах и сыграл важную роль в обращении Уорда.

Когда был избран Папа Пий X и в Риме началась реформа духовной музыки, Янг помог поддержать ее в Нью-Йорке в качестве музыкального руководителя церкви Святого Франциска Ксавьера в Нью-Йорке. Янг помогал Уорд со многими музыкальными элементами ее метода, числовой записью, интонацией и вокальными упражнениями, которым он научился у французских музыкальных педагогов Пьера Галена и Эмиля Шеве, а также в школе обучения вокалу бельканто. Первые издания метода Уорда «Музыка первого и второго года» были опубликованы в 1919 г.13. В 1920 году Уорд познакомился и начал изучать григорианские песнопения с Домом Андре Мокеро, основателем Solesmes Method ритмической интерпретации григорианских песнопений. Под его влиянием она пересмотрела ритмические части своего метода в 1920-х годах и установила тот метод, который известен сегодня.

ВОСПИТАНИЕ В ПРАВДЕ И КРАСОТЕ

Один из первых психологов-педагогов в стране, о. Томас Шилдс считал, что с самых ранних лет необходимо развивать эмоции ребенка, чтобы привести к формированию достойного характера. В статье для «Католического образовательного обозрения» он однажды сказал: «Настоящие основы характера находятся не в интеллекте, а в эмоциях и воле, должным образом просветленных посредством интеллекта, и именно благодаря музыке и искусству воображение и эмоции могут быть достигнуты и эффективно развиты». Шилдс воспринимал это и как психолог, и как католический священник. Католическая церковь на протяжении всей своей истории поощряла искусство. Зная, что человек состоит из тела и духа, Церковь понимает потребность человека в чувственных, осязаемых вещах, связывающих тело и дух. С помощью метода Уорда дети знакомятся с правдой и красотой через музыку, поэтому они будут реагировать на эмоциональные стимулы более высокого порядка.

THAT ALL MAY SING

Шилдс учил, что информация должна быть представлена ​​ребенку таким образом, который соответствует стадии развития ребенка. Если ребенку дать правильный стимул в нужное время в развитии, любой ребенок должен быть в состоянии учиться. Предмет должен быть разбит на фундаментальные принципы. Каждый урок должен включать в себя процесс соотнесения известного с неизвестным. Затем ребенка можно стимулировать к использованию этих новых истин через личный опыт. Уорд применил эти принципы к музыке, разделив музыкальные элементы каждого урока. Дети открывают для себя вокальные и интонационные упражнения, считают метр и воспринимают ритм как движение. Они творчески используют каждый музыкальный элемент в упражнениях, играх и собственных композициях. Таким образом, когда детям в конце урока предъявляют новую песню, они легко могут отделить, а затем снова соединить содержащиеся в ней музыкальные элементы.

РИТМИЧЕСКИЕ МЕТОДЫ SOLESMES

Основатель метода Solesmes Моккеро не изобретал правила, которым нужно следовать при пении. Его идеи были более сложными, чем это. Он переопределил ритм в свете своего изучения древних и средневековых текстов. Существует много споров о ритме пения и методе Солесмес, и многие критики не могут понять подход Моккеро. Уорд, однако, смог взять принципы ритма и через движение тела выразить их таким образом, что их может начать понимать шестилетний ребенок. Мокеро похвалил Уорд за пересмотр ее метода. Будучи своей ученицей, Уорд не только усвоила знания своего учителя, но и расширила и развила их. Его учение теперь стало доступно всем людям, детям и взрослым, составляющим церковные собрания.

РОСТ

В 1920-е годы использование метода Уорда распространилось по всей территории Соединенных Штатов. В 1925 году Уорд привезла свой метод в Голландию. Под руководством Джозефа Леннарда он распространился как по католическим, так и по протестантским школам Нидерландов. Голландские правительственные чиновники заинтересовались этим методом и предоставили субсидии для обучения учителей. Метод начали использовать в государственных школах. Затем метод был представлен в Бельгии и Франции, а затем распространен на Англию, Ирландию, Новую Зеландию, Китай и Италию. Во время Второй мировой войны его использование распространилось по всей Центральной и Южной Америке. После войны он использовался в Канаде, Африке и на Дальнем Востоке. В 1972 государство Израиль ввело метод Уорда, предложив курс для лучших классов Государственного колледжа учителей музыки в Тель-Авиве.

ТУРБУЛЕНТНЫЕ ВРЕМЕНА

В эти бурные годы католическая церковь и вся ее католическая система образования столкнулись с трудностями. Соответственно, система не смогла привлечь клиентуру и, таким образом, лишилась финансовой поддержки. В то же время священники, монахини и братья, составлявшие основную часть фактически неоплачиваемого персонала американской католической системы образования, отказывались от своих профессий, да и от религиозной жизни во многих случаях. Не имея поддержки, метод Уорда встретил почти полное затмение.

ВОЗРОЖДЕНИЕ

Метод продолжает знакомиться с новыми поколениями каждый год.

______________

Эми Зубербюлер живет и преподает в Сан-Антонио, штат Техас.

Следуйте плану урока Брандта

Метод Уорда (метод минимальной дисперсии)


Кластеризация >


Что такое метод Уорда?

Метод Уорда (он же Метод минимальной дисперсии или Метод кластеризации минимальной дисперсии Уорда ) является альтернативой одноканальной кластеризации. Популярный в таких областях, как лингвистика, он нравится, потому что обычно создает компактные кластеры одинакового размера (Szmrecsanyi, 2012).

Как и большинство других методов кластеризации, метод Уорда требует больших вычислительных ресурсов. Однако метод Уорда требует значительно меньше вычислений, чем другие методы. Недостатком является то, что это обычно приводит к менее чем оптимальным кластерам. Тем не менее, полученные кластеры обычно достаточно хороши для большинства целей.

Индекс суммы квадратов, E

Как и другие методы кластеризации, метод Уорда начинается с n кластеров, каждый из которых содержит один объект. Эти кластеры n объединяются в один кластер, содержащий все объекты. На каждом шаге процесс создает новый кластер, который минимизирует дисперсию, измеряемую индексом E (также называемым индексом суммы квадратов ).

На каждом шаге выполняются следующие вычисления для нахождения E :

  1. Найдите среднее значение для каждого кластера.
  2. Вычислите расстояние между каждым объектом в определенном кластере и средним значением этого кластера.
  3. Уравнять отличия от шага 2.
  4. Суммируйте (сложите) квадраты значений из шага 3.
  5. Сложите все суммы квадратов из шага 4.

Чтобы выбрать новый кластер на каждом шаге, необходимо рассмотреть все возможные комбинации кластеров. Вся эта громоздкая процедура делает практически невозможным ее выполнение вручную, что делает компьютер необходимым для большинства наборов данных, содержащих более нескольких точек данных. Тем не менее, «Кластерный анализ для исследователей» Чарльза Ромесберга включает в себя очень подробный и простой пример для расчета E вручную на небольшом наборе данных (начиная со страницы 130).

Метод Уорда доступен для запуска во многих популярных программах, включая SPSS, SYSTAT и S-PLUS.

В SPSS:

  1. Нажмите «Анализ>Классификация>Иерархическая кластеризация».
  2. Нажмите «Метод»

  3. Выберите «Метод Уорда» в раскрывающемся меню «Кластерный метод».

Ссылки

Romesburg, C. (2004. Кластерный анализ для исследователей Lulu.com.
Szmrecsanyi, B. (2012). Grammatical Variation in British English Dialects: A Study in Corpus-Based Dialectometry. Cambridge University Press.

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Метод Уорда (Метод минимальной дисперсии)» Из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *