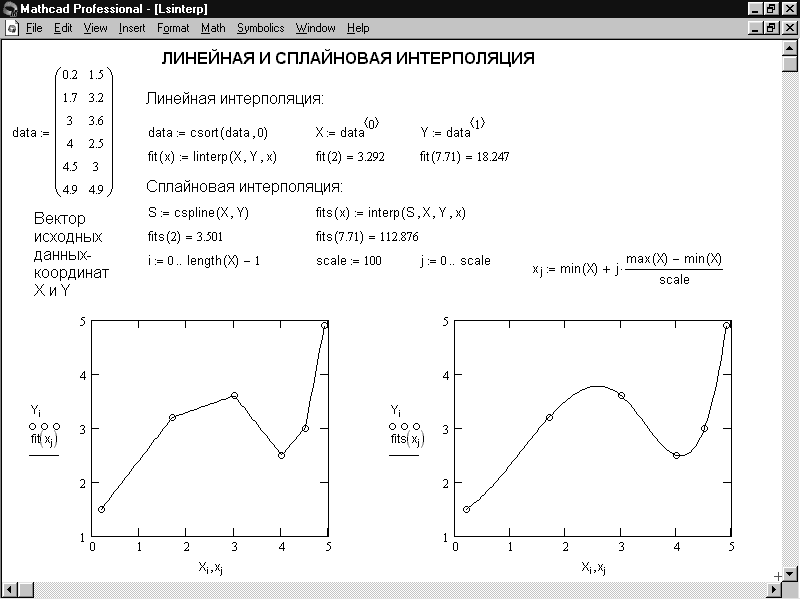
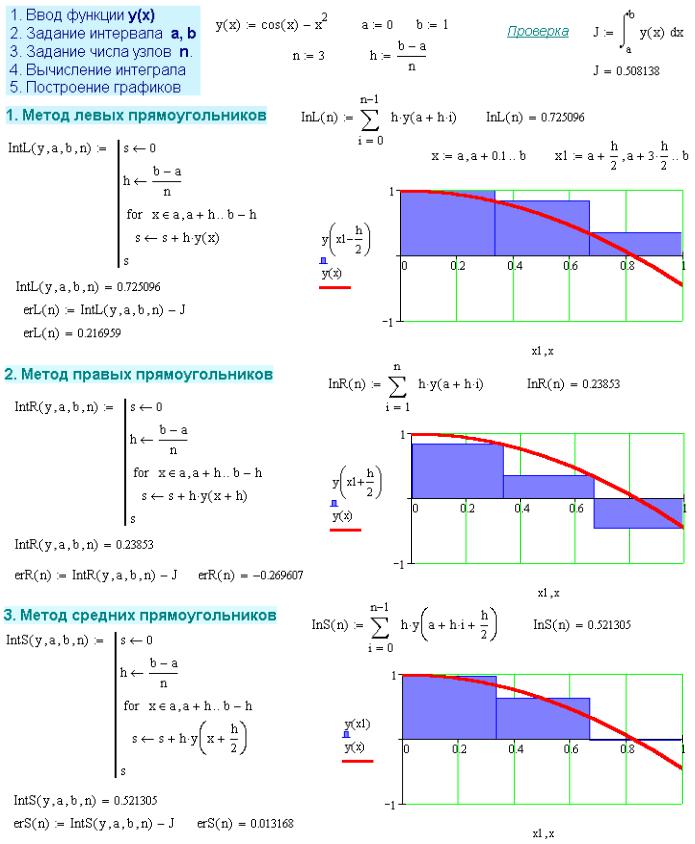
Метод дихотомии | MATHCAD | Mc-Plc.Ru
MATHCAD
Для примера выберем функцию у = х3– 75x.Для поиска экстремума в MathCAD методом дихотомии (от греч. dica – на две части и …tomh – сечение) воспользуемся программой-функцией. Чтобы её записать, введём имя будущей программы-функции Xmax. Затем нужно создать тело программы-функции, для чего открыть панель «Programming», выбрав в главном меню «Вид – Панели инструментов – Программирование», и на появившейся панели щёлкнуть левой кнопкой мыши на «Add line». После чего на экране появится вертикальная черта и вертикальный столбец с двумя полями для ввода операторов, образующих тело программы-функции:
.
Теперь заполним поля программы-функции операторами. Чтобы перейти в первое
сверху поле, нужно щёлкнуть на нём мышью, после чего ввести первый оператор
тела программы-функции. Так как самое нижнее поле всегда предназначено для
определения возвращаемого программой значения, то поля ввода для дополнительных
операторов открываются с помощью щелчка на кнопке «Add line»
панели программирования.
Для построения графика необходимо выбрать в главном меню «Вид – Панели инструментов –
График», далее на появившейся панели «Graph» выбрать
элемент «Декартов график», после
чего на рабочей области программы MathCAD появится область построения графика. По оси
ординат области построения графика необходимо ввести « y(x), y(Xmax)», а по оси абсцисс – «x, Xmax». Далее двойным щелчком левой
кнопки мыши по области построения графика необходимо вызвать панель форматирования
графика, на которой выбрать закладку «Трассировки»,
выделить мышью «trace2» и в поле «Символ» выбрать «dmnd».
Кроме того, для удобства можно установить диапазон значений по оси абсцисс
путём ввода соответствующих значений в области на оси x графика. Поскольку значения по оси
х изменяются от a = –10 до b =10, их
и введём.
Далее двойным щелчком левой
кнопки мыши по области построения графика необходимо вызвать панель форматирования
графика, на которой выбрать закладку «Трассировки»,
выделить мышью «trace2» и в поле «Символ» выбрать «dmnd».
Кроме того, для удобства можно установить диапазон значений по оси абсцисс
путём ввода соответствующих значений в области на оси x графика. Поскольку значения по оси
х изменяются от a = –10 до b =10, их
и введём.
Чтобы получить численное значение экстремума функции y(x), нужно написать в рабочей области MathCAD интересующую нас переменную и поставить знак равенства, после чего программа автоматически выведет значение экстремума. При Хmax = –5,063 получим уmax(Хmax) = 249,94.
Проверить результат машинного поиска экстремума функции у = х3 – 75x можно аналитически. Для этого приравняем нулю
её первую производную y‘ =
3х2– 75. При y‘ = 0 получаем x = ±5, что совпадает
с расчётами, сделанными на MathCAD. Тогда уmax(Хmax = –5) = 250, что соответствует машинному
расчёту.
График функции и результат поиска экстремума показан на рис. 1.
Рис. 1. График функции у = х3 – 75x и результат поиска экстремума (максимума) методом деления отрезка пополам
ЛАБОРАТОРНАЯ РАБОТА «МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ (ДИХОТОМИИ)»
ВВЕДЕНИЕ.
 F(x) = F'(x) =… = F (k — 1) (x) = 0.
F(x) = F'(x) =… = F (k — 1) (x) = 0.Задача отделения корней. Уточнение корней методом половинного деления (метод дихотомии). Бондаренко В.Ю., Китайчик В.Ю. Донской Государственный Технический Университет (ДГТУ) Ростов-на-Дону, Россия The
Методы решения нелинейного уравнения
Министерство общего и профессионального образования Российской Федерации МАТИ Российский Государственный технологический Университет им. К. Э. Циолковского ——————————————————————————————————————
ПодробнееВергазова Ольга Бухтияровна
УДК по дисциплине «Методы оптимизации» (160403) (519.677 Решения задач математического анализа и прикладных задач) для специальности 1604030065. Рецензенты: Фурсов Андрей Серафимович — кандидат физикоматематических
ПодробнееМЕТОДЫ БЕЗУСЛОВНОЙ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ
Министерство образования Российской федерации Новокузнецкий филиал институт Кемеровского государственного университета Кафедра информационных систем и управления МЕТОДЫ БЕЗУСЛОВНОЙ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ
ПодробнееОбразовательный портал «РЕШУ ЕГЭ» (
Применение производной к исследованию функций 1. На рисунке изображен график производной функции, определенной на интервале Найдите промежутки возрастания функции В ответе укажите сумму целых точек, входящих
На рисунке изображен график производной функции, определенной на интервале Найдите промежутки возрастания функции В ответе укажите сумму целых точек, входящих
Pascal 13. Решение нелинейных уравнений.
Pascal 13. Решение нелинейных уравнений. Нелинейные уравнения можно разделить на 2 класса — алгебраические и трансцендентные. Алгебраическими уравнениями называют уравнения, содержащие только алгебраические
ПодробнееМатематический анализ. Лекция 3.3
Московский Государственный Технический Университет им. Н.Э. Баумана Факультет Фундаментальные науки Кафедра Высшая математика Математический анализ Модуль 3. Дифференциальное исчисление функций одной переменной
ПодробнееРостов-на-Дону, Россия
ЛАБОРАТОРНАЯ РАБОТА «Сбалансированная транспортная задача. Распределение однородных ресурсов» Гамидов М.М. Донской государственный технический университет Ростов-на-Дону, Россия LABORATORY WORK of a «Balanced
Распределение однородных ресурсов» Гамидов М.М. Донской государственный технический университет Ростов-на-Дону, Россия LABORATORY WORK of a «Balanced
Математика (БкПл-100, БкК-100)
Математика (БкПл-100, БкК-100) М.П. Харламов 2009/2010 учебный год, 2-й семестр Лекция 5. Исследование функций с помощью производных 1 1. Понятие о производных высших порядков Опр. Пусть дана функция f(x)
ПодробнееЧисленное решение задач оптимизации
Цель работы: получение практических навыков построения алгоритмов решения задач оптимизации, их программной реализации на компьютере, оценки погрешности решения, сравнение эффективности различных методов
ПодробнееB14 (повышенный уровень, время 6 мин)
B14 (повышенный уровень, время 6 мин) Тема: Анализ программы с подпрограммами. Что нужно знать: функция это вспомогательный алгоритм, который возвращает некоторое значение результат в Паскале функция располагается
Что нужно знать: функция это вспомогательный алгоритм, который возвращает некоторое значение результат в Паскале функция располагается
Чтение графиков функций
Материалы для выполнения внеаудиторной (домашней самостоятельной работы) нацеленные на устранение пробелов знаний и умений по дисциплине «Математика: алгебра и начала математического анализа, геометрия»
Тема 9 «Функция. Свойства функций»
Тема 9 «Функция. Свойства функций» Пусть X некоторое непустое множество действительных чисел. И пусть указан закон f, по которому каждому числу х ϵ X ставится в соответствие единственное число y ϵ Y, обозначаемое
ПодробнееЛабораторная работа 2
Лабораторная работа Цель работы: Закрепление навыков работы с основными синтаксическими конструкциями языка Си и умения организовывать циклы и выполнять вычисления.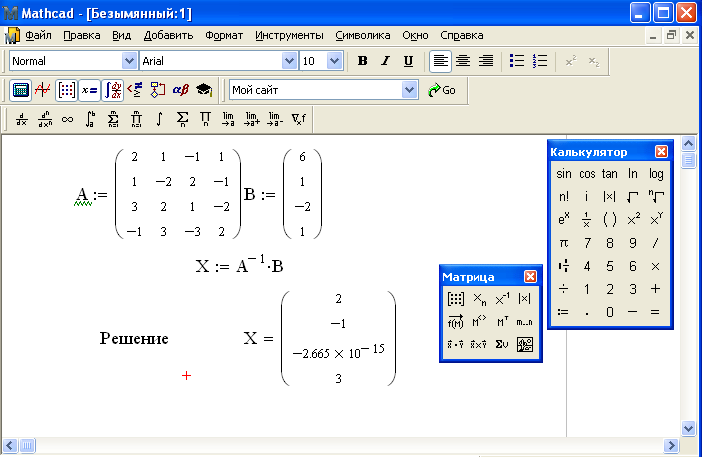 . ТЕОРЕТИЧЕСКАЯ ЧАСТЬ.. Методы решения
. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ.. Методы решения
Тема 39. «Производные функций»
Тема 39. «Производные функций» Функция Производной функции в точке х 0 называется предел отношения приращения функции к приращению переменной, то есть = lim = lim + ( ) Таблица производных: Производная
ПодробнееB14 (повышенный уровень, время 6 мин)
B14 (повышенный уровень, время 6 мин) Тема: Анализ программы с подпрограммами. Что нужно знать: функция это вспомогательный алгоритм, который возвращает некоторое значение результат в Паскале функция располагается
ПодробнееМЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ
Министерство образования и науки Российской федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Тихоокеанский государственный университет»
Подробнее ОДНОМЕРНАЯ ОПТИМИЗАЦИЯ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА НИКОЛАЯ II» Кафедра «Высшая и вычислительная математика»
ПодробнееМетоды решения нелинейных уравнений
Лекция стр. Лекция Методы решения нелинейных уравнений Постановка задачи Дано: нелинейное уравнение f () =, где f () функция определенная и непрерывная на некотором промежутке. Требуется найти корни уравнения,
Лекция Методы решения нелинейных уравнений Постановка задачи Дано: нелинейное уравнение f () =, где f () функция определенная и непрерывная на некотором промежутке. Требуется найти корни уравнения,
2 Численные методы решения уравнений.
2 Численные методы решения уравнений. 2.1 Классификация уравнений, их систем и методов решения. Уравнения и системы уравнений делятся на: 1) алгебраические: уравнение называется алгебраическим, если над
ПодробнееДифференциальное исчисление
Дифференциальное исчисление Основные понятия и формулы Определение 1 Производной функции в точке называется предел отношения приращения функции к приращению аргумента, при условии, что приращение аргумента
ПодробнееСИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ
УДК 004. 02 СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ Сидорова Т.В. (студ.) Южно-Российский Государственный Политехнический Университет ЮРГПУ (НПИ) им. М.И. Платова Новочеркасск, Россия Symbolic computation in MathCAD Sidorova
02 СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ Сидорова Т.В. (студ.) Южно-Российский Государственный Политехнический Университет ЮРГПУ (НПИ) им. М.И. Платова Новочеркасск, Россия Symbolic computation in MathCAD Sidorova
ОГЛАВЛЕНИЕ ВВЕДЕНИЕ… 8
ОГЛАВЛЕНИЕ ВВЕДЕНИЕ… 8 1. ЗАДАЧИ ПО РАЗРАБОТКЕ АЛГОРИТМОВ И ПРОГРАММ… 10 1.1. Линейные вычислительные процессы… 10 1.2. Циклические вычислительные процессы… 11 1.3. Вычислительные процессы с использованием
ПодробнееТема6. «Методы оптимизации.»
Министерство образования Республики Беларусь УО «Витебский государственный технологический университет» Тема6. «Методы оптимизации.» Кафедра теоретичской и прикладной математики. разработана доц. Е.Б.Дуниной
ПодробнееРисунок 1 Метод простых итераций
Информатика. Осень 2014. Уточнение корней уравнений. Для численного решения алгебраических уравнений разработано множество итерационных методов (методов последовательного приближения к точному значению)
Осень 2014. Уточнение корней уравнений. Для численного решения алгебраических уравнений разработано множество итерационных методов (методов последовательного приближения к точному значению)
Задание 8. Варганова Л.Ю
Задание 8 y f (x) у x 0 х Варганова Л.Ю Кодификатор элементов содержания Кодификатор требований http://shpargalkaege.ru/egeb8 Повторить материал по темам: Производная Понятие о производной функции, геометрический
ПодробнееМатематический анализ
Кафедра математики и информатики Математический анализ Учебно-методический комплекс для студентов ВПО, обучающихся с применением дистанционных технологий Модуль 4 Приложения производной Составитель: доцент
ПодробнееИССЛЕДОВАНИЕ ФУНКЦИЙ
Министерство образования Российской Федерации Российский государственный университет нефти и газа имени И. М. Губкина В.И. Иванов С.И. Васин Методические указания к изучению темы ИССЛЕДОВАНИЕ ФУНКЦИЙ (для
М. Губкина В.И. Иванов С.И. Васин Методические указания к изучению темы ИССЛЕДОВАНИЕ ФУНКЦИЙ (для
Моделирование в электроэнергетике — Численные методы решения нелинейных уравнений. Метод хорд.
Численные методы решения нелинейных уравнений. Метод хорд.
Метод хорд (метод также известен как Метод секущих) один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения . Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность .
В отличие от метода половинного деления, метод хорд предлагает, что деление рассматриваемого интервала будет выполняться не в его середине, а в точке пересечения хорды с осью абсцисс (ось — Х). Следует отметить, что под хордой понимается отрезок, который проведен через точки рассматриваемой функции по концам рассматриваемого интервала. Рассматриваемый метод обеспечивает более быстрое нахождение корня, чем метод половинного деления, при условии задания одинакового рассматриваемого интервала.
Следует отметить, что под хордой понимается отрезок, который проведен через точки рассматриваемой функции по концам рассматриваемого интервала. Рассматриваемый метод обеспечивает более быстрое нахождение корня, чем метод половинного деления, при условии задания одинакового рассматриваемого интервала.
Геометрически метод хорд эквивалентен замене кривой хордой, проходящей через точки и (см. рис.1.).
Рис.1. Построение отрезка (хорды) к функции .
Уравнение прямой (хорды), которая проходит через точки А и В имеет следующий вид:
Данное уравнение является типовым уравнением для описания прямой вы декартовой системе координат. Наклон кривой задается по ординате и абсциссе с помощью значений в знаменателе и , соответственно.
Для точки пресечения прямой с осью абсцисс записанное выше уравнение перепишется в следующем виде:
В качестве нового интервала для прохождения итерационного процесса выбираем один из двух или , на концах которого функция принимает значения разных знаков. Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:
Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:
или .
Итерационный процесс уточнения корня заканчивается, когда условие близости двух последовательных приближений станет меньше заданной точности, т.е.
.
Рис.2. Пояснение к определению погрешности расчета.
Следует отметить, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.
Алгоритм нахождения корня нелинейного уравнения по методу хорд
1. Найти начальный интервал неопределенности одним из методов отделения корней. Задать погрешность расчета (малое положительное число ) и начальный шаг итерации ().
2. Найти точку пересечения хорды с осью абсцисс:
3. Необходимо найти значение функции в точках , и . Далее необходимо проверить два условия:
Необходимо найти значение функции в точках , и . Далее необходимо проверить два условия:
— если выполняется условие , то искомый корень находится внутри левого отрезка положить, ;
— если выполняется условие , то искомый корень находится внутри правого отрезка принять , .
В результате находится новый интервал неопределенности, на котором находится искомых корень уравнения:
4. Проверяем приближенное значение корня уравнения на предмет заданной точности, в случае:
— если разность двух последовательных приближений станет меньше заданной точности , то итерационный процесс заканчивается. Приближенное значение корня определяется по формуле:
— если разность двух последовательных приближений не достигает необходимой точности , то необходимо продолжить итерационный процесс и перейти к п.2 рассматриваемого алгоритма.
В качестве примера, рассмотрим решение нелинейного уравнения методом хорд. Корень необходимо найти в рассматриваемом диапазоне с точностью .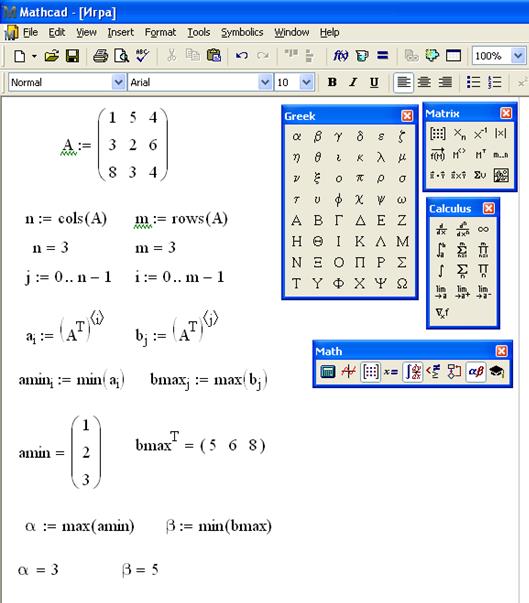
Вариант решения нелинейного уравнения в программном комплексе MathCAD.
Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага итерации представлены в графической форме (см. рис.1).
Рис.1. Результаты расчета по методу хорд
Для обеспечения заданной точности при поиске уравнения в диапазоне необходимо выполнить 6 итераций. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением: .
Примечание:
Модификацией данного метода является метод ложного положения (False Position Method), который отличается от метода секущих только тем, что всякий раз берутся не последние 2 точки, а те точки, которые находятся вокруг корня.
Следует отметить, что в случае если от нелинейной функции можно взять вторую производную алгоритм поиска может быть упрощен. Предположим, что вторая производная сохраняет постоянный знак, и рассмотрим два случая:
Предположим, что вторая производная сохраняет постоянный знак, и рассмотрим два случая:
Случай №1:
Из первого условия получается, что неподвижной стороной отрезка является – сторона a.
Случай №2:
Из второго условия получается, что неподвижной стороной отрезка является – сторона b.
В общем виде, для выявления неподвижного конца можно записать следующее условие: , где или .
Рис. 3. Примеры убывающей или возрастающей функции
Таким образом, в зависимости от вида функции получаются два выражения для упрощения поиска корня функции:
— если функция соответствует первому случаю (см. рис. 3), тогда формула будет иметь следующий вид:
, где k=0,1,2,…
— если функция соответствует второму случаю (см. рис. 3), тогда формула будет иметь следующий вид:
, где k=0,1,2,…
Случай сводится к рассматриваемому, если уравнение записать в форме: .
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
Численные методы на базе Mathcad
%PDF-1.6 % 43025 0 obj > endobj 43026 0 obj >/Font>>>/Fields[]>> endobj 43012 0 obj > endobj 43013 0 obj >stream Acrobat Distiller 5.0 (Windows)2009-02-06T14:01:22Z2013-05-23T17:41:15+04:002013-05-23T17:41:15+04:00PSCRIPT.DRV …… 4.0application/pdf
 ‘8’浉}h>3CsއH~*’S/؝%2|V9
‘8’浉}h>3CsއH~*’S/؝%2|V9Численные методы решения задач оптимизации
Численное решение задач оптимизации
Актуализация опорных знаний.
Численные методы одномерной оптимизации.
Метод дихотомии.
Метод золотого сечения.
Метод Фибоначчи.
Встроенные функции MathCAD для поиска локального минимума/максимума.
Пример использования.
Условный экстремум.
Экстремум функции многих переменных.
Контрольные вопросы.
Литература
Царегородцева, В. В. Вычислительная математика: лабораторный практикум по курсам «Численные методы» и «Вычислительная математика» для студентов всех специальностей и направлений подготовки / В. В. Царегородцева, Г. И. Севодина; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2014. – 78 с.
Актуализация опорных знаний
Постановка задачи оптимизации сводится к отысканию экстремума (наибольшего или наименьшего значения) скалярной функции f(х) одной или многих переменных.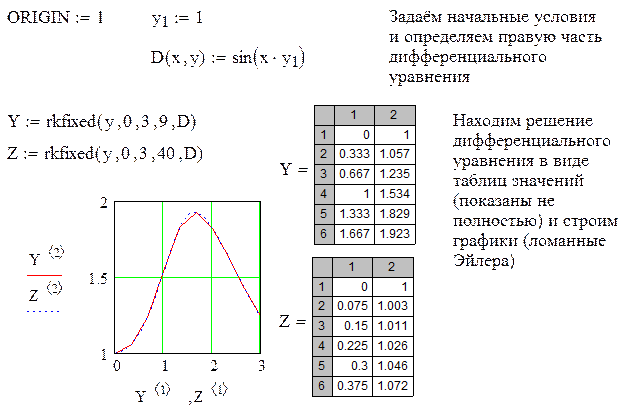
Оптимизируемую функцию f(x) называют целевой функцией, или критерием оптимальности.
Рассмотрим задачу поиска минимального значения функции f(x) одной переменной и запишем эту задачу следующим образом:
Значение х*, определяющее минимум целевой функции, называется оптимальным.
Отметим, что задачу максимизации можно заменить эквивалентной ей задачей минимизации или наоборот: минимальное значение функции равно максимальному значению функции , взятому с противоположным знаком, т. е.
Если на переменную х или некоторые функции, характеризующие качественные свойства объекта, накладываются ограничения в виде равенств или неравенств, то такую задачу называют задачей условной оптимизации. При отсутствии ограничений имеет место задача безусловной оптимизации.
На заданной области определения независимой переменной у функции может быть несколько локальных минимумов и максимумов, а также по одному глобальному минимуму и максимуму (рисунок 1).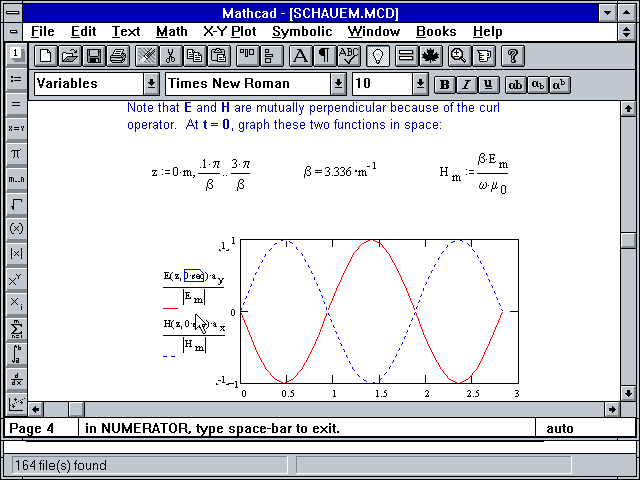 На отрезке – точки локального максимума, а – локального минимума. В точке реализуется глобальный максимум, а в точке – глобальный минимум.
На отрезке – точки локального максимума, а – локального минимума. В точке реализуется глобальный максимум, а в точке – глобальный минимум.
Рисунок 1 – Экстремумы функции
Как известно, в курсе математического анализа для определения точки оптимума используют необходимое условие существования экстремума – равенство нулю первой производной функции одной переменной или равенство нулю частных производных для функции многих переменных. Однако при решении практических задач вычисление производных функции бывает затруднительно или невозможно, если функция выражена неявно. В этих случаях приходится использовать аппарат численных методов для нахождения приближенного значения решения задачи с заранее заданной степенью точности.
На данном занятии рассматриваются только некоторые безградиентные методы одномерного поиска экстремума.
Численные методы одномерной оптимизации
К численным методам одномерной оптимизации относятся методы:
— дихотомического деления,
— золотого сечения,
— чисел Фибоначчи,
— полиномиальной аппроксимации
и ряд их модификаций.
Основная идея этих методов заключается в разбиении интервала поиска экстремума на несколько частей в определённом отношении, вычислении функции в этих точках и выборе наименьшего значения. После этого интервал поиска сужается, и процедура повторяется. Критерием окончания поиска может служить соотношение:
т. е. длина нового, суженного интервала поиска экстремума по модулю на i-й итерации меньше или равна заданной степени точности решения задачи.
Метод дихотомии
Пусть задан отрезок , на котором имеется один минимум (в общем случае нечетное число минимумов). Согласно методу дихотомического деления (рисунок 2, а) отрезок делят пополам и в точках, отстоящих от центра с отрезка на величину допустимой погрешности , рассчитывают значения целевой функции и .
Рисунок 2 – Одномерная минимизация:
а – дихотомическое деление; б – золотое сечение
Если окажется, что , то минимум находится на отрезке , если , то минимум – на , если ) – на .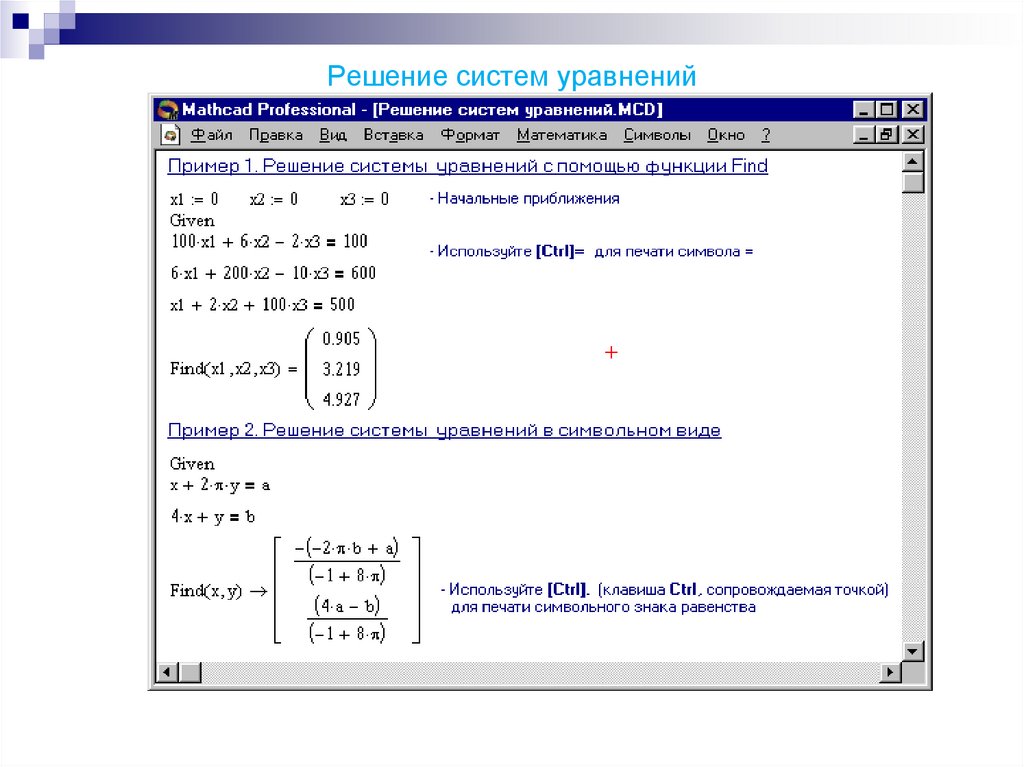 Таким образом, на следующем шаге вместо отрезка нужно исследовать суженный отрезок , или . Шаги повторяются, пока длина отрезка не уменьшится до величины погрешности . Таким образом, требуется не более n шагов, где n – ближайшее к целое значение, но на каждом шаге целевую функцию следует вычислять дважды.
Таким образом, на следующем шаге вместо отрезка нужно исследовать суженный отрезок , или . Шаги повторяются, пока длина отрезка не уменьшится до величины погрешности . Таким образом, требуется не более n шагов, где n – ближайшее к целое значение, но на каждом шаге целевую функцию следует вычислять дважды.
Пример 1. Пусть задана функция одной переменной вида
Найти её минимальное значение на интервале [2, 5 ] с заданной точностью методом дихотомического деления.
Программа, реализованная в системе MathCAD, приведена на рисунке 3. Для получения результата с заданной степенью точности потребовалось выполнить 19 итераций.
Метод золотого сечения
В соответствии с методом золотого сечения (рис. 2, б) внутри отрезка выделяют две промежуточные точки и на расстоянии от его конечных точек, где – длина отрезка. Затем вычисляют значения целевой функции в точках и . Если , то то минимум находится на отрезке , если , то на отрезке , если , то на отрезке .
Рис. 3. Программа поиска минимума методом дихотомического деления
Следовательно, вместо отрезка теперь можно рассматривать отрезок , или , т. е. длина отрезка уменьшилась не менее чем в
раз. Если подобрать значение α так, чтобы в полученном отрезке меньшей длины одна из промежуточных точек совпадала с промежуточной точкой от предыдущего шага, т. е. в случае выбора отрезка точка будет совпадать с точкой , а в случае выбора отрезка точка – с точкой , то это позволит сократить число вычислений целевой функции на всех шагах (кроме первого) в 2 раза.
Условие получения такого значения формулируется следующим образом:
откуда с учетом (*) имеем = 0,382. Это значение и называют золотым сечением.
Алгоритм поиска экстремума складывается из следующих этапов:
1) вычисляются значения функции на концах исходного интервала ;
2) вычисляются промежуточные точки интервала по формулам:
а также значения функции в этих точках;
3) по найденным значениям функции определяется её минимальное значение на интервале;
4) в зависимости от того в какой точке расположен минимум ( или ) определяется подынтервал, в котором локализован минимум – или ;
5) в новом интервале определяется точка по одной из формул п. 2 и итерационный процесс поиска продолжается с п. 3 до тех пор пока не будет достигнут критерий окончания поиска, например, такой:
2 и итерационный процесс поиска продолжается с п. 3 до тех пор пока не будет достигнут критерий окончания поиска, например, такой:
Пример 2. Для функции (см. пример 1) найти минимальное значение методом золотого сечения. Программа поиска решения приведена на рисунке 4. Здесь интервал поиска задан вектором с, а точки деления интервала в заданном соотношении заданы вектором z.
Процедура отсечения интервала задаётся функцией , в которой на каждой итерации из четырёх значений функции выбирается минимальное, а затем определяется новый соответствующий подынтервал. Координаты точек деления в новом интервале и соответствующие значения целевой функции находятся в процедуре-функции ming(eps, c, f).
Здесь задаётся число eps – точность решения задачи, вектор c и функция f. Как видно из приведенных результатов, для достижения заданной точности в методе золотого сечения требуется сделать 28 итераций. Этот метод гарантирует нахождение экстремума в самых неблагоприятных для поиска областях, однако обладает медленной сходимостью.
Рис.4. Метод золотого сечения
Метод Фибоначчи
Рис. 5. Метод Фибоначчи
Встроенные функции MathCAD для поиска локального минимума/максимума
Для численного решения задач поиска локального максимума и минимума в MathCAD имеются встроенные функции Minerr, Minimize и Maximize.
Чтобы найти глобальный максимум (или минимум), требуется сначала просканировать с некоторым шагом рассматриваемую область и вычислить все локальные значения и потом выбрать из них наибольший (наименьший). Другим вариантом будет простое сканирование с вычислением значений функции, позволяющее выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности.
Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно:
Пример использования
Всем аргументам функции предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примеры вычисления локальных экстремумов функций одной перемен-ной показаны на рисунке 7.7.
Примеры вычисления локальных экстремумов функций одной перемен-ной показаны на рисунке 7.7.
Если начальное приближение выбрать удачно, то итерационный процесс алгоритма сойдется к экстремуму функции, а если выбрать его вдали от него, на участке, где функция неограниченно возрастает, численный метод вообще не справится с задачей, выдавая сообщение об ошибке. Например, при поиске максимума (см. рисунок 7) начальное приближение (x = 10) выбрано далеко от области локального максимума, и поиск решения уходит в сторону увеличения функции.
Условный экстремум
Экстремум функции многих переменных
Контрольные вопросы
1. Сформулируйте постановку задачи оптимизации.
2. Что такое локальный и глобальный экстремумы?
3. Какие ограничения имеет применение классических методов поиска оптимума?
4. Назовите численные методы поиска оптимума функции одной переменной.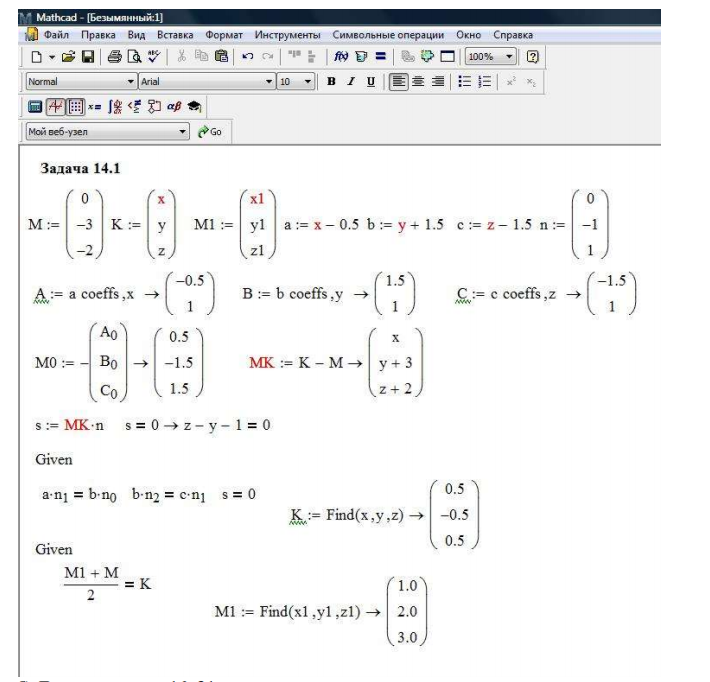
5. Разберите алгоритмы методов одномерного поиска оптимума: дихотомии, золотого сечения, чисел Фибоначчи.
6. Сформулируйте критерий окончания поиска решения в итерационных методах.
7. Какие встроенные в MathCAD функции для решения задачи оптимизации вы знаете?
8. Какие функции могут применяться для решения задачи условной оптимизации?
Практическое занятие. Инструкционная карта
на выполнение практического занятия по дисциплине «Компьютерная математика»Тема: Численное решение задач оптимизации
Цель работы: освоить численное решение задач одномерной оптимизации различными методами; изучить возможности пакета MathCAD для поиска экстремума функции одной и двух переменных
Норма времени: 2 часа.
После выполненных работ студент должен
знать: основные методы одномерной оптимизации: дихотомии, золотого сечения, Фибоначчи;
уметь: решать задачи оптимизации с использованием пакета MathCAD.
Оснащение рабочего места: ПК, инструкционные карты, конспект.
Вводный инструктаж.
Метод дихотомии (половинного деления).
Метод золотого сечения.
Метод Фибоначчи.
Встроенные функции MathCAD для поиска локального минимума/максимума.
Условный экстремум.
Экстремум функции нескольких переменных.
Задания для самостоятельного выполнения.
Задание 1 . Поиск минимума функции одной переменной.
Задание 2. Поиск оптимума функции двух переменных.
Контрольные вопросы.
Литература:
Царегородцева, В. В. Вычислительная математика: лабораторный практикум по курсам «Численные методы» и «Вычислительная математика» для студентов всех специальностей и направлений подготовки / В. В. Царегородцева, Г. И. Севодина; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2014. – 78 с.
Вводный инструктаж
Постановка задачи оптимизации сводится к отысканию экстремума (наибольшего или наименьшего значения) скалярной функции f(х) одной или многих переменных.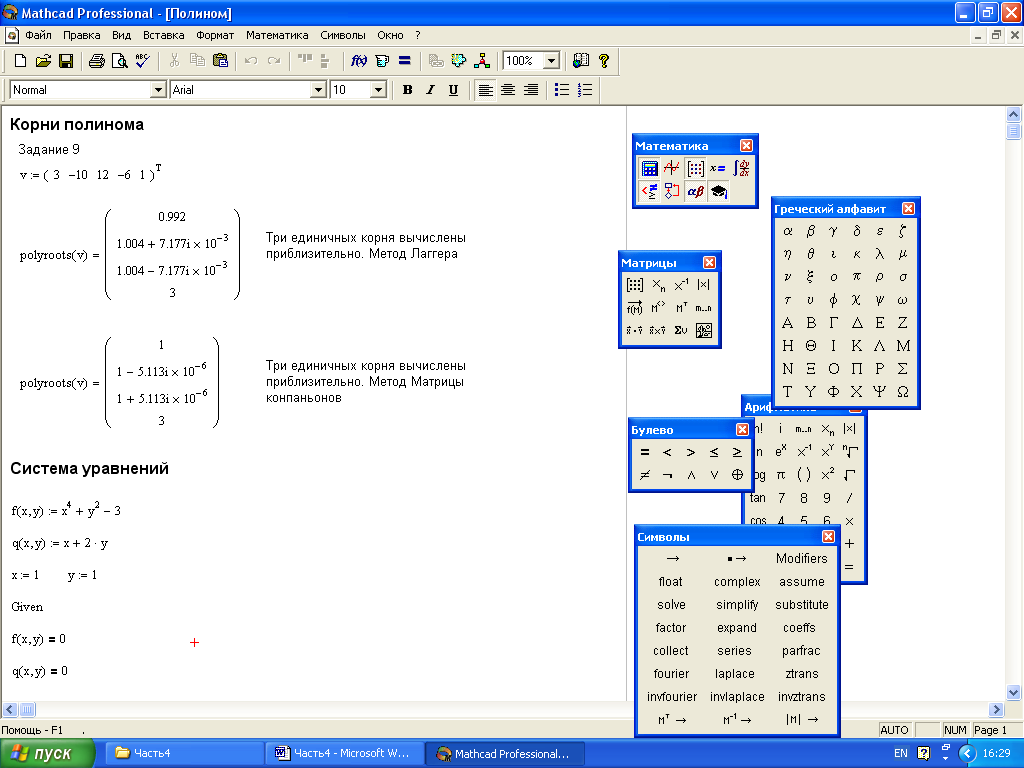
Оптимизируемую функцию f(x) называют целевой функцией, или критерием оптимальности.
К численным методам одномерной оптимизации относятся методы: дихотомического деления; золотого сечения; чисел Фибоначчи; полиномиальной аппроксимации.
Основная идея этих методов заключается в разбиении интервала поиска экстремума на несколько частей в определённом отношении, вычислении функции в этих точках и выборе наименьшего значения. После этого интервал поиска сужается, и процедура повторяется. Критерием окончания поиска может служить соотношение:
т. е. длина нового, суженного интервала поиска экстремума по модулю на i-й итерации меньше или равна заданной степени точности решения задачи.
Метод дихотомии (половинного деления)
Согласно методу дихотомического деления отрезок делят пополам и в точках, отстоящих от центра с отрезка на величину допустимой погрешности , рассчитывают значения целевой функции и .
Если окажется, что , то минимум находится на отрезке , если , то минимум – на , если ) – на . Таким образом, на следующем шаге вместо отрезка нужно исследовать суженный отрезок , или . Шаги повторяются, пока длина отрезка не уменьшится до величины погрешности . Таким образом, требуется не более n шагов, где n – ближайшее к целое значение, но на каждом шаге целевую функцию следует вычислять дважды.
Таким образом, на следующем шаге вместо отрезка нужно исследовать суженный отрезок , или . Шаги повторяются, пока длина отрезка не уменьшится до величины погрешности . Таким образом, требуется не более n шагов, где n – ближайшее к целое значение, но на каждом шаге целевую функцию следует вычислять дважды.
Пример программы поиска минимума методом дихотомии приведен на рис.1.
Метод золотого сечения
В соответствии с методом золотого сечения внутри отрезка выделяют две промежуточные точки и на расстоянии от его конечных точек, где – длина отрезка. Затем вычисляют значения целевой функции в точках и . Если , то то минимум находится на отрезке , если , то на отрезке , если , то на отрезке .
Алгоритм метода золотого сечения складывается из следующих этапов:
1) вычисляются значения функции на концах исходного интервала ;
2) вычисляются промежуточные точки интервала по формулам: , а также значения функции в этих точках;
3) по найденным значениям функции определяется её минимальное значение на интервале;
4) в зависимости от того в какой точке расположен минимум ( или ) определяется подынтервал, в котором локализован минимум – или ;
5) в новом интервале определяется точка по одной из формул п. 2 и итерационный процесс поиска продолжается с п. 3 до тех пор пока не будет достигнут критерий окончания поиска, например, такой:
2 и итерационный процесс поиска продолжается с п. 3 до тех пор пока не будет достигнут критерий окончания поиска, например, такой:
Пример программы приведен на рис. 2.
Рис. 1. Программа поиска минимума методом дихотомического деления
Рис. 2. Метод золотого сечения
Метод Фибоначчи
Согласно этому методу при разбиении отрезка используют числа Фибоначчи . Последовательность Фибоначчи образуется по правилу:
Ряд Фибоначчи имеет вид: 1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144 …
Алгоритм поиска с использованием числе Фибоначчи включает следующие шаги:
1) По заданной точности рассчитывается вспомогательное число ;
2) находится ближайшее к N число Фибоначчи ;
3) определяется минимальный шаг поиска по формуле ;
4) задается начальное значение счетчика шагов i = 0;
5) вычисляются значения и соответствующие значения функции в этих точках и ;
6) в зависимости от соотношения и выбирается новый интервал локализации минимума: или ;
7) внутри полученного интервала (значение счетчика i увеличивается на 1) находится новая точка (x или x1) , симметричная к уже имеющейся точке и отстоящая от конца интервала на величину , где i – номер шага. В этой точке рассчитывается значение f(x). Указанный процесс продолжается с пункта 5 до тех пор, пока не будут исчерпаны все числа Фибоначчи в убывающей последовательности , i = 0; 1; 2; …, т. е. пока i не станет равно s – 2. Это будет соответствовать ситуации достижения решения с заданной точностью.
В этой точке рассчитывается значение f(x). Указанный процесс продолжается с пункта 5 до тех пор, пока не будут исчерпаны все числа Фибоначчи в убывающей последовательности , i = 0; 1; 2; …, т. е. пока i не станет равно s – 2. Это будет соответствовать ситуации достижения решения с заданной точностью.
Пример программы приведен на рис. 3.
Рис. 3. Метод Фибоначчи
Встроенные функции MathCAD для поиска локального минимума/максимума
Для численного решения задач поиска локального максимума и минимума в MathCAD имеются встроенные функции Minerr, Minimize и Maximize. Пример приведен на рис.4.
Рис. 4. Поиск локальных экстремумов
Условный экстремум
В задачах на условный экстремум встроенные функции минимизации и максимиза-ции должны быть включены в вычислительный блок (solve block), который имеет следующую структуру:
Начальные приближения переменных
Given
Ограничительные условия
Выражения с функциями Minerr, Minimize или Maximize
Экстремум функции нескольких переменных
Вычисление экстремума функции многих переменных не несет принципиальных осо-бенностей по сравнению с функциями одной переменной. Пример нахождения максимума и минимума функции, показанной в виде графика трехмерной поверхности, приведен на рис. 5. Следует обратить внимание к тому, как с помощью неравенств, задается область на плоскости (x, y).
Пример нахождения максимума и минимума функции, показанной в виде графика трехмерной поверхности, приведен на рис. 5. Следует обратить внимание к тому, как с помощью неравенств, задается область на плоскости (x, y).
Задания для самостоятельного выполнения
Задание 1 . Поиск минимума функции одной переменной
Постройте графики функций одной переменной. Напишите программы в среде MathCAD и рассчитайте минимальное значение функции с заданной точностью методами дихотомии, золотого сечения, с использованием чисел Фибоначчи, с помощью встроенной функции Minner. Сравните результаты. Оцените количество итераций, необходимых для достижения заданной точности (таблица 1).
Задание 2. Поиск оптимума функции двух переменных
С помощью встроенных функций MathCAD решите задачу поиска оптимума функции двух переменных F(x, y), предварительно исследовав функцию графически.
Контрольные вопросы
1. Сформулируйте постановку задачи оптимизации.
Сформулируйте постановку задачи оптимизации.
2. Что такое локальный и глобальный экстремумы?
3. Какие ограничения имеет применение классических методов поиска оптимума?
4. Назовите численные методы поиска оптимума функции одной переменной.
5. Разберите алгоритмы методов одномерного поиска оптимума: дихотомии, золотого сечения, чисел Фибоначчи.
6. Сформулируйте критерий окончания поиска решения в итерационных методах.
7. Какие встроенные в MathCAD функции для решения задачи оптимизации вы знаете?
8. Какие функции могут применяться для решения задачи условной оптимизации?
1.3 Уточнение корней методом хорд
Рисунок 3 – Метод хорд.
Рассматриваемый метод так же, как и метод половинного деления, предназначен для уточнения корня на интервале, на концах которого функция принимает значения разных знаков. Очередное приближение в отличие от метода половинного деления берем не в середине отрезка, а в точке , где пересекает ось абсцисс прямая линия (хорда), проведенная через точки А и В (рис. 3).
3).
Запишем уравнение прямой, проходящей через точки А и В:
.
Для точки пересечения прямой с осью абсцисс ( ) получим уравнение
. (10)
В качестве нового интервала для продолжения итерационного процесса выбираем тот из двух и , на концах которого функция принимает значения разных знаков. Для рассматриваемого случая (рис. 3) выбираем отрезок, так как . Следующая итерация состоит в определении нового приближения как точки пересечения хорды с осью абсцисс и т.д.
Заканчиваем процесс уточнения корня, когда расстояние между очередными приближениями станет меньше заданной точности, т.е.
(11)
или при выполнении условия (9).
Рисунок 4 – О сходимости метода хорд
Замечание. Метод половинного деления и метод хорд очень похожи, в частности, процедурой проверки знаков функции на концах отрезка. При этом второй их них в ряде случаев дает более быструю сходимость итерационного процесса. Однако в некоторых случаях метод хорд может сходится существенно медленнее метода половинного деления. Такая ситуация показана на рис. 4. Оба рассмотренных метода не требуют знания дополнительной информации о функции. Например, не требуется, чтобы функция была дифференцируема. Даже для разрывных функций рассмотренные методы обладают гарантированной сходимостью. Более сложные методы уточнения корня используют дополнительную информацию о функции, прежде всего свойство дифференцируемости. Как результат они обычно обладают более быстрой сходимостью, но в то же время, применимы для более узкого класса функций, и их сходимость не всегда гарантирована. Примером такого метода служит метод Ньютона.
При этом второй их них в ряде случаев дает более быструю сходимость итерационного процесса. Однако в некоторых случаях метод хорд может сходится существенно медленнее метода половинного деления. Такая ситуация показана на рис. 4. Оба рассмотренных метода не требуют знания дополнительной информации о функции. Например, не требуется, чтобы функция была дифференцируема. Даже для разрывных функций рассмотренные методы обладают гарантированной сходимостью. Более сложные методы уточнения корня используют дополнительную информацию о функции, прежде всего свойство дифференцируемости. Как результат они обычно обладают более быстрой сходимостью, но в то же время, применимы для более узкого класса функций, и их сходимость не всегда гарантирована. Примером такого метода служит метод Ньютона.
1.4 Уточнение корней методом Ньютона
Рисунок 5 – Метод Ньютона.
Пусть нам известно начальное приближение к корню (вопрос выбора начального приближение будет подробно рассмотрен ниже). Проведем в этой точке касательную к кривой (рис. 5). Эта касательная пересечет ось абсцисс в точке, которую будем рассматривать в качестве следующего приближения. Значение легко найти из рисунка:
Проведем в этой точке касательную к кривой (рис. 5). Эта касательная пересечет ось абсцисс в точке, которую будем рассматривать в качестве следующего приближения. Значение легко найти из рисунка:
,
выражая отсюда, получим
.
Аналогично могут быть найдены и следующие приближения. Формула для k+1-го приближения имеет вид
, (12)
Из формулы (12) вытекает условие применимости метода: функция должна быть дифференцируемой и в окрестности корня не должна менять знак.
Для окончания итерационного процесса могут быть использованы условия (9) или (11).
1.5 Пакет MathCad. Использование программных фрагментов
Mathcad —это популярная система компьютерной математики, предназначенная для автоматизации решения массовых математических задач в самых различных областях науки, техники и образования. Название системы происходит от двух слов — MATHmatica (математика) и CAD (Computer Aided Design — системы автоматического проектирования, или САПР).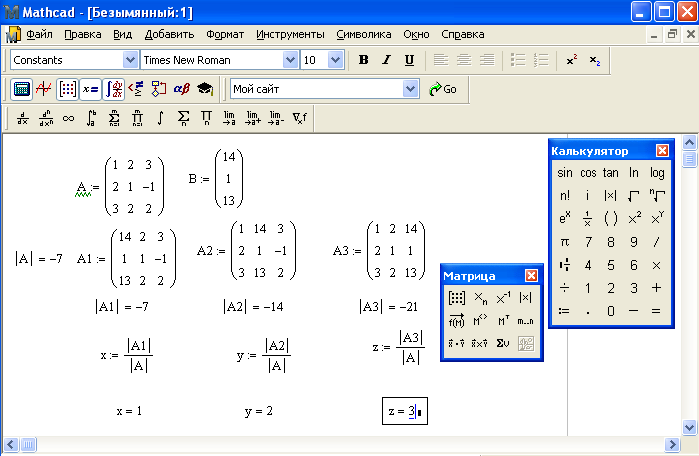 Так что вполне правомерно считать Mathcad математическими САПР.[1, стр 9]
Так что вполне правомерно считать Mathcad математическими САПР.[1, стр 9]
Как интегрированная система Mathcad 2000 содержит следующие основные компоненты:
1. Редактор документов — редактор с возможностью вставки математических выражений, шаблонов графиков и текстовых комментариев;
2. MathConnex — системный интегратор, обеспечивающий интеграцию Mathcad с рядом иных программных продуктов;
3. Центр ресурсов — система управления ресурсами системы;
4. Электронные книги — электронные книги с описанием типовых расчетов в различных областях науки и техники;
5. Справочная система — система для получения справочных данных по тематическому и индексному каталогу, а также для поиска нужных данных по ключевому слову или фразе;
6.Быстрые шпаргалки QuickSheets — короткие примеры с минимальными комментариями, описывающие применение всех встроенных операторов и функций системы;
7. Броузер Интернета — собственное средство выхода в Интернет.[1, стр.15]
Броузер Интернета — собственное средство выхода в Интернет.[1, стр.15]
Программа в Mathcad есть выражение, в свою очередь, состоящее из других выражений. Программы Mathcad содержат конструкции, во многом подобные программным конструкциям языков программирования: условные передачи управления, операторы циклов, области видимости переменных, использование подпрограмм и рекурсии.
Написание программ в Mathcad позволяет решить такие задачи, которые невозможно или очень трудно решить другим способом.
Программа Mathcad есть частный случай выражения Mathcad. Подобно любому выражению, программа возвращает значение, если за ней следует знак равенства. Точно так же, как переменную или функцию можно определить через выражение, их можно определить и с помощью программы.
Главным различием между программой и выражением является способ задания вычислений. При использовании выражения алгоритм получения ответа должен быть описан одним оператором. В программе может быть использовано столько операторов, сколько нужно. Можно рассматривать программу как “составное выражение.
Можно рассматривать программу как “составное выражение.
Условный оператор (if, otherwise)
Действие условного оператора if состоит из двух частей. Сначала проверяется логическое выражение (условие) справа от него. Если оно истинно, выполняется выражение слева от оператора if. Если ложно — ничего не происходит, а выполнение программы продолжается переходом к ее следующей строке. Вставить условный оператор в программу можно следующим образом:
1. Если необходимо, введите левую часть выражения и оператор присваивания.
2. Создайте новую строку программного кода, нажав на панели Programming (Программирование) кнопку Add Line (Добавить строку).
3. Нажмите кнопку условного оператора if.
4. Справа от оператора if введите условие. Пользуйтесь логическими операторами, вводя их с панели Boolean (Булевы операторы).
5. Выражение, которое должно выполняться, если условие оказывается выполненным, введите слева от оператора if.
6. Если в программе предусматриваются дополнительные условия, добавьте в программу еще одну строку нажатием кнопки Add Line и введите их таким же образом, используя оператор if или otherwise.
Оператор otherwise используется совместно с одним или несколькими условными операторами if и указывает на выражение, которое будет выполняться, если ни одно из условий не оказалось истинным.
Операторы цикла (for, while, break, continue)
В языке программирования MathCAD имеются два оператора цикла: for и while. Первый из них дает возможность организовать цикл по некоторой переменной, заставляя ее пробегать некоторый диапазон значений. Второй создает цикл с выходом из него по некоторому логическому условию. Чтобы вставить в программный модуль оператор цикла:
1. Создайте в программном модуле новую линию.
2. Вставьте один из операторов цикла for или while нажатием одноименной кнопки на панели Programming (Программирование).
3. Если выбран оператор for, то вставьте в соответствующие местозаполнители имя переменной и диапазон ее значений, а если while — то логическое выражение, при нарушении которого должен осуществляться выход из цикла.
4. В нижний местозаполнитель введите тело цикла, т. е. выражения, которые должны выполняться циклически.
5. При необходимости дополните программу другими строками и введите в них нужный код.
Диапазон значений переменной в условии цикла for можно задать как с помощью диапазона ранжированной переменной, так и с помощью вектора.
Оператор цикла for с ранжированной переменной
Оператор цикла for с вектором
Оператор цикла while ,
Иногда необходимо досрочно завершить цикл, т. е. не по условию в его заголовке, а в некоторой строке в теле цикла.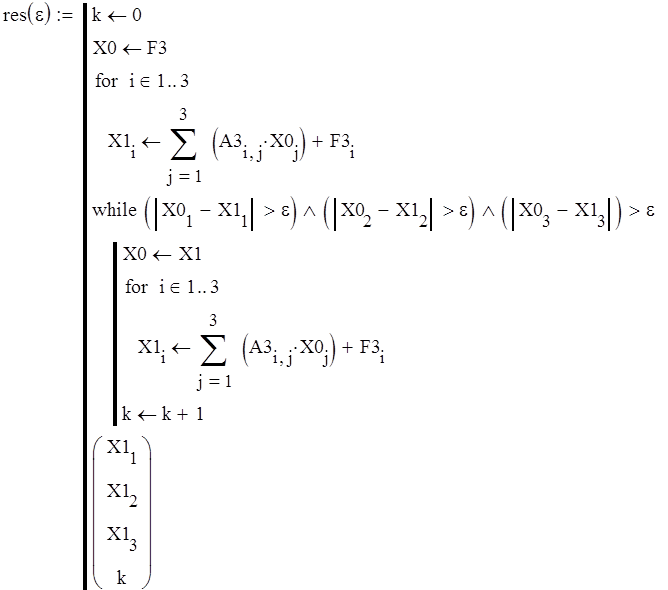 Для этого предназначен оператор break. Например, в листинге, как только значение переменной цикла i достигает 2, цикл, благодаря оператору break в последней строке программного модуля, прерывается. Соответственно, значение переменной х остается равным 0+1+2=3.
Для этого предназначен оператор break. Например, в листинге, как только значение переменной цикла i достигает 2, цикл, благодаря оператору break в последней строке программного модуля, прерывается. Соответственно, значение переменной х остается равным 0+1+2=3.
Оператор break внутри цикла for
Оператор break внутри цикла while
Чтобы четче обозначить границы завершения тела цикла, в его конце может использоваться дополнительная строка с оператором continue, который вводится одноименной кнопкой панели. Обычно используется для продолжения выполнения цикла путем возврата в начало тела цикла. Составим программу-функцию, формирующую новый вектор из положительных проекций исходного вектора.
Биссекция матки при вагинальной гистерэктомии
Несмотря на доказательства того, что вагинальный способ хирургии связан с более быстрым выздоровлением и меньшим количеством осложнений, почти 50% гистерэктомий во всем мире проводятся абдоминально. Для женщин основным показанием к вагинальной гистерэктомии остается лечение маточно-вагинального выпадения, в то время как другие общие показания к операции, такие как увеличение матки, нарушения менструального цикла, лечат абдоминальным путем путем абдоминальной гистерэктомии.Гинекологи не хотят делать вагинальную гистерэктомию до тех пор, пока матка не связана со значительной степенью выпадения. Это может быть связано с личными предпочтениями многих гинекологов, но в основном с отсутствием надлежащей подготовки или опыта, что приводит к нежеланию выполнять процедуру NDVH вагинальным путем в случаях увеличения матки, отсутствия опускания матки, предыдущих операций на тазовых органах или при гистерэктомии. совмещать с двусторонней сальпингоофорэктомией.
Для женщин основным показанием к вагинальной гистерэктомии остается лечение маточно-вагинального выпадения, в то время как другие общие показания к операции, такие как увеличение матки, нарушения менструального цикла, лечат абдоминальным путем путем абдоминальной гистерэктомии.Гинекологи не хотят делать вагинальную гистерэктомию до тех пор, пока матка не связана со значительной степенью выпадения. Это может быть связано с личными предпочтениями многих гинекологов, но в основном с отсутствием надлежащей подготовки или опыта, что приводит к нежеланию выполнять процедуру NDVH вагинальным путем в случаях увеличения матки, отсутствия опускания матки, предыдущих операций на тазовых органах или при гистерэктомии. совмещать с двусторонней сальпингоофорэктомией.
Удаление большой матки при лапароскопической гистерэктомии — это одна из проблем, которую можно решить, рассекая матку пополам. Эти взгляды сохраняются, несмотря на доказательства того, что вышеуказанные факторы являются не более чем относительными противопоказаниями для вагинального введения.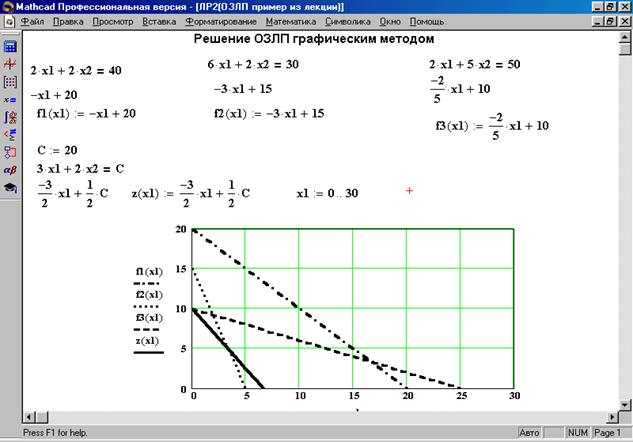 В различных публикациях и многочисленной литературе также описывается использование вагинальной гистерэктомии в этих ситуациях.
В различных публикациях и многочисленной литературе также описывается использование вагинальной гистерэктомии в этих ситуациях.
РАЗДЕЛЕНИЕ МАТКИ:
Биссекция — это наиболее часто используемый метод извлечения матки через влагалище.Шейка матки захватывается волчанкой или тенакулумом с двух сторон, как вы видите на видео выше, и матка была разрезана пополам в переднезаднем направлении ножом с постепенным перемещением волчанки до тех пор, пока не было достигнуто глазное дно и зажаты ножки. Биссекция матки — один из важных методов, который используется при NDVH, LAVH, а также TLH. В некоторых случаях требуется полное рассечение пополам, чтобы одна половина матки могла быть выведена во влагалище и зафиксирована ножка.
Шейку матки следует захватить с обеих сторон, а матку следует разрезать пополам по направлению к глазному дну с помощью ножа.Рассечение пополам, проводимое сначала вдоль задней стенки матки, должно сопровождаться повторным перемещением вульселлы близко к вершине разреза в сочетании с вращением шейной части матки вокруг лобковой дуги. При необходимости матку следует вернуть в исходное положение и провести рассечение кпереди. Полное рассечение пополам часто позволяло провести половину матки через влагалище и закрепить ножку яичника; то же самое было проделано с другой половиной матки.Даже матка с миомой часто сочетается с рассечением пополам или морцеллированием. Миомы меньшего размера могут быть удалены одним куском, а более крупные — морцеллированы и удалены фрагментами, при этом одна из вульселл всегда прикрепляется к остаточной массе миомы. Морцелляция выполняется на матке, когда, несмотря на рассечение пополам или миомэктомию, дальнейшее опускание невозможно. Биссекция возобновляется, как только станет возможным дальнейшее опускание матки после миомэктомии и морцелляции. Вырезание керна также выполняется вместо деления пополам при работе с маткой меньшего размера без какой-либо явной большой миомы.Окружной разрез делается на уровне перешейка матки примерно на 5 мм в субстанцию тела для облегчения извлечения. Затем иссекают центральную сердцевину ткани вокруг полости матки, постепенно подрезая серозную поверхность матки по направлению к дну.
При необходимости матку следует вернуть в исходное положение и провести рассечение кпереди. Полное рассечение пополам часто позволяло провести половину матки через влагалище и закрепить ножку яичника; то же самое было проделано с другой половиной матки.Даже матка с миомой часто сочетается с рассечением пополам или морцеллированием. Миомы меньшего размера могут быть удалены одним куском, а более крупные — морцеллированы и удалены фрагментами, при этом одна из вульселл всегда прикрепляется к остаточной массе миомы. Морцелляция выполняется на матке, когда, несмотря на рассечение пополам или миомэктомию, дальнейшее опускание невозможно. Биссекция возобновляется, как только станет возможным дальнейшее опускание матки после миомэктомии и морцелляции. Вырезание керна также выполняется вместо деления пополам при работе с маткой меньшего размера без какой-либо явной большой миомы.Окружной разрез делается на уровне перешейка матки примерно на 5 мм в субстанцию тела для облегчения извлечения. Затем иссекают центральную сердцевину ткани вокруг полости матки, постепенно подрезая серозную поверхность матки по направлению к дну. После того, как матка введена во влагалище, гистерэктомия была завершена обычным образом.
После того, как матка введена во влагалище, гистерэктомия была завершена обычным образом.
Помимо снятия напряжения связок, позволяющего опустить матку, он также помогает в удалении небольших миом во время курса лечения, уменьшая тем самым объем матки.Защита мочевого пузыря, прямой кишки и влагалища очень важна при таких процедурах, и эта защита достигается за счет использования соответствующих вагинальных зеркал. Используются два или три вагинальных зеркала. Верхнее влагалищное зеркало защитит от травм мочевого пузыря, а зеркало, наложенное ниже, защитит прямую кишку от травм. третье зеркало можно использовать для защиты от травм больших и малых половых губ. Некоторым гинекологам нравится накладывать швы на губы, чтобы предотвратить травмы и получить правильную визуализацию.
Трудно переоценить жизненно важную роль двух ассистентов, стоящих по обе стороны от гинеколога, выполняющего вагинальную гистерэктомию. Как известно каждому гинекологу, плохой ассистент может сделать легкую работу затруднительной во время гистерэктомии, а трудная работа — почти невозможной, в то время как хороший ассистент при гистерэктомии может сделать трудную гистерэктомию
При процедуре плетения (извлечение) стенка матки была разрезана по окружности на несколько миллиметров с шагом время поддерживая постоянную тягу шейки матки все время.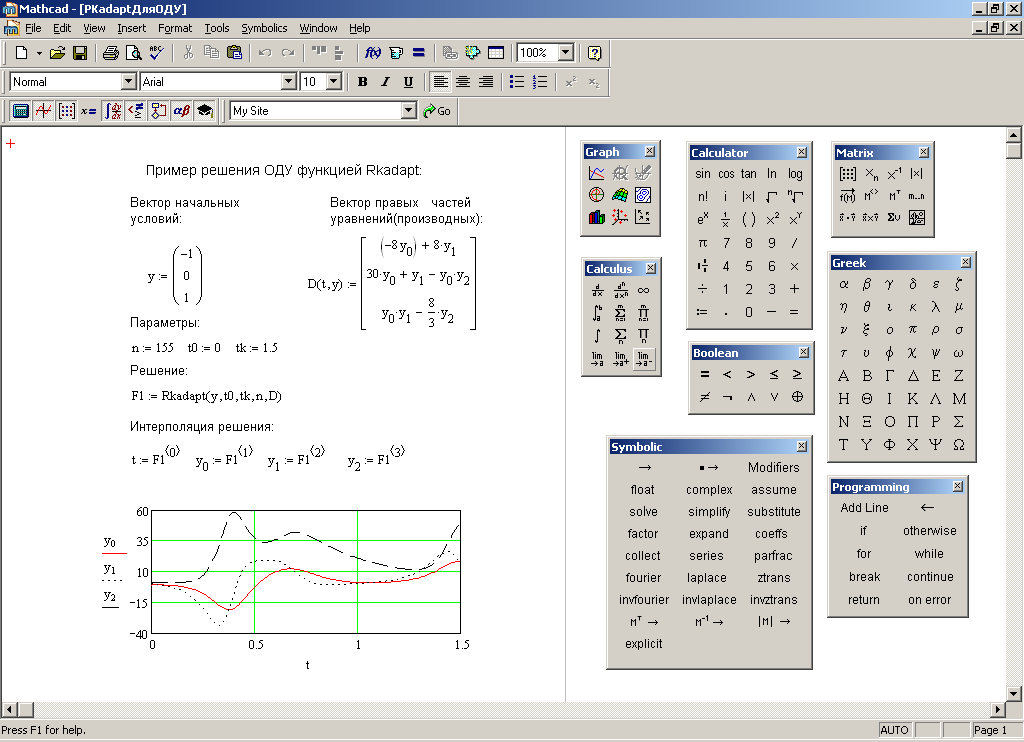 По мере того, как волокна разрезаются, матка В ТЕХНИКЕ НАПРЯЖЕНИЯ матка медленно удлиняется. Следующая серия разрезов матки выполняется на более высоком уровне до тех пор, пока не будет выведено дно. Только деление пополам требуется у 90 процентов пациентов, в то время как техника наращивания ресниц достаточна у 10 процентов пациентов. После того, как дно матки можно будет медленно доставить во влагалище путем рассечения пополам или конуса, гистерэктомия завершается обычным способом без каких-либо проблем. Выделение миометрия может оказаться неудачным, чем рассечение-морцелляция, особенно в случае узкой матки.Послеоперационная лихорадка также обнаруживается у некоторых пациентов значительно чаще после удаления корки миометрия. Обоим этим методам следует обучать гинеколога-резидента.
По мере того, как волокна разрезаются, матка В ТЕХНИКЕ НАПРЯЖЕНИЯ матка медленно удлиняется. Следующая серия разрезов матки выполняется на более высоком уровне до тех пор, пока не будет выведено дно. Только деление пополам требуется у 90 процентов пациентов, в то время как техника наращивания ресниц достаточна у 10 процентов пациентов. После того, как дно матки можно будет медленно доставить во влагалище путем рассечения пополам или конуса, гистерэктомия завершается обычным способом без каких-либо проблем. Выделение миометрия может оказаться неудачным, чем рассечение-морцелляция, особенно в случае узкой матки.Послеоперационная лихорадка также обнаруживается у некоторых пациентов значительно чаще после удаления корки миометрия. Обоим этим методам следует обучать гинеколога-резидента.
Как сказал знаменитый Кэмпбелл: «Большая часть матки, подлежащая удалению, не является противопоказанием для вагинального введения». В определенных пределах эти слова верны даже в сегодняшнюю эпоху лапароскопической хирургии. Умеренное увеличение матки не следует рассматривать как противопоказание к вагинальной гистерэктомии или лапароскопической ассистированной вагинальной гистерэктомии и, конечно же, не должно использоваться для оправдания использования абдоминальной и надшейной лапароскопической гистерэктомии.
Умеренное увеличение матки не следует рассматривать как противопоказание к вагинальной гистерэктомии или лапароскопической ассистированной вагинальной гистерэктомии и, конечно же, не должно использоваться для оправдания использования абдоминальной и надшейной лапароскопической гистерэктомии.
Биологические аспекты сумчато-плацентарной дихотомии в JSTOR
Abstract Филогенетическая дивергенция сумчатых и плацентарных млекопитающих, вероятно, произошла в раннем меловом периоде. В отличие от поздней юры, это было время исключительного ограничения межконтинентальной миграции наземных позвоночных из-за морских барьеров и, вероятно, время развития центров отчетливого эндемизма на «островном континенте». Палеонтологические и анатомические данные не предполагают происхождение сумчатых и плацентарных животных от разных пантотерианских предков, а, напротив, указывают на общий источник.Живые сумчатые рождаются после короткого периода внутренней беременности на чрезвычайно незрелой стадии органогенеза. По описанию доктора Фабиолы Мюллер, у них есть ряд временных закрытий для рта, глаз и ушей, которые развиваются незадолго до рождения и имеют функциональное значение после рождения в отношении прикрепления к соску, развития вторичного челюстного сустава и защиты. глаза и уши против высыхания в новой атмосферной среде. У живых здоровых животных обычно более длительный период внутренней беременности, чем у сумчатых, а у некоторых значительно увеличилось время внутриутробного развития.Однако даже у эутерианцев, которые могут родиться в преждевременном возрасте, внутриутробно на ранних стадиях развития образуются преходящие закрытия рта, глаз и ушей, которые могут быть потеряны задолго до рождения. Эти закрытия сегодня не работают у эутерианских нидифуг и кажутся лишь консервативными чертами, сохранившимися от эвтерианских предков, которые родились, как и современные сумчатые, в крайне болезненном состоянии после короткого периода внутренней беременности. Хотя продолжительность внутренней беременности современных сумчатых видов сильно варьируется (11-38 дней), все они рождаются на одинаковых стадиях органогенеза.
По описанию доктора Фабиолы Мюллер, у них есть ряд временных закрытий для рта, глаз и ушей, которые развиваются незадолго до рождения и имеют функциональное значение после рождения в отношении прикрепления к соску, развития вторичного челюстного сустава и защиты. глаза и уши против высыхания в новой атмосферной среде. У живых здоровых животных обычно более длительный период внутренней беременности, чем у сумчатых, а у некоторых значительно увеличилось время внутриутробного развития.Однако даже у эутерианцев, которые могут родиться в преждевременном возрасте, внутриутробно на ранних стадиях развития образуются преходящие закрытия рта, глаз и ушей, которые могут быть потеряны задолго до рождения. Эти закрытия сегодня не работают у эутерианских нидифуг и кажутся лишь консервативными чертами, сохранившимися от эвтерианских предков, которые родились, как и современные сумчатые, в крайне болезненном состоянии после короткого периода внутренней беременности. Хотя продолжительность внутренней беременности современных сумчатых видов сильно варьируется (11-38 дней), все они рождаются на одинаковых стадиях органогенеза.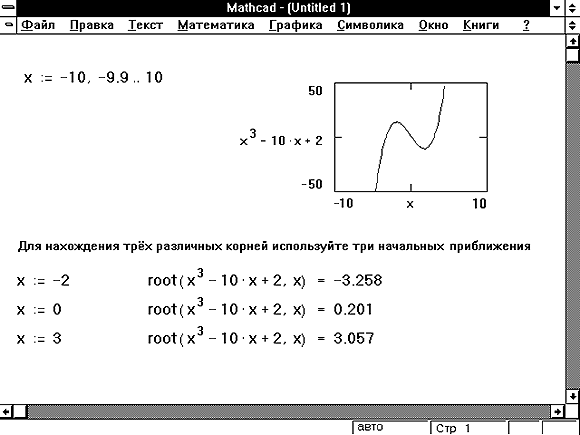 Таким образом, беременные с более длительным сроком беременности, в отличие от здоровых беременных, похоже, не «используют преимущества» полной продолжительности внутриутробной жизни для быстрого развития; у них отмечаются заметные остановки или замедление темпов органогенеза, и степень анатомического совершенства не обязательно коррелирует с продолжительностью беременности, как это обычно бывает у эутериан. Ранние стадии развития терианских млекопитающих в целом характеризуются почти полным отсутствием автономных запасов энергии (желток, белок), а постбластоцистозные эмбрионы почти полностью зависят от матери в получении питательных веществ.Эмбриональные потребности в энергии сравнительно невелики до стадии эмбриогенеза, характерной для сумчатых при рождении (и соответствующей анатомической стадии у здоровых животных), но затем резко возрастают. Растущие потребности эмбриона в энергии требуют тесной физической близости тканей плода и матери для обмена (т. Е. Плацентации). Сумчатые могут соединять свой желточный мешок и плаценту со стенкой матки только после внутриутробного «вылупления» из пористой яичной скорлупы — процесса, который происходит только в течение последней трети беременности у всех изученных видов.
Таким образом, беременные с более длительным сроком беременности, в отличие от здоровых беременных, похоже, не «используют преимущества» полной продолжительности внутриутробной жизни для быстрого развития; у них отмечаются заметные остановки или замедление темпов органогенеза, и степень анатомического совершенства не обязательно коррелирует с продолжительностью беременности, как это обычно бывает у эутериан. Ранние стадии развития терианских млекопитающих в целом характеризуются почти полным отсутствием автономных запасов энергии (желток, белок), а постбластоцистозные эмбрионы почти полностью зависят от матери в получении питательных веществ.Эмбриональные потребности в энергии сравнительно невелики до стадии эмбриогенеза, характерной для сумчатых при рождении (и соответствующей анатомической стадии у здоровых животных), но затем резко возрастают. Растущие потребности эмбриона в энергии требуют тесной физической близости тканей плода и матери для обмена (т. Е. Плацентации). Сумчатые могут соединять свой желточный мешок и плаценту со стенкой матки только после внутриутробного «вылупления» из пористой яичной скорлупы — процесса, который происходит только в течение последней трети беременности у всех изученных видов. Eutherians, с другой стороны, лишены яичной скорлупы и обладают эффектом близости плацентации (сначала желточный мешок, затем хориоаллантоис) на очень ранних стадиях эмбриогенеза. Эта близость возможна у здоровых людей только из-за еще плохо изученных свойств трофобласта, которые позволяют блокировать материнский иммунный ответ против отцовских антигенов, содержащихся в тканях плода. Инертная яичная скорлупа (материнского происхождения), по-видимому, выполняет эту задачу до поздних стадий беременности сумчатых, и они, вероятно, рождаются до того, как мать может завершить полноценную иммунологическую атаку на эмбрион.Сумчатое внутриутробное развитие — это исследование компромисса, который становится необходимым, когда интимная близость плода и матери в плацентации, необходимая для продвинутого морфологического развития, конфликтует с угрозой иммунологического отторжения при отсутствии защитных слоев. «Изобретение» трофобластических тканей первобытными эвтерианами было, вероятно, самым важным эволюционным событием в истории инфракласса. Способность трофобласта защищать эмбрион от иммунологической атаки и координировать эндокринологические события, источники питания и требования по удалению отходов были ключевыми особенностями в развитии длительной внутренней беременности в сочетании с устойчиво высокой скоростью органогенеза; Таким образом, было разрешено рождение анатомически развитого потомства.Сумчатый эмбриогенез строго регулируется естественным отбором, так как новорожденный должен быть способен самостоятельно перемещаться и прикрепляться к соску. Евтерианцам же, с другой стороны, позволена большая гибкость эмбриологической гетерохронии и анатомического «экспериментирования». Это особенно ярко проявляется в адаптации передних конечностей (с ластами, непротиворечивыми когтями, одиночными копытами и т. Д.), Частей тела, критически приспособленных к определенному образу жизни у всех видов. Обосновывается возможность того, что непосредственный общий предок сумчатых и плацентарных животных был живородящим и нидиколом, как и современные сумчатые.
Eutherians, с другой стороны, лишены яичной скорлупы и обладают эффектом близости плацентации (сначала желточный мешок, затем хориоаллантоис) на очень ранних стадиях эмбриогенеза. Эта близость возможна у здоровых людей только из-за еще плохо изученных свойств трофобласта, которые позволяют блокировать материнский иммунный ответ против отцовских антигенов, содержащихся в тканях плода. Инертная яичная скорлупа (материнского происхождения), по-видимому, выполняет эту задачу до поздних стадий беременности сумчатых, и они, вероятно, рождаются до того, как мать может завершить полноценную иммунологическую атаку на эмбрион.Сумчатое внутриутробное развитие — это исследование компромисса, который становится необходимым, когда интимная близость плода и матери в плацентации, необходимая для продвинутого морфологического развития, конфликтует с угрозой иммунологического отторжения при отсутствии защитных слоев. «Изобретение» трофобластических тканей первобытными эвтерианами было, вероятно, самым важным эволюционным событием в истории инфракласса. Способность трофобласта защищать эмбрион от иммунологической атаки и координировать эндокринологические события, источники питания и требования по удалению отходов были ключевыми особенностями в развитии длительной внутренней беременности в сочетании с устойчиво высокой скоростью органогенеза; Таким образом, было разрешено рождение анатомически развитого потомства.Сумчатый эмбриогенез строго регулируется естественным отбором, так как новорожденный должен быть способен самостоятельно перемещаться и прикрепляться к соску. Евтерианцам же, с другой стороны, позволена большая гибкость эмбриологической гетерохронии и анатомического «экспериментирования». Это особенно ярко проявляется в адаптации передних конечностей (с ластами, непротиворечивыми когтями, одиночными копытами и т. Д.), Частей тела, критически приспособленных к определенному образу жизни у всех видов. Обосновывается возможность того, что непосредственный общий предок сумчатых и плацентарных животных был живородящим и нидиколом, как и современные сумчатые.
Evolution, публикуемый для Общества изучения эволюции, является ведущим изданием, посвященным изучению органической эволюции и интеграции различных областей науки, связанных с эволюцией. В журнале представлены важные и оригинальные результаты, которые расширяют наше понимание эволюционных явлений и процессов.
Th2: Th3-дихотомия беременности и преждевременных родов
Беременность — это уникальное иммунологическое состояние, при котором необходим баланс иммунной толерантности и подавления для защиты плода без ущерба для матери.Давно установлено, что смещение от профиля цитокинов Т-хелперов 1 к профилю Т-хелперов 2 способствует успешному поддержанию беременности. Большинство публикаций, в которых сообщается об аберрантном балансе Th2: Th3, сосредоточены на ранней потере беременности и преэклампсии. За последние несколько десятилетий возросло понимание роли инфекции и воспаления в преждевременных родах, и поиск новых биомаркеров для прогнозирования преждевременных родов продолжается. В этой статье мы исследуем доказательства аберрантного профиля Th2: Th3, связанного с преждевременными родами.Мы также рассматриваем возможность его использования при скрининге женщин с высоким риском преждевременных родов и в качестве профилактических терапевтических мер для предотвращения преждевременных родов и связанных с ними неблагоприятных исходов у новорожденных.
1. Введение
Преждевременные роды встречаются примерно в 10% беременностей [1]. Во многих развитых странах ставки растут. Считается, что на рождение до 37 недель беременности приходится до 70% неонатальных смертей, а чрезвычайно высокие затраты на неонатальную интенсивную терапию, необходимые для поддержки выживших, делают преждевременные роды как социальным, так и экономическим бременем.В настоящее время широко признано, что этиология преждевременных родов многофакторна, и поэтому основная причина преждевременных родов часто неизвестна. Существует тесная связь между преждевременными родами и инфекцией и воспалением, и исследования в этой области резко увеличились за последние несколько десятилетий [2]. Однако мы до сих пор не добились значительного прогресса в профилактике преждевременных родов. Появляются доказательства пагубного прямого воздействия материнской инфекции / воспаления на исход новорожденных, но мы не до конца понимаем, принесут ли противовоспалительные терапевтические агенты пользу или вред новорожденному, рожденному в условиях преждевременных родов, вызванных инфекцией / воспалением.
Иммунология беременности сложна в том смысле, что мать должна переносить «чужеродный» плод и, следовательно, требует определенной степени иммуносупрессии, в то время как, с другой стороны, необходимо поддерживать иммунную функцию для борьбы с инфекцией. Одним из механизмов, который участвует в успешном поддержании беременности, является предлагаемый переход с профиля цитокинов Т-хелперов 1 (Th2) на профиль Т-хелперов 2 (Th3). В этой статье исследуются доказательства дисбаланса профиля Th2: Th3 у женщин с риском преждевременных родов и у которых уже установлены преждевременные роды.
2. Иммунология беременности
Плод можно описать как полуаллогенный трансплантат, являющийся продуктом двух гисто-несовместимых особей [3, 4]. Это создает проблему для матери, как терпеть, так и приспосабливать плод, который будет экспрессировать отцовские антигены и поддерживать способность отторжения в случае обширной инфекции [5]. Эта проблема частично решается иммунной системой. Иммунная система имеет две основные системы защиты: врожденную и адаптивную.Врожденный иммунный ответ — это неспецифическая реакция на чужеродные антигены, тогда как адаптивный ответ формирует очень специфическую реакцию на антигены [6]. Хотя в этих системах задействованы разные иммунные компоненты, между ними существует много совпадений и перекрестных помех. На рисунке 1 представлены основные элементы этих систем во время беременности.
Иммунные клетки, которые составляют адаптивный иммунный ответ, включают В- и Т-лимфоциты. Активация антигенпрезентирующими клетками и цитокинами приводит к высвобождению цитокинов Т-клетками при клеточно-опосредованном ответе или высвобождению антител В-клетками при гуморальном ответе [7].Хотя Медавар первоначально предположил, что беременность представляет собой время подавления иммунитета [8], недавно появилась более сложная картина, когда во время беременности происходит изменение соотношения и функции материнских лейкоцитов, а не полное подавление. Например, на ранних сроках беременности наблюдается увеличение общего количества лейкоцитов в периферической крови без изменения количества CD4 и CD8 [9]. В CD4-положительной популяции при беременности наблюдается увеличение Т-регуляторных клеток [10].Функция Т-лимфоцитов при беременности адаптируется к профилю цитокинов Т-хелперов 2, который более выражен на границе раздела матери и плода [11]. Неиммунные клетки, например трофобласты плаценты, также способствуют преобладанию цитокинов Th3 во время беременности [12].
Врожденная иммунная система дает менее специфический ответ, тем не менее, она имеет решающее значение для предотвращения микробной инвазии. Клеточные компоненты включают нейтрофилы, моноциты и макрофаги, которые защищают от патогенов путем фагоцитоза.Toll-подобные рецепторы (TLR) TLR2 и TLR4 представляют собой рецепторы распознавания образов, стимулируемые грамположительными и грамотрицательными бактериями соответственно [1]. TLR экспрессируются на неиммунных клетках плаценты и мембран плода, которые опосредуют часть врожденной иммунной системы на границе раздела матери и плода [13]. Мутации TLR2 и 4 связаны с повышенным риском преждевременных родов [14, 15]. Во время беременности существует жесткое регулирование и значительный перекрестный обмен между адаптивной и врожденной адаптивной иммунной системой, которая отвечает за предотвращение или активацию отторжения концепта.
3. Цитокины Th2: Th3
Подмножества Т-хелперов 1 и 2 происходят из недифференцированных клеток Th0 под влиянием гамма-интерферона (IFN- γ ) и интерлейкина-4 (IL-4) соответственно. Гормоны беременности, такие как прогестерон [16], лейкемический фактор ингибирования [17], эстрадиол [18] и простагландин D 2 (PGD 2 ) [19], способствуют клеточному профилю Т-хелперов 2 и, вероятно, частично отвечает за предубеждение Th3, связанное с беременностью.
CD4 + типа 1 Т-клетки (Th2) продуцируют ряд воспалительных цитокинов, включая IFN- γ [20], IL-2 [21] и фактор некроза опухоли альфа (TNF- α ) [ 22] и являются основными эффекторами опосредованной фагоцитами защиты хозяина, защищающими от внутриклеточных патогенов [21, 23, 24].CD4 + Т-клетки (Th3) типа 2 продуцируют ИЛ-4, ИЛ-5, ИЛ-13, ИЛ-10 [20] и ИЛ-6. В то время как IL-4 и IL-10 считаются противовоспалительными цитокинами [25], IL-6 обладает провоспалительными свойствами [26]. Хотя IL-10 и IL-6 часто называют цитокинами Th3 [27–32], они оба продуцируются другими типами клеток, включая клетки Th2, макрофаги и B-клетки для IL-10 [33, 34] и макрофаги. , фибробласты и В-клетки для IL-6 [35]. Цитокины Т-хелперов 2 обычно связаны с сильными ответами антител [36], например, IL-4 стимулирует продукцию антител IgE и IgG 1 [37].Однако цитокины Th3 также выполняют другие функции, например; ИЛ-5 способствует росту и дифференцировке эозинофилов, тогда как ИЛ-13 и ИЛ-10 подавляют активность макрофагов [37]. Ответы Т-хелперов 2 также связаны с защитой от паразитов, поскольку IL-4 опосредует продукцию IgE, а IL-5 опосредует эозинофилию, что является признаком паразитарной инфекции [38]. Важно отметить, что, хотя ответы Th2 и Th3 можно рассматривать как дискретные ответы, между функциями Т-хелперных клеток существует значительная перекрестная связь и перекрытие.Например, цитокины Th2 могут способствовать выработке связывающих комплемент антител, участвующих в антителозависимой клеточной цитотоксичности [39], и, таким образом, описанная дихотомия может быть упрощенным представлением сложной иммунной системы. Транскрипционная регуляция преобладающего цитокина Th3 IL-4 осуществляется с помощью STAT-6, c-maf, GATA-3 и NFAT [40], тогда как продукция цитокинов Th2 клетками транскрипционно регулируется T-bet и STAT-4 [11].
4. Th2: Th3 и поддержание беременности
Гипотеза преобладания Th3 и подавления Th2-ответа была выдвинута Вегманном и его коллегами [41] и подтверждена данными исследований на мышах и клинического течения состояний, основанных на Th3 и Th2. при беременности.IL-2, IFN- γ и TNF- α вызывают выкидыш у мышей, который может быть купирован ингибиторами цитокинов Th2 или введением противовоспалительного цитокина Th3 IL-10 [42, 43]. Аутоиммунные состояния, при которых Th2 участвует в патофизиологии, обычно улучшаются во время беременности (например, ревматоидный артрит [44]), тогда как аутоиммунный спектр Th3 имеет тенденцию к ухудшению (например, системная красная волчанка [45]). При смещении Th3: Th2 ослабленный клеточный иммунитет может быть ответственным за повышенную восприимчивость во время беременности к состояниям, вызванным внутриклеточным патогенезом (например,g., influenza, leprosy, и Listeria monocytogenes [46]).
4.1. Периферическая кровь
Существует несколько методов для определения функции клеток Th2 и Th3 во время беременности; твердофазный иммуноферментный анализ (ELISA) можно использовать для измерения интерлейкинов материнской сыворотки; периферические Т-клетки могут быть выделены и стимулированы митогеном, таким как форболмиристат ацетат (PMA) или фитогемагглютинин (PHA), для измерения продукции цитокинов с помощью ELISA или проточной цитометрии во время беременности по сравнению с небеременными контролями.
Marzi и его коллеги выделили PBMC, стимулировали их с помощью PHA и измерили секрецию интерлейкина с помощью ELISA, показав снижение IFN-, γ и IL-2 и увеличение IL-4 и IL-10 во время беременности по сравнению с небеременными контрольными людьми [ 47]. В поддержку этого исследования Reinhard et al. стимулировали клетки с помощью PMA и продемонстрировали с помощью проточной цитометрии снижение внутриклеточного IFN-, γ и IL-2, а также увеличение внутриклеточной продукции IL-4 во время беременности по сравнению с небеременными контролями [48]. In vivo подтверждение этой систематической ошибки с тех пор было продемонстрировано с помощью полимеразной цепной реакции (ПЦР), отражающей уменьшение рибонуклеиновой кислоты (мРНК) IFN-γ во время беременности и одновременное увеличение мРНК IL-4, достигающее пика на 7-м месяце по сравнению с небеременной контрольной группой [49]. Однако не все исследования подтверждают смещение Th2 к Th3. Shimaoka et al. сообщили о снижении стимулированного PMA IL-4 во время беременности [50], в то время как Matthiesen с коллегами представили данные, предполагающие увеличение как IL-4, так и IFN- γ секретирующих клеток во время беременности по сравнению с небеременными контрольными людьми [51, 52].Такие расхождения могут быть связаны с характеристиками профилей цитокинов либо в изолированных популяциях клеток, либо в цельной крови, причем последняя, возможно, является более биологически релевантной системой.
4.2. Материнский плодный интерфейс и неиммунные клетки
Хотя много исследований было посвящено циркулирующим цитокинам во время беременности, локальная продукция цитокинов на материнском интерфейсе может иметь большее значение, чем измерения, полученные в периферической крови [23]. Продукция IL-4, IL-10 и макрофагального колониестимулирующего фактора (m-CSF) Т-клетками на границе раздела матери и плода связана с успешной беременностью [23].Трофобласт, децидуальная оболочка и амнион — все вносят вклад в окружение цитокинов Th3 за счет продукции IL-13 [53], IL-10 [54], IL-4 и IL-6 [55, 56]. Совместное культивирование трофобластов и Т-клеток приводит к увеличению факторов транскрипции GATA-3 и STAT-6 (которые регулируют продукцию цитокинов Th3) и снижению фактора транскрипции Th2 STAT-4 и, следовательно, к снижению продукции IFN- γ . и TNF- α [57]. Плацента также синтезирует PGD 2 , который может действовать как хемоаттрактант клеток Th3 на границе материнского плода через классический Th3 рецептор CRTh3 (молекула, гомологичная рецептору хемоаттрактанта, экспрессируемая на клетках Th3) [28].Клетки CRTh3 + уменьшаются на границе раздела матери и плода у женщин, страдающих от повторяющейся потери, по сравнению с женщинами, перенесшими плановое прерывание [58].
Местная продукция IL-4 и IL-10 подавляет функцию как Th2-клеток, так и макрофагов, что предотвращает отторжение аллотрансплантата плода [59]. Другие противовоспалительные эффекты этих интерлейкинов приводят к ингибированию цитокина Th2 TNF- α [60] и TNF- α -индуцированной циклооксигеназы-2 (COX-2) и / или PGE 2 . синтез в клетках желаний, полученных из амниона.Подобные эффекты наблюдаются в децидуальных и плацентарных клетках in vitro [61–64], которые, как полагают, подавляют начало родов. В соответствии с такой ролью децидуальные CD4-положительные клетки женщин, перенесших необъяснимую рецидивирующую потерю беременности, обычно демонстрируют сниженную продукцию IL-4 и IL-10 [65].
5. Th2: Th3 цитокины в родах
5.1. Периферическая кровь
Было показано, что преобладание цитокинов Th3, которое существует во время беременности, возвращается к соотношению Th2: Th3 у небеременных через 4 недели после родов [66].Роды часто рассматриваются как провоспалительное состояние, знаменующее конец беременности, и поэтому вполне вероятно, что роды связаны с обратным смещением в сторону Th2, а не Th3. Скорее, Kuwajima и его коллеги показали, что соотношение Th3: Th2 оставалось постоянным в пользу Th3 во время беременности и родов, с возвращением к параметрам небеременных через 7 дней после родов [67]. Однако это открытие несколько противоречит более раннему отчету, показывающему, что уровни IL-4 в сыворотке, измеренные с помощью ELISA у женщин во время беременности и на разных этапах родов, были снижены в более позднем периоде родов и к 1 дню послеродового периода как у женщин с нормальным давлением, так и у женщин с преэклампсией. [68].В этом исследовании провоспалительный цитокин Th2 TNF- α достиг пика в ранние роды, что соответствует провоспалительному состоянию родов. В соответствии с этим, также сообщалось об увеличении IFN- γ и IL-1 β у женщин, ведущих активный период родов [69].
5.2. Интерфейс материнского плода и неиммунные клетки
Имеются убедительные доказательства того, что цитокины Th2 играют роль в инициировании родов в срок [22]. Важность местного, а не периферического производства цитокинов подчеркивается их прямым входом в биохимические пути, участвующие в родах.Мембраны плода [70, 71] и миометрий [72] продуцируют IL-1 β в срок, мощный индуктор NF- κ B [73]. Этот фактор транскрипции регулирует экспрессию многих генов, связанных с родом, включая COX-2, рецептор окситоцина, IL-8 и матриксную металлопротеиназу-9 (MMP-9) [74]. TNF- α и IL-1 β увеличиваются в амнионе, околоплодных водах и децидуальной оболочке в срок [75] и могут индуцировать продукцию PGE 2 в амниоцитах и децидуальных клетках in vitro [76, 77] .Несмотря на провоспалительную природу цитокинов Th2, они необходимы для успешной беременности, внося свой вклад в физиологию доношенных родов.
6. Цитокины Th2: Th3 при инфекции
Активация цитокинов Th2 происходит как специфический ответ на инфекцию, вызванную внутриклеточными бактериями, паразитами и вирусами [78]. Необходимый провоспалительный ответ типа 1, вызванный инфекцией, наряду с действием активированных Т-клеток, стимулирует местную и системную продукцию цитокинов, которая, если ее не контролировать, может быть вредной для хозяина [78].В некоторых ситуациях ответ Th2 уравновешивается производством цитокинов Th3, особенно IL-4 и IL-10 [79–82]. На ранних стадиях инфекции IL-12 продуцируется макрофагами и дендритными клетками [83, 84], что приводит к поляризации от клеток типа Th0 к клеткам типа Th2 [24]. IFN- γ усиливает развитие Th2 за счет активации рецептора IL-12 и ингибирования роста клеток Th3 [85]. IFN- γ также заставляет макрофаги начать фагоцитоз и стимулировать высвобождение интерлейкина-1 [86].
Хотя цитокиновый ответ Th2 может подавляться иммунной системой как матери, так и плода во время беременности [87], он по-прежнему сохраняет способность создавать защитный ответ в контексте инфекции. Например, мононуклеарные клетки пуповинной крови, культивируемые с липополисахаридом (LPS) in vitro , демонстрируют повышенную продукцию IFN-γ одновременно с пониженной секрецией IL-4 [88]. Точно так же новорожденные, подвергшиеся внутриутробной инфекции, имеют повышенный процент клеток, продуцирующих IFN- γ , а у некоторых новорожденных также наблюдается увеличение количества клеток, продуцирующих IL-4 [89].В ответ на ЛПС амнион, хорион, децидуас и плацента также выделяют провоспалительные цитокины [64, 90, 91].
7. Цитокины Th2: Th3 при преждевременных родах
Примерно 30% преждевременных родов связаны с инфекцией [92], с более высокой частотой 80–85% при преждевременных родах (<28 недель) [93]. Иммунные и неиммунные клетки способствуют созданию богатой цитокинами среды при наличии инфекции и воспаления. Провоспалительные цитокины, такие как TNF- α и IL-1 β , в конечном итоге приводят к продукции простагландинов и ММП [86] через NF- κ B.Это запускает каскад явлений пролаборации, включая сократимость матки и разрыв плодных оболочек, и если этот каскад активируется на ранних сроках беременности, могут последовать преждевременные роды.
7.1. Периферическая кровь
Как обсуждалось выше, периферический ответ может быть не таким сильным, как местный ответ Th2: Th3, и вместо этого может отражать более значительный воспалительный ответ в плацентарном компартменте плода. Большое исследование случай-контроль с участием 101042 датских женщин показало, что повышенный уровень IFN- γ в плазме в середине беременности был связан с умеренными и поздними самопроизвольными преждевременными родами, тогда как повышенного риска не наблюдалось при повышенном уровне TNF- α или IL-2 [ 94].Тем не менее, исследование, сравнивающее женщин с активными преждевременными родами и без родов, рассматривало стимулированную митогенами продукцию IFN-γ и цитокинов Th3 IL-4, IL-10 и IL-13, и не показало различий в средней продукции цитокинов у женщин. супернатант in vitro [86]. Различия в результатах этих исследований можно объяснить тем фактом, что в клетках in vitro отсутствуют другие клетки иммунной системы и, следовательно, отсутствует способность отражать сложность иммунной системы в целом.Однако это же исследование показало более высокий уровень IL-12 и более низкий уровень IL-4 в цервикальном секрете у женщин с преждевременными родами, что отражает локализованную дихотомию Th2: Th3. Бахар и его коллеги не продемонстрировали каких-либо различий в сыворотке TNF- α или IFN- γ у женщин с преждевременными родами по сравнению с доношенными или подобранными контрольными женщинами без родов [95]. Однако женщины из группы преждевременных родов получали индометацин, противовоспалительный ингибитор ЦОГ-2, который мог ослабить типичный провоспалительный ответ.Сыворотка, взятая у женщин с преждевременным разрывом плодных оболочек (pPROM), по сравнению с женщинами, родившими в срок, показывает более высокую концентрацию IFN- γ . Уровни IL-4 и IL-5 не определялись в обеих группах [96]. В исследовании 30 женщин с преждевременными родами, стимулированные митогеном и антигеном PBMC показали более высокую продукцию провоспалительных цитокинов IFN-, γ и IL-2, наряду с измененным соотношением Th2: Th3, благоприятствующим ответу Th2 по сравнению с с контрольными, которые родили в срок [97].Взятые вместе, эти результаты предполагают, что преждевременные роды, скорее, чем снижение ответа Th3, представляют активацию ответа Th2. Таким образом, будущая разработка терапевтических мишеней, вероятно, будет более эффективной, если будет направлена на модуляцию цитокинов Th2.
Дихотомия Th2: Th3, вероятно, представляет собой чрезмерное упрощение сложности перекрестных помех между цитокинами Th2 и Th3. Соотношение Th2: Th3, вероятно, будет иметь большее физиологическое значение, чем фактические производимые концентрации.В поддержку такого мнения, женщины с угрозой преждевременных родов с высокими уровнями сывороточного IL-12 (который индуцирует цитокиновый ответ Th2) и без изменений сывороточного IL-18 (который может вызывать как Th2-, так и Th3-ответ) не показывают значительных ассоциации с преждевременными родами. Однако женщины с высоким уровнем ИЛ-12 и низким уровнем ИЛ-18 и, следовательно, высоким соотношением ИЛ-12: ИЛ-18, увеличивающим преобладание Th2, связаны с двукратным риском преждевременных родов при наличии угрозы преждевременных родов [98].
7.2. Материнский плодный интерфейс и неиммунные клетки
Воспалительная реакция на материнском плодном интерфейсе более вероятно отражает истинное значение дихотомии Th2: Th3 и аберрантного профиля при преждевременных родах. Недавний метаанализ пришел к выводу, что провоспалительные цитокины на границе раздела матери и плода играют роль в событиях, ведущих к спонтанным преждевременным родам, в то время как системное воспаление, по-видимому, не проявляется у бессимптомных женщин на ранних сроках беременности, которые затем рожают преждевременные роды [ 99].Это согласуется с более локальным синдромом внутриутробной воспалительной реакции, при котором никакие организмы не идентифицируются. Понимание патофизиологии материнского интерфейса важно для разработки новых методов лечения преждевременных родов, вызванных воспалением, хотя использование таких локальных изменений для прогнозирования проблематично из-за отсутствия доступа к материнскому плодному интерфейсу.
Плаценты от женщин с pPROM и преждевременными родами имеют более высокий уровень Th2, индуцирующего цитокины [100], а плаценты от женщин после преждевременных родов по сравнению с доношенными родами демонстрируют смещение в сторону профиля Th2 со значительно более высокими уровнями IFN-, γ и IL. -2, а также Th2-индуцирующий цитокин IL-12 [100].Более того, доношенные плаценты демонстрируют сравнительно более высокие уровни цитокинов Th3, IL-4 и IL-10 по сравнению с недоношенными плацентами.
TNF- α увеличивается в хориодецидуальных тканях [71] и околоплодных водах [101] при преждевременных родах. TNF- α , как известно, стимулирует продукцию PG через рецептор 2 TNF, что приводит к сокращению матки, вероятно, через активацию NF- κ B, но также, вероятно, вносит вклад в продукцию MMP-9, приводя к PROM через активацию его рецептор TNF Receptor 1 (TNFR1) [102].Интересно, что образцы миометрия, взятые у женщин с преждевременными родами, и образцы, собранные преждевременно до родов, экспрессируют сопоставимые уровни мРНК TNF- α . Однако уровни мРНК рецепторов, TNF R1 A и B, увеличиваются при преждевременных родах и срочных родах по сравнению с контрольной группой, не связанной с работой [103], что свидетельствует об опосредованном рецептором повышении чувствительности к TNF- α .
Хотя плацентарные, амнионные и хориодецидуальные клетки секретируют провоспалительные цитокины, уровни цитокинов в тканях от преждевременных родов (с внутриутробной инфекцией и без нее) коррелируют со степенью инфильтрации лейкоцитов в плодные оболочки [75].При наличии инфекции основным клеточным источником производства цитокинов в плодных оболочках, вероятно, будет инфильтрация лейкоцитов, а не амниоцитов или хориодецидуальных клеток. [75].
7.3. Полиморфизмы цитокинов Th2 и Th3
Изучение генетических полиморфизмов цитокинов Th2 и Th3 может предоставить новый метод скрининга для определения женщин с высоким риском преждевременных родов. Полиморфизмы, вызывающие функциональные изменения, также могут предоставить информацию о важности интерлейкинов при преждевременных родах.Пока еще не найдены какие-либо многообещающие генетические полиморфизмы, идентифицированные в цитокинах Th2: Th3 для прогнозирования преждевременных родов, проведенная работа заслуживает рассмотрения (см. Таблицу 1).
| |||||||||||||||||||||||||||||||||||||||
8. Не-Th2: Th3 интерлейкины
8.1. IL-8
Интерлейкин 8 — это хемокин, продуцируемый многими иммунными клетками, но в первую очередь макрофагами и моноцитами [116]. Его производство стимулируется LPS, TNF и IL-1 [117] и, в контексте беременности, считается, что он привлекает лейкоциты к тканям беременности и шейке матки в начале срочных и преждевременных родов.Сообщалось, что экспрессия мРНК IL-8 увеличивается более чем в 50 раз при преждевременных родах и более чем в 1000 раз при преждевременных родах с признаками хориоамнионита в амнионе и хориодециду [118]. Ряд исследований также выявил повышение уровня IL-8 в миометрии и шейке матки с началом родов [119, 120]. Плацентарный IL-8 также выше при преждевременных родах по сравнению с доношенными [71].
8.2. IL-6
Хотя IL-6 продуцируется клетками Th3, он является провоспалительным цитокином и основным медиатором реакции хозяина на воспаление и инфекцию [121].Уровни ИЛ-6 умеренно повышены в плаценте, значительно повышены в амнионе и хориодециду у женщин с преждевременными родами по сравнению с доношенными [71]. IL-6, по-видимому, является одним из наиболее чувствительных и специфических индикаторов преждевременных родов, связанных с инфекцией [122, 123]. Повышение уровня IL-6 в околоплодных водах и цервиковагинальной жидкости является независимым фактором риска преждевременных родов и неонатальной заболеваемости [124], включая церебральный паралич [125] и бронхолегочную дисплазию [126].
9. Терапевтическая модуляция профиля Th2 и Th3
Были предложены различные терапевтические стратегии для предотвращения преждевременных родов с основными целями (1) отсрочки родов для увеличения срока беременности во время родов и (2) улучшения состояния новорожденных при рождении [ 127]. В настоящее время многие стратегии, принятые для предотвращения преждевременных родов, включают нацеливание на предложенные пути и события, которые приводят к сокращению матки, укорочению и расширению шейки матки, а не на нацеливание на активацию иммунной системы.Как описано здесь, аберрантный провоспалительный профиль существует как при доношенных, так и при преждевременных родах, что связано с неонатальной заболеваемостью. Ограничением токолитиков является неспособность противодействовать воздействию на плод провоспалительных цитокинов, которые приводят к синдрому воспалительной реакции плода. Фактически это может ухудшить неонатальный исход из-за продления воздействия на плод враждебной окружающей среды. Появляется все больше доказательств того, что перивентрикулярная лейкомаляция и церебральный паралич связаны с воздействием на плод внутриамниотического воспаления и развитием синдрома воспалительной реакции плода [128].Таким образом, стратегия нацеливания на активацию иммунной системы посредством модуляции смещения Th2: Th3 может быть полезной как для предотвращения преждевременных родов, так и для уменьшения неврологического повреждения плода.
9.1. Прогестерон
Было проведено несколько исследований, показывающих положительный ответ на лечение прогестероном для предотвращения преждевременных родов у определенных групп пациентов [129–131]. Наиболее убедительные доказательства улучшения неонатальных исходов получены в последнем многоцентровом рандомизированном контролируемом исследовании, которое показало снижение частоты преждевременных родов (<33 недель) на 45% и респираторного дистресс-синдрома на сроке <33 недель при использовании 90 мг вагинального прогестерона. у женщин с короткой шейкой матки 10–20 мм [132].Механизм, с помощью которого прогестерон способствует поддержанию беременности, традиционно связывают с поддержанием покоя матки за счет увеличения циклического АМФ (цАМФ) и снижения внутриклеточного кальция, что снижает сократимость [133]. Более того, прогестерон, по-видимому, ингибирует фосфорилирование миозина, что является критическим шагом в активации сократительного аппарата миометрия, необходимого для начала родов [134, 135].
Прогестерон также оказывает иммуномодулирующее действие на смещение Th2: Th3.Прогестерон способен подавлять дифференцировку Th2 и усиливать дифференцировку Th3 в мононуклеарных клетках периферической крови in vitro [136]. Более мощный и перорально биодоступный прогестаген, дидрогестерон (6-дегидро-9 β , 10 α -прогестерон) активирует IL-4 и подавляет IFN- γ в PHA-стимулированных PBMC в большей степени, чем прогестерон in vitro . [137]. Также имеется in vivo доказательств противовоспалительного эффекта длительного вагинального введения прогестерона.В исследовании беременных женщин, получавших прогестерон или плацебо от 24 до 34 недель, лейкоциты периферической крови были собраны до и после лечения [138]. мРНК провоспалительных цитокинов IL-1 , β и IL-8 снижались при лечении прогестероном, тогда как противовоспалительный IL-10 повышался. Многоцентровое плацебо-контролируемое исследование (OPPTIMUM, https://www.opptimum.org.uk/: ISRCTN 14568373), основанное на неонатальном исходе, предоставит нам доказательства любого потенциального положительного эффекта вагинального прогестерона на недоношенных новорожденных.
9.2. Ингибиторы NF-
κ BИнгибирование активации NF- κ B — еще одна привлекательная стратегия для предотвращения преждевременных родов, поскольку активация NF- κ B является центральной для активации связанных с родами генов в родах [139]. Активация NF- κ B также приводит к провоспалительному ответу различных цитокинов, включая IFN- γ [140], IL-1 β [74], TNF- α и IL-8 [141]. Ex vivo Исследования с противовоспалительным сульфасалазином подавляют индуцированную ЛПС продукцию IL-6 и TNF- α в мембранах плода посредством ингибирования транслокации p65 в ядро [142].Сообщаемый профиль клинической безопасности сульфасалазина варьирует [143–145], однако при использовании во время беременности часто добавляют фолиевая кислота. Противовоспалительные характеристики циклопентенона PG, 15-дезокси-Δ 12,14 -простагландина J 2 (15dPGJ 2 ), по-видимому, обусловлены его способностью ингибировать активацию NF- κ B у человека. амнион и культура клеток миометрия [146]. Мы также показали, что 15dPGJ 2 ингибирует активацию NF- κ B в мононуклеарных клетках периферической крови человека и снижает процент клеток, продуцирующих провоспалительные цитокины, IFN- γ и TNF- α , [147] .Работа, проведенная в нашей лаборатории, также показала, что 15dPGJ 2 способен задерживать роды и обеспечивать нейрозащиту за счет снижения смертности детенышей с 75% до 5% на мышиной модели преждевременных родов, вызванных воспалением [148].
10. Заключение
Дихотомия Th2: Th3 для поддержания успешной беременности вызвала большой интерес. Тенденция к профилю цитокинов Th3 и подавление профиля цитокинов Th2, по-видимому, существует как в периферической крови, так и в большей степени на границе раздела матери и плода.Активация провоспалительного профиля Th2 — а не подавление профиля Th3 — очевидна при преждевременных родах и, таким образом, должна рассматриваться как логическая цель для иммуномодулирующей терапии для предотвращения преждевременных родов и улучшения неонатального исхода.
Благодарности
Л. Сайкс поддерживается организацией «Благополучие женщин». П. Р. Беннет и Д. А. Макинтайр поддерживаются Фондом здравоохранения Имперского колледжа NHS Trust и Центром биомедицинских исследований NIHR.
Кто решает, кому делать гистерэктомию?
В этой статье научный сотрудник NSF из Центра выпускников CUNY Андр é a Беккер обсуждает, кто решает, кому будет сделана гистерэктомия, и что происходит, когда женщины не контролируют свое репродуктивное здоровье .
Гистерэктомия, удаление матки, — вторая по распространенности операция у женщин в США, уступающая только кесарево сечению. Это шокирующая мелочь, о которой большинство людей не подозревает. Но этот чрезвычайно высокий показатель вызван не причинами, которые вы могли себе представить, и цифры сложнее, чем кажется на первый взгляд.
Люди по всей стране борются за удаление матки как последний призыв к борьбе с годами изнурительной боли и кровотечений из-за хронических репродуктивных проблем, которые врачи просто «не могут понять».«Возьмем, к примеру, историю Лены Данхэм о том, как ей пришлось бороться за гистерэктомию после многих лет борьбы с эндометриозом. Даже могущественной знаменитости приходится бороться с медицинским истеблишментом за то, что ей нужно. Следует отметить, что нет никакой гарантии, что гистерэктомия предотвратит эндометриоз, но люди с другими состояниями, при которых гистерэктомия с большей вероятностью подействует, часто сталкиваются с той же проблемой.
История Лены обычна для людей с такими заболеваниями, как эндометриоз и миома — они просят об операции для облегчения, но врачи настаивают на сохранении их фертильности.Некоторые врачи говорят, что гистерэктомия не обязательно является идеальным средством для этих состояний и что это часто является пластырем при недостаточно изученных проблемах — это справедливый повод для колебаний, прежде чем назначать пациенту серьезную операцию. Но очень часто женщины сталкиваются с тем, что врачи не решаются делать операцию из-за фертильности, даже если женщина уверена, что не хочет детей. Точно так же людям, которые не хотят иметь детей и просят перевязку маточных труб, часто отказывают в этой процедуре по той же причине.Несмотря на свою решимость, им приходится бороться с сексистскими нарративами врачей о том, что «может быть, вы когда-нибудь передумаете и захотите детей…» и «что подумает ваш будущий муж…?»
Между тем, недавно появились сообщения о том, что женщин, содержащихся в учреждении ICE в Джорджии, принуждали к гистерэктомии без их полностью осознанного согласия врач, названный в жалобе «сборщиком матки». Несколько заключенных утверждают, что гистерэктомия проводилась — часто без полного понимания пациентом.ICE отвергла это требование, как и врач, о котором идет речь, и больница, где, как сообщалось, были проведены предполагаемые операции. Если такие процедуры действительно имели место, это напоминает долгую историю принудительной стерилизации цветных людей в этой стране. Более того, резкий контраст в подходах врачей к гистерэктомии рассказывает нам более широкую историю о гендере и о том, что материнство продолжает значить в медицине и за ее пределами.
Это история двух гистерэктомий: в одной из них американским гражданам неоднократно отказывали в доступе к хирургической операции, которую они отчаянно хотели, чтобы улучшить качество своей жизни.С другой стороны, цветных женщин и криминализованных женщин исторически подвергали насильственной стерилизации и лишали органа, который многие женщины по-прежнему считают центральным для своей идентичности.
В то время как все мы хотели бы верить, что врачи дают медицинские рекомендации, основанные на исследованиях, основанных на фактах, медицинские социологи знают, что взаимодействие врача и пациента не является невосприимчивым к социальным предубеждениям и предрассудкам. Мы видим, что предвзятость поставщиков услуг играет роль в непропорционально высоких показателях материнской смертности, например, среди чернокожих женщин.О чем меньше говорят, так это о том, как наш культурный акцент (даже навязчивая идея) на материнство продолжает по-разному влиять на медицину. С того момента, как девочка-подросток достигает половой зрелости, ее тело рассматривается как потенциальный сосуд для жизни человека. Как врачи, так и эксперты в области общественного здравоохранения дают медицинские рекомендации по подготовке женского тела к будущей беременности («уход до беременности») и, похоже, предполагают, что все, кому при рождении назначена женщина, однажды захотят забеременеть — даже если они в настоящее время решительно настроен против него.
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследовать
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
Метод деления пополам — математический Python
Простейшим алгоритмом поиска корня является метод деления пополам.Алгоритм применяется к любой непрерывной функции $ f (x) $ на интервале $ [a, b] $, где значение функции $ f (x) $ меняет знак с $ a $ на $ b $. Идея проста: разделите интервал пополам, решение должно существовать в пределах одного подынтервала, выберите подынтервал, на котором знак $ f (x) $ изменится, и повторите.
Алгоритм
Методика деления пополам:
- Выберите начальный интервал $ [a_0, b_0] $ так, чтобы $ f (a_0) f (b_0) <0 $.
- Вычислить $ f (m_0) $, где $ m_0 = (a_0 + b_0) / 2 $ — средняя точка.
- Определить следующий подинтервал $ [a_1, b_1] $:
- Если $ f (a_0) f (m_0) <0 $, то пусть $ [a_1, b_1] $ будет следующим интервалом с $ a_1 = a_0 $ и $ b_1 = m_0 $.
- Если $ f (b_0) f (m_0) <0 $, тогда пусть $ [a_1, b_1] $ будет следующим интервалом с $ a_1 = m_0 $ и $ b_1 = b_0 $.
- Повторяйте (2) и (3), пока интервал $ [a_N, b_N] $ не достигнет некоторой заданной длины.
- Вернуть значение средней точки $ m_N = (a_N + b_N) / 2 $.
Решение уравнения $ f (x) = 0 $ в интервале $ [a, b] $ гарантируется теоремой о промежуточном значении при условии, что $ f (x) $ непрерывно на $ [a, b] $ и $ f (a) f (b) <0 $.Другими словами, функция меняет знак на интервале и, следовательно, должна быть равна 0 в некоторой точке интервала $ [a, b] $.
Абсолютная ошибка
Метод деления пополам (в общем случае) не дает точного решения уравнения $ f (x) = 0 $. Однако мы можем дать оценку абсолютной погрешности приближения.
Теорема . Пусть $ f (x) $ — непрерывная функция на $ [a, b] $ такая, что $ f (a) f (b) <0 $. После $ N $ итераций метода biection пусть $ x_N $ будет средней точкой в $ N $ -м подынтервале $ [a_N, b_N] $
.$$ x_N = \ frac {a_N + b_N} {2}
$Существует точное решение $ x _ {\ mathrm {true}} $ уравнения $ f (x) = 0 $ на подынтервале $ [a_N, b_N] $, а абсолютная ошибка равна
.$$ \ left | \ x _ {\ text {true}} — x_N \, \ right | \ leq \ frac {b-a} {2 ^ {N + 1}}
$Обратите внимание, что мы можем изменить привязку ошибки, чтобы увидеть минимальное количество итераций, необходимое для гарантии абсолютной ошибки меньше предписанной $ \ epsilon $:
\ begin {align}
\ frac {b-a} {2 ^ {N + 1}} & <\ epsilon \\
\ frac {b-a} {\ epsilon} & <2 ^ {N + 1} \\
\ ln \ left (\ frac {b-a} {\ epsilon} \ right) & <(N + 1) \ ln (2) \\
\ frac {\ ln \ left (\ frac {b-a} {\ epsilon} \ right)} {\ ln (2)} - 1 & Напишите функцию под названием Давайте проверим, что абсолютная ошибка больше, чем граница этой ошибки: Строится CHARLESTON, W.Вирджиния - Бывший комиссар здравоохранения Западной Вирджинии описал, что врачи годами выписывали больше рецептов на опиоиды своим пациентам, чем необходимо, в ходе знаменательного испытания, в ходе которого местные власти обвиняли трех крупных дистрибьюторов лекарств в разжигании опиоидной эпидемии в США. В четверг доктор Рахул Гупта засвидетельствовал, что у врачей была «культура попыток уменьшить боль до нулевого уровня для каждого американца, для каждого жителя Западной Вирджинии». «Намерение было хорошим - для хороших врачей.Но из-за этого они выписали рецепты «дольше, чем нужно», - добавил он. «Плохие врачи регулярно и ритуально выписывают большое количество рецептов». Это был четвертый день судебного разбирательства в Чарльстоне, и он включал перекрестный допрос свидетелей от адвокатов защиты и показания работника службы экстренной помощи, который занимается лечением передозировок в Хантингтоне. Подобные иски привели к многомиллионным расчетам, но это первый случай, когда обвинения были рассмотрены в федеральном суде.Результат может иметь огромное влияние на сотни подобных исков, которые были поданы по всей стране. Округ Кэбелл и город Хантингтон утверждают, что дистрибьюторы лекарств AmerisourceBergen Drug Co., Cardinal Health Inc. и McKesson Corp создали «общественное неудобство», затопив территорию 80 миллионами доз опиоидов в течение восьми лет и игнорируя признаки того, что сообщество был опустошен зависимостью. Адвокаты компаний пытались доказать, что Западная Вирджиния могла иметь более высокую потребность в опиоидных обезболивающих, чем в других регионах, из-за старения населения штата и большого количества рабочих в угледобывающем и промышленном секторах.Несколько часов они допрашивали Гупту в качестве свидетелей. Они также рассмотрели проблему отмены опиоидов у младенцев, матери которых употребляли опиоиды во время беременности. Тимоти Хестер, поверенный McKesson Corp., сказал, что Центры по контролю и профилактике заболеваний никогда не исключали использования рецептов на опиоиды для беременных женщин, даже несмотря на то, что они призывали к осторожности. История продолжается Гупта сказал, что существует ряд «дополнительных рисков», включая эффекты абстиненции, для младенцев, получавших рецепты на опиоиды в утробе матери, добавив, что врачи и пациенты должны серьезно подумать о серьезных рисках. Хантингтон когда-то был эпицентром эпидемии наркомании, пока программа быстрого реагирования, разработанная в 2017 году, не снизила уровень передозировок. Тогда пандемия во многом свела на нет прогресс. Истцы позвонили Конни Придди, координатору программы команды Хантингтона, которая сказала, что эпидемия поразила людей из всех слоев общества. Ее команда сидела в домах «с земляным полом и матрасом, и они сидят в домах за миллион долларов, - сказала она. - Это не касается пола, расы, любой социально-экономической линии».Нет типичного человека, который принимает передозировку ». Ранее на этой неделе защита также попыталась переложить вину на своих клиентов, заявив, что то, что происходит после доставки, находится вне контроля поставщиков. Реализация
bisection , которая принимает 4 входных параметра f , a , b и N и возвращает аппроксимацию решения $ f (x) = 0 $, полученного за $ N $ итераций. метода деления пополам.Если $ f (a_n) f (b_n) \ geq 0 $ в любой точке итерации (вызвано либо неправильным начальным интервалом, либо ошибкой округления в вычислениях), то выведите «Метод деления пополам не работает». и возврат Нет .
по дефолту пополам (f, a, b, N):
'' 'Приближенное решение f (x) = 0 на интервале [a, b] методом деления пополам.
Параметры
----------
f: функция
Функция, для которой мы пытаемся аппроксимировать решение f (x) = 0.
а, б: числа
Интервал поиска решения.Функция возвращает
Нет, если f (a) * f (b)> = 0, поскольку решение не гарантировано.
N: (положительное) целое число
Количество реализуемых итераций.
Возврат
-------
x_N: номер
Середина N-го интервала, вычисленная методом деления пополам. В
начальный интервал [a_0, b_0] задается как [a, b]. Если f (m_n) == 0 для некоторого
midpoint m_n = (a_n + b_n) / 2, тогда функция возвращает это решение.
Если все знаки значений f (a_n), f (b_n) и f (m_n) одинаковы в любом
итерация метод деления пополам не работает и возвращает None.Примеры
--------
>>> f = лямбда x: x ** 2 - x - 1
>>> пополам (f, 1,2,25)
1.6180339939
>>> f = лямбда x: (2 * x - 1) * (x - 3)
>>> пополам (f, 0,1,10)
0,5
'' '
если f (a) * f (b)> = 0:
print («Метод деления пополам не работает.»)
return None
a_n = а
b_n = b
для n в диапазоне (1, N + 1):
m_n = (a_n + b_n) / 2
f_m_n = f (m_n)
если f (a_n) * f_m_n <0:
a_n = a_n
b_n = m_n
elif f (b_n) * f_m_n <0:
a_n = m_n
b_n = b_n
elif f_m_n == 0:
print ("Нашел точное решение.{26}) $ что:
error_bound = 2 ** (- 26)
печать (error_bound)
1.41193847656e-08
абс ((1 + 5 ** 0,5) / 2 - приблизительно_phi)
правда
Упражнения
Докторов выписали чрезмерное количество рецептов на опиоиды