polyfit() в MATLAB — GeeksforGeeks
Polyfit — это функция в MATLAB, которая подгоняет полином к набору точек данных. Он принимает три аргумента:
x: вектор x-координат точек данных
y: вектор y-координат точек данных
n: степень многочлена
polyfit возвращает вектор коэффициенты, представляющие подобранный полином в порядке убывания. В этой статье мы рассмотрим функцию полифита в MATLAB и то, как ее можно использовать для подбора многочлена к набору точек данных.
Синтаксис для polyfit следующий:
Синтаксис:
p = polyfit(x,y,n)
где x и y — векторы одинаковой длины, представляющие координаты x и y точек данных, соответственно, n — это степень полинома, а p — вектор коэффициентов, представляющий подобранный полином в порядке убывания.
Предположим, у нас есть следующие точки данных:
(1,2) (2,3) (3,4)
Мы можем использовать полифит, чтобы подогнать полином к этим точкам. Например:
Например:
Пример 1:
Matlab
|
Выход:
P = 1,0000 1,0000
. 1 (прямая) и имеет следующий вид:
y = x + 1
Мы можем использовать polyval, другую встроенную функцию в MATLAB, чтобы вычислить этот многочлен в определенной точке x. Например:
Пример 2:
Matlab
|
Выход:
3.0000
Это означает, что значение подходящего полинома в X = 2, что это 3, что это 3, это 3, что 3, что это 3, это 3, что это 3, это 3, что это 3, это 3, что это 3, это 3, что это 3, это 3, что это 3, это 3, что 3, что 3, это 3, что 3, что 3, это 3, что это 3, это 3, что это 3, это 3, что это 3, это 3, что 3, что это в качестве исходной точки данных.
Множественные степени
Мы также можем подгонять полиномы более высокой степени к точкам данных. Например, чтобы подобрать квадратичный многочлен (степень 2). В MATLAB функцию полифита можно использовать для подгонки полинома любой степени к набору точек данных. Степень полинома указывается в качестве третьего аргумента функции полифита.
Пример 3:
Matlab
|
Выход:
P = -0,0000 1,0000 1,0000
Заключение:
4449 .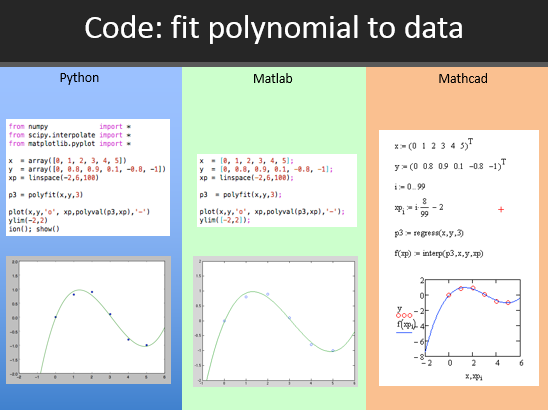 MATLAB для подгонки полинома к набору точек данных. Он прост в использовании и может сэкономить время при работе с полиномами в вашем коде.
MATLAB для подгонки полинома к набору точек данных. Он прост в использовании и может сэкономить время при работе с полиномами в вашем коде. numpy.polyfit — Руководство NumPy v1.24
- numpy.polyfit( x , y , град , rcond=Нет , full=Ложь , w=Нет , cov=Ложь )[источник]
Полиномиальная аппроксимация методом наименьших квадратов.
Примечание
Является частью старого полиномиального API. Начиная с версии 1.4, предпочтительнее новый полиномиальный API, определенный в
numpy.polynomial. Краткую информацию о различиях можно найти в руководство по переходу.Подбор полинома
p(x) = p[0] * x**deg + ... + p[deg]степени степени к точкам (х, у) . Возвращает вектор коэффициентов p , который минимизирует квадрат ошибки порядка град , град-1 , … 0 .Класс
Polynomial.метод рекомендуется для нового кода, так как он более устойчив численно. Видеть документацию метода для получения дополнительной информации. fit
fit - Параметры:
- x array_like, форма (M,)
x-координаты M точек выборки
(x[i], y[i]).- y array_like, форма (M,) или (M, K)
y-координаты точек выборки. Несколько наборов данных выборки точки, имеющие одни и те же координаты x, могут быть установлены сразу с помощью передавая 2D-массив, содержащий по одному набору данных на столбец.
- deg int
Степень аппроксимирующего полинома
- rcond поплавок, опция
Номер относительного состояния посадки. Сингулярные значения меньше, чем это относительно наибольшего единственного значения будет игнорироваться. значение по умолчанию — len(x)*eps, где eps — относительная точность поплавковый тип, в большинстве случаев около 2e-16.

- full bool, необязательный
Переключатель, определяющий характер возвращаемого значения. Когда оно ложно (т. по умолчанию) возвращаются только коэффициенты, когда истинная диагностика также возвращается информация из разложения по сингулярным числам.
- w array_like, форма (M,), опционально
Вес. Если не None, вес
w[i]применяется к неквадратичному остатокy[i] - y_hat[i]вx[i]. В идеале весы выбраны таким образом, чтобы все ошибки продуктовw[i]*y[i]имели такая же дисперсия. При использовании взвешивания с обратной дисперсией используйтеw[i] = 1/сигма(y[i]). Значение по умолчанию — Нет.- cov bool или str, опционально
Если задано, а не False , вернуть не только оценку, но и ее ковариационная матрица. По умолчанию ковариация масштабируется chi2/dof, где dof = M — (deg + 1), т.

cov='unscaled', что актуально для случая, когда веса w = 1/сигма, причем сигма, как известно, является надежной оценкой неопределенность.
- Возвращает:
- p ndarray, shape (градус + 1,) или (градус + 1, K)
Полиномиальные коэффициенты, сначала наивысшая степень. Если и были двумерными, то коэффициенты для k -го набора данных находятся в
p[:,k].- остатки, ранг, сингулярные_значения, rcond
Эти значения возвращаются, только если
full == TrueДополнительные сведения см. в разделе
numpy.linalg.lstsq 9.0041 .- V ndarray, форма (M,M) или (M,M,K)
Присутствует, только если
full == Falseиcov == True. Ковариация
матрица оценок коэффициентов полинома. Диагональ
эта матрица представляет собой оценки дисперсии для каждого коэффициента. Если у
представляет собой двумерный массив, то ковариационная матрица для k -го набора данных
находятся в
Ковариация
матрица оценок коэффициентов полинома. Диагональ
эта матрица представляет собой оценки дисперсии для каждого коэффициента. Если у
представляет собой двумерный массив, то ковариационная матрица для k -го набора данных
находятся в В[:,:,k]
- Предупреждает:
- Ранг Предупреждение
Ранг матрицы коэффициентов в аппроксимации методом наименьших квадратов равен неполноценный. Предупреждение возникает только в том случае, если
full == False.Предупреждения можно отключить с помощью
>>> предупреждения об импорте >>> warnings.simplefilter('игнорировать', np.RankWarning)
См. также
-
polyval Вычисление полиномиальных значений.
-
linalg.lstsq 92\]
в уравнениях:
x[0]**n * p[0] + ... + x[0] * p[n-1] + p[n] = y[0] x[1]**n * p[0] + .
 .. + x[1] * p[n-1] + p[n] = y[1]
...
x[k]**n * p[0] + ... + x[k] * p[n-1] + p[n] = y[k]
.. + x[1] * p[n-1] + p[n] = y[1]
...
x[k]**n * p[0] + ... + x[k] * p[n-1] + p[n] = y[k]
Матрица коэффициентов из коэффициентов p является матрицей Вандермонда.
polyfitвыдаетRankWarning, когда метод наименьших квадратов плохо подходит обусловленный. Это означает, что наилучшее соответствие не определено четко из-за к числовой ошибке. Результаты можно улучшить, понизив полином степени или заменой x на x - x .mean(). Параметр rcond также может быть установлено значение меньше значения по умолчанию, но в результате подгонка может быть ложной: включая вклады малого единственного числа значения могут добавить числовой шум к результату.Обратите внимание, что подходящие полиномиальные коэффициенты по своей сути плохо обусловлены когда степень многочлена велика или интервал точек выборки плохо центрируется. Качество подгонки следует всегда проверять в этих случаи. Когда полиномиальные подгонки неудовлетворительны, сплайны могут быть хорошими.
 альтернатива.
альтернатива.Ссылки
[1]
Википедия, «Подгонка кривой», https://en.wikipedia.org/wiki/Curve_fitting
[2]
Википедия, «Полиномиальная интерполяция», https://en.wikipedia.org/wiki/Полиномиальная_интерполяция
Примеры
>>> предупреждения об импорте >>> x = np.array([0.0, 1.0, 2.0, 3.0, 4.0, 5.0]) >>> y = np.array([0.0, 0.8, 0.9, 0.1, -0.8, -1.0]) >>> z = np.polyfit(x, y, 3) >
Удобно использовать объекты
poly1dдля работы с полиномами:>>> p = np.poly1d(z) >>> р(0,5) 0.6143849206349179 # может варьироваться >>> р(3.5) -0.34732142857143039 # может варьироваться >>> р(10) 22.579365079365115 # может варьироваться
Полиномы высокого порядка могут сильно колебаться:
>>> с warnings.catch_warnings(): ... warnings.simplefilter('игнорировать', np.