Форматы вывода результата вычислений и логические операции в MATLAB
Похожие презентации:
Matlab. Математические вычисления
Вычисления в MATLAB
Логические операции
Высказывание. Логические операции
Математическая логика. Логические операции и высказывания
Понятие предиката. Логические операции над предикатами
Логические выражения и логические операции. Школа детективов «Лунный Свет»
Предикат. Логические операции над предикатами
Элементарные логические операции
Базовые логические операции и функции. Таблицы истинности. Контактные схемы
1. Форматы вывода результата вычислений и логические операции в MATLAB
Выполнила студентка группыЭс/б33-о Васина А. Ю.
Встроенные математические функции MATLAB
позволяют находить значения различных
выражений. MATLAB предоставляет
возможность управления форматом вывода
результата.
Требуемый формат вывода результата определяется
пользователем из меню MATLAB.
 Необходимо
Необходимовыбрать в меню File пункт Preferences. На экране
следует перейти на вкладку Command Window.
Задание формата
производится из
раскрывающегося списка
Numeric Format панели Text
display.
Также задавать формат вывода можно
непосредственно из командной строки при
помощи команды format.
Наиболее распространенные форматы:
• Short – формат, при котором на
экране отображаются только
четыре цифры после десятичной
точки.
• Long – формат, при котором результат будет
отображаться в длинном формате с пятнадцатью цифрами
после десятичной точки.
Long применяется для получения
более точного результата
вычислений.
• Форматы Short e и Long e
предназначены для вывода
результата в
экспоненциальной форме с
четырьмя и пятнадцатью
цифрами после десятичной
точки соответственно.
• Short g – формат, при котором выбирается наилучшая
форма представления числа из форматов Short и Short e.

• Long g – формат, при котором выбирается наилучшая
форма представления числа из форматов Long и Long e.
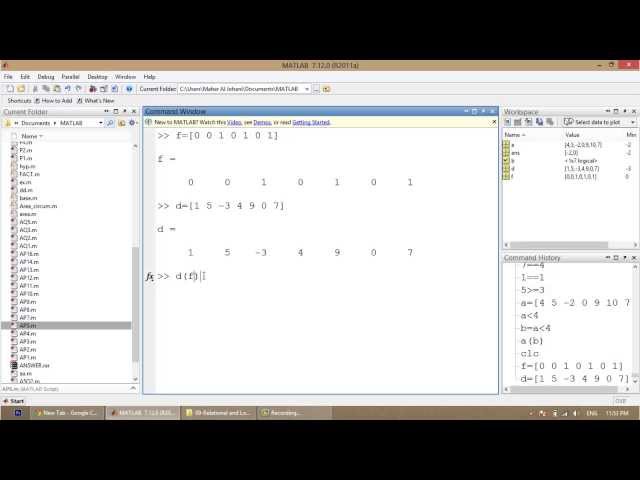
Логические операторы:
• AND – логическое И(AND)&
Логическое выражение
является истинным, если оба
элемента истинны и ложным,
если один из элементов
ложен. Если элементами
логического выражения
являются числа, то
выражение истинно, если оба
элемента отличны от нуля.
• OR – логическое ИЛИ(OR) |
Логическое выражение является
истинным, если один из элементов или
оба элемента истинны и ложным, если
оба элемента ложны.
• NOT – логическое НЕ(NOT) ~
Результат логически ложен, если
элемент истинен, и истинен, если
элемент ложен.
Логические функции:
• XOR – исключающее ИЛИ (EXCLUSIVE OR)
Выражение истинно, если один
из элементов истинен, а другой
ложен. Для числовых
1, если один из элементов
отличен от нуля, а другой — нуль.
• ANY – функция, при которой выражение истинно, если
хоть один из элементов истинен и ложно, если все
элементы ложны.

• ALL – функция, при которой выражение истинно, если все
элементы истинны и ложно, если хоть один элемент ложен.
English Русский Правила
Некоторые специфика выполнения арифметических и логических операций. — Информатика, информационные технологии
csaa Комментарии к записи Некоторые специфика выполнения арифметических и логических операций. отключены
При составлении арифметических выражений система MATLAB допускает использование традиционных знаков арифметических операций и символов специальных операций, представленных в таблице 2.6.1.
Вместе с тем, арифметические операции реализованы в MATLAB с некоторыми характерными особенностями. Наиболее привычным с этих позиций является сложение скалярных величин (т.е. массивов размерности 1х1), аналогичное соответствующему действию в большинстве языков программирования. Однако, если обоими операндами являются массивы одинаковой размерности, то осуществляется покомпонентное сложение элементов с одинаковыми индексами. Если же к массиву любой размерности добавляется скалярная величина, то она добавляется к каждому элементу
Если же к массиву любой размерности добавляется скалярная величина, то она добавляется к каждому элементу
Таблица 2.6.1. Знаки арифметических операций и символы специальных операций в системе MATLAB.
| Символ | Выполняемое действие | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Операции над числовыми величинами | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| + | Покомпонентное (поэлементное) сложение числовых массивов одинаковой размерности; добавление скалярной величины к каждому элементу массива. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| – | Покомпонентное вычитание числовых массивов одинаковой размерности; вычитание скалярной величины к каждому элементу массива. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | Умножение матриц в соответствии с правилами линейной алгебры; умножение всех элементов массива на скаляр. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .* | Покомпонентное умножение элементов массивов одинаковой размерности. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| / | Деление скаляра на скаляр; покомпонентное деление всех элементов массива на скаляр; A/B=A*B-1 (A, B – квадратные матрицы одного порядка). | Покомпонентное возведение в степень элементов массива. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ‘ | Вычисление сопряженной матрицы. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .’ | Транспонирование матрицы. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Логические операции | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Логическое умножение скаляров; логическое покомпонентное умножение массивов одинаковой размерности; логическое умножение массива на скаляр. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | | Логическое сложение скаляров; логическое покомпонентное сложение массивов одинаковой размерности; логическое сложение массива со скаляром. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ~ | Логическое отрицание скаляра или всех элементов массива. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Операции отношения (операции сравнения) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = = | Проверка на равенство. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ~= | Проверка на неравенство. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Проверка на «больше». | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | Проверка на «больше или равно». | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Проверка на «меньше». | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Проверка на «меньше или равно». для обозначения операции возведения в степень использовался в языке программирования Basic, а позднее он же стал использоваться в MATLAB. С сожалением приходится констатировать, что такие популярные языки программирования как C и Pascal даже не включили операцию возведения в степень в набор элементарных действий (для соответствующих целей приходится использовать специальные библиотечные функции). для обозначения операции возведения в степень использовался в языке программирования Basic, а позднее он же стал использоваться в MATLAB. С сожалением приходится констатировать, что такие популярные языки программирования как C и Pascal даже не включили операцию возведения в степень в набор элементарных действий (для соответствующих целей приходится использовать специальные библиотечные функции).Лекция 323. Atmega 8: Принцип работы АЛУлогических (булевых) операций — MATLAB и Симулинк — MathWorks ИндияПерейти к содержимомуОсновное содержание Истинно или ложно условия MATLAB ® представляет булевы данные с использованием логического Функции
Topics
Связанная информация
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: Вы также можете выбрать веб-сайт из следующего списка: Америка
Европа
Азиатско-Тихоокеанский регион
Обратитесь в местный офис
логических операторов: Elementwise & | ~ (функции MATLAB)логические операторы: поэлементно & | ~ (функции MATLAB)
Поэлементные логические операции над массивами Синтаксис
Описание Символы Оператор
Приоритет логических операторов по отношению друг к другу:
Примечания MATLAB всегда дает оператору Эти логические операторы имеют эквиваленты функций М-файла, как показано.
Примеры Этот пример показывает логическое См. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Некоторые функции и операторы MATLAB возвращают логические значения для указания
выполнение условия. Вы можете использовать эти логические значения для индексации в
массив или выполнить условный код. Дополнительные сведения см. в разделе, как найти элементы массива, соответствующие условию.
Некоторые функции и операторы MATLAB возвращают логические значения для указания
выполнение условия. Вы можете использовать эти логические значения для индексации в
массив или выполнить условный код. Дополнительные сведения см. в разделе, как найти элементы массива, соответствующие условию.
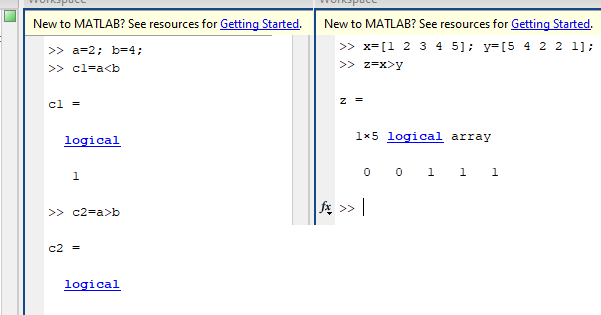
 Они работают с массивами поэлементно, где логические
Они работают с массивами поэлементно, где логические  Хотя MATLAB обычно вычисляет выражения слева направо, выражение
Хотя MATLAB обычно вычисляет выражения слева направо, выражение