Matlab квадратный корень: Справочник по MATLAB - Математические функции (В.Г.Потемкин)

Содержание

Самоучитель MathCAD

Однако (для положительных X и Y) mod(–x,y)
= rem(–x,y)+y. Примеры:
>> M = mod(5,2)
M=
1
>> mod(10,4)
ans = 2
• pow2(Y) – возвращает массив X, где каждый элемент есть 2Y;
• pow2(F,E) – вычисляет X=F*2E для соответствующих элементов F и E. Ар
гументы F и E – массивы действительных и целых чисел соответственно.
Пример:
>> d=pow2(pi/4,2)
d=
3.1416
• [N,D] = rat(X) – возвращает массивы N и D, такие, что N./D аппрокси
мирует X с точностью 1.e–6*norm(X(:),1). Даже при том, что все чис
ла с плавающей запятой – рациональные, иногда желательно аппрок
симировать их дробями, у которых числитель и знаменатель являются по
возможности малыми целыми числами. Функция rat пытается это сде
лать;
• [N,D] = rat(X,tol) – возвращает массивы N и D, такие, что N./D аппрок
симирует X с точностью tol;
• rat(X) без выходных параметров просто выдает на экран массив цепных

дробей;
• rats(X,strlen) – возвращает ряд, полученный путем упрощенной раци
ональной аппроксимации элементов O.

Аргумент strlen – длина возвра
щаемой строки. Функция возвращает знак «*», если полученное значение
не может быть напечатано в строке, длина которой задана значением
strlen. По умолчанию strlen=13. Тот же алгоритм аппроксимации ис
пользуется в командном окне MATLAB при задании рационального форма
та вывода командой format rat. Пример:
>> [g,j]=rat(pi,1e-10)
g=
312689
j=
99532
• p = nextpow2(A) – возвращает такой показатель степени ?, что 2p ?
abs(A). Эта функция эффективно применяется для выполнения быстрого

172
Программные средства математических вычислений
Встроенные элементарные функции
173
• sqrt(A) – возвращает квадратный корень каждого элемента массива X.
Для отрицательных и комплексных элементов X функция sqrt(X) вычис
ляет комплексный результат. Пример:

>> A=[25 21.23 55.8 3];
>> sqrt(A)
ans = 5.0
4.6076
7.4699
символ x окажется наложенным на наименование функций нижних графиков,
которое команда ezplot выводит над графиками автоматически.

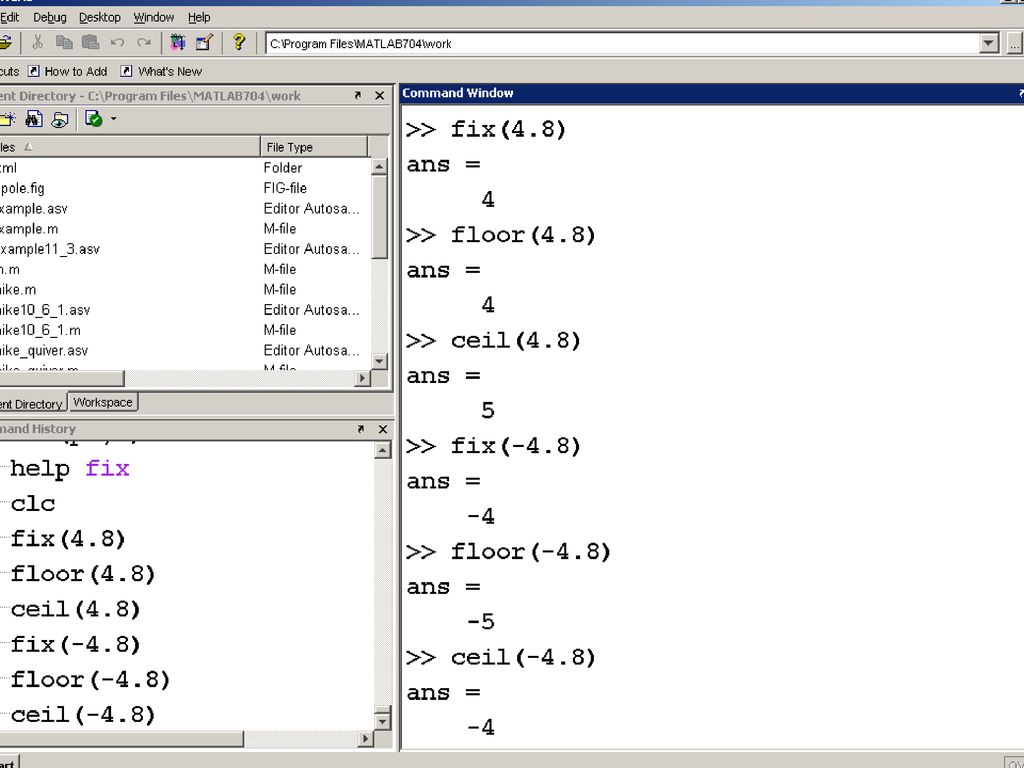
1.7321
3.4.2. Тригонометрические и обратные
тригонометрические функции
В системе MATLAB определены следующие тригонометрические и обратные три
гонометрические функции.

<< Назад 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 Вперед >>

Теория и обработка сигналов MATLAB в ТОС

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Кафедра Систем Сбора и Обработки Данных

Теория и обработка сигналов

MATLAB В ТОС

Доц. Ю. И. Щетинин

Новосибирск

2009

Введение
Что такое MATLAB?

Система MATLAB (сокращение от MATrix LABoratory – матричная лаборатория) фирмы MathWorks Inc. — интерактивная программа для инженерных и научных расчетов, ориентированная на работу с массивами (векторами и матрицами) данных. Система поддерживает:

§ вычисления с матрицами,

· комплексную арифметику,

· вычисления с полиномами,

· решение нелинейных уравнений,

· решение дифференциальных и разностных уравнений,

· задачи оптимизации,

· задачи цифровой обработки сигналов,

· приложения теории автоматического управления,

· построение графиков в декартовой и полярной системах координат,

· построение трехмерных графиков и линий уровня,

· возможность обращения к программам на языках C, C++, Fortran,

· высокоуровневые функции и другие возможности решения математических задач, не прибегая к рутинному программированию.

MATLAB имеет расширения в виде нескольких десятков дополнительных программных пакетов для вычислений и обработки данных в самых различных областях. Среди этих пакетов — расширений MATLAB можно отметить следующие:

ü Simulink – пакет моделирования динамических систем,

ü Signal Processing Toolbox – пакет для анализа, моделирования и проектирования устройств обработки сигналов,

ü Control System Toolbox – пакет для моделирования, анализа и проектирования систем автоматического управления,

ü Symbolic Math Toolbox – пакет программ для решения задач в символьном (аналитическом) виде,

ü Statistics Toolbox – пакет прикладных программ по статистике и др.

В курсе «Теория и обработка сигналов» используется пакет «Signal Processing Toolbox».

Система Matlab является средой для математических вычислений (преобразований) и в то же время предоставляет пользователю собственный язык программирования. На языке Matlab можно написать необходимые пользователям функции и программы (сценарии) в виде M – файлов с расширением .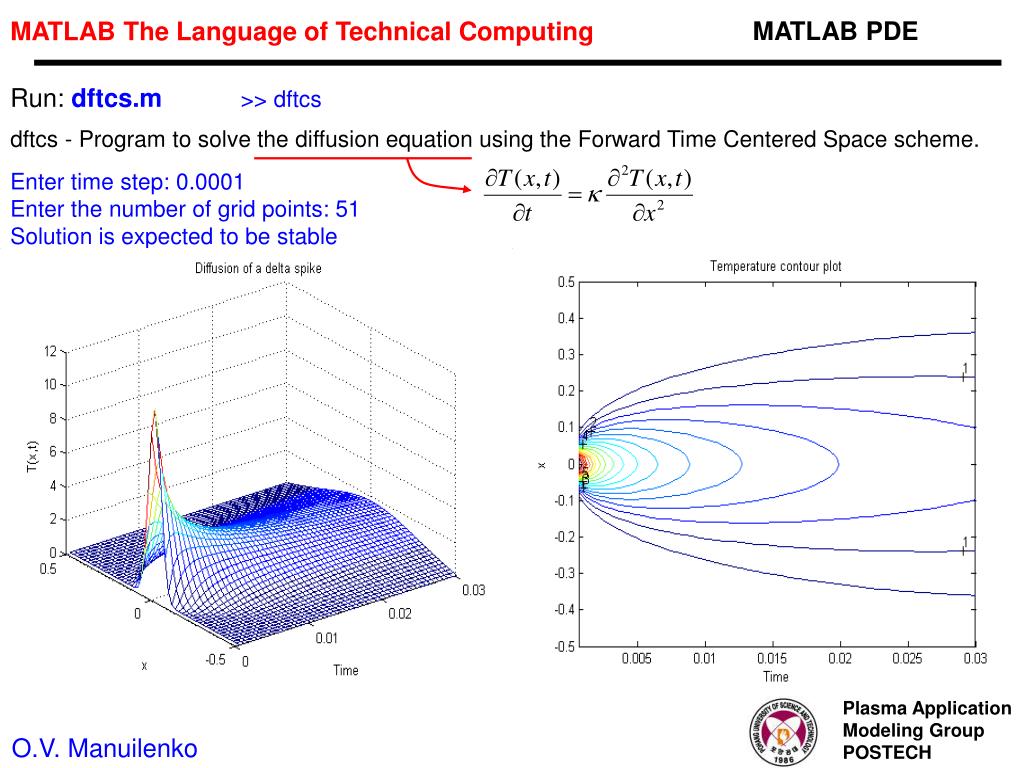

В Matlab любые (подчас весьма сложные) вычисления можно выполнять в режиме прямых вычислений, то есть без подготовки программы. В этом режиме Matlab используется как мощный калькулятор, который способен производить не только обычные для калькуляторов вычисления, но и операции с векторами и матрицами, комплексными числами, рядами и полиномами. Можно также задавать и выводить графики различных функций — от простой синусоиды до сложной трехмерной фигуры.

После загрузки программы на экран выводится командное окно среды Matlab. Работа в режиме прямых вычислений имеет диалоговый характер. При этом вводятся команды и отображаются результаты их выполнения. Ввод и редактирование команды Matlab заканчивается нажатием клавиши «Enter» («Return»). Если для вводимого выражения не хватает одной строки, то часть выражения можно перенести на новую строку с помощью многоточия «…» — 3 или более точек.

Все команды Matlab должны вводиться в нижнем регистре символов.

Например, команда

» sqrt(43.7)

ans =

6.6106e+000

вычисляет квадратный корень из 43,7 и присваивает результат переменной ans.

Остановить процесс вычислений или вывода на экран в MATLAB при необходимости можно командой CTRL+BREAK.

Клавиши управления перемещением курсора «вверх» (key up) и «вниз» (key down) позволяют вывести предыдущие команды командной строки в соответствующем порядке.

Выход из Matlab осуществляется с помощью команды

>> quit

Символ (команда) ‘ %’ обозначает комментарий MATLAB.

Команда

>> ; % ( точка с запятой) подавляет вывод результатов на экран. Если % опустить эту команду, то на экране после выполнения команды % может наблюдаться поток вывода из большого количества

% данных.

Сеанс работы с Matlab называется сессией (session). Используемые в сессии переменные и функции можно сохранить на диске в файлах типа .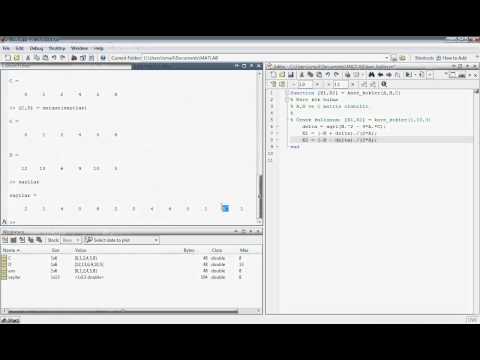 2+15/3-2

x =

Переменные Matlab

Имена переменных должны начинаться с буквы, максимальная длина имени — 31 символ. Имена не должны совпадать с именами функций и процедур и системных переменных. Имена чувствительны к регистру.

Операция присваивания

<имя переменной> = <выражение>; %

Здесь команда “;” подавляет эхо-вывод результатов вычисления (присваивания) на экран.

Примеры

Действительные скаляры (числа)

>> x =2

x = 2

Комплексные скаляры

>> x = 5+10j

x =

5.0000 +10.0000i

Вектор – строка (1 x 3)

>> x = [1 2 3]

x =

1 2 3

Вектор — столбец (3 x 1)

>> x = [1; 2 ; 3];

>> x

x =

Предопределенные системные переменные Matlab

>> ans имя переменной по умолчанию для результата вычислений.

>> ; подавляет вывод результатов на экран.

>> eps переменная машинной точности вычислений, имеет порядок 10^-16.

>> exit завершение (окончание) работы Matlab.

>> i или j мнимая единица, т.е. .

>> pi число π.

>> Inf обозначение бесконечности.

>> NaN не числовой результат, т.е. 0/0.

2 — квадратное целое число, тогда a определяется как квадратный корень из этого числа.

Например, 16 — это число в совершенной квадратной форме, и его квадратный корень может быть равен 4 или -4. Есть много методов, которые используются в математике, чтобы найти квадратный корень числа.

Работа и использование квадратного корня в Matlab с примерами

Matlab выполняет все математические функции, поэтому существуют также методы нахождения квадратного корня из числа. В Matlab мы используем функцию sqrt(), чтобы найти квадратный корень числа или каждого элемента, определенного в массиве. Входные аргументы, которые используются в функции, могут быть скалярными, векторными, массивными или многомерными массивами. Они также могут быть положительными, отрицательными или сложными по своей природе. Если ввод сложный или отрицательный по своей природе, то он приводит к комплексному числу. 9Пример №1

-3 -2 -1 0 1 2 3

A = SQRT (Y)

Выход:

(0,0000 + 1,7320i) (0,0000 + 1,4142i) (0,0000 + 1,0000 (0,0000 + 0,0000i) (1,0000 + 0,0000i) (1,4142 + 0,0000i) (1,7320+0,0000i)

Пример №2

Y = -5: -3

Таким образом, вход находится в форме 1*4

-5 -4 -3

A = SQRT (Y)

Выход:

(0,0000+2,2360I) (0,000014

(0,0000+2,2360i) +2.0000i) (0.0000+1.7320i)

Мы знаем, что если ввод массива отрицательный, то он приводит к комплексному числу. В приведенных выше двух примерах мы видим, что диапазон состоит из отрицательных и положительных чисел, поэтому его выход представляет собой комплексное число. Некоторые операции в Matlab отличаются от стандарта IEEE, например, квадратный корень из отрицательного нуля равен 0 в Matlab, тогда как в IEEE он равен -0, квадратный корень из значений меньше нуля приводит к комплексному числу в Matlab, в то время как то же самое недоступно в IEEE.

Если мы хотим найти квадратный корень только из положительных целых чисел в массиве, мы можем использовать функцию realsqrt() в Matlab. В отличие от функции sqrt(), она выдает сообщения об ошибках, когда мы передаем ввод как отрицательное или комплексное число. Итак, если мы хотим просмотреть результат отрицательного или комплексного числа, то предпочтительнее использовать функцию sqrt(). Размер вывода и размер ввода должны быть одинаковыми, если мы используем realsqrt().

Пример 3

Входные данные представляют собой матрицу 4*4 с именем A

Y=realsqrt(A)

Вывод:

В приведенном выше примере вычисляется квадратный корень каждого элемента матрицы. Входные аргументы могут быть матрицей, массивом, вектором, скаляром или многомерным массивом, и они должны быть положительными и действительными целыми числами. Существуют различные свойства квадратного корня в Matlab, которые следует отметить:

Квадратный корень из любого четного числа, являющегося полным квадратом, всегда должен быть четным.

Например: 16,36,64,100 и т.д.

Здесь 16, 36, 64 и 100 — четные числа, являющиеся полным квадратом, а квадратный корень из этих чисел — 4, 6, 8 и 10, которые также являются четными числами.

Умножение квадратных корней одного и того же числа приводит к положительному целому числу, в то время как квадратные корни числа также можно умножать и давать результат.

Например: √4 * √4 = 4

√3 * √2=√6

Квадратный корень любого нечетного числа, являющегося полным квадратом, всегда должен быть нечетным.

Например: 25,9,49,81

Здесь 25,9,47,81 — все квадраты нечетных чисел, а квадратный корень из этих чисел — 5,3,7,9, которые также являются нечетными числами. Единичная цифра элемента не может быть 3,2,8 или 7, чтобы быть полным квадратом.

Заключение

Квадратные корни широко используются в Matlab для различных бизнес-требований. Они широко используются при решении любых квадратных уравнений, таких темах машинного обучения, как вычисление стандартного отклонения и дисперсии. Таким образом, это важная функция во всех математических областях.

Как рассчитать стандартную ошибку с помощью MATLAB?

По

Андрей Блохин

Полная биография

Андрей Блохин имеет более 5 лет профессионального опыта работы в области государственного бухгалтерского учета, личных инвестиций и в качестве старшего аудитора в Ernst & Young.

Узнайте о нашем редакционная политика

Обновлено 27 мая 2021 г.

Рассмотрено

Эрик Эстевес

Рассмотрено Эрик Эстевес

Полная биография

Эрик является должным образом лицензированным независимым страховым брокером, имеющим лицензию на страхование жизни, здоровья, имущества и страхования от несчастных случаев. Он проработал более 13 лет как в государственном, так и в частном бухгалтерском учете и более четырех лет имел лицензию страхового агента. Его опыт в области налогового учета послужил прочной основой для его текущей деловой книги.

Узнайте о нашем Совет по финансовому обзору

В MATLAB можно рассчитать стандартную ошибку, выполнив однострочную команду. MATLAB — это платформа программирования от MathWorks, разработанная для ученых и инженеров и используемая ими.

Что такое стандартная ошибка?

В статистике стандартная ошибка — это стандартное отклонение статистической меры выборки, и она чаще всего используется для среднего значения выборки. Стандартная ошибка измеряет, насколько точно выборка представляет реальную совокупность, из которой она была составлена.

Поскольку из генеральной совокупности могут быть взяты разные выборки, существует распределение выборочных средних. Стандартная ошибка измеряет стандартное отклонение всех средних значений выборки, взятых из генеральной совокупности.

Формула для расчета стандартной ошибки среднего представляет собой стандартное отклонение выборки, деленное на квадратный корень размера выборки.

Команда для стандартной ошибки в MATLAB

Чтобы вычислить стандартную ошибку среднего значения в выборке, пользователю необходимо запустить однострочную команду в MATLAB:

стандартная ошибка знак равно std( данные ) / sqrt( длина ( данные )) куда: данные знак равно Массив с образцами значений станд. знак равно Функция MATLAB, вычисляющая стандартные отклонение образца кв знак равно Функция MATLAB, вычисляющая квадрат корень из неотрицательного числа длина знак равно Функция MATLAB, которая вычисляет общее количество количество наблюдений в выборке \begin{выровнено} &\text{stderror} = \text{ std(данные) / sqrt(длина(данные))}\\ &\textbf{где:}\\ &\text{данные} = \text{An массив значений выборки}\\ &\text{std} = \text{Функция MATLAB, вычисляющая стандарт} \\ &\text{отклонение выборки}\\ &\text{sqrt} = \text{Функция MATLAB которая вычисляет квадрат} \\ &\text{корень неотрицательного числа}\\ &\text{длина} = \text{Функция MATLAB, которая вычисляет общее} \\ &\text{количество наблюдений в образец}\\ \end{выровнено} stderror= std( data ) / sqrt( length( data )) где:data=массив со значениями выборки std=функция MATLAB, вычисляющая стандартное отклонение выборокqrt=функция MATLAB, вычисляющая квадратный корень из неотрицательного числаlength= Функция MATLAB, вычисляющая общее количество наблюдений в выборке.

Matlab квадратный корень: Справочник по MATLAB — Математические функции (В.Г.Потемкин)