Matlab график трехмерный: 04. Построение трехмерных графиков в Matlab.

Урок 9. 3D-графики функций в Mathcad

Павел Демидов 11.06.2014 Уроки Mathcad 1

Графики двух переменных в PTC Mathcad схожи с 2D-графиками. Однако существуют различия, о которых следует знать. В PTC Mathcad есть два типа 3D-графиков:

1. Контурный график.
2. 3D-график поверхности, в трех осях.

Контурный график

Контурный график отражает изменение поверхности по высоте. Он представляет собой линий равных высот. Чтобы вставить контурный график, выберите Графики –> Кривые –> Вставить график –> Контурный график:

Построим график параболоида:

Функция имеет минимум в начале координат и возрастает при увеличении расстояния от начала координат. Цвет графика зависит от величины функции z:

Диапазоны по умолчанию: -10<x<10, -10<y<10. По оси zдиапазон подбирается автоматически в зависимости от величины функции. Изменить эти диапазоны можно, меняя величину первой и последней меток, а расстояние между метками – изменением величины второй метки.

Кроме того, можно выбрать среди нескольких цветовых схем и добавлять величины к контурным линиям:

3

D-график

Прежде всего, рассмотрим элементы 3D-графика.

У графика есть три оси: X, Y и Z. Ось Z обычно вертикальная. Сам график (здесь – розовая поверхность с красной сеткой) заключена в прямоугольную область, ограниченную осями. В 2D-графиках были отдельные местозаполнители для осей X и Y. Здесь есть только один местозаполнитель для оси Z.

В правом верхнем углу есть кнопка для выбора осей. Выбранная ось будет подсвечена синим, как на кнопке выбора, так и в области графика. Вы можете изменять значение первой, второй и последней метки, как на 2D-графике. Так можно менять диапазоны по осям и число меток.

Вы можете перемещать, сжимать и расширять область с графиком с помощью кнопок на границе области. С помощью кнопок в левом верхнем углу можно перемещать, вращать и масштабировать график, а также сбросить вид графика (что-то вроде кнопки «Отменить»).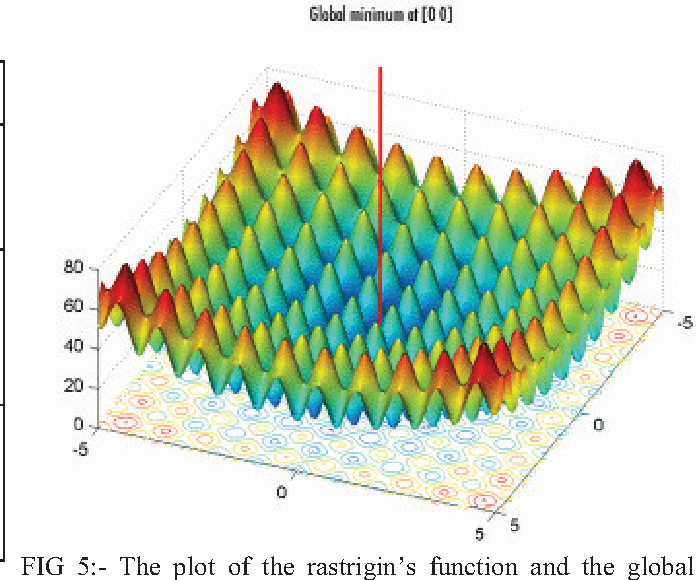

Параболоид

Мы собираемся построить график нашего параболоида. Поместите курсор на пустой области, затем нажмите Графики –> Кривые –> Вставить график –> 3D-график. В местозаполнителе введите [z(x,y] и щелкните по пустой области. Появится график:

Попробуйте использовать кнопки для управления видом графика в левом верхнем углу, потом нажмите «Сброс вида».

Щелкните по оси Z на кнопке выбора оси. Измените значение последней (верхней) метки с 200 на 400, затем щелкните по пустой области, чтобы посмотреть, что получилось. Если нужно изменить значение обратно на 200, то нужно сделать это вручную – кнопка сброса вида здесь не сработает.

На втором графике мы изменили цвет графика и добавили заливку поверхности. Попробуйте сделать это с помощью меню Графики –>Стили:

Две функции

Чтобы добавить график второй функции, поместите курсор на местозаполнитель с легендой и нажмите Графики –> Кривые –> Добавить кривую. Ниже мы построили графики параболоида и плоскости:

Для графиков выбрали контрастные цвета, чтобы можно было увидеть их пересечение. Повращайте график, чтобы изучить форму этого пересечения.

Использование вектора

Мы строили 2D-графики с помощью векторов. Нечто похожее можно проделать для 3D-графиков, но нужен вектор со значениями по осям X, Y и Z. Мы показали это на примере функции, известной под названием «Мексиканская шляпа»:

Сфера

Построить параметрическую поверхность несколько сложнее, чем 2D-график, так как Вы можете добавить лишь значение Z на график. Мы проиллюстрируем, как это сделать на примере построения графика сферы с помощью функции CreateMesh. Параметрические уравнения сферы:

Параметр ? называется азимутальным углом, а параметр ? – зенитным углом. Необходимые диапазоны изменения параметров:

Матрица для построения поверхности формируется функцией CreateMesh:

Поместите имя переменной-матрицы в местозаполнитель 3D-графика. и щелкните по пустой области, чтобы увидеть результат:

Резюме

Трехмерные графики имеют некоторые существенные отличия от двухмерных графиков, рассмотренных в предыдущих уроках:

1. Есть 2 вида графиков функций двух переменных: контурные графики и 3D-графики. Их можно ставить из меню Графики –> Кривые –> Вставить график.
2. Контурный график похож на карту с линиями уровня.
3. 3D-график похож на 2D-график, но у него три оси. Оси выбираются с помощью кнопки выбора и редактируется каждая в отдельности. Диапазон значений и расстояние между метками редактируются с помощью первой, второй и последней метки.
4. Выделите область графика с помощью щелчка мыши при зажатой клавише [Ctrl]. Перемещайте, сжимайте и расширяйте область графика с помощью кнопок на границе области.
5. Вращайте и перемещайте график с помощью кнопок управления в левом верхнем углу.
6. Для быстрого построения поверхности определите функцию z(x,y), вставьте область графика и введите имя функции в местозаполнитель.
7. Можно также создать вектор, содержащий значения по осям X, Y, Z и поместить имя вектора в местозаполнитель.

About Павел Демидов

Выпускник МГТУ им. Н.Э. Баумана, технический специалист по продуктам PTC Mathcad и Solid Edge.

View all posts by Павел Демидов →

Mathcad

Урок 8. 2D-графики функций в Mathcad

Урок 10. Обозначения и единицы измерения в Mathcad

Matplotlib. Урок 5. Построение 3D графиков. Работа с mplot3d Toolkit

До этого момента все графики, которые мы строили были двумерные, Matplotlib позволяет строить 3D графики. Этой теме посвящен данный урок.

• Линейный 3D-график
• Точечный 3D-график
• Каркасная поверхность
• Поверхность

Импортируем необходимые модули для работы с 3D:

import matplotlib. pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

В библиотеке доступны инструменты для построения различных типов графиков. Рассмотрим некоторые из них более подробно.

Линейный график

Для построения линейного графика используется функция plot().

Axes3D.plot(self, xs, ys, *args, zdir=’z’, **kwargs)

• xs: 1D массив
  • x координаты.
• ys: 1D массив
  • y
    координаты.
• zs: скалярное значение или 1D массив
  • z координаты. Если передан скаляр, то он будет присвоен всем точкам графика.
• zdir: {‘x’, ‘y’, ‘z’}
  • Определяет ось, которая будет принята за z направление, значение по умолчанию: ‘z’.
• **kwargs
  • Дополнительные аргументы, аналогичные тем, что используются в функции plot() для построения двумерных графиков.

x = np. linspace(-np.pi, np.pi, 50)
y = x
z = np.cos(x)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(x, y, z, label='parametric curve')

Точечный график

Для построения точечного графика используется функция scatter().

Axes3D.scatter(self, xs, ys, zs=0, zdir=’z’, s=20, c=None, depthshade=True, *args, **kwargs)

• xs, ys: массив
  • Координаты точек по осям x и y.
• zs: float или массив, optional
  • Координаты точек по оси z. Если передан скаляр, то он будет присвоен всем точкам графика. Значение по умолчанию: 0.
• zdir: {‘x’, ‘y’, ‘z’, ‘-x’, ‘-y’, ‘-z’}, optional
  • Определяет ось, которая будет принята за z направление, значение по умолчанию: ‘z’
• s: скаляр или массив, optional
  • Размер маркера. Значение по умолчанию: 20.
• c: color, массив, массив значений цвета, optional
  • Цвет маркера. Возможные значения:
    • Строковое значение цвета для всех маркеров.
    • Массив строковых значений цвета.
    • Массив чисел, которые могут быть отображены в цвета через функции cmap и norm.
    • 2D массив, элементами которого являются RGB или RGBA.
• depthshade: bool, optional
  • Затенение маркеров для придания эффекта глубины.
• **kwargs
  • Дополнительные аргументы, аналогичные тем, что используются в функции scatter() для построения двумерных графиков.

np.random.seed(123)
x = np.random.randint(-5, 5, 40)
y = np.random.randint(0, 10, 40)
z = np.random.randint(-5, 5, 40)
s = np.random.randint(10, 100, 20)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, s=s)

Каркасная поверхность

Для построения каркасной поверхности используется функция plot_wireframe().

plot_wireframe(self, X, Y, Z, *args, **kwargs)

• X, Y, Z: 2D массивы
  • Данные для построения поверхности.
• rcount, ccount: int
  • Максимальное количество элементов каркаса, которое будет использовано в каждом из направлений. Значение по умолчанию: 50.
• rstride, cstride: int
  • Параметры определяют величину шага, с которым будут браться элементы строки / столбца из переданных массивов. Параметры rstride, cstride и rcount, ccount являются взаимоисключающими.
• **kwargs
  • Дополнительные аргументы, определяемые Line3DCollection.

u, v = np.mgrid[0:2*np.pi:20j, 0:np.pi:10j]
x = np.cos(u)*np.sin(v)
y = np.sin(u)*np.sin(v)
z = np.cos(v)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_wireframe(x, y, z)
ax.legend()

Поверхность

Для построения поверхности используйте функцию plot_surface().

plot_surface(self, X, Y, Z, *args, norm=None, vmin=None, vmax=None, lightsource=None, **kwargs)

• X, Y, Z : 2D массивы
  • Данные для построения поверхности.
• rcount, ccount : int
  • см. rcount, ccount в “Каркасная поверхность“.
• rstride, cstride : int
  • см.rstride, cstride в “Каркасная поверхность“.
• color: color
  • Цвет для элементов поверхности.
• cmap: Colormap
  • Colormap для элементов поверхности.
• facecolors: массив элементов color
  • Индивидуальный цвет для каждого элемента поверхности.
• norm: Normalize
  • Нормализация для colormap.
• vmin, vmax: float
  • Границы нормализации.
• shade: bool
  • Использование тени для facecolors. Значение по умолчанию: True.
• lightsource: LightSource
  • Объект класса LightSource – определяет источник света, используется, только если shade = True.
• **kwargs
  • Дополнительные аргументы, определяемые  Poly3DCollection.

u, v = np.mgrid[0:2*np.pi:20j, 0:np.pi:10j]
x = np.cos(u)*np.sin(v)
y = np.sin(u)*np.sin(v)
z = np.cos(v)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='inferno')
ax.legend()

P.S.

Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas.  Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.

MATLAB-3D-LINE-PLOT-Google Suce

ALLBILDERVIDEOSSHOPPINGMAPSNEWSBücher

SUCOOPTIONEN

3-D POINT или LINE STUP-MATLAB STUT3-MATHWORKS

WWW.MATHWORKS.com ›…› LINE

WWW.MATHWORKS.com ›… Функция MATLAB отображает координаты в трехмерном пространстве. … plot3( X , Y , Z , LineSpec ) создает график с использованием указанного стиля линии, маркера и цвета.

Синтаксис · Описание · Примеры · Входные параметры

Способ построить несколько линий в 3D с указанием начальной и конечной точек?

www.mathworks.com › matlabcentral › ответы › 4…

Узнайте больше о трехмерных графиках, графиках, линиях MATLAB. … Есть ли способ построить несколько линий по 3 осям и указать начальную и конечную точки.

Ähnliche Fragen

Как построить трехмерную линию в MATLAB?

Как создать трехмерный график в Matplotlib?

Как создать трехмерную функцию в MATLAB?

Создание трехмерных графиков — пример MATLAB и Simulink — MathWorks

www. mathworks.com › … › Графики поверхности и сетки

В этом примере показано, как создавать различные трехмерные графики в MATLAB®. … Функция контура используется для создания графика с линиями контура постоянного значения.

Трехмерный линейный график в MATLAB | Команда Matlab для построения графика | Matlab Graph #matlab

www.youtube.com › смотреть

31.12.2021 · Трехмерный график в Matlab В этом видео показано, как создавать трехмерные линейные графики в MATLAB с помощью plot3 …
Дата: 0:59
Прислан: 31.12.2021

3D-графики в Matlab — YouTube

www.youtube.com › смотреть

19.10.2018 · В этом учебном пособии показано, как создавать 3D-графики в Matlab. Мы исследуем концепцию того, как …
Dauer: 34:58
Прислан: 19.10.2018

Трехмерные графики в MATLAB — Plotly

plotly.com › matlab › Трехмерные графики

Более 12 примеров трехмерных линейных графиков, включая изменение цвета, размера, логарифмических осей и т. д. в MATLAB.

Трехмерный график в Matplotlib | Наука о данных Python …

jakevdp.github.io › PythonDataScienceHandbook

axes(projection=’3d’) # Данные для трехмерной линии zline = np.linspace(0, 15, 1000) xline = …

Matlab: У меня есть две точки на трехмерном графике, и я хочу соединить их…

stackoverflow.com › вопросы › matlab-i-have-two-…

Я просто хочу построить видимую линию, соединяющую эти две баллы … Я пробовал plot3 (0,0,0, 13,-11,19) и другие вещи, но все, что я пробовал, не помогло …

Создание трехмерных графиков в Matlab: полное руководство по графике в Matlab в MATLAB вы должны использовать функцию «plot3». Эта функция позволит вам отображать данные в трех измерениях. Чтобы использовать …

Построить линию в 3D: r/matlab — Reddit

www.reddit.com › matlab › комментарии › ynsi48 › pl…

20.11.2022 · У меня есть параметрическая форма линия в 3D-пространстве. Я хочу построить его в 3D, но он кажется коротким. Я делаю что-то не так? код: xt = @(t) …

Ähnliche Suchanfragen

MATLAB 3D plot

MATLAB plot 3d line between two points

MATLAB 3d plot surface

matlab 3d plot x y z

MATLAB 3d point plot

MATLAB surf

MATLAB 3D plot matrix

MATLAB 3d plot function

Элементарное трехмерное построение (черчение в трех измерениях) (MATLAB), часть 1

Мы живем в трехмерном мире, и большая часть нашей информации лучше всего раскрывается с помощью трехмерных методов. К счастью, MATLAB предоставляет вам изобилие графических функций, позволяющих быстро создавать трехмерные графики и визуализировать ваши данные. Этот раздел предназначен для того, чтобы познакомить вас с этими функциями и привести к хорошему пониманию встроенной способности MATLAB визуализировать в трех измерениях. Мы начнем с изучения plot3, т. е. трехмерного аналога plot, а затем рассмотрим различные методы создания поверхностей, затем контурные графики и, наконец, представим специальные функции MATLAB для визуализации объемов.

Использование Plot3

Функция plot3 используется почти так же, как и plot , за исключением того, что для предоставления данных для третьего измерения используется дополнительная переменная z. Например, давайте воспользуемся формой plot3(x,y,z), набрав

, чтобы получить рисунок 4.1. Обратите внимание, как оси были помечены с помощью xlabel, ylabel, и здесь мы вводим новую команду маркировки, zlabel, форма которой такая же, как у ее братьев и сестер.

Рисунок 4.1 Трехмерный график с использованием plot3.

Общая форма этой функции — plot3(x, y, z, ‘string’), однако то, что она делает,    определяется характером переданных ей переменных, а именно:

Если x, y , и z являются векторами одинаковой длины, трехмерная линия создается путем соединения координат, заданных элементами векторов x, y и z.

Если x, y, и z являются матрицами, имеющими одинаковое количество строк и столбцов, то из столбцов матриц будет создано несколько строк.

Если некоторые из входных переменных являются матрицами, а другие являются векторами, а длина векторов равна количеству строк или столбцов в матрицах, MATLAB будет «реплицировать» векторы таким образом, чтобы несколько строк может быть создан. Если размеры векторов или матриц не позволяют этого, MATLAB вернет сообщение об ошибке.

Переменная string представляет собой строку из 1, 2 или 3 символов, состоящую из символов, совместимых с функцией построения графика (см. Таблицу 3.3.1).

Вы можете изменить перспективу , то есть угол обзора графика одним из двух способов. Во-первых, вы можете выбрать инструмент Rotate 3-D в окне Figure.

Это позволит вам интерактивно вращать оси графика, удерживая нажатой кнопку мыши и перемещая ее. Конкретные значения азимута и возвышения будут показаны в левом нижнем углу рисунка, пока вы вращаете оси.

Второй вариант — использовать функцию просмотра . Общая форма этой функции — view(az, el) или view([az, el]), и с ее помощью вы можете указать точные значения азимута и возвышения, на которые вы хотите повернуть оси. Следующий код создаст различные представления, показанные на рис. 4.2.

 

 

 

Хотя в MATLAB исходной единицей измерения угла являются радианы, в представлении используются градусы для единиц измерения азимута и эл. Есть еще несколько интересных аспектов обзора, которые мы сохраним для последующего обсуждения, а сейчас вам нужно знать, что по умолчанию для трехмерных графиков используется вид az = -37,5° и el = 30°. Использование az = 0o и el = 90o даст двухмерный вид по умолчанию; вы также можете получить это, используя представление (2). Что, если вы так сильно повернули свои оси, что запутались и устали пытаться исправить это, перетаскивая мышь? Вы можете быстро вернуться к трехмерному виду по умолчанию, набрав view(3).

Создание трехмерных сеток и поверхностей

По мере того, как мы переходим к большему количеству методов построения трехмерных графиков, мы обнаружим, что часто нам приходится иметь дело с упорядоченными парами, т. е. данными, которые зависят как от x, так и от y стоимость. Многие математические функции имеют две переменные, то есть для каждой пары x и y существует z. Вы видели, что это указано как z = f(x,y). Одним из способов вычисления z для каждой пары x y может быть повторение вложенного цикла, но одно из основных преимуществ MATLAB состоит в том, что он может работать с матрицами, не прибегая к циклу. Все, что вам нужно, это каким-то образом преобразовать ваши данные в матричный формат. Если у вас есть вектор значений x и вектор значений y, MATLAB предоставляет полезную функцию, называемую meshgrid, которую можно использовать для упрощения генерации массивов матриц X и Y, используемых в трехмерных графиках. Он вызывается с использованием формы [X,Y] = meshgrid (x,y), где x и y — векторы, помогающие указать область, в которой будут лежать координаты, определяемые парами элементов матриц X и Y. Матрица X будет содержать реплицированные строки вектора x, а Y будет содержать реплицированные столбцы вектора y. Сначала это может показаться немного сложным, но пример поможет прояснить ситуацию. Рассмотрим два вектора, переданные здесь в meshgrid.

MATLAB возвращает

Как вы можете видеть , X формируется путем репликации вектора x в виде строк для каждого столбца в y, а Y формируется вектором y в виде столбцов для каждого элемента в Икс. Каждый элемент в x соответствует каждому элементу в y. Имейте в виду, что ввод meshgrid(x) эквивалентен meshgrid(x,x). Функция meshgrid будет использоваться в нескольких примерах этого раздела.

Первую функцию построения графика поверхности мы будем обсудить это сетка. Он создает множество перекрещивающихся линий, которые выглядят как сеть, накинутая на поверхность, определенную вашими данными. Чтобы понять, что рисует команда, рассмотрим три матрицы размером M на N, X, Y и Z, которые вместе задают координаты некоторой поверхности в трехмерном пространстве. Сетчатый график этих матриц можно создать с помощью команды mesh(X,Y,Z). Каждая (x(i,j),y(i,j),z(i,j)) тройка, соответствующая элементу в i-й строке и j-м столбце каждой из матриц X, Y и Z, связана к триплетам, определенным элементами в соседних столбцах и строках. Вершины, определенные тройками, созданными из элементов, которые не находятся ни во внешней (то есть первой, ни в последней) строке или столбце матрицы, будут, следовательно, соединены с четырьмя соседними вершинами. Вершины на краю поверхности будут соединены с тремя соседними. Наконец, вершины, определяющие углы поверхности, будут присоединены только к двум соседним. Помимо обеспечения визуальной перспективы формы поверхности, такое использование сетки автоматически выбирает цвета графика сетки, пропорциональные высоте поверхности. Рассмотрим следующий пример, который создаст график, показанный на рис. 4.3.

 

 

 

 

Существует несколько способов вызова команды сетки . Мы только что рассмотрели mesh(X,Y,Z), однако еще более общий вызов функции можно сделать с помощью mesh(X,Y,Z,C), где матрица C задает цвет графика сетки. Когда эта матрица C отсутствует в команде, функция предполагает, что C = Z, таким образом, обеспечивая пропорциональное сопоставление между цветом и высотой поверхности. Пока вам достаточно понять, что минимальное и максимальное значения матрицы C определяют диапазон значений, связанных с цветовой картой фигуры, т. е. со списком цветовых векторов RGB. Минимальное значение C будет связано с первой строкой в ​​карте цветов, а максимальное значение C будет связано с последней строкой в ​​карте цветов. Все значения C, лежащие между минимумом и максимумом, должны быть связаны с цветом в этом списке. Например, если элемент C, соответствующий одной из вершин, находится посередине между минимальным и максимальным значениями C, цвет, связанный с этой вершиной, будет лежать посередине между первой и последней строкой цветовой карты. Вот пример того, что демонстрирует использование манипуляции с цветовой картой для выделения областей с одинаковым уклоном. Рассмотрим поверхность, созданную

Мы можем использовать сетку для построения этой поверхности, однако сетка будет производить цвета на основе значений z. Мы можем использовать функцию градиента, чтобы исследовать эту поверхность и определить, где наклоны совпадают по осям x и y. Общая форма такова: [Cx,Cy]=gradient(Z), где Cx — численное решение уравнения ±Z/±x, а Cy — ±Z/±y. (Фактический градиент представляет собой векторную сумму Cx и Cy.) Поскольку производная функции представляет собой ее наклон, производная, взятая в точке на поверхности, представляет собой наклон поверхности. Используя результаты градиента в качестве нашей цветовой карты, мы можем выявить те области на графике, которые имеют одинаковый наклон по отношению к осям x или y. Код, который покажет постоянный наклон по оси x,

Функция градиента предполагает приращение 1 , поэтому мы указали его здесь, чтобы согласовать с нашей сеткой. На Рисунке 4.4 и Таблице 1* показана рассматриваемая нами поверхность, построенная с помощью сетки с ее раскраской по умолчанию, которая меняется в зависимости от амплитуды z. На Рисунке 4.5 и Таблице 2 показаны равные наклоны с Cx от градиента. На рис. 4.6 показан наклон по оси Y.

Рисунок 4.4 График сетки по умолчанию с цветом, присвоенным высоте.

Рис. 4.5 Определение областей наклона относительно оси x.

Рисунок 4.6 Определение областей наклона относительно оси Y.

Вы должны попробовать этот пример на своем компьютере, чтобы лучше понять преимущества цвета. Цвет, когда он используется для фактической передачи информации, может сделать сюжет более информативным и дает понимание, которое невозможно было бы получить в противном случае.

Чтобы завершить обсуждение функции сетки мы должны упомянуть, что график сетки также можно создать, передав два вектора, x и y, вместо матриц, X и Y, используя либо сетку (x, y, Z), либо сетку (x, y, З, С). Вектор длины x должен быть равен количеству столбцов в Z, а длина вектора y должна быть равна количеству строк в Z. При использовании этой формы команды a (x(j),y(i ),Z(i,j)) определяет вершины над i строками и j столбцами Z.