Тригонометрические и обратные им функции MatLab
Арифметические операторы и функции
Операторы отношения и их функции
Логические операторы
Специальные символы
Системные переменные и константы
Функции поразрядной обработки
Функции обработки множеств
Функции времени и даты
Элементарные функции
Алгебраические и арифметические функции
Тригонометрические и обратные им функции
Гиперболические и обратные им функции
Функции округления и знака
Функции комплексного аргумента
Что нового мы узнали?
В системе MATLAB определены следующие тригонометрические и обратные тригонометрические функции. Функции вычисляются для каждого элемента массива. Входной массив допускает комплексные значения. Напоминаем, что все углы в функциях задаются в радианах.
Э acos (X)
— возвращает арккосинус для каждого элемента X. Для действительных значений
X в области [-1, 1] acos(X) возвращает действительное значение из диапазона
диапазона [0, р], для действительных значений X вне области [-1, 1] acos(X)
возвращает комплексное число.
Примеры:
»Y = acos (0.5)
1.0472
» acos([0.5 1 2])
ans =
1.0472
0 0 + 1.31701
acot (X) — возвращает арккотангенс для каждого элемента X. Пример:
» Y=acot(0.l)
у =
1.4711
acsc(X)
— возвращает арккосеканс для каждого элемента X. Пример:
» Y= acsc(3)
0.3398
asec(X)
— возвращает арксеканс для каждого элемента X. Пример:
Пример:
» Y=asec(0.5)
Y =
0
+ 1.31701
asin(X) — возвращает арксинус для каждого элемента X. Для действительных значений X в области [-1, 1] asin(X) возвращает действительное число из диапазона [-р/2, р/2], для действительных значений X вне области [-1, 1] asin(X) возвращает комплексное число. Пример:
» Y= asin (0.278)
0.2817
atan(X) — возвращает арктангенс для каждого элемента X. Для действительных значений X atan(X) находится в области [-р/2, р/2]. Пример:
» Y=atan(1)
Y =
0. 7854
7854
atan2 (Y, X) — возвращает массив Р той же размерности, что X и Y, содержащий поэлементно арктангенсы отношения вещественных частей Y и X. Мнимые части игнорируются. Элементы Р находятся в интервале [-р, р]. Специфический квадрант определен функциями sign(Y) и sign(X). Это отличает полученный результат от результата atan(Y/X), который ограничен интервалом [-л/2, л/2].
Пример:
» atan2(l,2)
ans =
0.4636
cos(X)
— возвращает косинус для каждого элемента X. Пример:
»Х=[123];
» cos(X)
ans =
0. 5403
-0.4161 -0.9900
5403
-0.4161 -0.9900
cot(X) — возвращает котангенс для каждого элемента X. Пример:
» Y = cot(2)
-0.4577
csc(X) — возвращает косеканс для каждого элемента X. Пример:
» Х=[2 4.678 5:0.987 1 3];
» Y = csc(X)
Y =
1.0998
-1.0006 -1.0428
1.1985
1.1884 7.0862
sec(X) — возвращает массив той же размерности что и X, состоящий из секансов элементов X. Пример:
» X=[pi/10 pi/3 pi/5];
» sec(X)
ans =
1.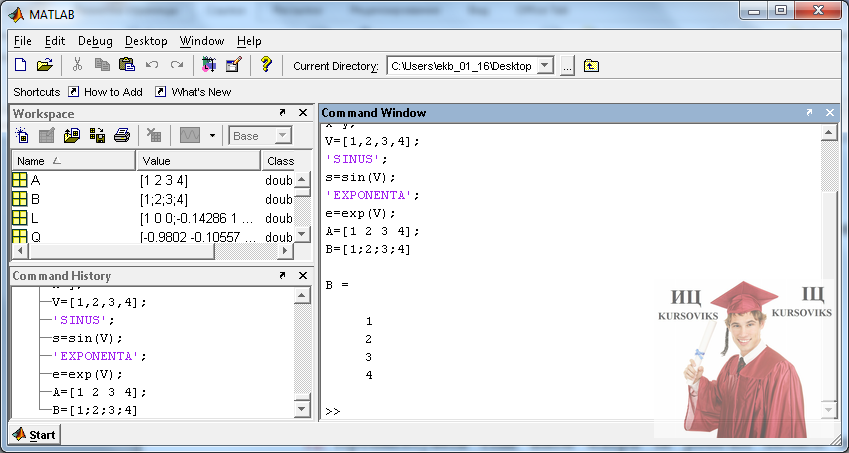
sin(X) — возвращает синус для каждого элемента X. Пример:
» X=[pi/2 pi/4 pi/6 pi];
» sin(X)
ans =
1.0000 0.7071 0.5000 0.0000
tan(X) — возвращает тангенс для каждого элемента X.
Рис. 8.2. Графики четырех тригонометрических функций
Пример:
» Х=[0.08 0.06 1.09]
X=
0.0800 0.0600 1.0900
» tan(X)
ans=
0. 802
0.0601 1.9171
802
0.0601 1.9171
Следующий файл-сценарий позволяет наблюдать графики четырех тригонометрических функций (рис. 8.2):
syms xsubplot(2.2.1).ezplot(sin(x),[-5 5]).xlabel(«),gnd on
subplot(2.2.2),ezp»lot(tan(x).[-5 5]).xlabel(«).grid on
subplot(2,2,3),ezplot(asin(x),[-1 1]).grid on
subplot(2.2.4),ezplot(atan(x).[-5 5]),grid on
Поскольку
многие тригонометрические функции периодичны, появляется возможность формирования
из них любопытных комбинаций, позволяющих создавать типовые тестовые сигналы,
используемые при моделировании радиоэлектронных устройств. Следующий файл-сценарий
строит графики для таких комбинаций, создающих из синусоиды три наиболее распространенных
сигнала — прямоугольные, пилообразные и треугольные импульсы:[
В пакете расширения
Signal Processing Toolbox есть специальные функции для генерации таких сигналов
— square и sawtooth. — Примеч. ред.
]
— Примеч. ред.
]
х=-10:0.01:10;
subplot(2,2.1).plot(x.0.8*sin(x))
.x label(‘0.8*sin(x)’)
subplot(2.2,2).plot(x,0.8*sign(sin(x)))
.x1abel(‘0.8*sgn(sin(x))’)
subplot(2.2.3),plot(x.atan(tan(x/2)))
.xlabel(‘atan(tan(x/2))’)
subplot(2.2.4),plot(x,asin(sin(x)))
.xlabel(‘asin(sin(x))’)
Соответствующие графики представлены на рис. 8.3.
Рис. 8.3. Графики синусоиды, прямоугольных, пилообразных и треугольных колебаний
Дополнительный
ряд графиков, полученных комбинациями элементарных функций, показан на рис. 8.4. Эти графики строятся следующим файлом-сценарием:
8.4. Эти графики строятся следующим файлом-сценарием:
х=-10:0.01:10;
subplot(2.2.1).plot(x.sin(x). A 3).x1abel(‘sin(xr3’)
subplot(2.2.2).plot(x,abs(s1n(x)))
.xlabel(‘abs(sin(x))’).axis([-10 10 -1 1]),
subplot(2.2,3),plot(x,tan(cos(x)))
.xlabel(‘tanCcos(x))’)
subplot(2.2.4).plot(x.csch(sec(x))),xlabeK’csch(sec(x))’)
Рис. 8.4. Графики периодических сигналов без разрывов
Эти графики
неплохо моделируют сигналы, получаемые при выпрямлении синусоидального напряжения
(или тока) и при прохождении синусоидальных сигналов через нелинейные цепи.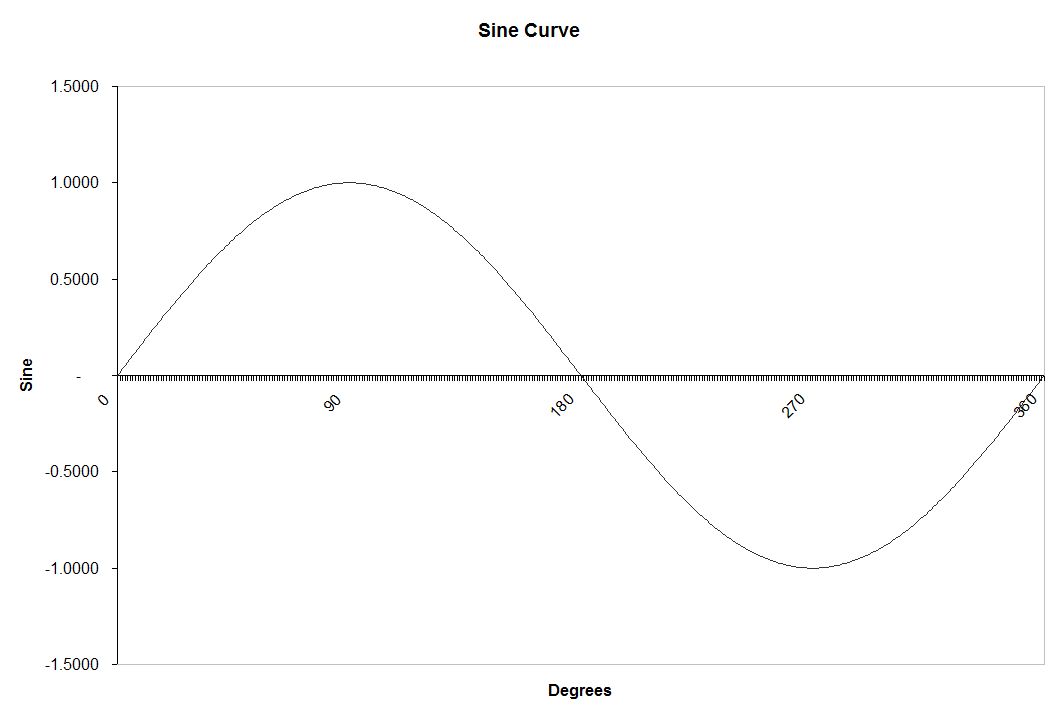
Нравится
Твитнуть
Элементарные математические функции. — Студопедия
Поделись
В систему MATLAB встроены все основные элементарные математические функции, которые представлены в таблице 1.1.4. Вместе с тем, следует отметить, что список функций, приведенный в данном пункте, составляет лишь крохотную часть всего набора библиотечных функций, встроенных в MATLAB.
Таблица 1.4. Основные элементарные математические функции.
| Обозначение | Выполняемое действие |
| Тригонометрические функции | |
| sin | sin(X) вычисляет синус от аргумента X, указанного в радианах. |
| sind | sind(X) вычисляет синус от аргумента X, указанного в градусах. |
| cos | cos(X) вычисляет косинус от аргумента X, указанного в радианах.
|
| cosd | cosd(X) вычисляет косинус от аргумента X, указанного в градусах. |
| tan | tan(X) вычисляет тангенс от аргумента X, указанного в радианах. |
| tand | tand(X) вычисляет тангенс от аргумента X, указанного в градусах. |
| cot | cot(X) вычисляет котангенс от аргумента X, указанного в радианах. |
| cotd | cotd(X) вычисляет котангенс от аргумента X, указанного в градусах. |
| sec | sec(X) вычисляет секанс от аргумента X, указанного в радианах. |
| secd | secd(X) вычисляет секанс от аргумента X, указанного в градусах. |
| csc | csc(X) вычисляет косеканс от аргумента X, указанного в радианах. |
| cscd | cscd(X) вычисляет косеканс от аргумента X, указанного в градусах.
|
| Обратные тригонометрические функции | |
| asin | asin(X) вычисляет арксинус от аргумента X. Результат представлен в радианах. |
| asind | asind(X) вычисляет арксинус от аргумента X. Результат представлен в градусах. |
| acos | acos(X) вычисляет арккосинус от аргумента X. Результат представлен в радианах. |
| acosd | acosd(X) вычисляет арккосинус от аргумента X. Результат представлен в градусах. |
| atan | atan(X) вычисляет арктангенс от аргумента X. Результат представлен в радианах. |
| atand | atand(X) вычисляет арктангенс от аргумента X. Результат представлен в градусах. |
| acot | acot(X) вычисляет арккотангенс от аргумента X. Результат представлен в радианах. |
| acotd | acotd(X) вычисляет арккотангенс от аргумента X. Результат представлен в градусах. Результат представлен в градусах.
|
| asec | asec(X) вычисляет арксеканс от аргумента X. Результат представлен в радианах. |
| asecd | asecd(X) вычисляет арксеканс от аргумента X. Результат представлен в градусах. |
| acsc | acsc(X) вычисляет арккосеканс от аргумента X. Результат представлен в радианах. |
| acscd | acscd(X) вычисляет арккосеканс от аргумента X. Результат представлен в градусах. |
| Показательные функции | |
| exp | exp(X) вычисляет экспоненциальную функцию от аргумента X. |
| pow2 | Функция может вызываться с одним или двумя аргументами. Если у функции один аргумент и функция вызывается в формате Y=pow2(X), то вычисляется показательная функция по основанию 2 от аргумента X. Если функция вызывается с двумя аргументами в формате Z=pow2(X,Y), причем X – целочисленный операнд, а Y – вещественный операнд, то результатом является Z=X*2Y.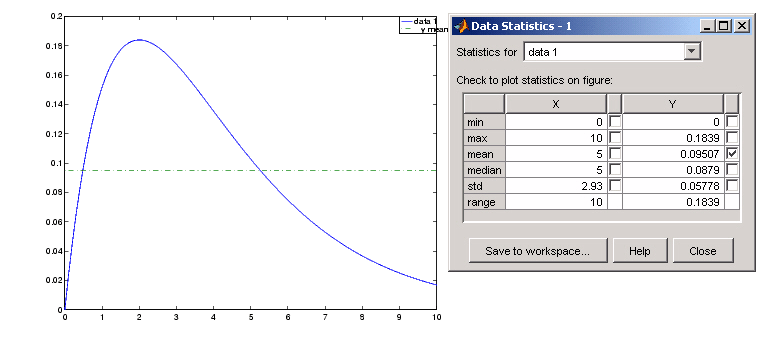
|
| Логарифмические функции | |
| log | log(X) вычисляет натуральный логарифм от аргумента X. |
| log2 | log2(X) вычисляет логарифм по основанию 2 от аргумента X. |
| log10 | log10(X) вычисляет десятичный логарифм от аргумента X. |
| Комплексные функции | |
| abs | abs(X) вычисляет модуль комплексного аргумента X. |
| conj | conj(X) вычисляет комплексное сопряжение для комплексного аргумента X. |
| imag | imag(X) выдает мнимую часть для комплексного аргумента X. |
| real | real(X) выдает вещественную часть для комплексного аргумента X. |
| isreal | K=isreal(A) равно 1, если аргумент X – вещественное число;
K=isreal(A) равно 0 в любом другом случае.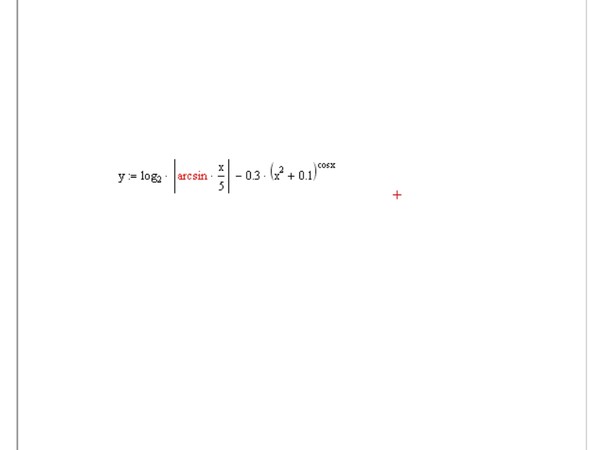
|
| Функции округления и вычисления остатков | |
| floor | floor(A) округляет вещественный аргумент A в сторону -inf (т.е. до ближайшего меньшего числа). |
| ceil | ceil(A) округляет вещественный аргумент A в сторону inf (т.е. до ближайшего большего числа). |
| fix | fix(X) округляет вещественный аргумент X в сторону нуля (т.е. просто отбрасывает дробную часть). |
| round | round(X) округляет вещественный аргумент X до ближайшего целого. |
| mod | M=mod(X,Y) возвращает остаток от деления X на Y. |
| rem | M=rem(X,Y) возвращает целую часть от деления X на Y. |
| sign | sign(x) возвращает -1, если x<0, 0, если x=0 и 1, если x>0. |
matlabʵarcsin_ٶ֪
- ٶҳ
- ̳
- ע
- ¼
- ҳ
- Ѷ
- Ƶ
- ͼƬ
- ֪
- Ŀ
- ɹ
- ͼ
matlabдʵַҺĹ. ..
matlab д ʵַҺĹ
չ
..
matlab д ʵַҺĹ
չ
ѡó⣿
{@each tagList as item}
ֻش㣬ȤAPP
ύɹ
Ƿش⣿
ֻش㣬ȤAPP
չȫ
>> sin(pi/6)
ans =
0.5000
>> asin(0.5)
ans =
0.5236
>> pi/6
ans =
0.5236
2022-09-12
Excel2022ѧϰءExcelֻapp.ƷʺڸиҵĹԱʹá
www.qinzhe.com
ܹעact.evkworld.cn U1Yk0ZDqzrXl1VHpUy7YUA7B_Xa11PUfzog5dh7zmLPGU6KY5UZ6_t1jJ0KGUHYzn160Iybq0ZKGujY1PsKWpyfqn0KBpHY1njD0uMfqn0KspjYs0Aq15H00mMTqn0K8IjYs0ZPl5fKzuLw9u1Ys0A4vTjYsQW0snj0snj0s0ANzu1Ys0Zwzmyw-5H00mhwGujY0uAPWujY0mgPxpywW5gK1Qy4J0ATqILP8TsKzIjYVnfKkTA-b5H00TyPGujYs0A7B5HKxn0KsTjYs0AdYTjYs0AwbUL0qn0KzpWYk0ZwdT1YkPW64nWndPWckP1RLnWbzrjmkn0K9m1Yk0ZK85H00TA7Ygvu_myTqn0K-TLfqn0K-IA-b5iYk0A71TAPW5H00IgKGUhPW5H00uhPdIjYs0A7buhk9u1Yk0ZIhThqV5fKBIjYk0Z91IZRqn1fsnHDsrHT0ThNkIjYkPWm1nHbkPjbvPj6k0ZPGujYsnWR1rHwbuH63uAuWmhfL0AqY5H00ULFsIjYsc10WwDuRc10Wnansc108nanscYwANanscYwAN0KopHYs0AdY5HcYnj60Uynqn0KVmdqhThqV5H00uA78IyF-gLK_my4GuZnqn0K9uZ745UZ6_t12ktJzsef0mywkIjYs0A-1mvsqn0KkUgfqn0K9u7q1ULNzmvRqnW6WIgF_gL7dugF4cdqxgdq8TzPdThsWmLwWIMFkgv94IWf0mLFW5HnvP1T&jump=http%3A%2F%2Fjubao.baidu.com%2Fjubao%2Faccu%2F%3Ftitle%3D%25E5%2594%25A4%25E5%25A2%2583%25E5%25BC%2595%25E6%2593%258E%25E2%2580%2594%25E2%2580%2594%25E5%2585%258D%25E7%25BC%2596%25E7%25A8%258B%25E6%25B8%25B8%25E6%2588%258F%25E5%2588%25B6%25E4%25BD%259C%25E5%25B7%25A5%25E5%2585%25B7%26q%3D%E5%A6%82%E4%BD%95%E5%9C%A8matlab%E7%BC%96%E7%A8%8B%E4%B8%AD%E5%AE%9E%E7%8E%B0arcsin&key=surl» jubao=»»/> ѧϰܵԱ!Ʒʣϲ۸! Ա̼ңƷ!֧ǣ! simba. ҪѧЩ-Ա! ҪѧЩ-ԱƼᣬ!ʡģƷʺûԱ! simba.taobao.com U1Y10ZDqzrXl1VHpUy7YUA7B_Xa11PUfzog5dh7zmLPGU6KY5UZ6_t1clt57YJowGtHDY2b0pyYqnWn30ZNG5fKspyfqn1T0mv-b5H00mhbqn10k0AuY5H00TA6qn0KET1Ys0AFL5H00UMfqn0K1XWY0ThIYmyTqn0K8IM0qna3snj0snj0sn0K-ThTqn0KYTh7buHYs0AFbpyfq0AwWmvfq0A71gv-bm1dsTzd8p6KM5gI1UMn0TMfqQHD0TgKGujYs0Z7Wpyfqn0K9mWYsg100TZ0qn0KVIZ0qn0KbuAqs5H00ThCqn0KYIgnqPHmYPjb4nWTkn1cYn1RYnWm1PfK9m1Yk0ZK85H00TA7Ygvu_myTqn0K-TLfqn0K-IA-b5iYk0A71TAPW5H00IgKGUhPW5H00uhPdIjYs0A7buhk9u1Yk0ZIhThqV5fKBIjYk0ZF-TgfqnHmvn1D4nHf4PWf3nfK1pyfqnjcdn1bYuAR3rAwhmvFbPsKEIjYs0AqzTZfqnanscYwANansc10WnansQW0WnaPDw-fWnaPDw-f0pvbqn0KVIjY0Uynq0AdWgvuzUvYq0Aw9UMNBuNqsUA78pyw15fK9uZ745UZ6_t12ktJzsef0mywkIjYs0A-1mvsqn0KkUgfqn0K9u7q1ULNzmvRqnW6WIgF_gL7dugF4cdqxgdq8TzPdThsWmLwWIMFkgv94IWf0mLFW5Hn4PHmk&jump=http%3A%2F%2Fjubao.baidu.com%2Fjubao%2Faccu%2F%3Ftitle%3D%25E7%25BC%2596%25E7%25A8%258B%25E5%2585%25A5%25E9%2597%25A8%25E8%25A6%2581%25E5%25AD%25A6%25E5%2593%25AA%25E4%25BA%259B-%25E4%25B9%25B0%25E4%25B8%259C%25E8%25A5%25BF%25E9%2580%259B%25E6%25B7%2598%25E5%25AE%259D%25EF%25BC%258C%25E6%25A6%259C%25E5%258D%2595%25E5%25A5%25BD%25E7%2589%25A9%25E9%259A%258F%25E5%25BF%2583%25E5%2585%25A5!%26q%3D%E5%A6%82%E4%BD%95%E5%9C%A8matlab%E7%BC%96%E7%A8%8B%E4%B8%AD%E5%AE%9E%E7%8E%B0arcsin&key=surl» jubao=»»/> |
ΪƼ
ذٶ֪APP
ʹðٶ֪APP顣ֻͷб֪Ĵ𰸡
ɨά
- ˡҵȨͶ
- ΥкϢ,·ѡύ
- ɫ
- Υ
- ʱϢʵ
- ʹˮ
ǻͨϢȷʽ콫ٱ֪ͨ
˵
10
50
100
200
б. ..
..
ģ ʽ
Комплексные числа и операции с ними
Содержание
Введение Комплексная плоскость и мнимая единица Модуль и фаза комплексного числа Показательная форма комплексного числа. Формула Эйлера Операции над комплексными числами. Комплексно-сопряженные числа Выводы Список литературы | DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов Распространяется под лицензией LGPL v3 Страница проекта на SourceForge |
Обнаружили ошибку? Выделите ее мышью и нажмите
Введение
Известно, что область определения некоторых функций на множестве вещественных чисел ограничена. Например функция определена для , аналогично можно вспомнить, что функция определена для , а функция определена для .
Однако, ограниченная область определения функций на множестве вещественных чисел не означает,
что , или не имеют смысла.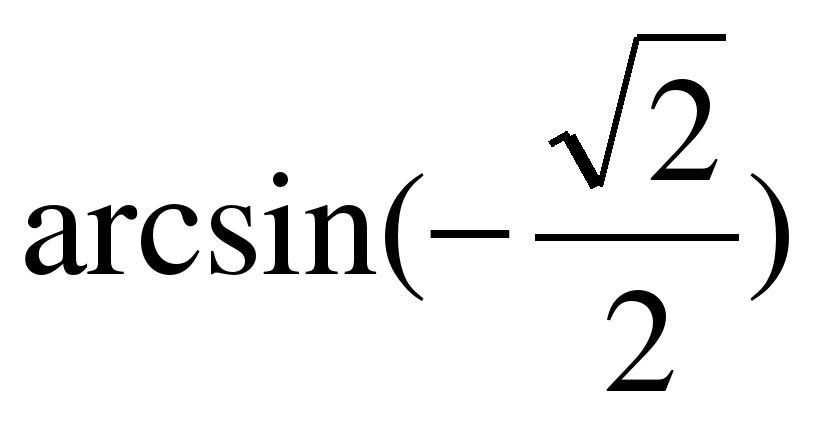 Ограниченная область определения функций на множестве вещественных чисел говорит лишь о том,
что не может быть представлено вещественным числом.
Действительно, среди вещественных чисел не найти такого числа , квадрат которого был бы равен .
Ограниченная область определения функций на множестве вещественных чисел говорит лишь о том,
что не может быть представлено вещественным числом.
Действительно, среди вещественных чисел не найти такого числа , квадрат которого был бы равен .
При решении квадратных уравнений часто возникает ситуация, когда дискриминант отрицательный. В этом случае это означает что парабола не пересекает прямую абсцисс ни в одной точке. Другими словами, корни квадратного уравнения не существуют среди вещественных значений и их также надо искать за пределами вещественных чисел.
Все бесконечное множество вещественных чисел можно представить в виде одной числовой прямой (смотри рисунок 1),
на которой мы можем откладывать рациональные и иррациональные вещественные числа.
Но на этой прямой нет числа , значит его надо искать вне числовой прямой.
Таким образом мы должны расширить множество вещественных чисел до множества в котором значения ,
или уже не бессмысленны, а являются такими же обычными числами в этом расширенном множестве,
как на множестве вещественных чисел.
Комплексная плоскость и мнимая единица
Естественным расширением числовой прямой является плоскость, которую называют комплексной плоскостью. Числовая прямая вещественных чисел и ее расширение до комплексной плоскости показано на рисунке 1. Любая точка на комплексной плоскости определяет одно комплексное число. Например на рисунке 1 показано число .
Рисунок 1. Расширение множества вещественных чисел до множества комплексных числел
Значение вещественного числа однозначно определяет его позицию на числовой прямой, однако для определения позиции на плоскости одного числа недостаточно.
Для «навигации» по комплексной плоскости вводятся две прямые и , которые пересекаются в начале координат. Прямая это числовая прямая, называемая реальной осью, на которой лежат все вещественные числа. Прямая называется мнимой осью и она перпендикулярна реальной оси . Оси и делят комплексную плоскость на четверти, как это показано на рисунке 1.
Любая точка комплексной плоскости задается двумя координатами и по осям и соответственно. При этом само комплексное число можно записать как , где называется реальной частью
и задает координату точки комплексной плоскости на вещественной прямой , а называется мнимой частью
и задает координату точки комплексной плоскости на мнимой оси .
При этом само комплексное число можно записать как , где называется реальной частью
и задает координату точки комплексной плоскости на вещественной прямой , а называется мнимой частью
и задает координату точки комплексной плоскости на мнимой оси .
Для того чтобы отделить одну координату от другой (реальную и мнимую части) вводят число , называемое мнимой единицей. Это так раз то число, которого не существует на множестве действительных чисел. Оно обладает особым свойством: . Тогда комплексное число может не только перемещаться по вещественной прямой вправо и влево, но и двигаться по комплексной плоскости потому что мы добавили ему слагаемое с мнимой единицей .
Мнимую единицу в математической литературе принято обозначать как , но в технике буква уже закреплена за обозначением электрического тока, поэтому чтобы избежать путаницы мы будем обозначать мнимую единицу буквой .
Если и , тогда число является действительным и располагается на реальной оси .
Если и , тогда число является чисто мнимым и располагается на мнимой оси .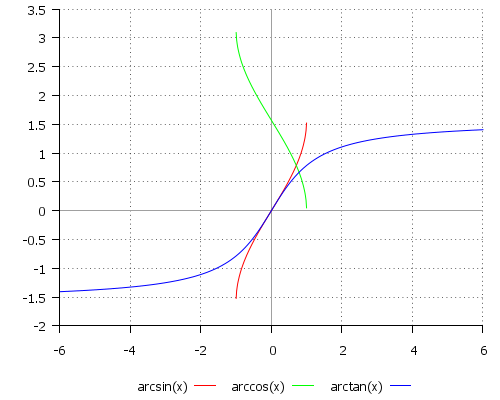
Если и , тогда число располагается в одной из четвертей комплексной плоскости.
Модуль и фаза комплексного числа
Представление комплексного числа как называют алгебраической формой записи. Если из начала координат комплексной плоскости к точке восстановить вектор (смотри рисунок 1), то можно вычислить длину этого вектора как
(1)
— неотрицательное вещественное число характеризующее длину вектора и называется модулем комплексного числа. При этом сам вектор комплексного числа повернут относительно реальной оси на некоторый угол , называемый фазой. Фаза комплексного числа может быть положительной или отрицательной, в зависимости от того в каком направлении относительно оси отсчитывать угол. Если угол поворота вектора на комплексной плоскости отсчитывать против часовой стрелки (как это показано на рисунке 1), то фаза будет принимать положительные значения, а если по часовой — то отрицательные.
Связь реальной и мнимой частей комплексного числа с его амплитудой и фазой представлено следующим выражением:
(2)
Тогда комплексное число можно представить в тригонометрической форме:
(3)
Связь угла поворота вектора комплексного числа с реальной и мнимой частью комплексного числа, представленного в алгебраической форме:
(4)
тогда
(5)
где учитывает четверть комплексной плоскости в которой расположено число :
(6)
Необходимость поправки возникает из-за того, что функция
периодическая функция с периодом рад. В результате возвращает корректные значения только в интервале
.
Таким образом функция арктангенса не отличает четверть I от четверти III
(в обоих случаях отношение положительное),
а также не отличает четверть II от четверти IV (отношение отрицательное).
В результате возвращает корректные значения только в интервале
.
Таким образом функция арктангенса не отличает четверть I от четверти III
(в обоих случаях отношение положительное),
а также не отличает четверть II от четверти IV (отношение отрицательное).
На рисунке 2 показаны значения параметра , в зависимости от того в какой четверти комплексной плоскости расположено число.
Рисунок 2. Значение поправки фазы комплексного числа в зависимости от расположения на комплексной плоскости.
На рисунке 2а исходное комплексное число расположено в первой четверти комплексной плоскости и .
Тогда и значение фазы комплексного числа равно:
(7)
Рассмотрим случай, когда комплексное число расположено во второй четверти комплексной плоскости (рисунок 2б), т.е. и . В этом случае и угол также будет отрицательным (красная пунктирная линия). Тогда для того, чтобы получить корректное значение фазы необходимо ввести поправку рад:
(8)
Пусть комплексное число расположено в третьей четверти комплексной плоскости (рисунок 2в),
т. е. и .
В этом случае и угол будет
положительным (красная пунктирная линия).
Тогда для того, чтобы получить корректное значение фазы необходимо ввести поправку рад:
е. и .
В этом случае и угол будет
положительным (красная пунктирная линия).
Тогда для того, чтобы получить корректное значение фазы необходимо ввести поправку рад:
(9)
Если расположено в четвертой четверти комплексной плоскости (рисунок 2г), т.е. и , то в этом случае и угол будет отрицательным и равным фазе комплексного числа без поправок ( рад):
(10)
Функция которая позволяет получить фазу комплексного числа c учетом четверти комплексной плоскости в которой расположено комплексное число называется функция арктангенс-2 и обозначается .
Функция арктангенс-2 присутствует во всех математических приложениях и может быть использована для расчета верного угла поворота вектора комплексного числа.
Показательная форма комплексного числа. Формула Эйлера
Мы уже рассмотрели алгебраическую и тригонометрическую формы записи комплексного числа. Помимо алгебраической и тригонометрической формы существует также показательная форма комплексного числа:
(11)
связанная с тригонометрической формой формулой Эйлера:
(12)
Cоотношение (12) легко доказать, если произвести разложение экспоненты в ряд Тейлора:
(13)
Представим ряд (13) в виде суммы четных и нечетных членов последовательности:
(14)
Рассмотрим более подробно мнимую единицу в четной и нечетной степенях.
Из определения мнимой единицы можно сделать вывод, что , тогда , в свою очередь .
Таким образом, можно сделать вывод что .
Построим аналогичным образом соотношение для нечетных степеней: , тогда , в свою очередь и окончательно можно записать: . Тогда (14) можно представить как:
(15)
В выражении (15) первая сумма по четным степеням дает разложение в ряд Тейлора функции , а вторая сумма по нечетным степеням дает разложение в ряд Тейлора функции . Таким образом, получено доказательство справедливости формулы Эйлера (12).
Необходимо отметить, что формула Эйлера является одной из важнейших в теории функций комплексного переменного. Так например при помощи формулы Эйлера можно связать математические константы и с использованием мнимой единицы :
(16)
Операции над комплексными числами. Комплексно-сопряженные числа
В данном параграфе мы кратко рассмотрим операции над комплексными числами. Сумма двух комплексных чисел и представляет собой комплексное число :
(17)
При сложении реальные и мнимые части комплексного числа также складываются. На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных
чисел по правилу параллелограмма (рисунок 3а).
На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных
чисел по правилу параллелограмма (рисунок 3а).
Рисунок 3. Операции над комплексными числами
Разность двух комплексных чисел и представляет собой комплексное число
(18)
При вычитании реальные и мнимые части комплексного числа также вычитаются. На комплексной плоскости операцию вычитания можно реализовать как вычитание векторов по правилу параллелограмма (рисунок 3б). На первом шаге из вектора формируется вектор (обозначенный пунктирной линией на рисунке 3б), после чего вектор складывается с вектором по правилу параллелограмма.
Для того чтобы получить формулу для умножения комплексных числен необходимо перемножить два комплексных числа по правилу умножения многочленов:
(19)
Умножение комплексных проще выполнять если числа представлены в показательной форме:
(20)
При перемножении в показательной форме модули комплексных чисел перемножаются а фазы складываются. Операция произведения комплексных чисел показано на рисунке 3в.
Операция произведения комплексных чисел показано на рисунке 3в.
Введем понятие комплексно-сопряженного числа. Число является комплексно-сопряженным числу .
Комплексно-сопряженные числа отличаются знаком перед мнимой частью.
Графически комплексно-сопряженные числа показаны на рисунке 3г.
При этом можно заметить, что модули комплексно-сопряженных чисел равны , а фазы имеют противоположные знаки.
Произведение комплексно-сопряженных чисел
(21)
представляет собой действительное число равное квадрату модуля этих чисел.
Из элементарных операций нам осталось рассмотреть лишь деление комплексных чисел. Рассмотрим результат деления комплексных чисел в показательной форме:
(22)
Таким образом, при делении комплексных чисел модуль частного равен частному модулей исходных чисел, а фаза равна разности фаз исходных чисел.
При этом необходимо потребовать, чтобы был не равен нулю,
иначе у нас появится деление на ноль при расчете модуля частного.
Рассмотрим теперь деление комплексных чисел в алгебраической форме:
(23)
Домножим и числитель и знаменатель на число, комплексно-сопряженное знаменателю:
(24)
Выводы
В данной статье введено понятие комплексного числа и рассмотрены основные его свойства. Введено понятие мнимой единицы.
Подробно рассмотрена комплексная плоскость и представление комплексных чисел в алгебраической, тригонометрической и показательной формах. Введены понятия модуля и фазы комплексного числа.
Рассмотрены основные арифметические операции над комплексными числами.
Показано как выполнять операции сложения, вычитания в алгебраической форме, введено понятие комплексно-сопряженных чисел, а также операции умножения и деления в показательной и алгебраической формах.
Информация была полезна? Поделитесь с друзьями!
Список литературы
[1]
Пантелеев А.В., Якимова А.С.
Теория функций комплексного переменного и операционное исчисление в примерах и задачах. М: Высшая школа, 2011.
М: Высшая школа, 2011.
[2] Дубровин В.Т. Теория функций комплексного переменного. Теория и практика Казань: Казанский государственный университет, 2010. [PDF]
Последнее изменение страницы: 12.05.2022 (19:41:15)
Страница создана Latex to HTML translator ver. 5.20.11.14
Как сделать обратный синус? – Book Vea
Содержание
Как вычислить обратный синус?
В тригонометрии функция, обратная синусу, обозначается как arcsin или sin-1. Значение функции arcsin зависит от заданного угла. Например, если значение sin 30 градусов равно 1/2, то значение sin -1(1/2) будет равно 30 градусам.
Какова обратная величина греха?
g finverse( f ) возвращает обратную функцию f , такую что f(g(x)) x . Если f содержит более одной переменной, используйте следующий синтаксис, чтобы указать независимую переменную. g finverse( f , var ) использует символьную переменную var как независимую переменную, такую, что f(g(var)) var .
Есть ли в Matlab обратная функция?
пример. asin( X ) возвращает функцию обратного синуса (функция арксинуса) X . Все углы в радианах. Для реальных значений X в интервале [-1,1] asin(X) возвращает значения в интервале [-pi/2,pi/2] .
asin( X ) возвращает функцию обратного синуса (функция арксинуса) X . Все углы в радианах. Для реальных значений X в интервале [-1,1] asin(X) возвращает значения в интервале [-pi/2,pi/2] .
Что противоположно греху?
Арксинус
Каково значение sin, обратное 1?
Итак, обратная функция sin 1 обозначается как 90xb0 или u03c0/2. 9-1(x) или arcsin(x). Обратные функции меняют местами значения x и y, поэтому диапазон обратного синуса составляет от -pi/2 до /2, а область определения — от -1 до 1.
Что является обратным значением sin и cos?
Функция обратного синуса ysinu22121x означает xsin y. Функция обратного синуса иногда называется функцией арксинуса и обозначается как arcsin x. Функция арккосинуса ycosu22121x означает xcos y. Функция арккосинуса иногда называется функцией арккосинуса и обозначается как arccos x. 9(-1) эквивалентно inv(X) .
Как написать обратный загар в Matlab?
Y atand( X ) возвращает арктангенс (tan -1) элементов X в градусах. Функция принимает как вещественные, так и комплексные входные данные. Для реальных значений X atand(X) возвращает значения в интервале [-90, 90].
Как использовать Arcsin в Matlab?
Y asin( X ) возвращает обратный синус (sin -1) элементов X в радианах. Функция принимает как вещественные, так и комплексные входные данные. Для реальных значений X в интервале [-1, 1] asin(X) возвращает значения в интервале [-u03c0/2, u03c0/2].
Как вы используете Finverse?
Эта команда используется, если в функции несколько переменных. эта команда используется, если в функции есть только одна зависимая переменная. 4. Инверсия log (x-y)Входной кодКомандное окноКомментарииfinverse ( log ( x y ), y )ans x exp ( y )Вывод функции по отношению к двум переменным1 еще строка
Является ли CSC обратным sin?
Косеканс ( csc u2061 ) (csc) (csc) Косеканс является обратной величиной синуса. Это отношение гипотенузы к катету, противолежащему данному углу прямоугольного треугольника.
Это отношение гипотенузы к катету, противолежащему данному углу прямоугольного треугольника.
Что является обратным синусу 1?
u03c0/2
Как найти инверсию sin 1?
Итак, обратная функция sin 1 обозначается как 90xb0 или u03c0/2. Это максимальное значение функции синуса.
Каково обратное значение sin?
Sin-1 является обратной функцией синуса.
Является ли инверсия sin sin 1?
Значение arctan 1 или tan inverse 1 равно u03c0/4 радиана или 45 градусов.
Где функция обратного синуса?
Функция обратного синуса или Sin-1 принимает соотношение Противоположная сторона / Сторона гипотенузы и дает угол u03b8. Это также записывается как arcsin. Давайте посмотрим на пример обратной функции синуса. Пример: В треугольнике ABC, AB 4,9м, ВС4,0 м, СА2,8 м и угол В 35xb0.
Как найти инверсию sin-1?
Функция обратного синуса Отвечает на вопрос, синус какого угла равен противолежащему/гипотенузе? Символ обратного синуса — sin-1 или иногда арксинус.
Как найти инверсию sin вручную?
Обратный синус 1, т. е. sin-1 (1), является уникальным значением функции обратного синуса. Sin-1(x) даст нам угол, синус которого равен x. Следовательно, sin-1 (1) равно углу, синус которого равен 1. Так как обратный sin -1 (1) равно 90xb0 или u03a0/2.
Как найти обратную величину синуса и косинуса?
Обратный синус
Обратный sin равен cos?
Арккосинус 9(-1) эквивалентно inv(X) .
Как найти обратную функцию синуса в Matlab?
Y asind( X ) возвращает арксинус (sin -1) элементов X в градусах. Функция принимает как вещественные, так и комплексные входные данные. Для реальных значений X в интервале [-1, 1] asind(X) возвращает значения в интервале [-90, 90].
Функция принимает как вещественные, так и комплексные входные данные. Для реальных значений X в интервале [-1, 1] asind(X) возвращает значения в интервале [-90, 90].
Как найти обратную функцию?
Чтобы найти обратную функцию, запишите функцию y как функцию x, т. е. y f(x), а затем найдите x как функцию y
CMSC 455, лекция 12, Комплексные функции
CMSC 455, лекция 12 , Комплексные функции
<- предыдущий индекс следующий ->
Лекция 12, сложные функции
Некоторые сложные функции могут быть точно вычислены из базовых определение. Но, сохраняя относительную точность по всему область нескольких сложных функций требует специальных методов. Обратите внимание, что домен и диапазон сложных функций могут не очевидно для обычного пользователя. Во-первых, посмотрите на сопоставления домена z1 с диапазоном z2 для некоторых сложные функции: С включенными апплетами Java Если это не сработает, Скриншоты сложных функций Различные тождества для элементарных функций на комплексной плоскости, включая реализацию сложной функции с использованием только реальных функций.Пусть z = x + i y тогда arg z = arctan y/x реальная функция, использующая знаки x и y модуль z = sqrt(x*x+y*y) = |z| длина комплексного вектора конъюгат (z) = x - iy г = х я г = у SQRT я (аргумент z)/2 sqrt z = sqrt (| z |) e таким образом, получается половина угла с величиной sqrt(|z|) модуль z + re z модуль z - re z sqrt z = sqrt ---------------- +/- i sqrt ---------------- 2 2 где знак мнимой части результата равен знак мнимой части z 2 3 з з з sqrt 1+z = 1 + - - -- + -- - ... 2 8 16 кврт( 0 + i0) = 0 + i0 sqrt(-0 + i0) = 0 + i0 sqrt( 0 - i0) = 0 - i0 sqrt(-0 - i0) = 0 - i0 кврт(г)**2 = г sqrt(z*z) = z re z > 0 sqrt(1/z) = 1/sqrt(z) не для -0 или отрицательной действительной оси сопряженный (sqrt (z)) = sqrt (сопряженный (z)) не для -0 или отрицательной действительной оси Обрезка ветки: Срез ветви лежит вдоль отрицательной действительной оси.
Домен: Математически неограниченный Диапазон: Правая полуплоскость, включая мнимую ось. Алгебраический знак действительной части положительна. Знак мнимой части результата тот же, что и знак im z. ЖУРНАЛ log z = ln (модуль z) + i аргумент z 2 3 з з log 1+z = z - -- + -- - ... для |z| В 'БОЛЬШОЙ iz -iz limit = i когда im z ln 'БОЛЬШОЙ iz -iz limit = -i, когда im z 1 2 4 6 4з 32з 288з 2 arcsin z = arctan(z/sqrt(1-z)) исправить результат арксинус z = 2 2 1/2 2 2 1/2 arcsin(1/2 (x + 2 x + 1 + y) - 1/2 (x - 2 x + 1 + y)) + я 2 2 1/2 2 2 1/2 csgn(-i x + y) ln(1/2 (x + 2 x + 1 + y) + 1/2 (x - 2 x + 1 + y) 2 2 1/2 2 2 1/2 2 1/2 + ((1/2 (х + 2 х + 1 + у) + 1/2 (х - 2 х + 1 + у )) - 1)) Примечание. Функция csgn используется для определения, в какой полуплоскости ("слева" или "справа") комплексное выражение или число x лежит.
Это определяется / 1, если Re(x) > 0 или Re(x) = 0 и Im(x) > 0 csgn(x) = 1/sqrt(эпсилон) arccos z = 2 2 1/2 2 2 1/2 arccos(1/2 (x + 2 x + 1 + y) - 1/2 (x - 2 x + 1 + y)) + я 2 2 1/2 2 2 1/2 csgn(I x - y) ln(1/2 (x + 2 x + 1 + y) + 1/2 (x - 2 x + 1 + y) 2 2 1/2 2 2 1/2 2 1/2 + ((1/2 (х + 2 х + 1 + у) + 1/2 (х - 2 х + 1 + у )) - 1)) 2 arccos z = arctan(sqrt(1-z)/z) fix re результата arccos z = pi/2 - arcsin z arccos(cos(z)) = z Обрезка ветки: Реальная ось не в [-1.0, 1.0] Домен: Математически неограниченный Диапазон: Мнимая часть математически неограничена, действительная часть в [0.0, Pi] АРКТАН arctan z = -i (ln(1 + i z) - ln(1 - i z))/2 я я+г arctan z = - ln --- должен быть зафиксирован на щели для iz 1 2 4 6 4з 32з 288з arcsinh z = -i arcsin iz arcsinh (sinh (z)) = z arcsinh z = 2 2 1/2 2 2 1/2 csgn(x + I y) ln(1/2 (x + y + 2 y + 1) + 1/2 (x + y - 2 y + 1) 2 2 1/2 2 2 1/2 2 1/2 + ((1/2 (х + у + 2 у + 1) + 1/2 (х + у - 2 у + 1)) - 1)) + я 2 2 1/2 2 2 1/2 arcsin(1/2 (x + y + 2 y + 1) - 1/2 (x + y - 2 y + 1)) АРККОШ г+я г-я arccosh z = 2 ln( sqrt --- + sqrt --- ) 2 2 arccosh z = ln(z + sqrt(z-1) sqrt(z+1)) не sqrt(z**2-1) 1 3 15 arccosh z = ln(2z) --- -- -- -- -- --- -- .
.. для |z| > 1 2 4 6 4з 32з 288з arccosh(ch(z)) = z арккош z = 2 2 1/2 - csgn(I - I x + y) csgn(I x - y) ln(1/2 (x + 2 x + 1 + y ) 2 2 1/2 + 1/2 (х - 2 х + 1 + у) 2 2 1/2 2 2 1/2 2 1/2 + ((1/2 (х + 2 х + 1 + у) + 1/2 (х - 2 х + 1 + у )) - 1)) + я csgn(I - I x + y) 2 2 1/2 2 2 1/2 arccos(1/2 (x + 2 x + 1 + y) - 1/2 (x - 2 x + 1 + y)) АРКТАНГ arcthz = (ln(1+z) - ln(1-z))/2 1 1+з arctanh z = - ln --- должен зафиксироваться на щели для z > 1 2 1-з 3 5 7 з з з arcth z = z + -- + -- + -- + ... для |z| generic_complex_elementary_functions.ads Фортран 90 имеет несколько сложных функций Исходный код complex_func.f90 Вывод complex_func_f90.out Python имеет много сложных функций Исходный код test_complex.py3 вывод test_complex_py3.out Haskell имеет много сложных функций Исходный код test_complex.
hs вывод test_complex_hs.out Модуль библиотеки Complex.hs Я запрограммировал некоторые сложные функции и утилиты на java. Исходный код Complex.java Тест исходного кода TestComplex.java Вывод TestComplex_java.out Исходный код Csimeq.java test_Csimeq.java тест исходного кода test_Csimeq_java.out вывод теста Исходный код Cinvert.java Тест исходного кода test_Cinvert.java test_Cinvert_java.out вывод теста Исходный код Cnuderiv.java Тест исходного кода test2_Cnuderiv.java test2_Cnuderiv_java.out вывод теста Я запрограммировал некоторые сложные функции и утилиты в балерине. Исходный код complex_math.bal Вывод теста complex_math_bal.out Решение PDE со сложными функциями, сложными решениями и сложными границами: Первая реальная, двойная, версия второго порядка, двухмерная pdenu22_eq.java реальный тест исходного кода pdenu22_eq_java.out тестовый вывод Затем преобразовать в сложную, сложную, версию (используя утилиты выше) pdeCnu22_eq.java Сложный тест исходного кода pdeCnu22_eq_java.out вывод теста Первая настоящая, двойная, версия четвертого порядка, четыре измерения pde44h_eq.
java реальный тест исходного кода Выходные данные теста pde44h_eq_java.out Затем преобразовать в сложную, сложную, версию (используя утилиты выше) pdeC44h_eq.java Сложный тест исходного кода Вывод теста pdeC44h_eq_java.out Гораздо более простое преобразование в комплекс на Фортране simeqC.f90 сложный исходный код исходный код сложного кода inverseC.f90 Комплексный исходный код nuderivC.f90 nuderivC_test.f90 сложный исходный код Результат теста nuderivC_test_f90.out pdeC44h_eq.f90 Комплексный тест исходного кода pdeC44h_eq_f90.out тестовый вывод Одинаковые максимальные ошибки в реальном и сложном коде MatLab перегружает все функции, которые принимают значения с плавающей запятой. также работать с комплексными числами. Python нужно использовать cmath.
<- предыдущий индекс следующий ->
Другие ссылки
- Домашняя страница CMSC 455
- Программа — даты занятий и предметов, даты домашних заданий, задания по чтению
- Домашнее задание — подробности
- Проекты —
- Частичные конспекты лекций, по одной на веб-страницу
- Частичные конспекты лекций, одна большая страница для печати
- Загружаемые образцы, исходный код и исполняемые файлы
- Несколько кратких заметок о Matlab
- Несколько кратких заметок о Python
- Несколько кратких заметок о Fortran 95
- Несколько кратких заметок об Аде 95
- Математическая библиотека Ады (gnatmath95)
- Конечно-разностные аппроксимации для производных
- Примеры MATLAB, некоторые ODE, некоторые PDE
- примеры параллельных потоков
- Справочные страницы по рядам Тейлора, тождествам, системам координат
, дифференциальным операторам - избранные новости, связанные с численными вычислениями
Наверх
Symbolab Math Solver — Пошаговый калькулятор
| \bold{\mathrm{Basic}} | \жирный {\альфа\бета\гамма} | \bold{\mathrm{AB\Gamma}} | \жирный{\sin\cos} 9{\ квадрат} | \sqrt{\square} | \nthroot[\msquare]{\square} | \frac{\msquare}{\msquare} | \log_{\msquare} | \pi | \ тета | \infty | \внутр | \frac{d}{dx} |
| \ле | \cdot 9{\msquare} | \лим | \сумма | \sin | \cos | \загар | детская кроватка | \csc | мс |
| \альфа | \бета | \гамма | \дельта | \дзета | \эта | \ тета | \йота | \каппа | \лямбда | \мю |
| \ню | \xi | \pi | \ро | \сигма | \тау | \ипсилон | \фи | \чи | \psi | \омега |
| А | Б | \Гамма | \Дельта | Е | З | Н | \Тета | К | \лямбда | М |
| С | \Xi | \Пи | П | \Сигма | Т | \Ипсилон | \Фи | Х | \пси | \Омега |
| \sin | \cos | \загар | детская кроватка | мс | \csc | \ш | \кош | \танх | \сеч | |
| \arcsin | \арккос | Арктан | \аркот | \арксек | \arccsc | \arcsinh | \арккош | Арктанх | \арккот | Арксеч |
| \begin{case}\square\\\square\end{case} | \begin{case}\square\\\square\\\square\end{cases} | = | \ne | \дел | \cdot | \раз | < | > 9{\circ} | \rightarrow | \lпол\квадрат\rпол | \lceil\square\rceil |
| \overline{\square} | \vec{\square} | \в | \для всех | \не в | \есть | \mathbb{R} | \mathbb{C} | 9{»} | \frac{\partial}{\partial x} |
| (2\раз2) | (2\раз3) | (3\раз3) | (3\раз2) | (4\раз2) | (4\раз3) | (4\4) | (3\4) | (2\раз4) | (5\х5) | |
| (1\раз2) | (1\раз3) | (1\4 раза) | (1\раз5) | (1×6) | (2\раз1) | (3\раз1) | (4\раз1) | (5\раз1) | (6\раз1) | (7\раз1) |
| \mathrm{Радианы} | \mathrm{Градусы} | \квадрат! | ( | ) | % | \mathrm{очистить} |
| \arcsin | \sin | \sqrt{\square} | 7 | 8 | 9 | \дел |
| \арккос | \cos | \лн | 4 | 5 | 6 | \раз |
| Арктан | \ желто-коричневый | \лог | 1 | 2 | 3 | — |
| \pi | е 9{\ квадрат} | 0 | «> . | \жирный{=} | + |
Анализ данных в науках о Земле
Для биномиального распределения дисперсия является функцией среднего, достигая максимального значения при пропорции 0,5 и уменьшаясь до нуля при пропорциях нуля и единицы. Преобразования, стабилизирующие дисперсию, используются для исправления этой проблемы в биномиальных данных, и два из наиболее распространенных преобразований, стабилизирующих дисперсию, — это логит-преобразования и преобразования арксинуса. Эти преобразования также используются для процентных данных, которые могут не соответствовать биномиальному распределению.
Логит-преобразование
Логит-преобразование — это логарифм отношения шансов, то есть логарифм пропорции, деленной на единицу минус пропорция. Основание логарифма не имеет значения, а e — обычное основание.
logitTransform <- function(p) { log(p/(1-p)) }
Эффект логит-преобразования заключается, прежде всего, в том, чтобы вытащить концы распределения. В широком диапазоне промежуточных значений пропорции (p) зависимость logit(p) и p почти линейна. Один из способов думать об этом состоит в том, что логит-преобразование расширяет концы шкалы, так что небольшие различия в p (скажем, переход от 0,9от 8 до 0,99) имеют большую разницу в логит-шкале.
В широком диапазоне промежуточных значений пропорции (p) зависимость logit(p) и p почти линейна. Один из способов думать об этом состоит в том, что логит-преобразование расширяет концы шкалы, так что небольшие различия в p (скажем, переход от 0,9от 8 до 0,99) имеют большую разницу в логит-шкале.
p <- seq(0.001, 0.999, 0.001)
pLogit <- logitTransform(p)
plot(p, pLogit, type=’l’, lwd=2, col=’red’, las=1, xlab=’p ‘, ylab=’logit(p)’)
Преобразование арксинуса
Преобразование арксинуса (также называемое преобразованием арксинуса квадратного корня или угловым преобразованием) вычисляется как удвоение арксинуса квадратного корня из пропорция. В некоторых случаях результат не умножается на два (Сокаль и Рольф 1995). Умножение на два приводит к изменению шкалы арксинуса от нуля до пи; если не умножить на два, шкала остановится на пи/2. Выбор произвольный.
asinTransform <- function(p) { asin(sqrt(p)) }
Эффект преобразования арксинуса аналогичен логит-преобразованию в том смысле, что оно вытягивает концы распределения, но не до такой степени, что логит-преобразование делает.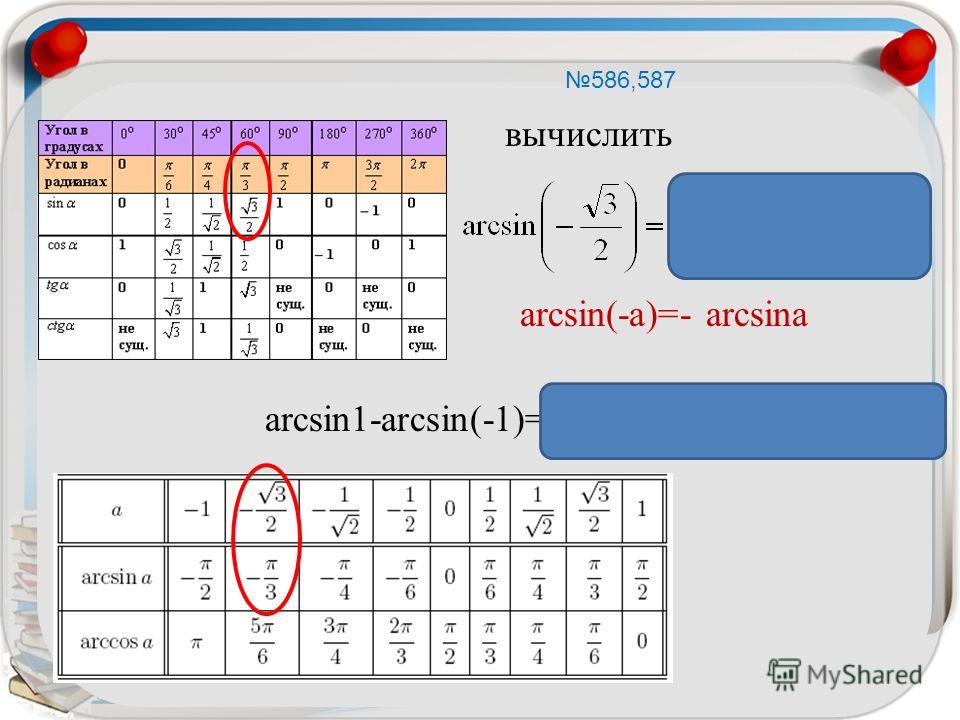
pAsin <- asinTransform(p)
plot(p, pAsin, type=’l’, lwd=2, col=’blue’, las=1, xlab=’p’, ylab=’arcsine(p)’)
Сравнение эффектов
Чтобы оценить различные эффекты этих двух преобразований, полезно показать их преобразования в одном масштабе. Для этого я буду масштабировать преобразования, чтобы они имели одинаковый диапазон.
rangeScale <- function(x) { (x-min(x)) / (max(x)-min(x)) }
pAsin.scaled <- rangeScale(pAsin)
pLogit.scaled <- rangeScale(pLogit)
plot(p, pAsin.scaled, las=1, type=’l’, lwd=2, col=’blue’, xlab=’p’, ylab=’p преобразованный’)
точек (p, pLogit.scaled, type=’l’, lwd=2, col=’red’)
text(0.8, 0.8, ‘asin’, col=’blue’)
text(0.8, 0.5, ‘ logit’, col=’red’)
Оба преобразования в основном линейны в диапазоне 0,3–0,7, с большей кривизной ближе к концам. Кривизна логит-преобразования гораздо более выражена, поэтому логит-преобразование имеет гораздо более сильный эффект, чем преобразование арксинуса.
Рекомендации
Для регрессии логит-преобразование предпочтительнее по трем причинам (Warton and Hui 2011). Во-первых, логит-шкала охватывает все действительные числа, а не ограничивается определенным диапазоном. Например, точно так же, как пропорция ограничена 0–1, масштаб квадратного корня арксинуса ограничен от 0 до pi. Напротив, пределы логит-шкалы — отрицательная бесконечность и положительная бесконечность. Это особенно важно, когда требуется прогнозирование, поскольку ограниченная шкала может давать бессмысленные результаты (например, более 100 % или менее 0 %). Во-вторых, логит-шкала более интуитивно понятна, поскольку представляет собой логарифмическую вероятность. Это особенно полезно при интерпретации наклонов логистической регрессии, в которой логит-преобразование является центральным. В-третьих, логит-шкала правильно моделирует взаимосвязь между средним значением и дисперсией в биномиальных данных, где дисперсия равна p(1-p)/n.
В многомерных исследованиях, таких как ординационный или кластерный анализ, предпочтение отдается преобразованию арксинуса.
 taobao.com baidu.com%2Fjubao%2Faccu%2F%3Ftitle%3D%25E4%25B9%25B0%25E5%25AD%25A6%25E4%25B9%25A0%25E5%259F%25BA%25E7%25A1%2580%25E7%25BC%2596%25E7%25A8%258B%25E4%25B8%258A%25E4%25B8%2587%25E8%2583%25BD%25E7%259A%2584%25E6%25B7%2598%25E5%25AE%259D!%25E4%25BC%2598%25E4%25BA%25AB%25E5%2593%2581%25E8%25B4%25A8%25EF%25BC%258C%25E6%2583%258A%25E5%2596%259C%25E4%25BB%25B7%25E6%25A0%25BC!%26q%3D%E5%A6%82%E4%BD%95%E5%9C%A8matlab%E7%BC%96%E7%A8%8B%E4%B8%AD%E5%AE%9E%E7%8E%B0arcsin&key=surl» jubao=»»/>
taobao.com baidu.com%2Fjubao%2Faccu%2F%3Ftitle%3D%25E4%25B9%25B0%25E5%25AD%25A6%25E4%25B9%25A0%25E5%259F%25BA%25E7%25A1%2580%25E7%25BC%2596%25E7%25A8%258B%25E4%25B8%258A%25E4%25B8%2587%25E8%2583%25BD%25E7%259A%2584%25E6%25B7%2598%25E5%25AE%259D!%25E4%25BC%2598%25E4%25BA%25AB%25E5%2593%2581%25E8%25B4%25A8%25EF%25BC%258C%25E6%2583%258A%25E5%2596%259C%25E4%25BB%25B7%25E6%25A0%25BC!%26q%3D%E5%A6%82%E4%BD%95%E5%9C%A8matlab%E7%BC%96%E7%A8%8B%E4%B8%AD%E5%AE%9E%E7%8E%B0arcsin&key=surl» jubao=»»/>