Практическая часть
Хотя MathCAD предназначен для сложных математических вычислений, его можно использовать, например, как калькулятор. Для этого:
Щёлкните в любом месте рабочего документа, появится небольшой крестик. Весь ввод с клавиатуры будет размещаться теперь в рабочем документе, начиная с места расположения крестика.
Напечатайте 20-4/103.2= . После набора знака= MathCAD вычисляет выражение и выводит результат.
Этот пример демонстрирует особенности работы с MathCAD.
MathCAD отображает формулы в точности в том виде, как их печатают в книгах или пишут на доске – по всей площади экрана; подбирает размеры для дробных черт, скобок и других математических символов, чтобы они выглядели так, как их обычно пишут на бумаге.
MathCAD понимает, какую операцию выполнять первой. После ввода знака равенства = MathCAD показывает результат.

После ввода оператора MathCAD показывает небольшой прямоугольник, называемый полем ввода. Поле ввода содержит места для ввода чисел и выражений.
Выражение на экране можно редактировать, устанавливая в нужном месте указатель и печатая новые символы, цифры или операторы.
В пакете MathCAD можно оперировать переменными и функциями. При помощи переменных и функций становится возможным связь уравнений и использование промежуточных результатов в дальнейших вычислениях.
Правила определения переменных.
Напечатать имя переменной, которую нужно определить.
Напечатать двоеточие (:), чтобы ввести символ присваивания ( MathCAD показывает : сопровождаемое символом присваивания : =).
Напечатать значение, присваиваемое переменной. Оно может содержать числовые константы и любые, ранее определённые переменные и функции.

Слева от знака := могут стоять:
имя простой переменной, например x;
имя переменной с нижними индексами;
матрица с элементами, являющимися простыми переменными или переменными с нижними индексами;
имя функции со списком аргументов, состоящих из имен простых переменных, например f(x,y,z);
имя переменных с верхними индексами.
Пример 1. Задание переменных.
MathCAD
читает рабочий документ сверху вниз и
слева направо. Определив переменную,
ее можно использовать в вычислениях
везде ниже и правее области, в которой
она определена. Попробуйте задать
переменную сами, используя следующий
алгоритм.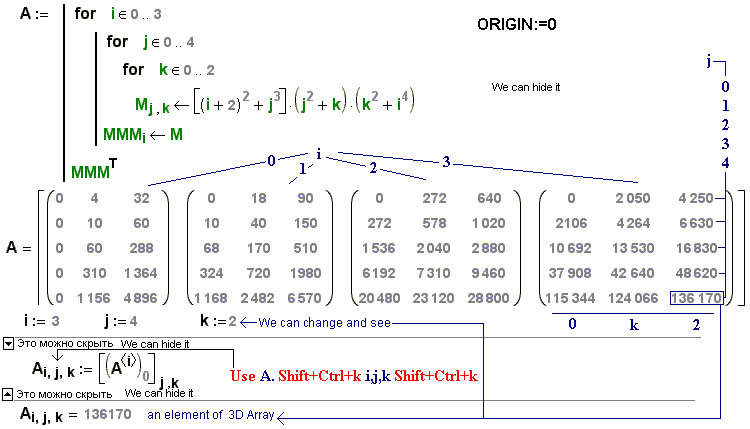 означает
возведение в степень, * ¾
знак умножения, а наклонная черта вправо
( / ) ¾
деление.
означает
возведение в степень, * ¾
знак умножения, а наклонная черта вправо
( / ) ¾
деление.
После ввода формулы MathCAD возвращает результат. Окно рабочего документа содержит одно определение, которое определяет переменную, и одно вычисление, которое дает результат. MathCAD пересчитывает результаты сразу после внесения любых изменений в рабочий документ. Если заменить, например, число 11 в примере на какое-либо другое, MathCAD изменит результат, как только будет введен [Enter], или Вы щелкнете мышью вне формулы.
Переменные могут быть определены в одном и том же рабочем документе неоднократно, например, дважды. MathCAD будет просто использовать первое определение для всех выражений ниже первого определения и выше второго. В выражениях, находящихся ниже второго определения, MathCAD использует второе определение.
MathCAD
может выполнять повторяющиеся или
итерационные вычисления также легко,
как вычисления отдельных выражений. Для этого MathCAD использует специальный
тип переменных
дискретные аргументы. Переменная типа
дискретный аргумент принимает диапазон
значений. Если в выражении присутствует
дискретный аргумент, то MathCAD вычисляет
выражение столько раз, сколько значений
содержит дискретный аргумент. Итак, для
определения дискретного аргумента
должны быть заданы:
Для этого MathCAD использует специальный
тип переменных
дискретные аргументы. Переменная типа
дискретный аргумент принимает диапазон
значений. Если в выражении присутствует
дискретный аргумент, то MathCAD вычисляет
выражение столько раз, сколько значений
содержит дискретный аргумент. Итак, для
определения дискретного аргумента
должны быть заданы:
имя переменной слева;
или := или в середине;
допустимый диапазон справа.
Для того чтобы вычислить выражение для диапазона значений, сначала определите дискретный аргумент.
напечатайте j и затем нажмите клавишу двоеточия :. Пустое поле означает, что MathCAD ожидает определение для j, не зная, будет ли j обычной переменной или дискретным аргументом.
Напечатайте 1. Затем нажмите клавишу точку с запятой ;. Это сообщает MathCAD, что определяется дискретный аргумент.
 MathCAD показывает
; как две точки .., что означает диапазон.
Завершите определение дискретного
аргумента, печатая 15 в оставшемся поле.
MathCAD показывает
; как две точки .., что означает диапазон.
Завершите определение дискретного
аргумента, печатая 15 в оставшемся поле.Это определение указывает, что j принимает значения 1, 2 .. 15. Чтобы определить дискретный аргумент с шагом, отличным от единицы, нужно сделать следующее:
напечатать k: 1, 1.5 ;15
На экране это будет выглядеть как
k:= 1,1.5 .. 15 .
В этом определении диапазона:
переменная k – имя дискретного аргумента. Это должно быть простое имя
число 0 – первое значение переменной k
число 1.5 – второе значение в диапазоне. Это не размер шага. Размер шага в этом примере 0.5 – разница между 1.5 и 1
число 2 – последнее значение в диапазоне.
 Если третье число в определении диапазона
не равно целому числу приращений
начального значения, аргумент все равно
не выйдет за его пределы.
Если третье число в определении диапазона
не равно целому числу приращений
начального значения, аргумент все равно
не выйдет за его пределы.
Нельзя
определить простую переменную через
дискретный аргумент. Например, если
определив j, теперь записать i := j + 1,то MathCAD истолкует это как попытку
приравнять скалярную переменную
дискретному аргументу и отметит уравнение
сообщением “нескалярная величина”. Если дискретный аргумент используется
в выражении, MathCAD вычисляет выражение
один раз для каждого значения дискретного
аргумента. Этот принцип выражает различие
между выражениями с дискретным аргументом
и без него. Выражения, которые не содержат
дискретный аргумент, имеют только одно
значение. Выражения, содержащие дискретные
аргументы, принимают много значений,
которые соответствуют каждому значению
каждого аргумента.
Этот принцип выражает различие
между выражениями с дискретным аргументом
и без него. Выражения, которые не содержат
дискретный аргумент, имеют только одно
значение. Выражения, содержащие дискретные
аргументы, принимают много значений,
которые соответствуют каждому значению
каждого аргумента.
П ример 2. Определение дискретного аргумента.
Определение функции аналогично определению переменной. Имя функции должно стоять слева, знак присваивания := посередине, а выражение — справа. Основное различие состоит в том, что имя теперь включает список аргументов.
Правила определения функций.
напечатать имя функции, например f ;
напечатать левую скобку, а вслед за ней – имя или список имен, разделенных запятой. Для завершения списка аргументов нужно напечатать правую скобку. Не имеет значение, были ранее определены или использованы в рабочем документе имена из списка аргументов.

ввести : . Появится знак оператора присваивания :=;
напечатать выражение, задающее функцию. Оно может содержать любые ранее определенные функции и переменные.
Определенная таким образом функция может быть использована везде ниже определения, также как используются переменные.
При использовании функции в выражении MathCAD
вычисляет значения аргументов, указанных в скобках;
заменяет формальные параметры (аргументы в определении функции) фактическими значениями аргументов, указанных в скобках;
выполняет вычисления, предписанные определением функции, и возвращает результат вычислений как значение функции.
Пример 3. Задание
функций.
Если в определении функции используется имя переменной, которой нет в списке аргументов, то оно должно быть определено прежде определения функции. Значение этой переменной в момент ввода определения функции становится постоянной частью функции.
Каким
образом строятся математические
выражения в MathCAD? Многие математические
выражения можно создавать, просто
печатая последовательность символов.
Часть символов – буквы и цифры – служат
для ввода чисел и имен функций и
переменных, другие символы – для создания
операторов. Можно напечатать многие из
этих операторов, нажимая соответствующие
кнопки на различных палитрах операторов.
Например, арифметическую палитру можно
открыть, нажав кнопку с изображением
калькулятора. Математические выражения
имеют строго определенную структуру,
и редактор формул MathCAD разработан с
учетом этого. В MathCAD математические
выражения не столько печатаются, сколько
строятся. MathCAD собирает различные части
выражения, используя правила старшинства
операций и некоторые дополнительные
правила, которые упрощают ввод
знаменателей, показателей степени и
выражений в радикалах.
Правила редактирования существующего выражения.
Чтобы отредактировать имя или число:
щелкните на нем – это поместит маркер ввода в нужное место
при необходимости нажмите клавиши управления курсором, чтобы переместить маркер
если напечатать символ, он появится слева от маркера ввода.
 Нажатие клавиши [Backspace]
удаляет символ слева от маркера ввода.
Нажатие клавиши [Backspace]
удаляет символ слева от маркера ввода.
Для замены оператора:
щелкните на знаке мышью или используйте клавиши курсора
нажмите клавишу [Del] или клавишу [Backspace]. Повторное нажатие удаляет все выражение.
нажмите другой знак.
Вставка оператора.
Проще вставить оператор между двумя буквами или цифрами, стоящими рядом. Например, чтобы вставить знак деления между двумя символами, стоящими рядом, нужно:
Столь же просто вставлять операторы,
которые требуют только одного операнда.
Примеры таких операндов – квадратный
корень, модуль и комплексное сопряжение.
Чтобы вставить один из них, выделите
все выражение, к которому нужно применить
оператор и наберите соответствующую
комбинацию клавиш. Многие из этих
операторов также доступны на арифметической
палитре.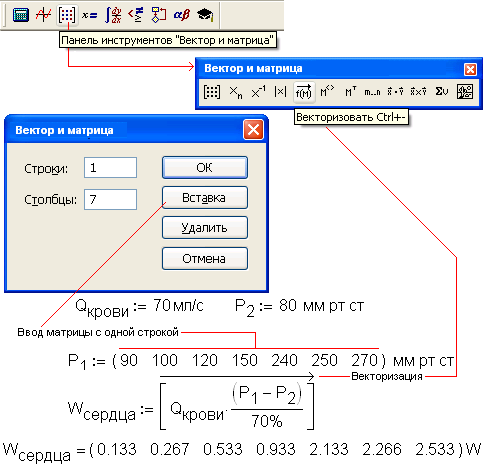
Удаление оператора.
Можно удалить оператор, соединяющий два имени переменных или две константы, а также операторы, требующие только одного операнда.
Или
Чтобы удалить оператор, который имеет только один операнд типа |x |, x! :
Чтобы вычислить выражение, нужно:
напечатать выражение, содержащее любую допустимую комбинацию чисел, переменных и функций. Любые переменные или функции, используемые в этом выражении, должны быть определены в рабочем документе;
нажать клавишу =.
Прерывание вычислений.
Для того чтобы прервать процесс вычислений, нажмите клавишу [Esc]. После появления диалогового окна нужно щелкнуть по кнопке OK, для остановки процесса вычислений или по кнопке “отмена” для его продолжения.
Исправление
ошибок.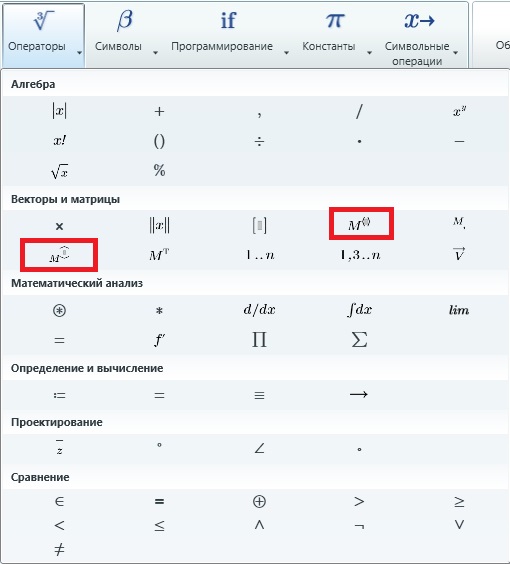
Определив выражение, вызвавшее ошибку, нужно его отредактировать с целью устранения ошибки или исправить определение переменной, приведшей к ошибке. После щелчка по выражению и начала редактирования MathCAD удаляет сообщение об ошибке. После щелчка вне уравнения (или нажатия клавиши [F9]), MathCAD повторно вычисляет выражение. Если ошибка устранена, то MathCAD затем повторно вычисляет другие выражения, зависящие от измененного.
Выражение, отмеченное сообщением об ошибке, не обязательно содержит ее причину. Причиной ошибки могут быть функции или переменные, определенные в рабочем документе значительно ранее. Для устранения ошибки придется отредактировать именно ее.
Рассмотрим допустимые в MathCAD имена переменных и функций. Имена в MathCAD могут содержать любые из следующих символов:
прописные и строчные латинские буквы;
цифры от 0 до 9
знак подчеркивания _
штрих ` Это не апостроф.
 Находится на одной
клавише с тильдой ~
Находится на одной
клавише с тильдой ~символ процента %
греческие буквы. Есть два способа набрать греческую букву: напечатать римский эквивалент и нажать [Ctrl]+G или щелкнуть по соответствующему символу на палитре греческих символов
символ бесконечности, который можно задать как комбинацию клавиш[Ctrl]+[Shift]+Z.
Имена переменных и функций не могут включать пробелы или любые другие символы, не перечисленные выше.
MathCAD
не делает различий между именами
переменных и именами функций. Если
определить вначале f(x), а затем переменную
f, окажется невозможным использовать
f(x) где-либо ниже определения f некоторые
имена уже используются MathCAD для встроенных
констант, единиц измерения и функций.
Хотя эти имена можно переопределить,
этот уничтожит их встроенные значения. 307 – машинная
бесконечность;
307 – машинная
бесконечность;
% =0.01 – процент.
MathCAD интерпретирует все, начинающееся цифрой, как число. Цифра может сопровождаться:
другими цифрами;
десятичной точкой;
цифрами после десятичной точки;
символами h или o для шеснадцатеричных и восьмеричных чисел; символами i или j для комплексных чисел. Комплексные числа MathCAD воспринимает в форме a+bi (или a+bj). Специальные функции и операторы для работы с комплексными числами:
Re(z) – вещественная часть числа z;
Im(z) – мнимая часть числа z;
Arg(z) – аргумент числа z (угол в комплексной плоскости между вещественной осью и радиус-вектором, определяемым числом z);
|z| – модуль числа z.
Одиночное число в MathCAD называют скаляром. Столбец чисел называется вектором, а прямоугольная таблица чисел матрицей. Способы создания массива:
Можно различать имена векторов, матриц и скаляров, используя различный шрифт для их описания.
Правила создания вектора (матрицы).
Щелкните мышью в свободном месте рабочего документа и напечатайте имя вектора V или матрицы M, сопровождаемое символом двоеточия.
Выберите матрицы из меню Вставка (Insert) или нажмите комбинацию клавиш [Ctrl]+m или щёлкните мышью на соответствующей палитре. Появится диалоговое окно, где Rows – количество строк, а Columns – количество столбцов.
Нажмите Ok . MathCAD создает вектор (матрицу) с пустыми полями для заполнения.
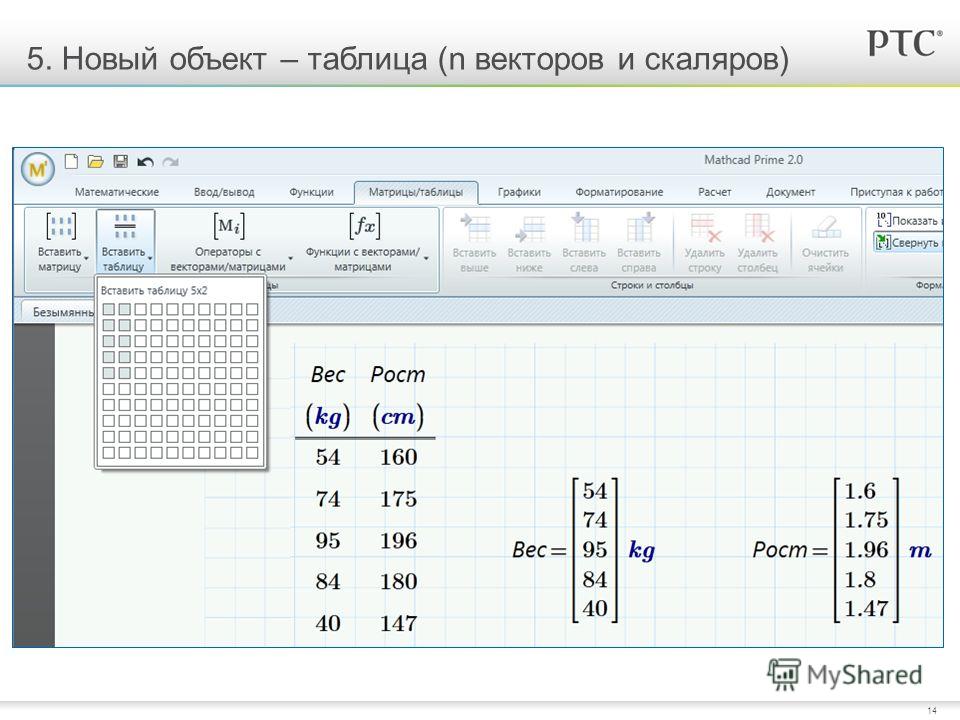 Заполните эти
поля скалярными выражениями.
Заполните эти
поля скалярными выражениями.
Можно теперь использовать имя вектора (матрицы) в любом выражении. Имя вектора (матрицы) и сам вектор (матрица) взаимозаменяемы. Как только вектор определен, можно определить через него другие вектора. Можно обращаться к отдельным элементам массива, используя нижние и верхние индексы. Чтобы напечатать нижний индекс, используйте клавишу нижней скобки [ . Чтобы вставить оператор верхнего индекса, нажмите комбинацию клавиш [Ctrl]+6. Нижние индексы, подобно делению и возведению в степень, удерживают ввод. Чтобы не печаталось после [ ,все остается в нижнем индексе, пока не будет нажат пробел , чтобы выйти оттуда. Когда определены элементы вектора (матрицы), часть из них можно оставить неопределенными. Если V был не определен и третий элемент вектора определяется равным 10, то нулевой, первый и второй элементы не определены. MathCAD заполняет эти элементы нулями, пока в них не будут внесены необходимые значения
П
ример 4. Определение и просмотр элементов
матрицы (вектора).
Определение и просмотр элементов
матрицы (вектора).
Можно создать большие массивы, используя дискретный аргумент. Если массив имеет более чем 9 строк или столбцов, MathCAD автоматически отображает его в виде таблицы вывода с полосами прокрутки.
Векторные и матричные операторы. Некоторые из операторов MathCAD имеют особые значения в применении к векторам и матрицам. Например, символ умножения означает просто умножение, когда применяется к двум числам, но он же означает скалярное произведение, когда применяется к векторам и умножение матриц, когда применяется к матрицам. Многие из этих операторов доступны из палитры символов. Обратите внимание, что операторы, которые ожидают в качестве аргумента вектор, всегда ожидают вектор-столбец, а не вектор-строку. MathCAD располагает следующими встроенными функциями для работы с векторами и матрицами:
cols(M) – число строк в матрице M;
rows(M) – число столбцов в матрице M;
min(M), max(M) – минимальный и максимальный элементы матрицы M;
length(V) – число элементов вектора V;
last(V) –индекс последнего элемента в векторе V.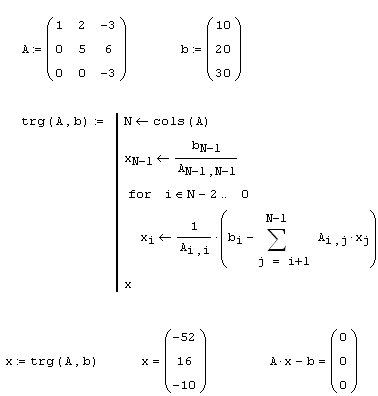
Пример 5. Векторные и матричные функции.
П ример 6. Векторные и матричные операции.
С умма элементов вектора: Скалярное и векторное произведение
Определитель матрицы Транспонированная матрица
Обратная матрица:
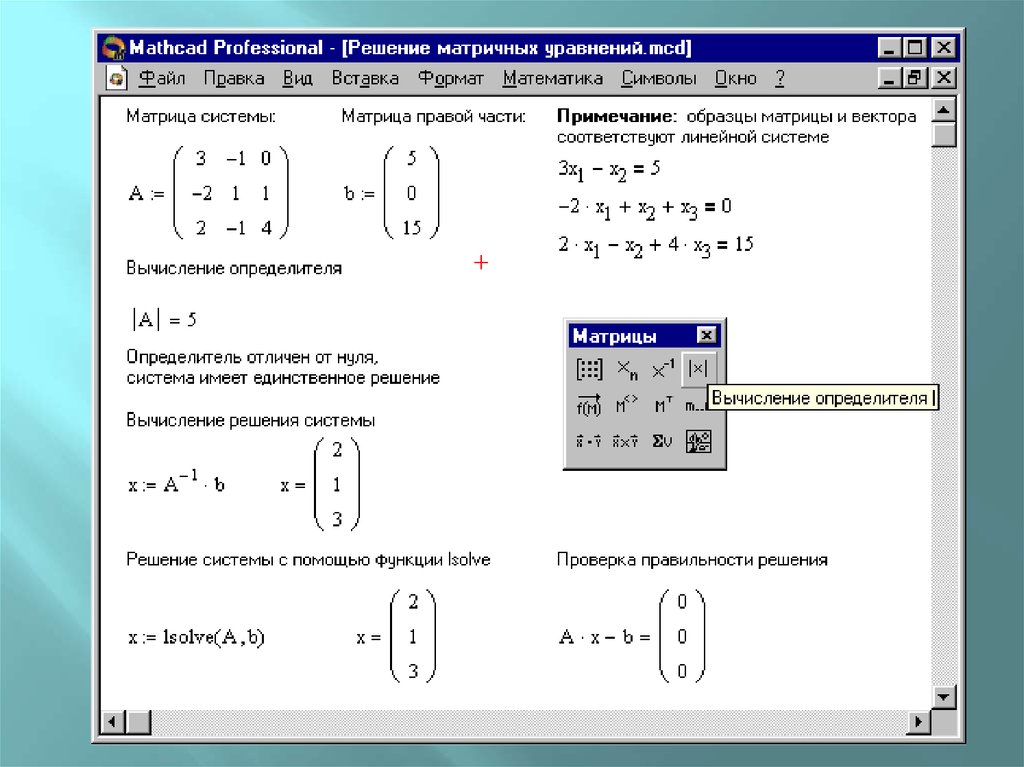
Решение матричных уравнений.
Матричные уравнения представляют собой систему линейных алгебраических уравнений и решаются путем обращения матрицы коэффициентов .
Кром того, MathCAD есть также оператор lsolve, позволяющий решать систему уравнений в случае невырожденной матрицы .
Пример 7. Решение системы линейных уравнений.
Как из вектора сделать скаляр в маткаде
Как из вектора сделать скаляр в маткаде
Операции, выполняемые над векторами и матрицами в Mathcad, можно разбить на две большие группы. К первой группе относятся операции, которые применяются к отдельным векторам и матрицами. Например, транспонирование матрицы или вычисление обратной матрицы в Mathcad. Ко второй группе относятся операции, которые выполняются над группой векторов и матриц. Как правило, они выполняются над двумя матрицами или матрицей и вектором. Например, сложение, вычитание матриц, перемножение матриц или умножение матрицы и вектора. К векторам и матрицам в Mathcad, при выполнении операций над ними, могут предъявляться определенные требования в соответствии с требованиями классической математики. Например, при перемножении матрицы и вектора, количество столбцов матрицы должно быть равно количеству срок вектора. Поэтому при работе с векторами и матрицами пользователь должен иметь необходимую математическую подготовку. В таблице приведены основные операции, выполняемые над векторами и матрицами, используемые в Mathcad. В таблице приняты следующие обозначение: А – массив, под которым понимается вектор или матрица, М – матрица, z — скаляр, v – вектор.
Ко второй группе относятся операции, которые выполняются над группой векторов и матриц. Как правило, они выполняются над двумя матрицами или матрицей и вектором. Например, сложение, вычитание матриц, перемножение матриц или умножение матрицы и вектора. К векторам и матрицам в Mathcad, при выполнении операций над ними, могут предъявляться определенные требования в соответствии с требованиями классической математики. Например, при перемножении матрицы и вектора, количество столбцов матрицы должно быть равно количеству срок вектора. Поэтому при работе с векторами и матрицами пользователь должен иметь необходимую математическую подготовку. В таблице приведены основные операции, выполняемые над векторами и матрицами, используемые в Mathcad. В таблице приняты следующие обозначение: А – массив, под которым понимается вектор или матрица, М – матрица, z — скаляр, v – вектор.
Наиболее удобно выполнять матричные вычисления с использованием кнопок панели инструментов “Матрица”. По умолчанию индексация строк и столбцов элементов матрицы начинается с 0.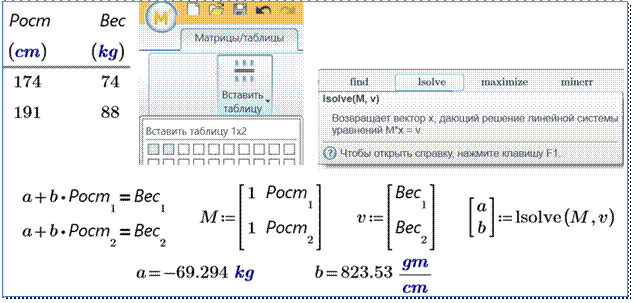 Для того чтобы индексация начиналась с 1, необходимо системной переменной ORIGIN присвоить значение 1. На листинге приведен пример матричных вычислений в Mathсad.
Для того чтобы индексация начиналась с 1, необходимо системной переменной ORIGIN присвоить значение 1. На листинге приведен пример матричных вычислений в Mathсad.
Значение должно быть скаляром, MathCad.
В примере, как работать с Маткадом, всё работает (изображение 1):
Когда я делаю тоже самое, появляется ошибка, что значения не является скаляром:
Как исправить? Помогите, пожалуйста.
Оно может быть скаляром, только если размеры матриц A и B совпадают.
Решение системы линейных уравнений — это ВСЕГДА вектор. Скаляром оно быть не может по определению.
В ошибочной строке справа после знака равенства есть какой-то символ перед В. Попробуй его убрать. Еще, этот самый знак равенства должен, похоже, вводиться через Ctrl =.
7.2.2. Скалярное произведение MathCAD 12 руководство
Скалярное произведение векторов ( vector inner product ) определяется как скаляр, равный сумме попарных произведений соответствующих элементов. Векторы должны иметь одинаковую размерность, скалярное произведение имеет ту же размерность.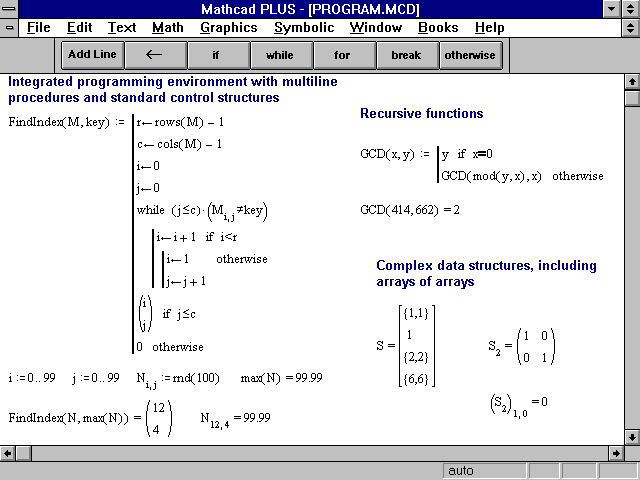 Скалярное произведение двух векторов u и v равно uv=|u||v|cos0 , где 0 — угол между векторами. Если векторы ортогональны, то их скалярное произведение равно нулю. Обозначается скалярное произведение тем же символом, что и умножение (листинг 7.9).
Скалярное произведение двух векторов u и v равно uv=|u||v|cos0 , где 0 — угол между векторами. Если векторы ортогональны, то их скалярное произведение равно нулю. Обозначается скалярное произведение тем же символом, что и умножение (листинг 7.9).
Для обозначения скалярного произведения пользователю позволяется выбирать представление оператора умножения при помощи контекстного меню (подобно умножению скалярных величин). Однако никогда не применяйте для обозначения скалярного произведения символ х , который является общеупотребительным символом векторного произведения (см. разд. 7.2.3).
Листинг 7.9 . Скалярное произведение векторов
С осторожностью перемножайте несколько (более двух) векторов. По-разному расставленные скобки полностью изменяют результат умножения. Примеры такого умножения приведены в листинге 7.10.
Листинг 7.10. Скалярное произведение векторов, умноженное на третий вектор
Значение должно быть скалярным
Значение должно быть скалярным
Не понимаю почему он пишет что значение "е" должно быть скалярным точнее почему он стал.
