Mathematica 5. Самоучитель. Система символьных, графических и чи
Шмидский Яков Константинович Кол-во страниц: 592 Оглавление | Дополнительные материалы | | Купить книгу: Книга в типографии |
Эта книга — самоучитель и практическое руководство по новейшей версии пакета компьютерной алгебры Mathematica 5. В ней доступно и подробно рассмотрены примеры решения всех типовых задач основных разделов элементарной и высшей математики: арифметики, алгебры, геометрии, математического анализа и теории дифференциальных уравнений.
Подробно рассмотрено построение графиков функций в декартовой и полярной системах координат. Для функций двух переменных описано построения поверхностей, контурных графиков, линий уровня и графиков плотности. Даны примеры решения типовых задач математического анализа — нахождение пределов, производных и интегралов. Обсуждаются также мультимедийные средства системы Mathematica — обработка звука и изображений, в частности мультипликация. В заключительной главе обсуждается новый вид науки — наука о сложном — и поведение клеточных автоматов. Предварительное знакомство читателя с компьютерной алгеброй не предполагается.
Расскажи про книгу своим друзьям и коллегам:
Твитнуть
Нравится
| ISBN | 5-8459-0678-4 |
| ISBN ENG | |
| Кол-во страниц | 592 |
| Год выпуска | 2004 |
| Формат | 70×100/16 |
| Тип переплета | мягкий переплет |
| Тип бумаги | газетная |
| Серия | Самоучитель |
| Автор | Шмидский Яков Константинович |
Название ориг. | |
| Автор ориг. | |
Вас, возможно, заинтересуют следующие книги
|
Оглавление к книге Mathematica 5. Самоучитель. Система символьных, графических и численных вычислений.
ОглавлениеБлагодарности 12
Введение 14
Глава 1.
Исторический обзор и первое знакомство 20
Глава 2. Первое знакомство — калькулятор 34
Глава 3. Числа, их представление и операции над ними 57
Глава 4. Арифметика: разложение целых чисел на простые множители 114
Глава 5. Арифметика: простые числа 136
Глава 6. Арифметика: наибольший общий делитель
и наименьшее общее кратное 167
Глава 7. Модулярная арифметика: деление с остатком, вычеты,
сравнения и китайская теорема об остатках 186
Глава 8. Числовые функции 215
Глава 9. Мультимедиа: геометрия, графика, кино, звук 241
Глава 11. За гранью простого 369
Приложение A. Ответы и решения задач 388
Приложение Б. Таблицы 410
Предметный указатель 572
Материалы к книге Mathematica 5. Самоучитель. Система символьных, графических и численных вычислений.
Полное содержаниеDemonstratio Mathematica Volume 5 Issue 4
Contents
Retrieving citations for document.
..
Publicly Available December 19, 2017
Titelei
Page range: I-I
Download PDF
Retrieving citations for document…
Contents
Page range: II-II
Download PDF
Retrieving citations for document…
Open Access December 19, 2017
О НЕКОТОРЫХ СВОЙСТВАХ МНОЖЕСТВ Ω , H
0 (ω) и H(ω1,ω2,ω)Вхи Гра&овскиЯ
Page range: 213-230
Download PDF
Retrieving citations for document.
..
Open Access December 19, 2017
THE DETERMINATION OF NON-HOMOGENEOUS LINEAR GEOMETRIC OBJECTS OF THE FIRST CLASS FOR WHICH THE NUMBER OF COORDINATES IS NOT GREATER THAN THE DIMENSION OF THE SPACE
Jan Luchter
Page range: 231-240
Download PDF
Retrieving citations for document…
Open Access December 19, 2017
ON SOME MULTIPLICATIVE FUNCTIONAL EQUATION DEFINED ON A DIFFERENTIAL GROUP
Jan Luchter
Page range: 241-256
Download PDF
Retrieving citations for document.
..
Open Access December 19, 2017
APPLICATION OF SOME SYSTEM OF FUNCTIONAL EQUATIONS TO THE INVESTIGATION OF BOUNDARY-VALUE PROBLEMS FOR PARTIAL DIFFERENTIAL EQUATIONS
Henryk Adamczyk
Page range: 257-268
Download PDF
Retrieving citations for document…
Open Access December 19, 2017
EIN BEITRAG ZUR AXIOMATISIERUNG DES BEGRIFFS DES SKALARPRODUKTES
Stanislaw Gol*b
Page range: 269-284
Download PDF
Retrieving citations for document.
..
Open Access December 19, 2017
О АСИМПТОТИЧЕСКОМ ПОВЕДЕНИИ РЕШЕНИЙ НЕКОТОРОЙ ГИПЕРБОЛИЧЕСКОЙ ЗАДАЧИ, I.
Ирена Маковецкая, Ежи Мугаинскнй
Page range: 285-294
Download PDF
Retrieving citations for document…
Open Access December 19, 2017
REPRESENTATIONS OF RINGS OF STRUCTURAL NUMBERS
Stanislaw Bellert, Tadeusz Traczyk
Page range: 295-306
Download PDF
Retrieving citations for document.
..
УСТОЙЧИВОСТЬ РКШКНИЙ АНСТРАКТНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНКНИЙ В ГИЛЬКККГОВОМ ПРОСТРАНСТВЕ, I.
М. А. Велиев, Я. Д. Мамедов
Page range: 307-326
Download PDF
Retrieving citations for document…
Open Access December 19, 2017
ОБ ОСТАТОЧНОЙ ОГРАНИЧЕННОСТИ И ДРУГИХ СВОЙСТВАХ РЕШЕНИЙ НЕКОТОРОЙ СМЕШАННОЙ ЗАДАЧИ
Ежи Мушинскип
Page range: 327-356
Download PDF
Journal Overview
Новости MathWorld: Mathematica 5 выпущена
Эрик В.
Вайсштейн23 июня 2003 г. — сегодня компания Wolfram Research, расположенная в Шампейне, штат Иллинойс, объявила о выпуске новой крупной версии своей мощной система математических вычислений Mathematica. Математика 5 содержит множество новых математических и программных функций, а также полная переработка числового движка, обеспечивающая впечатляющий прирост скорости в арифметике произвольной точности, а также молниеносных числовых линейных алгебра. Обладая впечатляющей скоростью и функциональными улучшениями, Mathematica 5 основана на надежных технологиях предыдущих версий. которым пользовались миллионы людей во всем мире за последние 15 лет.
23 июня — особенно подходящая дата выхода для такого крупный новый выпуск, поскольку он также отмечает 15-летие основания компании Wolfram Research. Как указано в графике работы компании истории Mathematica 5 разрабатывалась четыре года, с предыдущим выпуском в марте 1999 года.
Читатели MathWorld получат большую пользу от новых и
расширенные возможности Mathematica 5, которые использовались
широко в вычислениях и выводах, появляющихся на сайте
а в загружаемых блокнотах Mathematica предусмотрено больше
более 1000 отдельных записей.
Встроенные статистические функции
В версии 5 общие статистические функции, такие как Среднее, Variance и Median теперь встроены в ядро. и больше не требуют загрузки через пакеты. Кроме того, удобный новая функция Total теперь может использоваться для эффективного добавления списков чисел.
SeedRandom[1234]; данные = Таблица[Случайное[Целое число, {1, 10}], {10}] {1, 4, 5, 5, 1, 9, 8, 4, 5, 9} Всего[данные] 51 Медиана[данные] 5 Среднее [данные] 51/10 Дисперсия [данные] 749/90
Встроенные векторные и матричные нормы
В системе Mathematica 5 вектор и
матричные нормы теперь встроены.
поэтому новая функция Norm обеспечивает удобный способ
для вычисления различных математических норм.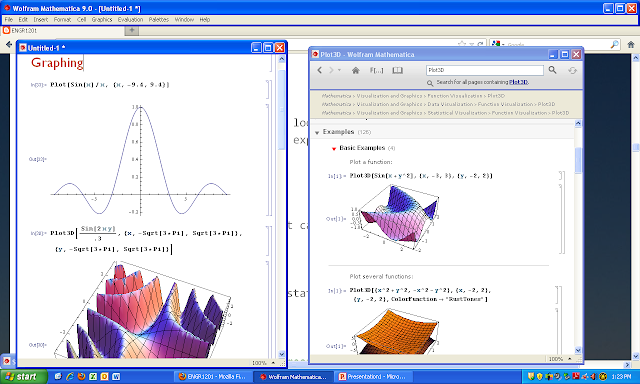
Эта же команда также
можно использовать для вычисления комплексных норм.
Норма[Диапазон[4], #]& /@ {1, 2, Бесконечность} {10, кв.[30], 4} Норма[Раздел[Диапазон[9], 3], #]& /@ {1, 2, Фробениус, Бесконечность} {18, Sqrt[(3*(95 + Sqrt[8881]))/2], Sqrt[285], 24} Норма[1 + 2I] кв[5]
Расширенные возможности интеграции
Возможности Mathematica Integrate были
упрощено, улучшено и систематически расширено в версии 5.
В частности, генерация состояний резко изменилась.
улучшено для параметров с произвольными комплексными значениями при определенном интегрировании. Когда
в сочетании с расширенными предположениями Mathematica 5 и новыми
Если говорить о технологиях, это обеспечивает прочную основу для
вычисление сложных интегралов, даже тех,
со сложными параметрами, с беспрецедентной точностью и строгостью.
92], {х1, 0, 1}, {х2, 0, 1},
{у1, 0, 1}, {у2, 0, 1}] (2 + Sqrt[2] + 5*ArcSinh[1])/15 Интегрировать [Log [x], {x, a, b}, предположения -> 0 < a Команда RSolve была полностью переписана для
Mathematica 5 и переведена в функцию ядра. Уравнение Пелла — простой пример
квадратичного диофантова
уравнение. Уравнение Пелла Благодаря новому мощному синтаксису Reduce в Mathematica 5,
общее решение этого уравнения над целыми числами может быть легко
найден с помощью следующей команды.
92 == 1 && х > 0 && 0
х == 1766319049 && у == 226153980 Mathematica 5 теперь может строго доказывать многие геометрические тождества. Демонстрация этого вручную — хорошее упражнение для изучающего геометрию.
но не то, для чего хорошо подходит компьютер. Однако
можно строго показать, что тождество выполняется, если сформулировать проблему как
логическое выражение «Для всех a, b и c, которые соответствуют сторонам
треугольника выполняется тождество (3)», а затем оценивая
чтобы увидеть, является ли результат True (предложение верно)
или False (предложение неверно). отмечая, что
дано условие того, что три числа являются длинами сторон треугольника
к Истинный Так как результат истинен, то предложение доказано. Wolfram Research, Inc. «Mathematica 5».
http://www.wolfram.com/mathematica/ Wolfram Research, Inc. «Что нового в версии 5».
http://www.wolfram.com/mathematica/newin5/ Mathematica 5 — это крупное обновление знакового приложения для инженеров, ученых и других людей, работающих со сложной математикой. В нем много новых функций, но более важно то, что большинство старых функций работают намного быстрее, чем в версии 4.2 ( ;
ноябрь 2002 г.). Есть только одно разочарование: Mathematica 5 оптимизирована для многих 64-битных систем, но не для Power Mac G5 — пока. Тем не менее, на G5 программа работает как подарок от дружественного космического корабля пришельцев. Система Mathematica всегда состояла из двух частей: интерфейса и основного вычислительного движка, или ядра. Теперь, 15 лет спустя, вы можете сформулировать свою задачу в виде уравнения или набора уравнений и условий, и в этот момент Mathematica обычно берет на себя ответственность и выдает ответ без помощи программирования. Ядро, всегда являющееся последним словом в области символьной математики, было переоснащено численными методами и решателями, которые конкурируют с лучшими практиками в специализированных математических пакетах. Раньше был класс задач, с которыми можно было работать быстрее всего, программируя непосредственно на C и используя оптимизированную библиотеку численных алгоритмов. Больше нет: в версии 5 несколько строк кода Mathematica заменяют страницы C. Большая часть числового увеличения скорости связана с кодом выбора алгоритма версии 5. В случае дифференциальных уравнений, решаемых с помощью NDSolve, вы можете сами выбрать алгоритм решения и посмотреть промежуточные результаты. Хотя Mathematica 5 выполняет сложные функции автоматически, опытные пользователи могут отменить большинство ее автоматических решений. Mathematica 5 также добавляет хороший набор видимых функций — как простых, так и сложных. Одной из основных функций является поддержка новых типов графических файлов: SVG (масштабируемая векторная графика, научно-технический стандарт), PNG (портативная сетевая графика, веб-стандарт) и DICOM (цифровая визуализация и обмен данными в медицине, для МРТ и других диагностических изображений). Также в эту категорию входят улучшенные инструменты разработки Mathematica 5. Теперь есть инструменты для сравнения разных блокнотов Mathematica, полезные для отслеживания меняющихся версий блокнотов. Поскольку серьезная работа Mathematica в конечном итоге может быть представлена аудитории, теперь существует специальная авторская палитра для слайд-шоу. Одной из сложных новых функций является новая функция Rsolve для решения разностных уравнений (также называемых рекуррентными уравнениями). Они описывают изменения, происходящие за конечные временные интервалы, и проявляются в широком диапазоне областей помимо науки и техники, включая бизнес и финансы. Mathematica по-прежнему позволяет вам создавать собственные программы для решения разностных уравнений, но Rsolve избавляет вас от этих усилий и может справиться с этой задачей лучше, чем вы (некоторые задачи с разностными уравнениями известны своей сложностью). Еще одно усовершенствование: числовые функции FindFit, FindRoot, FindMaximum и FindMinimum — а также самые простые числовые функции — теперь работают с векторными и массивными переменными, поэтому однострочные программы в версии 5 могут заменить десятки строк в версии 5. код 4.2. Матрица представляет собой прямоугольный массив чисел; многие важные расчеты в электротехнике и машиностроении представлены в виде матричных задач. Поскольку матрицы могут быть огромными — обычно 1000 на 1000 чисел или больше — существует множество специальных приемов для их быстрого вычисления. Чем больше библиотека матричных ярлыков программы, тем меньше грубой силы программа должна использовать. Первоначальная Mathematica была довольно слабой в этой области по сравнению с Matlab от MathWorks (что, в конце концов, означает «лаборатория матриц»). Помимо повышения скорости, матричные функции Mathematica 5 теперь включают обобщенные собственные значения, разложение Шура и Холецкого, матричные нормы и ранг, а также характеристические полиномы. Практически каждая операция, описанная в учебнике по матричной математике, теперь соответствует функции Mathematica. Если вы уже пользуетесь системой Mathematica, вам следует обновить ее до версии 5 — достаточно только повышения скорости. Переработанные матричные операции программы делают Mathematica конкурентоспособной с Matlab в большинстве инженерных матричных задач, а новые решения для бизнес-задач окажутся полезными в финансовом моделировании. Обновленный Решатель Рекуррентных Уравнений
Это содержит
современный решатель, который может решать большие классы общих рекуррентных уравнений. Например,
RSolve теперь может найти решения для трех точно решаемых задач.
случаи логистического уравнения x Нет +1 = х н (1- х н ). 9n*ArcCos[1 — 2*x0]])/2}}} Решение уравнения Пелла с редукцией
х 2 — г у 2 = 1, (2) Геометрические доказательства с Resolve
и неравенства с использованием квантификатора
устранение. Например, красивое тождество из геометрии треугольника утверждает
что радиус r и
радиус описанной окружности R треугольника с длинами сторон a , b ,
и c с соответствующими углами А , В и С связаны 1 + r / R = cos A + cos B + cos C . (3) а , б , в > 0, а + б > в , б + в > а , а + в > б . 
2)/(2#2#3)]&@@@NestList[Повернуть влево, {a, b, c}, 2])]
}]] Математика 5 | Macworld
Модернизация движка
Первоначальным ядром была в основном программа символьной математики Стивена Вольфрама, адаптированная для численных вычислений и объединенная с общим C-подобным языком. Пользователи могли использовать язык и большую библиотеку математических функций для решения научных и инженерных задач.
Для решения нетривиальных числовых задач (ярким примером являются обыкновенные дифференциальные уравнения) система Mathematica преобразует задачу в символьное выражение для наилучшего соответствия доступным алгоритмам, выбирает условия числовой точности и отслеживает ход выполнения, при необходимости переключая методы для получения более быстрых результатов. Обычно вы ничего этого не видите, но вы увидите, что большинство числовых вычислений выполняются в 5–500 раз быстрее, чем в версии 4.2. Новые трюки старого пса
Это важно, потому что Mathematica может быть самой мощной в мире средой для анализа изображений. Еще одной базовой функцией является дополнительный пакет StatisticsPlot, который добавляет множество полезных статистических графиков из учебников.
Новая функция также обрабатывает системы разностных уравнений (линейных и нелинейных) и алгебраических разностных уравнений. The Matrix, Revisited
Версия 5, однако, идет лицом к лицу с Matlab: из восьми общих тестов скорости для вычисления матриц Mathematica 5 выиграла четыре и примерно разделила два. Пользователи Matlab, которые написали свои собственные библиотеки кода для конкретных задач, не увидят необходимости переключаться, но теперь пользователи Mathematica могут выполнять крупномасштабные инженерные расчеты, которые раньше были домашней территорией Matlab. Macworld’s Buying Advice
