Математический оператор: Недопустимое название | Математика | Fandom

Математика. Операции и операторы. Функции. Подстановки

Допустим, я прошу Дениса посчитать, сколько конфет я съел за день.

— До обеда я съел $3$ конфеты, а после обеда $2$ конфеты, — диктую я.

Денис записывает карандашом выражение:

$3 + 2$

— Э, нет, постой, после обеда я съел не $2$ конфеты, а… Сейчас, подожди-ка, дай припомнить.

Денис берет резинку и стирает число $2$. На его месте осталось сероватое пятнышко. Поскольку среди типографских знаков сероватых пятнышек нет, я вместо него напишу многоточие, заключенное в скобки:

$3 + (…)$

То, что при этом получилось, является типичным примером оператора. Вообще говоря, оператор — это то, что остается от выражения, если стереть в нем одно или несколько чисел, оставив все знаки арифметических действий нетронутыми. Сам по себе оператор — вещь совершенно бессмысленная. Это всего лишь заготовка, которая превращается в полноценное выражение, только если заполнить подобающим образом прилагаемые к нему «свободные» места.

— Ага, вспомнил! — говорю я Денису. — После обеда я съел $5$ конфет.

Денис записывает:

$3 + 5 = 8$.

Говорят, что Денис подействовал оператором

$3 + (…)$

на число $5$ и в результате получил $8$. В некотором смысле оператор — это своеобразная машина по переработке чисел. В данном случае Денис ввел в машину число $5$, а та переработала его в число $8$. Такая переработка на математическом языке называется операцией.

Оператор может действовать не только на числа, но и на выражения. Например, я мог бы сказать Денису, что $4$ конфеты я съел сразу после обеда и еще одну конфету спустя некоторое время. Тогда Денис записал бы число конфет, съеденных мной после обеда, в виде выражения

$4 + 1$.

Подействовав на это выражение оператором

$3 + (…)$,

он бы нашел общее число съеденных за день конфет в следующем виде:

$3 + (4 + 1)$.

Правило действия оператора на выражение таково: мы просто вписываем выражение на место многоточия, а скобки сохраняем.

Потом, при желании, их можно раскрыть, но это уже отдельная процедура.

Необходимость сохранения скобок легко понять на следующем примере. Допустим, я говорю Денису:

— Всего за день я съел $8$ конфет. Интересно, сколько конфет я съел до обеда, если после обеда я съел… я съел… Подожди минуточку, сейчас припомню…

Денис тем временем уже заготавливает оператор

$8 — (…)$.

Я же продолжаю:

— Вначале я съел $4$ конфеты, а потом еще одну.

Денис действует заготовленным оператором на выражение

$4 + 1$

и получает

$8 − (4 + 1)$.

Если бы он не сохранил скобки, то получилось бы

$8 − 4 + 1$,

что, конечно же, неверно.

Итак, чтобы изготовить оператор, надо взять какое-то выражение, стереть в нем некоторые числа и на их место поставить многоточие, заключенное в скобки (…). Если мы стерли лишь одно единственное число, то такой оператор называется

унарным (то есть одинарным или одноместным). Вот примеры унарных операторов:

$3 + (. ..)$

$4 — (…)$

$(…) + 5$

$(…) — 6$

$10 + ((…) — 2)$

На практике, последовательность символов ${(…)}$ писать не принято, если и без того ясно, в какое место следует поставить недостающее число. Поэтому первые четыре оператора лучше переписать так:

$3~+$

$4~-$

$+~5$

$-~6$

Лишь последний оператор из этой серии придется пока оставить, как есть:

$10 + ((…) — 2)$.

Но тогда сразу возникает вопрос. Как же тогда отличить оператор $+~5$ от целого положительного числа $+5$ и как отличить оператор $-~6$ от целого отрицательного числа $-6$?

А никак. Потому что такой оператор — это одна из многих форм, которые могут принимать числа. Мы знаем, что числа, в зависимости от ситуации, можно представлять себе либо в виде кучек из конфет, либо в виде ступенек лестницы, либо в виде команд по перемещению по лестнице. Теперь этот ряд возможностей у нас еще немножко расширился.

Давайте вспомним, какие задачи мы решали с помощью целых чисел. Кузнечик прыгает по лестнице, начиная с этажа, где находится квартира Дениса. Сперва он прыгнул на $2$ ступеньки вниз, потом на $5$ ступенек вверх, потом опять на $7$ ступенек вниз. На сколько ступенек и в каком направлении переместился кузнечик?

Мы не знаем номера ступеньки, на которой сидел кузнечик первоначально. Но в любом случае, если мы подействуем на этот номер оператором $-~2$, то спустимся вниз на две ступеньки. Поэтому положение кузнечика после первого прыжка можно представить в виде

$(…) — 2$,

или, короче:

$-2$.

Далее, мы действует на эту запись оператором $+~5$ и поднимаем кузнечика на пять ступенек вверх:

$((…) — 2) + 5$,

или, короче:

$-2 + 5$.

И, наконец, с помощью оператора $-~7$ опускаем его на семь ступенек вниз:

$(((…) — 2) + 5) — 7$,

или, короче:

$-2 + 5 — 7$.

Хотите — понимайте это выражение как сумму целых чисел, хотите — просто как ряд целых чисел, выписанных друг за другом, хотите — как цепочку операторов. Это уж дело вкуса. Но мы уже умеем вычислять значение подобных выражения:

$-2 + 5 — 7 = -4$.

Значит, и цепочку операторов мы можем записать короче, или, как говорят математики, упростить:

$(((…) — 2) + 5) — 7 = (…) — 4$.

Мы получили так называемое операторное равенство. Предполагается, что на стертые с обеих сторон места ${(…)}$ следует вписать одно и то же число. Пока мы не знаем, каким будет это число, можно вместо него поставить какую-нибудь переменную, например, $x$:

$((x — 2) + 5) — 7 = x — 4$.

Это не что иное, как тождество, которое, после раскрытия скобок, принимает вид:

$x — 2 + 5 — 7 = x — 4$.

Конечно, такая запись короче и удобнее, чем запись с многоточием. К тому же, тут уже сразу ясно, что и слева, и справа от знака равенстсва вместо переменной $x$ должно стоять одно и то же число. Никаких дополнительных пояснений на этот счет делать не требуется.

Поэтому на практике, запись с многоточием ${(…)}$ никогда не употребляется. Либо многоточие и окружающие его скобки просто удаляют (и тогда запись ${(…) — 2}$ превращается просто в $-2$), либо ставят на их место какую-нибудь переменную.

Нам недавно встречался оператор

$10 + ((…) — 2)$.

Очевидно, отсюда нельзя просто убрать ${(…)}$, так как тогда получилось бы

$10 + (-2)$,

а такая запись имеет совсем другой смысл. Здесь, по необходимости, приходится вводить переменную. В качестве такой переменной подойдет любая буква, но особенно часто употребляются последние три буквы латинского алфавита, то есть $x$, $y$ или $z$. Таким образом, наш оператор можно записать, например, так:

$10 + (y — 2)$.

Правда, в таком виде это называется уже не оператором, а функцией (или, если уж совсем точно, то функцией от независимой переменной $y$), но суть от перемены названия не меняется. Функция отличается от оператора только способом записи. Когда мы просто удаляем символы ${(…)}$, то оператор остается оператором, а когда мы вместо этих символов пишем переменную, то оператор превращается в функцию.

Функции действуют на числа и выражения точно так же, как и операторы, хотя описывается это действие несколько в других словах. Например, принято говорить, что мы находим значение функции

$8 — z$

при

$z = 4 — 1$.

Это делается с помощью так называемой подстановки. На место переменной $z$ в записи $8 — z$ мы подставляем то выражение, которому эта переменная равна, то есть $4 — 1$. При этом, во избежание неприятностей, подставляемое выражение обязательно брать в скобки:

$8 — (4 — 1)$.

Отсюда, искомое значение функции равно:

$8 — (4 — 1) = 8 — 3 = 5$.

По сути, это значит абсолютно то же самое, что подействовать оператором

$8 — (…)$

на выражение

$4 — 1$.

Фактически, функции — это не что иное, как уже знакомые нам выражения с переменными. Поэтому вместо слов «найти значение функции» часто говорят «найти значение выражения».

Всякий оператор можно записать в виде функции, но это не всегда удобно. Операторная запись часто оказывается значительно проще.

Для того чтобы подействовать, например, оператором $- 2$ на число $3$, не надо думать ни о каких подстановках, а достаточно просто это число приписать слева от оператора:

$3 — 2$.

Обычно в тех случаях, когда можно построить оператор, действующий посредством «приписывания», математики предпочитают пользоваться именно оператором. Но если такого оператора построить нельзя, как в рассмотренном ранее примере

$10 + ((…) — 2)$,

то приходиться прибегать к функциям.

До сих пор мы рассматривали только унарные (одноместные) операторы. Но можно также взять какое-то выражение и стереть в нем не одно, а сразу два числа. Тогда мы получим так называемый бинарный (или двуместный) оператор. Вот примеры бинарных операторов:

$(…) + 5 — (…) + 3$,

$2 — ((…) + 1) + (…)$.

Впрочем, эти примеры хороши лишь как примеры. На практике подобными операторами пользуются редко, потому что в таких случаях удобнее иметь дело с функциями двух независимых переменных:

$x + 5 − y + 3$,

$2 − (u + 1) + v$.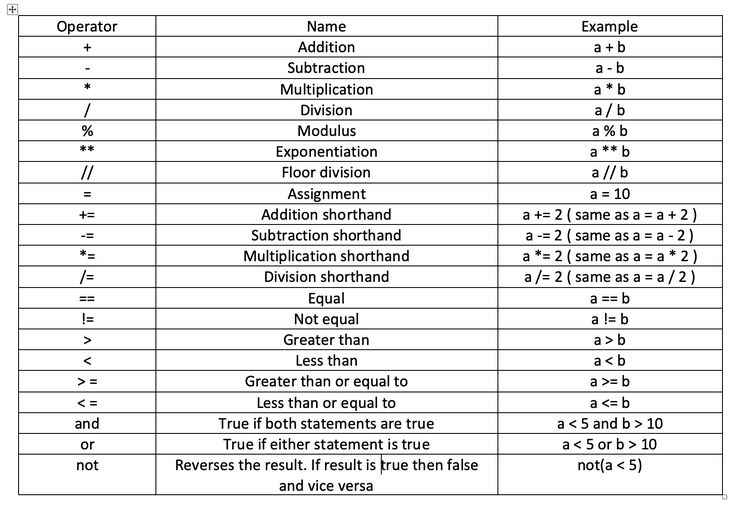

Однако есть и такие бинарные операторы, которые применяются очень широко. Например:

$(…) + (…)$

или в более короткой записи:

$+$

Этот оператор называется «плюс» и определяет операцию сложения. Как и всякий оператор, сам по себе он совершенно бессмыслен. Он приобретает смысл только тогда, когда по обе стороны от него приписывается по числу.

А вот другой, не менее распространенный оператор:

$(…) — (…)$

или же

$-$

Он, как нетрудно догадаться, называется «минус» и определяет операцию вычитания.

Мы настолько часто сталкиваемся с этими операторами, что приводить тут какие-то дополнительные пояснительные примеры, по-видимому, совершенно излишне.

Разумеется, если у бинарного оператора занять только одно свободное место, то получится унарный оператор. Особое значение имеют два следующих унарных оператора:

$0 + (…)$,
$0 — (…)$.

Это так называемые унарный плюс и унарный минус. Обычно при их написании опускают не только многоточие со скобками, но и стоящий слева ноль. В результате, по написанию они ничем не отличаются от бинарного плюса и бинарного минуса. К путанице это обычно не приводит, потому что сами по себе операторы всё равно бессмысленны и приобретают смысл только при наличии определенного окружения, а по этому окружению всегда можно догадаться, о чем, собственно, идет речь.

 

Например, когда мы говорим, что кузнечик сидит на ступеньке номер $-2$, мы имеем дело с унарным минусом, потому что $-2$ это на самом деле ${0 — 2}$. Это отражает тот факт, что номер ступеньки совпадает с командой, которую надо выполнить, чтобы переместиться на эту ступеньку с нулевого уровня.

 

Когда же мы говорим, что кузнечик прыгнул со ступеньки номер $3$ на две ступеньки вниз:

$3 — 2$,

речь идет, конечно, о бинарном минусе. Впрочем, это выражение можно записать и по-другому:

$3 + (-2)$.

Здесь снова на сцену выходит унарный минус, потому что более подробная запись выглядела бы так:

$3 + (0 — 2)$.

Возвращаясь к вопросу о том, какая разница между оператором $-~6$ и отрицательным числом $-6$, можно сказать, что, если уж делать между ними различие, то оператор — это

$(. ..) — 6$,

а число — это

$0 — 6$.

Кстати, машина по переработке чисел с помощью операторов существует в реальности и называется калькулятор. У всякого калькулятора есть кнопки, соответствующие бинарному плюсу, бинарному минусу и унарному минусу. Унарный плюс, впрочем, отсутствует за ненадобностью.

Конспект

1. Берем числовое выражение, заменяем в нем одно из чисел на многоточие, заключенное в скобки — то есть ${(…)}$ — и получаем унарный (или одноместный) оператор. Например, выражение ${3 + 2}$ можно превратить в оператор ${3 + (…)}$. На место многоточия $…$ мы можем теперь вписать любое другое число, например пятерку: ${3 + 5}$. Говорят, что мы подействовали оператором ${3 + (…)}$ на число $5$. Иначе говоря, оператор $3 + (…)$ перерабатывает число $5$ в число, равное ${3 + 5 = 8}$. Такая переработка называется операцией. Оператор может действовать не только на числа, но и на выражения. Например, если подействовать оператором ${3 + (. ..)}$ на выражение ${4 + 1}$, то получится ${3 + (4 + 1)}$.

2. Символы ${(…)}$ можно не писать, если и без того понятно, где они должны находиться. Например, вместо ${(…) — 6}$ достаточно написать ${-~6}$. Оператор ${-~6}$ фактически не отличается от отрицательного числа $-6$. Целые числа (иначе говоря: числа со знаками) можно представлять себе именно как разновидность операторов.

3. Пока мы не знаем, какое число поставить на место ${(…)}$, можно вписать туда какую-нибудь переменную. Например, вместо ${8 — (…)}$ написать ${8 — x}$. В результате получается функция от независимой переменной $x$. Впоследствии переменную $x$ можно будет заменить на какое-нибудь число или выражение, то есть сделать подстановку. Например, значение функции ${8 — x}$ при ${x = 4 — 1}$ с помощью подстановки находится так:

${8 — x = 8 — (4 — 1) = 8 — 3 = 5}$.

4. Если в числовом выражении заменить два числа на $(…)$, то получится бинарный (или двуместный) оператор. Примеры бинарных операторов:

${(…) + (…)}$, или сокращенно   $+$  (бинарный плюс)

${(…) — (…)}$, или сокращенно   $-$   (бинарный минус)

5. Помимо бинарного плюса и бинарного минуса, существуют также унарный плюс и унарный минус:

$0 + (…)$

$0 — (…)$

6. На практике запись операторов с ${(…)}$ не употребляется. Если простое стирание ${(…)}$ приводит к искажению смысла, то вместо операторов используются функции. В унарном плюсе и минусе опускается не только ${(…)}$, но и $0$. Действуя этими операторами на числа, мы пишем, например, $+2$ или $-3$.

Задачи

2.7.1. Подействовать оператором на данное выражение и вычислить результат. (Здесь и далее требуется вначале выполнить подстановку, а потом произвести вычисления.)

 

Оператор		Выражение
$22~-$		$10 + 2$
$-~8$		$14 + 13$
$1~+$		$41 — 2$
и т. п.

2.7.2. Подействовать оператором на данное выражение с параметром и упростить результат.

 

Оператор		Выражение
$38~-$		$a + 12$
$-~14$		$a — 13$
$12~+$		$11 — a$
и т.п.

2.7.3. Подействовать бинарным оператором на данные выражения и вычислить результат (первое выражение поставить слева, а второе — справа от оператора).

 

Оператор		Первое выражение		Второе выражение
$+$		$13 — 8$		$38 — 3$
$-$		$27 — 14$		$17 — 44$
$+~15~-$		$25 — 12$		$59 + 14$
и т. п.

2.7.4. Подействовать бинарным оператором на данные выражения c параметром и упростить результат (первое выражение поставить слева, а второе — справа от оператора).

 

Оператор		Первое выражение		Второе выражение
$+$		$a — 8$		$38 — 3$
$-$		$27 — 14$		$17 — a$
$+~1~-$		$a — 12$		$59 — a$
и т. п.

2.7.5. Вычислить значение функции при заданном значении переменной.

 

Функция		Значение переменной
$x + 10$		$x = 5$
$55 — x$		$x = 14$
$23 + (34 — x)$		$x = 18$
и т.п.

2.7.6. Выразить значение функции через параметр a при заданном значении переменной $x$.

 

Функция		Значение переменной
$x + 10$		$x = a − 5$
$55 − x$		$x = 14 − a$
$23 + (34 − x)$		$x = 18 − a$
и т. п.

2.7.7. Вычислить значение функции от двух переменных.

 

Функция		Значение переменных
$x + y$		$x = 15, ~y = 62$
$x — (5 — y)$		$x = 90, ~y = 20$
$(90 — x) — (45 — y)$		$x = 16, ~y = 10$
и т.п.

2.7.8. Выразить значение функции через параметр a при заданном значении переменных $x$ и $y$.

 

Функция		Значение переменных
$x + y$		$x = 12 — a, ~y = 14$
$x — (38 — y)$		$x = 55, ~y = 20 + a$
$(62 — x) — (29 + y)$		$x = 1 + a, ~y = 11$
и т. п.

Из «бесконечного» сборника типовых упражнений

Подбор операторов («+» или «−») в примерах в два действия

 

Базовые математические операторы

Введение

Python имеет общие математические операции в своем распоряжении, включая целочисленное деление, деление с плавающей точкой, умножение, возведение в степень, сложение и вычитание. Математический модуль (включен во все стандартные версии Python) предлагает расширенную функциональность как тригонометрические функции, извлечение корня, логарифмы и многое другое.

Сложение в Python

a, b = 1, 2
# Используется "+" оператор:
a + b                  # = 3
# Используется "+=" оператор для сложения и назначения:
a += b                 # a = 3 (эквивалентно a = a + b)
import operator        # поддерживает 2 аргумента арифметических функций для примеров
operator.add(a, b)     # = 5  since a is set to 3 right before this line
# Оператор "+=" эквивалентен: 
a = operator. iadd(a, b)    # a = 5 since a is set to 3 right before this line

Возможные комбинации (встроенные типы):

• int и int (дает int )
• int и float (дает float )
• int и complex (дает complex )
• float и float (дает float )
• float и complex (дает complex )
• complex и complex (дает complex )

Примечание: + оператор также используется для конкатенации строк, списков и кортежей:

"first string " + "second string"
>>>Out: 'first string second string'
[1, 2, 3] + [4, 5, 6]                # = [1, 2, 3, 4, 5, 6]
>>>Out: [1, 2, 3, 4, 5, 6]

Вычитание в python

a, b = 1, 2
# для вычитания используется "-" оператор:
b - a
>>>Out: 1
import operator        # поддерживает 2 аргумента арифметических функций
operator. sub(b, a)
>>>Out: 1
 

Возможные комбинации (встроенные типы):

• int и int (дает int )
• int и float (дает float )
• int и complex (дает complex )
• float и float (дает float )
• float и complex (дает complex )
• complex и complex (дает complex )

умножение в python

 a, b = 2, 3
a * b                  
>>>Out: 6
import operator
operator.mul(a, b)     
>>>Out: 6

Возможные комбинации (встроенные типы):

• int и int (дает int )
• int и float (дает float )
• int и complex (дает complex )
• float и float (дает float )
• float и complex (дает complex )
• complex и complex (дает complex )

Примечание: * оператор также используется для повторной конкатенации строк, списков и кортежей:

 3 * 'ab'  # = 'ababab'
3 *('a', 'b')  # =('a', 'b', 'a', 'b', 'a', 'b') 

Деление

Python выполняет целочисленное деление, когда оба операнда являются целыми числами. Поведение операторов деления Python изменились с 2.x и 3.x Python.

 a, b, c, d, e = 3, 2, 2.0, -3, 10
 

В Python 2 результат оператора / зависит от типа числителя и знаменателя. a / b # = 1
a / c # = 1,5
d / b # = -2
b / a # = 0
d / e # = -1

Обратите внимание, что поскольку a и b являются int, то результат является int. Результат всегда округляется до нуля. Поскольку c является float, результатом a / c является float. Вы также можете использовать модуль оператора: оператор #. Модуль оператора предоставляет арифметические функции с двумя аргументами operator.div (a, b) # = 1 оператор .__ div __ (a, b) # = 1

Что делать, если вы хотите разделить поплавки:

Рекомендуемые:

 from __future__ import division # applies Python 3 style division to the entire module
a / b                  # = 1.5 
a // b                 # = 1
 

Хорошо (если вы не хотите применять ко всему модулю):

 a / (b * 1. 0)          # = 1.5
1.0 * a / b            # = 1.5
a / b * 1.0            # = 1.0    (careful with order of operations)
from operator import truediv
truediv(a, b)          # = 1.5
 

Не рекомендуется (может вызывать TypeError, например, если аргумент сложный):

 float(a) / b           # = 1.5
a / float(b)           # = 1.5
 

Оператор «//» в Python 2 вызывает разделение по этажам независимо от типа. a // b # = 1 a // c # = 1.0

В Python 3, / оператор выполняет «истинные» разделения независимо от типа. // оператор выполняет вольные деление и поддерживает тип.

 a / b                  # = 1.5 
e / b                  # = 5.0
a // b                 # = 1
a // c                 # = 1.0
import operator            # the operator module provides 2-argument arithmetic functions
operator.truediv(a, b)     # = 1.5
operator.floordiv(a, b)    # = 1
operator.floordiv(a, c)    # = 1.0
 

Возможные комбинации (встроенные типы):

• int и int (дает int в Python 2 и float в Python 3)
• int и float (дает float )
• int и complex (дает complex )
• float и float (дает float )
• float и complex (дает complex )
• complex и complex (дает complex )

См PEP 238 для получения дополнительной информации.

возведения

 a, b = 2, 3
(a ** b)               # = 8
pow(a, b)              # = 8
import math
math.pow(a, b)         # = 8.0 (always float; does not allow complex results)
import operator
operator.pow(a, b)     # = 8
 

Еще одно различия между встроенным pow и math.pow является то , что встроенный pow может принимать три аргумента:

 a, b, c = 2, 3, 2
pow(2, 3, 2)           # 0, calculates (2 ** 3) % 2, but as per Python docs,
                       #    does so more efficiently
 

Специальные функции

Функция math.sqrt(x) вычисляет квадратный корень из x .

 import math
import cmath
c = 4
math.sqrt(c)           # = 2.0 (always float; does not allow complex results)
cmath.sqrt(c)          # = (2+0j) (always complex)
 

Чтобы вычислить другие корни, такие как кубический корень, увеличьте число до величины, обратной степени корня. Это может быть сделано с любой из показательных функций или оператора.

  import math
 x = 8
 math.pow(x, 1/3) # evaluates to 2.0
 x**(1/3) # evaluates to 2.0
 

Функция math.exp(x) вычисляет e ** x .

 math.exp(0)  # 1.0
math.exp(1)  # 2.718281828459045 (e)
 

Функция math.expm1(x) вычисляет e ** x - 1.Когда x мала, то это дает значительно лучшую точность , чем math.exp(x) - 1 .

 math.expm1(0)       # 0.0
math.exp(1e-6) - 1  # 1.0000004999621837e-06
math.expm1(1e-6)    # 1.0000005000001665e-06
# exact result      # 1.000000500000166666708333341666... 

Логарифмы

По умолчанию math.log функция вычисляет логарифм числа, по основанию е. Вы можете при желании указать базу в качестве второго аргумента.

 import math
import cmath
math.log(5)         # = 1.6094379124341003
# optional base argument. Default is math.e
math.log(5, math.e) # = 1.6094379124341003
cmath.log(5)        # = (1.6094379124341003+0j)
math.log(1000, 10)   # 3. 0 (always returns float)
cmath.log(1000, 10)  # (3+0j)
 

Специальные вариации math.log функции существуют для различных оснований.

 # Logarithm base e - 1 (higher precision for low values)
math.log1p(5)       # = 1.791759469228055
# Logarithm base 2
math.log2(8)        # = 3.0
# Logarithm base 10
math.log10(100)     # = 2.0
cmath.log10(100)    # = (2+0j) 

Операции на месте

В приложениях обычно требуется такой код:

 a = a + 1
 

или же

 a = a * 2
 

Для этих операций на месте есть эффективный ярлык:

 a += 1
# and
a *= 2
 

Любой математический оператор может использоваться перед символом ‘=’для выполнения операции на месте:

• -= декремент переменной в месте
• += Приращение переменной в месте
• *= Умножить переменную на месте
• /= Разделить переменную на месте
• //= пол разделить переменную на месте # Python 3
• %= Возвращают модуль переменной вместо
• **= поднять на мощность в месте

Другие в месте операторов существуют для поразрядных операторов ( ^ , | и т. д.)

Тригонометрические функции

 a, b = 1, 2
import math
math.sin(a)  # returns the sine of 'a' in radians
# Out: 0.8414709848078965
math.cosh(b)  # returns the inverse hyperbolic cosine of 'b' in radians
# Out: 3.7621956910836314
math.atan(math.pi)  # returns the arc tangent of 'pi' in radians
# Out: 1.2626272556789115
math.hypot(a, b) # returns the Euclidean norm, same as math.sqrt(a*a + b*b)
# Out: 2.23606797749979
 

Обратите внимание , что math.hypot(x, y) также длина вектора (или евклидово расстояние) от начала координат (0, 0) до точки (x, y) .

Для вычисления евклидова расстояния между двумя точками (x1, y1) и (x2, y2) можно использовать math.hypot следующих

 math.hypot(x2-x1, y2-y1) 

Для преобразования из радиана -> степеней и степеней -> радиан соответственно использовать math.degrees и math.radians

 math.degrees(a)
# Out: 57. 29577951308232
math.radians(57.29577951308232)
# Out: 1.0 

модуль

Как и во многих других языках, Python использует % оператор для вычисления модуля.

 3 % 4     # 3
10 % 2    # 0
6 % 4     # 2
 

Или с помощью operator модуля:

 import operator
operator.mod(3 , 4)     # 3
operator.mod(10 , 2)    # 0
operator.mod(6 , 4)     # 2
 

Вы также можете использовать отрицательные числа.

 -9 % 7     # 5
9 % -7     # -5
-9 % -7    # -2
 

Если вам необходимо найти результат целочисленного деления и модуля, вы можете использовать divmod функцию в качестве ярлыка:

quotient, remainder = divmod(9, 4)
# quotient = 2, remainder = 1 as 4 * 2 + 1 == 9

Синтаксис

Параметры

Примечания

Математические операторы

Операторы

• Арифметика
• Алгебра
• Линейная алгебра
• Исчисление
• Булева логика
• Набор

Математические операторы определяют основные операции, которые воздействуют на числа и другие математические конструкции.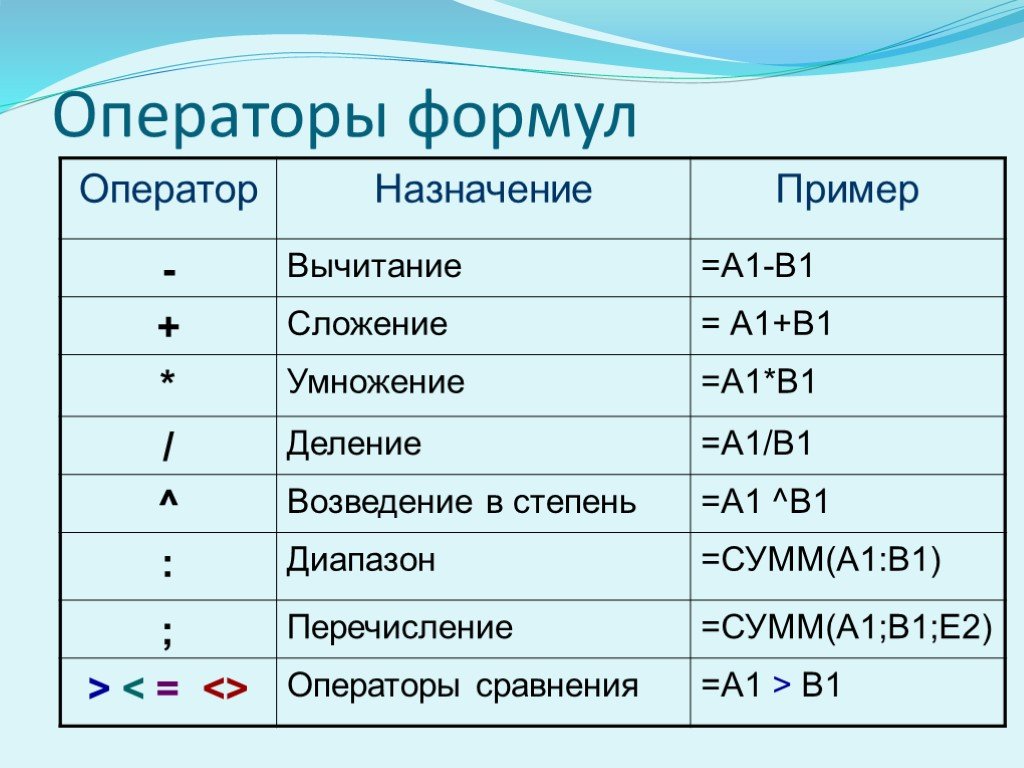 Обычно операторы принимают от одного до двух чисел на вход и возвращают число на выходе. Таким образом, два математика, чтобы получить один и тот же результат при заданном выражении, определяют порядок операций, чтобы результат был однозначным.

Арифметика

Основными арифметическими операциями являются сложение, вычитание, умножение и деление. Представленные в элементарной математике, они описывают способы манипулирования числами. По мере того, как понятие числа становится более сложным, их определения расширяются за пределы дискретных чисел, и вводятся свойства, чтобы сделать концепцию числа и операций более связной. Например, в алгебре операторы расширены для работы с дробями и частичными числами.

Оператор сложения

Сложение — это основная операция в математике для объединения двух чисел. Это бинарная операция, обозначаемая знаком плюс с выражением слева и выражением справа.

Оператор вычитания

Вычитание — это основная арифметическая операция вычитания одного числа из другого числа.

Оператор умножения

Умножение — это основная арифметическая операция, выполняемая над двумя числами. Умножение числа на другое число равносильно взятию n групп другого числа.

Оператор деления

Оператор деления возвращает результат деления одного числа на другое число.

Алгебра

Эти продвинутые операторы охватывают некоторые более сложные закономерности, встречающиеся в математике. Например, оператор факториала представляет шаблоны, найденные в комбинациях и перестановках. Другим примером являются операторы экспоненты и логарифма, которые описывают экспоненциальный рост и затухание.

Оператор абсолютного значения

Оператор абсолютного значения возвращает расстояние от нуля в числовой строке числа.

Оператор квадратного корня

Возвращает квадратный корень предоставленного выражения.

Радикальный оператор

Радикальный оператор возвращает n-й корень заданного выражения. Радикальный оператор — это альтернативный способ записи дробного показателя.

Оператор возведения в степень

Оператор возведения в степень является бинарным оператором. Основание — это выражение или число, которое возводится в некоторый показатель степени. Выражение экспоненты обозначается надстрочным текстом.

Оператор логарифмирования

Логарифмирование числа является операцией, обратной возведению в степень. Число нижнего индекса является основанием логарифма, а выражение является операндом.

Оператор факториала

Оператор факториала обозначается восклицательным знаком. Оператор является унарным, что означает, что он работает только с одним выражением. Оператор полезен при расчете комбинаций и перестановок.

Оператор модуля

Оператор модуля возвращает остаток от деления первого выражения на второе выражение.

Оператор суммирования

Оператор суммирования представлен символом Σ (заглавная сигма) и представляет собой операцию суммирования последовательности выражений вместе. Оператор используется в математике для представления последовательности и ряда.

Оператор произведения

Оператор произведения представлен символом Π (заглавная пи) и используется для представления операции умножения последовательности выражений вместе.

Линейная алгебра

Оператор перекрестного произведения

Перекрестное произведение работает с двумя векторами и в результате дает другой вектор.

Оператор величины

Величина векторного оператора, обозначенная двумя вертикальными линиями по обе стороны от выражения, возвращает длину вектора.

Оператор скалярного произведения

Скалярное произведение принимает на вход два вектора и производит число на выходе.

Оператор умножения матриц

Умножение матриц объединяет две матрицы для создания третьей матричной функции.

Оператор транспонирования матрицы

Транспонирование матрицы — это оператор, который отображает матрицу по ее диагонали.

Оператор определителя матрицы

Оператор определителя вычисляет скалярное значение из квадратной матрицы.

Исчисление

Обозначение лимита

Синтаксис для лимита — это аббревиатура «lim», следующая за выражением. Под буквами «lim» указано значение, к которому приближается переменная в выражении, обозначаемом как переменная со стрелкой, указывающей значение, к которому она приближается.

Интегральный оператор

Интеграл можно геометрически интерпретировать как площадь под кривой функции между двумя точками a и b. Интегралы являются основным оператором исчисления и используются в физике и математике более высокого уровня.

Оператор производной

Производная функции по переменной возвращает функцию, представляющую изменение функции во времени.

Оператор градиента

Оператор градиента возвращает вектор, представляющий изменение функции в точке. Оператор подобен производному оператору исчисления, с той разницей, что он работает с функциями более высоких размерностей.

Булева логика

Операторы логической логики работают с логическими выражениями — значениями, которые либо истинны, либо ложны. Обычно бинарные логические операторы принимают два логических значения и в результате возвращают логическое значение. При вычислениях числа и более сложные данные можно сравнивать с данными того же типа для проверки лексикографического порядка (меньше, больше) и равенства для получения логического значения.

Логический оператор «И»

Логический оператор «и» возвращает значение «истина», если и левое выражение, и левое выражение имеют значение «истина», в противном случае оператор возвращает значение «ложь».

Логический оператор «ИЛИ»

Логический оператор «или» возвращает значение «истина», если либо левое выражение оценивается как «истина», либо правостороннее выражение оценивается как «истина», в противном случае возвращает значение «ложь».

Логический оператор исключающего ИЛИ

Логический оператор исключающего ИЛИ (сокращенно xor) возвращает истину, если левая сторона оценивается как истина, а правая — как ложь. Оператор также возвращает значение true, если левая сторона оценивается как false, а правая — как true. В противном случае возвращает ложь.

Логический оператор импликации

Логический оператор импликации возвращает истину, если левое и правое выражения оцениваются как истинные или если левое выражение ложно.

Обозначение отрицания

Символ отрицания используется для представления унарного оператора отрицания, который инвертирует значение выражения, к которому он применяется.

Обозначение «меньше чем»

Символ < представляет логическое выражение, согласно которому левая часть меньше правой.

Обозначение «больше чем»

Символ > представляет логическое выражение, согласно которому левая часть больше правой.

Обозначение равенства

Две сложенные горизонтальные линии представляют символ равенства в математике. Два выражения с обеих сторон равны или одинаковы, если между ними поставить знак равенства.

Комплект

Операторы множеств — это бинарные операторы, используемые в теории множеств для работы с множествами.

Union Operator

Установленная операция объединения обозначается символом чашки. Объединение двух наборов возвращает объединенные элементы обоих наборов. Дубликаты игнорируются.

Оператор пересечения

Оператор пересечения множества возвращает общие элементы между двумя множествами. Оператор обозначается заглавной буквой.

Обозначение разности множеств

Символ минус используется в теории множеств для представления оператора разности двух множеств. Операция удаляет все элементы, найденные в одном наборе, из другого и возвращает результирующий набор.

Обозначение подмножества

Оператор подмножества обозначается U-образным символом, повернутым на девяносто градусов вправо с горизонтальной линией под ним.

Обозначение надмножества

Оператор надмножества в теории множеств обозначается с помощью символа надмножества, который выглядит как U, повернутый на девяносто градусов против часовой стрелки, с горизонтальной линией под ним.

Обозначение подмножества

Правильное подмножество обозначается символом ⊂

Правильное обозначение супермножества

Правильный надмножество обозначается символом надмножества, который выглядит как буква U, повернутая на девяносто градусов влево.

Элемент обозначения

Элемент обозначения описывает принадлежность к множеству. При чтении уравнения символ может быть прочитан как «в» или «принадлежит».

Ссылки

© 2022 Kurt Bruns

Оператор

| математика и логика

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• В этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Самые популярные вопросы
• Обзор недели
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.

• Студенческий портал
  Britannica — это лучший ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.