Статистические функции в Excel
Статистическая обработка данных – это сбор, упорядочивание, обобщение и анализ информации с возможностью определения тенденции и прогноза по изучаемому явлению. В Excel есть огромное количество инструментов, которые помогают проводить исследования в данной области. Последние версии этой программы в плане возможностей практически ничем не уступают специализированным приложениям в области статистики. Главными инструментами для выполнения расчетов и анализа являются функции. Давайте изучим общие особенности работы с ними, а также подробнее остановимся на отдельных наиболее полезных инструментах.
Статистические функции
Как и любые другие функции в Экселе, статистические функции оперируют аргументами, которые могут иметь вид постоянных чисел, ссылок на ячейки или массивы.
Выражения можно вводить вручную в определенную ячейку или в строку формул, если хорошо знать синтаксис конкретного из них. Но намного удобнее воспользоваться специальным окном аргументов, которое содержит подсказки и уже готовые поля для ввода данных.
Запустить Мастер функций можно тремя способами:
- Кликнуть по пиктограмме «Вставить функцию» слева от строки формул.
- Находясь во вкладке «Формулы», кликнуть на ленте по кнопке «Вставить функцию» в блоке инструментов «Библиотека функций».
- Набрать на клавиатуре сочетание клавиш Shift+F3.
При выполнении любого из вышеперечисленных вариантов откроется окно «Мастера функций».
Затем нужно кликнуть по полю «Категория» и выбрать значение «Статистические».
После этого откроется список статистических выражений. Всего их насчитывается более сотни. Чтобы перейти в окно аргументов любого из них, нужно просто выделить его и нажать на кнопку «OK».
Для того, чтобы перейти к нужным нам элементам через ленту, перемещаемся во вкладку «Формулы». В группе инструментов на ленте «Библиотека функций» кликаем по кнопке «Другие функции». В открывшемся списке выбираем категорию «Статистические». Откроется перечень доступных элементов нужной нам направленности. Для перехода в окно аргументов достаточно кликнуть по одному из них.
В группе инструментов на ленте «Библиотека функций» кликаем по кнопке «Другие функции». В открывшемся списке выбираем категорию «Статистические». Откроется перечень доступных элементов нужной нам направленности. Для перехода в окно аргументов достаточно кликнуть по одному из них.
Урок: Мастер функций в Excel
МАКС
Оператор МАКС предназначен для определения максимального числа из выборки. Он имеет следующий синтаксис:
=МАКС(число1;число2;…)
В поля аргументов нужно ввести диапазоны ячеек, в которых находится числовой ряд. Наибольшее число из него эта формула выводит в ту ячейку, в которой находится сама.
МИН
По названию функции МИН понятно, что её задачи прямо противоположны предыдущей формуле – она ищет из множества чисел наименьшее и выводит его в заданную ячейку. Имеет такой синтаксис:
=МИН(число1;число2;…)
СРЗНАЧ
Функция СРЗНАЧ ищет число в указанном диапазоне, которое ближе всего находится к среднему арифметическому значению.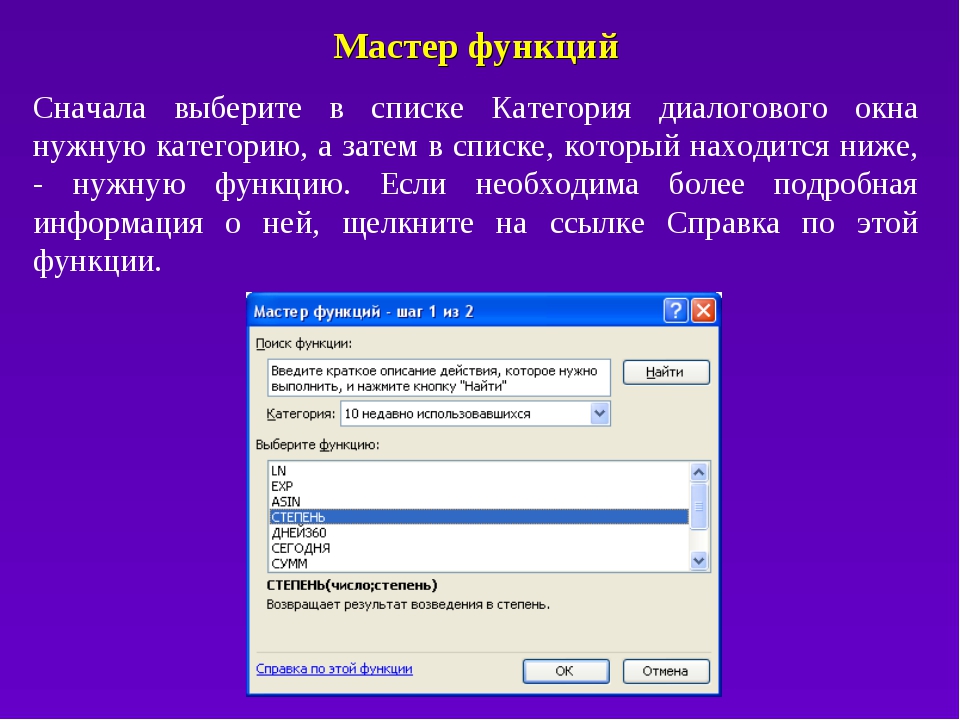 Результат этого расчета выводится в отдельную ячейку, в которой и содержится формула. Шаблон у неё следующий:
Результат этого расчета выводится в отдельную ячейку, в которой и содержится формула. Шаблон у неё следующий:
=СРЗНАЧ(число1;число2;…)
СРЗНАЧЕСЛИ
Функция СРЗНАЧЕСЛИ имеет те же задачи, что и предыдущая, но в ней существует возможность задать дополнительное условие. Например, больше, меньше, не равно определенному числу. Оно задается в отдельном поле для аргумента. Кроме того, в качестве необязательного аргумента может быть добавлен диапазон усреднения. Синтаксис следующий:
=СРЗНАЧЕСЛИ(число1;число2;…;условие;[диапазон_усреднения])
МОДА.ОДН
Формула МОДА.ОДН выводит в ячейку то число из набора, которое встречается чаще всего. В старых версиях Эксель существовала функция МОДА, но в более поздних она была разбита на две: МОДА.ОДН (для отдельных чисел) и МОДА.НСК(для массивов). Впрочем, старый вариант тоже остался в отдельной группе, в которой собраны элементы из прошлых версий программы для обеспечения совместимости документов.
=МОДА.ОДН(число1;число2;…)
=МОДА.НСК(число1;число2;…)
МЕДИАНА
Оператор МЕДИАНА определяет среднее значение в диапазоне чисел. То есть, устанавливает не среднее арифметическое, а просто среднюю величину между наибольшим и наименьшим числом области значений. Синтаксис выглядит так:
=МЕДИАНА(число1;число2;…)
СТАНДОТКЛОН
=СТАНДОТКЛОН.В(число1;число2;…)
=СТАНДОТКЛОН.Г(число1;число2;…)
Урок: Формула среднего квадратичного отклонения в Excel
НАИБОЛЬШИЙ
Данный оператор показывает в выбранной ячейке указанное в порядке убывания число из совокупности. То есть, если мы имеем совокупность 12,97,89,65, а аргументом позиции укажем 3, то функция в ячейку вернет третье по величине число. В данном случае, это 65. Синтаксис оператора такой:
То есть, если мы имеем совокупность 12,97,89,65, а аргументом позиции укажем 3, то функция в ячейку вернет третье по величине число. В данном случае, это 65. Синтаксис оператора такой:
=НАИБОЛЬШИЙ(массив;k)
В данном случае, k — это порядковый номер величины.
НАИМЕНЬШИЙ
Данная функция является зеркальным отражением предыдущего оператора. В ней также вторым аргументом является порядковый номер числа. Вот только в данном случае порядок считается от меньшего. Синтаксис такой:
=НАИМЕНЬШИЙ(массив;k)
РАНГ.СР
Эта функция имеет действие, обратное предыдущим. В указанную ячейку она выдает порядковый номер конкретного числа в выборке по условию, которое указано в отдельном аргументе. Это может быть порядок по возрастанию или по убыванию. Последний установлен по умолчанию, если поле «Порядок» оставить пустым или поставить туда цифру 0. Синтаксис этого выражения выглядит следующим образом:
=РАНГ.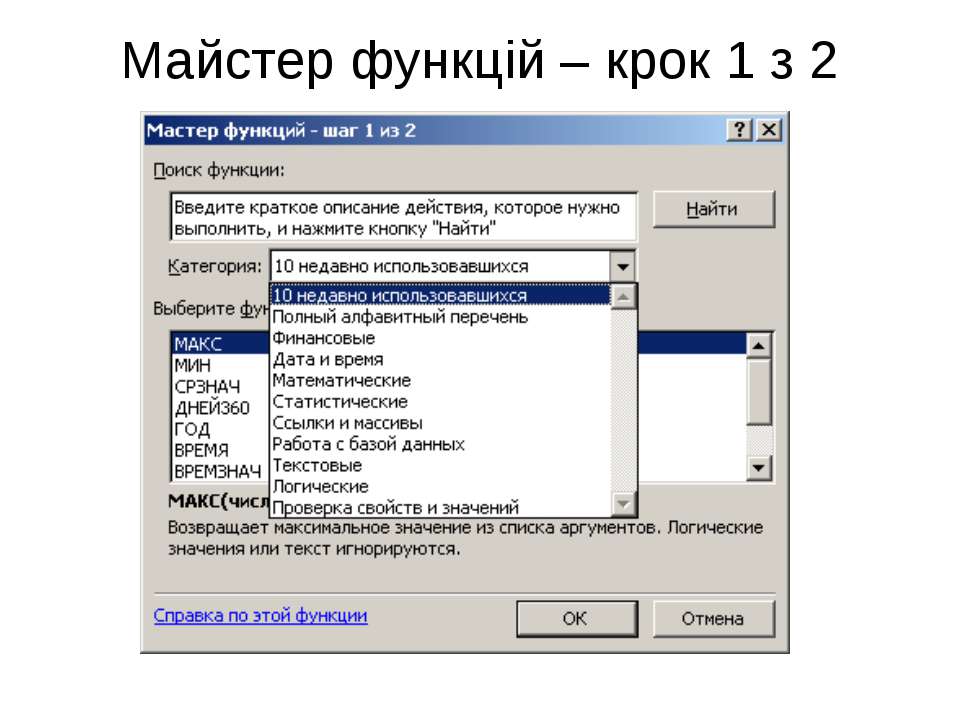 СР(число;массив;порядок)
СР(число;массив;порядок)
Выше были описаны только самые популярные и востребованные статистические функции в Экселе. На самом деле их в разы больше. Тем не менее, основной принцип действий у них похожий: обработка массива данных и возврат в указанную ячейку результата вычислительных действий.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТМатематические функции в Excel: подробное описание
Чаще всего среди доступных групп функций пользователи Экселя обращаются к математическим. С помощью них можно производить различные арифметические и алгебраические действия. Их часто используют при планировании и научных вычислениях. Узнаем, что представляет собой данная группа операторов в целом, и более подробно остановимся на самых популярных из них.
Применение математических функций
С помощью математических функций можно проводить различные расчеты. Они будут полезны студентам и школьникам, инженерам, ученым, бухгалтерам, планировщикам. В эту группу входят около 80 операторов. Мы же подробно остановимся на десяти самых популярных из них.
Они будут полезны студентам и школьникам, инженерам, ученым, бухгалтерам, планировщикам. В эту группу входят около 80 операторов. Мы же подробно остановимся на десяти самых популярных из них.
Открыть список математических формул можно несколькими путями. Проще всего запустить Мастер функций, нажав на кнопку «Вставить функцию», которая размещена слева от строки формул. При этом нужно предварительно выделить ячейку, куда будет выводиться результат обработки данных. Этот метод хорош тем, что его можно реализовать, находясь в любой вкладке.
Также можно запустить Мастер функций, перейдя во вкладку «Формулы». Там нужно нажать на кнопку «Вставить функцию», расположенную на самом левом краю ленты в блоке инструментов «Библиотека функций».
Существует и третий способ активации Мастера функций. Он осуществляется с помощью нажатия комбинации клавиш на клавиатуре Shift+F3.
После того, как пользователь произвел любое из вышеуказанных действий, открывается Мастер функций.
Открывается выпадающий список. Выбираем в нем позицию «Математические».
После этого в окне появляется список всех математических функций в Excel. Чтобы перейти к введению аргументов, выделяем конкретную из них и жмем на кнопку «OK».
Существует также способ выбора конкретного математического оператора без открытия главного окна Мастера функций. Для этого переходим в уже знакомую для нас вкладку «Формулы» и жмем на кнопку «Математические», расположенную на ленте в группе инструментов «Библиотека функций». Открывается список, из которого нужно выбрать требуемую формулу для решения конкретной задачи, после чего откроется окно её аргументов.
Правда, нужно заметить, что в этом списке представлены не все формулы математической группы, хотя и большинство из них. Если вы не найдете нужного оператора, то следует кликнуть по пункту «Вставить функцию…» в самом низу списка, после чего откроется уже знакомый нам Мастер функций.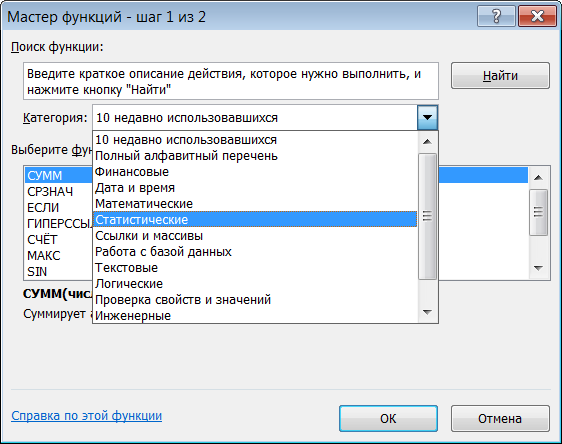
Урок: Мастер функций в Excel
СУММ
Наиболее часто используется функция СУММ. Этот оператор предназначен для сложения данных в нескольких ячейках. Хотя его можно использовать и для обычного суммирования чисел. Синтаксис, который можно применять при ручном вводе, выглядит следующим образом:
=СУММ(число1;число2;…)
В окне аргументов в поля следует вводить ссылки на ячейки с данными или на диапазоны. Оператор складывает содержимое и выводит общую сумму в отдельную ячейку.
Урок: Как посчитать сумму в Экселе
СУММЕСЛИ
Оператор СУММЕСЛИ также подсчитывает общую сумму чисел в ячейках. Но, в отличие от предыдущей функции, в данном операторе можно задать условие, которое будет определять, какие именно значения участвуют в расчете, а какие нет. При указании условия можно использовать знаки «>» («больше»), «<» («меньше»), «< >» («не равно»).
=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)
ОКРУГЛ
Как можно понять из названия функции ОКРУГЛ, служит она для округления чисел. Первым аргументом данного оператора является число или ссылка на ячейку, в которой содержится числовой элемент. В отличие от большинства других функций, у этой диапазон значением выступать не может. Вторым аргументом является количество десятичных знаков, до которых нужно произвести округление. Округления проводится по общематематическим правилам, то есть, к ближайшему по модулю числу. Синтаксис у этой формулы такой:
=ОКРУГЛ(число;число_разрядов)
Кроме того, в Экселе существуют такие функции, как ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые соответственно округляют числа до ближайшего большего и меньшего по модулю.
Урок: Округление чисел в Excel
ПРОИЗВЕД
Задачей оператора ПРИЗВЕД является умножение отдельных чисел или тех, которые расположены в ячейках листа. Аргументами этой функции являются ссылки на ячейки, в которых содержатся данные для перемножения. Всего может быть использовано до 255 таких ссылок. Результат умножения выводится в отдельную ячейку. Синтаксис данного оператора выглядит так:
=ПРОИЗВЕД(число;число;…)
Урок: Как правильно умножать в Excel
ABS
С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:
=ABS(число)
Урок: Функция модуля в Excel
СТЕПЕНЬ
Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:
У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:
=СТЕПЕНЬ(число;степень)
Урок: Как возводить в степень в Экселе
КОРЕНЬ
Задачей функции КОРЕНЬ является извлечение квадратного корня. Данный оператор имеет только один аргумент – «Число». В его роли может выступать ссылка на ячейку, содержащую данные. Синтаксис принимает такую форму:
=КОРЕНЬ(число)
Урок: Как посчитать корень в Экселе
СЛУЧМЕЖДУ
Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:
Синтаксис у него такой:
=СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница)
ЧАСТНОЕ
Оператор ЧАСТНОЕ применяется для деления чисел. Но в результатах деления он выводит только четное число, округленное к меньшему по модулю. Аргументами этой формулы являются ссылки на ячейки, содержащие делимое и делитель. Синтаксис следующий:
=ЧАСТНОЕ(Числитель;Знаменатель)
Урок: Формула деления в Экселе
РИМСКОЕ
Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:
=РИМСКОЕ(Число;Форма)
Выше были описаны только наиболее популярные математические функции Эксель. Они помогают в значительной мере упростить различные вычисления в данной программе. При помощи этих формул можно выполнять как простейшие арифметические действия, так и более сложные вычисления.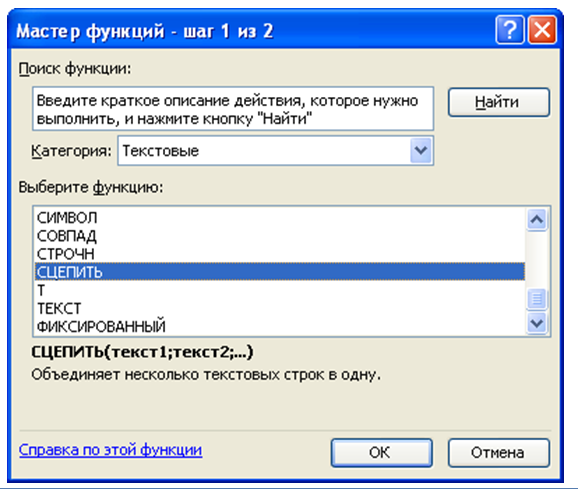 Особенно они помогают в тех случаях, когда нужно производить массовые расчеты.
Особенно они помогают в тех случаях, когда нужно производить массовые расчеты.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТМастер функций — Энциклопедия по экономике
Для включения в формулу встроенной функции используется Мастер функций, который вызывается различным образом [c.376]Нажать кнопку fx для вызова Мастера функций. [c.379]
Иного способа вставки вложенной встроенной функции нет. Если функция отсутствует в списке, выбирается Другие функции…, выводится окно Мастера функций для выбора категории и функции. [c.379]
| Рис. 1.1. Диалоговое окно Мастер функций |
Рис.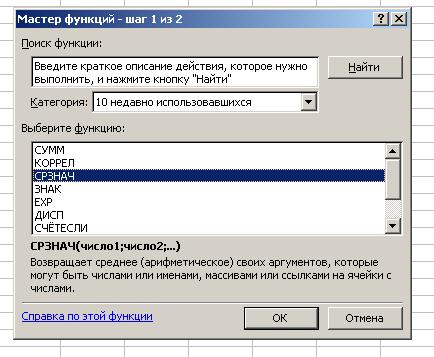 1.3. Ввод формулы для расчета ЦФ в окно «Мастер функций» 1.3. Ввод формулы для расчета ЦФ в окно «Мастер функций»
|
Знак вставлен перед ячейкой А31 для того, чтобы она не изменялась при копировании. Удобнее первую часть этой формулы получить командой в меню , а остальные члены добавить при редактировании формулы. Полученную формулу надо из ячейки В34 скопировать в остальные ячейки С34—Н34. Последующие операции вращения симплекса придется повторять много раз подряд, пока не будут получены приемлемые результаты. [c.70]
При анализе структуры затрат рабочего времени было установлено, что с развитием бригадной организации труда прослеживается тенденция к увеличению удельного веса затрат на выполнение свойственных мастеру функций и соответствующему снижению удельного веса но свойственных ему функций (см. табл. 19).
[c.213]
табл. 19).
[c.213]
Если щелкнуть на кнопке со значком fx, на экран поступит диалоговое окно Мастера функций (рис. 11.13), рассмотренное в п. 11.9.1. Вы можете ввести функцию. [c.157]
Ввод функций. Вместо того, чтобы набирать функции вручную, можно щелкнуть на кнопке со значком fx в панели инструментов Стандартная (рис. 11.2, (4)), — на экране появится диалоговое окно Мастера функций. С его помощью можно ввести и отредактировать любую функцию (см. п.11.9.1). [c.165]
Что такое Мастер функций [c.172]
В этом окне вы можете ввести аргумент (аргументы) функций. В правом верхнем углу в поле Значение отображается значение функции при набранных аргументах (на рисунке — sin(3.141). Поскольку аргументом может быть другая функция, вам предоставляется возможность вызвать вложенный Мастер функций (кнопка fx). [c.178]
Назовите два способа вызова на экран Мастера функций. [c.186]
Далее определим коэффициент корреляции с помощью Мастера функций. Вначале выполним расчет для соотношения Количество пойманных мышей — средняя дневная температура .
[c.20]
Вначале выполним расчет для соотношения Количество пойманных мышей — средняя дневная температура .
[c.20]
| Рис.4. Диалоговое окно Мастер функций |
Для вставки функции выполняем команду Вставка > Функция и в открывшемся окне мастера функций в раскрывающемся списке Категория выбираем [c.46]
Статистические функции (80 функций), вызываются через окно Мастер функций. [c.101]
Диспетчерские группы производств и цехов возглавляет заместитель начальника производства или цеха, который в соответствии с этим выполняет функции старшего диспетчера. Работа по оперативному контролю и регулированию хода производственного процесса непосредственно в каждом цехе возложена на начальников смен и сменных мастеров. В крупных производствах помимо этого создается служба сменных диспетчеров.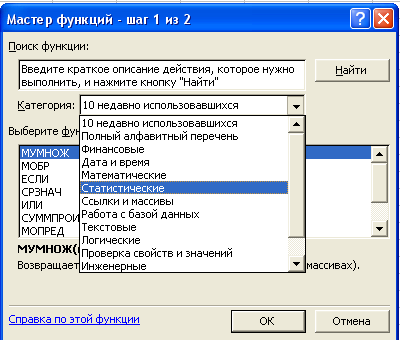 [c.201]
[c.201]
Специализированные подразделения или отдельные технологи могут территориально размещаться непосредственно в цехах предприятия и административно подчиняться руководителю цеха. В этом случае они именуются цеховыми, их функциями являются оказание повседневной технической помощи мастерам, рабочим, решение оперативных технических вопросов в цехе и обеспечение связи с отделом главного технолога и другими службами. [c.6]
Мастера занимают высокое положение в западногерманском обществе, обладая весомым престижем. Им предоставлены особые привилегии, а в больших фирмах они часто становятся начальниками участков и цехов. Их функции охватывают обучение других рабочих, наблюдение за процессом производства и контроль качества. Поэтому они не столь уж редко оказываются в жесткой оппозиции к указаниям руководителей производственных отделений. При переходе из категории ученика в категорию мастера заработная плата увеличивается чуть ли не вдвое. Если мастера не удовлетворены положением дел в фирме, то могут быстро найти новую работу.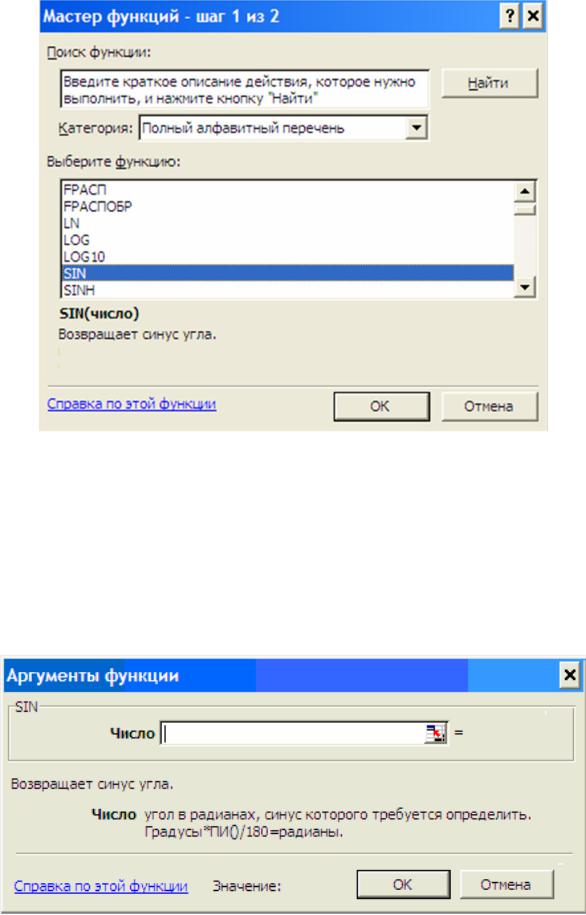 [c.97]
[c.97]
Каждая группа работает под началом лидера. В большинстве случаев это мастер или бригадир (в первые годы движения за качество лидерами становились преимущественно рядовые работники). Он не наделен диктаторскими полномочиями и организует деятельность участников группы на основе общего согласия. Лидер, в частности, выполняет функцию направляющего дискуссию. В ряде случаев ему помогает инструктор, который ведет журнал заседаний и следит за выполнением программ тренировки. Если на предприятии возникает достаточно большое количество групп, то выбирается координатор, основной задачей которого является осуществление связи одних групп с другими, с советом групп качества при фирме, с администрацией. [c.131]
Константы и знаки операций при построении вычисляемых выражений вводятся вручную, ссылки на ячейки или диапазоны ячеек формируются с помощью курсорного путевождения. Для этого нажимается правая кнопка ( красная кнопка), находящаяся справа от поля ввода. После нажатия красной кнопки диалоговое окно Мастера функций скрывается, на экран выводится окно построителя выражения. При выводе окна построителя выражения можно
[c.377]
При выводе окна построителя выражения можно
[c.377]
Для заданного вам вида фруктов (товаров), используя средства электронной таблицы, составьте формулы и рассчитайте (в строках 10— 22таблицы) расходы и другие параметры, приведенные выше в списке условных обозначений, строго соблюдая их последовательность. При расчетах по кредиту и оплате хранения фруктов неполные сутки рассматриваются как полные. Поэтому нужно подсчитать округленное число суток, используя окно и команду . В строке 10 получится округленное значение времени продаж для каждого вида фруктов, а в ячейку НО надо записать выбранное с помощью команды максимальное время продажи (в сутках). При расчете затрат на перевозку не забудьте, что они состоят из двух частей оплаты заказа автомашины и отдельно покилометровой оплаты. Напомним, что в столбце А набиваются только условные обозначения. (Опыт работы показал, что время, расходуемое на составление формул, существенно различается у разных студентов. Если вы отстали от других, то это означает, что вам нужно дополнительно потренироваться в элементарных экономических расчетах на компьютере или вручную.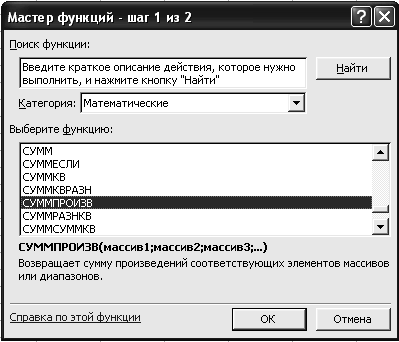 )
[c.65]
)
[c.65]
Как уже упоминалось, такие суммы произведений коэффициентов и переменных решений в выражениях для целевых функций и для левых частей ограничений типичны для моделей линейного программирования. В MS-Ex el имеется специальная математическая функция СУММПРОИЗВ (в английской версии -SUMPRODU T), позволяющая быстро вычислять такие суммы произведений. При вызове этой функции с помощью мастера функций последний просит указать две одинаковые строчки или два одинаковых столбика чисел (массивы), элементы которых нужно почленно перемножить и эти произведения сложить. [c.41]
Следует отметить, что поскольку па первом уровне бригадный механизм еще практически не отработан, то управленческие функции бригадиров являются частью традиционных обязанностей, выполняемых раньше мастерами. Функции же, рожденные самой бригадной формой организации труда, практически отсутствуют. Невысок и объем времени, затрачиваемого бригадирами на выполнение управленческих функций 15—20% внутри-сменпого фонда рабочего времени. [c.218]
[c.218]
С помощью пары кнопок (4) выполняются операции, упрощающие ввод функций в ячейку электронной таблицы. Если вы щелкнете на кнопке со знаком суммы, то в текущей ячейке появится заготовка функции =СУММ(…), аргументы которой Ex el подставит по соглашению (см. п.11.7.1). Вы можете отредактировать эту функцию или зафиксировать в ячейке без редактирования. После щелчка на кнопке fx на экран поступит диалоговое окно Мастера функций (см. п.11.9.1), и вы сможете выбрать и отредактировать функцию, вводимую в текущую ячейку. [c.152]
Для упрощения ввода функций в Ex el предусмотрен специальный Мастер функций, который можно вызвать либо нажатием кнопки fx на панели инструментов Стандартная (группа (4), рис. 11.2), либо командой [Вставка-Функция…]. Не забудьте предварительно выделить ячейку. Мастер функций имеет два окна — два шага. [c.177]
В левом списке первого окна Мастера функций (рис. 11.13) вы можете выбрать категорию функций (например, Математи-
[c. 177]
177]
Теперь займемся вычислением показателя % крит. Для этого применим функцию ХИ2ОБР. Для ее запуска
| gif» valign=»top»> TOP 10 1. Counter-Strike cs_mansion 2. | ||||
Временная сложность рекурсивных функций [Основная теорема] · YourBasic
yourbasic.org
Часто можно вычислить временную сложность рекурсивной функции путем формулирования и решения рекуррентного отношения.
Этот текст содержит несколько примеров и формулу, «основную теорему», что дает решение класса рекуррентных соотношений, которые часто появляются при анализе рекурсивных функций.
Мы также показываем, как анализировать рекурсивные алгоритмы, зависящие от размера и форма структуры данных.
Соотношение рецидивов
В качестве введения покажем, что следующая рекурсивная функция имеет линейную временную сложность.
// Sum возвращает сумму 1 + 2 + ... + n, где n> = 1.
func Sum (n int) int {
if n == 1 {
возврат 1
}
вернуть n + Sum (n-1)
}
Пусть функция T ( n ) обозначает число
элементарных операций, выполняемых вызовом функции Sum (n) .
Мы идентифицируем два свойства T ( n ).
- Так как
Sum (1)вычисляется с использованием фиксированного числа операции к 1 , Т (1) = к 1 . - Если n > 1, функция будет выполнять фиксированное число
операций к 2 , а кроме того,
он выполнит рекурсивный вызов
Sum (n-1). Этот рекурсивный вызов будет выполнять операции T ( n -1). Итого получаем T ( n ) = k 2 + T ( n -1).
Если мы ищем только асимптотическую оценку временной сложности,
нам не нужно указывать фактические значения
константы k 1 и к 2 .Вместо этого мы полагаем k 1 = k 2 = 1.
Чтобы найти временную сложность для функции Sum затем сводится к решению рекуррентного соотношения
- Т (1) = 1, (*)
- T ( n ) = 1 + T ( n -1), когда n > 1. (**)
Повторно применяя эти соотношения, мы можем вычислить T ( n ) для любого положительного числа n .
T ( n ) = (**)
1 + T ( n -1) = (**)
1 + (1 + T ( n -2)) = 2 + T ( n -2) = (**)
2 + (1 + T ( n -3)) = 3 + T ( n -3) =…
k + T ( n — k ) =…
n — 1 + T (1) = (*)
n — 1 + 1 = Θ ( № )
Двоичный поиск
Тот же метод можно использовать и для более сложных рекурсивных алгоритмов.Сформулировать повторения просто, но решить их иногда труднее.
Давайте попробуем вычислить временную сложность этой рекурсивной реализации. бинарного поиска.
// Find возвращает наименьший индекс i, при котором x Мы используем обозначение T ( n ) для обозначения количества элементарные операции, выполняемые этим алгоритмом в худшем случае, когда задан отсортированный срез из n элементов.
Еще раз, мы упрощаем задачу, вычисляя только асимптотическую временную сложность, и пусть все константы равны 1.Тогда повторения станут
- Т (1) = 1, (*)
- T ( n ) = 1 + T ( n /2), когда n > 1. (**)
Уравнение (**) учитывает тот факт, что функция выполняет постоянную работу (это тот) и один рекурсивный вызов среза размером n /2.
(Фактически, срез может также содержать n /2 + 1 элементов. Нас это не беспокоит, так как мы ищем только асимптотическую оценку.)
И снова можно найти решение путем повторной подстановки.
T ( n ) = (**)
1 + T ( n /2) = (**)
1 + (1 + T ( n /4)) = 2 + T ( n / 4) = (**)
2 + (1 + T ( n /8)) = 3 + T ( n /8) = …
k + T ( n /2 k ) = …
журнал n + T ( n /2 журнал n ) = журнал n + T (1) = (*)
журнал n + 1 = Θ (журнал n ).
Основная теорема
Основная теорема — это рецепт, который дает асимптотические оценки для класса рекуррентные отношения, которые часто возникают при анализе рекурсивных алгоритмов.
Пусть a ≥ 1 и b> 1 — константы, пусть f ( n ) — функция, и пусть T ( n ) — функция над положительными числами определяется повторением
Т ( n ) = aT ( n / b) + f ( n ).
Если f ( n ) = Θ ( n d ), где d ≥ 0, то
- T ( n ) = Θ ( n d ) если a d ,
- T ( n ) = Θ ( n d журнал n ) если a = b d ,
- T ( n ) = Θ ( n журнал b a ) если a> b d .
Доказательство опустим. Несложно, но долго. Фактически, вы можете использовать повторную замену точно так же, как и в предыдущие примеры.
Давайте проверим, что основная теорема дает правильное решение к повторению в примере двоичного поиска. В этом случае a = 1, b = 2 и функция f ( n ) = 1. Отсюда следует, что f ( n ) = Θ ( n 0 ), то есть d = 0. Мы видим, что a = b d , и можем использовать вторую точку маркера основной теоремы, чтобы заключить, что
T ( n ) = Θ ( n 0 log n ),
, что правильно.
Анализ без повторения
Для алгоритмов, работающих со структурой данных, обычно невозможно найти повторяющиеся
GMR Master Clocks — NTP Server, PTP Grandmaster, Time Code Generator, Frequency Generator — Masterclock, Inc.
Продукты Мастер Часы NTP-серверы Генераторы временного кода Многоцветные часы Часы часовых поясов Цифровые часы Цифро-аналоговые часы Контроллер счета Двухканальный производственный таймер Усилители-распределители Карты для ПК Регистраторы последовательности событий Переключатель временного кода Программного обеспечения Аксессуары Устаревшие продукты Компания Новости и обновления О нас Истории успеха Служба поддержки Техподдержка Планы поддержки Информация о гарантии Информация о RMA Информация для заказа Ресурсы Сделать запрос Продукты Мастер Часы NTP-серверы Генераторы временного кода Многоцветные часы Часы часовых поясов Цифровые часы Цифро-аналоговые часы Контроллер счета Двухканальный производственный таймер Усилители-распределители Карты для ПК Регистраторы последовательности событий Переключатель временного кода Программного обеспечения Аксессуары Устаревшие продукты Компания Новости и обновления О нас Истории успеха Служба поддержки Техподдержка Планы поддержки Информация о гарантии Информация о RMA Информация для заказа Ресурсы Сделать запрос- Продукты
- Мастер-часы
- Серверы NTP
- Генераторы временного кода
- Многоцветные часы
- Часы часовых поясов
- Цифровые часы
- Цифро-аналоговые часы
 0
0