Матрицы и массивы
Скрипт Open Live Script
MATLAB является сокращением от «матричной лаборатории». В то время как другие языки программирования в основном работают с числами по одному, MATLAB® спроектирован, чтобы работать, в основном, с целыми матрицами и массивами.
Все переменные MATLAB являются многомерными массивами, неважно какого типа данных. Матрица A является двумерным массивом, часто используемым для линейной алгебры.
Создание массивов
Чтобы создать массив из четырех элементов в одной строке, разделите элементы любым запятая (,) или пробел.
a = [1 2 3 4]
a = 1×4
1 2 3 4
Этот тип массива является вектором-строкой.
Чтобы создать матрицу, которая имеет несколько строк, разделите строки точками с запятой.
a = [1 3 5; 2 4 6; 7 8 10]
a = 3×3
1 3 5
2 4 6
7 8 10
Другой способ создать матрицу состоит в том, чтобы использовать функцию, такую как onesнули, или rand. Например, создайте вектор — столбец размером 5 на 1 из нулей.
Например, создайте вектор — столбец размером 5 на 1 из нулей.
z = zeros(5,1)
z = 5×1
0
0
0
0
0
Матричные операции и операции над массивами
MATLAB позволяет вам обрабатывать все значения в матрице с помощью одного арифметического оператора или функции.
a + 10
ans = 3×3
11 13 15
12 14 16
17 18 20
sin(a)
ans = 3×3
0.8415 0.1411 -0.9589
0.9093 -0.7568 -0.2794
0.6570 0.9894 -0.5440
Чтобы транспонировать матрицу, используйте одинарную кавычку ('):
ans = 3×3
1 2 7
3 4 8
5 6 10
Можно выполнить стандартное умножение матриц, которое вычисляет скалярные произведения между строками и столбцами, с помощью * оператор. Например, подтвердите, что матрица, умноженная на её обратную матрицу, возвращает единичную матрицу:
p = a*inv(a)
p = 3×3
1. 0000 0.0000 -0.0000
0 1.0000 -0.0000
0 0.0000 1.0000
0000 0.0000 -0.0000
0 1.0000 -0.0000
0 0.0000 1.0000
Заметьте, что p не матрица целочисленных значений. MATLAB хранит числа как значения с плавающей точкой, и арифметические операции чувствительны к небольшим различиям между фактическим значением и его представлением с плавающей точкой. Можно отобразить больше десятичных цифр с помощью format команда:
format long p = a*inv(a)
p = 3×3
1.0000 0.0000 -0.0000
0 1.0000 -0.0000
0 0.0000 1.0000
Сбросьте отображение к более короткому формату используя
format short
format влияет только на отображение чисел, а не то, как MATLAB вычисляет или сохраняет их.
Чтобы выполнить поэлементное умножение, а не умножение матриц, используйте .* оператор:
p = a.*a
p = 3×3
1 9 25
4 16 36
49 64 100
Для каждого из матричных операторов умножения, деления и возведения в степень существует соответствующий оператор для поэлементных операций.
a в третью степень:ans = 3×3
1 27 125
8 64 216
343 512 1000
Конкатенация
Конкатенация является процессом слияния массивов для создания бОльших массивов. На самом деле вы сделали свой первый массив путем конкатенации его отдельных элементов. Пара квадратных скобок [] оператор конкатенации.
A = [a,a]
A = 3×6
1 3 5 1 3 5
2 4 6 2 4 6
7 8 10 7 8 10
Конкатенация массивов друг с другом, с использованием запятых, называется горизонтальной конкатенацией. Каждый массив должен иметь одинаковое число строк. Точно так же, когда массивы имеют одинаковое число столбцов, можно конкатенировать вертикально с использованием точки с запятой.
A = [a; a]
A = 6×3
1 3 5
2 4 6
7 8 10
1 3 5
2 4 6
7 8 10
Комплексные числа
Комплексные числа имеют и действительные и мнимые части, где мнимая единица является квадратным корнем из -1.
sqrt(-1)
ans = 0.0000 + 1.0000i
Чтобы представлять мнимую часть комплексных чисел, используйте любой i или j.
c = [3+4i, 4+3j; -i, 10j]
c = 2×2 complex 3.0000 + 4.0000i 4.0000 + 3.0000i 0.0000 - 1.0000i 0.0000 +10.0000i
Начало работы с MATLAB
Затем
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
- Примеры
- Функции
- Информация о релизах
- PDF-документация
- MATLAB Answers
- Помощь в установке
- Отчеты об ошибках
- Требования к продукту
- Загрузка программного обеспечения
Пустой массив в матлаб
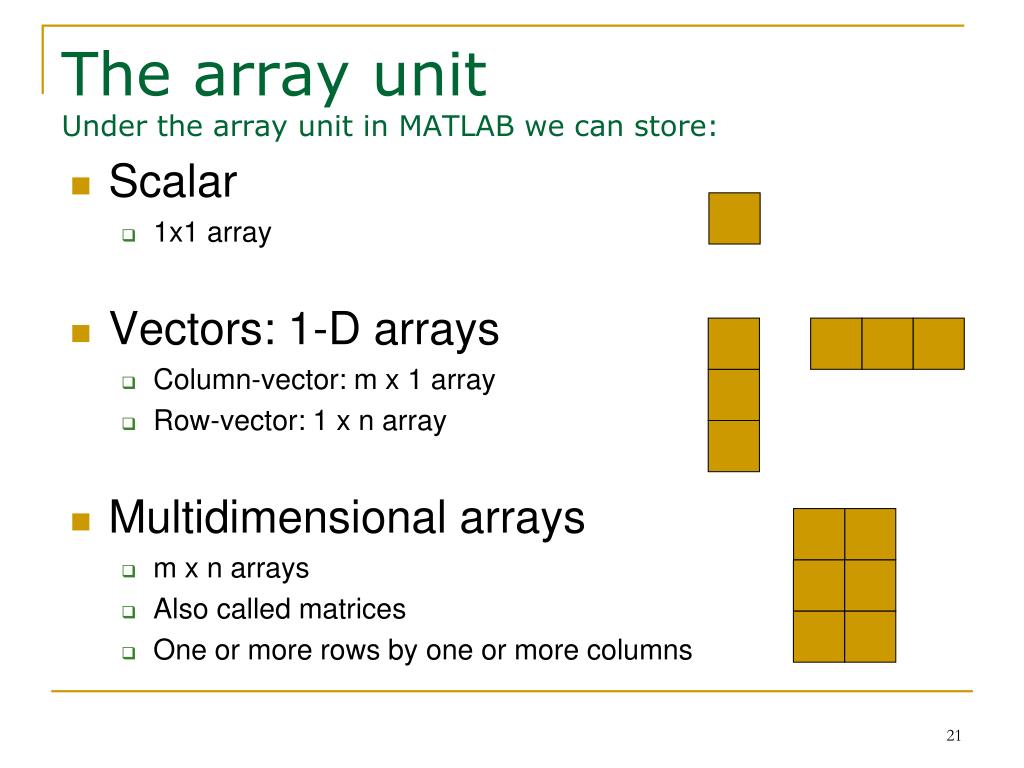
Наборы чисел в программировании принято называть массивами. Всему массиву присваивается одно имя, а доступ к отдельным элементам массива осуществляется по целочисленному индексу, то есть номеру элемента в массиве. Массивы бывают одномерными, когда используется единственный индекс (номер), а могут быть и многомерными (в частности — двумерными).
Массивы бывают одномерными, когда используется единственный индекс (номер), а могут быть и многомерными (в частности — двумерными).
Сначала рассмотрим одномерные массивы. Это линейные наборы чисел (элементов), в которых позиция каждого элемента задаётся единственным числом — его номером. Можно говорить о первом элементе массива, о втором и т.д.
Для задания одномерного массива, состоящего из нескольких чисел (вещественных или комплексных), используется операция конкатенации, обозначаемая с помощью квадратных скобок — [] . Например, следующее выражение
формирует переменную с именем a1 , являющуюся одномерным массивом из трёх элементов (вещественных чисел). Объединяемые в массив элементы должны отделяться друг от друга либо пробелом, либо запятой. Так что выражение
абсолютно идентично предыдущему.
Для доступа к индивидуальному элементу одномерного массива нужно после его имени указать в круглых скобках индекс (номер) этого элемента. Например, третий элемент массива a1 обозначается как a1(3) , первый элемент — как a1(1) , второй элемент — как a1(2) .
Если требуется изменить третий элемент уже сформированного выше операцией конкатенации массива a1 , то можно применить операцию присваивания:
Пусть, к примеру, второй элемент массива a1 должен стать равным среднему арифметическому первого и третьего элементов. Для этого выполняем следующее действие:
Количество элементов в одномерном массиве всегда можно узнать с помощью функции length :
При попытке чтения несуществующего элемента (напрмер, четвёртого элемента массива a1 ) в командном окне MATLABа появляется сообщение об ошибке:
В этом сообщении утверждается, что индекс превысил размер массива.
В то же время запись несуществующего элемента вполне допустима — она означает добавление нового элемента к уже существующему массиву:
Применяя к массиву a1 функцию length , находим, что количество элементов в этом массиве возросло до четырёх:
То же самое действие — «удлинение массива a1 » ,можно выполнить и с помощью операции конкатенации:
Здесь операндами операции конкатенации являются массив a1 , состоящий из трёх элементов, и добавляемый к нему четвёртый элемент, равный 7 .
Теперь создадим ещё один одномерный массив a2 , причём для его создания не будем использовать операцию конкатенации (как мы поступили выше). Вместо этого будем прописывать каждый элемент создаваемого массива по-отдельности:
a2(1) = 67
a2(2) = 7.8
a2(3) = 0.017
Из двух существующих массивов — массива a1 с четырьмя элементами и массива a2 с тремя элементами, можно одной (групповой) операцией конкатенации создать одномерный массив b из семи элементов:
Массивы могут состоять не только из вещественных чисел. Выражение
d = [ 1+2i, 2+3i, 3-7i ]
формирует одномерный массив d комплексных чисел. Разделителем элементов формируемого одномерного массива может быть либо пробел, либо запятая. При использовании выражений и комплексных чисел использование запятой предпочтительнее.
Теперь рассмотрим двумерные массивы, которые можно трактовать как набор чисел, упорядоченный в виде прямоугольной таблицы

Двумерный массив характеризуется количеством строк и количеством столбцов. Составим массив a3 , состоящий из двух столбцов и трёх строк:
Из этого рисунка хорошо видно, что в качестве разделителя строк в формируемом с помощью операции конкатенации двумерном массиве служит точка с запятой.
Как и в случае одномерных массивов двумерный массив можно создать, индивидуально прописывая его элементы:
a3(1,1) = 1
a3(1,2) = 2
a3(2,1) = 3
a3(2,2) = 4
a3(3,1) = 5
a3(3,2) = 6
Для доступа к отдельным элементам двумерного массива используется выражение с круглыми скобками, в которых через запятую перечисляются его индексы. Первым указывается номер строки, вторым — номер столбца.
Система MATLAB может работать и с массивами больших размерностей. Они будут рассматриваться позже в следующем разделе.
Вернёмся к двумерным массивам, которые в математике принято называть матрицами. Любая строка матрицы является одномерным массивом, и любой столбец матрицы также является одномерным массивом. Однако есть некоторая разница в упорядочении их элементов с точки зрения матриц: элементы первого одномерного массива упорядочены вдоль строк матрицы (горизонтально), а элементы второго — вдоль столбцов (вертикально). Если явно учитывать в понятии одномерного массива эту разницу, то тогда массивы первого типа называют вектор-строками, а второго типа — вектор-столбцами. В этом случае также можно считать, что вектор-строки являются частным случаем матрицы с количеством строк, равным единице, а вектор-столбцы являются частным случаем матрицы с количеством столбцов, равным единице.
Однако есть некоторая разница в упорядочении их элементов с точки зрения матриц: элементы первого одномерного массива упорядочены вдоль строк матрицы (горизонтально), а элементы второго — вдоль столбцов (вертикально). Если явно учитывать в понятии одномерного массива эту разницу, то тогда массивы первого типа называют вектор-строками, а второго типа — вектор-столбцами. В этом случае также можно считать, что вектор-строки являются частным случаем матрицы с количеством строк, равным единице, а вектор-столбцы являются частным случаем матрицы с количеством столбцов, равным единице.
В системе MATLAB все одномерные массивы трактуются либо как вектор-строки, либо как вектор-столбцы. До сих пор мы вводили только вектор-строки. Следующее выражение, использующее операцию конкатенации, задаёт вектор-столбец
состоящий из трёх строк, так как точка с запятой в операции конкатенации означает переход на новую строку.
Для массива a4 функция length(a4) возвращает число 3 , так как действительно этот массив состоит из трёх элементов. Функция length не различает вектор-строки и вектор-столбцы.
Функция length не различает вектор-строки и вектор-столбцы.
Если попросить систему MATLAB показать значение переменной a4 , то мы увидим следующую картину:
То есть MATLAB распознаёт «геометрию» этого одномерного массива и наглядно отображает его, располагая элементы для показа в своём окне вертикально.
Чтобы отразить правильно геометрию вектор-столбцов и вектор-строк, а также узнать размеры двумерного массива в обоих направлениях, используют функцию size . Для двумерного массива a3 получается следующий результат:
причём первым показывается число строк, а вторым — число столбцов.
Применяем эту же функцию к одномерным массивам. Вот, что из этого получается для вектор-строки a2
состоящего из одной строки и трёх столбцов. Для вектор-столбца a4 , состоящего из трёх строк и одного столбца, имеем следующий результат применения функции size :
Наконец, попробуем применить эту функцию к переменной, состоящей из единственного числового значения, то есть к скаляру:
var1 = 5
size(var1)
ans =
1 1
Отсюда видно, что система MATLAB трактует даже по-существу скалярные величины как массивы с размером 1×1. Это ровным счётом ничего не меняет для пользователя, так как он может не обращать на это никакого внимания. MATLAB переходит от скаляров к массивам прозрачно, не требуя от пользователя дополнительных действий.
Это ровным счётом ничего не меняет для пользователя, так как он может не обращать на это никакого внимания. MATLAB переходит от скаляров к массивам прозрачно, не требуя от пользователя дополнительных действий.
Итак, всё, с чем работает MATLAB, является массивами различной размерности. Все массивы из текущего сеанса работы (текущего Рабочего пространства) можно просмотреть
с точки зрения их структуры с помощью команды whos .
выше код дает следующее сообщение об ошибке:
. Неопределенная функция или метод «хромосомы» для входных аргументов типа «двойного».
Мне нужен пустой массив символов имени chromosomes . Я попытался добавить следующую строку перед выше петлями.
но он не работает. Это дает ошибку
. Index of element to remove exceeds matrix dimensions.
Вы хотите хромосом быть массивом символов (если все строки имеют одинаковый размер) или массив ячеек (с переменным размером Ith элементов)?
В первом случае вы определяете переменную:
Затем в течение цикла:
В случае массива ячеек:
EDIT :
На самом деле вы можете применить DEC2BIN на весь массив чисел сразу. Это также выглядит как переменная parameters одинаковы для каждой -й строки. Тогда вы можете сделать:
Это также выглядит как переменная parameters одинаковы для каждой -й строки. Тогда вы можете сделать:
Все переменные всех типов данных в MATLAB являются многомерными массивами. Вектор – это одномерный массив, а матрица – это двумерный массив.
Мы уже обсуждали векторы и матрицы. В этой главе мы обсудим многомерные массивы. Однако перед этим давайте обсудим некоторые специальные типы массивов.
Специальные массивы в MATLAB
В этом разделе мы обсудим некоторые функции, которые создают специальные массивы. Для всех этих функций один аргумент создает квадратный массив, двойные аргументы создают прямоугольный массив.
Функция нулей () создает массив всех нулей –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Функция ones () создает массив всех единиц –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Функция eye () создает единичную матрицу.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Функция rand () создает массив равномерно распределенных случайных чисел по (0,1) –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Магический Квадрат
Магический квадрат – это квадрат, который дает одинаковую сумму, когда его элементы добавляются построчно, по столбцам или по диагонали.
Функция magic () создает массив магических квадратов. Требуется исключительный аргумент, который дает размер квадрата. Аргумент должен быть скаляром, большим или равным 3.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Многомерные массивы
В MATLAB массив, имеющий более двух измерений, называется многомерным массивом. Многомерные массивы в MATLAB являются расширением нормальной двумерной матрицы.
Обычно для создания многомерного массива мы сначала создаем двумерный массив и расширяем его.
Например, давайте создадим двумерный массив a.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Массив a является массивом 3 на 3; мы можем добавить третье измерение к, предоставив такие значения, как –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Мы также можем создавать многомерные массивы, используя функции ones (), zeros () или rand ().
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Мы также можем использовать функцию cat () для построения многомерных массивов. Он объединяет список массивов по указанному измерению –
Он объединяет список массивов по указанному измерению –
Синтаксис для функции cat () –
B – новый созданный массив
A1 , A2 , … массивы, которые будут объединены
dim – это размер, по которому объединяются массивы.
B – новый созданный массив
A1 , A2 , … массивы, которые будут объединены
dim – это размер, по которому объединяются массивы.
пример
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он отображает –
Функции массива
MATLAB предоставляет следующие функции для сортировки, вращения, перестановки, изменения формы или смещения содержимого массива.
| функция | Цель |
|---|---|
| длина | Длина вектора или наибольшее измерение массива |
| ndims | Количество размеров массива |
| numel | Количество элементов массива |
| размер | Размеры массива |
| iscolumn | Определяет, является ли ввод вектором столбца |
| пустой | Определяет, является ли массив пустым |
| ismatrix | Определяет, является ли ввод матричным |
| isrow | Определяет, является ли ввод вектором строки |
| isscalar | Определяет, является ли вход скалярным |
| isvector | Определяет, является ли входной вектор |
| blkdiag | Создает блочную диагональную матрицу из входных аргументов. |
| circshift | Смещает массив по кругу |
| ctranspose | Комплексное сопряженное транспонирование |
| диаг | Диагональные матрицы и диагонали матрицы |
| flipdim | Переворачивает массив по указанному измерению |
| fliplr | Отразить матрицу слева направо |
| flipud | Переворачивает матрицу вверх-вниз |
| ipermute | Инвертирует перестановочные размеры массива ND |
| переставлять | Переставляет размеры массива ND |
| repmat | Реплики и массив плиток |
| перекроить | Перекраивает массив |
| rot90 | Поворот матрицы на 90 градусов |
| shiftdim | Смещает размеры |
| issorted | Определяет, находятся ли заданные элементы в отсортированном порядке |
| Сортировать | Сортирует элементы массива в порядке возрастания или убывания |
| sortrows | Сортирует строки в порядке возрастания |
| выжимать | Удаляет одиночные размеры |
| транспонировать | транспонировать |
| векторизовать | Векторизованное выражение |
Примеры
Следующие примеры иллюстрируют некоторые из функций, упомянутых выше.
Длина, Размер и Количество элементов –
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Круговое смещение элементов массива –
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Сортировка массивов
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Cell Array
Массивы ячеек – это массивы индексированных ячеек, где каждая ячейка может хранить массив разных измерений и типов данных.
Функция cell используется для создания массива cell. Синтаксис для функции ячейки –
С – массив ячеек;
dim – скалярное целое число или вектор целых чисел, который определяет размеры массива ячеек C;
dim1, …, dimN – скалярные целые числа, которые определяют размеры C;
obj является одним из следующих –
- Массив или объект Java
- .
 NET массив типа System.String или System.Object
NET массив типа System.String или System.Object
С – массив ячеек;
dim – скалярное целое число или вектор целых чисел, который определяет размеры массива ячеек C;
dim1, …, dimN – скалярные целые числа, которые определяют размеры C;
obj является одним из следующих –
пример
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Доступ к данным в массивах ячеек
Существует два способа обращения к элементам массива ячеек:
- Заключение индексов в первую скобку () для ссылки на наборы ячеек
- Заключение индексов в фигурные скобки <> для ссылки на данные в отдельных ячейках
Когда вы заключаете индексы в первую скобку, это относится к набору ячеек.
Индексы массива ячеек в гладких скобках относятся к наборам ячеек.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Вы также можете получить доступ к содержимому ячеек путем индексации с помощью фигурных скобок.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Функции для работы с массивами в Matlab
Похожие презентации:
3D печать и 3D принтер
Системы менеджмента качества требования. Развитие стандарта ISO 9001
Операционная система. Назначение и основные функции
Adobe Photoshop
AutoCAD история и возможности
Microsoft Excel
Облачные технологии
Корпорация Microsoft и ее особенности
Веб-дизайн
Тема 2. Пакеты прикладных программ
1. Функции для работы с массивами в Matlab
Лекция 3Функции для работы
с массивами в Matlab
2. Умножение матриц
23. Умножение матрицы на число
34. Транспонирование вещественных матриц
Транспонирование матрицы, так жекак и вектора, производится с помощью
символа ‘ (апостроф).
4
Пример.
5
6. Транспонирование матриц, содержащих комплексные числа
Эта операция выполняется командой‘ (апостроф).
 .
.Только квадратные матрицы могут быть
возведены в степень.
8
Пример.
9
10. Поэлементные операции с матрицами
1011. Создание матриц специального вида
• Для работы с матрицами удобно пользоватьсяследующими функциями
ones – формирование массива из единиц
zeros – формирование массива из нулей
eye – формирование единичной матрицы
rand – формирование массива из чисел, случайно
распределённых на отрезке [0, 1]
randn – формирование массива из чисел, нормально
распределённых на отрезке [-1, 1]
magic – формирование магического квадрата
pascal – формирование квадрата Паскаля
diag – диагональная матрица
и др.
11
12. Матрицы специального вида
• Рассмотрим основной синтаксис напримере функции создания единичной
матрицы (eye)
• eye(m) – создание единичной матрицы
размера [m, m]
• eye(m,n) – создание единичной
матрицы размера [m, n]
– «лишние» строки или столбцы
дополняются нулями
12
13.
 Матрицы специального вида13
Матрицы специального вида1314. Матрицы специального вида
1415. Матрицы специального вида
1516. Матрицы специального вида
1617. Матрицы специального вида
• Функция diag: работа с диагональнымиматрицами
– у которых ненулевые элементы расположены на
диагоналях
• Синтаксис:
– X = diag(v) – на главной диагонали матрицы X
расположены элементы вектора v
– X = diag(v,k) – на k-ой диагонали матрицы X
расположены элементы вектора v (по умолчанию k=0)
– v = diag(X,k) – извлечь из матрицы X k-ую
диагональ и сохранить её в векторе v
17
18. Матрицы специального вида
1819. Матрицы специального вида
1920. Вычисления с элементами массивов
• Простейшие операции над элементамимассивов:
–
–
–
–
–
–
–
sum: сумма элементов
prod: произведение элементов
cumsum: кумулятивная сумма элементов
cumprod: кумулятивное произведение элементов
max: нахождение максимального элемента
min: нахождение минимального элемента
sort: сортировка элементов
20
21.
 Вычисления с элементами массивов• Рассмотрим работу некоторых из этих
Вычисления с элементами массивов• Рассмотрим работу некоторых из этихфункций на примере sum
• Для векторов эта функция возвращает
сумму элементов.
• Для массивов – сумму элементов по
каждому из столбцов
– результат – вектор-строка
21
Суммирование элементов массива
можно проводить командой:
sum(A,[ ],dim) – возвращает сумму
элементов массива по столбцам (dim=1),
по строкам (dim=2).
22
23. Вычисления с элементами массивов
Здесь round(X) возвращает значения, округленные доближайшего целого.
23
24. Произведение элементов массива
Синтаксис: prod(X), cumprod(X)Описание:
Функция prod(X) в случае одномерного
массива возвращает произведение элементов
массива; в случае двумерного массива — это
вектор-строка, содержащая произведения
элементов каждого столбца.
Функция cumprod(X), кроме того,
возвращает все промежуточные результаты.
24
25
Произведение элементов массива
можно проводить командой:
prod(A,[ ],dim) – возвращает матрицу (массив
размерности два) с произведение элементов
массива А по столбцам (dim=1), по строкам
(dim=2).

26
27. Поворот матрицы
rot90(A) — осуществляет поворот матрицыА на 90° против часовой стрелки;
rot90(A,k) — осуществляет поворот матрицы
А на величину 90*k градусов, где k — целое
число.
27
28
29. Вычисления с элементами массивов
• Кумулятивная суммавычисляется так же,
только происходит
накопление
вычисленных
значений в
элементах массива:
29
30. Вычисления с элементами массивов
• Максимальный иминимальный
элементы:
30
31. Вычисления с элементами массивов
• Вызов функцийmax/min с двумя
выходными
параметрами
позволяет
определить и индекс
найденного
элемента:
31
32. Вычисления с элементами массивов
• Функцияsort(имя массива)
производит
сортировку элементов
матрицы по
возрастанию.
Сортировка
производится по
столбцам:
32
33. Вычисления с элементами массивов
Сортировкаэлементов
массива по
убыванию
осуществляется с
помощью
искусственного
приема:
-sort(-имя массива)
33
34.
 Логические функции• All(v) –
Логические функции• All(v) –возвращает истину,
если все элементы
вектора v отличны
от нуля. Для
матриц выдаёт
вектор-строку с
аналогичным
результатом для
каждого столбца
34
35. Логические функции
• Any(v) –возвращает истину,
если хотя бы один
элемент вектора v
отличен от нуля.
Для матриц выдаёт
вектор-строку с
аналогичным
результатом для
каждого столбца
35
36. Логические функции
3637. Поиск в массиве
• find: определяетиндексы
элементов,
удовлетворяющих
заданному
условию
37
38. Поиск в массиве
• Пример применениякоманды find к
массивам:
38
39. Поиск в массиве
Пример. Найтииндексы
максимального
элемента в
массиве.
39
40. Математические матричные операции
• det – вычислениеопределителя
квадратной матрицы
40
41. Матричные и поэлементные операции
• При работе с матрицами можноиспользовать два вида операторов:
– матричные: производят действия по
правилам матричной алгебры.
 поэлементное
поэлементноевозведение в степень
• .\ поэлементное
деление «слева»
42
43. Матричные и поэлементные операции
4344. Матричные и поэлементные операции
• Такие операции часто используются, если нужно применить какуюлибо функцию ко всем элементам матрицы.
44
45. Матричные и поэлементные операции
• Некоторыеоперации по
умолчанию
считаются
поэлементными:
45
English Русский Правила
Иллюстрированный самоучитель по MatLab › Массивы ячеек › Функции преобразования типов данных [страница — 276] | Самоучители по математическим пакетам
Тематика: Самоучители по математическим пакетам
При обработке сложных данных возникает необходимость в преобразовании их типов. Ниже представлены такие функции, имеющие отношение к массивам ячеек:
- num2cell (A,DIM) – преобразует массив чисел А в массив ячеек, помещая в одну и ту же ячейку элементы, соответствующие одному значению индекса вдоль измерения, указанного параметром DIM.
 Например, num2cell(A.2) преобразует каждый ряд массива А в отдельную ячейку, cat(DIM.C{:}) осуществляет обратное преобразование.
Например, num2cell(A.2) преобразует каждый ряд массива А в отдельную ячейку, cat(DIM.C{:}) осуществляет обратное преобразование. - num2cell (A) – преобразует массив чисел А в массив ячеек и возвращает последний. Каждый элемент А превращается в отдельную ячейку. Возвращаемый массив имеет тот же размер и ту же размерность, что и исходный массив А.
Примеры применения данных функций:
>>A=[12; 34: 56]
A=
12
34
56
>>C=num2cell(A.
2)
C=
[1x2double]
[1x2double]
[1x2double]
>>C{1.1}
ans =
12
>>C{2.1}
ans =
34
>>C{3.1}
ans =
56
>>cat(2. C{:})
C{:})
ans =
123456
ans =
12
34
56
>>num2cell(A.[12])
ans =
[3x2double]
- cell2struct(C. FIELDS. DIM) – преобразует массив ячеек С в массив структур, превращая размерность DIM массива ячеек С в поля структуры S. Размерность 1 – столбцы. Размерность 2 – строки. FILEDS – массив символов или строковый массив ячеек.
Пример преобразования:
>>C={' Привет! '.123. 2+31}
C =
'Привет!'[123] [2.0000+3.00001]
>>f={ 'name', 'number', 'complex'};
>>S=cell2struct(C,f,2)
S =
name: 'Привет! '
number: 123
complex: 2. 0000
0000+3.0000i
- struct2cell (S) – преобразует массив структур S размером тхп, в котором содержатся р полей, в массив ячеек, так что возвращаемый массив будет иметь размер рхтхп. Если массив структур многомерный, то возвращаемый массив ячеек будет иметь размер, равный [р size(S)]. Схему структуры с названиями полей возвращаемый массив ячеек не содержит. Пример такого преобразования приводится ниже:
>>C=struct2cellS)
C =
'Привет!'
[ 123]
[2.0000+3.0000i]
- « первая
- ‹ предыдущая
- …
- 271
- 272
- 273
- 274
- 275
- 276
- 277
- 278
- 279
- 280
- 281
- …
- следующая ›
- последняя »
Если Вы заметили ошибку, выделите, пожалуйста, необходимый текст и нажмите CTRL + Enter, чтобы сообщить об этом редактору.
Matlab индекс элемента массива • Вэб-шпаргалка для интернет предпринимателей!
Содержание
- 1 Специальные массивы в MATLAB
- 2 Магический Квадрат
- 3 Многомерные массивы
- 3.1 пример
- 4 Функции массива
- 4.1 Примеры
- 5 Сортировка массивов
- 6 Cell Array
- 6.1 пример
- 7 Доступ к данным в массивах ячеек
- 7.1 Рекомендуем к прочтению
Предположим, что у меня есть массив, a = [2 5 4 7] . Какова функция, возвращающая максимальное значение и его индекс?
Например, в моем случае эта функция должна возвращать 7 как максимальное значение, а 4 — как индекс.
Функция max . Чтобы получить первое максимальное значение, вы должны сделать
val — максимальное значение, а idx — его индекс.
В случае 2D-массива (матрицы) вы можете использовать:
Часть idx будет содержать номер столбца, содержащий максимальный элемент каждой строки.
Вы можете использовать max() для получения максимального значения. Функция max также может возвращать индекс максимального значения в векторе. Чтобы получить это, назначьте результат вызова max в вектор двух элементов вместо одной переменной.
Функция max также может возвращать индекс максимального значения в векторе. Чтобы получить это, назначьте результат вызова max в вектор двух элементов вместо одной переменной.
например. z — ваш массив,
Здесь 7 — наибольшее число в 4-й позиции (индекс).
Для матрицы вы можете использовать это:
I — индекс A (:), содержащий наибольший элемент.
Теперь используйте функцию ind2sub для извлечения индексов строк и столбцов A, соответствующих самому большому элементу.
В.Г.Потемкин «Введение в Matlab» (v 5.3)
Глава 3. Программирование в среде Matlab 5
3.5. Индексы и подындексы
Индексы. Элемент массива А, расположенный на пересечении строки i и столбца j, обозначается как А(i, j).
Пример
Рассмотрим в качестве массива А матрицу magic(4):
А = magic(4)
А =
| 16 | 2 | 3 | 13 |
| 5 | 11 | 10 | 8 |
| 9 | 7 | 6 | 12 |
| 4 | 14 | 15 | 1 |
Тогда А(4, 3) — это элемент, расположенный на пересечении строки 4 и столбца 3, равный 15.
Можно также вычислить сумму элементов четвертого столбца
A(1, 4) + A(2, 4) + A(3, 4) + A(4, 4)
ans = 34
На элементы массива А можно ссылаться, используя единственный индекс, А(k). Это обычный способ ссылки на элементы векторов. Но точно так же можно ссылаться на элементы двумерного массива, и в этом случае этот массив рассматривается как один длинный вектор-столбец, сформированный из столбцов исходного массива. В рассматриваемом примере А(12) — это другой способ ссылки на значение 15, соответствующее элементу А(4, 3).
Если будет сделана попытка обратиться к элементу вне матрицы, то программа выдаст ошибку:
t = A(4, 5)
. Index exceeds matrix dimensions. Индекс превышает размерность матрицы.
Если же выполняется присвоение значения элементу с индексами, выходящими за пределы массива, то система MATLAB автоматически увеличивает размер матрицы.
Пример:
X = A;
X (4, 5) = 17
X =
| 16 | 2 | 3 | 13 | |
| 5 | 11 | 10 | 8 | |
| 9 | 7 | 6 | 12 | |
| 4 | 14 | 15 | 1 | 17 |
Выделение подблоков массива. Если в индексных выражениях использовать двоеточие, то можно ссылаться на подблоки массива. Так индексное выражение A(1:k, j) ссылается на блок из k элементов столбца j.
Если в индексных выражениях использовать двоеточие, то можно ссылаться на подблоки массива. Так индексное выражение A(1:k, j) ссылается на блок из k элементов столбца j.
Пример:
A(1:4,3)
ans =
| 3 |
| 10 |
| 6 |
| 15 |
Здесь выделен столбец 3 матрицы magic(4).
sum(A(1:4, 3))
ans = 34
вычисляет сумму элементов столбца 3.
Однако существует способ лучше. Поскольку двоеточие само по себе ссылается на все элементы строки или столбца, то последнюю сумму можно вычислить так
sum(A(:,3))
ans = 34
Кроме того, начиная с версии 5.0, на последнюю строку или столбец массива можно ссылаться с помощью ключевого слова end. Таким образом, оператор
sum(A(:, end))
ans = 34
вычисляет сумму элементов в последнего столбца матрицы A.
Объдинение подблоков в массив. Операция объединения отдельных подблоков в массив называется конкатенацией. Даже при формировании исходной матрицу, когда объдиняются отдельные элементы, осуществляется операция конкатенации.Оператор конкатенации — это пара квадратных скобок [ ], внутри которых указываются отдельные элементы или блоки массива.
Пример.
Используя матрицу A, равную magic(4), образуем новую матрицу B размера 8×8
B = [A A+32; A+48 A+16]
B =
| 16 | 2 | 3 | 13 | 48 | 34 | 35 | 45 |
| 5 | 11 | 10 | 8 | 37 | 43 | 42 | 40 |
| 9 | 7 | 6 | 12 | 41 | 39 | 38 | 44 |
| 4 | 14 | 15 | 1 | 36 | 46 | 47 | 33 |
| 64 | 50 | 51 | 61 | 32 | 18 | 19 | 29 |
| 53 | 59 | 58 | 56 | 21 | 27 | 26 | 24 |
| 57 | 55 | 54 | 60 | 25 | 23 | 22 | 28 |
| 52 | 62 | 63 | 49 | 20 | 30 | 31 | 17 |
Эта матрица состоит из четырех блоков размера 4×4
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
Эта матрица есть половина другого волшебного квадрата, элементы которого находятся в диапазоне целых чисел 1:64. Суммы по столбцам уже имеют правильное значение для волшебного квадрата размера 8х8:
Суммы по столбцам уже имеют правильное значение для волшебного квадрата размера 8х8:
sum(B)
ans = 260 260 260 260 260 260 260 260
Однако сумма строк
sum (B’)
ans = 196 196 196 196 324 324 324 324
Попробуйте найти те перестановки элементов, которые приводят матрицу B к истинному волшебному квадрату порядка 8.
Удаление строк и столбцов. Используя понятие пустого массива, можно легко удалять строки, столбцы и целые подблоки.
X = A
X =
| 16 | 2 | 3 | 13 |
| 5 | 11 | 10 | 8 |
| 9 | 7 | 6 | 12 |
| 4 | 14 | 15 | 1 |
Чтобы удалить второй столбец массива X достаточно применить оператор
X (:, 2) = [ ]
X =
| 16 | 3 | 13 |
| 5 | 10 | 8 |
| 9 | 6 | 12 |
| 4 | 15 | 1 |
При попытке улалить отдельный элемент массива возникает ошибка, поскольку результат не является массивом:
X (1, 2) = []
. Indexed empty matrix assignment is not allowed.
Indexed empty matrix assignment is not allowed.
Запрещено присвоение пустой матрицы индексному выражению.
Однако использование единственного индекса позволяет удалить одиночный элемент или последовательность элементов, при этом остающиеся элементы преобразуются в вектор-строку.
X = A;
X(:, 2) = [ ]
X =
| 16 | 3 | 13 |
| 5 | 10 | 8 |
| 9 | 6 | 12 |
| 4 | 15 | 1 |
X(2:1:12) = [ ]
X = 16
или
X = A;
X(:, 2) = [ ]
X =
| 16 | 3 | 13 |
| 5 | 10 | 8 |
| 9 | 6 | 12 |
| 4 | 15 | 1 |
X(2 : 2 : 10) = [ ]
X = 16 9 3 6 13 12 1
Индексация многомерных массивов. В системе MATLAB принято хранить каждый массив, независимо от его размерности, как вектор-столбец. Этот вектор образован объединением (конкатенацией) столбцов исходного массива.
В системе MATLAB принято хранить каждый массив, независимо от его размерности, как вектор-столбец. Этот вектор образован объединением (конкатенацией) столбцов исходного массива.
Пример.
Система MATLAB хранит массив A
A = [2 6 9; 4 2 8; 3 0 1]
в виде следующего вектора-столбца
| 2 |
| 4 |
| 3 |
| 6 |
| 2 |
| 9 |
| 8 |
| 1 |
При обращении к массиву А с указанием единственного индекса происходит непосредственное обращение к этому вектору-столбцу. Обращение A(3) ссылается на третье значение в столбце; А(7) — на седьмое и так далее.
Если количество индексов массива больше 1, то MATLAB вычисляет индекс в столбце хранения, используя значения размерностей массива. Если двумерный массив А имеет размер [d1 d2], где d1 — число строк, а d2 — число столбцов, то для элемента с номером (i, j) его позиция в векторе хранения определяется как (j-1)*d1+i.
Если двумерный массив А имеет размер [d1 d2], где d1 — число строк, а d2 — число столбцов, то для элемента с номером (i, j) его позиция в векторе хранения определяется как (j-1)*d1+i.
Пример
Для элемента A(3, 2) MATLAB вычисляет следующую позицию в векторе хранения (2-1)*3+3 = 6. Элементу с номером 6 соответствует значение 0.
Этот способ хранения и индексная схема распространяются и на многомерные массивы. В этом случае MATLAB использует схему постраничного объединения, чтобы создать столбец хранения.
Использование единственного индекса приводит к непосредственному обращению к вектору хранения.
Если задано два индекса (i, j), то MATLAB вычисляет позицию описанным выше способом, причем только для первой страницы многомерного массива и при условии, что эти индексы находятся внутри диапазона размерностей исходного массива.
Если задано более двух индексов, схему индексации усложняется. Если задано четыре индекса (i, j, k, l) для четырехмерного массиву размера d1xd2xd3xd4, то позиция элемента в векторе хранения вычисляется следующим образом
s = (l-1)(d3)(d2)(d1)+(k-1)(d2)(d1)+(j-1)(d1)+i.
Общая формула для позиции элемента в векторе хранения, соответствующего элементу (j1 j2 . jn-1 jn) n-мерного массива размера d1xd2xd3x . xdn, имеет вид
s = (jn-1)(dn-1)(dn-2). (d1)+(jn-1-1)(dn-2). (d1)+. +(j2-1)(d1)+j1.
Пример
Рассмотрим многомерный массив C размера 5х4х3х2. На рис. 3.2 показаны форматы вывода на экран и хранения.
Все переменные всех типов данных в MATLAB являются многомерными массивами. Вектор – это одномерный массив, а матрица – это двумерный массив.
Мы уже обсуждали векторы и матрицы. В этой главе мы обсудим многомерные массивы. Однако перед этим давайте обсудим некоторые специальные типы массивов.
Специальные массивы в MATLAB
В этом разделе мы обсудим некоторые функции, которые создают специальные массивы. Для всех этих функций один аргумент создает квадратный массив, двойные аргументы создают прямоугольный массив.
Функция нулей () создает массив всех нулей –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Функция ones () создает массив всех единиц –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Функция eye () создает единичную матрицу.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Функция rand () создает массив равномерно распределенных случайных чисел по (0,1) –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Магический Квадрат
Магический квадрат – это квадрат, который дает одинаковую сумму, когда его элементы добавляются построчно, по столбцам или по диагонали.
Функция magic () создает массив магических квадратов. Требуется исключительный аргумент, который дает размер квадрата. Аргумент должен быть скаляром, большим или равным 3.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Многомерные массивы
В MATLAB массив, имеющий более двух измерений, называется многомерным массивом. Многомерные массивы в MATLAB являются расширением нормальной двумерной матрицы.
Обычно для создания многомерного массива мы сначала создаем двумерный массив и расширяем его.
Например, давайте создадим двумерный массив a.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Массив a является массивом 3 на 3; мы можем добавить третье измерение к, предоставив такие значения, как –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Мы также можем создавать многомерные массивы, используя функции ones (), zeros () или rand ().
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Мы также можем использовать функцию cat () для построения многомерных массивов. Он объединяет список массивов по указанному измерению –
Синтаксис для функции cat () –
B – новый созданный массив
A1 , A2 , … массивы, которые будут объединены
dim – это размер, по которому объединяются массивы.
B – новый созданный массив
A1 , A2 , … массивы, которые будут объединены
dim – это размер, по которому объединяются массивы.
пример
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он отображает –
Функции массива
MATLAB предоставляет следующие функции для сортировки, вращения, перестановки, изменения формы или смещения содержимого массива.
| функция | Цель |
|---|---|
| длина | Длина вектора или наибольшее измерение массива |
| ndims | Количество размеров массива |
| numel | Количество элементов массива |
| размер | Размеры массива |
| iscolumn | Определяет, является ли ввод вектором столбца |
| пустой | Определяет, является ли массив пустым |
| ismatrix | Определяет, является ли ввод матричным |
| isrow | Определяет, является ли ввод вектором строки |
| isscalar | Определяет, является ли вход скалярным |
| isvector | Определяет, является ли входной вектор |
| blkdiag | Создает блочную диагональную матрицу из входных аргументов. |
| circshift | Смещает массив по кругу |
| ctranspose | Комплексное сопряженное транспонирование |
| диаг | Диагональные матрицы и диагонали матрицы |
| flipdim | Переворачивает массив по указанному измерению |
| fliplr | Отразить матрицу слева направо |
| flipud | Переворачивает матрицу вверх-вниз |
| ipermute | Инвертирует перестановочные размеры массива ND |
| переставлять | Переставляет размеры массива ND |
| repmat | Реплики и массив плиток |
| перекроить | Перекраивает массив |
| rot90 | Поворот матрицы на 90 градусов |
| shiftdim | Смещает размеры |
| issorted | Определяет, находятся ли заданные элементы в отсортированном порядке |
| Сортировать | Сортирует элементы массива в порядке возрастания или убывания |
| sortrows | Сортирует строки в порядке возрастания |
| выжимать | Удаляет одиночные размеры |
| транспонировать | транспонировать |
| векторизовать | Векторизованное выражение |
Примеры
Следующие примеры иллюстрируют некоторые из функций, упомянутых выше.
Длина, Размер и Количество элементов –
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Круговое смещение элементов массива –
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Сортировка массивов
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Cell Array
Массивы ячеек – это массивы индексированных ячеек, где каждая ячейка может хранить массив разных измерений и типов данных.
Функция cell используется для создания массива cell. Синтаксис для функции ячейки –
С – массив ячеек;
dim – скалярное целое число или вектор целых чисел, который определяет размеры массива ячеек C;
dim1, …, dimN – скалярные целые числа, которые определяют размеры C;
obj является одним из следующих –
- Массив или объект Java
- .
 NET массив типа System.String или System.Object
NET массив типа System.String или System.Object
С – массив ячеек;
dim – скалярное целое число или вектор целых чисел, который определяет размеры массива ячеек C;
dim1, …, dimN – скалярные целые числа, которые определяют размеры C;
obj является одним из следующих –
пример
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Доступ к данным в массивах ячеек
Существует два способа обращения к элементам массива ячеек:
- Заключение индексов в первую скобку () для ссылки на наборы ячеек
- Заключение индексов в фигурные скобки <> для ссылки на данные в отдельных ячейках
Когда вы заключаете индексы в первую скобку, это относится к набору ячеек.
Индексы массива ячеек в гладких скобках относятся к наборам ячеек.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Вы также можете получить доступ к содержимому ячеек путем индексации с помощью фигурных скобок.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Как соединить массивы матлаб
Создание, конкатенация и расширение матрицы
Самая основная структура данных MATLAB® является матрицей. Матрица A является двумерным, прямоугольным массивом элементов данных, расположенных в строках и столбцах. Элементами могут быть числа, логические значения ( true или false ), даты и времена, строки или некоторый другой тип данных MATLAB.
Даже один номер хранится как матрица. Например, переменная, содержащая значение 100, хранится как матрица 1 на 1 типа double .
Построение матрицы данных
Если у вас есть определенный набор данных, можно расположить элементы в матрице с помощью квадратных скобок. Одна строка данных имеет пробелы или запятые между элементами, а точка с запятой разделяет строки. Например, создайте одну строку четырех числовых элементов. Размер получившейся матрицы 1 на 4, поскольку она имеет 1 строку и 4 столбца. Матрица A этой формы часто упоминается как вектор-строка.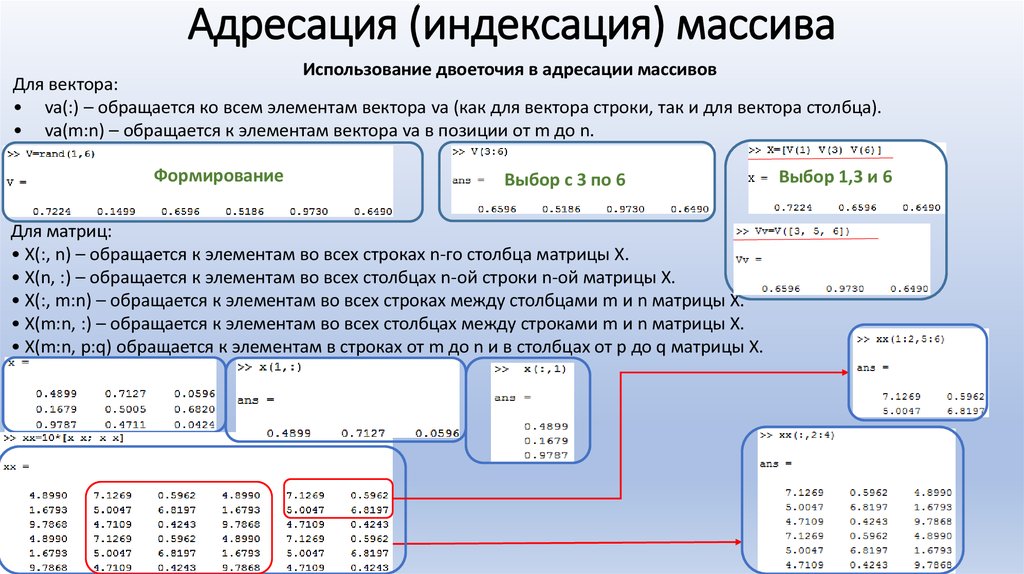
Теперь создайте матрицу с теми же числами, но расположите их в двух строках. Эта матрица имеет две строки и два столбца.
Специализированные матричные функции
MATLAB имеет много функций, которые помогают создавать матрицы с определенными значениями или конкретной структурой. Например, zeros и ones функции создают матрицы всех нулей или всех единиц. Первые и вторые аргументы этих функций являются количеством строк и количеством столбцов матрицы, соответственно.
diag функционируйте помещает входные элементы в диагональ матрицы. Например, создайте вектор-строку A содержащий четыре элемента. Затем создайте матрицу 4 на 4, диагональными элементами которой являются элементы A .
Конкатенация матриц
Можно также использовать квадратные скобки, чтобы соединить существующие матрицы вместе. Этот способ создать матрицу называется конкатенацией . Например, конкатенируйте два вектора-строки, чтобы сделать еще более длинный вектор-строку.
Располагать A и B как две строки матрицы, используйте точку с запятой.
Чтобы конкатенировать две матрицы, у них должны быть совместимые размеры. Другими словами, когда вы конкатенируете матрицы горизонтально, у них должно быть одинаковое число строк. Когда вы конкатенируете их вертикально, у них должно быть одинаковое число столбцов. Например, горизонтально конкатенируйте две матрицы, что у обоих есть две строки.
Альтернативный способ конкатенировать матрицы состоит в том, чтобы использовать функции конкатенации, такие как horzcat , который горизонтально конкатенирует две совместимых входных матрицы.
Генерация числовой последовательности
colon удобный путь состоит в том, чтобы создать матрицы, элементы которых последовательны и равномерно расположены с интервалами. Например, создайте вектор-строку, элементами которого являются целые числа от 1 до 10.
Можно использовать оператор двоеточия, чтобы создать последовательность чисел в любой области значений, с единичным шагом.
Чтобы изменить значение шага последовательности, задайте шаг между начальным и конечным значением области значений, разделенных двоеточиями.
Чтобы постепенно уменьшиться, используйте отрицательное число.
Можно также постепенно увеличиться значениями нецелого числа. Если инкрементное значение равномерно не делит заданную область, MATLAB автоматически заканчивает последовательность в последнем значении, которого это может достигнуть прежде, чем превысить область значений.
Расширение матрицы
Можно добавить один или несколько элементов в матрицу путем размещения их за пределами существующих контуров индекса строки и столбца. MATLAB автоматически заполняет матрицу нулями, чтобы сохранить его прямоугольным. Например, создайте матрицу 2 на 3 и добавьте дополнительную строку и столбец в него путем вставки элемента в (3,4) положение.
Можно также расширить размер путем вставки новой матрицы за пределами существующих областей значений индекса.
Расширять размер матрицы неоднократно, такой как в for цикл, обычно лучше предварительно выделить место для самой большой матрицы, которую вы ожидаете создавать. Без предварительного выделения MATLAB должен выделить память каждый раз увеличения размера, замедлив операции. Например, предварительно выделите матрицу, которая содержит до 10 000 строк и 10 000 столбцов путем инициализации ее элементов, чтобы обнулить.
Без предварительного выделения MATLAB должен выделить память каждый раз увеличения размера, замедлив операции. Например, предварительно выделите матрицу, которая содержит до 10 000 строк и 10 000 столбцов путем инициализации ее элементов, чтобы обнулить.
Если необходимо предварительно выделить дополнительные элементы позже, можно расширить его путем присвоения за пределами матричных областей значений индекса или конкатенировать другую предварительно выделенную матрицу к A .
Пустые массивы
Пустой массив в MATLAB является массивом по крайней мере с одной равной нулю длиной размерности. Пустые массивы полезны для представления концепции «ничего» программно. Например, предположите, что вы хотите найти все элементы вектора, которые меньше 0, но нет ни одного. find функция возвращает пустой вектор индексов, указывая, что она не могла найти элементы меньше чем 0.
Много алгоритмов содержат вызовы функции, которые могут возвратить пустые массивы. Часто полезно позволить пустым массивам течь через эти алгоритмы как аргументы функции вместо того, чтобы обработать их как особый случай. Если действительно необходимо настроить обработку пустого массива, можно проверять на них использующий isempty функция.
Если действительно необходимо настроить обработку пустого массива, можно проверять на них использующий isempty функция.
Похожие темы
Открытый пример
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
Документация MATLAB
Поддержка
© 1994-2021 The MathWorks, Inc.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста — например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.
MathCAD. MatLab
В пакете расширения Statistics Toolbox можно найти множество статистичес
ких функций, в том числе для генерации случайных чисел с различными законами
распределения и определения их статистических характеристик.
4.2. Операции с матрицами
4.2.1. Конкатенация матриц
Конкатенацией называют объединение массивов и матриц. Это реализует сле
дующая функция:
• C = cat(dim,A,B) – объединяет массивы A и B в соответствии со специфи
кацией размерности dim и возвращает объединенный массив; dim=1 – го
ризонтальная конкатенация, dim=2 – вертикальная, dim=3 – многомерный
массив размерности 3 и т. д.;
• C = cat(dim,A1,A2,A3,A4,…) объединяет все входные массивы (A1, A2,
A3, A4 и т. д.) в соответствии со спецификацией размерности dim и возвра
щает объединенный массив;
4. 1.7. Создание массивов с логическими
1.7. Создание массивов с логическими
значениями элементов
Уже в версии MATLAB 6.5 были введены функции true(m,n) и false(m,n) для ге
нерации массивов размера m?n, содержащих соответственно логические 1 и 0.
Примеры:
MATLAB – Массивы
Все переменные всех типов данных в MATLAB являются многомерными массивами. Вектор – это одномерный массив, а матрица – это двумерный массив.
Мы уже обсуждали векторы и матрицы. В этой главе мы обсудим многомерные массивы. Однако перед этим давайте обсудим некоторые специальные типы массивов.
Специальные массивы в MATLAB
В этом разделе мы обсудим некоторые функции, которые создают специальные массивы. Для всех этих функций один аргумент создает квадратный массив, двойные аргументы создают прямоугольный массив.
Функция нулей () создает массив всех нулей –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Функция ones () создает массив всех единиц –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Функция eye () создает единичную матрицу.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Функция rand () создает массив равномерно распределенных случайных чисел по (0,1) –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Магический Квадрат
Магический квадрат – это квадрат, который дает одинаковую сумму, когда его элементы добавляются построчно, по столбцам или по диагонали.
Функция magic () создает массив магических квадратов. Требуется исключительный аргумент, который дает размер квадрата. Аргумент должен быть скаляром, большим или равным 3.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Многомерные массивы
В MATLAB массив, имеющий более двух измерений, называется многомерным массивом. Многомерные массивы в MATLAB являются расширением нормальной двумерной матрицы.
Обычно для создания многомерного массива мы сначала создаем двумерный массив и расширяем его.
Например, давайте создадим двумерный массив a.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Массив a является массивом 3 на 3; мы можем добавить третье измерение к, предоставив такие значения, как –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Мы также можем создавать многомерные массивы, используя функции ones (), zeros () или rand ().
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Мы также можем использовать функцию cat () для построения многомерных массивов. Он объединяет список массивов по указанному измерению –
Синтаксис для функции cat () –
B – новый созданный массив
A1 , A2 , … массивы, которые будут объединены
dim – это размер, по которому объединяются массивы.
B – новый созданный массив
A1 , A2 , … массивы, которые будут объединены
dim – это размер, по которому объединяются массивы.
пример
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он отображает –
Функции массива
MATLAB предоставляет следующие функции для сортировки, вращения, перестановки, изменения формы или смещения содержимого массива.
| функция | Цель |
|---|---|
| длина | Длина вектора или наибольшее измерение массива |
| ndims | Количество размеров массива |
| numel | Количество элементов массива |
| размер | Размеры массива |
| iscolumn | Определяет, является ли ввод вектором столбца |
| пустой | Определяет, является ли массив пустым |
| ismatrix | Определяет, является ли ввод матричным |
| isrow | Определяет, является ли ввод вектором строки |
| isscalar | Определяет, является ли вход скалярным |
| isvector | Определяет, является ли входной вектор |
| blkdiag | Создает блочную диагональную матрицу из входных аргументов. |
| circshift | Смещает массив по кругу |
| ctranspose | Комплексное сопряженное транспонирование |
| диаг | Диагональные матрицы и диагонали матрицы |
| flipdim | Переворачивает массив по указанному измерению |
| fliplr | Отразить матрицу слева направо |
| flipud | Переворачивает матрицу вверх-вниз |
| ipermute | Инвертирует перестановочные размеры массива ND |
| переставлять | Переставляет размеры массива ND |
| repmat | Реплики и массив плиток |
| перекроить | Перекраивает массив |
| rot90 | Поворот матрицы на 90 градусов |
| shiftdim | Смещает размеры |
| issorted | Определяет, находятся ли заданные элементы в отсортированном порядке |
| Сортировать | Сортирует элементы массива в порядке возрастания или убывания |
| sortrows | Сортирует строки в порядке возрастания |
| выжимать | Удаляет одиночные размеры |
| транспонировать | транспонировать |
| векторизовать | Векторизованное выражение |
Примеры
Следующие примеры иллюстрируют некоторые из функций, упомянутых выше.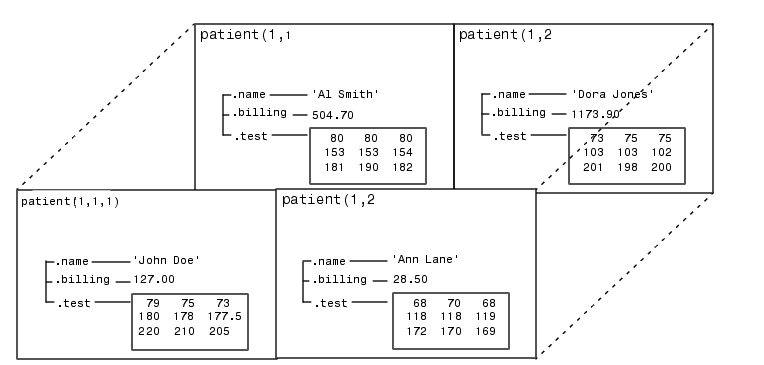
Длина, Размер и Количество элементов –
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Круговое смещение элементов массива –
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Сортировка массивов
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Cell Array
Массивы ячеек – это массивы индексированных ячеек, где каждая ячейка может хранить массив разных измерений и типов данных.
Функция cell используется для создания массива cell. Синтаксис для функции ячейки –
С – массив ячеек;
dim – скалярное целое число или вектор целых чисел, который определяет размеры массива ячеек C;
dim1, …, dimN – скалярные целые числа, которые определяют размеры C;
obj является одним из следующих –
- Массив или объект Java
- .
 NET массив типа System.String или System.Object
NET массив типа System.String или System.Object
С – массив ячеек;
dim – скалярное целое число или вектор целых чисел, который определяет размеры массива ячеек C;
dim1, …, dimN – скалярные целые числа, которые определяют размеры C;
obj является одним из следующих –
пример
Создайте файл сценария и введите в него следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Доступ к данным в массивах ячеек
Существует два способа обращения к элементам массива ячеек:
- Заключение индексов в первую скобку () для ссылки на наборы ячеек
- Заключение индексов в фигурные скобки для ссылки на данные в отдельных ячейках
Когда вы заключаете индексы в первую скобку, это относится к набору ячеек.
Индексы массива ячеек в гладких скобках относятся к наборам ячеек.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Вы также можете получить доступ к содержимому ячеек путем индексации с помощью фигурных скобок.
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
структурных массивов — MATLAB & Simulink
Массивы структур
Если у вас есть данные, которые вы хотите организовать по имени, вы можете использовать структуры для хранения Это. Структуры хранят данные в контейнерах, называемых полями , которые вы можете затем доступ по указанным вами именам. Используйте точечную нотацию для создания, назначения и доступа к данным в поля структуры. Если значение, хранящееся в поле, является массивом, вы можете использовать массив индексирование для доступа к элементам массива. Когда вы сохраняете несколько структур как структуру массива, вы можете использовать индексацию массива и точечную нотацию для доступа к отдельным структурам и их поля.
Создать скалярную структуру
Сначала создайте структуру с именем пациент , в которой есть поля для хранения данных о пациенте.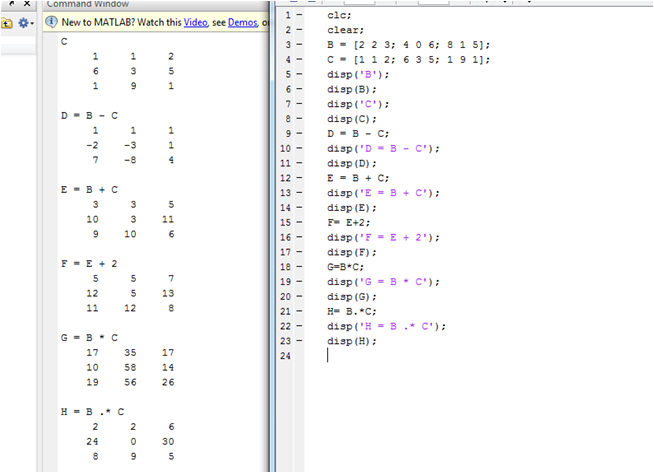 На диаграмме показано, как структура хранит данные. Структура типа
На диаграмме показано, как структура хранит данные. Структура типа пациента также называется скалярной структурой , поскольку переменная хранит одну структуру.
Используйте запись через точку, чтобы добавить поля имя , выставление счетов и тест , назначив данные каждому полю. В этом примере синтаксис имя_пациента создает как структуру, так и ее первое поле. Следующие команды добавляют дополнительные поля.
patient.name = 'Джон Доу'; пациент.биллинг = 127; пациент.тест = [79 75 73; 180 178 177,5; 220 210 205]
пациента = структура с полями:
имя: 'Джон Доу'
биллинг: 127
тест: [3x3 двойной]
Доступ к значениям в полях
После создания поля вы можете продолжать использовать запись через точку для доступа и изменения хранимого в нем значения.
Например, измените значение поля выставления счетов .
пациента.биллинг = 512.00
пациента = структура с полями:
имя: 'Джон Доу'
биллинг: 512
тест: [3x3 двойной]
С точечной нотацией вы также можете получить доступ к значению любого поля. Например, создайте столбчатую диаграмму значений в patient.test . Добавьте заголовок с текстом patient.name . Если в поле хранится массив, этот синтаксис возвращает весь массив.
бар(тест пациента)
title("Результаты теста для " + пациента.имя) Чтобы получить доступ к части массива, хранящегося в поле, добавьте индексы, соответствующие размеру и типу массива. Например, создайте гистограмму данных в одном столбце patient.test .
bar(patient.test(:,1))
Индекс в нескалярном массиве структур
Массивы структур могут быть нескалярными. Вы можете создать массив структур любого размера, если каждая структура в массиве имеет одинаковые поля.
Например, добавьте вторую структуру к пациентам , имеющим данные о втором пациенте. Кроме того, присвойте исходное значение
Кроме того, присвойте исходное значение 127 полю Billing первой структуры. Поскольку массив теперь имеет две структуры, вы должны получить доступ к первой структуре с помощью индексации, например, patient(1).billing = 127 .
пациент(2).name = 'Энн Лейн'; пациент(2).биллинг = 28,50; пациент(2).тест = [68 70 68; 118 118 119; 172 170 169]; пациент(1).биллинг = 127
пациент = Массив структур 1×2 с полями:
имя
выставление счетов
тест
В результате пациента представляет собой массив структур 1 на 2 с содержимым, показанным на диаграмме.
Каждая запись пациента в массиве представляет собой структуру класса struct . Массив структур иногда называют массивом структур . Однако термины массив структур и массив структур означают одно и то же. Как и другие массивы MATLAB®, массив структур может иметь любые размеры.
Массив структур имеет следующие свойства:
Все структуры в массиве имеют одинаковое количество полей.
Все структуры имеют одинаковые имена полей.
Поля с одним и тем же именем в разных структурах могут содержать разные типы или размеры данных.
Если добавить в массив новую структуру без указания всех ее полей, то неуказанные поля будут содержать пустые массивы.
пациент(3).name = 'Новое имя'; пациент(3)
анс = структура с полями:
имя: 'Новое имя'
выставление счетов: []
тест: []
Чтобы проиндексировать массив структур, используйте индексацию массива. Например, пациента(2) возвращает вторую структуру.
пациент(2)
анс = структура с полями:
имя: 'Энн Лейн'
биллинг: 28.5000
тест: [3x3 двойной]
Для доступа к полю используйте индексацию массива и запись через точку. Например, вернуть значение счета 9Поле 0012 для второго пациента.
пациент(2).биллинг
анс = 28,5000
Вы также можете индексировать массив, хранящийся в поле. Создайте столбчатую диаграмму, отображающую только первые два столбца пациента
Создайте столбчатую диаграмму, отображающую только первые два столбца пациента (2).test .
бар(пациент(2).тест(:,[1 2]))
См. также
структура | имена полей | Айсфилд
См. также
- Доступ к элементам массива нескалярных структур
- Создание имен полей из переменных
- Создание массива ячеек
- Сравнение ячеек и массивов структур
- Создание таблиц и присвоение им данных
- Преимущества использования таблиц
Матрицы и массивы - MATLAB & Simulink
Основное содержание
Open Live Script
MATLAB — это сокращение от «матричная лаборатория». В то время как другие языки программирования в основном работают с числами по одному, MATLAB® предназначен для работы в основном с целыми матрицами и массивами.
Все переменные MATLAB являются многомерными массивами , независимо от типа данных. Матрица — это двумерный массив, часто используемый для линейной алгебры.
Матрица — это двумерный массив, часто используемый для линейной алгебры.
Создание массива
Чтобы создать массив из четырех элементов в одной строке, разделите элементы запятой ( , ) или пробелом.
а = [1 2 3 4]
а = 1×4
1 2 3 4
Этот тип массива представляет собой вектор-строку .
Чтобы создать матрицу из нескольких строк, разделите строки точкой с запятой.
а = [1 3 5; 2 4 6; 7 8 10]
а = 3×3
1 3 5
2 4 6
7 8 10
Другой способ создать матрицу — использовать функцию, например единиц , нулей или ранд . Например, создайте вектор-столбец 5 на 1 из нулей.
z = нули (5,1)
z = 5×1
0
0
0
0
0
Операции с матрицами и массивами
MATLAB позволяет обрабатывать все значения в матрице с помощью одного арифметического оператора или функции.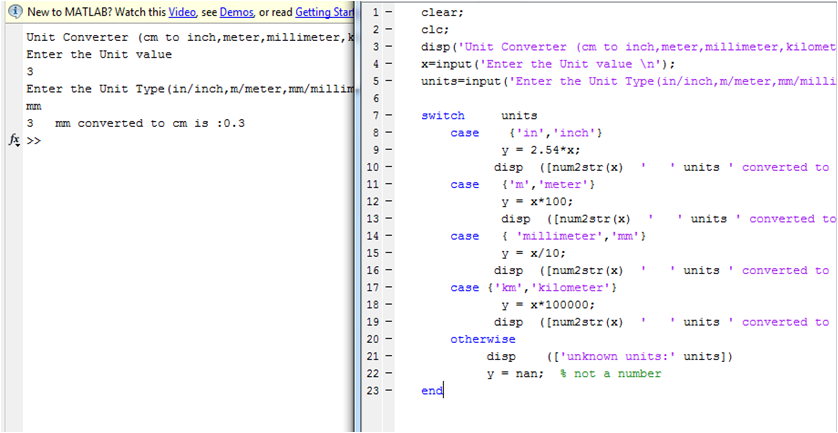
а + 10
анс = 3×3
11 13 15
12 14 16
17 18 20
sin(a)
ans = 3×3
0,8415 0,1411 -0,9589
0,9093 -0,7568 -0,2794
0,6570 0,9894 -0,5440
Чтобы транспонировать матрицу, используйте одинарную кавычку ( ' ):
и = 3×3
1 2 7
3 4 8
5 6 10
С помощью оператора * можно выполнить стандартное умножение матриц, при котором вычисляются внутренние произведения между строками и столбцами. Например, подтвердите, что матрица, умноженная на свою обратную, возвращает единичную матрицу:
p = a*inv(a)
p = 3×3
1,0000 0,0000 -0,0000
0 1,0000 -0,0000
0 0,0000 1,0000
Обратите внимание, что p не является матрицей целых значений. MATLAB хранит числа как значения с плавающей запятой, а арифметические операции чувствительны к небольшим различиям между фактическим значением и его представлением с плавающей запятой. Вы можете отобразить больше десятичных цифр, используя команду
Вы можете отобразить больше десятичных цифр, используя команду format :
format long p = a*inv(a)
p = 3×3
0,999999999999996 0,000000000000007 -0,000000000000002
0 1.000000000000000 -0.000000000000003
0 0,000000000000014 0,999999999999995
Сбросьте отображение на более короткий формат, используя
формат short
формат влияет только на отображение чисел, а не на то, как MATLAB их вычисляет или сохраняет.
Для выполнения поэлементного умножения вместо умножения матриц используйте оператор .* :
p = a.*a
p = 3×3
1 9 25
4 16 36
49 64 100
Каждому из матричных операторов умножения, деления и возведения в степень соответствует оператор массива, работающий поэлементно. Например, поднимите каждый элемент a в третьей степени:
инс = 3×3
1 27 125
8 64 216
343 512 1000
Конкатенация
Конкатенация — это процесс объединения массивов для создания больших массивов. Фактически вы создали свой первый массив, объединив его отдельные элементы. Пара квадратных скобок
Фактически вы создали свой первый массив, объединив его отдельные элементы. Пара квадратных скобок [] — это оператор конкатенации.
А = [а, а]
А = 3×6
1 3 5 1 3 5
2 4 6 2 4 6
7 8 10 7 8 10
Объединение массивов рядом друг с другом с помощью запятых называется горизонтальной конкатенацией. Каждый массив должен иметь одинаковое количество строк. Точно так же, когда массивы имеют одинаковое количество столбцов, вы можете объединить по вертикали с , используя точку с запятой.
А = [а; а]
А = 6×3
1 3 5
2 4 6
7 8 10
1 3 5
2 4 6
7 8 10
Комплексные числа
Комплексные числа имеют как действительную, так и мнимую части, где мнимой единицей является квадратный корень из -1 .
sqrt(-1)
анс = 0,0000 + 1,0000i
Для представления мнимой части комплексных чисел используйте i или j .
с = [3+4i, 4+3j; -i, 10j]
c = Комплекс 2×2 3.0000 + 4.0000i 4.0000 + 3.0000i 0,0000 - 1,0000i 0,0000 +10,0000i
Начало работы с MATLAB
Следующий
У вас есть модифицированная версия этого примера. Хотите открыть этот пример со своими правками?
Вы щелкнули ссылку, соответствующую этой команде MATLAB:
Запустите команду, введя ее в командном окне MATLAB. Веб-браузеры не поддерживают команды MATLAB.
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Европа
Свяжитесь с местным офисом
- Пробная версия программного обеспечения
- Пробная версия ПО
- Обновления продукта
- Обновления продукта
Многомерные массивы - MATLAB & Simulink
Open Live Script
Многомерный массив в MATLAB® — это массив с более чем двумя измерениями. В матрице два измерения представлены строками и столбцами.
В матрице два измерения представлены строками и столбцами.
Каждый элемент определяется двумя нижними индексами: индексом строки и индексом столбца. Многомерные массивы являются расширением двумерных матриц и используют дополнительные индексы для индексации. Трехмерный массив, например, использует три нижних индекса. Первые два похожи на матрицу, но третье измерение представляет собой страниц или листов элементов.
Создание многомерных массивов
Многомерный массив можно создать, сначала создав двумерную матрицу, а затем расширив ее. Например, сначала определите матрицу 3 на 3 как первую страницу в трехмерном массиве.
А = [1 2 3; 4 5 6; 7 8 9]
А = 3×3
1 2 3
4 5 6
7 8 9
Теперь добавьте вторую страницу. Для этого назначьте другую матрицу 3 на 3 значению индекса 2 в третьем измерении. Синтаксис A(:,:,2) использует двоеточие в первом и втором измерениях для включения всех строк и всех столбцов из правой части назначения.
А(:,:,2) = [10 11 12; 13 14 15; 16 17 18]
А =
А(:,:,1) =
1 2 3
4 5 6
7 8 9А(:,:,2) =
10 11 12
13 14 15
16 17 18
Функция cat может быть полезным инструментом для построения многомерных массивов. Например, создайте новый трехмерный массив B , соединив A с третьей страницей. Первый аргумент указывает, какое измерение следует конкатенировать.
B = кошка(3,A,[3 2 1; 0 9 8; 5 3 7])
B =
В(:,:,1) =
1 2 3
4 5 6
7 8 9
В(:,:,2) =
10 11 12
13 14 15
16 17 18
В(:,:,3) =
3 2 1
0 98
5 3 7
Еще один способ быстро расширить многомерный массив — назначить один элемент на всю страницу. Например, добавьте к B четвертую страницу, содержащую все нули.
Б(:,:,4) = 0
Б =
В(:,:,1) =
1 2 3
4 5 6
7 8 9
В(:,:,2) =
10 11 12
13 14 15
16 17 18
В(:,:,3) =
3 2 1
0 9 8
5 3 7
В(:,:,4) =
0 0 0
0 0 0
0 0 0
Доступ к элементам
Для доступа к элементам в многомерном массиве используйте целочисленные индексы так же, как для векторов и матриц. Например, найдите элемент 1,2,2
Например, найдите элемент 1,2,2 A , который находится в первой строке, втором столбце и на второй странице A .
А =
А(:,:,1) =
1 2 3
4 5 6
7 8 9
А(:,:,2) =
10 11 12
13 14 15
16 17 18
элА = А(1,2,2)
элА = 11
Используйте индексный вектор [1 3] во втором измерении, чтобы получить доступ только к первому и последнему столбцам каждой страницы A .
С = А(:,[1 3],:)
С =
С(:,:,1) =
1 3
4 6
7 9
С(:,:,2) =
10 12
13 15
16 18
Чтобы найти вторую и третью строки каждой страницы, используйте оператор двоеточия для создания индексного вектора.
Д = А(2:3,:,:)
Д =
Д(:,:,1) =
4 5 6
7 8 9Д(:,:,2) =
13 14 15
16 17 18
Манипулирование массивами
Элементы многомерных массивов можно перемещать разными способами, подобно векторам и матрицам. изменить форму , переставить и сжать — полезные функции для перестановки элементов. Рассмотрим трехмерный массив с двумя страницами.
Рассмотрим трехмерный массив с двумя страницами.
Изменение формы многомерного массива может быть полезно для выполнения определенных операций или визуализации данных. Используйте изменение формы , чтобы переставить элементы трехмерного массива в матрицу 6 на 5.
А = [1 2 3 4 5; 9 0 6 3 7; 8 1 5 0 2]; A(:,:,2) = [9 7 8 5 2; 3 5 8 5 1; 6 9 4 3 3]; B = изменить форму (A, [6 5])
B = 6×5
1 3 5 7 5
9 6 7 5 5
8 5 2 9 3
2 4 9 8 2
0 3 3 8 1
1 0 6 4 3
reshape работает по столбцам, создавая новую матрицу, перемещая последовательные элементы вниз по каждому столбцу из A , начиная с первой страницы, затем переходя ко второй странице.
Перестановки используются для изменения порядка измерений массива. Рассмотрим трехмерный массив M .
М(:,:,1) = [1 2 3; 4 5 6; 7 8 9]; М(:,:,2) = [0 5 4; 2 7 6; 9 3 1]
М =
М(:,:,1) =
1 2 3
4 5 6
7 8 9
М(:,:,2) =
0 5 4
2 7 6
9 3 1
Используйте функцию permute , чтобы поменять местами индексы строк и столбцов на каждой странице, указав порядок измерений во втором аргументе.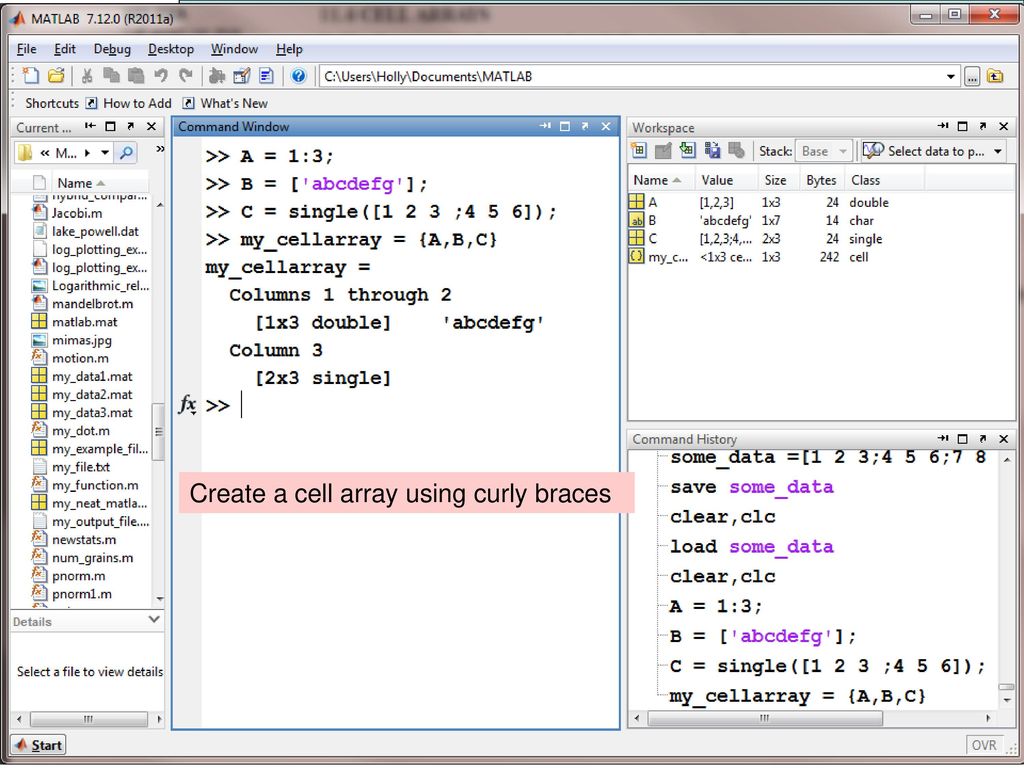 Исходные ряды
Исходные ряды M теперь являются столбцами, а столбцы теперь строками.
P1 = переставить (M,[2 1 3])
P1 =
Р1(:,:,1) =
1 4 7
2 5 8
3 6 9
Р1(:,:,2) =
0 2 9
5 7 3
4 6 1
Аналогичным образом поменяйте местами индексы строк и страниц M .
P2 = переставить (M, [3 2 1])
P2 =
Р2(:,:,1) =
1 2 3
0 5 4
Р2(:,:,2) =
4 5 6
2 7 6
Р2(:,:,3) =
7 8 99 3 1
При работе с многомерными массивами вы можете столкнуться с тем, что он имеет ненужную размерность длины 1. Функция сжатия выполняет другой тип манипуляции, исключающий размерности длины 1. Например, используйте функцию repmat для создания Массив 2 на 3 на 1 на 4, элементы которого равны 5, а третье измерение имеет длину 1.
A = repmat(5,[2 3 1 4])
A =
А(:,:,1,1) =
5 5 5
5 5 5
А(:,:,1,2) =
5 5 5
5 5 5
А(:,:,1,3) =
5 5 5
5 5 5
А(:,:,1,4) =
5 5 5
5 5 5
размер A = размер (A)
размер A = 1×4
2 3 1 4
numdimsA = ndims(A)
numdimsA = 4
Используйте функцию сжатия , чтобы удалить третье измерение, в результате чего получится трехмерный массив.
B = сжать(A)
B =
В(:,:,1) =
5 5 5
5 5 5
В(:,:,2) =
5 5 5
5 5 5
В(:,:,3) =
5 5 5
5 5 5
В(:,:,4) =
5 5 5
5 5 5
szB = размер(B)
szB = 1×3
2 3 4
numdimsB = ndims(B)
numdimsB = 3
- Создание, объединение и расширение матриц
- Индексирование массивов
- Изменение формы и реорганизация массивов
У вас есть модифицированная версия этого примера. Хотите открыть этот пример со своими правками?
Вы щелкнули ссылку, соответствующую этой команде MATLAB:
Запустите команду, введя ее в командном окне MATLAB. Веб-браузеры не поддерживают команды MATLAB.
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Европа
Обратитесь в местный офис
Массивы в Matlab | Краткий обзор массивов в Matlab
Массив представляет собой набор чисел или строк символов, хранящихся в памяти. Каждый элемент представляет собой массив с порядковым номером, и индексация начинается с 0 9.0573-я позиция и может упоминаться как первый элемент в массиве. В Matlab мы используем массив, который может собирать числа и к которому можно получить доступ с помощью индекса. В Matlab присутствуют различные специальные функции для выполнения операций с массивами, подобными нулям(), diag(), единицам() и т. д. . В двух измерениях элементы массива могут быть представлены с помощью строк и столбцов, а в трех и более измерениях используются листы или страницы элементов. Есть много операций, которые могут быть выполнены в массиве. Пожалуйста, найдите следующие примеры для справки:
Пример:
M1= [4,3,2;7,6,5;9,8,7]
Это первая страница трехмерного массива. Мы также можем продолжать добавлять страницы, используя функцию «кошка».
Мы также можем продолжать добавлять страницы, используя функцию «кошка».
M=cat (размер, M1)
Здесь
- M = новый массив.
- Dimension = измерение для добавления массивов.
- M1 = массив для объединения.
М1 = [4,3,2;7,6,5;9,8,7]
М2 = [9,8,7;6,5,4;3,2,1]
M = кат (1,M1,M2)
Выход:
Мы также можем использовать различные функции, такие как rand(), one(), zeroes(), для создания многомерных массивов.
1. rand ()
Эта функция используется для создания массива случайно распределенных чисел в диапазоне от 0 до 1. 3 колонки.
Пример:
ранд (4,3)
Вывод:
2. нули ()
Эта функция используется для создания массива нулей в зависимости от количества строк и столбцов.
нулей (4): Это создает массив нулей.
Пример:
нулей(4)
Вывод:
3.
 Единицы ()
Единицы ()Эта функция создает массив в зависимости от указанного количества единиц.
единиц (4): Это создает массив единиц.
Пример:
единиц (4)
Вывод:
Работа с массивами с примерами
, которые включают в себя комбинацию символов в MATB. Как и с числовыми массивами, с символьными массивами можно выполнять различные операции. Мы всегда можем преобразовать массив в символьный тип данных, используя функцию char.
Массивы созданы в MATLAB и могут быть проиндексированы с помощью следующих различных методов индексации:
1. Индексирование элемента по положению
Этот подход используется для поиска элемента массива путем указания номера строки и номера столбца для поиска одного элемента. Мы также можем получить доступ к нескольким элементам, указав номер строки и положение элементов в соответствующей строке. Мы также можем получить доступ к диапазону элементов, указав диапазон строк и столбцов. Ниже приведены примеры для лучшего понимания:
Ниже приведены примеры для лучшего понимания:
Пример:
I = [10,11,12,13;14,15,16,17;18,19,20,21;22,23,24,25]
I= 4*4
Вывод:
- Чтобы найти единственный элемент массива:
I (2,3)
Вывод:
Это дает третий элемент из второй строки.
- Чтобы найти несколько элементов в массиве:
I (2, [1,2])
Вывод:
Это дает первый и второй элементы из второй строки.
- Чтобы найти диапазон элементов в массиве:
I (1:3,2:4)
Вывод:
2. Индексирование с помощью единого индекса
Независимо от упоминания строк и столбцов в синтаксисе, мы можем прямо указать единственный индекс и найти элемент. Этот метод также известен как линейная индексация. Здесь элементы будут храниться в одном столбце. См. приведенный ниже пример:
См. приведенный ниже пример:
Пример:
J= [20,23,31; 34,45,56;78,87,67]
JLin=J (:)
Здесь он сохраняет вышеуказанные элементы в одном столбце.
Вывод:
Мы можем получить доступ к элементу, используя один индексный номер, такой как JLin (5), который дает 45.
3. Индексирование с использованием логических значений
логические значения, такие как True или False, и мы можем найти элементы, которые имеют истинное значение. Пожалуйста, найдите приведенный ниже пример
Пример:
L1 = [11,23,45;67,78,89]
L2 = [10,24,46;68,77,88]
i=L1
Вывод:
Это проверяет элементы с использованием условных выражений (L1 Вывод: Вывод: Использование массивов в различных языках программирования упростило выполнение ручных задач и используется программистами. Это руководство по работе с массивами в Matlab. Здесь мы обсуждаем основную концепцию, операции с массивами в Matlab, а также различные примеры и их реализацию. Вы также можете просмотреть наши рекомендуемые статьи, чтобы узнать больше – Обучение: 15 мин. Вопросы Объективы Теперь, когда мы понимаем, какие данные можно хранить в массиве,
нам нужно изучить правильный синтаксис для работы с массивами в MATLAB. Давайте начнем с создания «волшебной» матрицы 8 на 8: Мы хотим получить доступ к одному значению из матрицы: Для этого мы должны предоставить
его индекс в скобках: Индексы представлены в виде (строка, столбец). Итак, индекс Индекс типа мы можем сделать: Предоставление и столбцы: Чтобы выбрать подматрицу, мы должны взять срезы в обоих измерениях: Нам не нужно брать все значения в срезе — если мы предоставим
шаг. А еще мы можем выбирать значения в «шахматной доске», , предприняв соответствующие шаги в обоих измерениях: Часть массива называется срезом. Мы также можем взять фрагменты строк символов: Каково значение элемента Для массива любого размера MATLAB позволяет нам индексировать с помощью одного оператора двоеточия ( Упражнения с использованием срезов Оператор двоеточия «выравнивает» вектор или матрицу в вектор-столбец.
Порядок элементов в результирующем векторе определяется добавлением
каждый столбец исходного массива по очереди. Описание Типы данных в MATLAB Сложные матрицы двойной точности Числовые матрицы Строки MATLAB Разреженные матрицы Массивы ячеек Конструкции Объекты Pos= L1(i) Pos= L2(i) Заключение
 Существует много преимуществ использования массива, доступ к элементам в массиве прост и может быть выполнен с помощью простых шагов, в программе нет проблем с производительностью, правильное использование памяти, более быстрое выполнение и полезность в реализации программ, использующих стек, связанный список, деревья и т. д.
Существует много преимуществ использования массива, доступ к элементам в массиве прост и может быть выполнен с помощью простых шагов, в программе нет проблем с производительностью, правильное использование памяти, более быстрое выполнение и полезность в реализации программ, использующих стек, связанный список, деревья и т. д. Рекомендуемые статьи
Массивы — Программирование с помощью MATLAB
Обзор
Упражнения: 5 мин Индексация массива
 Для этого мы начнем с обсуждения массива , индексирующего , который является
метод, с помощью которого мы можем выбрать один или несколько различных элементов
множество. Четкое понимание индексации массива очень поможет
наша способность организовать наши данные.
Для этого мы начнем с обсуждения массива , индексирующего , который является
метод, с помощью которого мы можем выбрать один или несколько различных элементов
множество. Четкое понимание индексации массива очень поможет
наша способность организовать наши данные. >> М = магия (8)
ответ =
64 2 3 61 60 6 7 57
9 55 54 12 13 51 50 16
17 47 46 20 21 43 42 24
40 26 27 37 36 30 31 33
32 34 35 29 28 38 39 25
41 23 22 44 45 19 18 48
49 15 14 52 53 11 10 56
8 58 59 5 4 62 63 1
>> М(5, 6)
и = 38
(5, 6) выбирает элемент
в пятой строке и шестом столбце. (5, 6) выбирает один элемент
массив, но мы также можем получить доступ к разделам матрицы или срезам. Чтобы получить доступ к строке значений:
Чтобы получить доступ к строке значений: >> М(5, :)
ответ =
32 34 35 29 28 38 39 25
: в качестве индекса для измерения выбирает всех элементов
вдоль этого измерения.
Итак, индекс (5, :) выбирает
элементы в строке 5 и во всех столбцах — фактически вся строка.
Мы также можем
выбрать несколько строк, >> М(1:4, :)
ответ =
64 2 3 61 60 6 7 57
9 55 54 12 13 51 50 16
17 47 46 20 21 43 42 24
40 26 27 37 36 30 31 33
>> М(:, 6:конец)
ответ =
6 7 57
51 50 16
43 42 24
30 31 33
38 39 25
19 18 48
11 10 56
62 63 1
>> М(4:6, 5:7)
ответ =
36 30 31
28 38 39
45 19 18
 Допустим, мы хотим начать с строки 9.0011 2 ,
и впоследствии выберите каждую третью строку:
Допустим, мы хотим начать с строки 9.0011 2 ,
и впоследствии выберите каждую третью строку: >> М(2:3:конец, :)
ответ =
9 55 54 12 13 51 50 16
32 34 35 29 28 38 39 25
8 58 59 5 4 62 63 1
>> М(1:3:конец, 2:2:конец)
ответ =
2 61 6 57
26 37 30 33
15 52 11 56
Нарезка
>> элемент = 'кислород';
>> disp(['первые три символа: ', element(1:3)])
>> disp(['последние три символа: ', element(4:6)])
первые три символа: окси
последние три символа: gen
(4: конец) ? Как насчет элемента (1: 2: конец) ? Или элемент (2: конец - 1) ? : ). Это может иметь удивительные эффекты.
Например, сравните элемент
Это может иметь удивительные эффекты.
Например, сравните элемент с элементом element(:) . Что такое размер (элемент) по сравнению с размером (элемент (:)) ?
Окончательно,
попробуйте использовать одно двоеточие в матрице M выше: M(:) .
Что происходит, когда мы используем оператор с одним двоеточием для нарезки? Решение
element(4:end) % Выбрать все элементы с 4-го по последний
ответ =
'ген'
element(1:2:end) % Выберите все остальные элементы, начиная с первого
ответ =
эй
element(2:end-1) % Выбрать элементы, начиная со 2-го, до предпоследнего
ответ =
ксиге
 Посмотрите на порядок значений в
Посмотрите на порядок значений в М(:) против М Ключевые моменты
The MATLAB Array (интерфейс прикладной программы MATLAB)
The MATLAB Array (интерфейс прикладной программы MATLAB) Интерфейс прикладной программы MATLAB Перейти к функции: Поиск Справочная служба Массив MATLAB mxArray . Структура
Структура mxArray содержит, среди прочего:
Хранение данных
Все данные MATLAB хранятся по столбцам. Вот как Fortran хранит матрицы; MATLAB использует это соглашение, потому что изначально он был написан на Фортране. Например, учитывая матрицу: а=['дом'; 'пол'; 'порог']
а =
дом
пол
порог
его размеры: размер(а)
ответ =
3 5
и его данные хранятся как: double и имеют размерность м на n , где м — количество строк, а n — количество столбцов. Данные хранятся в виде двух векторов чисел двойной точности — один содержит действительные данные, а другой содержит мнимые данные. Указатели на эти данные обозначаются как
Данные хранятся в виде двух векторов чисел двойной точности — один содержит действительные данные, а другой содержит мнимые данные. Указатели на эти данные обозначаются как pr (указатель на реальные данные) и pi (указатель на мнимые данные) соответственно. Только вещественная матрица с двойной точностью — это та, у которой pi равно NULL . Параметры
Параметры pr и pi по-прежнему являются массивами чисел двойной точности, но есть три дополнительных параметра: nzmax , ir и jc : nzmax — целое число, содержащее длину ir , pr и, если оно существует, pi . Это максимально возможное количество ненулевых элементов в разреженной матрице. ir указывает на массив целых чисел длиной nzmax , содержащий индексы строк соответствующих элементов в pr и pi . jc указывает на целочисленный массив длины N+1 , который содержит информацию об индексе столбца. Для j , в диапазоне 0 j N-1 , jc[j] является индексом в ir и pr (и 2pi (и 2pi 900) первого ненулевого запись в j -м столбце и
jc[j+1] - 1 индекс последней ненулевой записи. В результате
В результате jc[N] также равно nnz , количеству ненулевых элементов в матрице. Если ннз меньше, чем nzmax , то в массив можно вставить больше ненулевых элементов без выделения дополнительной памяти. mxArray упоминается как ячейка. Это позволяет хранить массивы MATLAB разных типов вместе. Массивы ячеек хранятся аналогично числовым матрицам, за исключением того, что часть данных содержит один вектор указателей на mxArrays . Члены этого вектора называются клетками. Каждая ячейка может иметь любой поддерживаемый тип данных, даже другой массив ячеек. n — количество полей в структуре. Элементы вектора данных называются полями. Каждое поле связано с именем, хранящимся в массиве mxArray .